|
Для гиперболы (6) число p = |
b2 |
называется ее фокальным |
|
|
a |
|||
|
параметром. |
|||
|
Замечание. Гипербола, полуоси |
которой равны a = b , |
называется равносторонней. Ее каноническое уравнение имеет вид
|
x2 − y2 = a2 . |
Асимптоты |
равносторонней |
гиперболы |
|
перпендикулярны. |
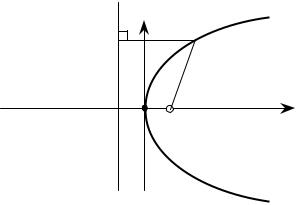
Параболой γ называется множество всех точек плоскости,
расстояние от каждой из которых до данной точки F равно расстоянию до данной прямой d , не проходящей через точку F . Точка F называется фокусом параболы, а прямая d – ее директрисой. Расстояние от фокуса до директрисы называется фокальным параметром параболы и обозначается через p .
d
y
x
F
Рис. 3
Найдем уравнение параболы в декартовой системе координат Oxy . Пусть O – середина отрезка FD , где D – ортогональная проекция точки F на прямую d . В этой системе координат фокус F
|
имеет |
координаты |
F |
p |
,0 |
, |
а директриса d |
– |
уравнение |
||
|
2 |
||||||||||
|
x + |
p |
= 0 . Пусть |
M (x, y) γ |
– произвольная |
точка |
параболы. |
||||
|
2 |
||||||||||
Расстояния от точки M до фокуса F и директрисы d вычисляются
|
p 2 |
2 |
p |
||||||||||
|
по формулам: |
FM = |
x − |
+ y |
, |
ρ(M , d) = |
x + |
. |
Из |
||||
|
2 |
||||||||||||
|
2 |
определения параболы следует равенство:
|
p 2 |
2 |
p |
|||||
|
x − |
+ y |
= x + |
2 |
. |
|||
|
2 |
Возводя обе части этого равенства в квадрат, получим следующее уравнение
Доказали, что точки параболы удовлетворяют уравнению (7). Как обычно, докажем обратное: точка M , координаты которой удовлетворяют уравнению (7), принадлежит параболе. В самом деле, подставим выражение (7) в формулу расстояния FM , получаем:
|
FM = |
p |
2 |
2 |
= |
x |
2 |
− px + |
p2 |
+ 2 px = |
p 2 |
= |
x + |
p |
||
|
x − |
+ y |
4 |
x + |
2 |
|||||||||||
|
2 |
2 |
Следовательно, FM = ρ(M , d) , т.е M (x, y) γ . Уравнение (7)
называется каноническим уравнением параболы.
Из уравнения (7) следуют следующие свойства параболы. Все точки параболы принадлежат полуплоскости, определяемой неравенством x ≥ 0 . Так как переменная y входит в уравнение (7) во второй степени, то из того, что M (x0 , y0 ) γ следует, что
M (x0 , − y0 ) γ . Следовательно, парабола симметрична относительно

оси OF . Точка O пересечения этой оси с параболой называется
вершиной параболы.
По определению считают, что эксцентриситет параболы ε =1.
4. Пара пересекающихся прямых.
Рассмотрим линию второго порядка, заданную уравнением
|
x2 |
− |
y2 |
= 0, |
(8) |
|||||||
|
a2 |
b2 |
||||||||||
|
где a > 0,b > 0 . Уравнение |
(8) |
равносильно |
совокупности: |
||||||||
|
y − |
b |
x = 0 , |
y + |
b |
x = 0 . Значит, |
кривая, заданная |
уравнением (8), |
||||
|
a |
a |
распадается на пару пересекающихся прямых (рис. 4). Эти прямые проходят через начало координат. Оси координат являются осями симметрии пары прямых, а начало координат – их центром симметрии.
|
y |
y |
|||||||||
|
b |
a |
|||||||||
|
– a |
a |
x |
x |
|||||||
|
– b |
– a |
|||||||||
|
Рис. 4 |
Рис. 5 |
5. Пара параллельных прямых. |
||||
|
Рассмотрим линию второго порядка, заданную уравнением |
||||
|
y2 − a2 |
= 0, |
(9) |
||
|
где a > 0. |
Уравнение (9) |
равносильно совокупности: y − a = 0 , |
||
|
y + a = 0 . |
Следовательно, |
кривая, |
заданная уравнением |
(9), |
распадается на пару параллельных прямых (рис. 5). Эти прямые отстоят на одинаковом расстоянии от оси ox , следовательно, ось ox является их осью симметрии.
6. Пара совпавших прямых.
Рассмотрим линию второго порядка, заданную уравнением
y2 = 0 . (10)
Уравнение (10) распадается на пару совпавших прямых y = 0 .
7. Мнимый эллипс.
Кривая второго порядка, которая задается уравнением вида
|
x2 |
+ |
y2 |
= −1, |
(11) |
|
|
a2 |
b2 |
||||
где a > 0,b > 0 , не имеет ни одной вещественной точки и называется
мнимым эллипсом. Этому уравнению удовлетворяют лишь точки с комплексными координатами.
Исследование уравнений второго порядка
Преобразование координат в уравнении второго порядка.
В общей декартовой системе координат линия второго порядка может быть задана уравнением
$$
Ax^ <2>+ 2Bxy + Cy^ <2>+ 2Dx + 2Ey + F = 0,label
$$
в котором коэффициенты (A), (B) и (C) не равны нулю одновременно. Исследуем множество точек, которые ему удовлетворяют, не предполагая заранее, что хоть одна такая точка существует. С этой целью мы будем менять систему координат так, чтобы уравнение стало возможно проще. С самого начала можно считать систему координат декартовой прямоугольной, так как при переходе к прямоугольной системе координат общий вид уравнения eqref не изменится.
При повороте базиса декартовой прямоугольной системы координат на угол (varphi) старые координаты точки (x), (y) будут связаны с ее новыми координатами (x’), (y’) формулами
$$
x = x’cos varphi-y’sin varphi,\ y = x’sin varphi + y’cos varphi.nonumber
$$
В новых координатах уравнение eqref примет вид
$$
A(x’cos varphi-y’sin varphi)^ <2>+ 2B(x’cos varphi-y’sin varphi) times \ times (x’sin varphi + y’cos varphi) + C(x’sin varphi + y’cos varphi) + … = 0.nonumber
$$
Здесь многоточием обозначены члены первой степени относительно (x’), (y’) и свободный член, которые нет необходимости выписывать. Нас будет интересовать член с произведением (x’y’) в преобразованном уравнении. В невыписанные члены это произведение не входит, и мы подсчитаем, что половина коэффициента при (x’y’) есть
$$
B’ = -Asin varphi cos varphi + B(cos^<2>varphi-sin^<2>varphi) + Csin varphi cos varphi.nonumber
$$
Если (B = 0), то поворачивать систему координат не будем. Если же (B neq 0), то выберем угол (varphi) так, чтобы (B’) обратилось в нуль.
Это требование приведет к уравнению
$$
2B cos 2varphi = (A-C)sin 2varphi.label
$$
Если (A = C), то (cos 2varphi = 0), и можно положить (varphi = pi/4). Если же (A neq C), то выбираем (varphi = displaystylefrac<1> <2>operatorname left[frac<2B>right]). Для нас сейчас важно то, что хоть один такой угол обязательно существует. После поворота системы координат на этот угол линия будет иметь уравнение
$$
A’x’^ < 2>+ C’y’^ < 2>+ 2D’x’ + 2E’y’ + F’ = 0.label
$$
Выражения для коэффициентов уравнения eqref через коэффициенты eqref подсчитать не трудно, но это не нужно. Теперь коэффициент при произведении переменных равен нулю, а остальные члены мы по-прежнему считаем произвольными.
Если в уравнение eqref входит с ненулевым коэффициентом квадрат одной из координат, то при помощи переноса начала координат вдоль соответствующей оси можно обратить в нуль член с первой степенью этой координаты.
В самом деле, пусть, например, (A’ neq 0). Перепишем eqref в виде
$$
A’left(x’^ < 2>+ frac<2D’>x’ + frac>>right) + C’y’^ < 2>+ 2E’y’ + F’-frac = 0.nonumber
$$
Если мы сделаем перенос начала координат, определяемый формулами (x″ = x’ + D’/A’), (y″ = y’), то уравнение приведется к виду
$$
A’x″^ < 2>+ C’y″^ < 2>+ 2E’y″ + F″ = 0,nonumber
$$
как и требовалось.
Канонические виды уравнений второго порядка.
Предположим, что (A’C’ neq 0), то есть оба коэффициента отличны от нуля. Согласно утверждению 1 при помощи переноса начала координат уравнение приведется к виду
$$
A’x″^ < 2>+ C’y″^ < 2>+ F″ = 0.label
$$
Могут быть сделаны следующие предположения относительно знаков коэффициентов в этом уравнении.
Случай A’C’ > 0.
Если (A’C’ > 0), то коэффициенты (A’) и (C’) имеют один знак. Для (F″) имеются следующие три возможности.
-
Знак (F″) противоположен знаку (A’) и (C’). Перенесем (F″) в другую часть равенства и разделим на него. Уравнение примет вид
$$
frac>> + frac>> = 1,label
$$
где (a^ <2>= -F″/A’), (b^ <2>= -F″/C’). Можно считать, что в этом уравнении (a > 0), (b > 0) и (a geq b). Действительно, если последнее условие не выполнено, то можно сделать дополнительную замену координат
$$
x^ <*>= y″, y^ <*>= x″.label
$$
Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением eqref при условии (a geq b), называется эллипсом, уравнение называется каноническим уравнением эллипса, а система координат — его канонической системой координат.
При (a = b) уравнение eqref есть уравнение окружности радиуса (a). Таким образом, окружность — частный случай эллипса.
$$
frac>> + frac>> = -1,label
$$
Этому уравнению не удовлетворяют координаты ни одной точки. Уравнение, которое приводится к каноническому виду eqref, называется уравнением мнимого эллипса.
$$
a^<2>x″^ < 2>+ c^<2>y″^ < 2>= 0.label
$$
Ему удовлетворяет только одна точка (x″ = 0), (y″ = 0). Уравнение, приводящееся к каноническому виду eqref, называется уравнением пары мнимых пересекающихся прямых. Основанием для этого названия служит сходство с приведенным ниже уравнением eqref.
Случай A’C’ Определение.
Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением eqref, называется гиперболой, уравнение называется каноническим уравнением гиперболы, а система координат — ее канонической системой координат.
Случай (A’C’ = 0).
Допустим теперь, что (A’C’ = 0), и, следовательно, один из коэффициентов (A’) или (C’) равен нулю. В случае необходимости, делая замену eqref, мы можем считать, что (A’ = 0). При этом (C neq 0), так как иначе порядок уравнения был бы меньше двух. Используя утверждение 1, мы приведем уравнение к виду
$$
C’y″^ < 2>+ 2D’x″ + F″ = 0.nonumber
$$
Пусть (D’ neq 0). Сгруппируем члены следующим образом:
$$
C’y″^ < 2>+ 2D’left(x″ + frac<2D’>right) = 0.nonumber
$$
Перенесем начало координат вдоль оси абсцисс в соответствии с формулами перехода (x^ <*>= x″ + F″/2D’), (y^ <*>= y″). Тогда уравнение примет вид
$$
C″y^ <*2>+ 2D’x^ <*>= 0,nonumber
$$
или
$$
y^ <*2>= 2px^<*>,label
$$
где (p = -D’/C″). Мы можем считать, что (p > 0), так как в противном случае можно сделать дополнительную замену координат, изменяющую направление оси абсцисс: (tilde = -x^<*>), (tilde = y^<*>).
Линия, которая в некоторой декартовой прямоугольной системе координат может быть задана уравнением eqref при условии (p > 0), называется параболой, уравнение называется каноническим уравнением параболы, а система координат — ее канонической системой координат.
Допустим, что (D’ = 0). Уравнение имеет вид (C’y″^ < 2>+ F″ = 0). Относительно (F″) есть следующие три возможности.
- Если (C’F″ 0) знаки (C’) и (F″) совпадают. Разделив на (C’), приведем уравнение к виду
$$
y″^ < 2>+ a^ <2>= 0.label
$$
Этому уравнению не удовлетворяют координаты ни одной точки. Уравнение, приводящееся к каноническому виду eqref, называют уравнением пары мнимых параллельных прямых. - Остался последний случай (F″ = 0). После деления на (C’) уравнение принимает вид
$$
y″^ < 2>= 0.label
$$
Это уравнение эквивалентно уравнению (y″ = 0), и потому определяет прямую линию. Уравнение, приводящееся к каноническому виду eqref, называется уравнением пары совпавших прямых.
Теперь мы можем объединить всё вместе.
Пусть в декартовой системе координат задано уравнение второго порядка eqref.
Тогда существует такая декартова прямоугольная система координат, в которой это уравнение принимает один из следующих девяти канонических видов:
- Уравнение эллипса.
$$
frac>> + frac>> = 1;nonumber
$$ - Мнимый эллипс. Данному уравнению не удовлетворяет ни одна точка.
$$
frac>> + frac>> = -1;nonumber
$$ - Уравнение пары мнимых пересекающихся прямых (точка).
$$
a^<2>x^ <2>+ c^<2>y^ <2>= 0;nonumber
$$ - Уравнение гиперболы.
$$
frac>>-frac>> = 1;nonumber
$$ - Пересекающиеся прямые.
$$
a^<2>x^<2>-c^<2>y^ <2>= 0;nonumber
$$ - Уравнение параболы.
$$
y^ <2>= 2px;nonumber
$$ - Пара параллельных прямых.
$$
y^<2>-a^ <2>= 0;nonumber
$$ - Пара мнимых параллельных прямых. Данному уравнению не удовлетворяет ни одна точка.
$$
y^ <2>+ a^ <2>= 0;nonumber
$$ - Прямая (пара совпавших прямых).
$$
y^ <2>= 0.nonumber
$$
Оптическое свойство кривых второго порядка. Касательные к эллипсу и гиперболе
По этой ссылке вы найдёте полный курс лекций по математике:
Предположим для определенности, что точка М0 лежит в первой четверти, т. е. х0 > О, Уо > 0. Тогда часть эллипса, лежащую в первой четверти, можно описать уравнением Пользуясь формулой (1), получаем уравнение касательной к эллипсу в точке Мо а так как точка (я0, уо) лежит на эллипсе, то Пусть mq(xо, уо) — точка эллипса и, значит, Полученное соотношение после несложных преобразований можно записать так: Отсюда с учетом тождества приходим к уравнению.
Оптическое свойство кривых второго порядка Касательные к эллипсу и гиперболе Касательные к параболе Оптическое свойство эллипса Оптическое свойство гиперболы Оптическое свойство параболы классификация кривых второго порядка Многочлены второй степени на плоскости Канонические уравнения кривых второго порядка (рис. 28). Полученное соотношение является уравнением касательной к эллипсу, проходящей через его точку (я0, Уо), и в обшем случае ее произвольного расположения, т.е. прилюбыхзнаках яо и у0. .
Уравнение касательной к гиперболе выводится аналогично и имеет следующий вид Подчеркнем, что точка (xq, Уо) лежит на гиперболе. Если кривая задана уравнением то уравнение касательной к ней, проходящей через точку (х0,у0), где уо = f(xо), можно записать в следующем виде Касательные к параболе Если кривая задана уравнением то уравнение касательной к ней, проходящей через точку (хо,2/о)> ГДе х0 = д(уо), можно записать в следующем виде Пусть Л/о(х0, уо) — точка параболы.
Пользуясь формулой (I), получаем уравнение касательной к параболе Отсюда в силу равенства yl = 2рх0 приходим к уравнению касательной вида Замечание. Сопоставляя канонические уравнения эллипса, гиперболы и параболы с уравнениями касательных к этим кривым, нетрудно заметить, чтодля получения последних не требуется специальных вычислений.
В самом деле, заменяя у2 на 3/3/0» а х2 на xxq (в случае параболы 2х нужно заменить на х + хо). приходим к уравнению соответствующей касательной. Еше раз отметим, что сказанное справедливо лишь в том случае, когда точка (го. Уо) лежит на кривой. 6.3. Оптическое свойство эллипса Пусть Мо — произвольная точка эллипса Как уже отмечалось, расстояния от нее до фокусов F„ и Fn — фокальные радиусы — равны соответственно.
Проведем через точку А/0 касательную к эллипсу, и вычислим, на каком расстоянии от этой касательной лежат фокусы Fn(
c, 0) и Fn(c, 0) (напомним, что для этого следует воспользоваться формулой (10) из §11.1). Имеем соответственно или — нормирующий м ножитель (рис. 29). Нетрудно проверить,что В самом деле, Обратившись к рис.29, заметим, что вычисленные отношения равны синусам углов, образованных касательной и фокальными радиусами точки касания.
Из того, что синусы этих углов равны, вытекает равенство и самих углов. Тем самым доказано оптическое свойство эллипса: касательная к эллипсу образует равные углы с фокальными радиусами точки касания. Это свойство называется оптическим по следующей причине: если поместить в один из фокусов эллипса с зеркальной «поверхностью» точечный источник Рис.29 света, то все лучи после отражения от «поверхности» эллипса сойдутся в другом его фокусе (рис. 30).
Оптическое свойство гиперболы Устанавливается аналогичными выкладками и заключается в следующем. Если поместить водин из фокусов гиперболы точечный источниксвета,то каждый луч после отражения от зеркальной «поверхности» гиперболы видится исходящим из другого фокуса (рис. 31). Оптическое свойство параболы Если в фокус параболы помешен точечный источник света, то все лучи, отраженные от зеркальной «поверхности» параболы, будут направлены параллельно оси параболы (рис.32).
Многочлены второй степени на плоскости Теорема. Пусть на плоскости введена прямоугольная декартова система координат Оху и пусть Оптическое свойство кривых второго порядка Касательные к эллипсу и гиперболе Касательные к параболе Оптическое свойство эллипса Оптическое свойство гиперболы Оптическое свойство параболы классификация кривых второго порядка Многочлены второй степени на плоскости Канонические уравнения кривых второго порядка — многочлен второй степени от переменных х и у.
Тогда на плоскости можно построить прямоугольную дека ртов у систему координат O’XY так, что после замены переменных х и у на переменные X uY исходный многочлен f(x, у) приведется к многочлену F(X, Y) одного из следующих трех видов: шаг. Поворотом координатных осей на подходящим образом выбранный угол всегда можно добиться того, чтобы коэффициент при произведении разноименных координат обратился в нуль. Пусть 6^0 (при этот шаг не нужен).
Возможно вам будут полезны данные страницы:
Повернем оси координат вокругточки О. Эта операция описывается следующими формулами Рис.33 При этом координатные оси исходной системы Оху поворачиваются на угол ^ (рис.33). Заменим переменные х и у в формуле (I) их выражениями (2) через и вычислим коэффициент 2b при произведении Он равен и обращается в нуль, если Так как полученное уравнение разрешимо относительно , то указанным преобразованием всегда можно добиться обращения в нуль нужного коэффициента.
Приступая ко второму этапу преобразования, будем считать, что исходный многочлен /(я, у) уже имеет вид где а2 + с2 >0.
Для определенности положим с Ф 0 (это не ограничивает общности наших рассуждений, так как заменой я и у в случае необходимости этого всегда можно добиться). 2-й шаг. Переносом начала координат можно достичьдальнейшего упрощения вида м ногочле-на f(x, у). Эта операция описывается следующими формулами: координатные оси новой системы получаются из координатных осей исходной системы Оху параллельным переносом в точку (-а, -р) (рис.34). Укажем конкретные значения а и р. Возможны три случая Тогда, полагая Рис. 34 О) е получаем глс .
Домножснием обеих частей уравнения из п. I на -1 и заменой X на У, а У на в случае необходимости) всегда можно добиться того, чтобы Полагая получим гиперболу Полагая получим — пару пересекающихся прямых: Название можно объяснить некоторым сходством этого уравнения с уравнением эллипса. Название можно объяснить некоторым сходством этого уравнения с уравнением лары пересекающихся прямых.
Всегда можно добиться того, чтобы В D (заменив, в случае необходимости, X на -X). Полагая получим параболу . Можно считать, что В 0. 1. Е Полагая получим — пару параллельных прямых. 2. Е > 0. Полагая получим На действительной плоскости нет ни одной точки, координаты которой обращали бы это уравнение (пары мнимых пара>1лелыыхпрямых) в тождество. 3. Е = 0. Тогда — пара совпадающих прямых. Чтобы определить тип кривой второго порядка, не обязательно проводить все указанные выше преобразования. Достаточно вычислить знаки некоторых выражений, составленных из коэффициентов уравнения.
Оптическое свойство кривых второго
порядка Касательные к эллипсу и гиперболе Касательные к параболе Оптическое свойство эллипса Оптическое свойство гиперболы Оптическое свойство параболы классификация кривых второго порядка Многочлены второй степени на плоскости Канонические уравнения кривых второго порядка уравнение линии второго порядка. Введем следующие обозначения Числа D и Д не зависят от выбора системы координат на плоскости и называются инвариантами.
Из приводимой таблицы видно, какому сочетанию знаков определителей D и Д соответствует та или иная линия второго порядка. Задача. Убедитесь в том, что d и Д при рассмотренных преобразованиях системы координат действительно остаются неизменными. ^ Название можно объяснить некоторым сходством этого уравнения с уравнением пары параллельных Эллипс Мнимый эллипс Пара мнимых пересекающихся прямых Гипербола Пара пересекающихся прямых Парабола Пара параллельных прямых Пара мнимых параллельных прямых Парасовпадаюших прямых
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
5.2.8. Примеры решения задач по теме «Кривые 2-го порядка»
Определить тип уравнения кривой 2-го порядка:
Если L1·L2 > 0, то уравнение эллиптического типа;
Если L1·L2 0, следовательно, перед нами уравнение эллиптического типа.
В уравнении отсутствует произведение Ху, следовательно, квадратичная форма его старших членов имеет канонический вид; поэтому коэффициенты при Х2 и У2 являются собственными числами матрицы квадратичной формы. Итак, L1 = 4, L2 = 9, L1·L2 > 0, следовательно, перед нами уравнение эллиптического типа.
Геометрические образы, определяемые уравнением эллиптического типа:
– пустое множество («мнимый эллипс»).
Для приведения уравнения к каноническому виду нужно исключить из него слагаемые. Содержащие первые степени переменных. Для этого преобразуем левую часть:
Зададим параллельный перенос осей координат:
Тогда в новых координатах уравнение примет вид:
Каноническое уравнение эллипса.
Ответ: уравнение эллипса, канонический вид 
Привести уравнение к каноническому виду и указать геометрический образ, который оно определяет:
Собственные числа имеют разные знаки, значит, тип уравнения – гиперболический.
Геометрические образы, определяемые уравнением гиперболического типа:
– пара пересекающихся прямых.
Собственные числа имеют разные знаки, значит, тип уравнения – гиперболический.
Геометрические образы, определяемые уравнением гиперболического типа:
– пара пересекающихся прямых.
Заметим, что для данного уравнения нет необходимости искать явный вид преобразования координат, приводящего квадратичную форму к каноническому виду. Это связано с тем, что уравнение не содержит линейных членов, а его свободный член не изменится при преобразовании вида
Найденные собственные числа будут коэффициентами при Х2 и У2 для канонического вида квадратичной формы. Следовательно, в соответствующей координатной системе уравнение примет вид:
Каноническое уравнение гиперболы.
Ответ: уравнение гиперболического типа, канонический вид

Привести уравнение к каноническому виду и указать геометрический образ, который оно определяет:
Перед нами полное уравнение 2-го порядка, и для приведения его к каноническому виду потребуется провести оба преобразования координатных осей: поворот на такой угол, чтобы новые оси стали параллельными собственным векторам матрицы квадратичной формы (это преобразование квадратичной формы к каноническому виду), и параллельный перенос.
Перед нами полное уравнение 2-го порядка, и для приведения его к каноническому виду потребуется провести оба преобразования координатных осей: поворот на такой угол, чтобы новые оси стали параллельными собственным векторам матрицы квадратичной формы (это преобразование квадратичной формы к каноническому виду), и параллельный перенос.
Итак, тип уравнения – гиперболический.
Матрица перехода к новому базису:

Собственные векторы следует выбирать так, чтобы определитель матрицы перехода равнялся +1 – при этом не нарушается взаимное расположение координатных осей.
Запишем исходное уравнение в новых координатах:
2) Параллельный перенос:
В новых координатах получаем уравнение
Пара пересекающихся прямых.
Ответ: уравнение гиперболического типа, определяет пару пересекающихся прямых, канонический вид: У″ = ± 2Х″.
Не проводя преобразования координат, установить, что уравнение
Определяет прямую, и найти уравнение этой прямой.
Обратите внимание на то, что квадратичная форма, образованная старшими членами уравнения, является полным квадратом.
Иногда привести уравнение к простому виду удается с помощью алгебраических приемов. Представим левую часть уравнения в виде:
Ответ: уравнение определяет прямую Х – 3У + 2 = 0.
Эллипс, симметричный относительно осей координат, проходит через точки
Найти его эксцентриситет.
По условию задачи оси координат являются осями симметрии эллипса, поэтому, во-первых, его уравнение имеет канонический вид, а во-вторых, полуось А равна абсциссе точки А.
По условию задачи оси координат являются осями симметрии эллипса, поэтому, во-первых, его уравнение имеет канонический вид:
А во-вторых, полуось А равна абсциссе точки А, т. е. А = 6. Найдем B, подставив в уравнение эллипса координаты точки М:
Итак, уравнение эллипса:
Тогда расстояние от фокуса до начала координат
Вычислим эксцентриситет эллипса:
Ответ: эксцентриситет
Составить уравнение эллипса, фокусы которого лежат на прямой У + 6 = 0, эксцентриситет равен 
Найдите расстояние от точки М до прямой У + 6 = 0, т. е. длину малой полуоси эллипса. Центром симметрии эллипса будет точка О пересечения прямых F1F2 (Y + 6 = 0) и МО, проходящей через точку М перпендикулярно F1F2.
Найдем расстояние от точки М до прямой У + 6 = 0, т. е. длину малой полуоси эллипса. Нормальный вид уравнения данной прямой: -у – 6 = 0, тогда
Центром симметрии эллипса будет точка О пересечения прямых F1F2 (Y + 6 = 0) и МО, проходящей через точку М перпендикулярно F1F2.
Поскольку прямая F1F2 параллельна оси абсцисс, прямая МО параллельна оси ординат; следовательно, ее уравнение: Х = 3. Тогда координаты точки О:
С учетом расположения осей эллипса можно утверждать, что в системе координат, полученной параллельным переносом начала координат в точку
О(3; -6), то есть заданной преобразованием
Уравнение эллипса имеет канонический вид:
Найдем А из условия, что
Подставим найденные значения А и B в уравнение эллипса:
Ответ: уравнение эллипса: Х2 + 2У2 – 6Х + 24У + 31 = 0.
Составить уравнения директрис гиперболы.
Приведите уравнение гиперболы к каноническому виду и составьте уравнения директрис в виде
Приведем уравнение гиперболы к каноническому виду:
Осями симметрии являются координатные оси, А = 3, B = 4. Тогда
Ответ: уравнения директрис:
Написать уравнение гиперболы, имеющей вершины в фокусах, а фокусы – в вершинах эллипса
Найдите вначале координаты вершин и фокусов эллипса, а затем определите коэффициенты А и B в каноническом уравнении гиперболы.
Координаты вершин гиперболы: (А; 0) и (-А; 0), координаты фокусов: (С; 0) и (–С; 0). Соответственно координаты вершин эллипса: (А1; 0) и (-А1; 0), координаты фокусов: (С1; 0) и (-С1; 0). У данного эллипса А1 = 5,
Тогда для гиперболы А = 4, С = 5, откуда

И уравнение гиперболы:
Ответ:
Составить уравнение касательной к гиперболе
В ее точке М=<15; 4
Найдите вначале координаты нормали к гиперболе в точке М (если кривая задана уравнением F(X,Y) = 0, То нормаль к ней в точке М0=<Х0;у0>
Имеет координаты: П = (F′X(X0;Y0);F′Y(X0;Y0))), а затем составьте уравнение прямой, проходящей через точку М=<15; 4
Найдем координаты нормали к гиперболе в точке М.
Уравнение прямой, проходящей через точку М0(х0;у0) перпендикулярно вектору П = <A, B>, имеет вид:
А(х – х0) + В(у – у0) = 0.
Запишем уравнение касательной:
Ответ: Уравнение касательной:
Составить уравнение параболы, если даны ее фокус F(2; -1) и директриса
Используйте определение параболы: параболой называется геометрическое место точек, для каждой из которых расстояние до фокуса равно расстоянию до директрисы.
Используем определение параболы:
Параболой называется геометрическое место точек, для каждой из которых расстояние до фокуса равно расстоянию до директрисы.
Пусть точка М(Х, У) лежит на параболе. Тогда ее расстояние до фокуса
Выразим через Х и У расстояние от точки М до директрисы.
Нормальное уравнение директрисы:
Из определения параболы DM = MF,
Ответ: уравнение параболы: Х2 + 2Ху + У2 – 6Х + 2У + 9 = 0.
Составить уравнение параболы с вершиной в начале координат, если известно, что парабола симметрична относительно оси Ох и проходит через точку А=<9; 6>. Найти координаты ее фокуса.
Из условий задачи следует, что данная парабола задается каноническим уравнением
Подставьте в это уравнение координаты точки А и найдите значение параметра Р параболы.
Из условий задачи следует, что данная парабола задается каноническим уравнением
Подставим в это уравнение координаты точки А: 36 = 2Р·9, откуда Р = 2.
Следовательно, уравнение параболы имеет вид: У2 = 4Х.
Координаты фокуса параболы задаются формулой: F=<0,5P; 0>, то есть F=<1; 0>.
Ответ: уравнение параболы: У2 = 4Х; фокус F=<1; 0>.
[spoiler title=”источники:”]
http://natalibrilenova.ru/opticheskoe-svojstvo-krivyih-vtorogo-poryadka-kasatelnyie-k-ellipsu-i-giperbole/
http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-i-analiticheskaia-geometriia/5-2-8-primery-resheniia-zadach-po-teme-krivye-2-go-poriadka
[/spoiler]
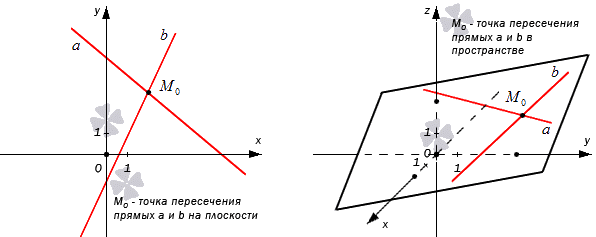
Для того, чтобы решить геометрическую задачу методом координат, необходима точка пересечения, координаты которой используются при решении. Возникает ситуация, когда требуется искать координаты пересечения двух прямых на плоскости или определить координаты тех же прямых в пространстве. Данная статья рассматривает случаи нахождения координат точек, где пересекаются заданные прямые.
Точка пересечения двух прямых – определение
Необходимо дать определение точкам пересечения двух прямых.
Раздел взаимного расположения прямых на плоскости показывает, что они могут совпадать , быть параллельными, пересекаться в одной общей точке или скрещивающимися. Две прямые, находящиеся в пространстве, называют пересекающимися, если они имеют одну общую точку.
Определение точки пересечения прямых звучит так:
Точка, в которой пересекаются две прямые, называют их точкой пересечения. Иначе говоря, что точка пересекающихся прямых и есть точка пересечения.
Рассмотрим на рисунке, приведенном ниже.
Нахождение координат точки пересечения двух прямых на плоскости
Перед нахождением координат точки пересечения двух прямых, необходимо рассмотреть предлагаемый ниже пример.
Если на плоскости имеется система координат Оху, то задаются две прямые a и b. Прямой a соответствует общее уравнение вида A1x+B1y+C1=0, для прямой b – A2x+B2y+C2=0. Тогда M0(x0, y0) является некоторой точкой плоскости необходимо выявить , будет ли точка М0 являться точкой пересечения этих прямых.
Чтобы решить поставленную задачу, необходимо придерживаться определения. Тогда прямые должны пересекаться в точке, координаты которой являются решением заданных уравнений A1x+B1y+C1=0 и A2x+B2y+C2=0. Значит, координаты точки пересечения подставляются во все заданные уравнения. Если они при подстановке дают верное тождество, тогда M0(x0, y0) считается их точкой пересечения.
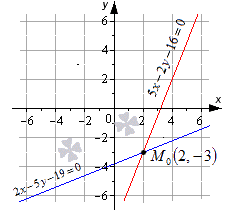
Даны две пересекающиеся прямые 5x-2y-16=0 и 2x-5y-19=0. Будет ли точка М0 с координатами (2,-3) являться точкой пересечения.
Решение
Чтобы пересечение прямых было действительным, необходимо, чтобы координаты точки М0 удовлетворяли уравнениям прямых. Это проверяется при помощи их подстановки. Получаем, что
5·2-2·(-3)-16=0⇔0=02·2-5·(-3)-19=0⇔0=0
Оба равенства верные, значит М0 (2, -3) является точкой пересечения заданных прямых.
Изобразим данное решение на координатной прямой рисунка, приведенного ниже.
Ответ: заданная точка с координатами (2,-3) будет являться точкой пересечения заданных прямых.
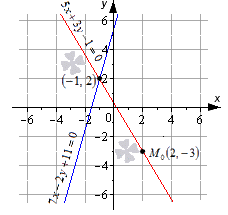
Пересекутся ли прямые 5x+3y-1=0 и 7x-2y+11=0 в точке M0 (2, -3)?
Решение
Для решения задачи необходимо подставить координаты точки во все уравнения. Получим, что
5·2+3·(-3)-1=0⇔0=07·2-2·(-3)+11=0⇔31=0
Второе равенство не является верным, значит, что заданная точка не принадлежит прямой 7x-2y+11=0. Отсюда имеем, что точка М0 не точка пересечения прямых.
Чертеж наглядно показывает, что М0 – это не точка пересечения прямых. Они имеют общую точку с координатами (-1,2).
Ответ: точка с координатами (2,-3) не является точкой пересечения заданных прямых.
Переходим к нахождению координат точек пересечения двух прямых при помощи заданных уравнений на плоскости.
Задаются две пересекающиеся прямые a и b уравнениями вида A1x+B1y+C1=0 и A2x+B2y+C2=0, расположенных в Оху. При обозначении точки пересечения М0 получим, что следует продолжить поиск координат по уравнениям A1x+B1y+C1=0 и A2x+B2y+C2=0.
Из определения очевидно, что М0 является общей точкой пересечения прямых. В этом случае ее координаты должны удовлетворять уравнениям A1x+B1y+C1=0 и A2x+B2y+C2=0. Иными словами это и есть решение полученной системы A1x+B1y+C1=0A2x+B2y+C2=0.
Значит, для нахождения координат точки пересечения , необходимо все уравнения добавить в систему и решить ее.
Заданы две прямые x-9y+14=0 и 5x-2y-16=0 на плоскости. необходимо найти их пересечение.
Решение
Данные по условию уравнения необходимо собрать в систему, после чего получим x-9y+14=05x-2y-16=0. Чтобы решить его, разрешается первое уравнение относительно x, подставляется выражение во второе:
x-9y+14=05x-2y-16=0⇔x=9y-145x-2y-16=0⇔⇔x=9y-145·9y-14-2y-16=0⇔x=9y-1443y-86=0⇔⇔x=9y-14y=2⇔x=9·2-14y=2⇔x=4y=2
Получившиеся числа являются координатами, которые необходимо было найти.
Ответ: M0 (4, 2) является точкой пересечения прямых x-9y+14=0 и 5x-2y-16=0.
Поиск координат сводится к решению системы линейных уравнений. Если по условию дан другой вид уравнения, тогда следует привести его к нормальному виду.
Определить координаты точек пересечения прямых x-5=y-4-3 и x=4+9·λy=2+λ, λ∈R.
Решение
Для начала необходимо привести уравнения к общему виду. Тогда получаем, что x=4+9·λy=2+λ, λ∈R преобразуется таким образом:
x=4+9·λy=2+λ⇔λ=x-49λ=y-21⇔x-49=y-21⇔⇔1·(x-4)=9·(y-2)⇔x-9y+14=0
После чего беремся за уравнение канонического вида x-5=y-4-3 и преобразуем. Получаем, что
x-5=y-4-3⇔-3·x=-5·y-4⇔3x-5y+20=0
Отсюда имеем, что координаты – это точка пересечения
x-9y+14=03x-5y+20=0⇔x-9y=-143x-5y=-20
Применим метод Крамера для нахождения координат:
∆=1-93-5=1·(-5)-(-9)·3=22∆x=-14-9-20-5=-14·(-5)-(-9)·(-20)=-110⇒x=∆x∆=-11022=-5∆y=1-143-20=1·(-20)-(-14)·3=22⇒y=∆y∆=2222=1
Ответ: M0 (-5, 1).
Имеется еще способ для нахождения координат точки пересечения прямых, находящихся на плоскости. Он применим, когда одна из прямых задается параметрическими уравнениями, имеющими вид x=x1+ax·λy=y1+ay·λ, λ∈R. Тогда вместо значения x подставляется x=x1+ax·λ и y=y1+ay·λ, где получим λ=λ0, соответствующее точке пересечения, имеющей координаты x1+ax·λ0, y1+ay·λ0.
Определить координаты точки пересечения прямой x=4+9·λy=2+λ, λ∈R и x-5=y-4-3.
Решение
Необходимо выполнить подстановку в x-5=y-4-3 выражением x=4+9·λ, y=2+λ, тогда получим:
4+9·λ-5=2+λ-4-3
При решении получаем, что λ=-1. Отсюда следует, что имеется точка пересечения между прямыми x=4+9·λy=2+λ, λ∈R и x-5=y-4-3. Для вычисления координат необходимо подставить выражение λ=-1 в параметрическое уравнение. Тогда получаем, что x=4+9·(-1)y=2+(-1)⇔x=-5y=1.
Ответ: M0 (-5, 1).
Для полного понимания темы, необходимо знать некоторые нюансы.
Предварительно необходимо понять расположение прямых. При их пересечении мы найдем координаты, в других случаях решения существовать не будет. Чтобы не делать эту проверку, можно составлять систему вида A1x+B1y+ C1=0A2x+B2+C2=0 При наличии решения делаем вывод о том, что прямые пересекаются. Если решение отсутствует, то они параллельны. Когда система имеет бесконечное множество решений, тогда говорят, что они совпадают.
Даны прямые x3+y-4=1 и y=43x-4. Определить, имеют ли они общую точку.
Решение
Упрощая заданные уравнения, получаем 13x-14y-1=0 и 43x-y-4=0.
Следует собрать уравнения в систему для последующего решения:
13x-14y-1=013x-y-4=0⇔13x-14y=143x-y=4
Отсюда видно, что уравнения выражаются друг через друга, тогда получим бесконечное множество решений. Тогда уравнения x3+y-4=1 и y=43x-4 определяют одну и ту же прямую. Поэтому нет точек пересечения.
Ответ: заданные уравнения определяют одну и ту же прямую.
Найти координаты точки пересекающихся прямых 2x+(2-3)y+7=0 и 23+2x-7y-1=0.
Решение
По условию возможно такое, прямые не будут пересекаться. Необходимо составить систему уравнений и решать. Для решения необходимо использовать метод Гаусса, так как с его помощью есть возможность проверить уравнение на совместимость. Получаем систему вида:
2x+(2-3)y+7=02(3+2)x-7y-1=0⇔2x+(2-3)y=-72(3+2)x-7y=1⇔⇔2x+2-3y=-72(3+2)x-7y+(2x+(2-3)y)·(-(3+2))=1+-7·(-(3+2))⇔⇔2x+(2-3)y=-70=22-72
Получили неверное равенство, значит система не имеет решений. Делаем вывод, что прямые являются параллельными. Точек пересечения нет.
Второй способ решения.
Для начала нужно определить наличие пересечения прямых.
n1→=(2, 2-3) является нормальным вектором прямой 2x+(2-3)y+7=0, тогда вектор n2→=(2(3+2), -7 – нормальный вектор для прямой 23+2x-7y-1=0.
Необходимо выполнить проверку коллинеарности векторов n1→=(2, 2-3) и n2→=(2(3+2), -7). Получим равенство вида 22(3+2)=2-3-7. Оно верное, потому как 223+2-2-3-7=7+2-3(3+2)7(3+2)=7-77(3+2)=0. Отсюда следует, что векторы коллинеарны. Значит, прямые являются параллельными и не имеют точек пересечения.
Ответ: точек пересечения нет, прямые параллельны.
Найти координаты пересечения заданных прямых 2x-1=0 и y=54x-2.
Решение
Для решения составляем систему уравнений. Получаем
2x-1=054x-y-2=0⇔2x=154x-y=2
Найдем определитель основной матрицы. Для этого 2054-1=2·(-1)-0·54=-2. Так как он не равен нулю, система имеет 1 решение. Отсюда следует, что прямые пересекаются. Решим систему для нахождения координат точек пересечения:
2x=154x-y=2⇔x=1245x-y=2⇔x=1254·12-y=2⇔x=12y=-118
Получили, что точка пересечения заданных прямых имеет координаты M0(12, -118).
Ответ: M0(12, -118).
Нахождения координат точки пересечения двух прямых в пространстве
Таким же образом находятся точки пересечения прямых пространства.
Когда заданы прямые a и b в координатной плоскости Охуz уравнениями пересекающихся плоскостей, то имеется прямая a , которая может быть определена при помощи заданной системы A1x+B1y+C1z+D1=0A2x+B2y+C2z+D1=0 а прямая b – A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0.
Когда точка М0 является точкой пересечения прямых, тогда ее координаты должны быть решениями обоих уравнений. Получим линейные уравнения в системе:
A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0
Рассмотрим подобные задания на примерах.
Найти координаты точки пересечения заданных прямых x-1=0y+2z+3=0 и 3x+2y+3=04x-2z-4=0
Решение
Составляем систему x-1=0y+2z+3=03x+2y+3=04x-2z-4=0 и решим ее. Чтобы найти координаты, необходимо решать через матрицу. Тогда получим основную матрицу вида A=10001232040-2 и расширенную T=1001012-340-24. Определяем ранг матрицы по Гауссу.
Получаем, что
1=1≠0, 1001=1≠0, 100012320=-4≠0, 1001012-3320-340-24=0
Отсюда следует, что ранг расширенной матрицы имеет значение 3. Тогда система уравнений x-1=0y+2z+3=03x+2y+3=04x-27-4=0 в результате дает только одно решение.
Базисный минор имеет определитель 100012320=-4≠0, тогда последнее уравнение не подходит. Получим, что x-1=0y+2z+3=03x+2y+3=04x-2z-4=0⇔x=1y+2z=-33x+2y-3 . Решение системы x=1y+2z=-33x+2y=-3⇔x=1y+2z=-33·1+2y=-3⇔x=1y+2z=-3y=-3⇔⇔x=1-3+2z=-3y=-3⇔x=1z=0y=-3.
Значит, имеем, что точка пересечения x-1=0y+2z+3=0 и 3x+2y+3=04x-2z-4=0 имеет координаты (1, -3, 0).
Ответ: (1, -3, 0).
Система вида A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0 имеет только одно решение. Значит, прямые a и b пересекаются.
В остальных случаях уравнение не имеет решения, то есть и общих точек тоже. То есть невозможно найти точку с координатами, так как ее нет.
Поэтому система вида A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0A3x+B3y+C3z+D3=0A4x+B4y+C4z+D4=0 решается методом Гаусса. При ее несовместимости прямые не являются пересекающимися. Если решений бесконечное множество, то они совпадают.
Можно произвести решение при помощи вычисления основного и расширенного ранга матрицы, после чего применить теорему Кронекера-Капелли. Получим одно, множество или полное отсутствие решений.
Заданы уравнения прямых x+2y-3z-4=02x-y+5=0 и x-3z=03x-2y+2z-1=0. Найти точку пересечения.
Решение
Для начала составим систему уравнений. Получим, что x+2y-3z-4=02x-y+5=0x-3z=03x-2y+2z-1=0 . решаем ее методом Гаусса:
12-342-10-510-303-221~12-340-56-130-20-40-811-11~~12-340-56-1300-125650075-1595~12-340-56-1300-1256500031110
Очевидно, что система не имеет решений, значит прямые не пересекаются. Точки пересечения нет.
Ответ: нет точки пересечения.
Если прямые заданы при помощи кононических или параметрических уравнений, нужно привести к виду уравнений пересекающихся плоскостей, после чего найти координаты.
Заданы две прямые x=-3-λy=-3·λz=-2+3·λ, λ∈R и x2=y-30=z5 в Охуz. Найти точку пересечения.
Решение
Задаем прямые уравнениями двух пересекающихся плоскостей. Получаем, что
x=-3-λy=-3·λz=-2+3·λ⇔λ=x+3-1λ=y-3λ=z+23⇔x+3-1=y-3=z+23⇔⇔x+3-1=y-3x+3-1=z+23⇔3x-y+9=03x+z+11=0x2=y-30=z5⇔y-3=0x2=z5⇔y-3=05x-2z=0
Находим координаты 3x-y+9=03x+z+11=0y-3=05x-2z=0, для этого посчитаем ранги матрицы. Ранг матрицы равен 3, а базисный минор 3-10301010=-3≠0, значит, что из системы необходимо исключить последнее уравнение. Получаем, что
3x-y+9=03x+z+11=0y-3=05x-2z=0⇔3x-y+9=03x+z+11=0y-3=0
Решим систему методом Крамер. Получаем, что x=-2y=3z=-5. Отсюда получаем, что пересечение заданных прямых дает точку с координатами (-2, 3, -5).
Ответ: (-2, 3, -5).
- Учебники
- 3 класс
- Математика 👍
- Рудницкая
- №33
авторы: Рудницкая, Юдачева.
издательство: “Вентана-Граф”
Раздел:
- Деление на 10 и на 100
ГДЗ учебник по математике 3 класс (часть 2) Рудницкая. Деление на 10 и на 100. Номер №33
- Предыдущее
- Следующее
Назови пары пересекающихся прямых.
reshalka.com
ГДЗ учебник по математике 3 класс (часть 2) Рудницкая. Деление на 10 и на 100. Номер №33
Решение
Ответ: 1 и 2; 1 и 3; 2 и 3.
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
-
Пересечение линии второго порядка и прямой.
Начать изучение
-
Тип линии.
Начать изучение
-
Диаметр линии второго порядка.
Начать изучение
-
Центр линии второго порядка.
Начать изучение
-
Сопряженные направления.
Начать изучение
-
Главные направления.
Начать изучение
-
Касательная к линии второго порядка.
Начать изучение
-
Особые точки.
Начать изучение
Пересечение линии второго порядка и прямой.
Рассмотрим линию второго порядка, заданную общим уравнением
$$
Ax^{2}+2Bxy+Cy^{2}+2Dx+2Ey+F=0label{ref1}
$$
в декартовой системе координат, и исследуем пересечение этой линии с произвольной прямой
$$
x=x_{0}+alpha t, y=y_{0}+beta t.label{ref2}
$$
Значения параметра (t), соответствующие точкам пересечения, должны удовлетворять уравнению, получаемому подстановкой eqref{ref2} в eqref{ref1}:
$$
A(x_{0}+alpha t)^{2}+2B(x_{0}+alpha t)(y_{0}+beta t)+C(y_{0}+beta t)^{2} +\+ 2D(x_{0}+alpha t)+2E(y_{0}+beta t)+F=0.label{ref3}
$$
Раскрывая скобки и приводя подобные члены, мы получим уравнение
$$
Pt^{2}+2Qt+R=0,label{ref4}
$$
в котором
$$
P=Aalpha^{2}+2Balphabeta+Cbeta^{2},label{ref5}
$$
$$
Q=(Ax_{0}+By_{0}+D)alpha+(Bx_{0}+Cy_{0}+E)beta,label{ref6}
$$
или, при другой группировке слагаемых,
$$
Q=(Aalpha+Bbeta)x_{0}+(Balpha+Cbeta)y_{0}+Dalpha+Ebeta.label{ref7}
$$
Свободный член — это значение многочлена при (t=0), то есть
$$
R=Ax_{0}^{2}+2Bx_{0}y_{0}+Cy_{0}^{2}+2Dx_{0}+2Ey_{0}+F=0.label{ref8}
$$
Вообще говоря, уравнение eqref{ref4} квадратное, имеет не больше двух корней, и прямая пересекает линию или в двух точках, или в одной точке (кратные корни), или не пересекает ее (комплексные корни). Но возможны “исключительные” прямые, для которых (P=0), то есть
$$
Aalpha^{2}+2Balphabeta+Cbeta^{2}=0,label{ref9}
$$
и, следовательно, уравнение eqref{ref4} является линейным. В этом случае оно имеет один корень при (Q neq 0), а при (Q=0) либо выполнено тождественно (если и (R=0)), либо не имеет решений. Следовательно, “исключительные” прямые или пересекают линию в единственной точке, или лежат на ней целиком, или не имеют с ней общих точек.
В равенство eqref{ref9} не входят координаты начальной точки прямой. Кроме того, оно остается справедливым, если умножить (alpha) и (beta) на общий ненулевой множитель.
Определение.
Направление, определяемое вектором, компоненты которого удовлетворяют уравнению eqref{ref9}, называется асимптотическим направлением линии второго порядка.
Тип линии.
Выясним, сколько асимптотических направлений может иметь линия второго порядка. Обозначив
$$
delta=begin{vmatrix}
A& B\
B& C
end{vmatrix},nonumber
$$
сформулируем следующее утверждение.
Утверждение 1.
Линия второго порядка имеет два асимптотических направления, если (delta < 0), одно, если (delta=0), и ни одного, если (delta > 0).
Доказательство.
Рассмотрим несколько случаев.
- Пусть (A=C=0). Тогда (B neq 0) и (delta=-B^{2} < 0). Уравнение eqref{ref9} имеет вид (2Balphabeta=0), и ему удовлетворяют векторы (1,0) и (0,1).
- Пусть (C neq 0). Тогда вектор (0,1) не является решением этого уравнения, и каждое решение можно задать угловым коэффициентом (k=beta/alpha), удовлетворяющим уравнению (Ck^{2}+2Bk+A=0). Дискриминант этого уравнения равен (B^{2}-AC=-delta). Следовательно, оно имеет два вещественных корня при (delta < 0), один корень при (delta=0) и не имеет вещественных корней при (delta > 0).
- Случай (A neq 0) исследуется аналогично случаю 2, только нужно рассматривать не угловой коэффициент, а отношение (alpha/beta).
Поскольку разобранные выше случаи исчерпывают все возможности, предложение доказано.
От противного нетрудно проверить, что и обратно число асимптотических направлений определяет знак (delta).
Мы определили асимптотические направления при помощи аналитического условия eqref{ref9}. Поэтому в принципе при изменении системы координат асимптотическое направление могло бы перестать быть асимптотическим, или, наоборот, обыкновенное направление стать асимптотическим. Из геометрического смысла асимптотических направлений видно, что в действительности асимптотические направления не зависят от выбора системы координат.
Используя канонические уравнения, легко проверить, что эллипс не имеет асимптотических направлений, парабола имеет одно, а гипербола — два асимптотических направления (рис. 9.1). Поэтому линии второго порядка называются линиями гиперболического, параболического или эллиптического типа, смотря по тому, имеют они два, одно или не имеют ни одного асимптотического направления.
Для линий гиперболического типа (delta < 0), для параболического типа (delta=0), а для эллиптического (delta > 0).
Диаметр линии второго порядка.
Назовем хордой любой отрезок, концы которого лежат на линии, а остальные точки на ней не лежат. Таким образом, хорда не может иметь асимптотического направления.
Предположим, что рассматриваемая линия второго порядка имеет по крайней мере одну хорду. Этому условию удовлетворяют эллипсы, гиперболы, пары пересекающихся прямых, параболы и пары параллельных прямых.
Фиксируем какое-нибудь неасимптотическое направление и исследуем множество середин хорд, имеющих это направление. Если начальная точка (M_{0}(x_{0}, y_{0})) секущей eqref{ref2} находится в середине хорды, то корни уравнения eqref{ref4} равны по абсолютной величине и отличаются знаком (рис. 9.2). Это будет так в том и только том случае, когда (Q=0). Используя eqref{ref7}, мы получаем, что середины хорд направления ((alpha, beta)^{2}) лежат на прямой
$$
(Aalpha+Bbeta)x+(Balpha+Cbeta)y+Dalpha+Ebeta=0.label{ref10}
$$
Определение.
Прямая eqref{ref10} называется диаметром линии второго порядка, сопряженным направлению ((alpha, beta)).
Стоит обратить внимание на то, что диаметром называется вся прямая. Это не означает, что середины хорд заполняют ее целиком. Так может быть, но возможно также, что множество середин хорд есть, например, отрезок или луч.
Конечно, остается сомнение, действительно ли уравнение eqref{ref10} определяет прямую: не окажутся ли в нем коэффициенты при переменных оба равными нулю? Допустим, что это так, то есть
$$
Aalpha+Bbeta=0, Balpha+Cbeta=0.nonumber
$$
Умножим первое из этих равенств на (alpha), второе — на (beta) и сложим. Мы получим равенство eqref{ref9}, которое по предположению не имеет места. Следовательно, уравнение eqref{ref10} определяет прямую.
Центр линии второго порядка.
Обозначим левую часть уравнения eqref{ref1} через (boldsymbol{Phi}(x, y)) и введем еще одно понятие.
Определение.
Точка (O(x_{0}, y_{0})) называется центром линии второго порядка (boldsymbol{Phi}(x, y)=0), если для любого вектора (boldsymbol{a}(alpha, beta)) выполнено равенство
$$
boldsymbol{Phi}(x_{0}+alpha, y_{0}+beta)=boldsymbol{Phi}(x_{0}-alpha, y_{0}-beta).label{ref11}
$$
По-видимому, это определение зависит от выбора системы координат, так как в нем участвует не линия, а многочлен, стоящий в левой части ее уравнения. Допустим, что координаты (x_{0}, y_{0}) точки (O) в некоторой системе координат удовлетворяют уравнению eqref{ref11}. Будут ли ее координаты ((tilde{x}_{0}, tilde{y}_{0})) в другой системе координат удовлетворять равенству того же вида для многочлена (tilde{boldsymbol{Phi}}(tilde{x}, tilde{y})), задающего ту же линию в новой системе координат? Легко видеть, что это так, потому что многочлен (tilde{boldsymbol{Phi}}) так и выбирается, чтобы для координат любой точки выполнялось равенство (tilde{boldsymbol{Phi}}(tilde{x}, tilde{y})=boldsymbol{Phi}(x, y)). Нам остается только выписать это равенство для точек, получаемых из (O) сдвигом на векторы (boldsymbol{a}) и (-boldsymbol{a}).
Ниже мы докажем, что в том случае, когда линия содержит хоть одну точку, центры линии и только они являются ее центрами симметрии. Однако понятие центра несколько более общее: линии, являющиеся пустыми множествами, имеют вполне определенные центры, хотя говорить об их центрах симметрии смысла нет. Например, каждая точка прямой (y=0) является центром линии с уравнением (y^{2}+1=0).
Получим систему уравнений для координат центра. С этой целью напишем подробнее равенство eqref{ref11}. Его левая часть равна
$$
A(x_{0}+alpha)^{2}+2B(x_{0}+alpha)(y_{0}+beta) +\+ C(y_{0}+beta)^{2}+2D(x_{0}+alpha)+2E(y_{0}+beta)+F.nonumber
$$
Правая часть отличается от левой только знаками у (alpha) и (beta). Поэтому при вычитании (boldsymbol{Phi}(x_{0}-alpha, y_{0}-beta)) из (boldsymbol{Phi}(x_{0}+alpha, y_{0}+beta)) уничтожаются все члены, кроме тех, в которые (alpha) и (beta) входят в первой степени, а члены с первыми степенями удвоятся. После упрощений мы получаем
$$
(Ax_{0}+By_{0}+D)alpha+(Bx_{0}+Cy_{0}+E)beta=0.label{ref12}
$$
Но равенство eqref{ref11}, а вместе с ним и равносильное равенство eqref{ref12} имеет место при любых (alpha) и (beta), в частности, при (alpha=1), (beta=0) и при (alpha=0), (beta=1). Отсюда следует, что координаты ((x_{0}, y_{0})) центра должны удовлетворять системе уравнений
$$
left{begin{array}{l}
Ax_{0}+By_{0}+D=0,\
Bx_{0}+Cy_{0}+E=0.
end{array}right.label{ref13}
$$
Легко видеть, что и обратно, если справедливы равенства eqref{ref13}, то, умножая их на произвольные числа (alpha) и (beta) и складывая, мы получим eqref{ref12}, а тем самым и eqref{ref11}.
Исследуем, обязательно ли существуют центры у линии второго порядка, а если они существуют, то сколько их и как они расположены. Система уравнений eqref{ref13} имеет единственное решение тогда и только тогда, когда
$$
delta=begin{vmatrix}
A& B\
B& C
end{vmatrix} neq 0.label{ref14}
$$
Таким образом, условие (delta neq 0) необходимо и достаточно для того, чтобы линия второго порядка имела единственный центр.
Линии второго порядка, имеющие единственный центр, называются центральными.
Полученное условие показывает, что центральными являются линии эллиптического и гиперболического типов.
Условие (delta=0) характеризует нецентральные линии. Это — линии параболического типа. При условии (delta=0) система eqref{ref13} либо не имеет решения, либо равносильна одному из составляющих ее уравнений (ранее мы уже доказывали этот факт). Это значит, что нецентральная линия либо не имеет центра (парабола), либо ее центры заполняют прямую линию (пары параллельных прямых, вещественных и мнимых, и пары совпавших прямых).
Утверждение 2.
Если линия второго порядка не является пустым множеством и имеет центр (O(x_{0}, y_{0})), то он — ее центр симметрии.
Доказательство.
В самом деле, рассмотрим произвольную точку линии (M(x, y)) и докажем, что симметричная ей относительно (O) точка (M_{1}(x_{1}, y_{1})) также лежит на линии. Точка (M_{1}) определяется равенством (overrightarrow{OM_{1}}=-overrightarrow{OM}). Если ((alpha, beta)) — координаты вектора (overrightarrow{OM}), то (x=x_{0}+alpha), (y=y_{0}+beta), а (x_{1}=x_{0}-alpha), (y_{1}=y_{0}-beta). Теперь ясно, что в силу eqref{ref11} из (boldsymbol{Phi}(x, y)=0) следует (boldsymbol{Phi}(x_{1}, y_{1})=0). Утверждение доказано.
Утверждение 3.
Если линия содержит хотя бы одну точку и имеет центр симметрии (O(x_{0}, y_{0})), то (O) является центром.
Доказательство.
Рассмотрим пересечение линии с прямой, проходящей через (O), приняв эту точку за начальную точку прямой. Имеются две возможности:
- Точка (O) лежит на линии. Пусть прямая имеет неасимптотическое направление. Тогда (O) — единственная точка пересечения, так как иначе с учетом симметрии точек пересечения было бы не меньше трех. Следовательно, уравнение eqref{ref4} имеет кратный корень (t=0), откуда вытекает (Q=0). Итак, координаты точки (O) удовлетворяют равенству (12) при любых (alpha) и (beta), соответствующих неасимптотическим направлениям. Выберем два различных неасимптотических направления ((alpha, beta)) и ((alpha’, beta’)) и рассмотрим равенства
$$
begin{array}{cc}
& (Ax_{0}+By_{0}+D)alpha+(Bx_{0}+Cy_{0}+E)beta=0,\
& (Ax_{0}+By_{0}+D)alpha’+(Bx_{0}+Cy_{0}+E)beta’=0.
end{array}nonumber
$$
как систему уравнений с коэффициентами (alpha), (beta), (alpha’), (beta’), причем ((alphabeta’-alpha’beta neq 0)). Мы получаем равенства eqref{ref13}, как и требовалось. - Точка (O) не лежит на линии. Если прямая пересекает линию в точке (M), которой соответствует значение параметра (t_{1} neq 0), то существует симметричная точка пересечения со значением параметра (-t_{1}). Тогда (Pt_{1}^{2}+2Qt_{1}+R=0) и (Pt_{1}^{2}-2Qt_{1}+R=0), откуда следует (Q=0).
Таким образом, если линия имеет точки пересечения с двумя различными прямыми, проходящими через (O), то, как и выше, мы можем получить равенства eqref{ref13} для координат (O). Докажем, что такие прямые обязательно найдутся. Действительно, в противном случае все точки линии лежат на одной прямой. Согласно теореме о существующих типах линий второго порядка линии только двух классов обладают этим свойством: пары совпавших прямых и пары мнимых пересекающихся прямых. Но и для того, и для другого класса все центры симметрии принадлежат линии, что противоречит сделанному предположению. Утверждение доказано.
Сопряженные направления.
Направление ((alpha’, beta’)), определяемое диаметром, сопряженным направлению ((alpha, beta)), называется сопряженным направлению ((alpha, beta)). Компоненты ((alpha’, beta’)), направляющего вектора диаметра eqref{ref10} согласно доказанному ранее утверждению 6 удовлетворяют условию
$$
(Aalpha+Bbeta)alpha’+(Balpha+Cbeta)beta’=0label{ref15}
$$
или
$$
Aalphaalpha’+B(alpha’beta+alphabeta’)+Cbetabeta’=0label{ref16}
$$
В последнее выражение пары чисел ((alpha, beta)) и ((alpha’, beta’)) входят симметричным образом. Поэтому имеет место следующее утверждение.
Утверждение 4.
Если направление ((alpha’, beta’)), сопряженное с ((alpha, beta)), не является асимптотическим, то сопряженным для ((alpha’, beta’)) будет направление ((alpha, beta)) (рис. 9.3).
Возникает вопрос, при каких условиях направление, сопряженное какому-нибудь направлению ((alpha, beta)) может оказаться асимптотическим. Это легко выяснить. Из равенства eqref{ref15} следует, что в качестве (alpha’) и (beta’) можно выбрать соответственно — (-(Balpha+Cbeta)) и ((Aalpha+Bbeta)). Подставим это в уравнение eqref{ref9} для асимптотических направлений:
$$
A(Balpha+Cbeta)^{2}-2B(Balpha+Cbeta)(Aalpha+Bbeta)+C(Aalpha+Bbeta)^{2}=0.nonumber
$$
После преобразований получаем ((AC-B^{2}) times (Aalpha^{2}+2Balphabeta+Cbeta^{2})=0). Поскольку исходное направление не асимптотическое, это произведение может обратиться в нуль только за счет первого сомножителя. Мы получаем новое утверждение.
Утверждение 5.
Если линия не центральная ((delta=0)), то для любого направления ((alpha, beta)) сопряженное направление — асимптотическое (рис. 9.4). Если линия центральная ((delta neq 0)), то направление, сопряженное любому направлению, не асимптотическое.
Главные направления.
Если диаметр перпендикулярен хордам, которым он сопряжен, то он является осью симметрии рассматриваемой линии.
Определение.
Направление ((alpha, beta)) и направление ((alpha’, beta’)) сопряженного ему диаметра называются главными направлениями, если они перпендикулярны.
Если система координат декартова прямоугольная, то для главного направления компоненты ((alpha, beta)) должны быть пропорциональны коэффициентам уравнения eqref{ref10}, то есть должно существовать такое число (lambda), что
$$
Aalpha+Bbeta=lambdaalpha, Balpha+Cbeta=lambdabeta.label{ref17}
$$
Исключая (lambda), мы получаем уравнение для (alpha) и (beta):
$$
(A-C)alphabeta+B(beta^{2}-alpha^{2})=0.label{ref18}
$$
Если положить (alpha=cos varphi), (beta=sin varphi), то уравнение eqref{ref18} превратится в уравнение (2B cos 2varphi = (A-C)sin 2varphi), которое, как мы видели, обязательно имеет решение относительно (varphi). Поэтому имеет место следующее утверждение.
Утверждение 6.
Каждая линия второго порядка имеет хотя бы одну пару главных направлений.
Более подробное исследование уравнения eqref{ref18} показывает, что либо эта пара единственная, либо каждая пара перпендикулярных направлений является главной. Последний случай имеет место, когда (A=C), (B=0). При этом уравнение линии приводится к одному из канонических видов: (x^{2}+y^{2}=a^{2}), (x^{2}+y^{2}=-a^{2}) или (x^{2}+y^{2}=0). В двух последних случаях линия не имеет хорд, и результат лишен геометрического смысла.
Касательная к линии второго порядка.
Как известно, касательной к какой-либо линии называется предельное положение секущей, когда хорда стягивается в точку. Выведем уравнение касательной к линии второго порядка, заданной уравнением eqref{ref1}. Дадим предварительно следующее определение.
Определение.
Особой точкой линии второго порядка называется ее центр, который лежит на линии.
Особыми точками являются: точка пересечения пары пересекающихся прямых, единственная точка пары мнимых пересекающихся прямых и каждая точка пары совпавших прямых. В особой точке касательная не определена. Если точка лежит на прямой, входящей в состав линии, то касательная в этой точке совпадает с прямой. Исключив эти случаи, мы фактически ограничиваемся рассмотрением касательных к эллипсам, гиперболам и параболам.
Рассмотрим точку (M_{0}(x_{0, y_{0}})), лежащую на линии (L), и прямую с начальной точкой (M_{0}), заданную уравнением eqref{ref2}. С нашей точки зрения, приведенное выше определение касательной означает, что уравнение eqref{ref4}, определяющее точки пересечения (L) и прямой, имеет два совпадающих корня.
Так как начальная точка принадлежит (L), в уравнении eqref{ref4} (R=0), и один из его корней равен нулю. Корни совпадают, если и второй корень равен нулю, для чего необходимо, чтобы (Q=0). Если при этом окажется, что и (P=0), то прямая принадлежит линии второго порядка. Этот случай мы исключили, и потому уравнение имеет кратный корень (t=0) в том и только том случае, когда (Q=0). Мы рассматриваем равенство (Q=0) как условие, определяющее направляющий вектор касательной:
$$
(Ax_{0}+By_{0}+D)alpha+(Bx_{0}+Cy_{0}+E)beta=0.label{ref19}
$$
Так как (M_{0}) не особая точка, обе скобки здесь одновременно в нуль не обращаются, и условие eqref{ref19} определяет (alpha) и (beta) с точностью до общего множителя. Точка (M(x, y)) лежит на касательной тогда и только тогда, когда вектор (overrightarrow{M_{0}M}) коллинеарен (boldsymbol{a}(alpha, beta)), то есть его координаты (x-x_{0}) и (y-y_{0}) удовлетворяют тому же условию, что и ((alpha, beta)):
$$
(Ax_{0}+By_{0}+D)(x-x_{0})+(Bx_{0}+Cy_{0}+E)(y-y_{0})=0.label{ref20}
$$
Это и есть уравнение касательной к линии (L) в точке (M_{0}), лежащей на линии. Уравнение eqref{ref20} можно записать и иначе, если заметить, что координаты (M_{0}) удовлетворяют уравнению eqref{ref1} и, следовательно,
$$
(Ax_{0}+By_{0}+D)x_{0}+(Bx_{0}+Cy_{0}+E)y_{0}+Dx_{0}+Ey_{0}+F=0.nonumber
$$
Прибавляя это равенство к eqref{ref20} и группируя слагаемые, получим окончательное уравнение
$$
Axx_{0}+B(xy_{0}+x_{0}y)+Cyy_{0}+D(x+x_{0})+E(y+y_{0})+F=0.label{ref21}
$$
Особые точки.
Напомним, что особая точка линии второго порядка — это ее центр, лежащий на линии. Исследуем, при каких условиях линия второго порядка имеет особую точку. Для координат ((x_{0}, y_{0})) особой точки должны быть справедливы равенства
$$
begin{array}{cc}
& Ax_{0}+By_{0}+D=0, Bx_{0}+Cy_{0}+E=0,\
& Ax_{0}^{2}+2Bx_{0}y_{0}+Cy_{0}^{2}+2Dx_{0}+2Ey_{0}+F=0.
end{array}nonumber
$$
Умножим первое из них на (x_{0}), второе на (y_{0}) и вычтем из третьего. Мы получим эквивалентную систему уравнений
$$
left{begin{array}{l}
Ax_{0}+By_{0}+D=0,\
Bx_{0}+Cy_{0}+E=0,\
Dx_{0}+Ey_{0}+F=0.
end{array}right.label{ref22}
$$
Выберем какой-нибудь базис в пространстве и рассмотрим вспомогательные векторы (boldsymbol{p}(A, B, D)), (boldsymbol{q}(B, C, E)) и (boldsymbol{r}(D, E, F)). Равенства eqref{ref22} представляют собой координатную запись векторного равенства
$$
x_{0}boldsymbol{p}+y_{0}boldsymbol{q}=-boldsymbol{r}.label{ref23}
$$
Отсюда следует, что при наличии особой точки векторы (boldsymbol{p}), (boldsymbol{q}) и (boldsymbol{r}) компланарны, и потому
$$
triangle=begin{vmatrix}
A& B& D\
B& C& E\
D& E& F
end{vmatrix}=0.label{ref24}
$$
Если линия центральная, то векторы (boldsymbol{p}) и (boldsymbol{q}) не коллинеарны, и условие компланарности eqref{ref24} равносильно существованию разложения eqref{ref23}, то есть существованию решения системы eqref{ref22}. Мы получили ещё одно утверждение.
Утверждение 7.
Центральная линия имеет особую точку тогда и только тогда, когда (triangle=0).
Итак, сочетание (delta < 0), (triangle=0) характеризует пары пересекающихся прямых, а (delta > 0), (triangle=0) — пары мнимых пересекающихся прямых.
Рассмотрим нецентральные линии. Для них существует центр, хотя бы не являющийся особой точкой, тогда и только тогда, когда (triangle=0). В этом (и только этом) случае векторы (boldsymbol{p}) и (boldsymbol{q}) коллинеарны. Действительно, так как (delta=0), по предложению 9 § 2 гл. II, если система уравнений eqref{ref13} имеет решение, она равносильна одному из составляющих ее уравнений: либо коэффициенты и свободный член одного из уравнений равны нулю, либо коэффициенты и свободные члены обоих уравнений пропорциональны. Тогда (triangle=0) независимо от (boldsymbol{r}).
Обратно, пусть для нецентральной линии (triangle=0). Докажем, что (boldsymbol{p}) и (boldsymbol{q}) коллинеарны, что равносильно совместности уравнений центра. Действительно, в противном случае (boldsymbol{r}) по ним раскладывается, и согласно eqref{ref23} существует особая точка. Она — центр, (boldsymbol{p}) и (boldsymbol{q}) коллинеарны, и мы получаем противоречие.
Утверждение 8.
Для нецентральных линий условие (triangle=0) равносильно существованию центра.
Итак, сочетание (delta=triangle=0) характеризует пары параллельных прямых (вещественных, мнимых или совпавших).
Из последних двух утверждений следует, что равенство (triangle=0) является инвариантным: оно не может измениться при переходе к другой системе координат.