Как найти паш раствора через концентрацию - Сайт, где вы сможете решить свои вопросы

Загрузить PDF

В быту под pH подразумевают обычно шкалу, используемую для описания нейтральности или, наоборот, недостатка нейтральности того или иного вещества. В научном значении величина pH соответствует количеству ионов в химическом растворе. Если вы изучаете химию или связанные с ней предметы, вам может понадобиться рассчитать уровень pH, основываясь на концентрации веществ в растворе. Значение pH находится по следующей формуле: pH = -lg[H₃O⁺].

1
Ознакомьтесь с понятием pH. Величина pH соответствует концентрации ионов водорода в растворе. Раствор с повышенной концентрацией ионов водорода называется кислотным, а раствор с пониженной концентрацией этих ионов – щелочным.^[1] Ионы водорода кратко обозначают как H⁺. Их можно представлять и в составе соединения, тогда они называются гидроксонием и записываются как H₃0⁺.
- Ознакомьтесь со шкалой pH. Значения на шкале pH изменяются от 1 до 14. Чем меньше число, тем более кислотным является данный раствор. И наоборот, чем выше значение, тем более щелочным является раствор.^[2] Например, pH апельсинового сока составляет 2, поскольку этот сок представляет собой довольно кислотную жидкость. У хлорного отбеливателя pH равно 12, так как в нем много щелочи.^[3] В середине шкалы располагаются относительно нейтральные растворы, такие как вода, pH которой составляет 7.
- Разница между двумя растворами на 1 пункт по шкале pH означает, что они различаются по кислотности в 10 раз. Например, если взять два раствора со значениями pH 6 и 7, кислотность первого раствора с pH 6 будет выше кислотности второго раствора с pH 7 в 10 раз. А, например, кислотность раствора с pH 6 выше кислотности раствора с pH 8 в 100 раз.^[4]
2
Запомните уравнение для определения pH. Шкала pH вычисляется с помощью отрицательного десятичного логарифма. Отрицательный десятичный логарифм соответствует числу нулей, стоящих перед единицей, включая и ноль целых: например, отрицательный десятичный логарифм числа 0,1 равен 1, числа 0,01 — 2, и так далее.^[5] Формула для нахождения pH выглядит следующим образом: pH = -lg[H₃O⁺].
- Иногда формулу записывают в виде pH = -lg[H⁺]. Неважно, стоит ли в уравнении H₃O⁺ или H⁺, обе формы записи равноценны.
- Для нахождения pH необязательно уметь рассчитывать десятичный логарифм, так как практически в каждом научном или инженерном калькуляторе есть опция его вычисления.
3

Ознакомьтесь с понятием концентрации. Концентрация какого-либо вещества соответствует числу частиц этого вещества, присутствующих в растворе.^[6] Как правило, концентрация выражается в количестве молей на единицу объема и обозначается как m/V, или M. В химических лабораториях концентрации растворов пишут на бутылках с ними. Если вы решаете химическую задачу, концентрация может быть дана в условии, либо ее требуется найти.

Реклама

1
Вспомните формулу для нахождения pH. Вот эта формула: pH = -lg[H₃O⁺].^[7] Убедитесь в том, что вы знакомы со всеми элементами, входящими в данную формулу. Посмотрите, какая величина соответствует концентрации.
- В химии квадратные скобки означают концентрацию чего-либо. Так что формула для расчета pH читается как «pH равно отрицательному логарифму концентрации гидроксоний-ионов».
2
Определите действительную концентрацию. Внимательно прочитайте условие задачи. Найдите в исходных данных концентрацию кислоты или щелочи. Запишите полную формулу на листке бумаги, подставив в нее известные величины.^[8] Чтобы не возникло путаницы, рядом с числами всегда указывайте единицы измерения.
- Например, если концентрация составляет 1,05 x 10⁵ M, запишите формулу для расчета pH в следующем виде: pH = -lg[1,05 x 10⁵ M]
3

Вычислите pH. Для этого удобно использовать научный калькулятор. Сначала введите знак минуса, нажав кнопку «+/-». Затем нажмите кнопку «log», соответствующую десятичному логарифму (в английском языке десятичный логарифм обозначается как log). На экране отобразится «-log».^[9] Затем нажмите левую скобку и введите концентрацию. При необходимости не забудьте указать значение степени.^[10] После этого закройте скобки.^[11] В результате на экране калькулятора вы увидите «-log(1,05×10⁵). Нажмите «=». У вас должно получиться значение pH, приблизительно равное 4,98.

Реклама

1

Определите, что дано и что требуется найти. Запишите формулу для вычисления pH. После этого выясните известные величины, выписав их значения под формулой. Например, если известно, что pH равно 10,1, запишите это число под pH в формуле.
2
Преобразуйте формулу. При этом вам понадобятся знания из школьного курса алгебры. Для вычисления концентрации по известному значению pH необходимо преобразовать формулу так, чтобы концентрация обособленно стояла с какой-либо из двух сторон уравнения. То есть необходимо, чтобы по одну сторону знака равенства было выражение, содержащее величину pH, а по другую — концентрация гидроксония. Сначала умножьте обе части уравнения на -1. Затем возведите 10 в степени, стоящие по обе стороны получившегося равенства.
- Преобразовывая равенство pH = -log[H₃O⁺], получаем формулу +[H₃O⁺] = 10^-pH, то есть концентрация ионов равна десяти в степени -pH. Теперь вместо pH подставляем известное значение, в нашем случае 10,1.
3
Решите уравнение. Для возведения десяти в степень в калькуляторе предусмотрена определенная процедура. Сначала наберите 10. Затем нажмите клавишу возведения в степень «EXP». Введите знак минуса и значение степени. Нажмите «=».
- В нашем примере pH равно 10,1. Наберите «10» и нажмите клавишу «EXP». После этого нажмите «-/+», меняя знак. И наконец, введите значение pH «10,1» и нажмите клавишу «=». В результате у вас должно получиться 1e-100. Это означает, что концентрация составляет 1,00 x 10^-100 M.
4

Обдумайте полученный ответ. Имеет ли он физический смысл? Если pH равно 10,1, это значит, что концентрация гидроксония чрезвычайно мала, и у вас щелочной раствор.^[12] Таким образом, найденная очень низкая концентрация соответствует

Реклама

Советы

Если вычисление уровня pH поначалу кажется вам трудным, не забывайте, что существует множество источников, позволяющих больше узнать об этом вопросе. Воспользуйтесь учебником химии или попросите преподавателя помочь вам.

Об этой статье

Эту страницу просматривали 130 094 раза.

Была ли эта статья полезной?

Источник

Расчет рН растворов сильных и слабых электролитов

Сильные
кислоты и основания
(табл.2.1) в растворах диссоциируют пол-

ностью,
поэтому концентрация ионов водорода и
ионов гидроксила равна

общей
концентрации сильного электролита.

Для
сильных оснований:
[OH^–]
= См;
для
сильных
кислот:
[H⁺]
=
См.

Таблица
2.1

Сильные электролиты

Класс	Формулы электролитов
Кислота	HNO₃, H₂SO₄, HCl, HBr, HI, HMnO₄, HClO₄
Основание	LiOH , KOH, RbOH, CsOH, NaOH, Ba(OH)₂, Ca(OH)₂, Sr(OH)₂
Соль	Растворимые соли

Слабым
электролитом
принято считать химические соединения,
молекулы которых даже в сильно разбавленных
растворах не полностью диссоциируют
на ионы. Степень диссоциации слабых
электролитов для децимолярных растворов
(0,1М) меньше 3%. Примеры слабых электролитов:
все органические кислоты, некоторые
неорганические кислоты (например, H₂S,
HCN), большинство гидроксидов (например,
Zn(OH)₂,
Cu(OH)₂).

Для
растворов слабых
кислот
концентрация ионов водорода [H⁺]
в растворе рассчитывается по формуле:

где:
Кк –
константа диссоциации слабой кислоты;
Ск –
концентрация кислоты, моль/дм³.

Для
растворов слабых
оснований
концентрация гидроксильных ионов
рассчитывается по формуле:

где:
Ко –
константа диссоциации слабого основания;
Сосн. –
концентрация основания, моль/дм³.

Таблица
2.2

Константы диссоциации слабых кислот и оснований при 25 оС

Формула	Константа диссоциации, Кд
СH₃COOH	1,86 • 10^–5
HCN	7,2 • 10^-10
HOCl	5,0 • 10^-8
HBO₂	7,5 • 10^-10
HOBr	2,5 • 10^-9
HF	6,2 • 10^-4
HNO₂	5,1 • 10^-4
HIO	2,3 • 10^-11
HOCN	2,7 • 10^-4
NH₄OH	1,79 • 10^-5
AgOH	5,0 • 10^-3

2.2.
Примеры решения индивидуального задания

Пример
№1.

Условие
задания: Определить
концентрацию
водородных и гидроксильных ионов в
растворе, если
рН =5,5.

Решение

Концентрация
ионов водорода рассчитывается по
формуле:

[Н⁺]
= 10^-рН

[Н⁺]
= 10^-5,5=
3,16 •10^-6
моль/дм³

Концентрация
гидроксильных ионов рассчитывается по
формуле:

[OН^–]
= 10^-рOН

рОН
= 14 – рН = 14 – 5,5 = 8,5

[OН^–]
= 10 ^-8,5
=
3 • 10^-9моль/дм³

Пример
№ 2.

Условие
задания: Вычислить
рН 0,001 М раствора HС1.

Решение

Кислота
HС1 является сильным электролитом
(табл.2.1) и в разбавленных растворах
практически полностью диссоциирует на
ионы:

HС1⇄
Н⁺+
С1^–

Поэтому
концентрация ионов [Н⁺]
равна общей концентрации кислоты:
[Н⁺]
= См = 0,001 М.

[Н⁺]
= 0,001= 1·10^-3
моль/дм³

Тогда:

рН
= – lg[H⁺]
= – lg 1 • 10^-3
= 3

Пример
№ 3.

Условие
задания:
Вычислить
рН 0,002 М раствора NaOH.

Решение

Основание
NaOH является сильным электролитом
(табл.2.1) и в разбавленных растворах
практически полностью диссоциирует на
ионы:

NaOH
⇄Na⁺+OH^–

Поэтому
концентрация гидроксильных ионов равна
общей концентрации основания: [ОH^–]=
См
= 0,002
М.

Тогда:

рОН
= – lg[ОН^–]
= – lgСм = – lg 2 •10^-3
= 2,7

Исходя
из формулы: рН + рОН = 14, находим рН
раствора:

рН
= 14 – 2,7 = 11,3

Пример
№4.

Условие
задания: Вычислить
рН 0,04 М раствора NH₄OH,
если
константа диссоциации Кд(NH₄OH)
= 1,79·10^-5
(табл.2.2).

Решение

Основание
NH₄OH
является слабым электролитом и в
разбавленных растворах очень незначительно
диссоциирует на ионы.

Концентрация
гидроксильных ионов [ОH^–]
в растворе слабого основания рассчитывается
по формуле:

моль/дм³

рОН
= – lg[ОH^–]
= – lg 8,5·10^-2
= 1,1

Исходя
из формулы: рН + рОН = 14, находим рН
раствора:

рН
= 14 – рOН = 14 – 1,1 = 12,9

Пример
№5.

Условие
задания: Вычислить
рН
0,17
М раствора
уксусной
кислоты (CH₃COOH),
если константа диссоциации Кд(CH₃COOH)
= 1,86 • 10^-5
(табл.2.2).

Решение

Кислота
CH₃COOH
является слабым электролитом и в
разбавленных растворах очень незначительно
диссоциирует на ионы.

Концентрация
ионов водорода [H⁺]
в растворе слабой кислоты рассчитывается
по формуле:

Тогда:

моль/дм³

Вычисляем
pH
раствора по формуле: рН = – lg [H⁺]

pH
= – lg 1,78 • 10^-3=
2,75

2.3.
Индивидуальные задания

Условия
заданий
(табл.
2.3):

Задание
№ 1.
Вычислить концентрацию водородных и
гидроксильных ионов в растворе при
определенном значении рН (см. пример №
1);

Задание
№ 2.
Вычислить рН раствора сильного электролита
(кислоты, основания) при заданной
концентрации (см. пример № 2, 3);

Задание
№ 3.
Вычислить рН раствора слабого электролита
(кислоты, основания) при заданной
концентрации (см. пример № 4, 5).

Таблица
2.3

Состав
исследуемой воды

№ задания	Условия заданий:
Задание № 1	Задание № 2	Задание № 3
рН	Сильный электролит	Концентрация, См	Слабый электролит	Концентрация, См
1	6,05	НСl	0,033	NH₄OH	0,01
2	8,5	HNO₃	0,091	HCN	0,09
3	5,5	HI	0,032	HOCl	0,05
4	7,7	NaOH	0,054	HBO₂	0,36
5	6,3	HBr	0,076	HOBr	0,22
6	6,5	KOH	0,045	HF	0,63
7	8,9	HClO₄	0,027	HNO₂	0,55
8	8,5	HMnO₄	0,005	HOI	0,03
9	6,5	CsOH	0,008	HOCN	0,19
10	6,1	HNO₃	0,004	NH₄OH	0,082
11	6,5	HI	0,001	AgOH	0,04
12	6,9	LiOH	0,009	СH₃COOH	0,26
13	8,8	HBr	0,005	HCN	0,075
14	6,9	RbOH	0,036	HOCl	0,07
15	7,3	HClO₄	0,0022	HBO₂	0,15
16	6,3	HMnO₄	0,063	HOBr	0,23
17	7,4	KOH	0,055	HF	0,34
18	6,7	HNO₃	0,003	HNO₂	0,18
19	8,2	HI	0,019	HOI	0,39
20	8,3	HNO₃	0,082	HOCN	0,15
21	6,1	CsOH	0,004	NH₄OH	0,33
22	6,9	HCl	0,026	AgOH	0,091
23	8,2	HClO₄	0,075	HBO₂	0,32
24	8,6	HMnO₄	0,007	HOBr	0,054
25	8,5	LiOH	0,015	HF	0,076
26	8,2	HNO₃	0,0023	HNO₂	0,045
27	8,0	HI	0,034	HOI	0,27

Продолжение
табл. 2.3

28	7,9	NaOH	0,018	HOCN	0,35
29	7,9	HBr	0,039	NH₄OH	0,08
30	8,1	HCl	0,015	AgOH	0,4
31	6,1	HNO₃	0,003	NH₄OH	0,032
32	6,5	HI	0,002	AgOH	0,02
33	6,9	LiOH	0,008	СH₃COOH	0,24
34	8,8	HBr	0,003	HCN	0,073
35	6,9	RbOH	0,033	HOCl	0,072
36	7,3	HClO₄	0,0012	HBO₂	0,16
37	6,3	HMnO₄	0,033	HOBr	0,24
38	7,4	KOH	0,045	HF	0,35
39	6,7	HNO₃	0,004	HNO₂	0,28
40	8,2	HI	0,029	HOI	0,29
41	8,3	HNO₃	0,081	HOCN	0,05
42	6,1	CsOH	0,006	NH₄OH	0,033
43	6,9	HCl	0,023	AgOH	0,29
44	8,2	HClO₄	0,078	HBO₂	0,62
45	8,6	HMnO₄	0,006	HOBr	0,024
46	8,5	LiOH	0,012	HF	0,036
47	8,2	HNO₃	0,0021	HNO₂	0,025
48	8,0	HI	0,037	HOI	0,027
49	7,9	NaOH	0,013	HOCN	0,015
50	7,9	HBr	0,034	NH₄OH	0,08

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
#
#
#
#
10.02.20161.72 Mб14referat_turbaza.docx
#
#
#
#
#
#

Источник

Download Article

You can calculate the pH of a chemical solution, or how acidic or basic it is, using the pH formula: pH = -log₁₀[H₃O⁺]. Anything less than 7 is acidic, and anything greater than 7 is basic. Check out the steps below to learn how to find the pH of any chemical solution using the pH formula.

1
Know what pH actually is. The pH is a measure of the concentration of hydrogen ions in a solution.^[1] A solution with a high concentration of hydrogen ions is acidic. A solution with a low amount of hydrogen ions is basic, or also known as alkaline. Hydrogen ions, also known as hydronium, are written shorthand as H⁺ or H₃O⁺.^[2]
- Know the pH scale. The pH scale is usually presented from 0 to 14. The lower the number, the more acidic the solution. The higher the number, the more basic the solution. For example, orange juice would have a pH of 2 because it is quite acidic. In contrast, bleach has a pH of 12 as it is quite basic. Numbers in the middle of the scale are neutral, such as water, with a pH of 7.
- One level of pH is a 10x difference. For example, when comparing pH 7 to pH 6, pH 6 is ten times more acidic than pH 7. Furthermore, pH 6 would be 100 times more acidic than pH 8.
2
Define pH in an equation. The pH scale is calculated by a negative logarithm. A negative logarithm of base b is simply how many times a number must be divided by b to reach 1.^[3] The pH equation can be seen as follows: pH = -log₁₀[H₃O⁺].^[4]
- The equation can sometimes be seen as pH = -log₁₀[H⁺]. Know that whether the equation has H₃O⁺ or H⁺, they are the same.
- It is not vital to have a firm understanding of what a negative log is to calculate pH. Most calculators used at high school and post secondary level will have a log button.
Advertisement
3

Understand concentration. Concentration is the number of particles of a compound in a solution relative to the volume of the same solution.^[5] For pH, you have to use molar concentration for the formula to work out. Molar concentration, which is also called molarity, denotes the number of moles of dissolved compound per liter of solution. Its units are moles per liter (mol/L), also called molar (M). If you’re using a solution in a lab, the concentration will be written on the bottle. When working on your chemistry homework, the concentration will usually be given to you.^[6]

1
Remember the pH equation. The pH equation is as follows: pH = -log₁₀[H₃O⁺].^[7] Ensure you know what all terms in the equation represent. Look at which term is used for concentration.
- In chemistry, square brackets usually indicate “concentration of”. So the equation of pH would be read as “pH equals the negative logarithm of the concentration of hydronium ions”.
2
Identify the actual concentration. Read over your chemistry question. Identify the concentration of the acid or base. Write down the entire equation on paper with the known values represented in the equation.^[8] Always include units to avoid confusion.
- For example, if the concentration is 1.05 x 10^-5 M, write the pH equation as: pH = -log₁₀(1.05 x 10^-5 M)
3

Solve the equation. When solving the pH equation, you must use a scientific calculator. First, hit the “negative” button. It is usually written as “+/-”. Now key in the “log” button. Your screen should display “-log”.^[9] Now hit an open bracket and enter in your concentration. Don’t forget to add exponents when necessary.^[10] Follow with a closed bracket.^[11] At this point, you should see “-log(1.05×10^-5). Hit solve. Your pH should be approximately 4.98.

1

Identify the known unknowns. First write out the pH equation. Next, identify the values you have by writing them directly below your equation. For example, if you know the pH is a value of 10.1, write it on the paper below the pH equation.
2
Rearrange the equation. Rearranging the equation will require a strong understanding of algebra. To calculate concentration from pH, you must understand that the inverse of log₁₀ is “10 to the power of …” Start by shifting the minus sign over from the log side to the pH side. Then raise 10 to the power of (each side). “10 to the power of” and log₁₀ are inverses of each other and cancels out.^[12]
- For example, pH = -log₁₀[H₃O⁺] will mold into [H₃O⁺] = 10^-pH. pH can then be filled in as 10.1
3
Solve the equation. When working with inverse log, the calculator process is unique. Remember that log is a type of multiplication by 10. To enter your equation, key in 10. Next, hit the “EXP” exponent button. Key in the negative sign followed by the value. Hit solve.
- For example, take a pH value of 10.1. Key in “10” followed by “EXP.” Now key in “-/+” to have our value be negative. Finally, key in the pH of “10.1”. Hit solve. You should get about 7.943ᴇ-11, or 7.943*10^-11. This means our concentration is 7.943*10^-11 M.
4

Think about your answer. A neutral pH of 7 equates to a hydronium ion concentration of 10^-7 M. A solution with a pH of 10.1 is basic, so it will have less hydronium ions than that. If we look at our answer, 7.943*10^-11, we do indeed see that this number is way smaller than 10^-7, so our answer does make sense.^[13]

Add New Question

Question

What are some natural indicators?

Dr. Chris Hasegawa was a Science Professor and the Dean at California State University Monterey Bay. Dr. Hasegawa specializes in teaching complex scientific concepts to students. He holds a BS in Biochemistry, a Master’s in Education, and his teaching credential from The University of California, Davis. He earned his PhD in Curriculum and Instruction from The University of Oregon. Before becoming a professor, Dr. Hasegawa conducted biochemical research in Neuropharmacology at the National Institute of Health. He also taught physical and life sciences and served as a teacher and administrator at public schools in California, Oregon, and Arizona.

Retired Science Professor & Dean

Expert Answer

Cabbage juice, celeries, and different kinds of flowers are all excellent, natural base indicators.
Question

What is the purpose of a titration lab?

Dr. Chris Hasegawa was a Science Professor and the Dean at California State University Monterey Bay. Dr. Hasegawa specializes in teaching complex scientific concepts to students. He holds a BS in Biochemistry, a Master’s in Education, and his teaching credential from The University of California, Davis. He earned his PhD in Curriculum and Instruction from The University of Oregon. Before becoming a professor, Dr. Hasegawa conducted biochemical research in Neuropharmacology at the National Institute of Health. He also taught physical and life sciences and served as a teacher and administrator at public schools in California, Oregon, and Arizona.

Retired Science Professor & Dean

Expert Answer

Titration labs let you titrate an unknown acid solution with a basic solution that you already know the pH and molarity of.
Question

What is the most accurate method of reading pH?

Dr. Chris Hasegawa was a Science Professor and the Dean at California State University Monterey Bay. Dr. Hasegawa specializes in teaching complex scientific concepts to students. He holds a BS in Biochemistry, a Master’s in Education, and his teaching credential from The University of California, Davis. He earned his PhD in Curriculum and Instruction from The University of Oregon. Before becoming a professor, Dr. Hasegawa conducted biochemical research in Neuropharmacology at the National Institute of Health. He also taught physical and life sciences and served as a teacher and administrator at public schools in California, Oregon, and Arizona.

Retired Science Professor & Dean

Expert Answer

A pH meter is the most accurate options, but most people don’t have those lying around at home. pH papers and other indicators can work, too.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

If calculating pH seems difficult to you, there are many sources available. Use your textbook and reach out to your teacher for further help.

References

About This Article

Article SummaryX

To calculate pH, remember that the pH scale goes from 0 to 14 with numbers below 7 being acidic and numbers above 7 being basic. If you are doing chemistry in a lab, you will need to determine the concentration by finding the moles per unit of volume (m/v or M). If you are doing a chemistry problem, look at the equation to identify the concentration. Then, use the formula pH = -log10[H3O+], where H equals Hydrogen ions, to find the pH. To learn how to use pH to calculate a concentration, keep reading!

Did this summary help you?

Thanks to all authors for creating a page that has been read 347,692 times.

Reader Success Stories

Roman Barasa

May 15, 2018

“I had been taught 3 times in class about pH calculations, but failed to grasp. However, I have now grasped this in…” more

Did this article help you?

Источник

Как правильно рассчитать рН растворов сильных и слабых электролитов

Задача 40.
Вычислите рН 0,025 М раствора КОН.
Решение:
КОН – сильный электролит, который диссциирует по схеме: КОН = К⁺ + ОН^–;

[ОН^–] = С_М(КОН) = 0,025 моль/дм³;

рОН = – lg[OH^–] = – lg2,5 · 10^–2 = 2 – lg2,5 = 2 – 0,6 = 1,4;

pOH + pH = 14;

pH = 14 – pOH = 14 – 1,4 = 12,6.

Ответ: рН = 12,6.

Задача 41.
Вычислите концентрацию ионов [H⁺] и рН 0,3 М раствора пропионовой кислоты С₂Н₅СООН, если К_D = 1,4 · 10^–5.
Решение:
С₂Н₅СООН – слабая кислота. Для слабых кислот [H⁺] вычисляется по формуле:

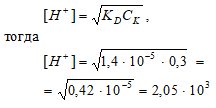
рН = –lg[H⁺] = –lg2,05 · 10^–3 = 3 – lg2,605 = 2,7.

Ответ: [H+] = 2,05 · 10^–3 моль/л; рН = 2,7.

Задача 42.
Вычислите рН 0,02 М раствора аммиака, если К_D = 1,76·10^–5.
Решение:
В водном растворе аммиака имеет место равновесие:

NH₃ + H₂O ⇔ NН₄⁺ + OH^–.

Поскольку К_О < 1 · 10^–2, полагаем, что равновесная концентрация недиссоциированного основания равна его общей концентрации: C_О(NH₄OH) = 0,02 моль/дм³. Для слабых оснований [H⁺] вычисляют по формуле:

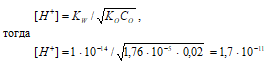
рН = –lg[H⁺] = –lg1,7 · 10^–11 = 11 – lg1,7 = 10,77.

Ответ: [H⁺] = 1,7 · 10^–11 моль/дм³; рН = 10,77.

Задача 43.
К 80 см³ 0,2 Н. раствора СН₃СООН прибавили 20 см³ 0,2 н. раствора СН₃СООNa. Рассчитайте рН полученного раствора, если Кк = 1,78 · 10^–5.
Решение:
Объём раствора, полученного после сливания исходных растворов, равен 80 + 20 = 100 см³.

Рассчитаем нормальность веществ в полученном растворе смеси, получим:

Сн(СН₃СООН) = [Сн(СН₃СООН) ^. V(СН₃СООН)]/V(p-pa) = (0,2 ^. 80)/100 = 0,16 моль/дм₃;
Сн(СН₃СООNa) = [Сн(СН₃СООNa) ^. V(СН₃СООNa)]/V(p-pa) = (0,2 ^. 20)/100 = 0,04 моль/дм³.

Для буферных растворов, образованных слабой кислотой и солью этой кислоты, [Н+] находят по формуле:

[H+] = Кк ^. (Ск/Cc);

Тогда

[H⁺] = 1,78 · 10^–5 ^. (0,16/0,04) = 7,12 · 10^–5 моль/дм³.

рН = –lg[H⁺]; pH = –lg7,12 · 10^–5 = 5 – lg7,12 = 4,15.

Ответ: [H⁺] = 7,12 · 10^–5 моль/дм³; рН = 4,15.

Задача 44.
Вычислите и сравните рН растворов: а) 0,1 М HCl и 0,1 М CH₃COOH; б) растворов, содержащих 7 г/дм³ HCl и 7 г/дм³ CH₃COOH.
Решение:

а) Расчет рН растворов: 0,1 М HCl, 0,1 М CH₃COOH

1. рассчитаем рН раствора 0,1 М HCl

HCl – сильная кислота, которая диссциирует полностью, поэтому [H⁺] = С_М(HCl) = 0,1 моль/дм³.

Тогда

рН = –lg[H⁺]; pH = –lg1 · 10^–1 = 1 – lg1 = 1.

2. рассчитаем рН раствора 0,1 М CH₃COOH

CH₃COOH (Кк = 1,78 · 10^–5) – слабая кислота. Для слабых кислот [H⁺] вычисляется по формуле:

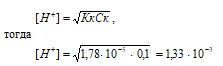
рН = –lg[H⁺] = –lg1,33 · 10^–3 = 3 – lg1,33 = 2,88.

б) Расчет рН растворов, содержащих 7 г/дм³ HCl и 7 г/дм³ CH₃COOH

1. Рассчитаем рН раствора HCl

Определим концентрацию HCl, получим:

С_М(HCl) = m(HCl)/M(HCl) = 7/36,5 = 0,19 = 1,9 · 10^–1

Так как HCl сильный электролит, то [H⁺] = См(HCl) = 0,19 = 1,9 · 10^–1 моль/дм³.

рН = –lg[H⁺]; pH = –lg1,9 · 10^–1 = 1 – lg1,9 = 0,72.

2. Рассчитаем рН раствора CH₃COOH

Определим концентрацию CH₃COOH, получим:

С_М(CH₃COOH) = m(CH₃COOH)/M(CH₃COOH) = 7/60 = 0,117.

CH₃COOH – слабая кислота. Для слабых кислот [H⁺] вычисляется по формуле:

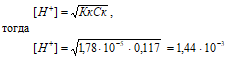
рН = –lg[H⁺]; pH = –lg1,44 · 10^–3 = 3 – lg1,44 = 2,85.

Ответ: а) 1 и 2,88; б) 0,72 и 2,85.

Источник

Калькуляторы ниже предназначены для решения химических задач. Или, если угодно, для проверки ответов. Первый калькулятор рассчитывает pH раствора сильной кислоты или сильного основания по заданным формуле вещества и молярности раствора. Второй калькулятор рассчитывает pH раствора слабой кислоты или слабого основания по заданным константе диссоциации и молярности раствора. Описание расчета с некоторой теорией можно найти под калькуляторами.

Расчет pH в растворах сильных кислот и оснований

Точность вычисления

Знаков после запятой: 3

Расчет pH в растворах слабых кислот и оснований

Точность вычисления

Знаков после запятой: 3

pH раствора

pH означает “pondus Hydrogenii”, “potential of hydrogen” или “power of hydrogen” – вес или потенциал водорода. pH вычисляется как величина, противоположная по знаку и равная по модулю десятичному логарифму активности водородных ионов, выраженной в молях на литр.
$ce {pH} = -log_{10}(a_{ce {H^+}})=log _{10}left({frac {1}{a_{{ce {H^+}}}}}right)$

pH является мерой кислотности водных растворов. Однако, в большинстве задач на растворы для описания раствора обычно используется молярная концентрация раствора или молярность. Как связаны эти две величины?

Активность ионов, конечно, зависит от их концентрации и эта зависимость описывается следующим уравнением:
$a_{H^+}=f cdot [H^+]$
где,
$a_{H^+}$ – активность ионов водорода
– коэффициент активности ионов водорода
[H^+] – концентрация ионов водорода

Коэффициент активности является функцией от концентрации ионов и стремится к 1 по мере разбавления раствора. При этом для идеальных растворов концентрации ионов равны концентрации растворенного вещества с учетом коэффициентов в формуле соединения. Поэтому для большинства задач, предполагающих идеальные растворы, можно использовать логарифм по основанию 10 от молярной концентрации раствора.

То, как проявляет себя водный раствор, как кислота или как основание, зависит от количества ионов водорода (H+). Вода, сама по себе, содержит некоторое количество ионов водорода¹ благодаря явлению автодиссоциации:

Известно, что в состоянии равновесия при стандартных условиях (750 мм.рт.ст. и 25°C), 1 литр чистой воды содержит $10^{-7}$ моль ионов H^+ и $10^{-7}$ моль ионов OH^- , следовательно, вода при стандартных условиях имеет pH равный 7. Кислоты отдают ионы водорода, так что водные растворы кислот содержат большее количество ионов H^+ чем нейтральная вода, и показатель pH таких растворов меньше 7. Основания принимают ионы водорода, которые возникают при автодиссоциации воды, так что водные растворы оснований содержат меньшее количество ионов водорода чем нейтральная вода и показатель pH таких растворов больше 7. То есть, низкое значение pH указывает на высокую концентрацию ионов водорода и наоборот.

Шкала pH является логарифмической, то есть разница значений в единицу означает разницу концентраций на порядок – в десять раз.

Расчет показателя pH по молярной концентрации раствора отличается в случаях сильных и слабых кислот и оснований.

Сильная кислота / Сильное основание

Сильные кислоты и основания – это вещества, которые, с практической точки зрения, полностью диссоциируют на ионы в воде. Следовательно, концентрацию ионов водорода в таких растворах можно принять равной концентрации вещества. Расчет pH в этом случае становится тривиальным:

Для кислот:
$pH=-log_{10}[H^+]$

Для растворов оснований известна концентрация основания, то есть, концентрация гидроксид ионов OH-. Следовательно можно рассчитать pOH:
$pOH=-log_{10}[OH^-]$

Исходя из равновесных концентраций H+ и OH− в воде, pH и pOH связаны соотношением , выполняющимся для любого водного раствора

Таким образом, для оснований:
$pH=14 - pOH=14 + log_{10}[OH^-]$

Всего семь кислот считаются сильными:

Соляная кислота HCl
Азотная кислота HNO3
Серная кислота H2SO4
Бромоводород HBr
Иодоводородная кислота HI
Хлорная кислота HClO4
Хлорноватия кислота HClO3

Сильных оснований не намного больше, и не все из них растворимы в воде. К растворимым относятся:

Гидроксид лития LiOH
Гидроксид натрия NaOH
Гидроксид калия KOH
Гидроксид рубидия RbOH
Гидроксид цезия CsOH

Раствор сильной кислоты с концентрацией 1 M (1 моль/литр) имеет pH равный 0. Раствор сильного основания с концентрацией 1 M (1 моль/литр) имеет pH равный 14. В большинстве задач значения pH будут лежать в границах от 0 до 14, однако отрицательные значения pH, также как и значения pH больше 14 вполне возможны.

Слабая кислота / слабое основание

Слабые кислоты и основания только частично диссоциируют в воде. Это усложняет вычисление pH. Хотя формула остается такой же: , для вычисления концентрации ионов [H+] понадобится еще константа диссоциации.

Формула константы диссоциации кислоты Ka:

$K_a =frac{[H^+][B^-]}{[HB]}$

где:
[H^+] – концентрация ионов H+
[B^-] – концентрация анионов
[HB] – концентрация недиссоциированного соединения
для реакции

Эта формула описывает состояние равновесия. Чтобы найти H+, составим следующую таблицу изменения концентрации. В таблице обозначим искомую концентрацию H+ как x:

	HB	H+	B-
Начальная концентрация	C M	0 M	0 M
Изменение концентрации	-x M	+x M	+x M
Концентрация в состоянии равновесия	(C-x) M	x M	x M

Используем эти величины в формуле для Ka:

$K_a =frac{x cdot x}{(C - x)}$

Получим квадратное уравнение:

$x^2 - K_a(C - x) = 0 \ x^2 + K_ax - K_aC = 0$

Решаем его, выбрав положительный корень. После чего найденное значение можно подставить в формулу pH.

Тот же самый способ применим и к растворам оснований, только используется константа диссоциации основания и сначала рассчитывается pOH.

Обычно константы диссоциации даны в условии задачи, либо их можно посмотреть в таблице для известных соединений.

Стоит заметить, что в таблицах для некоторых кислот указывается несколько значений Ka. Это многоосновные кислоты, которые могут отдать в раствор более чем один протон. Однако, из-за молекулярных сил, значение Ka для каждого следующего протона уменьшается на несколько порядков.

Например, для фосфорной кислоты:
$K_1 = 7.2 cdot 10^{-3} \ K_2 = 6.3 cdot 10^{-8} \ K_3 = 4.6 cdot 10^{-13}$

Поэтому в задачах обычно рассматривается отдача только одного протона, и для всех вычислений можно использовать стохиометрический коэффициент равный 1.

Источник

Советы

Об этой статье

Была ли эта статья полезной?

Расчет рН растворов сильных и слабых электролитов

Сильные электролиты

Константы диссоциации слабых кислот и оснований при 25 оС

References

About This Article

Reader Success Stories

Did this article help you?

Как правильно рассчитать рН растворов сильных и слабых электролитов

а) Расчет рН растворов: 0,1 М HCl, 0,1 М CH3COOH

1. рассчитаем рН раствора 0,1 М HCl

2. рассчитаем рН раствора 0,1 М CH3COOH

б) Расчет рН растворов, содержащих 7 г/дм3 HCl и 7 г/дм3 CH3COOH

2. Рассчитаем рН раствора CH3COOH

Расчет pH в растворах сильных кислот и оснований

Расчет pH в растворах слабых кислот и оснований

pH раствора

Сильная кислота / Сильное основание

Слабая кислота / слабое основание

Вам также может понравиться

Как исправить электронный больничный лист если заполнен неправильно медучреждением

Не начислялись налоги как исправить

Как найти массу уксусного альдегида

Добавить комментарий Отменить ответ

а) Расчет рН растворов: 0,1 М HCl, 0,1 М CH₃COOH

2. рассчитаем рН раствора 0,1 М CH₃COOH

б) Расчет рН растворов, содержащих 7 г/дм³ HCl и 7 г/дм³ CH₃COOH

2. Рассчитаем рН раствора CH₃COOH