
 Решение задач по теме «Давление. Закон Паскаля»
Решение задач по теме «Давление. Закон Паскаля»
Закон Паскаля:
1.
Давление, производимое на
жидкость или газ, передаётся в любую точку одинаково во всех направлениях.
2.
Газы и жидкости передают производимое на
них давление во все стороны одинаково.
Задача 1.
Какое давление
оказывает на грунт гранитовая колонна объемом 6
м3 , если площадь основания ее 1,5
м2. Плотность гранита 2600 ![]() .
.
Дано: Решение:
![]()
![]()
![]() = 2600
= 2600![]() m= · V =2600
m= · V =2600![]()
V = 6
м3 F = P = mg = 15600
кг ·10 ![]() = 156 000 Н
= 156 000 Н
![]() S =1,5 м2
S =1,5 м2
р=![]() =
=![]()
р
-? Ответ: 104
кПа
Задача 2.
Чему равно давление
на рельсы четырехосного вагона массой 60 т, если площадь соприкосновения одного
колеса с рельсами 10 см2.
![]()
![]() Дано:
Дано:
СИ Решение: N– число колес
m=60 т= 60 000кг
S=N· S1= 8·0,001 м2=0,008 м2– площадь всех колес =
площадь одного колеса S1 =10 cм2 =0,001м2 умножить
на число колес
N=8 F = P = mg = 60
000 кг ·10 ![]() = 600 000 Н
= 600 000 Н
p-? ![]() р=
р=![]() =
=![]()
Ответ: 75000 кПа
Задача 3.
Мальчик стоит на лыжах. Его масса 45
кг. Длина каждой лыжи 1,5 м, ширина 10
см. Какое давление он оказывает на снег?
![]()
![]() Дано:
Дано:
СИ Решение: N– число лыж
m=45 кг S1 = а ·b = 1,5
м ·0,1 м = 0,15 м2-площадь одной лыжи
а =1,5 м
S = N· S1 = 2 ·0,15 м2 = 0,3
м2 -площадь двух лыж = площадь одной лыжи
b =10cм = 0,1 м умножить на число лыж
![]() N=2 F = P = mg = 45
N=2 F = P = mg = 45
кг ·10 ![]() = 450 Н
= 450 Н
p-? р=![]() =
=![]()
Ответ: 1,5 кПа
Самостоятельная работа
|
Вариант |
Вариант |
|
1.Охотник стоит |
1. Охотник стоит |
|
2. Какое давление оказывает на грунт гранитовая колонна |
2. Какое давление оказывает на грунт гранитовая колонна |

 Решение задач по теме «Давление. Закон Паскаля»
Решение задач по теме «Давление. Закон Паскаля»
давление =![]()
р=![]() – давление
– давление
Чтобы определить давление, надо силу,
действующую перпендикулярно поверхности, разделить на площадь поверхности.
![]() =
=![]() =Па – паскаль-единица
=Па – паскаль-единица
давления
F = pS -сила S= ![]() -площадь
-площадь
Закон
Паскаля:
1.
Давление, производимое на
жидкость или газ, передаётся в любую точку одинаково во всех направлениях.
2.
Газы и
жидкости передают производимое на них давление во все стороны одинаково.
Давление
газа зависит:
- от объема (при
уменьшении объема газа его давление увеличивается) - от температуры (чем выше
температура, тем быстрее движутся молекулы газа, и сильнее и чаще
ударяются о стенки сосуда, тем больше давление)
Задача 1.
Спортсмен,
масса которого 80 кг, скользит на коньках. Какое давление он оказывает на лед,
если длина одного конька 40 см, а ширина его лезвия 3
мм?
![]()
![]() Дано:
Дано:
СИ Решение: N=1, так как коньковый ход
на одной ноге
m= 80
кг S1 = а ·b = 0,4
м ·0,003 м = 0,0012 м2-площадь одного конька
а =40 см
=0,4м F = P = mg = 80 кг ·10 ![]() = 800
= 800
Н
b = 3мм = 0,003
м
p-? р=![]() =
=![]()
Ответ: 666,7 кПа
 Задача 2. ,
Задача 2. ,
В сосуде под поршнем находится газ. Поршень
переместили из положения А в положение В. Одинаково ли увеличилось при этом
давление газа на стенки сосуда в точках 1,2,3,4,5?
Решение:
По закону Паскаля газы
передают производимое на них давление во все стороны одинаково. Давление газа в
точках 1,2,3,4,5 одинаково увеличилось.
Самостоятельная работа
|
Вариант |
Вариант |
|
1. Забавляясь, |
1. Если |
|
2. Человек стоит |
2. Человек стоит |
|
3. Как изменится |
3. Как изменится |
Данная тема посвящена решению задач на давление твердых тел,
жидкостей и газов, а также задач с применением закона Паскаля.
Задача 1. В четыре сосуда, вертикальные сечения
которых показаны на рисунке, налита вода. Одна клеточка на рисунке
соответствует 10 см. В каком из этих сосудов гидростатическое давление на дно
максимально и чему оно равно?
РЕШЕНИЕ
Гидростатическое давление — это давление
неподвижной жидкости, обусловленное ее весом.
Как видно из формулы, давление жидкости на дно сосуда не
зависит от его формы, а определяется только высотой уровня жидкости и ее
плотностью.
Так как во всех четырех сосудах находится вода, то
гидростатическое давление будет определяться только высотой ее столба в сосуде.
Как видно из рисунка, самый высокий уровень воды в третьем сосуде — 5 клеточек,
то есть пятьдесят сантиметров. Следовательно, в этом сосуде давление на дно
будет максимальным.
ОТВЕТ: гидростатическое давление максимальное в сосуде
№3 и равно 5 кПа.
Задача 2. Однородный кубик с ребром 10 см и плотностью
2500 кг/м3 лежит на дне сосуда с водой, высота уровня которой над
верхней гранью кубика равна 20 см. Атмосферное давление равно 100 кПа.
Определите силу давления кубика на дно сосуда. Считать, что вода под кубик не
подтекает.
Задача 3. Самолет совершает «мертвую петлю» радиусом
500 м со скоростью 792 км/ч. Определите давление бензина на дно бака,
заполненного до высоты 1 м, в верхней точке «мертвой петли».
Задача 4. В двух сообщающихся сосудах разного диаметра
находится вода. В широкий сосуд налили слой масла высотой 7 см, а в узкий
— слой бензина высотой 15 см. Определите разность уровней воды в сосудах.
Задача 5. Резиновая камера заполнена ртутью и
соединена со стеклянной трубкой так, как показано на рисунке. На камеру
положили доску массой 0,5 кг и гирю массой 12 кг. Определите высоту столба
ртути в трубке, если площадь доски равна 50 см2.
Задача 6. Малый поршень гидравлического пресса за один
ход опускается на 0,9 м, а большой поршень поднимается на 0,01 м. С какой силой
действуют на малый поршень пресса, если пресс действует на зажатое в нем тело с
силой 100 кН?
«Доводы, до которых человек
додумывается сам,
обычно убеждают его больше, нежели те,
которые пришли в голову другим»
Блез Паскаль
Задачи на давление жидкостей и газов
с ответами и решениями
Формулы, используемые на уроках «Задачи на давление жидкостей и газов».
Название величины |
Обозначение |
Единица измерения |
Формула |
Высота столба жидкости |
h |
м |
h = p / (pg) |
Плотность жидкости |
р |
кг/м3 |
p = p / (gh) |
Давление |
р |
Па |
p = pgh |
Постоянная |
g ≈ 10 или 9,8 или 9,81(зависит от условия задачи) |
Н/кг
|
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1.
Определить давление бензина на дно цистерны, если высота столба бензина 2,4 м, а его плотность 710 кг/м3.
ОТВЕТ: 17,04 кПа.

Задача № 2.
Какая жидкость находится в сосуде, если столб высотой 0,3 м оказывает давление 5400 Па ?
ОТВЕТ: Серная кислота (1800 кг/м3).

Задача № 3.
Плотность спирта 800 кг/м3. Какова будет высота столба спирта при давлении 2,4 кПа?
ОТВЕТ: 0,3 м. Чтобы увидеть решение, нажмите на спойлер ниже.
Смотреть РЕШЕНИЕ задачи в тетради

Задача № 4.
В цилиндре с маслом на поршень действует сила 40 Н. Чему равна сила давления на внутреннюю поверхность цилиндра площадью 8 дм2? Площадь поршня 2,5 см2. Вес масла не учитывайте.
ОТВЕТ: 12,8 кН.
Смотреть РЕШЕНИЕ задачи в тетради

Задача № 5.
Вычислите давление и силу давления керосина на дно бака площадью 50 дм2, если высота столба керосина в баке 40 см.
ОТВЕТ: 3200 Па; 1600 Н.
Смотреть РЕШЕНИЕ задачи в тетради

Задача № 6.
В мензурку, площадь дна которой 20 см2, налита вода до высоты 10 см. Сколько граммов воды налито? Чему равно давление воды на дно мензурки?
ОТВЕТ:
Смотреть РЕШЕНИЕ задачи в тетради

Задача № 7.
Рыба камбала находится на глубине 1200 м и имеет площадь поверхности 560 см2. С какой силой она сдавливается водой?
ОТВЕТ: 678 кН.
Смотреть РЕШЕНИЕ задачи в тетради

Задача № 8.
На какой глубине давление воды в море равно 412 кПа?
ОТВЕТ: 40 м.
Смотреть РЕШЕНИЕ задачи в тетради

Задача № 9.
Поршневой насос может произвести давление 5 • 105 Па. На какую высоту можно поднять воду этим насосом?
ОТВЕТ: 51 м.
Смотреть РЕШЕНИЕ задачи в тетради

Задача № 10.
В сталелитейном производстве «изложницей» называется чугунный стакан без дна, в который выливают расплавленный металл. Верхнее отверстие изложницы немного меньше нижнего для того, чтобы можно было изложницу снять с отвердевшего слитка, когда остынет металл. Чтобы металл снизу не выливался, изложницы ставят на плоское основание и делают их очень массивными. На рисунке слева изображена изложница, справа — подъем изложницы с отлитого слитка. Определите силу давления, которую производит на подложку изложницы налитый чугун, если высота изложницы 1,5 м, а площадь нижнего основания 1600 см2. Плотность чугуна 7000 кг/м3.
ОТВЕТ: 17 кН.
Смотреть РЕШЕНИЕ задачи в тетради

Задача № 11.
Как велика должна быть высота столба ртути и столба спирта, если этот столб производит давление в 105 Па?
ОТВЕТ: ртути — 75 см, спирта — 12,76 см.
Смотреть РЕШЕНИЕ задачи в тетради

Задача № 12.
Батискаф опустился в море на глубину 50 м. Каково давление на поверхность батискафа на данной глубине? (Плотность морской воды 1010 кг/м3.)
ОТВЕТ: 606 кПа.
Смотреть РЕШЕНИЕ задачи в тетради

Задача № 13.
Человек стоит на кожаном мешке с водой. Рассчитайте, на какую высоту поднимается вода в трубке, если масса человека 75 кг, площадь соприкасающейся с мешком поверхности платформы 1000 см2.
ОТВЕТ: 0,75 м.
Смотреть РЕШЕНИЕ задачи в тетради

Задача № 14 (повышенной сложности).
Брусок массой m = 2 кг имеет форму параллелепипеда. Лежа на одной из граней, он оказывает давление p1 = 1 кПа, лежа на другой — давление 2 кПа, стоя на третьей — давление 4 кПа. Каковы размеры бруска?
ОТВЕТ: 5 см, 10 см, 20 см.
Указание к РЕШЕНИЮ. Обозначим размеры бруска а, b, с, где а > b > с. Тогда из условия следует, что b = а/2, с = а/4, p1 = mg/(ab) = 2mg/a2. Отсюда , а = 20 см, b = 10 см, c = 5 см.
Задача № 15 (олимпиадный уровень).
Оцените массу атмосферы Земли (радиус Земли R = 6400 км)
ОТВЕТ: примерно 5 • 1018 кг.
Указание к РЕШЕНИЮ. Вес атмосферы равен силе давления воздуха на всю поверхность Земли, площадь которой S = 4πR2. Следовательно, mg = ра • 4πR2, где ра = 105 Па — атмосферное давление. Отсюда m = 4πR2 ра /g = 5 • 1018 кг. Эта величина составляет менее одной миллионной части полной массы нашей планеты. Такая простая оценка массы атмосферы возможна потому, что основная часть атмосферы сосредоточена на высотах, малых по сравнению с радиусом Земли. Поэтому можно считать, что вес атмосферы равен mg, где g — ускорение свободного падения вблизи поверхности Земли.
Краткая теория по теме «Задачи на давление жидкостей»
Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = ратм + p*g*h
Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.

Вы смотрели конспект урока «Задачи на Давление жидкостей с ответами и решениями». Выберите дальнейшие действия:
- Перейти к теме: ЗАДАЧИ на Давление твердых тел с ответами и решениями.
- Перейти к теме: ЗАДАЧИ на Сообщающиеся сосуды и гидравлический пресс с решениями.
- Вернуться к Списку конспектов по физике для 7-11 классов
- Найти конспект через Кодификатор ОГЭ по физике
- Найти конспект через Кодификатор ЕГЭ по физике
Давление жидкостей и газов. Закон Паскаля
- Особенности давления жидкостей и газов
- Закон Паскаля
- Давление столба жидкости
- Давление столба газа
- Задачи
п.1. Особенности давления жидкостей и газов
Давление жидкостей и газов отличается от давления твердых тел. Причина – в особенностях поведения частиц вещества в разных агрегатных состояниях (см. §16 данного справочника).
В отличие от твердых тел, молекулы жидкостей и газов подвижны.
Жидкость принимает форму сосуда, который предохраняет её от растекания. Поэтому жидкость в сосуде оказывает давление не только на дно, но и на стенки. Верхние слои жидкости давят на нижние, и давление растет с глубиной (с увеличением столба жидкости).
Газ заполняет весь предоставленный ему объем. В закрытом сосуде хаотически движущиеся молекулы газа будут сталкиваться с дном, стенками и крышкой сосуда. Таким образом, газ будет оказывать давление во все стороны: вниз, по бокам и даже вверх.
Давление газа также растет с увеличением высоты столба. Однако за счет малой плотности газов этот рост менее заметен по сравнению с жидкостями. В небольшом сосуде давление газа можно считать постоянным во всем объеме сосуда.
п.2. Закон Паскаля
При давлении на жидкость или газ в определенной области происходит сжатие; расстояние между молекулами становится меньше, начинают сильнее действовать силы отталкивания. В результате молекулы перемещаются из области сжатия с большим давлением в области с меньшим давлением. Это происходит достаточно быстро; например, у кислорода при 0°С средняя скорость молекул 425 м/с, у паров воды – 570 м/с. Поэтому в течение небольшого времени давление в сосуде выравнивается.
Закон Паскаля
Жидкости и газы передают давление по всем направлениям одинаково.
Для подтверждения закона Паскаля можно провести следующие эксперименты.
п.3. Давление столба жидкости
Как было замечено выше, давление жидкостей заметно увеличивается с глубиной. Это объясняется тем, что верхние слои давят на нижние.
Найдем давление столба жидкости высотой (h)
Согласно закону Паскаля, давление в жидкости передается во всех направлениях одинаково. Поэтому на данной глубине (h) в каждой точке уровня давление будет постоянно.
 |
Рассмотрим сосуд в форме прямоугольного параллелепипеда. Пусть в его основании – прямоугольник с длиной (a) и шириной (b). Нальем в этот сосуд воду до отметки высотой (h). Нас интересует давление воды на дно сосуда. Сила давления на дно направлена вертикально вниз и равна силе тяжести: $$ F=mg=rho Vg $$ Объем воды в сосуде: $$ V=abh $$ |
Получаем: $$ F=rhocdot abhcdot g $$ Давление на дно сосуда равно отношению силы давления к площади дна: $$ p=frac FS=frac{rhocdot abh cdot g}{ab}=rho gh $$
Давление столба жидкости
На глубине (h) давление жидкости равно $$ p=rho gh $$
Давление не зависит от площади дна, и, следовательно, не зависит от его формы.
Полученное выражение будет справедливо для вертикального столба жидкости высотой (h) с любым сечением (квадратным, круглым, треугольным, совершенно фантазийным).
Это интересно
 |
Давление не зависит ни от формы, ни от размеров сечения столба жидкости, зато резко увеличивается с высотой. Это свойство использовал Паскаль, продемонстрировав своим современникам забавный эксперимент. Он взял прочную дубовую бочку, наполнил ее доверху водой, плотно закрыл и вставил очень узкую, но очень длинную трубку (около 4 м). Затем он поднялся на второй этаж и вылил в трубку кружку воды. Бочка тут же …лопнула. Действительно, ведь давление в бочке увеличилось на (p=1000cdot 10cdot 4=40 text{кПа}): её будто «придавило» четырьмя тоннами воды, хотя понадобилась всего лишь кружка. Тем не менее, результат этого фокуса всегда кажется неожиданным. |
п.4. Давление столба газа
Газы, как и жидкости, также имеют некоторую плотность. Поэтому, рассматривая давление столба газа по аналогии с жидкостью, можно прийти к тем же результатам.
Давление столба газа
Давление столба газа высотой (h) равно $$ p=rho gh $$
Понимание того, что газ также оказывает разное давление в разных слоях, возникло не сразу. Это объясняется небольшой плотностью газов по сравнению с жидкостями.
 |
Для иллюстрации рассчитаем давление столба воды и столба воздуха высотой (h=1 text{м}). Плотность воды (rho_text{воды}=1000 text{кг/м}^3), плотность воздуха при 20°C (rho_text{возд}=1,2 text{кг/м}^3). Получаем: begin{gather*} p_text{вода}= rho_text{вода}ghapprox 1000cdot 10cdot 1=10000 (text{Па})\[7pt] p_text{возд}= rho_text{возд}ghapprox 1,2cdot 10cdot 1=12 (text{Па}) end{gather*} Из-за разности в плотности, давление отличается почти в 1000 раз, ведь масса кубометра воды – 1 тонна, а масса кубометра воздуха – всего 1,2 кг. |
Поэтому при изучении процессов в небольших сосудах разность в давлении газа в верхних и нижних слоях практически не заметна.
С другой стороны, если рассматривать значительные по высоте «столбы» газов, например, атмосферу планеты, давление становится существенной величиной. Так, на поверхности Земли атмосферное давление составляет около 100 000 (Па). Подробней этот вопрос будет рассмотрен в §31 данного справочника.
В итоге, для открытого сосуда с жидкостью, где на поверхность дополнительно оказывает давление атмосфера, давление жидкости на глубине h равно сумме: $$ p=p_text{атм}+rho gh $$
п.5. Задачи
Задача 1. Пятый этаж расположен выше первого на 15 м.
На каком этаже давление в трубах водопровода больше и на сколько?
Дано:
(h=15 text{м})
(p=1000 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(Delta p-?)
Давление в водопроводе на первом этаже $$ p_1=p_text{внеш}+rho gh, $$ где (p_text{внеш}) – давление, связанное с действием внешних сил (атмосфера, водонапорная башня, насос и т.п.), второе слагаемое – давление вертикального столба жидкости в трубе в доме.
Давление в водопроводе на пятом этаже (p_5=p_text{внеш}).
Давление больше на первом этаже.
Разность давлений $$ Delta p=p_1-p_5= p_text{внеш}+rho gh -p_text{внеш}=rho gh $$ Получаем: $$ Delta p=1000cdot 10cdot 15=150 000 (text{Па})=150 (text{кПа}) $$ Ответ: на первом; на 150 кПа
Задача 2. Давление в трубах водопровода (4cdot 10^5 text{Па}). На какую максимальную высоту можно достать струей воды в случае пожара, если подключить оборудование к пожарному гидранту на поверхности земли? Атмосферное давление примите равным (1cdot 10^5 text{Па})
Дано:
(p=4cdot 10^5 text{Па})
(p_text{атм}=1cdot 10^5 text{Па})
(p=1000 text{кг/м}^3)
(gapprox 10 text{м/с}^2)
__________________
(h-?)
При подключении на струю воды, направленную вертикально вверх, будет действовать снизу давление водопровода, сверху атмосферное давление.
Под действием разности этих давлений вода может подняться на высоту $$ h=frac{p-p_text{атм}}{rho g} $$ Получаем: $$ h=frac{(4-1)cdot 10^5}{1000cdot 10}=30 (text{м}) $$ Ответ: 30 м
Задача 3. Рассчитайте, какую силу давления воды должен выдерживать жесткий водолазный скафандр, предназначенный для глубоководных работ на глубине до 365 м, если общая поверхность скафандра составляет 2,5 м2?
(Плотность морской воды 1010 кг/м3, g=9,8 м/с2). Ответ округлите до меганьютонов.
Дано:
(rho=1010 text{кг/м}^3)
(g=9,8 text{м/с}^2)
(h=365 text{м})
(S=2,5 text{м}^2)
__________________
(F-?)
Давление воды на максимальной глубине $$ p=rho gh $$ Сила давления $$ F=pS=rho ghS $$ Получаем: $$ F=1010cdot 9,8cdot 365cdot 2,5approx 9,03cdot 10^6 (text{Н})=9 (text{МН}) $$ Ответ: ≈9 МН
Задача 4*. В цилиндрический сосуд налиты ртуть и вода. Общая высота столба жидкости 20 см. Чему равно давление, создаваемое жидкостями на дно сосуда, если:
а) объемы жидкостей одинаковы; б массы жидкостей одинаковы?
Дано:
(rho_1=1000 text{кг/м}^3)
(rho_2=13600 text{кг/м}^3)
(H=20 text{см}=0,2 text{м})
(gapprox 10 text{м/с}^2)
(text{а)} V_1=V_2; text{б)} m_1=m_2)
__________________
(p-?)
Ответ: а) 14,6 кПа; б) 3,7 кПа
Закон Паскаля для жидкостей и газов, теория и онлайн калькуляторы
Закон Паскаля для жидкостей и газов
Жидкости и газы передают давление, которое оказывается на них, по всем направлениям одинаково.
Данный закон был открыт в середине XIV века французским ученым Б. Паскалем и получил впоследствии его имя.
То, что жидкости и газы передают давление, объясняют большой подвижностью частиц, из которых они составлены, это существенным образом отличает их от твёрдых, тел, чьи частицы малоподвижны, и могут только совершать колебания около положений своего равновесия. Допустим, газ, находится в замкнутом сосуде с поршнем, его молекулы равномерно заполняют весь предоставленный ему объем. Передвинем поршень, уменьшив объем сосуда, слой газа, прилегающий к поршню, сожмется, молекулы газа будут располагаться плотнее, чем на некотором удалении от поршня. Но через некоторое время частицы газа, участвуя в хаотичном движении, перемешаются с другими частицами, плотность газа выровняется, но станет больше, чем до передвижения поршня. При этом количество ударов о дно и стенки сосуда возрастает, следовательно, давление поршня передается газом во всех направлениях одинаково и в каждой точке увеличивается на одну и ту же величину. Аналогичные рассуждения можно отнести к жидкости.
Формулировка закона Паскаля
Давление, производимое внешними силами на жидкость (газ), находящуюся в состоянии покоя, передается веществом во все стороны без изменения к любой точке жидкости (газа) и стенкам сосуда.
Закон Паскаля выполняется для несжимаемых и сжимаемых жидкостей и газов, если сжимаемостью пренебрегают. Этот закон – следствие закона сохранения энергии.
Гидростатическое давление жидкостей и газов
Жидкости и газы передают не только внешнее давление, но и давление, которое возникает благодаря существованию силы тяжести. Эта сила создает внутри жидкости (газа) давление, которое зависит от глубины погружения, при этом приложенные внешние силы увеличивают это давление в любой точке вещества на одну и ту же величину.
Давление, которое оказывает покоящаяся жидкость (газ), называют гидростатическим. Гидростатическое давление ($p$) на любой глубине внутри жидкости (газа) не зависит от формы сосуда, в котором она (он) находится и равно:
[p=rho gh left(1right),]
где $h$ – высота столба жидкости (газа); $rho $ – плотность вещества. Из формулы (1) для гидростатического давления следует, что во всех местах жидкости (газа), которые находятся на одной глубине, давление одно и то же. С увеличением глубины гидростатическое давление растет. Так, на глубине 10 км давление воды составляет приблизительно ${10}^8Па$.
Следствие закона Паскаля: давление в любой точке на одном горизонтальном уровне жидкости (газа), находящейся в состоянии равновесия имеет одну и ту же величину.
Примеры задач с решением
Пример 1
Задание. Даны три сосуда разной формы (рис.1). Площадь дна каждого сосуда равна $S$. В каком из сосудов давление одной и той же жидкости на дно наибольшее?
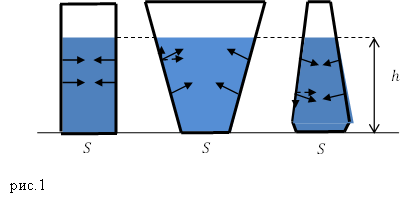
Решение. В данной задаче речь идет о гидростатическом парадоксе. Следствием закона Паскаля является то, что давление жидкости не зависит от формы сосуда, а определено высотой столба жидкости. Так как по условию задачи площадь дна каждого сосуда равна S, из рис.1 видим, что высота столбов жидкости одинакова, несмотря на разный вес жидкости, сила «весового» давления на дно во всех сосудах одинакова и равна весу жидкости в цилиндрическом сосуде. Объяснение этого парадокса заключено в том, что сила давления жидкости на наклонные стенки имеет вертикальную составляющую, которая направлена вниз в сужающемся к верху сосуде и направленную вверх в расширяющемся.
Пример 2
Задание. На рис.2 изображены два сообщающихся сосуда с жидкостью. Поперечное сечение одного из сосудов в $n $ раз меньше, чем второго. Сосуды закрыты поршнями. К малому поршню прикладывают силу $F_2. $Какой силой надо подействовать на большой поршень, чтобы система находилась в состоянии равновесия?
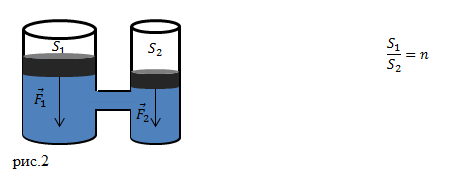
Решение. В задаче представлена схема гидравлического пресса, который работает на основе закона Паскаля. Давление, которое создает на жидкость первый поршень, равен:
[p_1=frac{F_1}{S_1}left(2.1right).]
Второй поршень оказывает на жидкость давление:
[p_2=frac{F_2}{S_2}left(2.2right).]
Если система находится в равновесии, $p_1$ и $p_2$ равны, запишем:
[frac{F_1}{S_1}=frac{F_2}{S_2}left(2.3right).]
Найдем модуль силы, приложенной к большому поршню:
[F_1=F_2frac{S_1}{S_2}=nF_{2.}]
Ответ. $F_1=nF_{2}$
Читать дальше: линейная скорость вращения.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
