В данной публикации мы рассмотрим, как можно вычислить площадь поверхности различных видов правильных пирамид: треугольной, четырехугольной и шестиугольной.
Правильная пирамида – это пирамида, вершина которой проецируется в центр основания, являющегося правильным многоугольником.
-
Формула площади правильной пирамиды
- 1. Общая формула
-
2. Площадь правильной треугольной пирамиды
- 3. Площадь правильной четырехугольной пирамиды
- 4. Площадь правильной шестиугольной пирамиды
Формула площади правильной пирамиды
1. Общая формула
Площадь (S) полной поверхности пирамиды равняется сумме площади ее боковой поверхности и основания.
Sполн. = Sбок. + Sосн.
Боковой гранью правильной пирамиды является равнобедренный треугольник.
Площадь треугольника вычисляется по формулам:
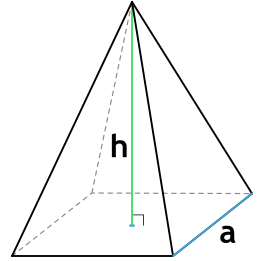
1. Через длину основания (a) и высоту (h):
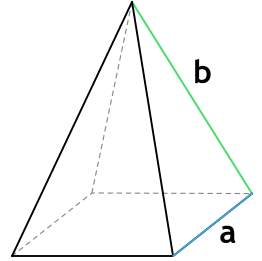
2. Через основание (a) и боковую сторону (b):
Формула площади основания правильной пирамиды зависит от вида многогранника. Далее мы рассмотрим самые популярные варианты.
2. Площадь правильной треугольной пирамиды
Основание: равносторонний треугольник.
L (апофема) – перпендикулярная линия, опущенная из вершины пирамиды на ребро основания. Т.е. апофема пирамиды является высотой (h) ее боковой грани.
3. Площадь правильной четырехугольной пирамиды
Основание: квадрат.
| Площадь | Формула |
| основание | Sосн. = a2 |
| боковая поверхность | Sбок. = 2aL |
 |
|
| полная | Sполн. = a2 + 2aL |
 |
microexcel.ru
4. Площадь правильной шестиугольной пирамиды
Основание: правильный шестиугольник

{S_{полн} = dfrac{1}{2}PL + S}
На странице вы найдете онлайн-калькуляторы, которые помогут найти площадь полной и боковой поверхности правильной пирамиды, а также треугольной, четырехугольной и шестиугольной пирамиды. Кроме того приводятся формулы, по которым вы можете произвести расчет самостоятельно.
- калькулятор площади поверхности пирамиды
- формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
- формула площади полной поверхности правильной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и боковую грань
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону и высоту
- формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной пирамиды через периметр и апофему
- формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
- формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
- примеры задач
Познакомьтесь с важными понятиями, которые необходимо знать для расчета площади поверхности пирамиды.
Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.
Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.
Площадь полной поверхности пирамиды – это сумма площадей боковых граней и площади основания.
Площадь боковой поверхности пирамиды – это совокупная площадь всех боковых граней пирамиды.
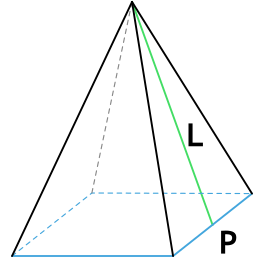
Апофема — перпендикуляр, опущенный из вершины пирамиды на ребро основания.
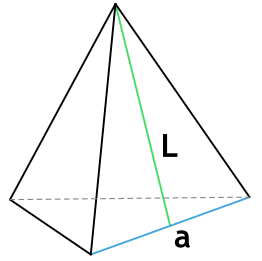
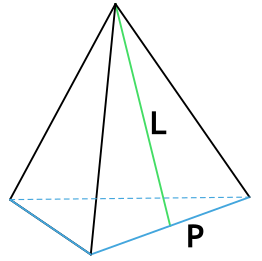
Формула площади полной поверхности правильной пирамиды через периметр, площадь и апофему
{S_{полн} = dfrac{1}{2}PL+S}
P – периметр основания пирамиды
L – апофема пирамиды
S – площадь основания пирамиды
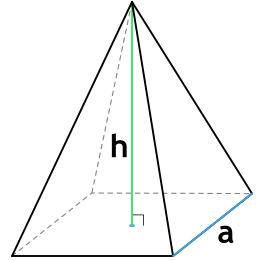
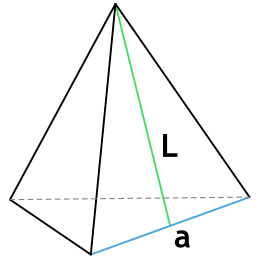
Формула площади полной поверхности правильной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{na}{2} {Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} + sqrt{h^2+ Bigg( dfrac{a}{2 \tg ( dfrac{180°}{n})} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
n – число сторон основания
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{a^2 sqrt{3}+6aL}{4}}
a – сторона основания пирамиды
L – апофема пирамиды
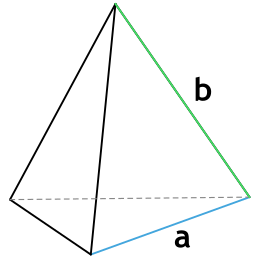
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{a^2 sqrt{3}+6a sqrt{b^2 – dfrac{a^2}{4}}}{4}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади полной поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{полн} = dfrac{3a}{2} {Bigg( dfrac{a}{2 tg ( 60°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{полн} = 2a {Bigg( dfrac{a}{2 tg ( 45°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
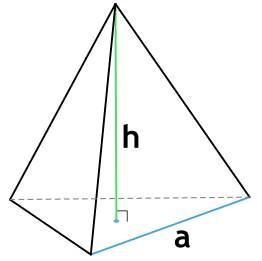
Формула площади полной поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{полн} = a^2+2aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{полн} = dfrac{3sqrt{3}a^2}{2}+3asqrt{b^2-dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади полной поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{полн} = 3a {Bigg( dfrac{a}{2 tg ( 30°)} + sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2} Bigg)}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади боковой поверхности правильной пирамиды через периметр и апофему
{S_{бок} = dfrac{1}{2}PL}
P – периметр основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{na}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( dfrac{180°}{n})} Bigg) ^2} }
a – сторона основания пирамиды
h – высота пирамиды
n – число сторон основания
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и апофему
{S_{бок} = dfrac{3}{2}aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и боковую грань
{S_{бок} = dfrac{3a sqrt{b^2 – dfrac{a^2}{4}}}{2}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через сторону основания и высоту
{S_{бок} = dfrac{3a}{2} sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 60°)} Bigg) ^2}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади боковой поверхности правильной треугольной пирамиды через периметр основания и апофему
{S_{бок} =dfrac{1}{2}PL}
P – периметр основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и апофему
{S_{бок} = 2aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 2a sqrt{b^2 – dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади боковой поверхности правильной четырехугольной пирамиды через сторону основания и высоту
{S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2}}
a – сторона основания пирамиды
h – высота пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и апофему
{S_{бок} = 3aL}
a – сторона основания пирамиды
L – апофема пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и боковую грань
{S_{бок} = 3asqrt{b^2-dfrac{a^2}{4}}}
a – сторона основания пирамиды
b – боковая грань пирамиды
Формула площади боковой поверхности правильной шестиугольной пирамиды через сторону основания и высоту
{S_{бок} = 3a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 30°)} Bigg) ^2}}
a – сторона основания пирамиды
h – высота пирамиды
Примеры задач на нахождение площади поверхности пирамиды
Задача 1
Стороны основания правильной четырехугольной пирамиды равны 60см, боковые ребра равны 78см. Найдите площадь поверхности этой пирамиды.
Решение
Так как пирамида правильная четырехугольная, то воспользуемся соответствующей формулой площади поверхности через сторону основания и боковую грань.
S_{полн} = a^2 + 2a sqrt{b^2- dfrac{a^2}{4}} = 60^2 + 2 cdot 60 sqrt{78^2- dfrac{60^2}{4}} = 3600 + 120 sqrt{6084- dfrac{3600}{4}} = 3600 + 120 sqrt{6084 – 900} = 3600 + 120 sqrt{5184} = 3600 + 120 cdot 72 = 3600 + 8640 = 12240 : см²
Ответ: 12240 см²
Проверим полученный ответ с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной треугольной пирамиды со стороной 6см и апофемой 10см.
Решение
Из условия мы знаем апофему и сторону правильной треугольной пирамиды, поэтому нам потребуется эта формула.
S_{бок} = dfrac{3}{2}aL = dfrac{3}{2} cdot 6 cdot 10 = dfrac{3}{2} cdot 60 = 90 : см²
Ответ: 90 см²
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найти площадь боковой поверхности правильной четырехугольной пирамиды сторона основания 6см и высота 4см.
Решение
Подставим значения в формулу и произведем расчет.
S_{бок} = 2a sqrt{h^2+ Bigg( dfrac{a}{2 tg ( 45°)} Bigg) ^2} = 2 cdot 6 sqrt{4^2+ Bigg( dfrac{6}{2 tg ( 45°)} Bigg) ^2} = 60 : см²
Ответ: 60 см²
Проверка .
Способ 1
Требуется найти площадь боковой поверхности (displaystyle S_{бок}) правильной пирамиды. Эта площадь равна сумме площадей всех боковых граней.
Боковые грани правильной пирамиды – равные треугольники. Следовательно, площади боковых граней равны.
У правильной треугольной пирамиды три боковых грани. Значит,
(displaystyle S_{бок}=S_{грани}+S_{грани}+S_{грани}=3S_{грани}small. )
Вычислим (displaystyle S_{грани}small. )
(displaystyle S_{грани}=18)
Получаем:
(displaystyle S_{бок}=3 cdot S_{грани}=3cdot 18 = 54small. )
Способ 2
Воспользуемся формулой для вычисления площади боковой поверхности пирамиды.
Правило
Площадь боковой поверхности правильной пирамиды
Площадь боковой поверхности правильной пирамиды (displaystyle S_{бок} ) равна половине произведения периметра основания на апофему.
(displaystyle S_{бок}=frac{1}{2}P_{осн} cdot l{ small ,} )
где (displaystyle P_{осн} ) – периметр основания,
(displaystyle l) – апофема.
Периметр основания правильной треугольной пирамиды равен
(displaystyle P_{осн}=3cdot AC{small .})
(displaystyle l=SK=4 )
Подставим найденные значения (displaystyle P_{осн}) и (displaystyle l) в формулу для (displaystyle S_{бок}{small :})
(displaystyle S_{бок}=frac{1}{2}P_{осн} cdot l{ small ,} )
(displaystyle S_{бок}=frac{1}{2}cdot 3 cdot AC cdot SK{ small .} )
Подставим значения (displaystyle AC) и (displaystyle SK{small :})
(displaystyle S_{бок}=frac{1}{2}cdot 3 cdot 9 cdot 4=54{ small .})
Ответ: (displaystyle 54{small .})
Пирамида — это многогранник, в основании которого лежит многоугольник, а грани его являются треугольниками.
Онлайн-калькулятор площади поверхности пирамиды
Стоит остановиться на определении некоторых составляющих пирамиды.
У нее, как и у других многогранников, есть ребра. Они сходятся к одной точке, которая называется вершиной пирамиды. В ее основании может лежать произвольный многоугольник. Гранью называется геометрическая фигура, образованная одной из сторон основания и двумя ближайшими ребрами. В нашем случае это треугольник. Высотой пирамиды называется расстояние от плоскости, в которой лежит ее основание, до вершины многогранника. Для правильной пирамиды существует еще понятие апофемы – это перпендикуляр, опущенный из вершины пирамиды к её основанию.
Виды пирамид
Существуют 3 вида пирамид:
- Прямоугольная — та, у которой какое-либо ребро образует прямой угол с основанием.
- Правильная — у нее основание – правильная геометрическая фигура, а вершина самого многоугольника является проекцией центра основания.
- Тетраэдр — пирамида, составленная из треугольников. Причем каждый из них может быть принят за основание.
Формула площади поверхности пирамиды
Для нахождения полной площади поверхности пирамиды нужно сложить площадь боковой поверхности и площадь основания.
Самой простой является случай правильной пирамиды, поэтому нею мы и займемся. Вычислим полную площадь поверхности такой пирамиды. Площадь боковой поверхности равна:
Sбок=12⋅l⋅pS_{text{бок}}=frac{1}{2}cdot lcdot p
ll — апофема пирамиды;
pp — периметр основания пирамиды.
Полная площадь поверхности пирамиды:
S=Sбок+SоснS=S_{text{бок}}+S_{text{осн}}
SбокS_{text{бок}} — площадь боковой поверхности пирамиды;
SоснS_{text{осн}} — площадь основания пирамиды.
Пример решения задачи.
Найти полную площадь треугольной пирамиды, если её апофема равна 8 (см.), а в основании лежит равносторонний треугольник со стороной 3 (см.)
Решение
l=8l=8
a=3a=3
Найдем периметр основания. Так как в основании лежит равносторонний треугольник со стороной aa, то его периметр pp (сумма всех его сторон):
p=a+a+a=3⋅a=3⋅3=9p=a+a+a=3cdot a=3cdot 3=9
Тогда боковая площадь пирамиды:
Sбок=12⋅l⋅p=12⋅8⋅9=36S_{text{бок}}=frac{1}{2}cdot lcdot p=frac{1}{2}cdot 8cdot 9=36 (см. кв.)
Теперь найдем площадь основания пирамиды, то есть площадь треугольника. В нашем случае треугольник равносторонний и его площадь можно вычислить по формуле:
Sосн=3⋅a24S_{text{осн}}=frac{sqrt{3}cdot a^2}{4}
aa — сторона треугольника.
Получаем:
Sосн=3⋅a24=3⋅324≈3.9S_{text{осн}}=frac{sqrt{3}cdot a^2}{4}=frac{sqrt{3}cdot 3^2}{4}approx3.9 (см. кв.)
Полная площадь:
S=Sбок+Sосн≈36+3.9=39.9S=S_{text{бок}}+S_{text{осн}}approx36+3.9=39.9 (см. кв.)
Ответ: 39.9 см. кв.
Еще один пример, немного сложнее.
Основанием пирамиды является квадрат с площадью 36 (см. кв.). Апофема многогранника в 3 раза больше стороны основания aa. Найти полную площадь поверхности данной фигуры.
Решение
Sквад=36S_{text{квад}}=36
l=3⋅al=3cdot a
Найдем сторону основания, то есть сторону квадрата. Его площадь и длина стороны связанны:
Sквад=a2S_{text{квад}}=a^2
36=a236=a^2
a=6a=6
Найдем периметр основания пирамиды (то есть, периметр квадрата):
p=a+a+a+a=4⋅a=4⋅6=24p=a+a+a+a=4cdot a=4cdot 6=24
Найдем длину апофемы:
l=3⋅a=3⋅6=18l=3cdot a=3cdot 6=18
В нашем случае:
Sквад=SоснS_{text{квад}}=S_{text{осн}}
Осталось найти только площадь боковой поверхности. По формуле:
Sбок=12⋅l⋅p=12⋅18⋅24=216S_{text{бок}}=frac{1}{2}cdot lcdot p=frac{1}{2}cdot 18cdot 24=216 (см. кв.)
Полная площадь:
S=Sбок+Sосн=216+36=252S=S_{text{бок}}+S_{text{осн}}=216+36=252 (см. кв.)
Ответ: 252 см. кв.
Возникают трудности с тем, чтобы найти площадь поверхности пирамиды? У нас вы можете заказать контрольную работу по геометрии!
2023-04-05
В треугольной пирамиде $PABC$ с основанием $ABC$ известно, что $AB=13$, $PB=15$, $cosangle PBA=frac{48}{65}$. Основанием высоты этой пирамиды является точка $C$. Прямые $PA$ и $BC$ перпендикулярны.
а) Докажите, что треугольник $ABC$ прямоугольный.
б) Найдите объём пирамиды $PABC$.
Решение:
а) Поскольку $PC$ – перпендикуляр к плоскости $ABC$, сторона $AC$ основания пирамиды – ортогональная проекция наклонной $PA$ на эту плоскость, а т.к. $PAperp BC$, то по теореме о трёх перпендикулярах $ACperp BC$. Следовательно, треугольник $ABC$ прямоугольный с прямым углом при вершине $C$.
б) По теореме косинусов
$AP^{2}=PB^{2}+AB^{2}-2PBcdot ABcosangle PBA=225+169-2cdot15cdot13cdotfrac{48}{65}=106.$
Пусть $PH$ – высота треугольника $APB$. Из прямоугольного треугольника $PHB$ находим, что
$BH=PBcosangle PBA=15cdotfrac{48}{65}=frac{144}{13}.$
По теореме о трёх перпендикулярах $CH$ – высота прямоугольного треугольника $ABC$, проведённая из вершины прямого угла. Значит,
$BC=sqrt{BHcdot AB}=sqrt{frac{144}{13}cdot13}=12$
(см. задачу 6185).
По теореме Пифагора из прямоугольного треугольника $ABC$ находим, что $AC=5$. Тогда
$PC=sqrt{AP^{2}-AC^{2}}=sqrt{106-25}=sqrt{81}=9.$
Следовательно,
$V_{PABC}=frac{1}{3}S_{ABC}cdot PC=frac{1}{2}ACcdot BCcdot PC=frac{1}{2}cdot5cdot12cdot9=90.$