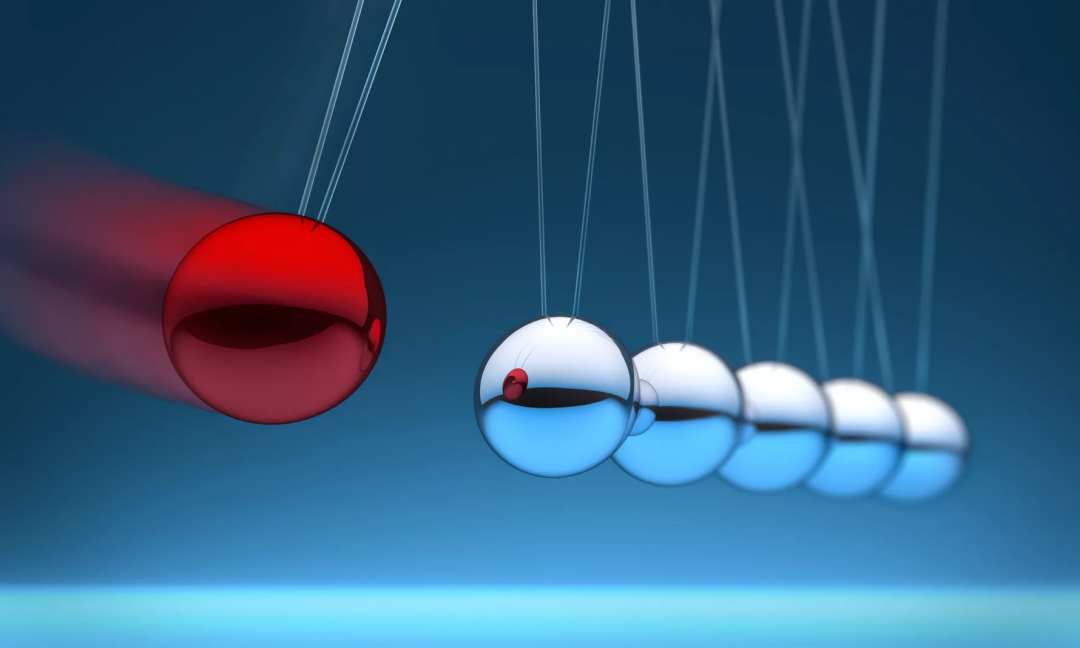
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой: |
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:
Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:
Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:
Подставим это выражение во второй закон Ньютона и получим:
Или:
F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:
Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:
Реактивная сила:
Второй закон Ньютона для ракеты:
Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:
Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
Отсюда ускорение равно:
Выразим формулу для скорости и сделаем вычисления:
Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:
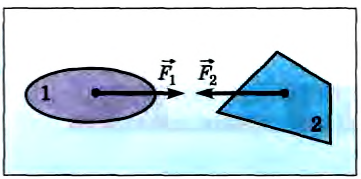
Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:
Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:
Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:
Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:
Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730

Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520

. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:
Сделаем чертеж:
Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:
Выразим массу груза:
Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 19.9k
В этой главе…
- Измеряем количество движения
- Вычисляем импульс
- Выясняем связь между силой и изменением импульса
- Разбираемся с законом сохранения импульса
- Знакомимся с разными типами столкновений
Эта глава посвящена понятиям, которые следует учитывать при изучении движения объектов, а именно с импульсом и моментом импульса. Оба эти понятия играют большую роль в двух разделах механики: кинематике, посвященной изучению движения объектов, и динамике, посвященной изучению взаимодействия объектов. Владея этими понятиями, можно легко описывать поведение объектов при столкновениях: с какой скоростью продолжат движение сталкивающиеся объекты (не хотелось бы, чтобы на их месте были ваш автомобиль или велосипед), в каком направлении продолжит движение теннисный мячик после столкновения с ракеткой, насколько глубоко дротик для игры в дартс вонзится в мишень и т.п. Чтобы получить ответы на эти и многие другие вопросы, нужно очень хорошо представлять себе, что такое импульс и момент импульса. Описанию именно этих понятий и посвящается данная глава.
Содержание
- Изучаем количество движения
- Получаем импульс
- Связываем работу силы и изменение импульса
- Пример: вычисляем импульс бильярдного шара
- Пример: определяем импульс капель дождя
- Изучаем закон сохранения импульса
- Измеряем скорость с помощью закона сохранения импульса
- Измеряем начальную скорость пули с помощью закона сохранения импульса
- Упругие и неупругие столкновения
- Когда сталкивающиеся объекты отскакивают друг от друга: упругие столкновения
- Когда сталкивающиеся объекты не отскакивают друг от друга: неупругие столкновения
- Упругие столкновение на прямой
- Упругое столкновение с более тяжелым объектом
- Упругое столкновение с более легким объектом
- Упругие столкновения в одной плоскости
Изучаем количество движения
В физике импульсом называется количество движения, которое приобретает тело под действием заданной силы за определенное время. Играя в бильярд, нетрудно убедиться в разнообразных проявлениях импульса. Чем сильнее и быстрее удар кия по шару, тем интенсивнее движется шар. Чем больше столкновений испытает шар, тем менее интенсивным становится его движение.
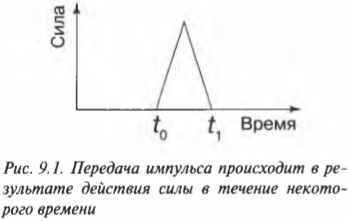
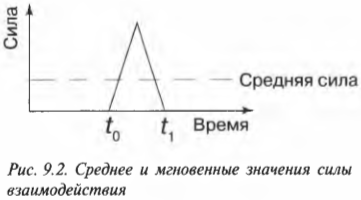
В повседневных ситуациях мы привыкли говорить, что тому или иному объекту или событию придают импульс. Рассмотрим процесс передачи импульса более подробно на примере бильярдного кия и шара. Процесс передачи импульса начинается в момент ( t_0 ) первого соприкосновения кия с шаром и заканчивается в момент ( t_1 ) утраты контакта между кием и шаром. В общем зависимость силы воздействия кия на шар от времени имеет сложный характер. Однако доя простоты можно положить, что она линейно возрастает от нулевого значения в момент ( t_0 ) первого соприкосновения, достигает максимального значения в момент наибольшего контакта, а потом снижается до нуля в момент ( t_1 ) утраты контакта между кием и шаром. Эта идеализированная зависимость силы взаимодействия кия и шара от времени графически показана на рис. 9.1.
Время взаимодействия кия и шара очень мало (несколько долей секунды), и зафиксировать характер изменения силы можно только с помощью очень точного оборудования. Обычно физики используют не точные мгновенные значения, а усредненные величины. Например, в данном примере приобретенный шаром импульс ( mathbf{p} ) равен произведению средней силы взаимодействия ( mathbf{overline{F}} ) и времени взаимодействия ( Delta{t}=t_1-t_0 ):
Обратите внимание, что эта формула связывает векторы силы и импульса. Действительно, импульс — это вектор, обладающий некоторой величиной и направлением, совпадающим с направлением силы, например результирующей векторной суммы всех действующих на объект сил.
Из этой формулы ясно, что изменение импульса измеряется в системе СИ в ньютонах в секунду (Н·с), а в системе СГС — в динах-секундах (дин·с).
Получаем импульс
Изменение импульса (т.е. определенного количества движения) объекта означает изменение характера его движения. Причем это изменение зависит от массы и скорости объекта, поскольку импульс равен произведению скорости и массы объекта. Импульс является очень важной физической концепцией, которая используется не только в начальном курсе физики, но и в некоторых очень сложных разделах физики, например в физике элементарных частиц, где компоненты атомов носятся с огромными скоростями. Именно на основании анализа импульсов до и после столкновения элементарных частиц ученые могут делать выводы о поведении субатомного мира.
Общая идея импульса понятна даже тем, кому незнакомо это понятие. Не так уж легко остановить тележку, которая катится по склону горы. Дело в том, что тележка массивна и обладает большой скоростью. Еще труднее остановить огромный нефтяной танкер. Порой для полной остановки крупного танкера требуется около 30 км тормозного пути! И все это из-за огромного импульса, которым он обладает.
Чем больше масса движущегося объекта (представьте себе огромный танкер) и чем больше скорость объекта (представьте себе быстро плывущий танкер), тем больше импульс объекта.
Итак, импульс объекта равен:
Как видите, импульс — это вектор с определенной величиной и направлением (о векторах подробнее рассказывается в главе 4). Импульс, как и количество движения, измеряется в системе СИ в ньютонах в секунду (Н·с), а в системе СГС — в динах-секундах (дин·с).
Связываем работу силы и изменение импульса
Придать объекту импульс так же просто, как ударить клюшкой для гольфа по мячу. Достаточно применить элементарные алгебраические преобразования ко второму закону Ньютона и мы получим связь между работой силы и изменением импульса. С чего начать? Начнем со связи силы и скорости. Как известно, ускорение определяется следующей формулой:
где ( Delta{v} ) — это изменение скорости за промежуток времени ( Delta{t} ), ( v_0 ) — это начальная скорость в момент времени ( t_0 ), a ( v_1 ) — это конечная скорость в момент времени ( t_1 ). Теперь, если умножить обе части этой формулы на массу объекта ( m ), то слева получим:
Теперь, чтобы получить связь силы с импульсом объекта, умножим эту формулу на промежуток времени ( Delta{t} ) и получим:
Посмотрите повнимательнее на правую часть формулы ( m(v_1-v_0) ). Поскольку импульс объекта с массой ( m ) равен ( p=mv ), то эта часть формулы выражает разницу конечного ( p_1=mv_1 ) и начального ( p_0=mv_0 ) импульса, т.е.:
Следовательно, в итоге получим:
Итак, справа имеем силу, умноженную на промежуток времени ее действия, т.е. ( FDelta{t} ), а слева — изменение импульса ( Delta{p} ). Убирая промежуточные выкладки, получим искомую формулу связи силы и изменения импульса объекта:
Произведение силы на время ее действия называется импульсом силы за то же время. (Его не следует путать с понятием импульс объекта ( p=mv ). Применение обоих этих понятий часто приводит к путанице, и потому понятие импульс силы используется довольно редко. — Примеч. ред.)
Пример: вычисляем импульс бильярдного шара
С помощью приведенных выше уравнений можно связать действующую на объект силу и приобретенный им импульс. Попробуем применить полученные знания при игре в бильярд. Допустим, что время контакта кия с бильярдным шаром приблизительно равно 5 мс (1 миллисекунда, или сокращенно 1 мс, равна 10-3 с). Насколько нужно изменить импульс неподвижного бильярдного шара, чтобы загнать его в лузу с отскоком от боковой стенки?
Пусть шар имеет массу 200 г (т.е. 0,2 кг). Допустим, что путем тщательных замеров и вычислений стало известно, что для попадания в лузу с отскоком от боковой стенки шару нужно приобрести скорость 20 м/с. Какую силу нужно приложить к кию для выполнения этой задачи?
Итак, в начальный момент времени шар покоится, т.е. начальная скорость ( v_0 ) = 0, а его конечная скорость ( v_1 ) должна быть равна 20 м/с. Вычислим необходимое изменение импульса по уже известной нам формуле:
Подставив значения получим:
Итак, необходимо изменить импульс шара на 4 кг·м/с. Вычислим, какую силу нужно для этого приложить за промежуток времени 5 мс по известной формуле:
откуда
Подставив значения, получим:
Итак, чтобы загнать бильярдный шар в лузу с отскоком от боковой стенки нужно прилагать к кию силу 800 Н в течение 5 мс.
Пример: определяем импульс капель дождя
После триумфальной демонстрации своих физических познаний в бильярдной попробуем использовать их в более привычной ситуации. Предположим, что на обратном пути домой внезапно начался дождь. Не беда, ведь под рукой есть зонт. Допустим, что на раскрытый зонт ежесекундно со средней скоростью около 10 м/с падает приблизительно 100 г капель воды. Вопрос: с какой силой нужно удерживать зонт массой 1 кг, чтобы удержать его под таким дождем?
Чтобы удержать зонт даже в отсутствие дождя, потребуется сила, равная весу зонта, то есть:
А как же подсчитать воздействие капель дождя? Предположим, что капли после падения на зонт почти мгновенно стекают по его почти горизонтальной поверхности. Даже в этом случае нам нужно учесть не только их массу, но и уменьшение скорости из-за встречи с зонтом. Действительно, летящие капли имеют начальную скорость 10 м/с, а после падения на зонт останавливаются, т.е. приобретают нулевую конечную скорость. Итак, имеем изменение импульса капель дождя, вызванное взаимодействием с зонтом. Попробуем оценить это изменение с помощью известной формулы:
Подставляя значения, получим:
Такое изменение импульса капель происходит ежесекундно. Свяжем теперь его с известной нам формулой:
Подставив значения, получим:
Итак, помимо силы 9,8 Н для удержания сухого зонта потребуется еще дополнительная сила 1 Н для компенсации торможения капель, т.е. всего потребуется сила 10,8 Н.
Наибольшую трудность при вычислениях изменения импульса под действием силы вызывает оценка времени действия этой силы. Поэтому при решении задач, связанных с изменением импульса, при столкновениях объектов обычно стремятся использовать другие параметры процесса, например скорость до и после столкновения, избегая оценок трудновычислимых параметров.
Изучаем закон сохранения импульса
Согласно этому закону, в изолированной системе без внешних сил общий импульс всех объектов системы до столкновений между ними равен общему импульсу всех объектов системы после столкновений между ними.
Если для анализа импульсов взаимодействующих объектов использовать приведенные выше формулировки с указанием силы и времени ее действия, то на это придется затратить чрезвычайно много усилий. Закон сохранения импульса позволяет избежать этих сложностей. Дело в том, что, применяя этот закон, можно полностью исключить из рассмотрения силы и время их действия.
Допустим, что два беспечных пилота космических кораблей А и Б не смогли избежать лобового столкновения своих машин. Во время столкновения корабль Б воздействовал на корабль А со средней силой ( F_{АБ} ). Согласно известной формуле о связи между силой и изменением импульса, получим для корабля А:
где ( m_{А} ) — это масса корабля A, ( v_{А1} ) — скорость корабля А после столкновения и ( v_{А0} ) — скорость корабля А до столкновения.
Аналогично, во время столкновения корабль А воздействовал на корабль Б со средней силой ( F_{БА} ). Опять по известной формуле о связи между силой и изменением импульса, получим для корабля Б:
где ( m_{Б} ) — это масса корабля Б, ( v_{Б1} ) — скорость корабля Б после столкновения и ( v_{Б0} ) — скорость корабля Б до столкновения.
Сложим оба последних равенства и получим следующее уравнение:
Опустим промежуточные выкладки и оставим только крайние левую и правую части этого равенства. Причем в правой части соберем отдельно члены начального и конечного состояний и получим:
Сумма ( m_Av_{A1}+m_Бv_{Б1} ) означает суммарный конечный импульс ( p_{1}=p_{A1}+p_{Б1} ) двух кораблей после столкновения, а сумма ( m_Av_{A0}+m_Бv_{Б0} ) — суммарный начальный импульс ( p_{0}=p_{A0}+p_{Б0} ) двух кораблей до столкновения. Следовательно, последнее уравнение можно переписать в следующем виде:
Если теперь ввести обозначение ( sum!{F} ) для суммы этих двух сил ( F_{АБ}+F_{БА} ), то получим:
При работе с изолированной, или замкнутой, системой объектов внешних сил нет. Именно такая ситуация рассматривается в данном примере.
Если два космических корабля столкнутся при отсутствии внешних сил, то согласно третьему закону Ньютона, ( F_{АБ}=-F_{БА} ). Иначе говоря, в замкнутой системе имеем:
А это означает, что:
Это равенство означает, что в изолированной системе без внешних сил начальный импульс двух сталкивающихся объектов до их столкновения равняется конечному импульсу после столкновения, что соответствует закону сохранения импульса.
Извлекаем тепло из суммарного импульса.
Всегда ли сохраняется суммарный импульс объектов при их лобовом столкновении и сцеплении? В реальном мире далеко не всегда. Дело в том, что часто при столкновениях объектов они необратимо деформируются и часть их кинетической энергии расходуется на необратимую деформацию и рассеивается в виде тепловой энергии. Однако для точного расчета такого преобразования кинетической энергии в тепловую требуется учесть много других сложных физических процессов. Эти процессы обычно не рассматриваются в начальном курсе физики, а тем более в этом курсе.
Измеряем скорость с помощью закона сохранения импульса
Попробуем применить закон сохранения импульса для расчета некоторых параметров движения. Предположим, что при игре в хоккей игрок А с массой 100 кг решил применить силовой прием против другого неподвижного игрока Б тоже с массой 100 кг (который оказался его братом-близнецом). Для этого игрок А разогнался до скорости 11 м/с, грубо толкнул игрока Б и, схватив его руками, устроил потасовку. С какой скоростью будут двигаться оба сцепившихся руками игрока после столкновения?
Будем считать, что в данном примере мы имеем дело с замкнутой системой (см. предыдущий раздел), поскольку мы пренебрегаем всеми внешними силами, включая силу трения. Хотя в вертикальном направлении на хоккеистов со стороны ледяного катка действует нормальная сила (подробнее о ней см. в главе 6), но она равна по величине весу игроков и противоположна по направлению и в сумме дает нуль.
Итак, рассмотрим горизонтальные проекции импульсов игроков. Согласно закону сохранения импульса, имеем:
Подставим в эту формулу массу и начальную скорость игроков (на самом деле нужно подставить массу ( m_А ) и начальную скорость ( v_{А0} ) только игрока А, поскольку игрок Б имел нулевую начальную скорость):
Конечный импульс ( p_1 ) должен быть равен произведению общей массы ( m_А+m_Б ) игроков на их конечную скорость ( v_{АБ1} ), т.е. получаем:
Из двух последних уравнений получаем:
откуда легко можно выразить конечную скорость ( v_{АБ1} ):
Подставляя значения, получим:
Конечная скорость двух игроков равна половине начальной скорости одного игрока. Этого следовало ожидать, ведь масса движущихся объектов увеличилась вдвое, а поскольку импульс сохраняется, то скорость должна уменьшиться во столько же раз.
Измеряем начальную скорость пули с помощью закона сохранения импульса
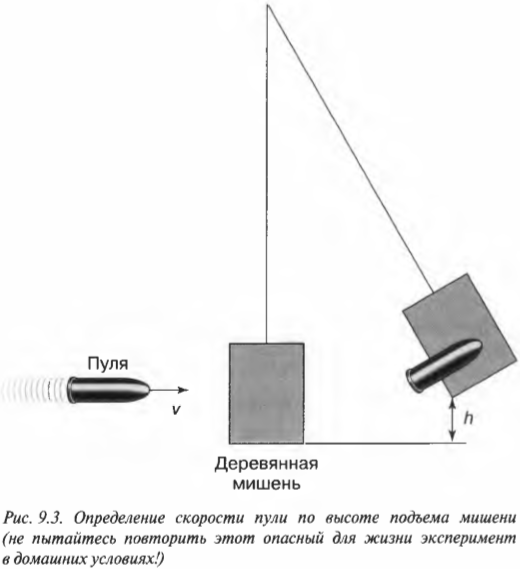
Закон сохранения импульса очень удобно использовать для определения скорости объекта, если ее нельзя или очень трудно измерить с помощью секундомера. Предположим, что изготовитель пуль хочет знать, какой будет начальная скорость новой пули. Как ему поступить? Для решения этой задачи ему предложили использовать приспособление, показанное на рис. 9.3.
Как оно может помочь? Оказывается, что если выстрелить пулей с массой ( m ) в массивную деревянную мишень с массой ( M ) и пуля застрянет в мишени, то, как и в примере с хоккеистами, конечная скорость мишени с пулей ( v_1 ) будет зависеть от начальной скорости пули ( v_0 ). Как именно? Для конкретного ответа на этот вопрос попробуем использовать закон сохранения импульса.
Итак, начальный суммарный импульс пули и мишени равен:
Поскольку пуля застряла в мишени, то конечный суммарный импульс пули и мишени равен:
Если пренебречь потерями энергии на преодоление трения при попадании пули в мишень, то согласно закону сохранения импульса, эти два импульса должны быть равны:
Тогда:
и искомая начальная скорость равна:
Итак, остается только определить конечную скорость ( v_1 ) мишени с застрявшей в ней пулей. Для этого нужно вспомнить закон сохранения энергии, который описывается в главе 8. Ведь после попадания пули мишень отклонится и поднимется на некоторую максимальную высоту ( h ), на которой ее скорость станет равной нулю. В этой точке ее кинетическая энергия ( frac{(m+M)v^2_1}{2} ) преобразуется в потенциальную ( (m+M)gh ). Итак, согласно закону сохранения энергии получим:
Откуда легко вывести формулу для конечной скорости мишени с застрявшей в ней пулей ( v_1 ):
Подставим эту формулу в прежнее выражение для искомой начальной скорости пули:
и получим:
Пусть пуля имеет массу 50 г, деревянная мишень — 10 кг, а после попадания пули в нее мишень отклонилась и поднялась на максимальную высоту 0,5 м. Подставляя значения в приведенную выше формулу, получим:
Таким образом, мы определили начальную скорость пули. Изготовитель пуль будет просто в восторге от такого простого и удобного способа.
Упругие и неупругие столкновения
Изучение физики на примере столкновений разных тел — это очень интересное и увлекательное занятие. Во многом это объясняется тем, что многие вычисления значительно упрощаются благодаря закону сохранения импульса (более подробно он рассматривается в предыдущих разделах этой главы). Однако, как мы уже убедились в предыдущих примерах, в некоторых столкновениях одного этого закона недостаточно и нужно применять закон сохранения энергии. Это особенно полезно для анализа столкновений объектов со скоростями, векторы которых направлены не вдоль одной прямой (как в предыдущих примерах), а лежат в одной плоскости.
В реальной жизни такие ситуации происходят сплошь и рядом. Например, при изучении причин дорожно-транспортного происшествия часто требуется проанализировать начальные и конечные скорости столкнувшихся автомобилей. При сортировке вагонов нужно учитывать начальные и конечные скорости сталкивающихся вагонов и составов.
Что происходит в таких столкновениях, если столкнувшиеся объекты не “слипаются” друг с другом? Рассмотрим более общий пример: пусть два бильярдных шара сталкиваются дуг с другом с разными скоростями, направленными друг к другу под произвольным углом. Как определить их величину и направление их скоростей после столкновения? Для этого потребуется не только закон сохранения импульса, но и закон сохранения энергии.
Когда сталкивающиеся объекты отскакивают друг от друга: упругие столкновения
В реальном мире при столкновении тел всегда наблюдаются потери энергии на деформацию и рассеивание тепла. В некоторых случаях эти потери столь малы, что ими можно пренебречь, как, например, при столкновении двух бильярдных шаров. В физике такие столкновения с сохранением кинетической энергии сталкивающихся объектов называют упругими столкновениями. Итак, в упругом столкновении сохраняется общая кинетическая энергия замкнутой системы объектов, т.е. суммарная кинетическая энергия после столкновения равна суммарной кинетической энергии до столкновения.
Когда сталкивающиеся объекты не отскакивают друг от друга: неупругие столкновения
Если во время столкновения объектов какая-то часть энергии тратится на работу каких-то неконсервативных сил (например, на преодоление силы трения, деформацию и т.п.), то кинетическая энергия системы не сохраняется. Она частично преобразуется в другие формы энергии. Такие столкновения в физике называют неупругими столкновениями. Итак, в неупругом столкновении общая кинетическая энергия замкнутой системы объектов не сохраняется, т.е. суммарная кинетическая энергия после столкновения не равна суммарной кинетической энергии до столкновения. Примеры неупругих столкновений можно наблюдать в дорожно-транспортных происшествиях, когда столкнувшиеся машины деформируют друг друга или даже сцепляются и движутся как единое целое.
Совсем не обязательно, чтобы после неупругого столкновения объекты сцеплялись друг с другом. Достаточно, чтобы часть кинетической энергии “утрачивалась”, т.е. переходила в другую форму, например в тепловую энергию. Неупругое столкновение внешне может быть очень похоже на упругое столкновение, например при касательном столкновении двух машин с образованием легких повреждений. На образование этих повреждений необратимо тратится часть кинетической энергии, но машины могут независимо продолжить движение.
Упругие столкновение на прямой
Итак, мы уже выяснили, что при упругом столкновении кинетическая энергия сталкивающихся объектов сохраняется. Проще всего изучать особенности упругого столкновения, когда векторы скоростей находятся на одной прямой. Рассмотрим идеализированный пример столкновения двух машин с совершенно упругими (т.е. недеформирую- щимися) бамперами, которые движутся по прямой.
Упругое столкновение с более тяжелым объектом
Предположим, что вы решили прокатиться на автомобиле А с массой 300 кг и на скорости около 10 м/с столкнулись с внезапно остановившимся перед вами другим автомобилем Б с массой 400 кг. Какими будут скорости обоих автомобилей после их упругого столкновения?
Итак, до столкновения автомобиль А с массой ( m_А ) = 300 кг имел начальную скорость ( v_{А0} ) = 10 м/с, а автомобиль Б с массой ( m_Б ) = 400 кг — начальную скорость ( v_{Б0} ) = 0. Если считать систему двух автомобилей замкнутой, то их общий импульс должен сохраняться, то есть:
где ( v_{А1} ) — это конечная скорость автомобиля А после столкновения, a ( v_{Б1} ) — это конечная скорость автомобиля Б после столкновения.
У нас есть одно уравнение с двумя неизвестными ( v_{А1} ) и ( v_{Б1} ). Чтобы их найти, нужно иметь еще одно уравнение, связывающее эти неизвестные. Как насчет кинетической энергии? Действительно, поскольку столкновение было упругим, то кинетическая энергия объектов должна сохраняться, т.е. должно выполняться равенство:
Теперь у нас есть два уравнения и две неизвестных величины. С помощью простых алгебраических операций можно легко получить выражения для неизвестных скоростей ( v_{А1} ) и ( v_{Б1} ):
и
Подставляя значения в обе эти формулы, получим:
и
Анализируя полученные значения, можно легко восстановить ход событий. Итак, автомобиль А на скорости 10 м/с столкнулся с неподвижным автомобилем Б. После столкновения автомобиль А отскочил назад (об этом свидетельствует отрицательный знак конечной скорости ( v_{А1} )) со скоростью 1,43 м/с, а автомобиль Б начал движение вперед со скоростью 8,57 м/с. Автомобиль А легче автомобиля Б, а что если бы было наоборот?
Упругое столкновение с более легким объектом
Предположим, что в предыдущем примере движущийся автомобиль А тяжелее неподвижного автомобиля Б. Пусть автомобиль А с массой 400 кг на скорости около 10 м/с сталкивается с внезапно остановившимся перед вами другим автомобилем Б с массой 300 кг. Вопрос остается прежним: какими будут скорости обоих автомобилей после их упругого столкновения?
Итак, до столкновения автомобиль А с массой ( m_А ) = 400 кг имеет начальную скорость ( v_{А0} ) = 10 м/с, а автомобиль Б с массой ( m_Б ) = 300 кг — начальную скорость ( v_{Б0} ) = 0. Используем уже известные нам формулы скоростей ( v_{А1} ) и ( v_{Б1} ):
и
Подставим в них новые значения и получим:
и
Как видите, более тяжелый движущийся автомобиль А после столкновения с более легким автомобилем Б смог продолжить движение в том же направлении, но с меньшей скоростью. Причем часть своего импульса он передал более легкому автомобилю Б.
Упругие столкновения в одной плоскости
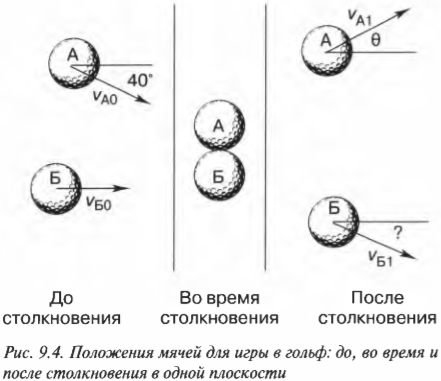
Столкновения объектов не всегда происходят по прямой линии. Например, бильярдные шары сталкиваются так, что векторы их скоростей могут быть направлены не вдоль одной прямой, а находится в одной плоскости под произвольным углом друг к другу. В этом случае нужно учитывать не только величину, но и направление скорости. Пусть во время игры в гольф два игрока одновременно (простим им это нарушение правил) ударяют по разным мячам А и Б, мячи упруго сталкиваются и продолжают движение, как показано на рис. 9.4. Какими будут скорости мячей после столкновения?
Попробуем решить эту задачу, учитывая, что мячи имеют одинаковую массу ( m ) = 46 г. Мяч А имеет начальную скорость ( v_{А0} ) = 1,0 м/с, а мяч Б — начальную скорость ( v_{Б0} ) = 2,0 м/с. Кроме того, пусть нам известны направления векторов начальных скоростей обоих мячей (см. рис. 9.4).
Для решения задачи нам потребуются закон сохранения импульса и закон сохранения энергии. Поскольку столкновение считается упругим, то кинетическая энергия системы сохраняется, т.е. согласно закону сохранения энергии, имеем:
или в более простой форме:
Если подставить вместо скоростей их компоненты по осям X и Y, то получим:
Так как трение здесь не учитывается, то в процессе столкновения внутренние силы упругого взаимодействия мячей направлены только по вертикальной оси Y. Эти силы не изменяют компоненты импульсов мячей по горизонтальной оси X:
и
Отсюда следует, что компоненты скоростей мячей по горизонтальной оси X после столкновения тоже не изменяются:
и
(То есть компоненты скоростей мячей по горизонтальной оси X в результате столкновения не изменились.)
Соотношение, полученное ранее из закона сохранения энергии:
с учетом постоянства компонент скоростей по оси X теперь будет иметь следующий вид:
или (поскольку ( v_{Б0у} ) = 0);
Согласно закону сохранения импульса, для компонент импульса по вертикальной оси Y имеем( mv_{А1у}+mv_{Б1у}=mv_{А0у}+mv_{Б0у} ) или в более простой форме (поскольку ( v_{Б0у} ) = 0):
Из двух последних равенств нетрудно получить выражения для компонент скоростей по вертикальной оси Y:
и
Как видите, при таком упругом столкновении у мячей остались прежними их компоненты скоростей по горизонтальной оси X, и они “обменялись” компонентами скоростей по вертикальной оси Y. Это значит, что мяч А продолжит движение с нулевой компонентой ( v_{А1у} ), т.е. по горизонтали, а мяч Б продолжит движение под углом ( alpha ), который легко вычислить по формуле:
где знак “минус” перед значением угла означает, что на рис. 9.4 угол откладывается в направлении против часовой стрелки.
А скорости мячей после столкновения будут равны
и:
Подставив значения, получим:
и
Глава 9. Двигаем объекты: количество движения и импульс
3 (60%) 5 votes
Если на тело массой m за определенный промежуток времени Δt действует сила F→, тогда следует изменение скорости тела ∆v→=v2→-v1→. Получаем, что за время Δt тело продолжает движение с ускорением:
a→=∆v→∆t=v2→-v1→∆t.
Основываясь на основном законе динамики, то есть втором законе Ньютона, имеем:
F→=ma→=mv2→-v1→∆t или F→∆t=mv2→-mv1→=m∆v→=∆mv→.
Изменение импульса
Импульс тела, или количество движения – это физическая величина, равная произведению массы тела на скорость его движения.
Импульс тела считается векторной величиной, которая измеряется в килограмм-метр в секунду (кг м/с).
Импульс силы – это физическая величина, равняющаяся произведению силы на время ее действия.
Импульс относят к векторным величинам. Существует еще одна формулировка определения.
Изменение импульса тела равняется импульсу силы.
При обозначении импульса p→ второй закон Ньютона записывается как:
F→∆t=∆p→.
Данный вид позволяет формулировать второй закон Ньютона. Сила F→ является равнодействующей всех сил, действующих на тело. Равенство записывается как проекции на координатные оси вида:
FxΔt=Δpx; FyΔt=Δpy; FzΔt=Δpz.
Рисунок 1.16.1. Модель импульса тела.
Изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось.
Одномерное движение – это движение тела по одной из координатный осей.
На примере рассмотрим свободное падение тела с начальной скоростью v0 под действием силы тяжести за промежуток времени t. При направлении оси OY вертикально вниз импульс силы тяжести Fт=mg, действующий за время t, равняется mgt. Такой импульс равняется изменению импульса тела:
Fтt=mgt=Δp=m(v–v0), откуда v=v0 + gt.
Запись совпадает с кинематической формулой определения скорости равноускоренного движения. По модулю сила не изменяется из всего интервала t. Когда она изменяема по величине, тогда формула импульса требует подстановки среднего значения силы Fср из временного промежутка t. Рисунок 1.16.2 показывает, каким образом определяется импульс силы, которая зависит от времени.
Рисунок 1.16.2. Вычисление импульса силы по графику зависимости F(t)
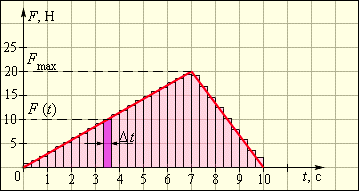
Необходимо выбрать на временной оси интервал Δt, видно, что сила F(t) практически неизменна. Импульс силы F(t)Δt за промежуток времени Δt будет равняться площади заштрихованной фигуры. При разделении временной оси на интервалы на Δti на промежутке от от 0 до t, сложить импульсы всех действующих сил из этих промежутков Δti, тогда суммарный импульс силы будет равняться площади образования при помощи ступенчатой и временной осей.
Применив предел (Δti→0), можно найти площадь, которая будет ограничиваться графиком F(t) и осью t. Использование определения импульса силы по графику применимо с любыми законами, где имеются изменяющиеся силы и время. Данное решение ведет к интегрированию функции F(t) из интервала [0; t].
Рисунок 1.16.2 показывает импульс силы, находящийся на интервале от t1=0 с до t2=10.
Из формулы получим, что Fср(t2-t1)=12Fmax(t2-t1)=100 Н·с=100 кг·м/с.
То есть, из примера видно Fср=12Fmax=10 Н.
Определение средней силы
Имеются случаи, когда определение средней силы Fср возможно при известных времени и данных о сообщенном импульсе. При сильной ударе по мячу с массой 0,415 кг можно сообщить скорость, равную v=30 м/с. Приблизительным временем удара является значение 8·10–3 с.
Тогда формула импульса приобретает вид:
p=mv=12,5 кг·м/с.
Чтобы определить среднюю силу Fср во время удара, необходимо Fср=p∆t=1,56·103 Н.
Получили очень большое значение, которое равняется телу массой 160 кг.
Когда движение происходит по криволинейной траектории, то начальное значение p1→ и конечное
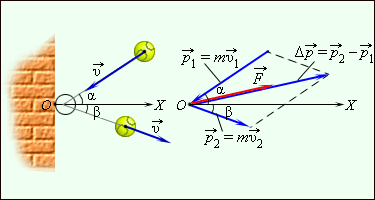
p2→ могут быть различны по модулю и по направлению. Для определения импульса ∆p→ применяют диаграмму импульсов, где имеются векторы p1→ и p2→, а ∆p→=p2→-p1→ построен по правилу параллелограмма.
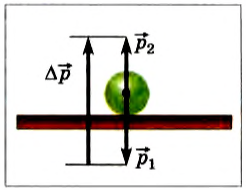
Для примера приводится рисунок 1.16.2, где нарисована схема импульсов мяча, отскакивающего от стены. При подаче мяч с массой m со скоростью v1→ налетает на поверхность под углом α к нормали и отскакивает со скоростью v2→ с углом β. При ударе в стену мяч подвергался действию силы F→, направленной также, как и вектор ∆p→.
Рисунок 1.16.3. Отскакивание мяча от шероховатой стенки и диаграмма импульсов.
Если происходит нормальное падение мяча с массой m на упругую поверхность со скоростью v1→=v→, тогда при отскоке она изменится на v2→=-v→. Значит, за определенный промежуток времени импульс изменится и будет равен ∆p→=-2mv→. Используя проекции на ОХ, результат запишется как Δpx=–2mvx. Из рисунка 1.16.3 видно, что ось ОХ направлена от стенки, тогда следует vx<0 и Δpx>0. Из формулы получим, что модуль Δp связан с модулем скорости, который принимает вид Δp=2mv.
Содержание:
Импульс:
Основное уравнение динамики (второй закон Ньютона)
Что такое импульс стела
Импульс тела — физическая векторная величина, совпадающая по направлению со скоростью тела в данный момент времени и равная произведению массы тела на его скорость. Как следует из определения, импульс тела измеряется в СИ в килограмм-метрах в секунду (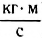
Впервые понятие импульса тела было введено в физику как произведение массы тела на модуль его скорости французским мыслителем и математиком P Декартом. Импульс тела как вектор был введен И. Ньютоном.
Хотя скорость и импульс тела связаны между собой простой зависимостью, они коренным образом отличаются друг от друга. Скорость тела — чисто кинематическая характеристика движения. Импульс тела является динамической характеристикой движения, связанной с причинами (силами), вызывающими движение.
C помощью важнейшего понятия импульса основное уравнение динамики запишется в виде:
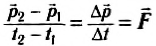
и может быть сформулировано следующим образом.
Изменение импульса тела в единицу времени равно векторной сумме всех сил, действующих на данное тело.
Это более общая формулировка второго закона Ньютона. Именно так сформулировал Ньютон свой основной закон в знаменитой книге «Математические начала натуральной философии».
На первый взгляд уравнение (4) идентично уравнению (I). Это верно в том случае, если масса тела при движении не меняется. Если же масса тела изменяется, например при движении ракет, осьминогов, катеров с водометными движителями и т. д., то для описания движения тел необходимо применять более общее уравнение (4), а не уравнение (1).
Уравнение (4) может быть записано еще и в виде:
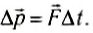
Данное выражение позволяет сделать важнейший вывод: для изменения импульса тела сила должна действовать определенный промежуток времени. Импульс, а следовательно, и скорость тела мгновенно изменить нельзя.
Величина 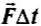
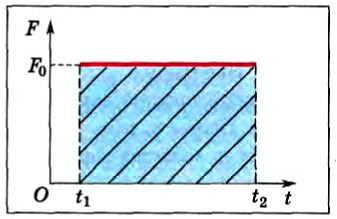
Действительно, предположим, что на тело действует постоянная сила F0 в течение некоторого промежутка времени ∆t = t2-t1. На рисунке 114 представлен график зависимости модуля силы от времени. Из формулы (5) следует, что величина модуля импульса этой силы численно равна площади прямоугольника.
Рис. 114
Если же сила непостоянна во времени, например линейно увеличивается: F = kt (рис. 115) от t1 = 0 до t2, то импульс этой силы тоже равен площади под прямой, т. е. площади треугольника. Очевидно, что импульс этой силы равен –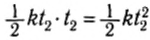
Рис. 115
Вычисленная таким образом сила называется средней силой и обозначается (F).
Поэтому выражение (4) часто записывается в виде:
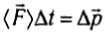
и используется для оценки средней силы при кратковременных взаимодействиях тел (ударах, толчках и т. п.).
Для примера оценим среднюю силу, действующую со стороны пола на теннисный мяч массой m при его падении с высоты h1. Как показывает опыт, после удара о пол мяч поднимается на меньшую высоту h2. По этим данным мы можем вычислить скорость мяча по известной формуле 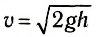
Рис. 116
Это выражение получено в предположении отсутствия сопротивления воздуха. Уменьшение высоты подъема мяча обусловлено тем, что удар неупругий.
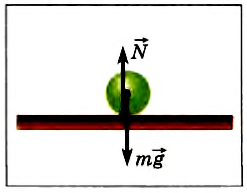
Во время удара на мяч действуют две силы: сила реакции пола 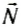
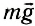
Следовательно,
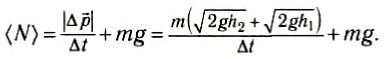
Опыт проводился с мячом массой m = 55 г. Его бросали без начальной скорости с высоты h1 = 1,0 м. После отскока от пола мяч поднимался на среднюю высоту h2 = 63 см. Считая, что удар происходил за время Δt = 0,15 с, после подстановки численных значений в формулу (7) и вычисления, получим, что (N) = 3,4 H = 6,3 mg.
Если мяч просто лежит на полу (рис. 117), то сила реакции N, действующая на него, равна mg. Значит, средняя сила реакции, действующая на мяч, при ударе в данном опыте в 6,3 раза превосходила силу тяжести.
Рис. 117
Главные выводы:
- Импульсом тела (количеством движения) называется векторная физическая величина, равная произведению массы тела на его скорость.
- Импульсом силы называется векторная физическая величина, равная произведению постоянной или средней силы на промежуток времени действия силы.
- Изменение импульса тела в единицу времени равно векторной сумме всех действующих на тело сил.
Определение импульса
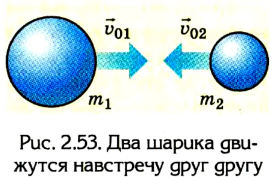
Существует несколько путей решения основной задачи механики. Одним из них является использование законов механики Ньютона. Однако это не всегда возможно. Если массу тела измерить сравнительно легко, то измерение силы связано со значительными трудностями. Для примера рассмотрим два стальных шарика, которые движутся навстречу друг другу и сталкиваются. По законам Ньютона каждый из них при столкновении приобретает некоторое ускорение, которое определяет скорость шариков после взаимодействия. Чтобы найти ускорение, необходимо знать силу, действующую на каждый из шариков во время взаимодействия.
Время, на протяжении которого взаимодействуют шарики, очень незначительное, а потому измерить силу или вызванное ей ускорение сложно.
Пусть два упругих шарика имеют массы 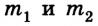
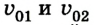
Будем считать, что действие других сил несущественно или скомпенсировано, т. е. шарики образуют замкнутую (изолированную) систему.
Во время столкновения шарики деформируются, вследствие чего возникают силы упругости, которые в соответствии с третьим законом Ньютона равны по модулям, но противоположны по направлению:
где 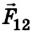
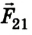
Отсюда 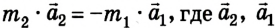
Если считать, что 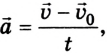
где 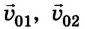
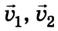
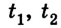
Поскольку время взаимодействия обоих шариков одинаково 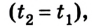
В левой и правой части уравнения суммируются произведения массы тела на его скорость. Как известно, данная физическая величина называется импульсом тела, или количеством движения.
Таким образом, чтобы определить результат взаимодействия, необязательно знать силы, которые возникают во время взаимодействия. Достаточно знать массу и скорость каждого тела: если два тела взаимодействуют только друг с другом, то сумма их импульсов до и после взаимодействия не изменяется.
Для более общего случая: в замкнутой (изолированной) системе сумма импульсов тел после любого взаимодействия между ними остается постоянной:
Закон сохранения импульса – один из основных законов природы. Согласно этому закону в замкнутой (изолированной) системе векторная сумма импульсов всех тел остается постоянной. Тела такой системы могут обмениваться импульсами, но суммарный импульс остается постоянным. Это положение справедливо для всех явлений природы.
Закон сохранения импульса
До сих пор мы рассматривали изменение скорости отдельного тела под действием некоторых сил. Теперь давайте рассмотрим вопрос об изменении импульсов нескольких тел под действием сил взаимодействия между ними.
В механике всякая группа тел, выделенная нами, называется механической системой.
Рассмотрим систему, состоящую из двух тележек с пружинными бамперами, находящихся на горизонтальных рельсах. На тележки действуют силы тяжести и силы реакции рельсов. Эти силы действуют со стороны тел, не входящих в систему, и поэтому называются внешними силами.
Итак, внешние силы — это силы, действующие на тела системы со стороны тел, не входящих в выделенную систему.
При столкновении тележек между ними возникают силы взаимодействия. Эти силы принято называть внутренними.
Внутренние силы в любой механической системе — это силы взаимодействия между телами, входящими в данную систему.
Если на тела системы действуют только внутренние силы, то такая система называется замкнутой. В том случае, когда на тела системы действуют еще внешние силы, система тел называется незамкнутой. Хорошим примером замкнутой системы является Солнечная система. Движение любой из планет относительно Солнца происходит вследствие, во-первых, силы притяжения к Солнцу и, во-вторых, сил притяжения к остальным планетам Солнечной системы. Очевидно, что система, состоящая из, например. Солнца, Земли и Луны, не является замкнутой.
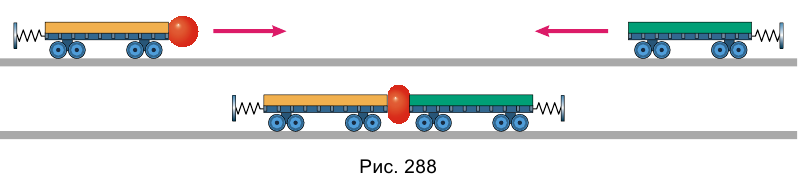
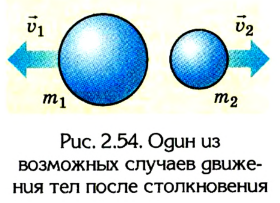
Теперь давайте рассмотрим опыт по столкновению двух одинаковых тележек.
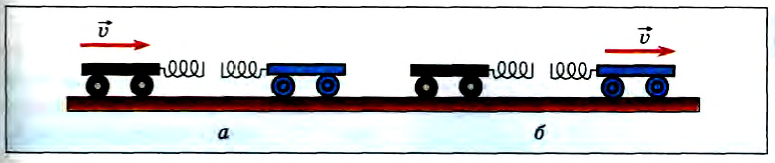
Толкнув одну из тележек, мы увидим, что она после столкновения остановится, а покоящаяся ранее тележка придет в движение (рис. 118, а, б) с той же скоростью, т. е. тележки обменяются скоростями.
Рис. 118
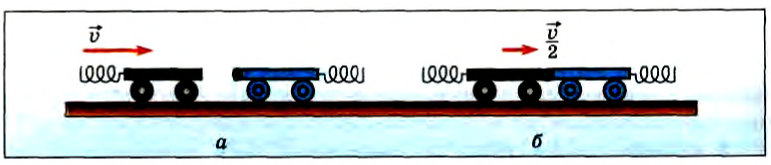
Видоизменим опыт. Повернем тележки так, чтобы они не были обращены друг к другу пружинными бамперами. На одну из тележек прикрепим пластилиновый шарик. Если толкнуть одну из тележек, то после столкновения с другой они будут двигаться вместе (рис. 119, а, б). При этом скорость тележек будет в 2 раза меньше скорости первой тележки до столкновения. Из этого опыта следует, что скорость изменяется в зависимости от типа столкновения. Однако можно заметить, импульс системы не изменяется. Действительно, до столкновения двигалась одна тележка, и ее импульс был равен 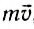
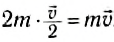
Рис. 119
Изменение скорости тележек происходит только под действием внутренних сил — сил взаимодействия между тележками. Импульс системы до взаимодействия равен импульсу системы после взаимодействия. Суммарный импульс системы не изменяется под действием внутренних сил.
Действительно, рассмотрим изменение состояния движения двух тел под действием только сил взаимодействия между ними. Внешние силы отсутствуют, т. е. наша система является замкнутой (рис. 120). По третьему закону Ньютона: 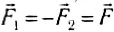
Рис. 120
Запишем уравнение (5) из § 22 для каждого из тел.
Для тела 1:
Для тела 2:
где 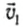
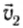
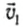
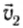
Сложим почленно эти равенства:
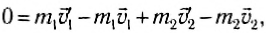
В левой части равенства (3) стоит сумма импульсов обоих тел до взаимодействия, а в правой — сумма их импульсов после взаимодействия. Импульс каждого тела изменился, но сумма осталась неизменной.
Очевидно, что если взаимодействуют не два, а несколько тел, то для каждой пары тел можно написать соотношения (I) и (2) и доказать, что векторная сумма импульсов тел замкнутой системы нс изменяется. В этом и состоит закон сохранения импульса системы.
Если в замкнутой системе п тел и их импульсы до взаимодействия — 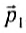
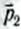
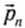
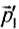
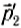
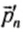
Векторная сумма импульсов всех тел, входящих в замкнутую систему, остается неизменной при любых движениях и взаимодействиях тел системы. Это и есть закон сохранения импульса. Всякий раз, когда под действием сил взаимодействия изменяется импульс одного из тел, непременно изменяются и импульсы других тел замкнутой системы так, что суммарный импульс всех тел остается неизменным.
Закон сохранения импульса для замкнутых систем является одним из фундаментальных законов природы, хотя мы его получили, опираясь на второй и третий законы Ньютона.
Поскольку импульс тела является физической векторной величиной, то, следовательно, закон должен выполняться и для проекций импульса на оси выбранной системы координат. Например, для проекций на ось Ox выбранной системы координат равенство (4) примет вид:
Поскольку при решении практических задач о движении тел в земных условиях в систему обычно Земля не включается, то такая система тел не будет замкнутой. Однако если в каждый момент взаимодействия тел сумма внешних сил в каком-то направлении равна нулю, то в этом направлении импульс системы не изменяется. В плоскости, перпендикулярной этому направлению, систему можно считать замкнутой и применять закон сохранения импульса для определения скоростей движения тел. Этот закон можно применять и для незамкнутых систем, когда внешние силы, действующие на тела, значительно меньше сил взаимодействия между телами системы.
Главные выводы:
- Закон сохранения импульса является фундаментальным законом природы. Он всегда выполняется для замкнутых систем.
- Если тела выделенной системы движутся только под действием сил взаимодействия между ними, то векторная сумма импульсов тел системы не изменяется с течением времени.
- Закон сохранения импульса можно использовать в земных условиях для систем тел. на которые действуют внешние силы, если они взаимно компенсируются или импульсом этих сил можно пренебречь по сравнению с импульсом сил взаимодействия.
Импульс тела и реактивное движение
Многие из вас видели игрушку «колыбель Ньютона» — несколько стальных шаров, подвешенных вплотную друг к другу. Если первый шар отвести в сторону и отпустить, после его удара о систему отклонится последний шар, причем примерно на такой же угол, на который был отведен первый. Вернувшись, последний шар ударит систему из оставшихся шаров, после чего снова отклонится первый шар, а затем все повторится. При этом шары посредине остаются практически неподвижными. Как объяснить действие этой игрушки?
Закон сохранения импульса:
Изучая, вы вспомнили закон сохранения механической энергии, а сейчас вспомните еще одну физическую величину, которая имеет свойство сохраняться, — импульс тела.
Импульс тела 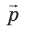
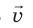
Единица импульса тела в СИ — килограммметр в секунду:
Запишем второй закон Ньютона в импульсном виде:
Величину 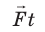
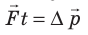
Рис. 17.1. Чем большая сила действует на тело и чем дольше ее действие, тем сильнее изменяется импульс тела
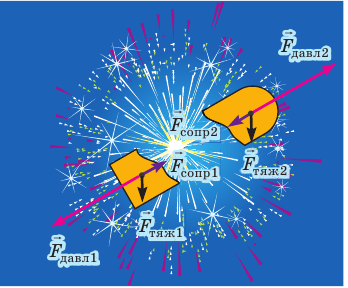
Рис. 17.2. При разрыве снаряда фейерверка суммарный импульс системы сохраняется, поскольку в момент разрыва внешние силы (сила тяжести и сила сопротивления) незначительны по сравнению с силами давления пороховых газов
В замкнутой системе тел — системе, в которой тела взаимодействуют только друг с другом, а внешние силы отсутствуют, уравновешены или пренебрежимо малы (см., например, рис. 17.2), суммарный импульс тел остается неизменным (сохраняется), то есть выполняется закон сохранения импульса:
В замкнутой системе тел векторная сумма импульсов тел до взаимодействия равна векторной сумме импульсов тел после взаимодействия:
где n — количество тел системы.
Учитывая, что импульс тела равен произведению массы m и скорости 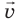
С проявлениями закона сохранения импульса мы имеем дело в природе, технике и т. д. Рассмотрим два примера применения данного закона: реактивное движение и столкновение тел.
- Заказать решение задач по физике
От чего отталкиваются ракеты
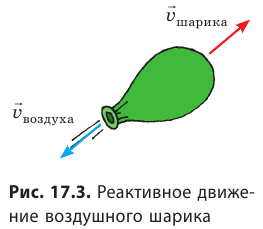
Вспомните опыт с шариком, который движется благодаря воздуху, вырывающемуся из его отверстия (рис. 17.3). Это движение — пример реактивного движения. Реактивное движение — это движение, возникающее при отделении с некоторой скоростью от тела его части.
Реактивное движение — это движение, возникающее при отделении с некоторой скоростью от тела его части.
Реактивное движение можно наблюдать в природе (рис. 17.4); его широко используют в технике: простейшие поливные системы, автомобили на реактивной тяге, катера с водометными двигателями, реактивные самолеты и, конечно, ракеты, ведь реактивное движение — это единственный способ передвижения в безвоздушном пространстве.
Рис. 17.4. Благодаря реактивному движению передвигаются многие обитатели морей и океанов (а); «бешеный огурец» может преодолеть расстояние до 12 м, рассеивая по пути семена (б)
Ракета — летательный аппарат, который движется в пространстве благодаря реактивной тяге, возникающей при отбросе ракетой части собственной массы.
Отделяющейся частью ракеты является струя горячего газа, образующегося при сгорании топлива. Когда газовая струя с огромной скоростью выбрасывается из сопла ракеты, оболочка ракеты получает мощный импульс, направленный в сторону, противоположную движению струи.
Если бы топливо сгорало мгновенно, а раскаленный газ сразу весь выбрасывался бы из ракеты, то закон сохранения импульса для системы «оболочка ракеты — раскаленный газ» выглядел бы так: 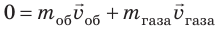
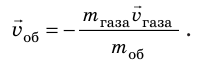
Именно на многоступенчатых ракетах были сделаны первые шаги человечества в космос: 4 октября 1957 г. советские ученые вывели на околоземную орбиту первый искусственный спутник Земли, а 12 апреля 1961 г. — космический корабль «Восток», на борту которого был первый в мире космонавт Юрий Алексеевич Гагарин; 21 июля 1969 г. американские астронавты Нил Армстронг и Базз Олдрин впервые высадились на Луне.
Прошло всего 60 лет, а мы уже не можем представить свою жизнь без космоса. Вспомните: спутниковое телевидение и спутниковая связь, система GPS и спутниковый Интернет, надежный прогноз погоды и спутниковые карты. Сейчас созданы космические корабли многоразового использования, космические аппараты высадились на Венеру, Марс и другие планеты Солнечной системы.
13 апреля 2018 г. исполнилось 25 лет со дня первого запуска ракеты-носителя «Зенит», созданной в конструкторском бюро «Южное» и на заводе «Южмаш» (Днепр). Сейчас усовершенствованная трехступенчатая ракета-носитель «Зенит-3SL» является самым большим и самым мощным летательным аппаратом своего класса в мире. Экологически чистый (работает на кислороде и керосине), недорогой, надежный «Зенит» может быть запущен при любых метеорологических условиях, способен вывести на околоземную орбиту спутники массой до 13 т. Изобретатель и предприниматель Илон Маск, основатель компании SpaceX, работающей в области строительства космического транспорта, на вопрос журналистки о любимой ракете ответил: «Лучшая ракета (после моей) — это “Зенит”».
Упругий и неупругий удары
Кратковременное взаимодействие тел, при котором тела непосредственно касаются друг друга, называют ударом. В системе сталкивающихся тел при ударе обычно возникают большие (по сравнению с внешними) внутренние силы, поэтому при ударе систему тел можно считать замкнутой и, рассматривая удары, использовать закон сохранения импульса. А вот полная механическая энергия сохраняется не всегда. Потенциальная энергия тел непосредственно до столкновения и сразу после него в большинстве случаев одинакова, поэтому далее речь пойдет только о кинетической энергии.
Рис. 17.5. Удар при столкновении бильярдных шаров (а), удары мяча по бетонной стене (б) можно считать упругими
Если после удара суммарная кинетическая энергия тел сохраняется, такой удар называют упругим (рис. 17.5).
Если после удара часть кинетической энергии превращается во внутреннюю энергию (тратится на деформацию и нагревание тел), такой удар называют неупругим.
Неупругий удар, после которого тела движутся как единое целое, называют абсолютно неупругим ударом (рис. 17.6).
Если скорости движения тел до и после удара (упругого или неупругого) направлены вдоль прямой, проходящей через центры масс этих тел, такой удар называют центральным.
Абсолютно неупругий центральный удар и упругий центральный удар рассмотрим на примерах решения задач.
Пример №1
Два шара массами 300 и 200 г, движущиеся со скоростями 4 и 2 м/с соответственно, испытывают центральный абсолютно неупругий удар. Определите, какое количество кинетической энергии шаров превратится во внутреннюю энергию, если: 1) шары двигались навстречу друг другу; 2) шары двигались друг за другом.
Анализ физической проблемы. Удар абсолютно неупругий, поэтому: 1) после столкновения шары движутся как одно целое; 2) суммарный импульс системы сохраняется; 3) кинетическая энергия системы уменьшается (часть энергии превращается во внутреннюю).
Решение:
Найдем суммарную кинетическую энергию системы шаров до столкновения:
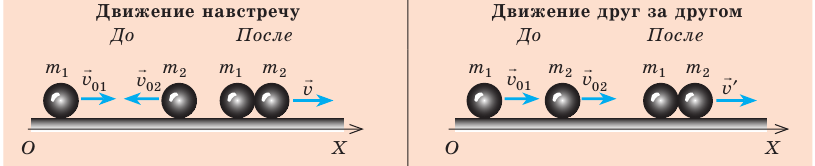
Выполним пояснительные рисунки; ось ОХ направим вдоль движения шаров.
Запишем закон сохранения импульса в векторном виде и в проекциях на ось OX:
Найдем скорость движения шаров после столкновения:
Найдем суммарную кинетическую энергию системы шаров после столкновения:
Выясним, на сколько уменьшилась кинетическая энергия системы шаров:
Ответ: 1) 2,16 Дж; 2) 0,24 Дж.
Анализ результатов. Видим, что в случае лобового удара шаров во внутреннюю энергию превращается значительно большее количество механической энергии.
Пример №2
Два шара одинаковой массы, движущиеся со скоростями 4 и 2 м/с соответственно, испытывают центральный упругий удар. Определите скорость движения шаров после столкновения, если: 1) шары двигались навстречу друг другу; 2) шары двигались друг за другом.
Решение:
Удар упругий, поэтому: 1) после столкновения шары движутся с разными скоростями; 2) суммарный импульс системы сохраняется, поскольку внешние силы, действующие на шары, скомпенсированы; 3) кинетическая энергия системы не изменяется. Для решения задачи воспользуемся законом сохранения импульса и законом сохранения механической энергии. Выполним пояснительные рисунки; ось ОХ направим вдоль движения шаров.
Запишем закон сохранения импульса в проекциях на ось ОХ и закон сохранения кинетической энергии:
Учтем, что 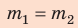
После простых преобразований получим:
Разделим второе уравнение системы на первое и получим более простую систему:
Решим полученную систему уравнений методом сложения и найдем скорости движения шаров после столкновения:
Ответ: для обоих случаев
Видим, что при упругом центральном ударе тела одинаковой массы обмениваются скоростями.
Выводы:
Вычисление импульса
Импульс тела — это векторная физическая величина, характеризующая движение, и определяется произведением массы тела и его скорости.
Обозначают импульс буквой р. Единицей импульса в СИ является один килограмм-метр в секунду (1 кг • м/с). Математически это записывают так:
Импульс силы — это векторная физическая величина, характеризующая действие силы за определенный интервал времени.
Определяется произведением среднего значения силы за определенный интервал времени и длительности этого интервала:
Импульсу присуще очень интересное и важное свойство, которое имеют немного физических величин. Это свойство сохранения. Оно заключается в том, что геометрическая сумма импульсов тел, взаимодействующих только друг с другом, сохраняется неизменной. Сами импульсы тел, конечно, изменяются, поскольку на каждое из тел действуют силы взаимодействия, но сумма импульсов остается неизменной (постоянной).
Это утверждение называют законом сохранения импульса. Закон сохранения импульса – один из самых важных законов природы. Его очень просто доказать, если взаимодействуют друг с другом два тела. Действительно, если первое тело действует на второе с силой 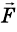
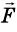
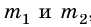
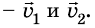
Тогда, согласно формуле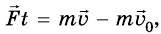
Изменив знаки обеих частей этого равенства на противоположные, перепишем его в виде:
В левой части этого равенства записана сумма начальных импульсов двух тел, а в правой – сумма импульсов этих же тел через время t. Эти суммы равны между собой. Таким образом, хотя импульс каждого из тел при взаимодействии изменяется, их полный импульс, то есть сумма импульсов обоих тел сохраняется неизменной. Что и требовалось доказать.
Можно также доказать, и опыты это подтверждают, если взаимодействуют не два, а много тел, то геометрическая сумма импульсов всех тел или системы тел остается неизменной. Важно только, чтобы эти тела взаимодействовали друг с другом и на них не действовали силы со стороны других тел, которые не входят в систему (или, чтобы эти внешние силы уравновешивались). Такую группу тел, которые не взаимодействуют с другими телами, не входящими в эту группу, называют замкнутой системой.
Именно для замкнутых систем и выполняется закон сохранения импульса:
- геометрическая сумма импульсов тел, образующих замкнутую систему, сохраняется постоянной при любых взаимодействиях тел этой системы между собой:
= const.
Отсюда следует, что взаимодействие тел сводится к тому, что одни тела передают часть своего импульса другим.
Импульс тела – это векторная величина. Следовательно, если сумма импульсов тел сохранится постоянной, то и сумма проекций этих импульсов на координатные оси также остается постоянной. Вследствие этого геометрическую сумму импульсов можно заменить суммой алгебраических их проекций.
Закон сохранения импульса можно проиллюстрировать такими опытами.
Опыт 1. Поставим на рельсы две тележки одинаковой массы m. К торцу одной тележки прикрепим пластилиновый шарик. Пусть тележки движутся навстречу друг другу с одинаковыми по модулю скоростями 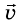
При столкновении обе тележки остановятся. Объяснить результаты опыта легко. До столкновения импульс левой тележки равен 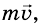
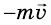
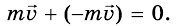
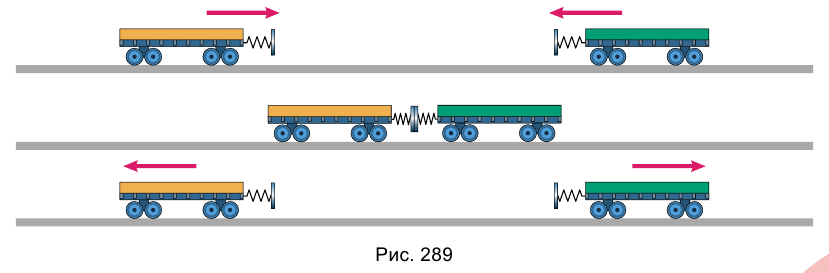
Опыт 2. Повернем тележки друг к другу пружинными буферами (рис. 289). Повторив опыт, убедимся в том, что после столкновения обе тележки разъедутся в противоположные стороны. При таком взаимодействии скорости движения тележек изменят свои направления на противоположные, модули скоростей останутся такими же, какими они были до
взаимодействия. Если до встречи импульс левой тележки равен 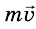
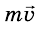
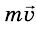
- Замкнутая система в физике
- Реактивное движение в физике
- Освоение космоса – история, этапы и достижения с фотографиями
- Закон сохранения механической энергии в физике
- Математика – язык физики
- Законы Ньютона в физике
- Гравитационные силы в физике
- Центр тяжести в физике (центр масс)




























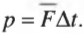
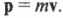
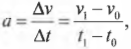
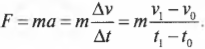
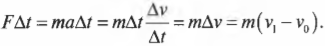
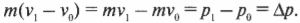
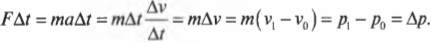
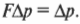
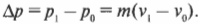
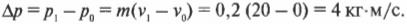
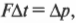
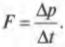
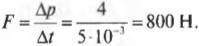
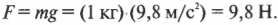
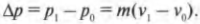
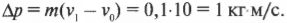
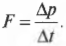
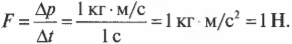
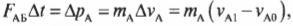
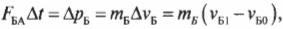
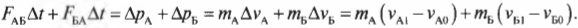
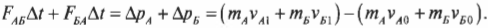
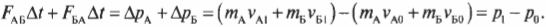
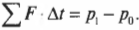
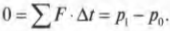

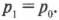
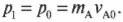
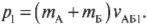
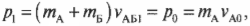
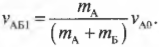
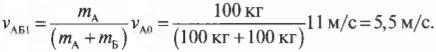
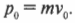
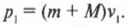
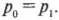
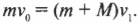
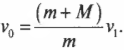
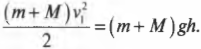
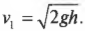
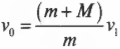
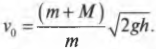
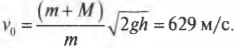
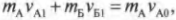
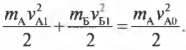
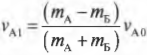
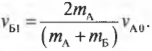
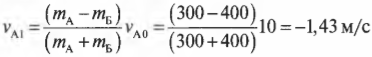
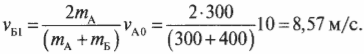
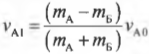
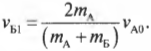
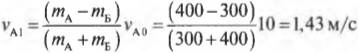
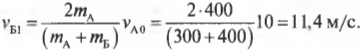
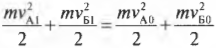
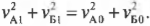
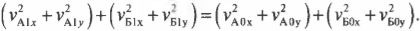
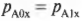
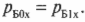
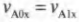
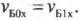
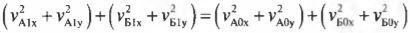
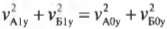
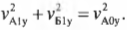
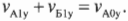
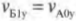
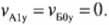
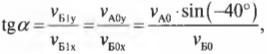
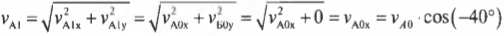
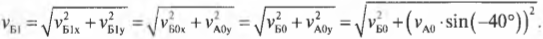
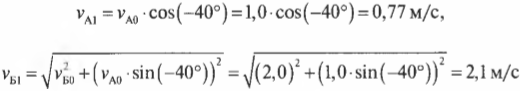
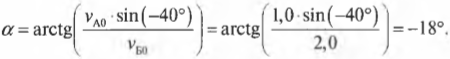
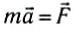
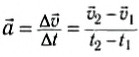
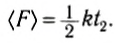
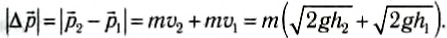
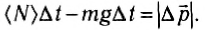
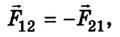
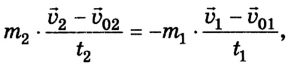
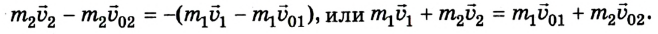
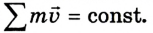
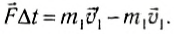
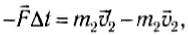
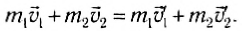
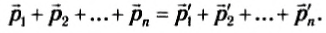
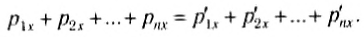

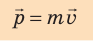
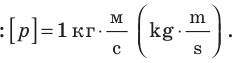
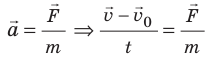
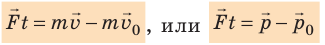

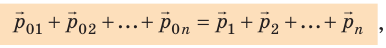
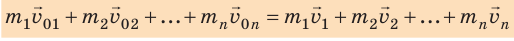





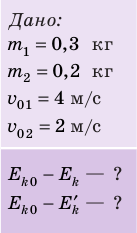
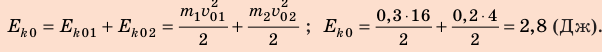



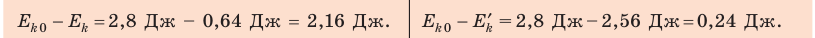
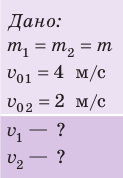






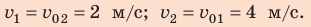
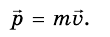
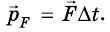
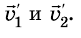
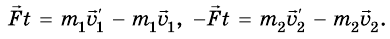
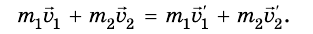
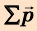 = const.
= const.