-
Определение передаточных чисел узлов трансмиссии
В первую очередь необходимо определить
передаточное число главной передачи,
коробки перемены передач и, если
требуется, колесной передачи.
2.1. Определение передаточного числа главной передачи
Передаточное число главной передачи
определяется по максимальной скорости
движения автомобиля, которая осуществима
на высшей передаче и на максимальной
частоте вращения двигателя по формуле
![]()
,
(5)
iквыс – высшая передача
коробки. Для автомобилей с высокооборотистым
двигателем iквыс=1,
т.е., прямая передача. Для автомобилей,
на которых установлен двигатель с
максимальной частотой вращения
коленчатого вала двигателя менее 2600
об/мин, iквыс=0,81…0,71 –
ускоряющая передача.
rк – радиус колеса, м;
Vmax – максимальная скорость,
км/ч.
Радиус колеса rк определяется
по формуле
![]()
,
(6)
где δш – коэффициент
деформации шины (δш=0,94 –
для грузовых автомобилей);
d – диаметр обода
колеса, дюймы; А – высота профиля
шины, дюймы. Следует учесть, что высота
профиля шины приблизительно равна
ширине профиля шины В, то есть,![]()
.
Для
подбора шин необходимо определить
нагрузку, приходящуюся на одно колесо
автомобиля. На задней оси у многих
автомобилей монтируется четыре шины,
однако, каждая шина задней оси испытывает
большую нагрузку, чем шина переднего
колеса, поэтому подбор шин грузового
автомобиля производится по весовой
нагрузке, приходящейся на одно заднее
колесо.
Маркировка колес включает ширину профиля
шины и посадочный диаметр обода, на
который одевается шина. Цифры 200, 220, 240,
280, 300 и т.д. обозначают ширину профиля
в миллиметрах, а 10.00, 11.00, 12.00 и т.д. – в
дюймах. Цифры 508, 610, 838 и др. – посадочный
диаметр обода в миллиметрах, а 13, 14, 15,
18, 20 и др. – в дюймах. В табл. П. 2 представлены
некоторые шины для автомобилей средней
грузоподъемности.
2.2. Определение числа ступеней коробки перемены передач
Число ступеней коробки переменных
передач для заданного автомобиля
выбирается по его типу.
Передаточное число первой передачи
(i1) определяется из условия
возможности движения
![]()
,
(7)
где Gсц -вес,
приходящийся на ведущие колеса полностью
груженого автомобиля, Н;
φ – коэффициент сцепления, φ=0,65;
ψmax – максимальный коэффициент
дорожного сопротивления; ψmax=0,3;
Memax – максимальный крутящий
момент двигателя, Нм;
η1 – трансмиссии на первой
передаче, η1=0,85.
2.3. Определение передаточных чисел промежуточных передач коробки
Передаточные числа промежуточных
передач коробки определяются по формуле
![]()
,
(8)
где n – число ступеней коробки передач,
выбираемое по типу автомобиля;
m – определяемая передача.
Передаточные числа, найденные по формуле
(8), являются ориентировочными и при
проектировании коробки передач могут
несколько изменяться в зависимости от
кинематического расчета всех элементов
коробки, но в задачу данной работы это
не входит.
Скорость автомобиля на соответствующей
передаче определяется по формуле
![]()
(9)
По
результатам расчета и выбранного
прототипа начертить кинематическую
схему автомобиля. Допускается изображение
структурной схемы автомобиля отдельно
от кинематических схем коробки передач
и дифференциала согласно рис. 2 – 4.
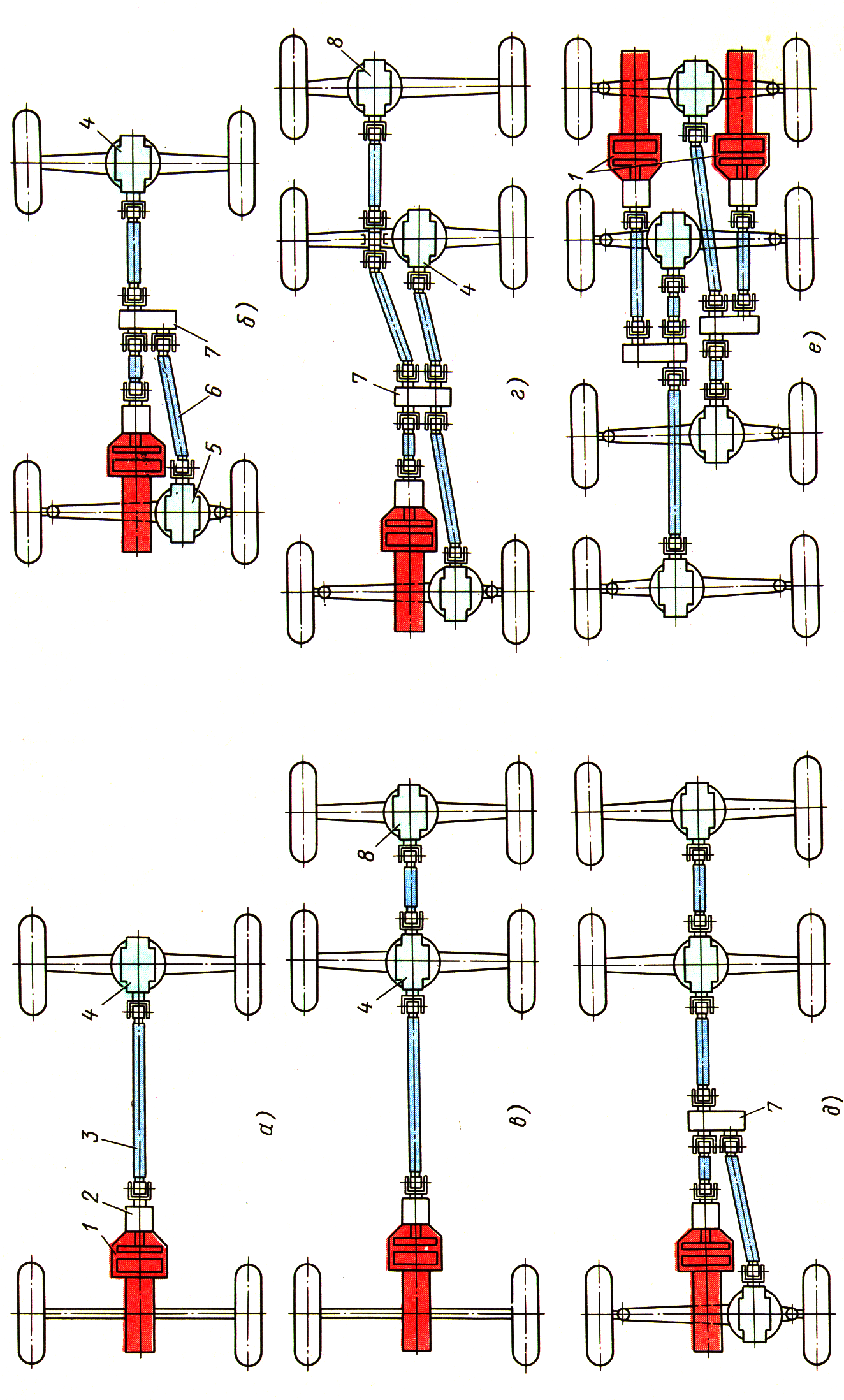

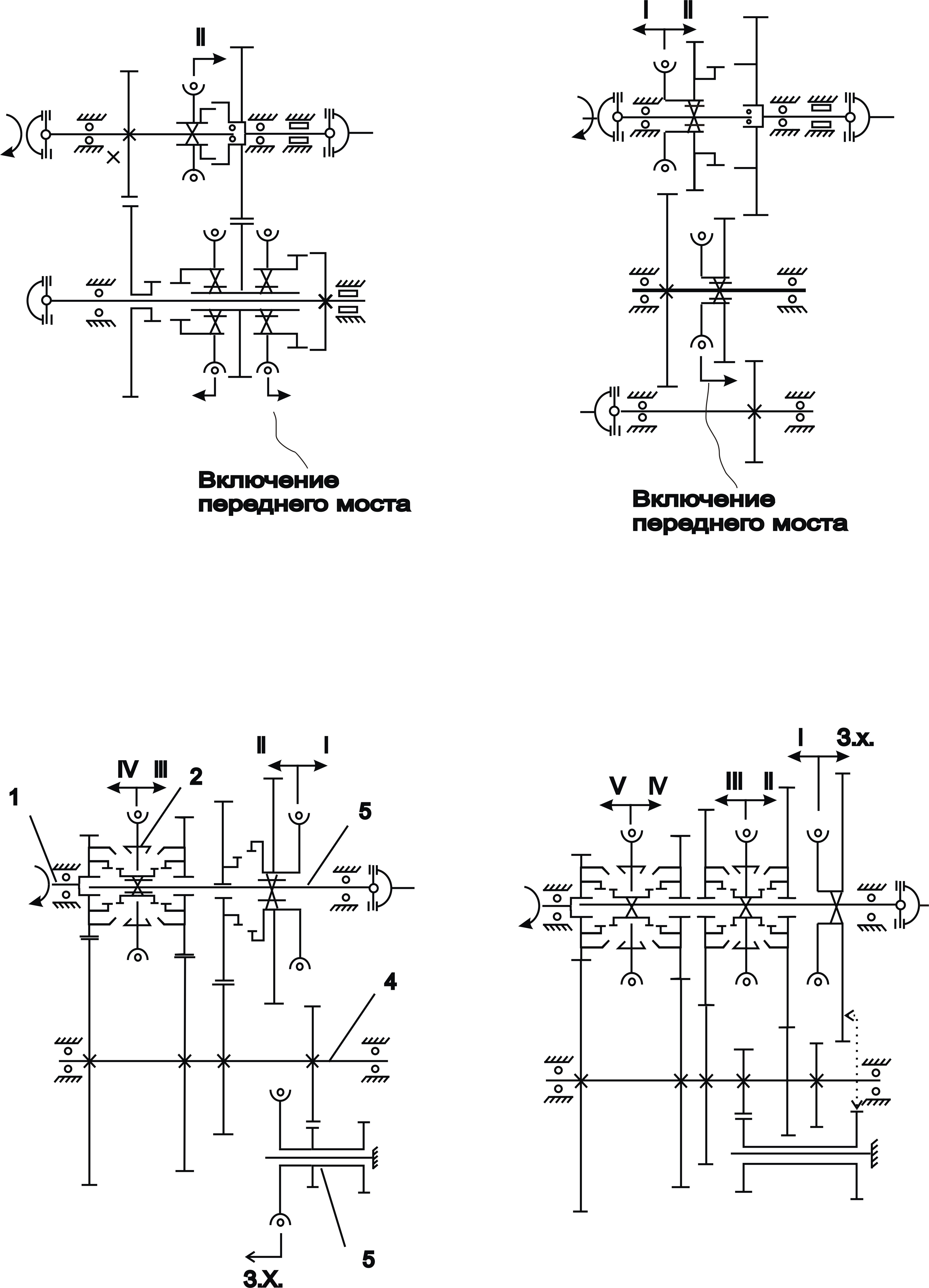
а б
в г
Рис. 3.
Кинематические схемы раздаточных
коробок и коробок передач
а –
трехвальная; б – четырехвальная;
в – трехвальная; г – четырехвальная;
1 –
первичный вал; 2– синхронизатор; 3
– вторичный вал; 4 – промежуточный
вал; 5 – блок шестерен заднего хода
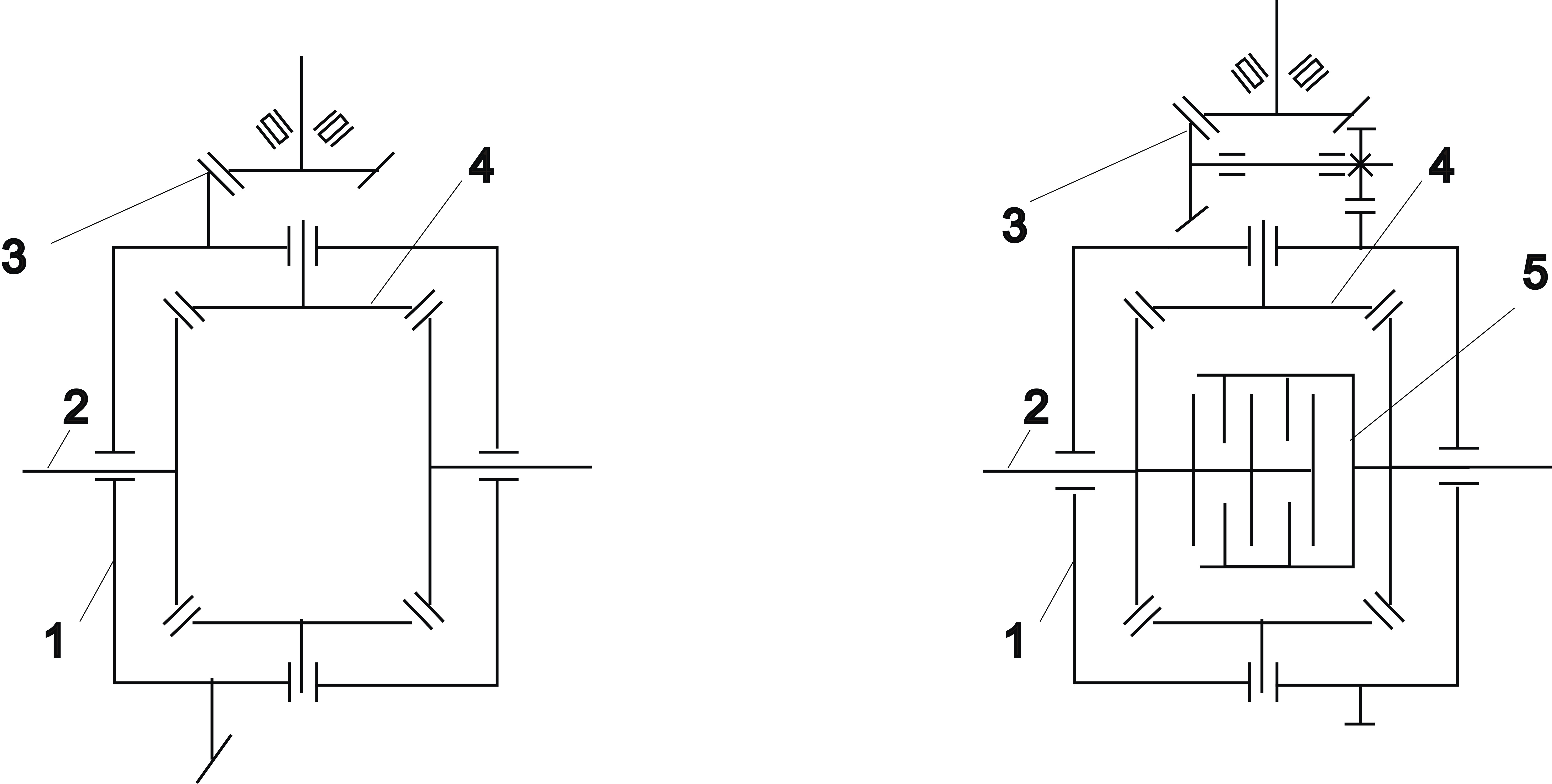
а б
Рис. 4.
Кинематические схемы дифференциалов
и главных передач:
а –
конический дифференциал с одноступенчатой
главной передачей;
б –
конический дифференциал с двухступенчатой
главной передачей и механизмом блокировки
дифференциала;
1 – коробка
дифференциала; 2– полуось колеса; 3
–главная передача;
4 –
сателлит; 5 – механизм блокировки
с внутренней муфтой постоянного момента
трения
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Любое подвижное соединение, передающее усилие и меняющее направление движения, имеет свои технические характеристики. Основным критерием, определяющим изменение угловой скорости и направления движения, является передаточное число. С ним неразрывно связано изменение силы – передаточное отношение. Оно вычисляется для каждой передачи: ременной, цепной, зубчатой при проектировании механизмов и машин.

Перед тем как узнать передаточное число, надо посчитать количество зубьев на шестернях. Затем разделить их количество на ведомом колесе на аналогичный показатель ведущей шестерни. Число больше 1 означает повышающую передачу, увеличивающую количество оборотов, скорость. Если меньше 1, то передача понижающая, увеличивающая мощность, силу воздействия.
Общее определение
Наглядный пример изменения числа оборотов проще всего наблюдать на простом велосипеде. Человек медленно крутит педали. Колесо вращается значительно быстрее. Изменение количества оборотов происходит за счет 2 звездочек, соединенных в цепь. Когда большая, вращающаяся вместе с педалями, делает один оборот, маленькая, стоящая на задней ступице, прокручивается несколько раз.
Передачи с крутящим моментом
В механизмах используют несколько видов передач, изменяющих крутящий момент. Они имеют свои особенности, положительные качества и недостатки. Наиболее распространенные передачи:
- ременная;
- цепная;
- зубчатая.
Ременная передача самая простая в исполнении. Используется при создании самодельных станков, в станочном оборудование для изменения скорости вращения рабочего узла, в автомобилях.
Ремень натягивается между 2 шкивами и передает вращение от ведущего в ведомому. Производительность низкая, поскольку ремень скользит по гладкой поверхности. Благодаря этому, ременной узел является самым безопасным способом передавать вращение. При перегрузке происходит проскальзывание ремня, и остановка ведомого вала.
Передаваемое количество оборотов зависит от диаметра шкивов и коэффициента сцепления. Направление вращения не меняется.

Переходной конструкцией является ременная зубчатая передача.
На ремне имеются выступы, на шестерне зубчики. Такой тип ремня расположен под капотом автомобиля и связывает звездочки на осях коленвала и карбюратора. При перегрузе ремень рвется, так как это самая дешевая деталь узла.
Цепная состоит из звездочек и цепи с роликами. Передающееся число оборотов, усилие и направление вращения не меняются. Цепные передачи широко применяются в транспортных механизмах, на конвейерах.
Характеристика зубчатой передачи
В зубчатой передаче ведущая и ведомая детали взаимодействуют непосредственно, за счет зацепления зубьев. Основное правило работы такого узла – модули должны быть одинаковыми. В противном случае механизм заклинит. Отсюда следует, что диаметры увеличиваются в прямой зависимости от количества зубьев. Одни значения можно в расчетах заменить другими.
Модуль – размер между одинаковыми точками двух соседних зубьев.
Например, между осями или точками на эвольвенте по средней линии Размер модуля состоит из ширины зуба и промежутка между ними. Измерять модуль лучше в точке пересечения линии основания и оси зубца. Чем меньше радиус, тем сильнее искажается промежуток между зубьями по наружному диаметру, он увеличивается к вершине от номинального размера. Идеальные формы эвольвенты практически могут быть только на рейке. Теоретически на колесе с максимально бесконечным радиусом.
Деталь с меньшим количеством зубьев называют шестерней. Обычно она ведущая, передает крутящий момент от двигателя.

Зубчатое колесо имеет больший диаметр и в паре ведомое. Оно соединено с рабочим узлом. Например, передает вращение с необходимой скоростью на колеса автомобиля, шпиндель станка.
Обычно посредством зубчатой передачи уменьшается количество оборотов и увеличивается мощность. Если в паре деталь, имеющая больший диаметр, ведущая, на выходе шестерня имеет большее количество оборотов, вращается быстрее, но мощность механизма падает. Такие передачи называют понижающими.
Зачем нужна паразитка
При взаимодействии шестерни и колеса происходит изменение сразу нескольких величин:
- количества оборотов;
- мощности;
- направление вращения.
Только в планетарных узлах с нарезкой зубьев по внутреннему диаметру венца сохраняется направление вращения. При наружном зацеплении ставится две одинаковые шестерни подряд. Их взаимодействие не меняет ничего, кроме направления движения. В этом случае обе зубчатые детали называются шестернями, колеса нет. Вторая, промежуточная, получила название «паразитка», поскольку в вычислениях не участвует, меняет только знак.

Виды зубчатых соединений
Зубчатое зацепление может иметь различную форму зуба на деталях. Это зависит от исходной нагрузки и расположения осей сопрягаемых деталей. Различают виды зубчатых подвижных соединений:
- прямозубая;
- косозубая;
- шевронная;
- коническая;
- винтовая;
- червячная.
Самое распространенное и простое в исполнении прямозубое зацепление. Наружная поверхность зуба цилиндрическая. Расположение осей шестерни и колеса параллельное. Зуб расположен под прямым углом к торцу детали.
Когда нет возможности увеличить ширину колеса, а надо передать большое усилие, зуб нарезают под углом и за счет этого увеличивают площадь соприкосновения. Расчет передаточного числа при этом не изменяется. Узел становится более компактным и мощным.
Недостаток косозубых зацеплений в дополнительной нагрузки на подшипники. Сила от давления ведущей детали действует перпендикулярно плоскости контакта. Кроме радиального, появляется осевое усилие.
Компенсировать напряжение вдоль оси и еще больше увеличить мощность позволяет шевронное соединение. Колесо и шестерня имеют 2 ряда косых зубьев, направленных в разные стороны. Передающее число рассчитывается аналогично прямозубому зацеплению по соотношению количества зубьев и диаметров. Шевронное зацепление сложное в исполнении. Оно ставится только на механизмах с очень большой нагрузкой.
В конической зубчатой передачи оси расположены под углом. Рабочий элемент нарезается по конической плоскости. Передаточное число таких пар может равняться 1, когда надо только изменить плоскость действия силы. Для увеличения мощности нарезается полукруглый зуб. Передающееся количество оборотов считается только по зубу, диаметр в основном используется при расчетах габаритов узла.

Винтовая передача имеет зуб, нарезанный под углом 45⁰. Это позволяет располагать оси рабочих элементов перпендикулярно в разных плоскостях. У червячной передачи нет шестерни, ее заменяет червяк. Оси деталей не пересекаются. Они расположены перпендикулярно в пространстве, но разных плоскостях. Передаточное число пары определяется количеством заходов резьбы на червяке.

Кроме перечисленных производят и другие виды передач, но они встречаются крайне редко и к стандартным не относятся.
Многоступенчатые редукторы
Как подобрать нужное передаточное число. Двигатель обычно выдает несколько тысяч оборотов в минуту. На выходе – колесах автомобиля и шпинделе станка, такая скорость вращения приведет к аварии. Мощности исполняющего механизма не хватит, чтобы рабочий инструмент мог резать металл, а колеса сдвинули автомобиль. Одна пара зубчатого зацепления не сможет обеспечить требуемое понижение или ведомая деталь должна иметь огромные размеры.
Создается многоступенчатый узел с несколькими парами зацеплений. Передаточное число редуктора считается как произведение чисел каждой пары.
Uр = U1×U2 × … ×Un;
Где:
Uр – передаточное число редуктора;
U1,2,n – каждой из пар.
Перед тем как подобрать передаточное число редуктора, надо определиться с количеством пар, направлением вращения выходного вала, и делать расчет в обратном порядке, исходя из максимально допустимых габаритов колес.

В многоступенчатом редукторе все зубчатые детали, находящиеся между ведущей шестерней на входе в редуктор и ведомым зубчатым венцом на выходном валу, называются промежуточными. Каждая отдельная пара имеет свое передающееся число, шестерню и колесо.
Редуктор и коробка скоростей
Любая коробка скоростей с зубчатым зацеплением является редуктором, но обратное утверждение неверно.
Коробка скоростей представляет собой редуктор с подвижным валом, на котором расположены шестерни разного размера. Смещаясь вдоль оси, он включает в работу то одну, то другую пару деталей. Изменение происходит за счет поочередного соединения различных шестерен и колес. Они отличаются диаметром и передающимся количеством оборотов. Это дает возможность изменять не только скорость, но и мощность.
Трансмиссия автомобиля
В машине поступательное движение поршня преобразуется во вращательное коленвала. Трансмиссия представляет собой сложный механизм с большим количеством различных узлов, взаимодействующих между собой. Ее назначение – передать вращение от двигателя на колеса и регулировка количества оборотов – скорости и мощности автомобиля.
В состав трансмиссии входит несколько редукторов. Это, прежде всего:
- коробка передач – скоростей;
- дифференциал.
Коробка передач в кинематической схеме стоит сразу за коленвалом, изменяет скорость и направление вращения.
Посредством переключения – перемещения вала, шестерни на валу соединяются поочередно с разными колесами. При включении задней скорости, через паразитку меняется направление вращения, автомобиль в результате движется назад.

Дифференциал представляет собой конический редуктор с двумя выходными валами, расположенными в одной оси напротив друг друга. Они смотрят в разные стороны. Передаточное число редуктора – дифференциала небольшое, в пределах 2 единиц. Он меняет положение оси вращения и направление. Благодаря расположению конических зубчатых колес напротив друг друга, при зацеплении с одной шестерней они крутятся в одном направлении относительно положения оси автомобиля, и передают вращательный момент непосредственно на колеса. Дифференциал изменяет скорость и направление вращения ведомых коничек, а за ними и колес.
Как рассчитать передаточное число
Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.
Расчет без учета сопротивления
В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.
u12 = ± Z2/Z1 и u21 = ± Z1/Z2,
Где u12 – передаточное число шестерни и колеса;
Z2 и Z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.
Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».
При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.
Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.
Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:
u16 = u12×u23×u45×u56 = z2/z1×z3/z2×z5/z4×z6/z5 = z3/z1×z6/z4
Способ расчета передаточного числа позволяет спроектировать редуктор с заранее заданными выходными значениями количества оборотов и теоретически найти передаточное отношение.
Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.
КПД зубчатой передачи
Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:
- трение соприкасаемых поверхностей;
- изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
- потери на шпонках и шлицах;
- трение в подшипниках.
Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.
Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.
При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.
Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.
Передаточное отношение зубчатой передачи
Значение передаточного числа зубчатой передачи совпадает передаточным отношением. Величина угловой скорости и момента силы изменяется пропорционально диаметру, и соответственно количеству зубьев, но имеет обратное значение.
Чем больше количество зубьев, тем меньше угловая скорость и сила воздействия – мощность.
При схематическом изображении величины силы и перемещения шестерню и колесо можно представить в виде рычага с опорой в точке контакта зубьев и сторонами, равными диаметрам сопрягаемых деталей. При смещении на 1 зубец их крайние точки проходят одинаковое расстояние. Но угол поворота и крутящий момент на каждой детали разный.
Например, шестерня с 10 зубьями проворачивается на 36°. Одновременно с ней деталь с 30 зубцами смещается на 12°. Угловая скорость детали с меньшим диаметром значительно больше, в 3 раза. Одновременно и путь, который проходит точка на наружном диаметре имеет обратно пропорциональное отношение. На шестерне перемещение наружного диаметра меньше. Момент силы увеличивается обратно пропорционально соотношению перемещения.
Крутящий момент увеличивается вместе с радиусом детали. Он прямо пропорционален размеру плеча воздействия – длине воображаемого рычага.

Передаточное отношение показывает, насколько изменился момент силы при передаче его через зубчатое зацепление. Цифровое значение совпадает с переданным числом оборотов.
Передаточное отношение редуктора вычисляется по формуле:
U12 = ±ω1/ω2=±n1/n2
где U12 – передаточное отношение шестерни относительно колеса;
ω1 и ω2 – угловые скорости ведущего и ведомого элемента соединения; n1 и n2 – частота вращения.

Отношение угловых скоростей можно считать через число зубьев. При этом направление вращения не учитывается и все цифры с положительным знаком.
Зубчатая передача имеет самый высокий КПД и наименьшую защиту от перегруза – ломается элемент приложения силы, приходится делать новую дорогостоящую деталь со сложной технологией изготовления.

Данная зубчатая передача имеет большую шестерню с 28 зубьями и меньшую шестерню с 10 зубьями.
Передаточное число (u) = 2.8 (28/10).
Передаточное отношение ( i ) данной передачи не очевидно и может быть равно как 2.8, так и 0.357.

Данная трёхзвенная планетарная передача имеет большое центральное зубчатое колесо в 56 зубьев и малое в 24 зуба. Её передаточное число (K) = 2,333 (56/24).
Понимание значения передаточного числа необходимо для того, чтобы рассчитать все шесть возможных передаточных отношений между двумя центральными зубчатыми колёсами и водилом.
Передаточное число — один из параметров пары зацепления из двух зубчатых колёс (двух шестерён), определяемый как соотношение числа зубьев большего зубчатого колеса к меньшему[1][2].
Формула расчёта[править | править код]
u = zБ / zМ
где
zБ – число зубьев большей шестерни;
zМ – число зубьев меньшей шестерни.
Трактовка определения[править | править код]
Определение передаточного числа одинаково применимо к любым механическим зубчатым передачам в виде пары зацепления из двух зубчатых колёс, независимо от типа: цилиндрическим, коническим, гипоидным, червячным.
Передаточное число всегда есть рациональное число. Для определения передаточного числа не имеет значения, какое зубчатое колесо является ведущим, а какое ведомым. Передаточное число показывает:
- Насколько данная пара зацепления в принципе может изменить крутящий момент в ту или иную сторону.
- Линейное соотношение диаметров зубчатых колёс.
Передаточное число не показывает:
- Передаточное отношение, для определения которого необходимо понимать, какое зубчатое колесо является ведущим, а какое ведомым.
Передаточное число планетарного механизма[править | править код]
Для любого простого или сложного планетарного механизма таковое определяется как соотношение зубьев большего центрального зубчатого колеса к меньшему[3][4].
Сходство и отличие от передаточного отношения[править | править код]
Передаточное число в отличие от передаточного отношения всегда положительное и больше или равно единице. Передаточное число характеризует передачу только количественно. Передаточное число и передаточное отношение могут совпадать только у передачи внутреннего зацепления. У передач внешнего зацепления они не совпадают, так как в любом случае имеют разные знаки: передаточное отношение – отрицательное, а передаточное число – положительное. Наиболее распространены понижающие передачи, так как частота вращения исполнительного механизма в большинстве случаев меньше частоты вращения вала двигателя.[5]
В современном техническом речевом обиходе термины передаточное отношение и передаточное число зачастую подразумеваются как синонимы. Объяснение этому проистекает из факта того, что подавляющее число зубчатых передач являются понижающими, а у таких передач передаточное отношение и передаточное число совпадают. Формально, такое смешение терминов есть ошибка, так как передаточное отношение всегда определяется через угловые и линейные перемещения ведущего и ведомого элемента[6]
[7], а передаточное число только через число зубьев пары зубчатых колёс и только для зубчатых передач вращением. Фактически, это настолько широко распространено, в том числе в технической литературе, что, вероятно, уже может считаться нормой.
Примеры современного употребления:
Для механизмов типа винт-гайка-сектор передаточное число определяется отношением радиуса начальной окружности зубьев сектора к шагу винта[8].
Передаточные числа червячных пар достаточно велики, достигая 26 и более, причём могут иметь переменное передаточное число в зависимости от угла поворота[9].
Примечания[править | править код]
- ↑ ГОСТ 16530-83, 1983, с. 19.
- ↑ ГОСТ 16530-83, 1983, с. 22.
- ↑ Анализ ПКП транспотных и тяговых машин, 2008, с. 17.
- ↑ ПКП колёсных и гусеничных машин, 2000, с. 12.
- ↑ Справочник конструктора; Машины и механизмы, 2019, с. 23.
- ↑ ГОСТ 19587-74, 1974, с. 11.
- ↑ ГОСТ 16530-83, 1983, с. 28.
- ↑ В зависимости от типа рулевой пары рулевые механизмы современных автомобилей разделяют на червячные, винтовые и … – Большая Энциклопедия Нефти и Газа. www.ngpedia.ru. Дата обращения: 14 февраля 2020.
- ↑ Для того чтобы облегчить управление в зоне наиболее частых поворотов рулевого колеса передаточное число рулевого … – Большая Энциклопедия Нефти и Газа. www.ngpedia.ru. Дата обращения: 14 февраля 2020.
Литература[править | править код]
- ГОСТ 16530-83. ПЕРЕДАЧИ ЗУБЧАТЫЕ; общие термины, определения и обозначения. — официальное. — Москва: ИПК Издательство стандартов, 1983. — 51 с.
- ГОСТ 19587-74. ПЕРЕДАЧИ ГИДРОДИНАМИЧЕСКИЕ; термины и определения. — официальное. — Москва: ИПК Издательство стандартов, 1974. — 37 с.
- Фещенко В. Н. Справочник конструктора. Книга 1. Машины и механизмы: учебно-практическое пособие / В. Н Фещенко. — 3-е изд. ипр. и доп. — М.: Инфра-Инженерия, 2019. — С. 23. — 400 с. — ISBN 978-5-9729-0252-1.
- Н.В.Филичкин. Анализ планетарных коробок передач транспортных и тяговых машин. — официальное. — Челябинск: ЮУрГУ, 2008. — 178 с. — ISBN 5-696-03134-X.
- В.М.Шарипов. Планетарные коробки передач колёсных и гусеничных машин. — официальное. — Москва: МГТУ МАМИ, 2000. — 142 с. — ISBN 5-94099-007-X.
Коробка передач для автомобиля – второй по важности (да и по стоимости) агрегат. Без неё автомобиль бы двигался в ограниченном диапазоне скоростей и был бы очень прожорливым. Именно трансмиссия ответственна за изменение передаваемого на привод крутящего момента.

Большинство современных КПП – ступенчатые, то есть позволяют изменять крутящий момент дискретно, по ступеням, что обеспечивается наличием зубчатой передачи. Схематически ступени можно представить себе в виде пар шестерёнок, характеризующихся разным передаточным числом.
Сегодня мы расскажем, что обозначает передаточное число коробки, как оно измеряется, на что влияет.
Общий принцип работы КПП
Классическая механическая коробка представляет собой редуктор, состоящий из множества ступеней. Основная задача редуктора – увеличить или уменьшить на выходе скорость вращения вала с одновременным изменением крутящего момента, передаваемого от коленвала силового агрегата на пару ведущих колёс. В МКПП работой редуктора управляют вручную, используя рычаг переключения передач, устанавливаемый в салоне ТС.
Увеличивая обороты мотора, водитель разгоняет машину, но на каждой конкретной передаче существует максимальная скорость, выше которой авто ехать не сможет Проблема решается переходом на другую передачу с увеличенным передаточным числом, что позволяет снизить обороты при примерно том же крутящем моменте.
Но что такое передаточное число коробки, о котором мы упоминаем?
Под этим термином понимают вполне конкретную величину: соотношение количества зубьев, имеющихся на ведомой шестерне, к числу зубьев на одной из ведущих шестерен. То есть при переключении передач на шестерню с 30 зубьями при 60 зубьях на ведомой шестерне будем иметь передаточное число, равное двум (60:30).
Это значит, что передаточное число коробки передач говорит о том, насколько быстрее будет вращаться ведомый вал по сравнению со скоростью вращения коленвала.
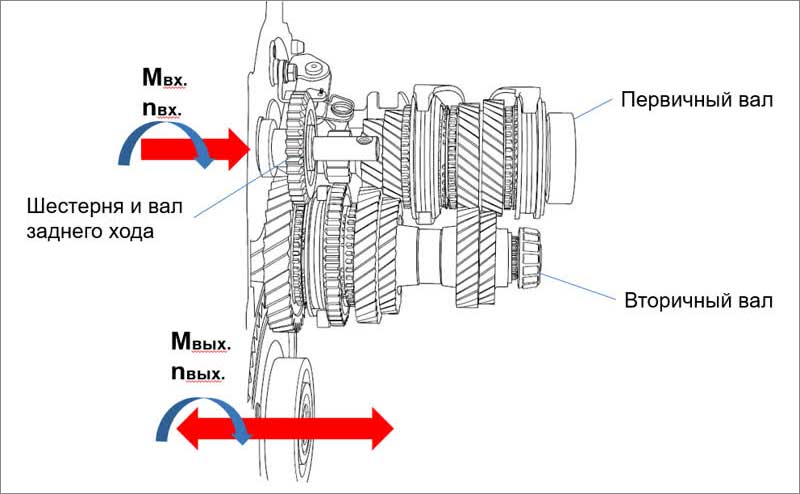
Как рассчитываются передаточные числа КПП
Алгоритм определения передаточного числа коробки:
- за базовую берём формулу К = Квм/Квщ, где Квм — число зубцов ведомой шестерни, Квщ — ведущей. Если, скажем, требуется определить ПЧ крутящего момента на колеса от трансмиссии, необходимо взять за исходные данные число зубцов шестерни дифференциала, которая будет ведомой, и количество зубцов шестерни вторичного вала КПП. Полученное значение называют ПЧ главной пары;
- итак, пускай на коробке, расположенной на вторичном валу, имеется 15 зубьев, на шестерне дифференциала – 53 зубца. Подставив эти значения в нашу формулу, получим значение ПЧ для этой пары, равное 3,5. Это означает, что вал дифференциала будет вращаться медленнее вторичного вала коробки в 3,5 раза;
- аналогичным образом рассчитываются ПЧ для каждой пары шестерен, присутствующих в трансмиссии. Чем ближе они будут находиться, тем плавнее будет осуществляться разгон авто, если передачи переключать последовательно друг за другом. По передаточным числам КПП можно произвести расчёт скорости вращения мотора, вернее, разницу скоростей между высшей и низшей передачами, разделив ПЧ первой передачи на ПЧ самой высокой;
- рост передаточного числа, приводит к более коростному разгону автомобиля, но придётся чаще переключаться. Чем меньше ПЧ, тем выше максимально достижимая скорость, но разгоняться придётся дольше.
В принципе такой способ расчёта применяется при разработке трансмиссии, но здесь многое зависит от точности подбора передаточных чисел – это влияет не только на максимальную скорость автомашины, но и её динамические характеристики.
Узнать ПЧ для конкретной модели авто можно просмотрев её технические характеристики в руководстве пользователя. Если таковые найти не удалось, посчитать отношение для каждых пар МКПП можно и самостоятельно.
Делается это следующим образом:
- машина загоняется на яму, все колёса, кроме одного ведущего, фиксируются противооткатными упорами;
- выставляем рычаг КП в нейтральное положение;
- мелом фиксируем текущее положение колеса, поставив метки на шине и полу (добиваясь их совмещения);
- аналогичную операцию выполняем с фланцем и корпусом редуктора;
- пуская помощник вращает колесо, а вы подсчитывайте, сколько оборотов сделает вал редуктора. Помощник добивается повторного совпадения меток, подсчитывая количество оборотов колеса;
- полученное значение делим пополам, а затем на количество оборотов, выполненных карданным валом. Результирующее значение и будет искомым передаточным числом.
Как динамика машины зависит от передаточного числа
Чем правильнее (читай – сбалансированнее) подобраны ПЧ, тем эффективнее будет работать коробка, а износ шестерней будет сведён к минимуму. Но такой подбор – задача нелёгкая, поскольку необходимо учитывать множество факторов: мощность силового агрегата, назначение транспортного средства, диаметр колеса и т. д.
Величина передаточного числа влияет на то, как изменяется крутящий момент на выходе конкретной пары, а в конечном итоге – на валу, идущему к ведущим колесам. Для изменения ПЧ подбирают шестерни с увеличенным или уменьшённым количеством зубьев.
При высоком ПЧ автомобиль будет разгоняться быстрее, то есть будет обладать большей динамикой, но длина передачи будет короткой. Под этим термином понимают, насколько быстро достигаются максимальные обороты коленвала (короткие передачи расположены снизу, и переключаться здесь нужно быстро).
При уменьшении ПЧ мы ухудшаем динамику авто, но зато можем разгонять её до больших скоростей. Именно поэтому на самой высокой передаче обгон выполнять не рекомендуется, нужно перейти на меньшую и переключиться на высшую после завершения манёвра.
Конструкторы, подбирая передаточные числа, стремятся найти компромиссное решение, когда и скорость высока, и разгонные характеристики не страдают.
В автоспорте многие гонщики стремятся сделать передаточные числа коробки передач со строго последовательным уменьшением на определённое значение. Это делается для того, чтобы спортсмен переключался при разгоне «на автомате», то есть длина передач делается примерно равной.
Высокая скорость – режим, характерный для движения по прямой. Если трасса извилистая, рекомендуется использовать ПЧ с большими значениями – такой подбор в зависимости от типа трассы приходит с опытом.

Тюнинг КПП с изменением передаточного отношения
Не все знают, что лучшие динамические показатели зависят не от мощности, а достигаются в том диапазоне оборотов, который характернее для максимального крутящего момента. То есть в граничных значениях частоты оборотов коленвала, наименьшем и наибольшем, крутящий момент не достигает своего максимума.
Другими словами, чем большей будет разница между текущими и максимальными оборотами, тем хуже будет происходить набор скорости. В классических коробках передаточные числа стараются подобрать таким образом, чтобы разгон авто был комфортен на низших передачах, а наивысшие использовать для поддержания высокой скорости, экономя при этом горючее.
Если экономичность не является критическим показателем, то можно улучшить динамику, изменяя ПЧ. В этом случае уменьшается диапазон скоростей вращения коленвала при движении на одной передаче, то есть она становится короче, при этом происходит сближение ПЧ рядом расположенных передач. Для этого даже есть свой термин – сближенный ряд КПП.
Что это означает с точки зрения водителя? Двигатель достигает максимальных оборотов на меньшей передаче, но при переходе на более высокую ступень обороты остаются на примерно том же уровне – падают, но не критично, оставаясь в поддиапазоне максимального крутящего момента.
Существует несколько путей решения этой задачи – например, установить колёса меньшего диаметра или изменить передаточное число главной пары (например, увеличить с 3,7 до 4,0). А можно и совместить эти методы.
Многие поступают так: если конкретная модель имеет комплектации с разными силовыми агрегатами (например, 1,1, 1,3 и 1,6 л.), то передаточное число главной пары для автомобиля с 1,6-литровым мотором делают равным ПЧ, характерному младшим версиям.
То есть в результате такого тюнинга при установке ПЧ в значение 4,0 вместо штатных 3,7 передаточное число на пятой передаче станет таким же, как на четвёртой. Если при этом «обуть» машину в покрышки с меньшим диаметром, это ещё больше понизит передаточное число. То есть машина будет разгоняться намного быстрее, но и бензина кушать больше.
После такого апгрейда на 5-й передаче двигатель будет раскручиваться «по полной», что не добавит комфорта пассажирам. Так что подобный тюнинг уместен только в случае острой необходимости с учётом других характеристик машины (её веса, мощности двигателя, режима эксплуатации).
Download Article
Download Article
In mechanical engineering, a gear ratio is a direct measure of the ratio of the rotational speeds of two or more interlocking gears. As a general rule, when dealing with two gears, if the drive gear (the one directly receiving rotational force from the engine, motor, etc.) is bigger than the driven gear, the latter will turn more quickly, and vice versa. We can express this basic concept with the formula Gear ratio = T2/T1, where T1 is the number of teeth on the first gear and T2 is the number of teeth on the second.
Two Gears
-

1
Start with a two-gear train. To be able to determine a gear ratio, you must have at least two gears engaged with each other — this is called a “gear train.” Usually, the first gear is a “drive gear” attached to the motor shaft and the second is a “driven gear” attached to the load shaft. There may also be any number of gears between these two to transmit power from the drive gear to the driven gear: these are called “idler gears.”[1]
- For now, let’s look at a gear train with only two gears in it. To be able to find a gear ratio, these gears have to be interacting with each other — in other words, their teeth need to be meshed and one should be turning the other. For example purposes, let’s say that you have one small drive gear (gear 1) turning a larger driven gear (gear 2).
-

2
Count the number of teeth on the drive gear. One simple way to find the gear ratio between two interlocking gears is to compare the number of teeth (the little peg-like protrusions at the edge of the wheel) that they both have. Start by determining how many teeth are on the drive gear. You can do this by counting manually or, sometimes, by checking for this information labeled on the gear itself.[2]
- For example purposes, let’s say that the smaller drive gear in our system has 20 teeth.
Advertisement
-

3
Count the number of teeth on the driven gear. Next, determine how many teeth are on the driven gear exactly as you did before for the drive gear.
- Let’s say that, in our example, the driven gear has 30 teeth.
-

4
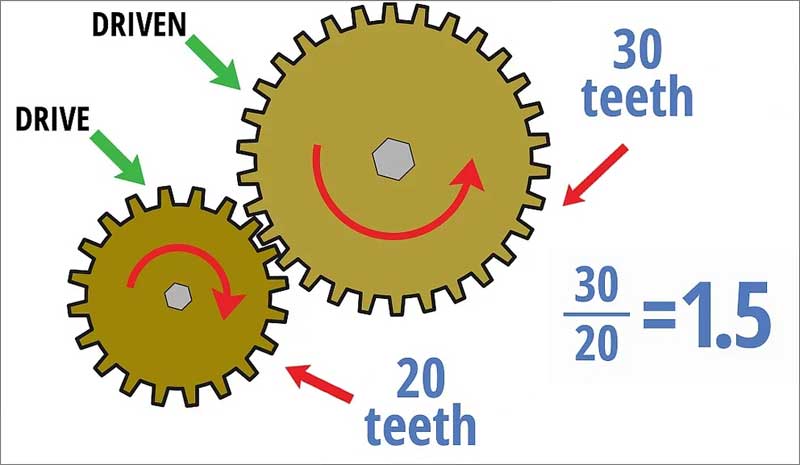
Divide one teeth count by the other. Now that you know how many teeth are on each gear, you can find the gear ratio relatively simply. Divide the driven gear teeth by the drive gear teeth. Depending on your assignment, you may write your answer as a decimal, a fraction, or in ratio form (i.e., x : y).[3]
- In our example, dividing the 30 teeth of the driven gear by the 20 teeth of the drive gear gets us 30/20 = 1.5. We can also write this as 3/2 or 1.5 : 1, etc.
- What this gear ratio means is that the smaller driver gear must turn one and a half times to get the larger driven gear to make one complete turn. This makes sense — since the driven gear is bigger, it will turn more slowly.
Advertisement
More than Two Gears
-

1
Start with a gear train of more than two gears. As its name suggests, a “gear train” can also be made from a long sequence of gears — not just a single driver gear and a single driven gear. In these cases, the first gear remains the driver gear, the last gear remains the driven gear, and the ones in the middle become “idler gears.” These are often used to change the direction of rotation or to connect two gears when direct gearing would make them unwieldy or not readily available.[4]
- Let’s say for example purposes that the two-gear train described above is now driven by a small seven-toothed gear. In this case, the 30-toothed gear remains the driven gear and the 20-toothed gear (which was the driver before) is now an idler gear.
-

2
Divide the teeth numbers of the drive and driven gears. The important thing to remember when dealing with gear trains with more than two gears is that only the driver and driven gears (usually the first and last ones) matter. In other words, the idler gears don’t affect the gear ratio of the overall train at all. When you’ve identified your driver gear and your driven gear, you can find the gear ratio exactly as before.
- In our example, we would find the gear ratio by dividing the thirty teeth of the driven gear by the seven teeth of our new driver. 30/7 = about 4.3 (or 4.3 : 1, etc.) This means that the driver gear has to turn about 4.3 times to get the much larger driven gear to turn once.
-

3
If desired, find the gear ratios for the intermediate gears. You can find the gear ratios involving the idler gears as well, and you may want to in certain situations. In these cases, start from the drive gear and work toward the load gear. Treat the preceding gear as if it were the drive gear as far as the next gear is concerned. Divide the number of teeth on each “driven” gear by the number of teeth on the “drive” gear for each interlocking set of gears to calculate the intermediate gear ratios.
- In our example, the intermediate gear ratios are 20/7 = 2.9 and 30/20 = 1.5. Note that neither of these are equal to the gear ratio for the entire train, 4.3.
- However, note also that (20/7) × (30/20) = 4.3. In general, the intermediate gear ratios of a gear train will multiply together to equal the overall gear ratio.
Advertisement
-

1
Find the rotational speed of your drive gear. Using the idea of gear ratios, it’s easy to figure out how quickly a driven gear is rotating based on the “input” speed of the drive gear. To start, find the rotational speed of your drive gear. In most gear calculations, this is given in rotations per minute (RPM), though other units of velocity will also work.[5]
- For example, let’s say that in the example gear train above with a seven-toothed driver gear and a 30-toothed driven gear, the drive gear is rotating at 130 RPMs. With this information, we’ll find the speed of the driven gear in the next few steps.
-

2
Plug your information into the formula S1 × T1 = S2 × T2. In this formula, S1 refers to the rotational speed of the drive gear, T1 refers to the teeth in the drive gear, and S2 and T2 to the speed and teeth of the driven gear. Fill in the variables until you have only one left undefined.
- Often, in these sorts of problems, you’ll be solving for S2, though it’s perfectly possible to solve for any of the variables. In our example, plugging in the information we have, we get this:
- 130 RPMs × 7 = S2 × 30
-

3
Solve. Finding your remaining variable is a matter of basic algebra. Just simplify the rest of the equation and isolate the variable on one side of the equals sign and you will have your answer. Don’t forget to label it with the correct units — you can lose points for this in schoolwork.
- In our example, we can solve like this:
- 130 RPMs × 7 = S2 × 30
- 910 = S2 × 30
- 910/30 = S2
- 30.33 RPMs = S2
- In other words, if the drive gear spins at 130 RPMs, the driven gear will spin at 30.33 RPMs. This makes sense — since the driven gear is much bigger, it will spin much slower.
Advertisement
Add New Question
-
Question
If a 38 tooth gear running at 360rpm is driving another gear at 144rpm, what is the number of teeth on the driven gear?

T1*S1=S2*T2 where, T1=number of teeth on the driver gear, S1= angular speed on the driver gear, T2=number of teeth on the driven gear and S2=angular speed on the driven gear. 38 teeth*360rpm=T2*144rpm. T2=95 teeth on the driven gear.
-
Question
How do I determine my gear ratio in my gear box?

If you can not see the gears you can mark the shaft and the start point on the gear box and count the number of times it revolves when you spin the other shaft one full rotation.
-
Question
What is gear up and gear down?

Gear up is when you drive a smaller gear with a larger gear thus creating a faster RPM at the output but less torque. Gear down is to drive a larger gear with a smaller gear creating a slower RPM at the output but more torque.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
The power needed to drive the load is geared up or down from the motor by the gear ratio. The motor must be sized to provide the power needed by the load after the gear ratio is taken in to consideration. A geared up system (where load RPM is greater than motor RPM) will require a motor that delivers optimal power at lower rotational speeds.
-
To see the principles of gear ratio in action, take a ride on your bike! Notice that it is easiest to go up hills when you have a small gear in front and a big one in the back. While it’s easier to turn the smaller gear with the leverage from your pedals, it takes many rotations to get your rear wheel to rotate compared to the gear settings you’d use for flat sections, making you go slower.
-
A geared down system (where load RPM is less than motor RPM) will require a motor that delivers optimal power at higher rotational speeds.
Advertisement
References
About This Article
Article SummaryX
To determine gear ratio of a gear train with 2 gears, start by identifying your gears. The gear attached to the motor shaft is considered the first gear, or the “drive gear”, and the other gear, whose teeth are meshed with the drive gear, is considered the second gear, or “driven gear.” Count the number of teeth on the drive gear and on the driven gear. Then, divide the number of teeth on the driven gear by the number of teeth on the drive gear to get the gear ratio. For example, if the drive gear has 20 teeth and the driven gear has 30 teeth, the gear ratio is 1.5. If you want to learn how to use the gear ratio to calculate the gears’ speeds, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,661,746 times.
Reader Success Stories
-

Marlo Deguzman
Aug 5, 2017
“I am currently in school for my airframe and power plant licenses, and this helped me gain the confidence work…” more
