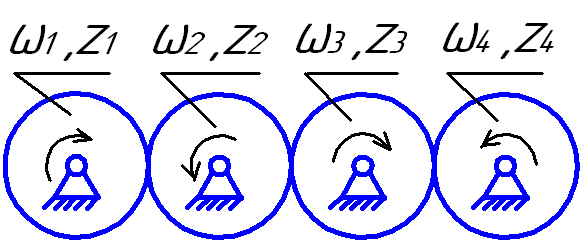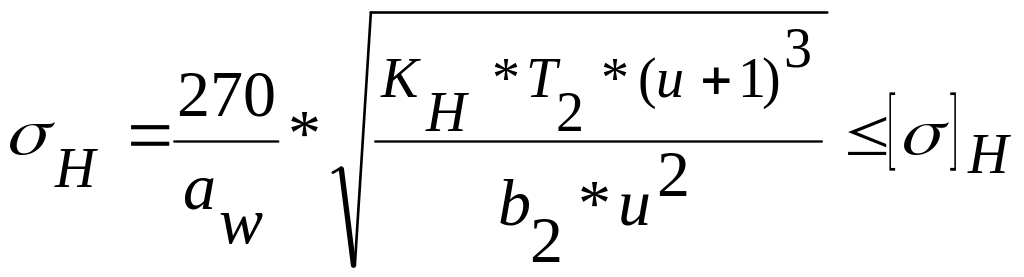Загрузить PDF
Загрузить PDF
В машиностроении передаточное отношение является показателем отношения частоты вращения двух или более сцепленных шестерен. Как правило, когда мы имеем дело с двумя шестернями, и ведущая шестерня (получающая поворачивающую силу непосредственно от двигателя) больше ведомой шестерни, то последняя вращается быстрее (и наоборот). Формула для вычисления: передаточное отношение = T2/ T1, где T1 — количество зубьев первой шестерни, Т2 — количество зубьев второй шестерни.[1]
Две шестерни
-
1
Для того чтобы определить передаточное отношение, у вас должно быть по крайней мере две шестерни, сцепленных друг с другом; такое сцепление называется зубчатой передачей. Как правило, первая шестерня является ведущей шестерней (крепится к валу двигателя), а вторая — ведомой шестерней (крепится к валу нагрузки). Между ведущей и ведомой шестернями может быть сколь угодно много шестерен. Они называются промежуточными.
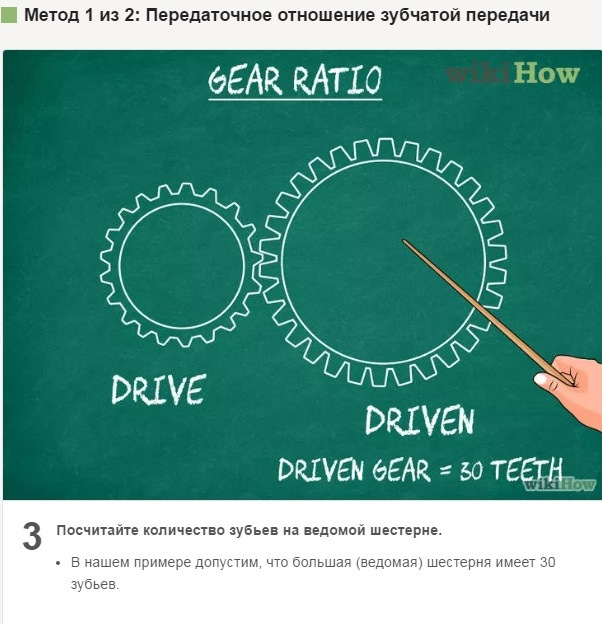
- Сейчас рассмотрим зубчатую передачу с двумя шестернями. Для определения передаточного отношения эти шестерни должны быть сцеплены друг с другом (то есть их зубья сцеплены и одна шестерня поворачивает другую). Например, дана небольшая ведущая шестерня (шестерня 1) и большая ведомая шестерня (шестерня 2).
-
2
Посчитайте количество зубьев на ведущей шестерне. Простейший способ найти передаточное отношение между двумя шестернями — сравнить количество зубьев на каждой из них. Начните с определения количества зубьев на ведущей шестерне. Вы можете сделать это вручную или посмотреть на маркировку шестерни.
- В нашем примере допустим, что меньшая (ведущая) шестерня имеет 20 зубьев.
-
3
Посчитайте количество зубьев на ведомой шестерне.
- В нашем примере допустим, что большая (ведомая) шестерня имеет 30 зубьев.
-
4
Разделите количество зубьев ведомой шестерни на количество зубьев ведущей шестерни, чтобы вычислить передаточное отношение. В зависимости от условий задачи вы можете записать ответ в виде десятичной дроби, обыкновенной дроби или в виде отношения (х:у).
- В нашем примере: 30/20 = 1,5. Вы также можете записать ответ в виде 3/2 или 1,5:1.
- Такое передаточное отношение означает, что меньшая ведущая шестерня должна совершить полтора оборота, чтобы большая ведомая шестерня совершила один оборот. Это имеет смысл, так как ведомая шестерня больше, а значит вращается медленнее.[2]
Реклама
Более двух шестерен
-
1
Зубчатая передача может включать сколь угодно большое количество шестерен. В этом случае первая шестерня является ведущей шестерней (крепится к валу двигателя), а последняя — ведомой шестерней (крепится к валу нагрузки). Между ведущей и ведомой шестернями может быть несколько промежуточных шестерен; они используются для изменения направления вращения или для сцепления двух шестерен (когда сцепление напрямую невозможно).[3]
- Рассмотрим пример, приведенный выше, но теперь ведущей шестерней станет шестерня с 7 зубьями, а шестерня с 20 зубьями превратится в промежуточную шестерню (ведомая шестерня с 30 зубьями остается той же).
-
2
Разделите количество зубьев ведомой шестерни на количество зубьев ведущей шестерни. Помните, что при определении передаточного отношения зубчатой передачи с несколькими шестернями важно знать только количество зубьев ведомой шестерни и количество зубьев ведущей шестерни, то есть промежуточные шестерни на значение передаточного отношения не влияют.
- В нашем примере: 30/7 = 4,3. Это означает, что ведущая шестерня должна совершить 4,3 оборота, чтобы ведомая (большая) шестерня совершила один оборот.
-
3
Если необходимо, найдите передаточные отношения для промежуточных шестерен. Для этого начните с ведущей шестерни и двигайтесь в направлении ведомой шестерни. При каждом новом вычислении передаточного отношения для промежуточных шестерен рассматривайте предыдущую шестерню в качестве ведущей (и делите количество зубьев ведомой шестерни на количество зубьев ведущей шестерни).
- В нашем примере передаточные отношения для промежуточной шестерни: 20/7 = 2,9 и 30/20 = 1,5. Заметьте, что передаточные отношения для промежуточной шестерни отличаются от передаточного отношения всей зубчатой передачи (4,3).
- Также заметьте, что (20/7) × (30/20) = 4,3. То есть для вычисления передаточного отношения всей зубчатой передачи необходимо перемножить значения передаточных отношений для промежуточных шестерен.
Реклама
-
1
Определите частоту вращения ведущей шестерни. Используя передаточное отношение и частоту вращения ведущей шестерни, можно запросто вычислить частоту вращения ведомой шестерни. Как правило, частота вращения измеряется в оборотах в минуту (rpm).
- Рассмотрим пример зубчатой передачи, описанной выше (с тремя шестернями). Здесь частота вращения ведущей шестерни равна 130 оборотам в минуту. Вычислим частоту вращения ведомой шестерни.
-
2
Подставьте соответствующие значения в формулу: S1 × T1 = S2 × T2, где S1, Т1 — частота вращения и количество зубьев ведущей шестерни; S2, Т2 — частота вращения и количество зубьев ведомой шестерни.
- В нашем примере нужно найти S2, но по этой формуле вы можете найти любую переменную.
- 130 rpm × 7 = S2 × 30
-
3
Теперь просто обособьте неизвестную переменную на одной стороне уравнения, чтобы получить ответ. Не забудьте приписать к нему соответствующую единицу измерения.
- В нашем примере:
- 130 rpm × 7 = S2 × 30
- 910 = S2 × 30
- 910/30 = S2
- 30,33 rpm = S2
- Другими словами, если ведущая шестерня вращается со скоростью 130 оборотов в минуту, ведомая шестерня будет вращаться со скоростью 30,33 оборотов в минуту. Это имеет смысл, так как ведомая шестерня значительно больше, а значит вращается намного медленнее.
Реклама
Советы
- Для того, чтобы понять принцип передаточного отношения в действии, покатайтесь на велосипеде! Обратите внимание, что проще всего ехать в гору, когда у вас небольшая шестерня спереди, а большая сзади. Хотя педалями легче крутить меньшую шестерню, понадобится множество вращений, чтобы заставить заднее колесо вращаться, то есть скорость велосипеда будет ниже.
- Мощность, необходимая для движения нагрузки, может увеличиваться или уменьшаться (относительно мощности двигателя) посредством зубчатой передачи. При проектировании двигателя необходимо учитывать передаточное отношение, чтобы мощность двигателя соответствовала характеру будущей нагрузки. Повышающая система (в которой обороты вала нагрузки выше, чем обороты двигателя) требует мотора, вырабатывающего оптимальную мощность при меньших скоростях вращения ведущего вала.
- С другой стороны, понижающая система (в которой обороты вала нагрузки ниже, чем обороты двигателя) требует мотора, вырабатывающего оптимальную мощность при больших скоростях вращения ведущего вала.
Реклама
Об этой статье
Эту страницу просматривали 256 816 раз.
Была ли эта статья полезной?
Вопрос возник еще в теме www.drive2.ru/l/5042113/ А что такое передаточное число и как его рассчитать? И на что оно влияет?
В машиностроении передаточное отношение является показателем отношения частоты вращения двух или более сцепленных шестерен. Как правило, когда мы имеем дело с двумя шестернями, и ведущая шестерня (получающая поворачивающую силу непосредственно от двигателя) больше ведомой шестерни, то последняя вращается быстрее (и наоборот). Формула для вычисления: передаточное отношение = T2/ T1, где T1 – количество зубьев первой шестерни, Т2 – количество зубьев второй шестерни
Источники и ссылки:
1. ↑ bowlesphysics.com/images/…Gears_and_Gear_Ratios.pdf
2. ↑ bowlesphysics.com/images/…Gears_and_Gear_Ratios.pdf
3. ↑ www.education.rec.ri.cmu.…um/multimedia/idler.shtml
4. ↑ www.schsm.org/html/gear_ratio_calculations.html
Download Article
Download Article
In mechanical engineering, a gear ratio is a direct measure of the ratio of the rotational speeds of two or more interlocking gears. As a general rule, when dealing with two gears, if the drive gear (the one directly receiving rotational force from the engine, motor, etc.) is bigger than the driven gear, the latter will turn more quickly, and vice versa. We can express this basic concept with the formula Gear ratio = T2/T1, where T1 is the number of teeth on the first gear and T2 is the number of teeth on the second.
Two Gears
-
1
Start with a two-gear train. To be able to determine a gear ratio, you must have at least two gears engaged with each other — this is called a “gear train.” Usually, the first gear is a “drive gear” attached to the motor shaft and the second is a “driven gear” attached to the load shaft. There may also be any number of gears between these two to transmit power from the drive gear to the driven gear: these are called “idler gears.”[1]
- For now, let’s look at a gear train with only two gears in it. To be able to find a gear ratio, these gears have to be interacting with each other — in other words, their teeth need to be meshed and one should be turning the other. For example purposes, let’s say that you have one small drive gear (gear 1) turning a larger driven gear (gear 2).
-
2
Count the number of teeth on the drive gear. One simple way to find the gear ratio between two interlocking gears is to compare the number of teeth (the little peg-like protrusions at the edge of the wheel) that they both have. Start by determining how many teeth are on the drive gear. You can do this by counting manually or, sometimes, by checking for this information labeled on the gear itself.[2]
- For example purposes, let’s say that the smaller drive gear in our system has 20 teeth.
Advertisement
-
3
Count the number of teeth on the driven gear. Next, determine how many teeth are on the driven gear exactly as you did before for the drive gear.
- Let’s say that, in our example, the driven gear has 30 teeth.
-
4
Divide one teeth count by the other. Now that you know how many teeth are on each gear, you can find the gear ratio relatively simply. Divide the driven gear teeth by the drive gear teeth. Depending on your assignment, you may write your answer as a decimal, a fraction, or in ratio form (i.e., x : y).[3]
- In our example, dividing the 30 teeth of the driven gear by the 20 teeth of the drive gear gets us 30/20 = 1.5. We can also write this as 3/2 or 1.5 : 1, etc.
- What this gear ratio means is that the smaller driver gear must turn one and a half times to get the larger driven gear to make one complete turn. This makes sense — since the driven gear is bigger, it will turn more slowly.
Advertisement
More than Two Gears
-
1
Start with a gear train of more than two gears. As its name suggests, a “gear train” can also be made from a long sequence of gears — not just a single driver gear and a single driven gear. In these cases, the first gear remains the driver gear, the last gear remains the driven gear, and the ones in the middle become “idler gears.” These are often used to change the direction of rotation or to connect two gears when direct gearing would make them unwieldy or not readily available.[4]
- Let’s say for example purposes that the two-gear train described above is now driven by a small seven-toothed gear. In this case, the 30-toothed gear remains the driven gear and the 20-toothed gear (which was the driver before) is now an idler gear.
-
2
Divide the teeth numbers of the drive and driven gears. The important thing to remember when dealing with gear trains with more than two gears is that only the driver and driven gears (usually the first and last ones) matter. In other words, the idler gears don’t affect the gear ratio of the overall train at all. When you’ve identified your driver gear and your driven gear, you can find the gear ratio exactly as before.
- In our example, we would find the gear ratio by dividing the thirty teeth of the driven gear by the seven teeth of our new driver. 30/7 = about 4.3 (or 4.3 : 1, etc.) This means that the driver gear has to turn about 4.3 times to get the much larger driven gear to turn once.
-
3
If desired, find the gear ratios for the intermediate gears. You can find the gear ratios involving the idler gears as well, and you may want to in certain situations. In these cases, start from the drive gear and work toward the load gear. Treat the preceding gear as if it were the drive gear as far as the next gear is concerned. Divide the number of teeth on each “driven” gear by the number of teeth on the “drive” gear for each interlocking set of gears to calculate the intermediate gear ratios.
- In our example, the intermediate gear ratios are 20/7 = 2.9 and 30/20 = 1.5. Note that neither of these are equal to the gear ratio for the entire train, 4.3.
- However, note also that (20/7) × (30/20) = 4.3. In general, the intermediate gear ratios of a gear train will multiply together to equal the overall gear ratio.
Advertisement
-
1
Find the rotational speed of your drive gear. Using the idea of gear ratios, it’s easy to figure out how quickly a driven gear is rotating based on the “input” speed of the drive gear. To start, find the rotational speed of your drive gear. In most gear calculations, this is given in rotations per minute (RPM), though other units of velocity will also work.[5]
- For example, let’s say that in the example gear train above with a seven-toothed driver gear and a 30-toothed driven gear, the drive gear is rotating at 130 RPMs. With this information, we’ll find the speed of the driven gear in the next few steps.
-
2
Plug your information into the formula S1 × T1 = S2 × T2. In this formula, S1 refers to the rotational speed of the drive gear, T1 refers to the teeth in the drive gear, and S2 and T2 to the speed and teeth of the driven gear. Fill in the variables until you have only one left undefined.
- Often, in these sorts of problems, you’ll be solving for S2, though it’s perfectly possible to solve for any of the variables. In our example, plugging in the information we have, we get this:
- 130 RPMs × 7 = S2 × 30
-
3
Solve. Finding your remaining variable is a matter of basic algebra. Just simplify the rest of the equation and isolate the variable on one side of the equals sign and you will have your answer. Don’t forget to label it with the correct units — you can lose points for this in schoolwork.
- In our example, we can solve like this:
- 130 RPMs × 7 = S2 × 30
- 910 = S2 × 30
- 910/30 = S2
- 30.33 RPMs = S2
- In other words, if the drive gear spins at 130 RPMs, the driven gear will spin at 30.33 RPMs. This makes sense — since the driven gear is much bigger, it will spin much slower.
Advertisement
Add New Question
-
Question
If a 38 tooth gear running at 360rpm is driving another gear at 144rpm, what is the number of teeth on the driven gear?
T1*S1=S2*T2 where, T1=number of teeth on the driver gear, S1= angular speed on the driver gear, T2=number of teeth on the driven gear and S2=angular speed on the driven gear. 38 teeth*360rpm=T2*144rpm. T2=95 teeth on the driven gear.
-
Question
How do I determine my gear ratio in my gear box?
If you can not see the gears you can mark the shaft and the start point on the gear box and count the number of times it revolves when you spin the other shaft one full rotation.
-
Question
What is gear up and gear down?
Gear up is when you drive a smaller gear with a larger gear thus creating a faster RPM at the output but less torque. Gear down is to drive a larger gear with a smaller gear creating a slower RPM at the output but more torque.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
The power needed to drive the load is geared up or down from the motor by the gear ratio. The motor must be sized to provide the power needed by the load after the gear ratio is taken in to consideration. A geared up system (where load RPM is greater than motor RPM) will require a motor that delivers optimal power at lower rotational speeds.
-
To see the principles of gear ratio in action, take a ride on your bike! Notice that it is easiest to go up hills when you have a small gear in front and a big one in the back. While it’s easier to turn the smaller gear with the leverage from your pedals, it takes many rotations to get your rear wheel to rotate compared to the gear settings you’d use for flat sections, making you go slower.
-
A geared down system (where load RPM is less than motor RPM) will require a motor that delivers optimal power at higher rotational speeds.
Advertisement
References
About This Article
Article SummaryX
To determine gear ratio of a gear train with 2 gears, start by identifying your gears. The gear attached to the motor shaft is considered the first gear, or the “drive gear”, and the other gear, whose teeth are meshed with the drive gear, is considered the second gear, or “driven gear.” Count the number of teeth on the drive gear and on the driven gear. Then, divide the number of teeth on the driven gear by the number of teeth on the drive gear to get the gear ratio. For example, if the drive gear has 20 teeth and the driven gear has 30 teeth, the gear ratio is 1.5. If you want to learn how to use the gear ratio to calculate the gears’ speeds, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,662,357 times.
Reader Success Stories
-
Marlo Deguzman
Aug 5, 2017
“I am currently in school for my airframe and power plant licenses, and this helped me gain the confidence work…” more
Did this article help you?
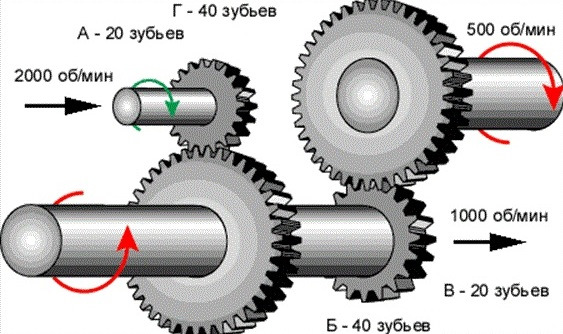
Любое подвижное соединение, передающее усилие и меняющее направление движения, имеет свои технические характеристики. Основным критерием, определяющим изменение угловой скорости и направления движения, является передаточное число. С ним неразрывно связано изменение силы – передаточное отношение. Оно вычисляется для каждой передачи: ременной, цепной, зубчатой при проектировании механизмов и машин.
Перед тем как узнать передаточное число, надо посчитать количество зубьев на шестернях. Затем разделить их количество на ведомом колесе на аналогичный показатель ведущей шестерни. Число больше 1 означает повышающую передачу, увеличивающую количество оборотов, скорость. Если меньше 1, то передача понижающая, увеличивающая мощность, силу воздействия.
Общее определение
Значение передаточного отношения у кинематических схем рассчитывается по стандартному математическому выражению. Результат получается при проведении математической операции деления значения угловой скорости ведущего вала или шестерёнки, на такой же параметр ведомого вала. Вместо этих значений используют отношение их частот вращения.
Современные кинематические схемы реализованы с использованием следующих механических соединений:
- с зубчатым зацеплением (в разных вариациях);
- червячных;
- фрикционных соединений;
- с помощью цепей;
- посредством специальных ремней;
- планетарных соединений.
Передача вращения основана на двух физических принципах: с помощью силы трения, с использованием механизмов зацепления. В зависимости от решаемой задачи механизмы изготавливаются с замедлением и ускорением. Первые называются редукторами, вторые — мультипликаторами. Обе разновидности бывают одноступенчатыми, двухступенчатыми, многоступенчатыми.
Пространственное расположение осей определяет следующие виды механизмов:
- параллельные (в них оба вала расположены параллельно друг относительно друга);
- пересекающиеся (зацепление происходит посредством пересечения);
- перекрещивающиеся механизмы (у них валы вступают в перекрестное зацепление).
Все типы механизмов бывают замедляющие и ускоряющие движение. Наиболее частое применение замедляющих конструкций объясняется более высокой скоростью используемых двигателей и необходимостью увеличить мощность выходного элемента кинематической схемы.
В зависимости от соотношения скоростей возникает вопрос: может ли передаточное отношение быть отрицательным? Этот коэффициент является отношением величин имеющих только положительные значения. Он не может быть отрицательным. В зависимости от отношения числителя к знаменателю результат получиться больше единицы или меньше. В первом случает, он справедлив для редукторов, во втором для мультипликаторов.
Таблица передаточных отношений является сводным документом. В ней приведены значения основных технических характеристик всех типов кинематических соединений.
В сводной таблице можно найти зависимость значения передаточного числа от допустимой мощности, которая передаётся конкретным видом соединения.
Зубчатая передача
Это механическое соединение двух или более вращающихся валов при помощи специальных колёс, на поверхности которых выточены зубья. Такой тип подразделяется по следующим характеристикам:
- форме и типу зубьев;
- относительному расположению валов в корпусе;
- расчётной скорости вращения колёс;
- степени защиты от внешних воздействий.
Важную роль в понимании работы всего механизма играет передаточное отношение зубчатой передачи. Его вычисляют, используя классическое выражение. Оно находится с подстановкой различных параметров. Например, подсчитывая численность изготовленных зубьев на ведущем и ведомом колесе. Формула позволяет получать результаты с высокой степенью точности:
Где i12 — передаточное отношение от звена 1 к звену 2 (звено 1 — ведущее, звено 2 — ведомое; d1,d2 — диаметры звеньев; z1, z2 — количество зубьев звеньев (если таковые имеются); M1, M2 — крутящие моменты звеньев; ω1, ω2 — угловые скорости звеньев; n1, n2 — частоты вращения звеньев.
В большей степени он зависит от количества зубьев расположенных на шестерёнке. Существенным достоинством зубчатого соединения является постоянство расчётного и реального передаточного отношения. Она связано с отсутствием эффекта проскальзывания.
Существенное влияние на величину этого показателя оказывает применяемое количество шестерней и число зубчатых колёс.
Для цилиндрической передачи этот параметр кроме приведенных выше параметров зависит от межосевого расстояния. Цилиндрические зубчатые передачи распространены в различных агрегатах легковых и грузовых автомобилей, тракторов, сельскохозяйственной техники. Их активно используют в трансмиссии.
Зубчатая передача обладает самым большим коэффициентом передачи мощности. Она способна отдавать мощность до 4500 кВт с передаточным числом достигающим 6,3.
Распространение получили зубчатые конструкции конического типа. Они обладают ортогональным сочленением. Расчёт конической передачи предполагает учёт таких параметров как: делительные диаметры, углы конусов, количество зубьев.
Для получения поступательного движения применяется реечное соединение. Конструктивно она состоит из шестерёнки, рейки с нанесёнными зубьями. Для реечной передачи учитывают диаметр окружности и количество зубьев на колесе, число зубьев расположенных на рейке.
Как рассчитать передаточное число
Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.
Расчет без учета сопротивления
В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.
u12 = ± Z2/Z1 и u21 = ± Z1/Z2,
Где u12 – передаточное число шестерни и колеса;
Z2 и Z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.
Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».
При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.
Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.
Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:
u16 = u12×u23×u45×u56 = z2/z1×z3/z2×z5/z4×z6/z5 = z3/z1×z6/z4
Способ расчета передаточного числа позволяет спроектировать редуктор с заранее заданными выходными значениями количества оборотов и теоретически найти передаточное отношение.
Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.
КПД зубчатой передачи
Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:
- трение соприкасаемых поверхностей;
- изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
- потери на шпонках и шлицах;
- трение в подшипниках.
Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.
Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.
При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.
Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.
Планетарная передача
Широко применяется так называемая планетарная кинематическая схема. Она представляет собой механизм, предназначенный для передачи, преобразования вращательного движения. С этой целью используются зубчатые колеса, расположенные на перемещающейся оси. Конструктивными элементами являются: центральные зубчатые колеса, закреплённые на неподвижных осях, боковые зубчатые колеса (расположены на перемещающихся осях). Для обеспечения наилучшего эффекта планетарные механизмы изготовляются на параллельных осях.
Максимальное значение передаточного числа достигает 9 единиц.
Коэффициент полезного действия достаточно высокий. Его значение приближается к 0,98. Наиболее распространёнными являются конструкции, в которых применяются нескольких сателлитов. Их располагают с угловыми шагами равной величины.
Такие конструкции выполняются с постоянным или переменным передаточным отношением. Некоторые из них имеют возможность регулировки этого параметра. Они разработаны обратимыми и необратимыми. В обратимых образцах предусмотрено движение в прямом и обратном направлении. В необратимых конструкциях такое движение невозможно. Изменение передаточного отношения бывает ступенчатым или бесступенчатым. Ярким представителем первого агрегата является механическая коробка передач автомобиля. Второй вариант применяется в вариаторах.
Рассмотренные передаточные отношения передач рассчитываются на этапе проектирования агрегата при выборе кинематической схемы. С их помощью производится выбор типа соединения, определяется эффективность. Оценивается надёжность всего механизма.
Выбор передаточных отношений промежуточных передач
Для выбора передаточных чисел 2 и 3 передач существуют два способа. Первый заключается в определении показателя разбивки передач q:
Здесь: – максимальная скорость на высшей передаче; – максимальная скорость на 1 передаче; m – порядковый номер наивысшей передачи. При этом остальные передаточные числа определяются из показателя разбивки:
При этом передачи равномерно распределены по диапазону, то есть для всех передач выполняется
Посмотрим, как соотносятся передачи в существующих транспортных средствах. В методичке «Тяговый расчет автомобиля» приведены передаточные отношения КПП различных автомобилей. Я обработал их статистически, определив средние значения показателей разбивки для различных групп автомобилей и мотоциклов.
Таблица. Показатели разбивки передач для различных транспортных средств.
В целом видно, что показатели автомобилей и мотоциклов довольно близки. Импортные авто в среднем имеют меньшие значения показателей в силу большего числа передач.
Показатели для низших передач в целом больше, чем показатели высших для всех видов транспортных средств. Это говорит о том, что высшие передачи стараются сближать за счет низших.
Средние значения показателей составляют 1,7 для 1-2 передач. На этом фоне выделяется Вояж, у него соотношение 1 и 2 передач составляет 1,88. Это довольно много, поэтому переключение с 1 на 2 передачу нагружает коробку передач значительным ударом, что приводит к ускоренному износу. Мне совершенно непонятно, зачем конструкторам потребовалось так отдалять первую и вторую передачу. Притом что вторая и третья сближены по сравнению с другими мотоциклами.
Высшая передача зачастую выполняется приближенной к предыдущей, когда ее назначение – снизить обороты двигателя на высокой скорости, то есть максимальная динамика и наибольшая скорость обеспечивается не на ней, а на предыдущей передаче (овердрайв). В этом случае показатель разбивки снижается до 1,18 … 1,2.
Второй способ разбивки передач состоит в индивидуальном подборе передаточных, с подбором показателей разбивки для каждой пары передач с анализом разгона по динамической характеристике.
Цепная передача
Хорошо известна цепная передача. Она относится к гибким конструкциям. Передаточное отношение цепной передачи рассчитывается расчёту зубчатых систем. Ведущая и ведомая звёздочка рассматриваются как зубчатые колеса. Значение этого параметра достигает 15.
Особенностью такой конструкции считается требование иметь определённое провисание цепи. Настройка этого параметра проводится с помощью специального регулирующего винта.
Достоинства подобного соединения сводятся к следующему:
- низкая критичность к возможным ошибкам при установке валов.
- передача мощности производится с использованием нескольких звездочек;
- длина передачи вращения может быть достаточно большой.
К недостаткам можно отнести быстрый износ соединительных элементов цепи. Это требует периодической смазки. Вторым недостатком считается высокий уровень шума.
Кроме передаточного числа для них рассчитывается величина статистической разрушающей силы. Этот параметр зависит от требуемого коэффициента безопасности. Его задают в интервале от 6 до 10. Он обеспечивает качественную работу всего механизма, высокую надёжность соединения и долговечность.
Червячная передача
Необходимость изменения вращательного движения под углом требует создания специального вида систем. К таким конструкциям относится червячная передача. Основной элемент такой передачи может быть цилиндрической формы, глобоидным, эвольвентным, архимедовым винтом. Это зависит от поверхности, на которой расположена резьба, и профиля резьбы.
В качестве параметров, используемых для расчёта передаточного числа подставляемых в выражение, используют существующее количество заходов червячного механизма. Обычно оно варьируется от одного до четырёх. Таблица передаточных отношений для червячной схемы позволяет рассчитать необходимое количество элементов зацепления. Приведенные в этой таблице данные, помогают правильно выбрать соединения для конкретного механизма.
Основными недостатками передачи являются:
- высокая температура нагрева элементов во время передачи вращения;
- наличие эффекта проскальзывания;
- затормаживание и заедание;
- низкий КПД;
- как следствие невысокую надёжность.
Мощность привода
Правильно рассчитанная мощность привода помогает преодолевать механическое сопротивление трения, возникающее при прямолинейных и вращательных движениях.
Элементарная формула расчета мощности – вычисление соотношения силы к скорости.
При вращательных движениях мощность вычисляется как соотношение крутящего момента к числу оборотов в минуту:
где M – крутящий момент; N – количество оборотов/мин.
Выходная мощность вычисляется по формуле:
где P – мощность; Sf – сервис-фактор (эксплуатационный коэффициент).
ВАЖНО!
Значение входной мощности всегда должно быть выше значения выходной мощности, что оправдано потерями при зацеплении:
Нельзя делать расчеты, используя приблизительное значение входной мощности, так как КПД могут существенно отличаться.
Как рассчитать передаточное число редуктора
Ременная передача
Данная конструкция является часто встречающейся. Её тип определяется расположением вала и направлением движения ремня. Их классифицируют следующим образом:
- открытого типа;
- перекрестной формы;
- ступенчатой системы;
- угловой.
Для повышения надёжности применяют спаренное соединение. Реализация подобных конструкций производится с помощью ремней различного сечения. Наиболее популярными являются три типа: прямоугольные, в форме трапеции, круглого сечения.
Значение передаточного отношения рассчитывается подстановкой в классическую формулу скоростей вращения ведущего и ведомого валов. Иногда в расчёте используют число оборотов каждого из валов. В качестве альтернативного варианта при расчёте этого параметра используются величины диаметров (радиусов) шкивов.
-
Передаточное отношение, передаточное число
Передаточное
отношение –
это отношение мгновенных угловых или
линейных скоростей ведущего
и ведомого
звеньев. u
= ω1/ω2.
Передаточное
число – это
отношение чисел зубьев или диаметров
(радиусов)
ведомого и ведущего звеньев.
i
= z2/z1.
В
производственном лексиконе эти два
понятия зачастую путают, поскольку в
численном выражении u
= i.
Определим u
и
i при
последовательном и параллельном
соединении зубчатых колес.
Последовательное
соединение (рис.4.3).
u
1-4
= ω1/ω2*
ω2/ω3*
ω3/ω4
= ω1/ω4
i
1-4
=
z2/z1*
z3/z2*
z4/z3
= z4/z1
Видим,
что промежуточные шестерни z2
и z3
не влияют
на передаточное отношение и передаточное
число. Эти шестерни называются паразитными.
Они
Рис.
4.3 устанавливаются
в двух случаях:
1 – для изменения направления
вращения; 2 – для получения большого
межосевого расстояния при малых
поперечных габаритах передачи.
Параллельное
соединение (рис.4.4).
u
1-4
= ω1/ω2*
ω3/ω4
= ω1/ω4,
ω2
= ω3
– это один вал.
i
1-4
=
z2/z1*
z4/z3
При
параллельном соединении нет паразитных
шестеренок. Больше того, у зубчатых
колес 1-й ступени (z1
и z2)
модуль меньше чем модуль колес 2-й ступени
(z3
и z4),
поскольку крутящий момент на входе 1-й
ступени в i
1-2
= z2/z1
раз меньше
момента на входе 2-й ступени (при условии,
что обе
Рис.
4.4 ступени
редукторные, то есть
z2
> z1
; z4
> z3
, соответственно
i
1-2 >
1 и
i
3-4
> 1).
Редуктор
–понижает
обороты, но увеличивает крутящий момент.
Мультипликатор
– повышает
обороты, но понижает крутящий момент.
-
Силы в зацеплении цилиндрических зубчатых колес
В
цилиндрической косозубой
передаче силу в зацеплении раскладывают
на составляющие (рис.4.5).
Окружная
сила Ft
определяется
по формуле
Ft
= 2T1/d1
,
(4.1)
где
T1
– крутящий
момент на валу шестерни;
d1
– делительный
диаметр
шестерни .
Радиальная сила
равна
Fr
= Ft*tq
α/cos
β
, (4.2)
Рис. 4.5
где
α = 20о
– стандартный
угол эвольвентного зацепления;
β
– угол
наклона зубьев.
Осевая сила равна
Fа
= Ft*tq
β
(4.3)
В
цилиндрической прямозубой
передаче β
= 0, поэтому
Fr
= Ft*tq
α, а Fа
= 0.
-
Прочностной расчет цилиндрических зубчатых передач
В инженерной
практике может возникнуть необходимость
в двух видах расчетов: проверочном и
проектировочном. В первом случае Вам
известны все элементы передачи, а так
же крутящие моменты на валах. Задача –
определить напряжения и сравнить с
допустимыми. Во втором случае необходимо
найти элементы передачи, удовлетворяющие
условию прочности.
Зубчатые
передачи рассчитывают на контактную
прочность (σH
≤ [σH])
и на изгиб зубьев (σF
≤ [σF])
.
-
Расчет зубьев на контактную прочность
Расчеты на контактную
прочность базируются на формуле Герца
,
(4.4)
где
q –
нагрузка на единицу длины контактной
линии;
Е
= 2*Е1*Е2/(
Е1+Е2)
– приведенный
модуль упругости материалов зубчатых
колес; ρпр
= ρ1*ρ2/(
ρ1+ρ2)
– приведенный
радиус кривизны контактирующих элементов;
μ
– коэффициент Пуассона.
Опуская
промежуточные выкладки (они описаны в
приведенной литературе), запишем условия
контактной прочности: прямозубых передач
;
(4.5)
косозубых передач
.
(4.6)
Здесь
aw
= a
– межосевое
расстояние; Т2
– крутящий
момент на валу зубчатого колеса;
b2
– ширина
колеса; u –
передаточное отношение пары зацепления;
KH
= KHa*
KHβ*
KHv
– комплексный коэффициент. KHa
– учитывает неравномерность распределения
нагрузки между зубьями; KHβ
– учитывает неравномерность распределения
нагрузки по ширине венца; KHv
– зависит от скорости и степени точности
передачи. Значения коэффициентов даны
в литературе.
Допускаемое
контактное напряжение [σ]H
определяется по формуле
[σ]H
= σН lim
b*KНL/[n]Н
, (4.7)
где
σН
lim
b
– предел контактной выносливости при
базовом числе циклов нагружения;
KНL
– коэффициент,
учитывающий число циклов ( в большинстве
случаев принимают KНL
= 1); [n]Н
– коэффициент безопасности; для колес
из нормализованной и улучшенной стали,
а также при объемной закалке принимают
[n]Н
= 1,1…1,2; при
поверхностном упрочнении зубьев [n]Н
= 1,2…1,3.
σН
lim
b
определяются
по формулам (см. таблицу 4.1).
Таблица
4.1
|
Способы обработки зубьев |
Твердость поверхностей зубьев |
Сталь |
σН МПа |
|
Нормализация |
< НВ 350 |
Углеродистая |
2 НВ + 70 |
|
Объемная закалка |
38…50 НRС |
Углеродистая |
18 НRС + 150 |
|
Поверхностная |
48…54 НRС |
Углеродистая |
17 НRС + 200 |
|
Цементация |
56…63 НRС |
Низкоуглеродистая |
23 НRС |
|
Азотирование |
57…67 НRС |
Легированная |
1050 |
В
таблице НВ
– твердость
по Бринеллю; НRС
– твердость
по Роквеллу. 1
НRС ≈ 10 НВ
Предположим,
Вы применили углеродистую Сталь 45,
термообработка – нормализация,
твердость НВ
200. Тогда σН
lim
b
= 2 НВ + 70 = 470 МПа. Эта же сталь при объемной
закалке может дать твердость 40
НRС. В этом
случае
σН
lim
b
= 18 НRС + 150 = 870 МПа. А если Вы применили
Сталь 12ХН3А, термообработка – цементация
и закалка, твердость
60 НRС,
то
σН
lim
b
= 23 НRС
= 1380 МПа. Разница весьма существенная.
Учитывая, что межосевое расстояние (aw)
обратно пропорционально допускаемому
напряжению (формулы 4.5 и 4.6), габаритные
размеры в 1-м и 3-ем случаях будут отличаться
почти в 3 раза. Если бы шестерни в коробках
передач автомобилей делали из не
термообработанной стали, то коробки
пришлось бы возить в кузове.
Для
косозубых передач рекомендуется
допускаемое контактное напряжение
определять по формуле
[σ]H
= 0,45*([σ]H1
+ [σ]H2),
(4.8)
где
[σ]H1
и [σ]H2
– допускаемые контактные напряжения
соответственно для шестерни и колеса.
По
формулам (4.5) и (4.6) проводится проверочный
расчет. При проектировочном расчете из
формул выделяют aw.
При этом ширина колеса b2
заменяется выражением b2
= Ψba*
aw.
Ψba
– коэффициент ширины зубчатого венца.
Рекомендуется:
для
прямозубых передач Ψba
= 0,125…0,25; для косозубых передач
Ψba
= 0,25…0,40. В результате получают формулы
для проектировочного
расчета:
прямозубых
передач
(4.9)
косозубых
передач
(4.10)
В
формулах (4.5); (4.6); (4.9); (4.10) для получения
требуемой размерности крутящий момент
Т2
следует подставлять в Н*мм.
После
определения межосевого расстояния
выбирают стандартный
нормальный модуль в
интервале
m
= mn
=
(0,01…0,02)*aw..
Определяют
суммарное число зубьев, предварительно
задавшись углом наклона зубьев (для
косозубых колес) в интервале β
= 8…15о.
z∑
= 2*aw*cos
β/mn
(4.11)
Определяют
числа зубьев шестерни и колеса
z
1
= z∑/(u
+ 1); z
2
= z
1*
u (4.12)
При
расчетах числа зубьев могут получиться
не целыми. Их округляют до ближайших
целых чисел и уточняют: для прямозубых
передач – межосевое расстояние; для
косозубых – угол наклона зубьев.
Затем,
по зависимостям, приведенным в п.4.1.1,
определяют все остальные элементы
шестерни и колеса.
В
завершение проводят проверку контактных
напряжений по формулам (4.5) или (4.6). В
случае невыполнения условия прочности
увеличивают b2
(при малых расхождениях σH
и [σ]H)
или увеличивают aw
(при значительных расхождениях σH
и
[σ]H).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
