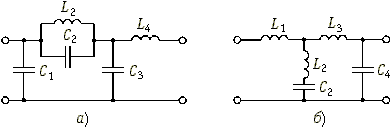-
Передаточная функция фильтра
Нu(j
)=
.
Представленные
выше звенья являются звеньями второго
порядка. Комплексная
передаточная функция (КПФ)
такого звена имеет вид:
Нu(j
)=
Здесь
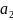
,
,
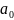
( т.е.

при

=
)
и
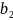
,

,

(т.е.

при

)
― действительные
(вещественные) положительные величины
при разных степенях аргумента

.
Максимальная
степень аргумента определяет порядок
звена
( звено 2-го порядка ).
Степень
числителя не может быть выше степени
знаменателя. Некоторые коэффициенты
могут быть нулевыми. В отличии от
числителя все коэффициенты знаменателя
ненулевые

0.
Степень полинома знаменателя равна 2
при наличии в схеме как минимум, двух
реактивных элементов с разным характером
реактивности. Коэффициенты
и
комплексной передаточной функции КПФ
определяются значениями L
и C
и структурой фильтра.
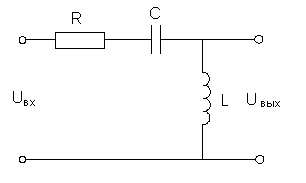
2.1 Определить комплексную передаточную функцю фильтра низких частот
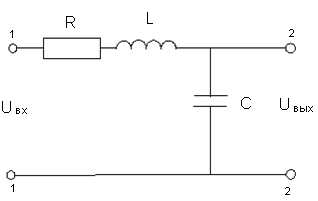
Нu(j
)=
.
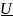
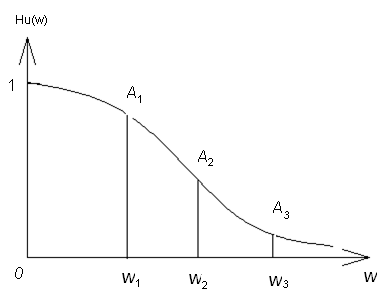
вых=
);
вх=

Значение
КПФ принимает вид:
Нu(j
)=
=
В
этом выражении КПФ В числителе а2=а1=0;
а0=1;
в знаменателе
=LC;
=RC;
=1.
Таким
образом, звено второго порядка является
фильтром низких частот при условии
а2=а1=0:
Нu(j
)=
Тогда
АЧХ ФНЧ определяется выражением | Нu(j
)|
Нu(
)=
С
помощью этого выражения можно рассчитать
коэффициент передачи на любой частоте.
Значение
Нu(
)
на нулевой частоте Нu(
=0)=
=1
H(
)=Н1
;
H(
)=H2
H(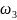
)=H3
Нu(j
)=
2.2) Фвч ― фильтр верхних частот.
Нu(j
)=
=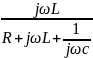
=
или
Нu(j
)=
.
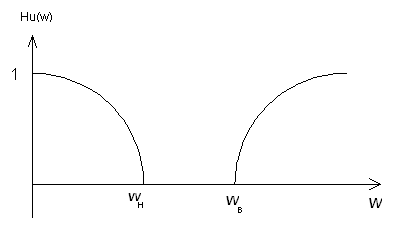
AЧХ
описывается выражением
Нu(
)=
.
При

Нu(
=
=
=1
2.3)
Для произвольного фильтра в виде звена
n-го
порядка КПФ имеет следующий вид:

j
=
Причем
n
≥ m.
В
зависимости от того, какие из коэффициентов
равны нулю, модуль КПФ

по разному зависит от частоты на разных
участках частотного диапазона. Формируют
АЧХ различного вида, которые соответствуют
различным видом фильтров.
-
Схемы пассивных lc-фильтров.
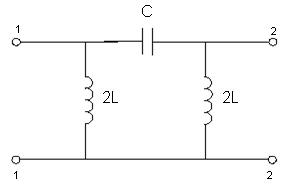
3.1)
ФНЧ
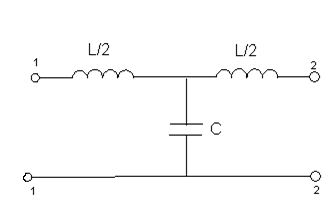
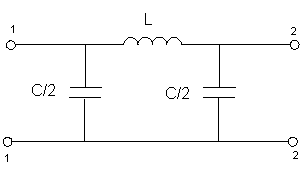
Т-образная
схема П-образная схема
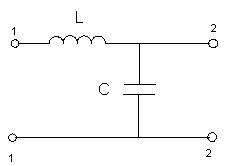
Г-образная

;
;
C=
;
L=
Для
расчета параметров фильтра заданным
являются граничная частота

и сопротивление нагрузки. Наилучших
частотных свойств можно застичь в режиме
согласования. Приближение к этому режиму

.
3.2) Фильтр верхних частот (фвч).
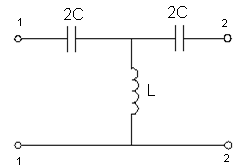
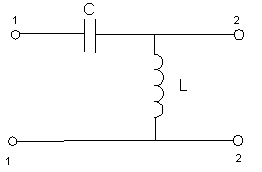

;

C=
;
L=
.
3.3) Полосовой фильтр
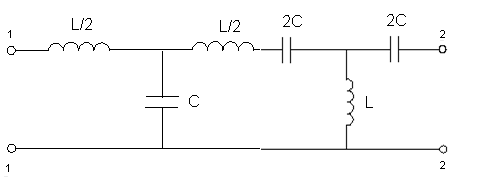
Каскадные
соединение ФНЧ и ФВЧ
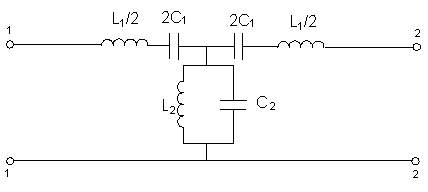
Более
практична в настройке последовательном
и параллельном КК настроено на одну
частоту.
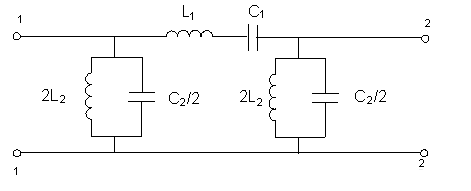
П-образная
схема.
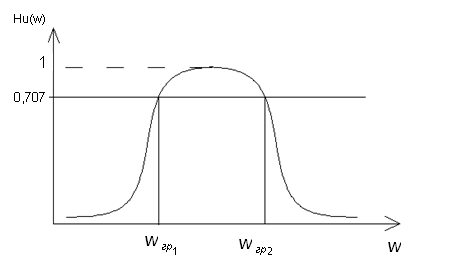
Комплексное
сопротивление последовательного
идеального колебательного контура,
который включается в продольную ветвь

,
на частоте
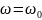
;

;
а параллельного, который включается в
поперечную ветвь

.
Эквивалентные
схемы полосового Т-образного фильтра
имеют следующий вид :
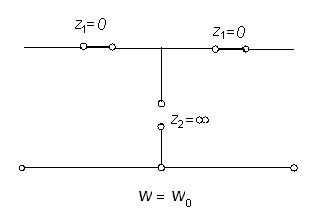
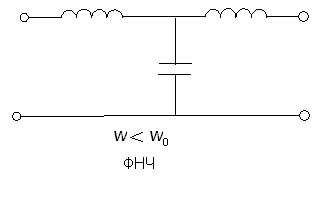
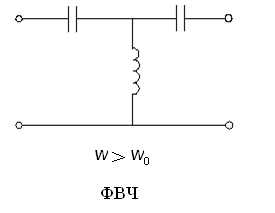
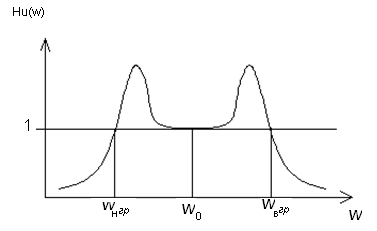
На
частотах
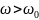
последовательные контуры ведут себя
как индуктивное сопротивление, а
параллельного контура, как емкостное
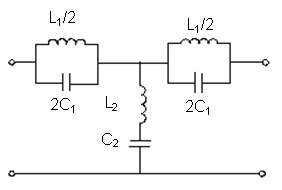
сопротивление. Эквивалентная схема
приобретает вид рис.2. Она подобна ФНЧ.
При
частоте ниже резонансной (
)
последовательные ветви ведут себя
емкостные, а параллельные ― как
индуктивные. Эквивалентная схема ФВЧ
. Для расчета задают

:
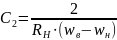
;

;

;

.
ZZZ///
ЧЕТЫРЁХПОЛЮСНИКИ
Ч
етырёхполюсником
называется часть электрической цепи,
имеющей два входных и два выходных
зажима. К входным зажимам присоединяется
источник, а к выходным – приёмник
энергии. Примерами четырёх-полюсников
(ЧП)
является усилитель,
Рисунок
1-Схемное обозначение ЧП
трансформатор,
электрический фильтр, линия связи и
т.д. Эти устройства, не похожие по
внутреннему содержанию, можно описать
общим набором параметров ЧП.
Ч
1′
R
етырёхполюсники могут быть пассивные
и активные, линейные и нелинейные,
симметричные и несимметричные.
ЧП называется
симметричным, если при взаимной замене
первичных 1-1′
и вторичных 2-2′
выводов токи и напряжение на входе и
выходе ЧП не поменяются.
Режим работы ЧП
полностью
определён, если известны
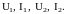
Основной задачей теории ЧП
является установление соотношений
между этими величинами. Уравнения,
которые дают зависимость между

называются уравнениями передачи
четырёхполюсника
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Понятие передаточных функций фильтров нижних частот
Добавлено 21 декабря 2019 в 07:01
Данная статья дает некоторое представление о взаимосвязи между передаточной функцией в s-области и поведением фильтра нижних частот первого порядка.
В последнее время я довольно много пишу на тему фильтров, и хотя я сосредоточился на практических соображениях, я чувствую необходимость объяснить некоторые важные теоретические концепции в пользу тех, кто хотел бы более подробно понять и проанализировать поведение аналоговых фильтров. В настоящее время каждый имеет доступ к программным инструментам, которые делают сложное проектирование фильтров относительно безболезненным, но я не думаю, что было бы разумно полностью игнорировать математические основы просто потому, что они не являются строго необходимыми для выполнения многих реальных задач проектирования.
s-область
Отклик фильтра может быть выражен передаточной функцией в s-области; переменная s появляется из преобразования Лапласа и представляет комплексную частоту. Например:
[T(s) = frac{K}{1+ left( frac{s}{omega_0} right) }]
Эта передаточная функция является математическим описанием поведения фильтра нижних частот первого порядка в частотной области. Выражение в s-области эффективно передает общие характеристики, и если мы хотим вычислить конкретную информацию об амплитуде и фазе, всё, что нам нужно сделать, это заменить s на jω, а затем вычислить выражение при заданной угловой частоте.
Вам может быть интересно, откуда берутся K и ω0 – вы, вероятно, никогда не видели принципиальной схемы, в которой значения компонентов были выражены в значениях K и ω0. Идея в том, что K и ω0 подобны частям шаблона, и в следующем разделе мы рассмотрим взаимосвязь между этим шаблоном и принципиальной схемой.
Анализ схем в s-области
RC фильтр нижних частот является частотно-зависимым делителем напряжения. При анализе в s-области импеданс резистора равен R, а импеданс конденсатора равен (frac{1}{sC}).
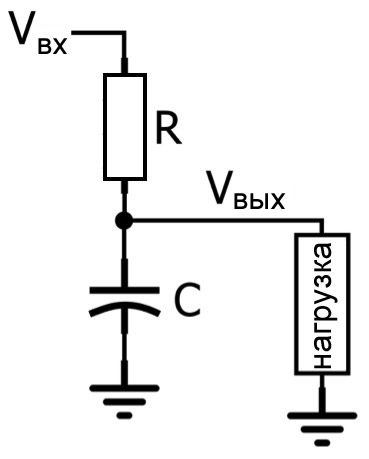
[frac{V_{вых}}{V_{вх}} = {frac{1}{sC} over frac{1}{sC} + R} = frac{1}{1+sRC}]
Если мы сравним это выражение с нормированной передаточной функцией, то увидим, что K = 1 и (omega_0 = frac{1}{RC}). Удобство использования нормированной формы становится понятным, как только вы узнаете, что представляют собой K и ω0: K – это коэффициент усиления схемы при постоянном напряжении, а ω0 – это частота среза. Таким образом, сравнивая передаточную функцию схемы с нормированной передаточной функцией, вы можете сразу же сформулировать выражения для двух определяющих характеристик фильтра нижних частот первого порядка, а именно для коэффициента усиления при постоянном напряжении и частоты среза.
Другой нормированной формой передаточной функции фильтра нижних частот первого порядка является следующее:
[T(s)=frac{a_0}{s+omega_0}]
Мы можем встроить передаточную функцию схемы в этот шаблон, если разделим числитель и знаменатель на RC:
[T(s)= frac{1}{1+sRC} rightarrow { frac{1}{RC} over s + frac{1}{RC} } ]
Таким образом, (a_0=frac{1}{RC}), и (omega_0 = frac{1}{RC}). Эта форма напрямую не дает нам коэффициент усиления по постоянному напряжению, но если мы вычислим нормированное выражение для s = 0, то получим
[T(s=0) = frac{a_0}{omega_0}]
Это означает, что коэффициент усиления по постоянному напряжению нашего RC-фильтра равен
[left( frac{1}{RC} right) / left( frac{1}{RC} right) = 1]
А коэффициент усиления по постоянному напряжению, равный единице, – это именно то, что мы ожидаем от пассивного фильтра нижних частот.
Понятие частоты среза
Мы видели, что ω0 в стандартной передаточной функции представляет частоту среза, но каково математическое основание этого факта?
Во-первых, давайте, преобразуем стандартную передаточную функцию в s-области в эквивалентную передаточную функцию jω.
[T(s) = frac{K}{1 + frac{s}{omega_0}} rightarrow T(jomega) = frac{K}{1 + jfrac{omega}{omega_0}}]
Теперь давайте вычислим выражение при частоте среза.
[T(jomega = jomega_0) = frac{K}{1 + jfrac{omega_0}{omega_0}}= frac{K}{1+j}]
Знаменатель является комплексным числом, поэтому модуль будет равен
[|T(jomega = jomega_0)|= frac{K}{sqrt{1^2+1^2}} = frac{K}{sqrt{2}}]
Поскольку K – это коэффициент усиления по постоянному напряжению, очень низкочастотный входной сигнал с амплитудой в один вольт приведет к выходному сигналу с амплитудой в K вольт. Если входная частота увеличивается до ω0 радиан в секунду, выходная амплитуда будет равна (frac{K}{sqrt{2}}). Коэффициент (frac{1}{sqrt{2}}) соответствует –3 дБ, и, как вы, вероятно, знаете, другое название частоты среза – это частота –3 дБ.
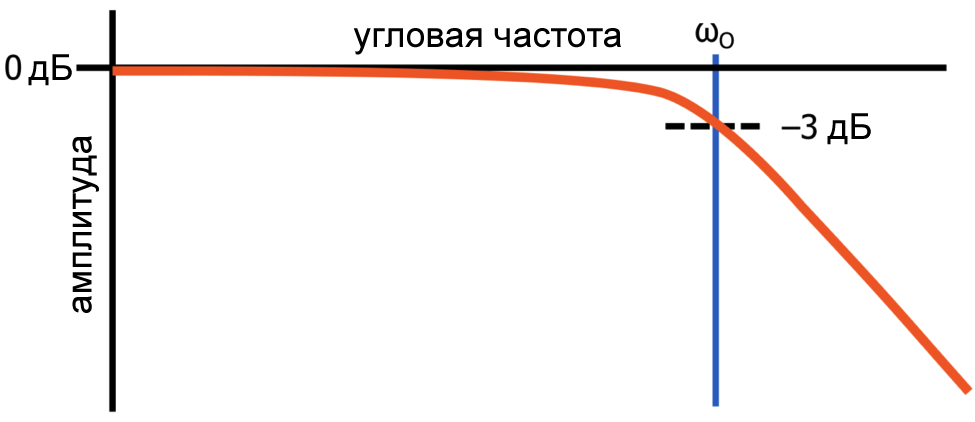
Этот простой анализ передаточной функции ясно продемонстрировал, что частота среза – это просто частота, на которой амплитудно-частотная характеристика фильтра снижается на 3 дБ относительно выходного уровня на очень низкой частоте.
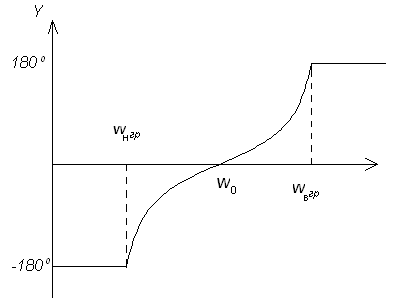
Частота среза и сдвиг фазы
Частота среза фильтра нижних частот имеет особое значение также в отношении фазо-частотной характеристики схемы. Если мы напишем комплексное число в форме x + jy, мы рассчитаем фазу следующим образом:
[theta=text{arctg}left( frac{y}{x} right)]
Таким образом, общая фазо-частотная характеристика нашего RC фильтра низких частот следующей:
[theta(omega)= -text{arctg}left( frac{frac{omega}{omega_0}}{1} right)= -text{arctg}left( frac{omega}{omega_0} right)]
Если мы вычислим это выражение при ω = ω0, сдвиг фазы будет равен
[-text{arctg}left( frac{omega_0}{omega_0} right) = -text{arctg}left( 1 right) = -45^circ]

Максимальный сдвиг фазы, создаваемый фильтром нижних частот первого порядка, составляет 90°, поэтому этот анализ говорит нам, что частота среза является «центром» фазо-частотной характеристики схемы – другими словами, это частота, на которой фильтр создает половину своего максимального сдвига фазы.
Заключение
Я надеюсь, что вам понравилось это краткое введение в концепции s-области и анализ передаточных функций. Поначалу математические основы схем аналоговых фильтров могут быть немного пугающими, но я думаю, что стоит потратить некоторое время на то, чтобы получить некоторое представление об этих темах. Я продолжу исследовать эту тему в будущих статьях.
Теги
s-областьАЧХ (амплитудно-частотная характеристика)Комплексные числаПередаточная функцияПреобразование ЛапласаСдвиг фазыФНЧ (фильтр нижних частот)ФЧХ (фазо-частотная характеристика)Частота среза
17.1. Классификация фильтров
17.2. Аппроксимация характеристик фильтров нижних частот
17.3. Реализация фильтров нижних частот
17.4. Переход от фильтров нижних частот к другим типам фильтров
17.5. Резонаторные фильтры
17.6. Вопросы и задания для самопроверки
17.1. Классификация фильтров
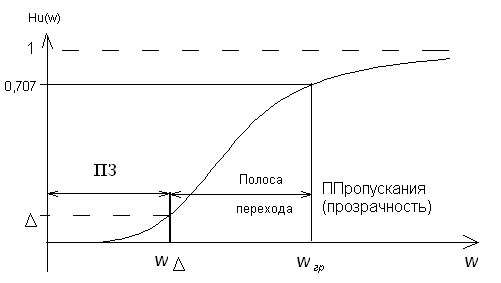
Электрический фильтр – это устройство, которое практически не ослабляет спектральные составляющие сигнала в заданной полосе частот и значительно ослабляет (подавляет) все спектральные составляющие вне этой полосы.
Полоса частот, в которой ослабление мало, называется полосой пропускания. Полоса частот, в которой ослабление велико, называется полосой непропускания (задерживания). Между этими полосами находится переходная область.
По расположению полосы пропускания на шкале частот различают следующие фильтры:
На рис. 17.1, а—г показаны также условные обозначения фильтров каждого типа в соответствии с ГОСТ.
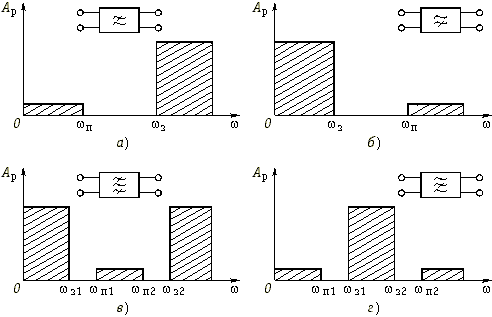
Рис. 17.1
В соответствии с используемой элементной базой к настоящему моменту выделились несколько классов фильтров. Исторически первыми (и все еще широко применяемыми) являются пассивные фильтры, содержащие элементы L и С. Они носят название LC-фильтров.
Во многих случаях на практике требовалась крайне высокая избирательность (различие ослаблений в полосах пропускания и непропускания в десятки тысяч раз). Это привело к появлению фильтров с механическими резонаторами: кварцевых, магнитострикционных, электромеханических.
По-видимому, самые значительные достижения в области теории и проектирования фильтров связаны с успехами микроэлектроники. Требования микроминиатюризации радиоэлектронной аппаратуры заставили отказаться от использования индуктивностей, которые имеют большие габаритные размеры, особенно на низких частотах, и не поддаются исполнению в микроминиатюрном виде. Появились активные RC-фильтры, состоящие из резисторов, конденсаторов и активных приборов (например, транзисторов). Эти фильтры могут быть выполнены в виде микромодульной конструкции или интегральной схемы. Применение активных RC-фильтров ограничивается пока сравнительно небольшим диапазоном частот до десятков (иногда сотен) килогерц.
Разработка цифровых систем связи и достижения в области цифровых вычислительных машин стимулировали создание фильтров на базе элементов цифровой и вычислительной техники – цифровых фильтров. В силу специфики элементной базы цифровых фильтров не будем далее упоминать о них, хотя расчет таких фильтров производится методами теории электрических цепей. Заинтересованные читатели могут обратиться к специальной литературе по цифровым фильтрам.
В идеальном случае (идеальный фильтр) характеристика рабочего ослабления, например для ФНЧ, имеет вид, показанный на рис. 17.2, а. С рабочим ослаблением связана рабочая амплитудно-частотная характеристика (АЧХ): ![]() . На рис. 17.2, б изображена АЧХ идеального фильтра нижних частот.
. На рис. 17.2, б изображена АЧХ идеального фильтра нижних частот.
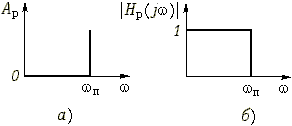
Рис. 17.2
Реальные фильтры (т. е. фильтры, состоящие из реальных элементов) имеют характеристики рабочего ослабления и амплитудно-частотную, отличные от идеальных.
Требования к электрическим характеристикам фильтров задаются в виде допустимых пределов изменения этих характеристик. Так, рабочее ослабление в полосе пропускания не должно превышать некоторого максимального допустимого значения Арmax, а в полосе непропускания не должно быть ниже некоторого минимально допустимого значения Арmin. Нетрудно изобразить эти требования графически, как это сделано на рис. 17.3, а для ФНЧ. На этом рисунке ![]() и
и ![]() – граничные частоты полос пропускания и непропускания.
– граничные частоты полос пропускания и непропускания.
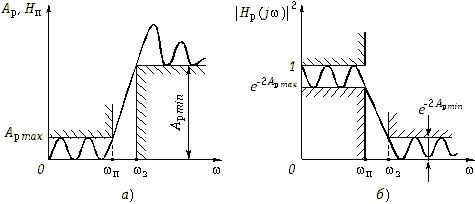
Рис. 17.3
Зная требования к Ар, можно пересчитать их в требования к АЧХ или, как это принято в теории фильтров, в требования к квадрату АЧХ (рис. 17.3, б): 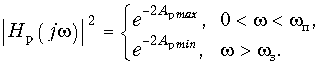
Характеристики проектируемых фильтров должны “укладываться” в эти требования (рис. 17.3, а и б).
Помимо требований к частотной зависимости рабочего ослабления (а значит, и к АЧХ) могут задаваться также требования к фазочастотной характеристике фильтра (скажем, допустимые отклонения от линейного закона) и величине нелинейных искажений (обусловленных, например, наличием железа в катушках индуктивности). Могут предъявляться требования и к другим характеристикам и параметрам фильтра. Ниже будем учитывать только требования к рабочему ослаблению и АЧХ.
Идеальные частотные характеристики фильтра (см. рис. 17.2, а) заведомо нереализуемы. Частотные характеристики реальных фильтров могут лишь приближаться к ним с той или иной степенью точности в зависимости от сложности схемы фильтра.
17.2. Аппроксимация характеристик фильтров нижних частот
Функция фильтрации. В общем виде электрические фильтры описываются передаточной функцией вида: 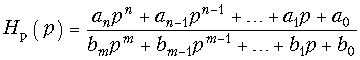 (17.1)
(17.1)
Квадрат амплитудно-частотной характеристики таких фильтров 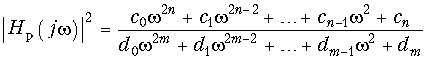 (17.2) и, следовательно, рабочее ослабление
(17.2) и, следовательно, рабочее ослабление 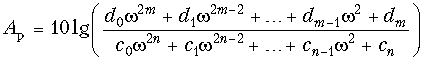 (17.3) могут при надлежащем выборе степени полинома (порядка фильтра) и коэффициентов dk удовлетворить заданным требования (см. рис. 17.3).
(17.3) могут при надлежащем выборе степени полинома (порядка фильтра) и коэффициентов dk удовлетворить заданным требования (см. рис. 17.3).
В теории фильтров принято иметь дело не с обычной угловой частотой ![]() , а с нормированной частотой
, а с нормированной частотой ![]() , где
, где ![]() – нормирующая частота. Обычно в качестве нормирующей частоты выбирают граничную частоту полосы пропускания
– нормирующая частота. Обычно в качестве нормирующей частоты выбирают граничную частоту полосы пропускания ![]() , так что
, так что ![]() .
.
В теории электрических фильтров вместо формул (17.2) и (17.3) используют другие, также универсальные для любого типа фильтра: 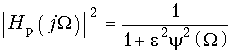 (17.4)
(17.4) ![]() (17.5)
(17.5)
Функция ![]() называется функцией фильтрации, а
называется функцией фильтрации, а ![]() – коэффициентом неравномерности ослабления. В общем случае
– коэффициентом неравномерности ослабления. В общем случае ![]() – это дробно-рациональная функция с вещественными коэффициентами (в частности полином), удовлетворяющая условиям: –1
– это дробно-рациональная функция с вещественными коэффициентами (в частности полином), удовлетворяющая условиям: –1 ![]()
![]()
![]() 1 в полосе пропускания и
1 в полосе пропускания и ![]() >> 1 в полосе непропускания фильтра.
>> 1 в полосе непропускания фильтра.
В зависимости от вида функции фильтрации получают различные типы фильтров. Если в качестве функции фильтрации используют полиномы, то фильтры называются полиномиальными. Среди полиномиальных фильтров широкое использование нашли фильтры Баттерворта и Чебышева. Если ![]() – дробно-рациональная функция, например, дробь Золотарева, то получают фильтр Золотарева. Все эти три типа фильтров будут рассмотрены в этой главе.
– дробно-рациональная функция, например, дробь Золотарева, то получают фильтр Золотарева. Все эти три типа фильтров будут рассмотрены в этой главе.
Следует отметить, что имеет смысл подробно изучать только фильтры нижних частот, т. к. другие типы фильтров (верхних частот, полосовые и заграждающие) могут быть легко получены из ФНЧ с помощью замены переменной (частоты). Для этого во всех выражениях, содержащих переменную ![]() , нужно произвести замену переменной таким образом, чтобы характеристики ФНЧ Ар(
, нужно произвести замену переменной таким образом, чтобы характеристики ФНЧ Ар(![]() ) и |Hр(j
) и |Hр(j![]() )|2 преобразовались в характеристики соответствующего фильтра. Подобная замена переменной
)|2 преобразовались в характеристики соответствующего фильтра. Подобная замена переменной ![]() называется преобразованием частоты, а исходный ФНЧ – фильтром НЧ-прототипа.
называется преобразованием частоты, а исходный ФНЧ – фильтром НЧ-прототипа.
Преобразование частоты позволяет установить соответствие между частотами полос пропускания и непропускания НЧ-прототипа и частотами фильтров верхних частот, полосового или заграждающего, а также преобразовать схему ФНЧ в схемы ФВЧ, ПФ или ЗФ. Более подробно вопросы, связанные с преобразованием частоты, будут рассматриваться в 17.5. Резонаторные фильтры.
Фильтры Баттерворта. Если в выражениях, описывающих квадрат АЧХ фильтра (17.4) и его рабочее ослабление (17.5), в качестве функции фильтрации используются полиномы Баттерворта ![]() = Bm(
= Bm(![]() ) =
) = ![]() m (по имени автора, предложившего использовать их для “конструирования” частотных характеристик фильтра), то такие фильтры называются фильтрами Баттерворта.
m (по имени автора, предложившего использовать их для “конструирования” частотных характеристик фильтра), то такие фильтры называются фильтрами Баттерворта.
Из формул (17.4) и (17.5) следует, что для фильтров Баттерворта на частоте ![]() = 0 значение квадрата АЧХ равно единице, а рабочего ослабления – нулю. С ростом частоты квадрат АЧХ фильтра Баттерворта уменьшается и падает до нуля на бесконечно большой частоте. Рабочее ослабление плавно растет до бесконечно большого значения. Таким образом, выражения (17.4) и (17.5) приближенно воспроизводят характеристики идеального фильтра.
= 0 значение квадрата АЧХ равно единице, а рабочего ослабления – нулю. С ростом частоты квадрат АЧХ фильтра Баттерворта уменьшается и падает до нуля на бесконечно большой частоте. Рабочее ослабление плавно растет до бесконечно большого значения. Таким образом, выражения (17.4) и (17.5) приближенно воспроизводят характеристики идеального фильтра.
Чтобы эти характеристики “вписывались” в предъявляемые к фильтру требования (см. рис. 17.3), необходимо иметь рабочее ослабление (17.5) в полосе пропускания меньшее Арmax, а в полосе непропускания большее Арmin. Первому условию можно удовлетворить, если потребовать на граничной частоте полосы пропускания (![]() = 1) выполнения равенства Ар(
= 1) выполнения равенства Ар(![]() )
)![]() =1 = Арmax или |Hр(j
=1 = Арmax или |Hр(j![]() )|
)|![]() =
= ![]() . Отсюда с учетом (17.5) или (17.4) имеем 1 +
. Отсюда с учетом (17.5) или (17.4) имеем 1 + ![]() 2 =
2 = ![]() и
и ![]() 2 =
2 = ![]() – 1. Вычисленный таким способом коэффициент
– 1. Вычисленный таким способом коэффициент ![]() :
: ![]() (17.6) называется коэффициентом неравномерности ослабления в полосе пропускания фильтра.
(17.6) называется коэффициентом неравномерности ослабления в полосе пропускания фильтра.
В формуле (17.6) величина Арmax имеет размерность непер. Если воспользоваться значениями Арmax в децибелах, то ![]() (17.7)
(17.7)
С учетом введенных обозначений квадрат АЧХ фильтра Баттерворта запишется в виде ![]() (17.8)
(17.8)
Эта функция удовлетворяет свойствам квадрата АЧХ реальных четырехполюсников, и поэтому ей можно сопоставить физически осуществимый электрический фильтр.
Рабочее ослабление фильтра Баттерворта: ![]() (17.9)
(17.9)
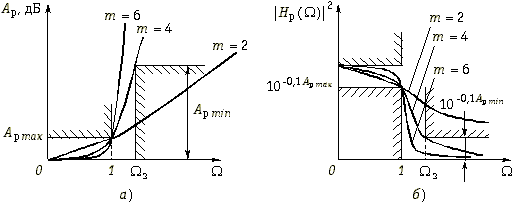
Рис. 17.4
Крутизна частотных характеристик (17.8) и (17.9) зависит от степени m (порядка фильтра). Чем больше степень m, тем выше крутизна характеристик. На рис. 17.4, а, и б показаны графики рабочего ослабления и квадрата АЧХ фильтра Баттерворта для различных m. Таким образом, для удовлетворения требований в полосе непропускания необходимо выбрать соответствующий порядок фильтра m. Его легко определить из условия: на граничной частоте полосы непропускания: ![]() з Ар(
з Ар(![]() з)
з) ![]() Арmin или |Hр (j
Арmin или |Hр (j![]() )|
)|![]()
![]()
![]() . С учетом этого условия получим 1 +
. С учетом этого условия получим 1 + ![]() 2
2![]()
![]() >
> ![]() , откуда
, откуда ![]()
![]()
![]() . Логарифмируя обе части неравенства, придем к выражению
. Логарифмируя обе части неравенства, придем к выражению 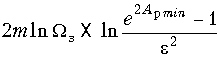
Из него находим окончательно
m ![]()
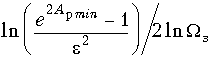 (17.10)
(17.10)
Величина Арmin входит в формулу в неперах. Если вычислять ее в децибелах, то: m ![]()
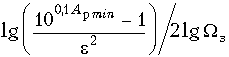 (17.11)
(17.11)
Передаточную функцию фильтра Баттерворта можно получить из (17.8), если положить j![]() = p:
= p: 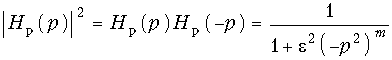 (17.12) и разложить знаменатель полученной функции на произведение сомножителей.
(17.12) и разложить знаменатель полученной функции на произведение сомножителей.
Вычислим корни знаменателя, т. е. полюсы функции Hр(p) X Hр(–p), отдельно для четных и нечетных значений m. Для четных значений m: ![]() и
и 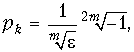 k = 1, 2, …, 2m.
k = 1, 2, …, 2m.
Так как: ![]() , имеем:
, имеем: 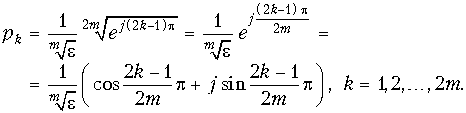 (17.13)
(17.13)
Для нечетных значений m: 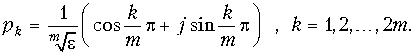
Выражение (17.12) примет вид: 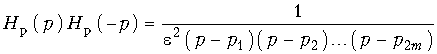 .
.
Половина полюсов функции Hр(p)Hр(–p) лежит в левой полуплоскости комплексной переменной p и может быть отнесена к передаточной функции реализуемого фильтра Hр(p). Другая половина полюсов, являясь зеркальным отражением первой, располагается в правой полуплоскости и относится к Hр(–p).
Построенная из полюсов, лежащих в левой полуплоскости, передаточная функция фильтра Баттерворта является полиномиальной передаточной функцией типа (17.1):  , где H = 1/
, где H = 1/![]() .
.
Пример. Найти выражения для частотной характеристики и передаточной функции фильтра нижних частот Баттерворта, удовлетворяющего следующим требованиям: Арmax = 3 дБ; Арmin = 12,2 дБ; fп = 159 кГц; fз = 318 кГц.
Определим нормированную частоту ![]() з = fз/fn = 2 и по формуле (17.7) коэффициент неравномерности ослабления
з = fз/fn = 2 и по формуле (17.7) коэффициент неравномерности ослабления ![]() 2 = 100,1×3 – 1 = 1. Порядок фильтра найдем согласно (17.11):
2 = 100,1×3 – 1 = 1. Порядок фильтра найдем согласно (17.11): ![]() .
.
Выберем m = 2. Тогда в соответствии с (17.8) и (17.9): ![]() .
.
Найдем передаточную функцию фильтра Hр(p). Значения полюсов функции |Hр(p)|2 = Hр(p)Hр(–p) = 1/ (1 + р4) вычислим из формулы (17.13): p1 = 0,707 + j0,707; p2 = – 0,707 + j0,707; p3 = – 0,707 – j0,707; p4 = 0,707 – j0,707. Расположение полюсов в комплексной плоскости показано на рис. 17.5, а.
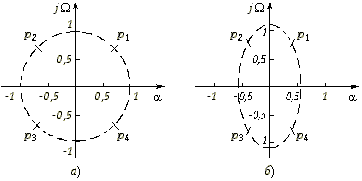
Рис. 17.5
По теореме Виета из полюсов в левой полуплоскости p2 и p3 формируем передаточную функцию: ![]() .
.
Используя введенное ранее обозначение Bm(![]() ) =
) = ![]() m полинома Баттерворта, можно представить частотные характеристики (17.8) и (17.9) фильтра Баттерворта в следующей форме:
m полинома Баттерворта, можно представить частотные характеристики (17.8) и (17.9) фильтра Баттерворта в следующей форме: 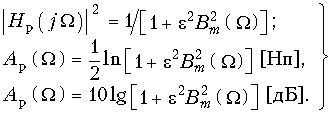 (17.14)
(17.14)
Фильтры Баттерворта называют также фильтрами с максимально плоским ослаблением в полосе пропускания (см. рис. 17.4, а).
Полиномиальные фильтры Чебышева. Если в качестве функции фильтрации в (17.4) и (17.5) использовать полином Чебышева, обозначаемый ![]() (
(![]() ) = Tm(
) = Tm(![]() ), то формулы (17.14) примут вид:
), то формулы (17.14) примут вид: 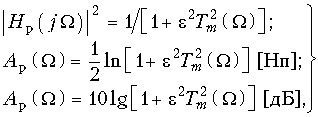 (17.15) где Tm(
(17.15) где Tm(![]() ) – полином Чебышева степени (порядка) m;
) – полином Чебышева степени (порядка) m; ![]() – коэффициент неравномерности, определяемый (17.6) или (17.7).
– коэффициент неравномерности, определяемый (17.6) или (17.7).
Фильтры с частотными характеристиками (17.15) называются фильтрами Чебышева. Проанализируем частотные характеристики фильтра Чебышева. Для этого вначале рассмотрим свойства полиномов Tm(![]() ). Ниже приведены шесть первых полиномов Чебышева:
). Ниже приведены шесть первых полиномов Чебышева: 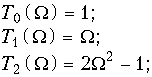
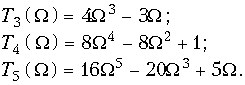 (17.16 а)
(17.16 а)
Любой полином Чебышева при m ![]() 2 может быть вычислен по рекуррентной формуле Tm(
2 может быть вычислен по рекуррентной формуле Tm(![]() ) = 2
) = 2![]() Tm–1(
Tm–1(![]() ) – Tm–2(
) – Tm–2(![]() ). Таким образом, выражения (17.15) удовлетворяют общим выражениям (17.1) – (17.3) характеристик полиномиальных фильтров.
). Таким образом, выражения (17.15) удовлетворяют общим выражениям (17.1) – (17.3) характеристик полиномиальных фильтров.
Существует единая тригонометрическая форма записи полиномов Чебышева в интервале –1 ![]()
![]()
![]() 1:
1:
![]() (17.16)
(17.16)
Действительно, T0(![]() ) = cos0arccos
) = cos0arccos![]() = 1; T1(
= 1; T1(![]() ) = cos1arccos
) = cos1arccos![]() = =
= = ![]() ; T2(
; T2(![]() ) = cos2arccos
) = cos2arccos![]() = 2cos2arccos
= 2cos2arccos![]() – 1 = 2
– 1 = 2![]() 2 – 1. Вне интервала –1
2 – 1. Вне интервала –1 ![]()
![]()
![]() 1 полиномы Tm(
1 полиномы Tm(![]() ) также представляются в тригонометрической форме:
) также представляются в тригонометрической форме:
![]() (17.16 в)
(17.16 в)
Анализ поведения полиномов Чебышева показывает, что в интервале –1 ![]()
![]()
![]() 1 угол
1 угол ![]() = arccos
= arccos![]() изменяется от –
изменяется от –![]() (при
(при ![]() = –1) до 0 (при
= –1) до 0 (при ![]() = 1), поэтому полином Tm(
= 1), поэтому полином Tm(![]() ) = cosm
) = cosm![]() ровно m раз принимает значения, равные нулю, и m + 1 раз достигает значений, равных +1 или –1 и чередующихся друг с другом. Вне интервала –1
ровно m раз принимает значения, равные нулю, и m + 1 раз достигает значений, равных +1 или –1 и чередующихся друг с другом. Вне интервала –1 ![]()
![]()
![]() 1 полином Tm(
1 полином Tm(![]() ) согласно формуле (17.16 в) монотонно возрастает. В качестве примера на рис. 17.6, а изображен график полинома Чебышева T4(
) согласно формуле (17.16 в) монотонно возрастает. В качестве примера на рис. 17.6, а изображен график полинома Чебышева T4(![]() ), т. е. полинома четвертого порядка.
), т. е. полинома четвертого порядка.
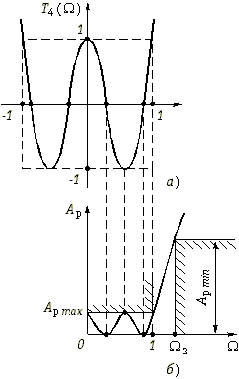
Рис. 17.6
В соответствии с (17.15) рабочее ослабление Ap(![]() ) фильтра Чебышева на тех частотах
) фильтра Чебышева на тех частотах ![]() , где полином Tm(
, где полином Tm(![]() ) обращается в нуль, также обращается в нуль. На частотах, на которых Tm(
) обращается в нуль, также обращается в нуль. На частотах, на которых Tm(![]() ) равен
) равен ![]() 1, рабочее ослабление достигает величины:
1, рабочее ослабление достигает величины: 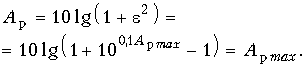
С ростом значений полинома Tm(![]() ) на частотах
) на частотах ![]() > 1 рабочее ослабление Ap(
> 1 рабочее ослабление Ap(![]() ) также монотонно растет. На рис. 17.6, б приведен график рабочего ослабления фильтра Чебышева четвертого порядка.
) также монотонно растет. На рис. 17.6, б приведен график рабочего ослабления фильтра Чебышева четвертого порядка.
Фильтры Чебышева называют также фильтрами с равноволновой характеристикой ослабления в полосе пропускания.
На рис. 17.7 показаны частотные зависимости квадрата АЧХ фильтра Чебышева для различных значений m, полученные для |Hр(j![]() )|2 из (17.15). Подобные зависимости могут быть построены для рабочего ослабления фильтра.
)|2 из (17.15). Подобные зависимости могут быть построены для рабочего ослабления фильтра.
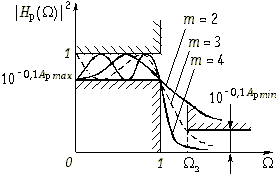
Рис. 17.7
Чтобы характеристики фильтра отвечали требованиям в полосе непропускания, необходимо выбрать порядок фильтра m из условия |Hр(j![]() )|
)|![]()
![]()
![]() . Для полосы непропускания Tm(
. Для полосы непропускания Tm(![]() ) определяется формулой (17.16 в), следовательно, 1 +
) определяется формулой (17.16 в), следовательно, 1 + ![]() 2сh2m X Arch
2сh2m X Arch![]() з
з ![]()
![]() . Отсюда сhmArch
. Отсюда сhmArch![]() з
з![]()
![]() . Далее mArch
. Далее mArch![]() з
з ![]()
![]() и m
и m ![]()
![]() .
.
В этой формуле величина Apmin измеряется в неперах. При использовании единицы децибел порядок фильтра вычисляется из выражения:
m ![]()
 (17.17 a)
(17.17 a)
Сравнивая частотные характеристики фильтров Баттерворта и Чебышева, следует указать, что полиномы Чебышева являются полиномами наилучшего приближения. Это означает, что при одинаковом значении m из всех полиномиальных фильтров, ослабления которых в полосе пропускания не превышают Apmax, наибольшие значения ослабления в полосе непропускания имеет фильтр Чебышева. В частности, рабочее ослабление фильтра Чебышева в полосе непропускания может превышать (и весьма значительно) рабочее ослабление фильтра Баттерворта при равных значениях m и Apmax. Однако характеристика рабочего ослабления фильтра Баттерворта имеет в полосе пропускания монотонный характер и легче поддается корректированию для устранения искажений передаваемых сигналов.
Выбор типа полиномиальных фильтров определяется конкретными условиями их применения в аппаратуре связи и радиотехнических устройствах.
Для получения передаточной функции фильтра Чебышева поступим аналогично тому, как делали это для фильтров Баттерворта. Заменим оператор j![]() на оператор р и перейдем от функции |Hр(j
на оператор р и перейдем от функции |Hр(j![]() )|2 к функции:
)|2 к функции: ![]() .
.
Представим полином Tm(![]() ) в виде (17.16 б) и найдем полюсы функции |Hр(p)|2, решив уравнение:
) в виде (17.16 б) и найдем полюсы функции |Hр(p)|2, решив уравнение: ![]() (17.17 б)
(17.17 б)
Поскольку согласно (17.16 а) коэффициент при старшем члене полинома Чебышева Tm(![]() ) равен 2m–1, то коэффициент при старшем члене полинома в левой части приведенного выше уравнения равен
) равен 2m–1, то коэффициент при старшем члене полинома в левой части приведенного выше уравнения равен ![]() 222(m–1).
222(m–1).
Корни уравнения (17.17 б), как можно доказать, определяются аналитически следующим выражением: ![]() (17.18) где
(17.18) где ![]() .
.
Из корней в левой полуплоскости составляются сомножители (p – pi), и по теореме Виета строится передаточная функция фильтра:  , где
, где ![]() .
.
Пример. Построить передаточную функцию фильтра Чебышева второго порядка (m = 2), рабочее ослабление в полосе пропускания (от 0 до 159 кГц) которого не превышает величину Apmax = 3 дБ. Граничная частота полосы непропускания 318 кГц.
Коэффициент неравномерности ![]() такого фильтра согласно (17.7) равен 1. Рабочее ослабление на частоте
такого фильтра согласно (17.7) равен 1. Рабочее ослабление на частоте ![]() з = 318/159 = 2 составляет Ap(
з = 318/159 = 2 составляет Ap(![]() )
)![]() =2 = 10lg(1 + ch22Arch2) = 17 дБ, что почти на 5 дБ превышает рабочее ослабление на этой же частоте фильтра Баттерворта второго порядка (см. предыдущий пример).
=2 = 10lg(1 + ch22Arch2) = 17 дБ, что почти на 5 дБ превышает рабочее ослабление на этой же частоте фильтра Баттерворта второго порядка (см. предыдущий пример).
Расчет полюсов функции Hp(p)Hp(–p) по формулам (17.18) дает величины: p1 = 0,322 + j0,777; p2 = 0,322 – j0,777; p3 = –0,322 – j0,777; p4 = –0,322 + j0,777. Расположение полюсов в комплексной плоскости показано на рис. 17.5, б.
Передаточная функция фильтра: ![]() .
.
В заключение отметим, что для полиномиальных фильтров в справочниках составлены весьма полные таблицы полюсов и коэффициентов передаточных функций для различных величин Apmax и m. Порядок же фильтров m определяется по специальным графикам, исходя из заданных величин Apmax, Apmin и ![]() з.
з.
Фильтры со всплесками ослабления (на основе дробей Чебышева и Золотарева). Частотные характеристики полиномиальных фильтров, описываемые выражениями (17.1)—(17.3), имеют монотонный характер в полосе непропускания. В частности, рабочее ослабление таких фильтров монотонно возрастает по мере удаления от полосы пропускания (рис. 17.4, а и 17.6, б).
При “жестких” требованиях к частотным характеристикам (малая переходная область между полосами пропускания и непропускания и большая величина рабочего ослабления в полосе непропускания) порядок фильтра m может получиться очень большим даже в случае применения полинома Чебышева. Это приведет к существенному усложнению фильтра и к излишнему “расходу” элементов.
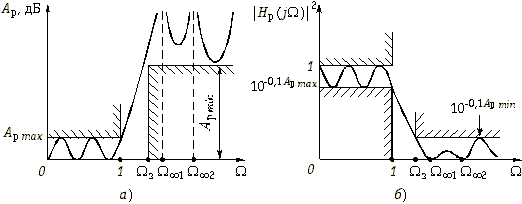
Рис. 17.8
В таких случаях целесообразно применять фильтры со всплесками рабочего ослабления в полосе непропускания (рис. 17.8, а). На частотах всплеска ![]()
![]() 1,
1, ![]()
![]() 2 и т. д. рабочее ослабление фильтра стремится к бесконечности; за счет этого возрастает крутизна характеристики ослабления в переходной области. Соответственно АЧХ фильтра на частотах
2 и т. д. рабочее ослабление фильтра стремится к бесконечности; за счет этого возрастает крутизна характеристики ослабления в переходной области. Соответственно АЧХ фильтра на частотах ![]()
![]() 1,
1, ![]()
![]() 2 и т. д. будет обращаться в нуль (рис. 17.8, б).
2 и т. д. будет обращаться в нуль (рис. 17.8, б).
Для выполнения указанных условий в выражениях (17.2)—(17.3) используют рациональные дроби вида: 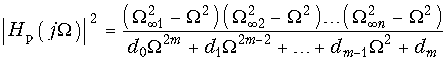 (17.19)
(17.19) 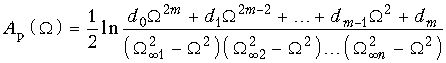 (17.20)
(17.20)
Действительно, когда ![]() принимает значения
принимает значения ![]()
![]() 1,
1, ![]()
![]() 2, …,
2, …, ![]()
![]() n, |Hр(j
n, |Hр(j![]() )|2 = 0 и Aр(
)|2 = 0 и Aр(![]() )
) ![]()
![]() .
.
Передаточная функция таких фильтров является дробно-рациональной: 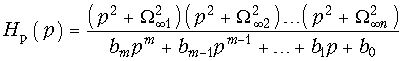 (17.21) и кроме полюсов p1, p2, …, pm имеет нули:
(17.21) и кроме полюсов p1, p2, …, pm имеет нули: ![]() .
.
Фильтры со всплесками рабочего ослабления называют еще фильтрами с нулями передачи.
Среди фильтров со всплесками ослабления наиболее широкое распространение получили фильтры, построенные на основе дробей Чебышева и Золотарева. Чтобы получить частотные характеристики фильтра на основе дробей Чебышева, нужно в формулах (17.14) или (17.15) использовать в качестве функции фильтрации дробь Чебышева. Обозначая ее Фm(![]() ), получим:
), получим: 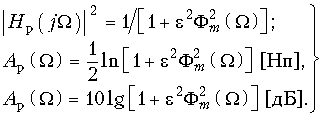 (17.22)
(17.22)
В качестве примера укажем дробь Чебышева пятого порядка, для которой построены графики Aр(![]() ) и |Hр(j
) и |Hр(j![]() )|2 на рис. 17.8, а и б:
)|2 на рис. 17.8, а и б: 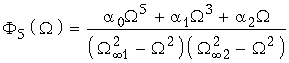 , где a0, a1 и a2 – коэффициенты, связанные с частотами всплеска
, где a0, a1 и a2 – коэффициенты, связанные с частотами всплеска ![]()
![]() 1 и
1 и ![]()
![]() 2.
2.
Очевидно, что подстановка этой дроби в (17.22) приведет после некоторых преобразований к выражениям общего вида (17.19) и (17.20).
В полосе пропускания дробь Чебышева ведет себя так же, как и полином Чебышева, т. е. рабочее ослабление фильтра носит равноволновый характер. На частотах всплеска ![]()
![]() 1 и
1 и ![]()
![]() 2 дробь Чебышева обращается в бесконечность, что приводит к бесконечно большому рабочему ослаблению.
2 дробь Чебышева обращается в бесконечность, что приводит к бесконечно большому рабочему ослаблению.
Следует отметить, что дробь Чебышева является дробью наилучшего приближения. Это означает, что фильтр на основе дроби Чебышева на любой частоте полосы непропускания имеет большее значение рабочего ослабления по сравнению с фильтрами на основе других дробей (и полиномов, как частных случаев дробей) при прочих равных условиях (при одинаковых порядках m, при таком же количестве и расположении частот всплеска и тех же величинах Apmax).
Частным случаем дробей Чебышева являются дроби Золотарева: ![]() (17.23) где
(17.23) где ![]() ,
, ![]() , значение S равно 0 для четных m и равно 1 для нечетных m; m – порядок дроби;
, значение S равно 0 для четных m и равно 1 для нечетных m; m – порядок дроби; ![]() 0V,
0V, ![]()
![]() V – нули и полюсы дроби, связанные соотношением
V – нули и полюсы дроби, связанные соотношением ![]()
![]() V =
V = ![]() з/
з/![]() 0V.
0V.
Используя в качестве функции фильтрации в (17.14) и (17.15) дроби Золотарева, получим: 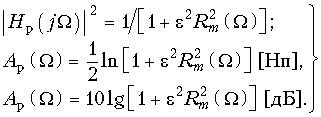 (17.24)
(17.24)
Из формул (17.23) и (17.24) следует, что нули функции Aр(![]() ) совпадают с нулями дроби Золотарева, а всплески функции Aр(
) совпадают с нулями дроби Золотарева, а всплески функции Aр(![]() ) – с полюсами этой же дроби. Нули и полюсы дроби Золотарева можно рассчитывать, однако обычно их определяют по каталогам для операторных передаточных функций ФНЧ. На рис. 17.9 показан график Aр(
) – с полюсами этой же дроби. Нули и полюсы дроби Золотарева можно рассчитывать, однако обычно их определяют по каталогам для операторных передаточных функций ФНЧ. На рис. 17.9 показан график Aр(![]() ) для фильтра Золотарева пятого порядка.
) для фильтра Золотарева пятого порядка.
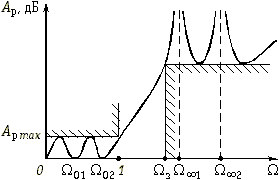
Рис. 17.9
Дроби Золотарева так же, как и полиномы Чебышева, дают равноволновую характеристику рабочего ослабления фильтра в полосе пропускания. Однако в полосе непропускания у фильтров Золотарева значения всех минимумов рабочего ослабления оказываются одинаковыми и равными значению рабочего ослабления на частоте ![]() з. Такие фильтры называются также фильтрами с изоэкстремальными характеристиками рабочего ослабления.
з. Такие фильтры называются также фильтрами с изоэкстремальными характеристиками рабочего ослабления.
Фильтры с характеристиками Золотарева можно рассматривать как частный случай фильтров с характеристиками Чебышева, когда значения минимумов ослабления фильтра в полосе непропускания выравнены, а число всплесков – максимально возможное при выбранном значении m.
17.3. Реализация фильтров нижних частот
Лестничные полиномиальные LC-фильтры. Любые из рассмотренных выше фильтров, как полиномиальные, так и со всплесками ослабления могут быть реализованы в виде пассивных LC-цепей.
Пассивные LC-фильтры обычно представляют собой реактивный лестничный четырехполюсник, включенный между генератором с активным внутренним сопротивление Rг и нагрузкой с активным сопротивлением Rн (рис. 17.10). Входное сопротивление реактивного четырехполюсника, нагруженного на сопротивление Rн, обозначено на рисунке Zвх1(р).
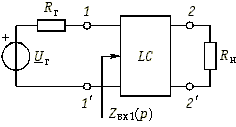
Рис. 17.10
Если фильтр со стороны зажимов 1—1′ рассматривать как двухполюсник, образованный реактивным четырехполюсником и нагрузкой Rн, то, зная выражение Zвх1(р), можно реализовать данный двухполюсник одним из известных в теории цепей методов синтеза двухполюсников. Таким образом, задача реализации фильтра сводится к реализации двухполюсника по его заданному входному сопротивлению. Идея данного подхода принадлежит С. Дарлингтону и метод реализации фильтров называется методом Дарлингтона.
На входе фильтра имеет место несогласованность, которую можно оценить, введя в рассмотрение коэффициент отражения (16.25) 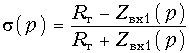 (17.25)
(17.25)
Решая (17.25) относительно Zвх1(р), получаем: 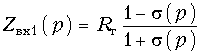 (17.26)
(17.26)
В (17.26) неизвестным является коэффициент отражения ![]() (р). В свою очередь, коэффициент отражения
(р). В свою очередь, коэффициент отражения ![]() (р) связан с передаточной функцией Hp(р) = w(р)/ v(р) соотношением (16.26 а):
(р) связан с передаточной функцией Hp(р) = w(р)/ v(р) соотношением (16.26 а): 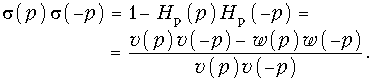 (17.27)
(17.27)
Из (17.27) следует, что знаменатель у ![]() (р) такой же, как и у Hp(р): им является полином v(р). Остается найти нули правой части выражения (17.7) и половину из них “приписать” полиному числителя
(р) такой же, как и у Hp(р): им является полином v(р). Остается найти нули правой части выражения (17.7) и половину из них “приписать” полиному числителя ![]() (р). Последний формируется из нулей по теореме Виета.
(р). Последний формируется из нулей по теореме Виета.
Пример. Реализовать фильтр нижних частот Баттерворта второго порядка в виде пассивной LC-схемы. Внутреннее сопротивление генератора 1 кОм.
В примере была получена передаточная функция Баттерворта второго порядка Hp(p) = 1/(p2 + 1,41p + 1) для нормированных значений частоты ![]() =
= ![]() /
/![]() н =
н = ![]() /(2
/(2![]() ×159× 103) =
×159× 103) = ![]() / 106, где
/ 106, где ![]() н =
н = ![]() п = 2
п = 2![]() fп. Реализация нормированной передаточной функции приведет к схеме с нормированными значениями реактивных элементов (обозначим их
fп. Реализация нормированной передаточной функции приведет к схеме с нормированными значениями реактивных элементов (обозначим их ![]() ), которые затем необходимо денормировать для получения реальных значений.
), которые затем необходимо денормировать для получения реальных значений.
В соответствии с (17.27) 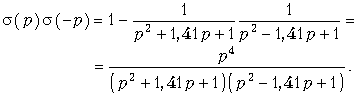 Нули этой функции p01, 02, 03, 04 = 0. Полином числителя
Нули этой функции p01, 02, 03, 04 = 0. Полином числителя ![]() (р) в соответствии с теоремой Виета равен (p – p01)× (p – p02) = p2. Отсюда
(р) в соответствии с теоремой Виета равен (p – p01)× (p – p02) = p2. Отсюда ![]() (р) = p2/(p2 + 1,41p + 1).
(р) = p2/(p2 + 1,41p + 1).
Согласно (17.26) 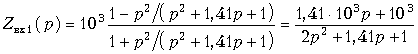 .
.
Реализацию двухполюсника со входным сопротивлением Zвх1(p) осуществим разложением в цепную (лестничную) дробь по методу Кауэра. Представим Zвх1(p) = 1/ Yвх1(p) и проведем разложение проводимости: 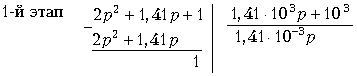
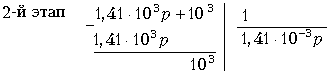
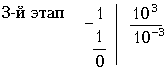
Процесс разложения закончен. Входное сопротивление Zвх1(p), представленное цепной дробью, имеет вид:
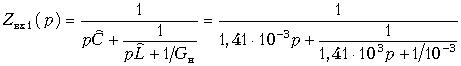 .
.
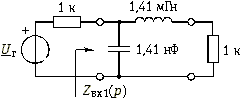
Рис. 17.11
Схема двухполюсника, входное сопротивление которого соответствует данной цепной (лестничной) дроби, приведена на рис. 17.11. Нормированные значения элементов ![]() = 1,41× 10–3,
= 1,41× 10–3, ![]() = 1,41× 103. Активная проводимость нагрузки не нормируется и равна Gн = 10–3 См, т. е. сопротивление нагрузки Rн = 1 кОм. Денормировать значения элементов можно следующим образом. Комплексная проводимость нормированной емкости
= 1,41× 103. Активная проводимость нагрузки не нормируется и равна Gн = 10–3 См, т. е. сопротивление нагрузки Rн = 1 кОм. Денормировать значения элементов можно следующим образом. Комплексная проводимость нормированной емкости ![]() , откуда ненормированное значение емкости
, откуда ненормированное значение емкости ![]() = 1,41×10–3/106 =nbsp;1,41×10–9 Ф = 1,41 нФ.
= 1,41×10–3/106 =nbsp;1,41×10–9 Ф = 1,41 нФ.
Подобным образом комплексное сопротивление нормированной индуктивности ![]() или
или ![]() = 1,41×103/106 = 1,41× 10–3 Гн = 1,41 мГн.
= 1,41×103/106 = 1,41× 10–3 Гн = 1,41 мГн.
Аналогично рассмотренному примеру решается задача реализации фильтра любого порядка. Например, полиномиальный ФНЧ пятого порядка (m = 5) реализуется в виде одной из двух схем, показанных на рис. 17.12, а и б. Количество реактивных элементов определяется порядком фильтра m. Отличие фильтра Баттерворта от фильтра Чебышева будет заключаться в этом случае только в разных значениях реактивных элементов, получаемых в процессе реализации соответствующих передаточных функций.
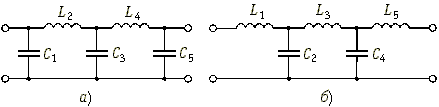
Рис. 17.12
Лестничные фильтры со всплесками ослабления. По подобной схеме осуществляется и реализация передаточных функций фильтров со всплесками ослабления (Чебышева или Золотарева). Разложение входного сопротивления таких фильтров в цепную дробь приведет к схемам, содержащим резонансные контуры, в которых резонансы происходят на частотах ![]()
![]() 1,
1, ![]()
![]() 2, … Наличие этих контуров и обеспечивает бесконечно большое затухание на частотах всплеска.
2, … Наличие этих контуров и обеспечивает бесконечно большое затухание на частотах всплеска.
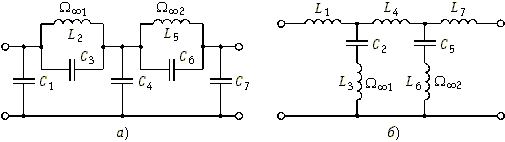
Рис. 17.13
Так, ФНЧ пятого порядка со всплесками ослабления на частотах ![]()
![]() 1 и
1 и ![]()
![]() 2 реализуется в виде одной из схем, приведенных на рис. 17.13, а и б. И в первой и во второй схемах контуры рассчитаны на резонансные частоты
2 реализуется в виде одной из схем, приведенных на рис. 17.13, а и б. И в первой и во второй схемах контуры рассчитаны на резонансные частоты ![]()
![]() 1 и
1 и ![]()
![]() 2. В первой схеме в параллельных контурах происходят резонансы токов; сопротивления контуров принимают бесконечно большие значения. В результате на частотах резонансов
2. В первой схеме в параллельных контурах происходят резонансы токов; сопротивления контуров принимают бесконечно большие значения. В результате на частотах резонансов ![]()
![]() 1 и
1 и ![]()
![]() 2 наблюдается “обрыв” продольных ветвей фильтра и сигнал от генератора в нагрузку не поступает, т. е. фильтр вносит бесконечно большое ослабление. Во второй схеме в последовательных контурах происходят резонансы напряжений; сопротивления контуров обращаются в нуль. Таким образом, здесь на частотах
2 наблюдается “обрыв” продольных ветвей фильтра и сигнал от генератора в нагрузку не поступает, т. е. фильтр вносит бесконечно большое ослабление. Во второй схеме в последовательных контурах происходят резонансы напряжений; сопротивления контуров обращаются в нуль. Таким образом, здесь на частотах ![]()
![]() 1 и
1 и ![]()
![]() 2 поперечные ветви “закорачивают” нагрузку и сигнал на выход фильтра не поступает. Таким образом, имеет место бесконечно большое ослабление.
2 поперечные ветви “закорачивают” нагрузку и сигнал на выход фильтра не поступает. Таким образом, имеет место бесконечно большое ослабление.
Реализация лестничных фильтров по каталогам. Из изложенного следует, что синтез фильтров представляет собой сложную процедуру, поэтому разработчики фильтров пытались облегчить ее. В результате были созданы обширные каталоги фильтров, применение которых значительно облегчает процедуру синтеза ФНЧ. Табл. 17.1 представляет собой страницу из такого каталога, где приведены нормированные элементы фильтра Золотарева четвертого порядка. В этой таблице ![]() s, As,
s, As, ![]() As – нормированная граничная частота полосы задерживания, минимальное ослабление в полосе задерживания, максимальное ослабление в полосе пропускания соответственно. Аналогичные каталоги существуют и для фильтров Баттерворта и Чебышева.
As – нормированная граничная частота полосы задерживания, минимальное ослабление в полосе задерживания, максимальное ослабление в полосе пропускания соответственно. Аналогичные каталоги существуют и для фильтров Баттерворта и Чебышева.
Таблица 17.1. Параметры элементов фильтров Золотарева четвертого порядка
|
|
As, дБ |
С1 |
С2 |
L2 |
|
С3 |
L4 |
|
при |
|||||||
|
3,98 3,39 2,96 2,63 |
56 50 45 41 |
0,7020 0,6871 0,6697 0,6497 |
0,04232 0,05952 0,08025 0,1049 |
1,241 1,215 1,186 1,152 |
4,364244 3,718173 3,241901 2,876673 |
1,282 1,272 1,261 1,248 |
0,7429 0,7440 0,7451 0,7465 |
|
при |
|||||||
|
3,76 3,23 2,84 2,45 |
56 50 45 40 |
0,7575 0,7422 0,7245 0,6968 |
0,044585 0,06339 0,08436 0,1183 |
1,282 1,256 1,226 1,287 |
4,124781 3,544141 3,109875 2,677264 |
1,326 1,316 1,305 1,287 |
0,8018 0,8027 0,8037 0,8052 |
|
при |
|||||||
|
3,39 2,96 2,53 2,22 |
56 51 45 40 |
0,8775 0,8612 0,8357 0,8057 |
0,05363 0,07202 0,1017 0,1382 |
1,349 1,321 1,278 1,229 |
3,718173 3,241901 2,773213 2,427221 |
1,400 0,390 1,373 1,354 |
0,9292 0,9297 0,9304 0,9311 |
|
при |
|||||||
|
3,09 2,73 2,37 2,09 |
55 50 45 40 |
0,9807 0,9630 0,9356 0,9040 |
0,063309 0,08273 0,1141 0,1522 |
1,382 1,353 1,308 1,257 |
3,386078 2,988543 2,588050 2,286311 |
1,443 1,432 1,414 1,394 |
1,041 1,041 1,041 1,041 |
|
|
|||||||
|
|
As, дБ |
L1 |
L2 |
С2 |
|
L3 |
С4 |
Процедура синтеза ФНЧ с помощью каталогов может выглядеть следующим образом: 1. По формуле (17.17 а) определяем порядок фильтра m. Если число m четное, то в числитель данной формулы добавляем слагаемое в соответствии с выражением (17.40) и уточняем порядок фильтра. 2. Из каталога фильтров выбираем таблицы, соответствующие данному порядку. 3. Из данных таблиц выбираем строку, для которой с минимально возможным отклонением выполняются неравенства ![]()
Нормированные элементы данной строки и будут нормированными элементами фильтра, схема которого приведена на рисунке к данной таблице. При этом, обозначения элементов вверху таблицы относятся к схеме а, а внизу – к схеме б. Истинные значения элементов получаются путем денормирования.
Активные RC-фильтры. Фильтры, представляющие собой комбинацию пассивной RC-цепи и активного элемента, называются активными RC-фильтрами. В качестве активного элемента чаще всего используются операционные усилители с двумя входами: инвертирующим и неинвертирующим.
Реализация передаточных функций фильтров на активных RC-цепях осуществляется следующим образом. Заданную функцию Hp(p) порядка m разбивают на произведение передаточных функций не выше второго порядка, т. е. Hp(p)=Hp1(p)Hp2(p) … Hpk(p). Каждую передаточную функцию Hpi(p) реализуют в виде ARC-звена первого или второго порядка. Схему ARC-фильтра получают путем каскадного соединения звеньев.
Пример. Пусть задана передаточная функция полиномиального фильтра Чебышева пятого порядка. ![]() .
.
Полюсы этой функции (корни знаменателя): р1 = –0,177; р2,3 = –0,143 ![]()
![]() j0,597; р4,5 = –0,0547
j0,597; р4,5 = –0,0547 ![]() j0,966. Вещественный полюс р1 дает по теореме Виета сомножитель первого порядка (р – р1) = р + 0,177; первая пара комплексно-сопряженных полюсов р2 и р3 – сомножитель второго порядка (р – р2)×(р – р3) = р2 + 0,286р + 0,377; вторая пара полюсов р4 и р5 – сомножитель (р – р4)(р – р5) = р2 + 0,110р + 0,936. Тогда
j0,966. Вещественный полюс р1 дает по теореме Виета сомножитель первого порядка (р – р1) = р + 0,177; первая пара комплексно-сопряженных полюсов р2 и р3 – сомножитель второго порядка (р – р2)×(р – р3) = р2 + 0,286р + 0,377; вторая пара полюсов р4 и р5 – сомножитель (р – р4)(р – р5) = р2 + 0,110р + 0,936. Тогда 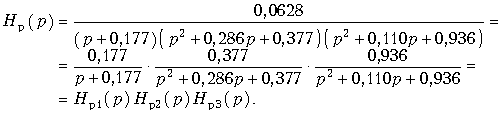
Таким образом, фильтр Чебышева пятого порядка может быть реализован двумя звеньями с передаточными функциями второго порядка и одним звеном с передаточной функцией первого порядка.
В практике проектирования активных RC-фильтров используется большое число схем, реализующих передаточные функции первого и второго порядка. Один из способов построения таких схем показан на рис. 17.14, а. Пассивная часть схемы представлена в виде цепи из элементов R и С. Между зажимами 2 и 3 включен операционный усилитель, в котором использован инвертирующий вход. Примером пассивной RC-цепи является схема, приведенная на рис. 17.14, б. Передаточная функция изображенной на рис. 17.14, б активной RC-цепи имеет вид: 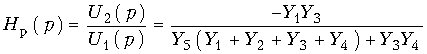 (17.28)
(17.28)
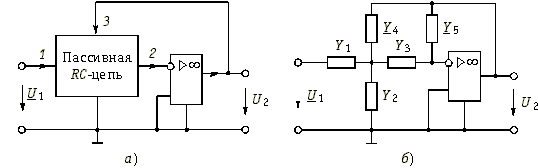
Рис. 17.14
Для реализации в виде такой цепи полиномиального фильтрового звена второго порядка с передаточной функцией 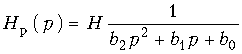 (17.29)
(17.29)
нужно выбрать проводимости Y1, Y3 и Y4 активными: G1, G3 и G4, а проводимости Y2 и Y5 – емкостными: pC2 и pC5. Тогда (17.28) запишется в следующей форме: 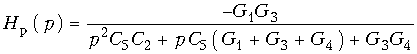 (17.30)
(17.30)
Сопоставление коэффициентов при р в соответствующих степенях и свободных членов из (17.30), выраженных через элементы фильтра, с заданными числовыми значениями коэффициентов при р и свободных членов из (17.29) позволяет определить значения элементов фильтра.
Пример. Реализовать фильтр нижних частот Баттерворта второго порядка из примера в виде активной RC-цепи.
Передаточная функция НЧ фильтра Баттерворта второго порядка Hp(p) = 1/ (p2 + 1,41p + 1). Для сопоставления с ней передаточной функции (17.30) представим последнюю в виде, когда коэффициент при p2 равен 1: 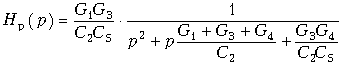 .
.
Приравнивая коэффициенты при р и свободные члены этих передаточных функций, получаем три уравнения с шестью неизвестными G1, G2, G3, G4, C1 и C2: ![]() ;
; ![]() ;
; ![]() .
.
Следует учесть, что в уравнения входят нормированные значения емкостей ![]() и
и ![]() , так как коэффициенты передаточной функции фильтра Баттерворта получены для нормированной частоты
, так как коэффициенты передаточной функции фильтра Баттерворта получены для нормированной частоты ![]() =
= ![]() /
/![]() н (где
н (где ![]() н =
н = ![]() ‘п = 2
‘п = 2![]() fп = 2
fп = 2![]() ×159×103 = 106 рад/с).
×159×103 = 106 рад/с).
Поскольку искомых величин больше, чем уравнений, зададимся частью из них. Выберем приемлемые значения проводимостей G1, G3 и G4, например G1 = G3 = G4 = 10–3 См, т. е. R1 = R3 = R4 = 1 кОм. Далее из второго уравнения легко получить ![]() , а из первого и третьего уравнений –
, а из первого и третьего уравнений – ![]() . Денормированные значения емкостей
. Денормированные значения емкостей ![]() 2,13 нФ,
2,13 нФ, ![]() 0,47 нФ.
0,47 нФ.
Схема фильтра приведена на рис. 17.15.
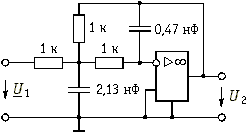
Рис. 17.15
Реализация фильтров со всплесками ослабления, передаточные функции которых описываются выражением (17.21), осуществляется так же, как и реализация полиномиальных фильтров. Передаточная функция (17.21) разбивается на произведение простейших (первого и второго порядков) передаточных функций; последние реализуются в виде фильтровых RC-звеньев первого и второго порядков, соединяемых каскадно в общую схему фильтра.
Для реализации передаточных функций второго порядка с нулем передачи Hpi(p) = (p2 + a 0)/(p2 + b1p + a 0) используются специальные фильтровые ARC-звенья.
Более подробно методику синтеза активных RC-фильтров со всплесками ослабления можно изучить, обратившись к специальной литературе.
17.4. Переход от фильтров нижних частот к другим типам фильтров
Преобразование шкалы частот ФНЧ. Для синтеза фильтров верхних частот (полосовых или заграждающих) и, в частности, для нахождения их передаточных функций, можно было бы заново повторить все преобразования, примененные к фильтрам нижних частот. Однако такой подход нерационален. Обычно для расчета ФВЧ, ПФ или ЗФ используют преобразование шкалы частот ФНЧ-прототипа.
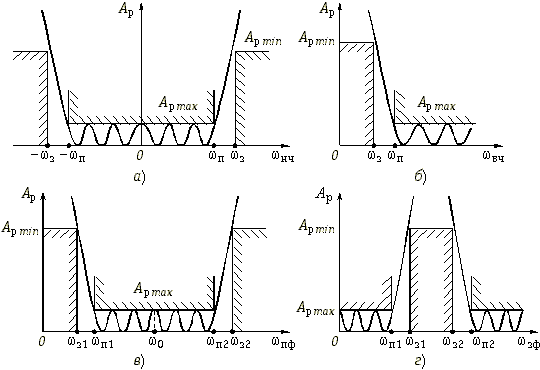
Рис. 17.16
На рис. 17.16 приведены характеристики ослабления фильтров: нижних частот (а), верхних частот (б) полосового (в) и заграждающего (г). Для ФНЧ эта характеристика построена как для положительных, так и для отрицательных частот. Шкала частот для каждого фильтра помечена для удобства буквенными обозначениями: “нч”, “вч”, “пф”, “зф”.
Из рис. 17.16, а и б видно, что характеристика ослабления ФНЧ в отрицательной области частот повторяет характеристику ФВЧ. Преобразовать характеристику ФНЧ в характеристику ФВЧ можно с помощью замены переменной: ![]() (17.31) где
(17.31) где ![]() n – граничная частота полосы пропускания ФНЧ и ФВЧ.
n – граничная частота полосы пропускания ФНЧ и ФВЧ.
График зависимости (17.31) представляет собой нижнюю ветвь гиперболы. На рис. 17.17 приведены характеристика ослабления ФНЧ, график преобразующей функции (17.31) и характеристика ослабления ФВЧ. Действительно, такое преобразование частоты приводит к соответствию: частоты ![]() н.ч = —
н.ч = —![]() частоте
частоте ![]() в.ч = 0; частоты
в.ч = 0; частоты ![]() н.ч = —
н.ч = —![]() п частоте
п частоте ![]() в.ч =
в.ч = ![]() п; частоты
п; частоты ![]() н.ч = 0 частоте
н.ч = 0 частоте ![]() в.ч =
в.ч = ![]() .
.
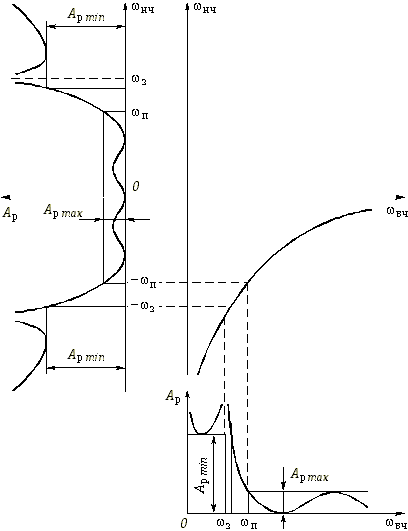
Рис. 17.17
Чтобы из характеристики ФНЧ получить характеристику ПФ (рис. 17.16, в), необходима замена переменной: 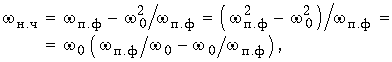 (17.32) где
(17.32) где ![]() ;
; ![]() п1 и
п1 и ![]() п2 – граничные частоты полосы пропускания ПФ;
п2 – граничные частоты полосы пропускания ПФ; ![]() з1 и
з1 и ![]() з2 – граничные частоты полосы нерпопускания ПФ.
з2 – граничные частоты полосы нерпопускания ПФ.
График функции (17.32) описывается более сложной кривой, чем у ФВЧ. На рис. 17.18 показано как происходит преобразование шкалы частот ФНЧ в шкалу частот ПФ с помощью преобразования частоты (17.32). Данное преобразование приводит к соответствию частоты ![]() н.ч = —
н.ч = —![]() частоте
частоте ![]() п.ф = 0, частоты
п.ф = 0, частоты ![]() н.ч = 0 частоте
н.ч = 0 частоте ![]() п.ф =
п.ф = ![]() 0, частоты
0, частоты ![]() н.ч =
н.ч = ![]() частоте
частоте ![]() п.ф =
п.ф = ![]() .
.
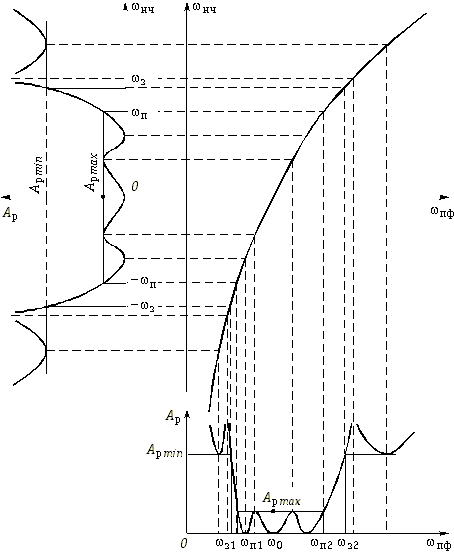
Рис. 17.18
Характеристику (рис. 17.16, г) заграждающего фильтра можно получить из характеристики ФНЧ, применяя преобразование частоты: 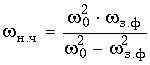 (17.33)
(17.33)
Преобразование схем пассивных LC-фильтров. Замена переменных (2.31) и (2.32) в выражении для квадрата АЧХ |Hp(j![]() )|2 фильтра нижних частот приводит при реализации этой функции к преобразованию схемы ФНЧ в схемы ФВЧ и ПФ. Индуктивное сопротивление ФНЧ j
)|2 фильтра нижних частот приводит при реализации этой функции к преобразованию схемы ФНЧ в схемы ФВЧ и ПФ. Индуктивное сопротивление ФНЧ j![]() н.чLн.ч переходит при преобразовании частот (17.31) в сопротивление:
н.чLн.ч переходит при преобразовании частот (17.31) в сопротивление: ![]() , т. е. в емкостное сопротивление ФВЧ, где Cв.ч = 1/
, т. е. в емкостное сопротивление ФВЧ, где Cв.ч = 1/![]() п2Lн.ч.
п2Lн.ч.
Емкостная проводимость: 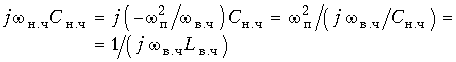 переходит в индуктивную проводимость фильтра ВЧ с индуктивностью Lв.ч = 1/
переходит в индуктивную проводимость фильтра ВЧ с индуктивностью Lв.ч = 1/ ![]() п2Cн.ч.
п2Cн.ч.
Преобразование частоты (17.32) приводит к замене индуктивного сопротивления ФНЧ: 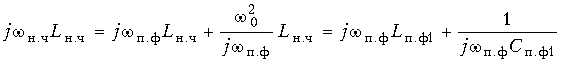
сопротивлением последовательного контура в ПФ с элементами Lп.ф1 = Lн.ч и Cп.ф1 = 1/ (![]() 02Lн.ч).
02Lн.ч).
Емкостная проводимость ФНЧ: 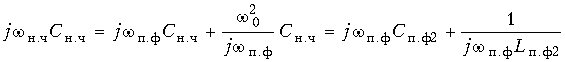 заменяется в ПФ проводимостью параллельного контура с элементами Cп.ф2 = Cн.ч и Lп.ф2 = 1/ (
заменяется в ПФ проводимостью параллельного контура с элементами Cп.ф2 = Cн.ч и Lп.ф2 = 1/ (![]() 02Cн.ч).
02Cн.ч).
Нетрудно убедиться также, что индуктивный элемент ФНЧ преобразуется в ЗФ в параллельный колебательный контур с резонансной частотой ![]() 0, а емкость ФНЧ – в последовательный колебательный контур с той же резонансной частотой.
0, а емкость ФНЧ – в последовательный колебательный контур с той же резонансной частотой.
Пример. Рассчитать полосовой фильтр с характеристиками Баттерворта, удовлетворяющий требованиям: Аpmax = 3 дБ; Аpmin=12,2 дБ; fп1=1241 кГц; fп2 = 1400 кГц; fз1 = 1168,5 кГц; fз2 = 1486 кГц.
Для решения поставленной задачи нужно сначала построить фильтр НЧ-прототипа, а затем с помощью преобразования частоты перейти к ПФ.
Пересчитаем требования ПФ (рис. 17.16, в) в требования к НЧ-прототипу (см. рис. 17.16, а). Воспользуемся формулой (17.32): f0 = ![]() =
= ![]() = 1734,4 кГц; fп = fп2 – f02/fп2 = fп2 – fп1= 159 кГц; fз = fз2 – f02/fз2 = = fз2 – fз1= 318 кГц. В качестве нормирующей частоты выберем fн = fп. Тогда нормированные частоты
= 1734,4 кГц; fп = fп2 – f02/fп2 = fп2 – fп1= 159 кГц; fз = fз2 – f02/fз2 = = fз2 – fз1= 318 кГц. В качестве нормирующей частоты выберем fн = fп. Тогда нормированные частоты ![]() п = 1 и
п = 1 и ![]() з = fз/fп = 2. Итак, требования к НЧ-прототипу имеют вид: Аpmax = 3 дБ; Аpmin = 12,2 дБ; fп = 159 кГц (
з = fз/fп = 2. Итак, требования к НЧ-прототипу имеют вид: Аpmax = 3 дБ; Аpmin = 12,2 дБ; fп = 159 кГц (![]() п = 1); fз = 318 кГц (
п = 1); fз = 318 кГц (![]() з = 2).
з = 2).
В примере для такого НЧ-фильтра были получены квадрат АЧХ |Hp(j![]() )|2 = 1/(1 +
)|2 = 1/(1 + ![]() 4), рабочее ослабление Аp = 10lg(1 +
4), рабочее ослабление Аp = 10lg(1 + ![]() 4) и передаточная функция Hp(p) = 1/(p2 + 1,41p + 1).
4) и передаточная функция Hp(p) = 1/(p2 + 1,41p + 1).
В другом примере этот фильтр был реализован в виде схемы, изображенной на рис. 17.11 с элементами Lн.ч = 1,41 мГн и Сн.ч = 1,41 нФ.
При переходе к требуемому полосовому фильтру необходимо индуктивность продольного плеча Lн.ч фильтра НЧ-прототипа заменить последовательным контуром с элементами Lп.ф1 = Lн.ч = 1,41 мГн и Сп.ф1 = ![]() = 6×10–12 Ф = 6,0 пФ.
= 6×10–12 Ф = 6,0 пФ.
Вместо емкости Сн.ч в поперечном плече полосового фильтра будет включен параллельный контур с элементами Сп.ф2 = Сн.ч = 1,41 нФ и Lп.ф2 = ![]() = 6×10–6 Гн = 6 мкГн.
= 6×10–6 Гн = 6 мкГн.
Схема искомого полосового фильтра приведена на рис. 17.19.
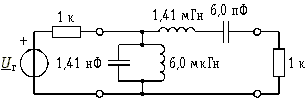
Рис. 17.19
Преобразование передаточных функций активных RC-фильтров. В активных RC-фильтрах для того, чтобы перейти от передаточной функции ФНЧ-прототипа к передаточным функциям ФВЧ и ПФ, следует осуществить замену комплексной переменной р. Из (17.31) получаем для ФВЧ ![]() или
или ![]() (17.34) где
(17.34) где ![]() н.ч =
н.ч = ![]() н.ч/
н.ч/![]() п и
п и ![]() в.ч =
в.ч = ![]() в.ч/
в.ч/ ![]() п.
п.
Заменяя в (17.34) оператор j![]() на оператор р, запишем преобразование переменной р в выражении нормированной по частоте передаточной функции ФНЧ-прототипа:
на оператор р, запишем преобразование переменной р в выражении нормированной по частоте передаточной функции ФНЧ-прототипа: ![]() (17.35)
(17.35)
Передаточная функция полиномиального звена второго порядка ФНЧ имеет вид: 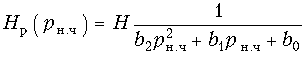 (17.36)
(17.36)
Замена переменной (17.35) в этом выражении приводит к передаточной функции полиномиального звена второго порядка ФВЧ: 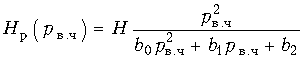 (17.37)
(17.37)
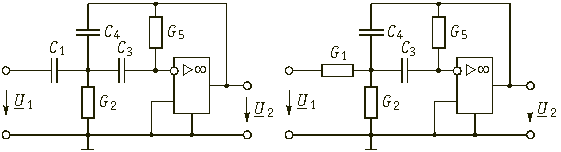
Для реализации звена с передаточной функцией (17.37) может быть использована схема рис. 17.14, б, в которой следует выбрать проводимости Y2 и Y5 – активными, т. е. Y2 = G2 и Y5 = G5, а проводимости Y1, Y3 и Y4 – емкостными, т. е. Y1 = pC1; Y3 = pC3 и Y4 = pC4. Подставляя эти значения проводимостей в выражение (17.28), получаем передаточную функцию 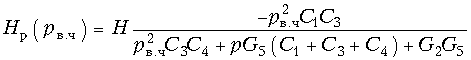 (17.38) ARC-звена ФВЧ второго порядка, схема которого дана на рис. 17.20. Значения элементов схемы будут найдены, если приравнять коэффициенты из (17.37) и (17.38) при соответствующих степенях р.
(17.38) ARC-звена ФВЧ второго порядка, схема которого дана на рис. 17.20. Значения элементов схемы будут найдены, если приравнять коэффициенты из (17.37) и (17.38) при соответствующих степенях р.
 |
|
| Рис. 17.20 | Рис. 17.21 |
Для перехода от НЧ-прототипа к полосовому фильтру воспользуемся (17.33): ![]() или
или ![]() (17.39) где
(17.39) где ![]() н.ч =
н.ч = ![]() н.ч
н.ч![]() п;
п; ![]() п.ф =
п.ф = ![]() п.ф/
п.ф/![]() п;
п; ![]() 0 =
0 = ![]() 0/
0/![]() п.
п.
Вводя переменную p = j![]() и учитывая, что p2 = –
и учитывая, что p2 = –![]() 2, находим из (17.39):
2, находим из (17.39): ![]() (17.40)
(17.40)
Такая замена переменной pн.ч в (17.36) приводит к передаточной функции полосового фильтра: 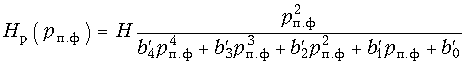 (17.41) где b‘4 = b2; b‘3 = b1; b‘2 = 2b2
(17.41) где b‘4 = b2; b‘3 = b1; b‘2 = 2b2![]() 02 + b0; b‘1 = b1
02 + b0; b‘1 = b1![]() 02; b‘0 = b2
02; b‘0 = b2![]() 04.
04.
Видим, что при переходе к ПФ порядок передаточной функции удваивается. Передаточную функцию (17.41) можно разбить на произведение передаточных функций второго порядка и каждую из них реализовать отдельной ARC-схемой.
Запишем передаточную функцию ПФ второго порядка: 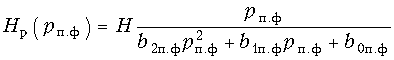 (17.42)
(17.42)
Подобную передаточную функцию имеет ARC-схема, изображенная на рис. 17.14, б при Y1 = G1, Y2 = G2, Y5 = G5 и Y3 = = pC3, Y4 = pC4. Действительно, из (17.28) находим: 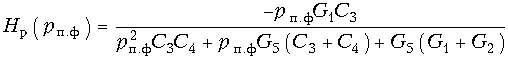 (17.43)
(17.43)
Элементы схемы фильтра (рис. 17.21) определяются сопоставлением (17.42) и (17.43).
Порядок синтеза ФВЧ, ПФ и ЗФ. С помощью преобразования частоты был осуществлен переход от ФНЧ к другим типам фильтра. Однако для их синтеза этого недостаточно, так как исходными при синтезе ФВЧ, ПФ и ЗФ являются требования не к ФНЧ, а к данным фильтрам. Поэтому вначале требуется выполнять обратный переход. Сформулируем порядок синтеза ФВЧ, ПФ, ЗФ: 1) по заданным требованиям к ФВЧ, ПФ и ЗФ необходимо определить требования к ФНЧ; 2) решить задачу аппроксимации для ФНЧ (получить квадрат АЧХ или операторную передаточную функцию); 3) реализовать квадрат АЧХ в виде лестничного ФНЧ и перейти с помощью преобразования частоты к схеме требуемого типа фильтра (если выбрана пассивная схема фильтра); 4) используя соответствующее преобразование частоты, перейти от операторной передаточной функции ФНЧ к операторной передаточной функции искомого фильтра и реализовать его в виде ARC-схемы (если выбран активный RCфильтр).
Рассмотрим более подробно первый пункт.
Пусть заданы требования к ФВЧ, т. е. заданы ![]() пв.ч,
пв.ч, ![]() зв.ч, Арmax и Арmin (см. рис. 17.17). Определим требования к ФНЧ. Если в выражение (17.31) вместо
зв.ч, Арmax и Арmin (см. рис. 17.17). Определим требования к ФНЧ. Если в выражение (17.31) вместо ![]() в.ч подставить
в.ч подставить ![]() пв.ч, то согласно рис. 17.17 получим
пв.ч, то согласно рис. 17.17 получим ![]()
Откуда: ![]()
Величины Арmax и Арmin остаются для ФНЧ такими же как и для ФВЧ. Таким образом получены требования к ФНЧ. По найденным требованиям к ФНЧ решаем задачу аппроксимации одним из методов, изложенных выше.
Пусть заданы требования к ПФ, т. е. известны ![]() з1,
з1, ![]() п1,
п1, ![]() п2,
п2, ![]() з2, а также ослабление в полосе пропускания Арmax и в полосе задерживания Арmin (см. рис. 17.18). Подставим в выражение (17.32) последовательно граничные частоты полос пропускания и задерживания полосового фильтра. Как видно из рис. 17.18, в результате такой подстановки получим:
з2, а также ослабление в полосе пропускания Арmax и в полосе задерживания Арmin (см. рис. 17.18). Подставим в выражение (17.32) последовательно граничные частоты полос пропускания и задерживания полосового фильтра. Как видно из рис. 17.18, в результате такой подстановки получим: ![]()
Учитывая, что ![]()
получим окончательно: ![]()
Требования по ослаблению к ФНЧ-прототипу остаются такими же, как и к ПФ. Следовательно, имеются все исходные данные для решения задачи аппроксимации ФНЧ.
Аналогично решается задача для ЗФ. Граничные частоты для ПП и ПЗ фильтров рассчитываются по формулам
![]()
17.5. Резонаторные фильтры
В многоканальных системах передачи разделение каналов по частоте осуществляется с помощью полосовых фильтров. Чтобы сигналы одного канала не попадали в другой, ПФ должны иметь высокую избирательность. Добротность резонансных контуров таких фильтров Q > 20 … 25f0/ (fп2 – fп1). Так, для фильтра с f0 = 62 кГц и полосой пропускания fп2 – fп1 = 4 кГц Q > 300, в то же время для фильтра с f0 = 106 кГц и fп2 – fп1 = 4 кГц Q > 1500.
В радиосвязи используются еще более высокие частоты (десятки и сотни мегагерц) и для построения избирательных фильтров нужны резонаторы с добротностью в тысячи и десятки тысяч единиц. Такие значения добротности никогда не обеспечиваются в LC-резонаторах (их добротность не превышает сотен единиц), поэтому в фильтрах применяют высокодобротные механические резонаторы, пьезоэлектрические, магнитострикционные и электромеханические.
В пьезоэлектрических фильтрах роль резонатора выполняет пластинка, вырезанная специальным образом из материала, обладающего пьезоэлектрическим эффектом (например, из кристалла кварца). Пьезоэффект кварцевой пластинки заключается в появлении на ее поверхностях электрических зарядов при механическом воздействии на пластинку. Существует и обратный пьезоэффект – возникновение механических колебаний пьезопластинки при помещении ее в переменное электрическое поле.
Если пьезопластинку поместить между металлическими обкладками и подать на обкладки переменное напряжение, то пластинка начнет совершать механические колебания. На поверхностях пластинки возникнут электрические заряды и во внешней цепи потечет ток. При совпадении частоты переменного напряжения и частоты собственных колебаний пластинки возникает механический резонанс; амплитуда колебаний достигнет максимума и ток во внешней цепи будет максимальным. Таким образом, механический резонанс в кварцевой пластине подобен резонансу напряжений в последовательном колебательном контуре.
Эквивалентная схема пьезоэлектрического (в частности, кварцевого) резонатора (рис. 17.22) помимо эквивалентных индуктивности L и емкости C резонатора содержит емкость кварцедержателя Cк, т. е. обкладок, между которыми помещена кварцевая пластинка.
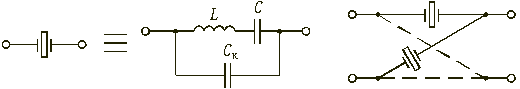 |
|
| Рис. 17.22 | Рис. 17.23 |
Пьезоэлектрические фильтры с кварцевыми резонаторами называют кварцевыми. Добротность кварцевых резонаторов достигает 10 … 20 тыс. ед. Кварцевые фильтры могут быть построены по мостовой схеме (рис. 17.23).
Магнитострикционные фильтры строятся на основе резонаторов из ферромагнитного материала, обладающего магнитострикционным эффектом (например, из сплава никеля с кобальтом). Магнитострикционный эффект состоит в том, что стержень из ферромагнетика, помещенный в переменное магнитное поле, изменяет свои геометрические размеры. Обратный эффект – изменение магнитной проницаемости стержня при механическом воздействии на него. Если, например, никель-кобальтовый стержень поместить внутрь катушки индуктивности, создающей переменное магнитное поле, его геометрические размеры начнут меняться. При этом будет меняться и его магнитная проницаемость. В катушке индуктивности наведется ЭДС, направленная против ЭДС генератора и уменьшающая ток во внешней цепи. При механическом резонансе амплитуда колебаний стержня будет максимальной, а ток во внешней цепи – минимальный. Таким образом, механический резонанс магнитострикционного стержня подобен резонансу токов параллельного колебательного контура.
Эквивалентная схема резонатора приведена на рис. 17.24 и включает в себя элементы Lм и См эквивалентного резонатору контура, а также индуктивность L0, учитывающую рассеяние магнитного потока при замыкании его через воздух.
Добротность магнитострикционных резонаторов ниже, чем кварцевых, и составляет 5 … 10 тыс. ед. Магнитострикционные фильтры строятся по мостовой схеме (рис. 17.25).
В электромеханических фильтрах резонаторами являются металлические тела (диски, шарики, стержни, пластинки), соединенные металлическими связками. На рис. 17.26 изображен трехрезонаторный стержневой электромеханический фильтр. Возбуждаются колебания в фильтре с помощью входного магнитострикционного преобразователя (МСП); снимаются колебания с выхода фильтра с помощью выходного МСП. Электромеханические фильтры являются также высокодобротными.
Кроме рассмотренных существуют и другие типы фильтров: фильтры с переключаемыми конденсаторами, кварцевые фильтры на поверхностных акустических волнах (ПАВ) и др. С некоторыми из них можно ознакомиться в [2] и специальной литературе.
17.6. Вопросы и задания для самопроверки
- Что такое электрический фильтр? Какие типы фильтров существуют?
- Характеристика рабочего ослабления фильтра изображена на рис. 17.3. Определить тип фильтра.
Ответ: ФНЧ Чебышева 5 порядка.
- Какой вид имеют функции фильтрации фильтров Баттерворта, Чебышева, Золотарева?
- Привести графики Ap(
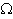 ) ФНЧ третьего порядка Баттерворта, Чебышева и Золотарева.
) ФНЧ третьего порядка Баттерворта, Чебышева и Золотарева. - Рассчитать коэффициент неравномерности ослабления в полосе пропускания и порядок фильтра Баттерворта, удовлетворяющего требованиям: Apmax = 2 дБ; Apmin = 25 дБ; fп = 15 кГц; fз = 26 кГц.
Ответ:
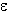 = 0,765; m = 6.
= 0,765; m = 6. - Найти выражение для передаточной функции ФНЧ Баттерворта, удовлетворяющего требованиям, приведенным в задаче 5.
Ответ:
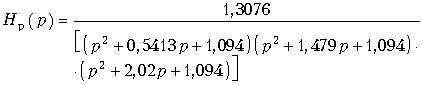 .
. - Рассчитать порядок и найти операторную передаточную функцию ФНЧ Чебышева, удовлетворяющего требованиям: Apmax = = 1,25 дБ; Apmin = 30 дБ; fп = 105 кГц; fз = 2,5×105 кГц.
Ответ:m = 3;
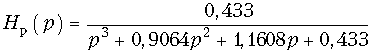 .
. - Привести LC-схемы фильтров, имеющих характеристики, изображенные на рис. 17.4.
- Привести LC-схему фильтра, характеристика которого изображена на рис. 17.3.
- Привести LC-схему фильтра НЧ Золотарева, а также график зависимости его рабочего ослабления от частоты.
- Каков алгоритм расчета фильтров методом Дарлингтона?
- Реализовать ФНЧ Баттерворта третьего порядка, имеющего передаточную функцию
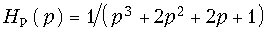 , в виде пассивной LC-схемы. Внутреннее сопротивление генератора
, в виде пассивной LC-схемы. Внутреннее сопротивление генератора 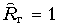 .
.
Ответ:![]() ,
, ![]() ,
, ![]() .
.
- Какие фильтры называются активными RC-фильтрами?
- Какие передаточные функции имеют RC-фильтровые звенья первого и второго порядков? Как получить передаточную функцию фильтра более высокого порядка?
- Реализовать активный RC-фильтр, имеющий передаточную функцию, приведенную в задаче 12.
- Как осуществить переход от ФНЧ к ФВЧ, ПФ, ЗФ?
- Доказать, что при переходе от ФНЧ к ЗФ индуктивность фильтра-прототипа преобразуется в параллельный контур в ЗФ, а емкость – в последовательный контур?
- Привести схемы LC-фильтров, имеющих характеристики, изображенные на рис. 17.16, б, в, г.
- Рассчитать ФВЧ с максимально плоской характеристикой ослабления, удовлетворяющий требованиям: Apmax = 1,5 дБ; Apmin = 20 дБ;
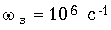 ;
; 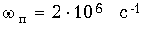 .
. - Как осуществляется переход от схемы НЧ-прототипа к схемам ФВЧ и ПФ в активных RC-фильтрах?
- Какие высокодобротные механические резонаторы используются для построения фильтров?
В одной главе невозможно подробно изложить основы теории фильтров, но мы постараемся в данном разделе дать ее основные положения и выводы. Здесь и далее 5 означает оператор Лапласа,

Активные RC-фильтры принадлежат к классу линейных схем с сосредоточенными параметрами. Передаточная функция линейной цепи  порядка с сосредоточенными параметрами описывается следующим выражением (порядок цепи определяется степенью полинома знаменателя):
порядка с сосредоточенными параметрами описывается следующим выражением (порядок цепи определяется степенью полинома знаменателя):

где  — полином числителя,
— полином числителя,  — полином знаменателя,
— полином знаменателя,  — вещественные коэффициенты,
— вещественные коэффициенты,  — передаточная функция схемы.
— передаточная функция схемы.
Заметим, что для реальных схем 
Полиномы  можно разложить на множители первого и второго порядков с вещественными коэффициентами. Следовательно, нужную характеристику можно получить, включив последовательно несколько фильтров первого и второго порядков. Рассмотрим далее передаточные функции таких фильтров.
можно разложить на множители первого и второго порядков с вещественными коэффициентами. Следовательно, нужную характеристику можно получить, включив последовательно несколько фильтров первого и второго порядков. Рассмотрим далее передаточные функции таких фильтров.
1. Характеристика ФНЧ первого порядка (рис. 6.2). Эта характеристика описывается простым выражением:

где  — коэффициент передачи на постоянном токе,
— коэффициент передачи на постоянном токе,  — частота полюса, которая в данном случае равна частоте, на которой коэффициент передачи снижается на 3 дБ по сравнению с
— частота полюса, которая в данном случае равна частоте, на которой коэффициент передачи снижается на 3 дБ по сравнению с 

Рис. 6.2. Частотная характеристика ФНЧ первого порядка.
2. Характеристика ФВЧ первого порядка (рис. 6.3). Эта харакгеристика также довольно простая:

где  — коэффициент передачи на высоких частотах,
— коэффициент передачи на высоких частотах,  — частота полюса, равная частоте, на которой коэффициент передачи снижается на 3 дБ по сравнению с
— частота полюса, равная частоте, на которой коэффициент передачи снижается на 3 дБ по сравнению с 
3. Характеристика фазового фильтра (ФФ) первого порядка (рис. 6.4). Коэффициент передачи этого фильтра имеет постоянное значение во всем частотном диапазоне, изменяется лишь вносимый фазовый сдвиг (временная задержка).
Характеристика фазового фильтра первого порядка:

где  — модуль коэффициента передачи,
— модуль коэффициента передачи,  — частота, на которой фазовый сдвиг равен 90°.
— частота, на которой фазовый сдвиг равен 90°.

Рис. 6.3. Частотная характеристика ФВЧ первого порядка.

Рис. 6.4. Частотная характеристика ФФ первого порядка.
4. Характеристика ФНЧ второго порядка (рис. 6.5). Эта характеристика имеет вид:

где  — коэффициент передачи на постоянном токе,
— коэффициент передачи на постоянном токе,  — частота полюса,
— частота полюса,  — добротность фильтра.
— добротность фильтра.
При  на амплитудно-частотной характеристике (АЧХ) появляется выброс на частоте:
на амплитудно-частотной характеристике (АЧХ) появляется выброс на частоте:

и значение коэффициента передачи на этой частоте равно:

причем частота среза по уровню -3 дБ составляет:

Для ФНЧ, характеристика которого показана на рис. 6.5, при малых  (т.е.
(т.е.  ) полюса передаточной функции вещественные, и его АЧХ оказывается плоской. Выражение для характеристики второго порядка можно разложить на два сомножителя первого порядка. Когда же
) полюса передаточной функции вещественные, и его АЧХ оказывается плоской. Выражение для характеристики второго порядка можно разложить на два сомножителя первого порядка. Когда же  превышает
превышает  на АЧХ появляется “выпуклость”. Амплитудно-частотная характеристика схем с большой добротностью имеет значительный выброс.
на АЧХ появляется “выпуклость”. Амплитудно-частотная характеристика схем с большой добротностью имеет значительный выброс.

Рис. 6.5. Частотная характеристика ФНЧ второго порядка.
5. Характеристика ФВЧ второго порядка (рис. 6.6). Эта характеристика описывается выражением:

где  — коэффициент передачи на высокой частоте,
— коэффициент передачи на высокой частоте,  — частота полюса,
— частота полюса,  — добротность фильтра.
— добротность фильтра.
Максимальный коэффициент передачи (в точке выброса — прим. ред.) при больших значениях  равен
равен  .
.

Рис. 6.6. Частотная характеристика ФВЧ второго порядка. Выброс на АЧХ возникает при  на частоте:
на частоте:

и значение коэффициента передачи при этом равно:

Частота среза по уровню —3 дБ равна:


Рис. 6.7. Частотная характеристика ПФ второго порядка.
6. Характеристика ПФ второго порядка (рис. 6.7). Эта характеристика описывается выражением:

ее можно представить в другом виде:

где  — коэффициент передачи на центральной частоте
— коэффициент передачи на центральной частоте  ,
,  — добротность фильтра.
— добротность фильтра.
Заметим, что  , где
, где  — частоты, на которых коэффициент передачи снижается на -3 дБ по сравнению с
— частоты, на которых коэффициент передачи снижается на -3 дБ по сравнению с 
Можно показать, что:

Ширина полосы пропускания по уровню -3 дБ составляет:

При малых добротностях  знаменатель передаточной функции можно разложить на два сомножителя с вещественными коэффициентами (т.е. передаточная функция может быть представлена в виде произведения двух функций первого порядка — прим. ред.), поэтому АЧХ и фазочастотная характеристика (ФЧХ) на рис. 6.7 выглядят достаточно пологими. При
знаменатель передаточной функции можно разложить на два сомножителя с вещественными коэффициентами (т.е. передаточная функция может быть представлена в виде произведения двух функций первого порядка — прим. ред.), поэтому АЧХ и фазочастотная характеристика (ФЧХ) на рис. 6.7 выглядят достаточно пологими. При  полюса передаточной функции становятся комплексными. С увеличением
полюса передаточной функции становятся комплексными. С увеличением  полоса пропускания сужается и характеристика фильтра становится более избирательной.
полоса пропускания сужается и характеристика фильтра становится более избирательной.
7. Характеристика ППФ (РФ или фильтра-“пробки”) второго порядка (рис. 6.8). Передаточная функция описывается выражением:

где  — коэффициент передачи на постоянном токе и на высокой частоте,
— коэффициент передачи на постоянном токе и на высокой частоте,  — центральная частота полосы подавления,
— центральная частота полосы подавления,  — добротность фильтра.
— добротность фильтра.

Рис. 6.8. Частотная характеристика ППФ.
Приведенное выше выражение можно записать по-другому:

т.е. в виде разности постоянного коэффициента передачи  и коэффициента передачи ПФ.
и коэффициента передачи ПФ.
Частоты среза по уровню -3 дБ такие же, как у полосового фильтра:

Ширина полосы подавления по уровню -3 дБ равна

8. Характеристика ФФ второго порядка (рис. 6.9). Характеристика фазового фильтра второго порядка описывается выражением:

Его можно переписать в следующем виде:

т.е. постоянный коэффициент минус удвоенная передаточная характеристика полосового фильтра.

Рис. 6.9. Частотная характеристика ФФ второго порядка.
17.2. Аппроксимация характеристик фильтров нижних частот
Функция фильтрации. В общем виде электрические фильтры описываются передаточной функцией вида:
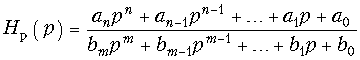 (17.1)
(17.1)
Квадрат амплитудно-частотной характеристики таких фильтров
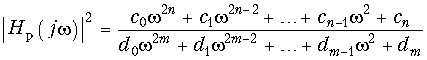 (17.2)
(17.2)
и, следовательно, рабочее ослабление
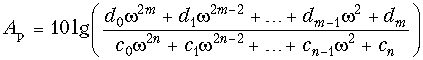 (17.3)
(17.3)
могут при надлежащем выборе степени полинома (порядка фильтра) и коэффициентов dk удовлетворить заданным требования (см. рис. 17.3).
В теории фильтров принято иметь дело не с обычной угловой частотой ![]() , а с нормированной частотой
, а с нормированной частотой ![]() , где
, где ![]() – нормирующая частота. Обычно в качестве нормирующей частоты выбирают граничную частоту полосы пропускания
– нормирующая частота. Обычно в качестве нормирующей частоты выбирают граничную частоту полосы пропускания ![]() , так что
, так что ![]() .
.
В теории электрических фильтров вместо формул (17.2) и (17.3) используют другие, также универсальные для любого типа фильтра:
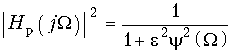 (17.4)
(17.4)
![]() (17.5)
(17.5)
Функция ![]() называется функцией фильтрации, а
называется функцией фильтрации, а ![]() – коэффициентом неравномерности ослабления. В общем случае
– коэффициентом неравномерности ослабления. В общем случае ![]() – это дробно-рациональная функция с вещественными коэффициентами (в частности полином), удовлетворяющая условиям: –1
– это дробно-рациональная функция с вещественными коэффициентами (в частности полином), удовлетворяющая условиям: –1 ![]()
![]()
![]() 1 в полосе пропускания и
1 в полосе пропускания и ![]() >> 1 в полосе непропускания фильтра.
>> 1 в полосе непропускания фильтра.
В зависимости от вида функции фильтрации получают различные типы фильтров. Если в качестве функции фильтрации используют полиномы, то фильтры называются полиномиальными. Среди полиномиальных фильтров широкое использование нашли фильтры Баттерворта и Чебышева. Если ![]() – дробно-рациональная функция, например, дробь Золотарева, то получают фильтр Золотарева. Все эти три типа фильтров будут рассмотрены в этой главе.
– дробно-рациональная функция, например, дробь Золотарева, то получают фильтр Золотарева. Все эти три типа фильтров будут рассмотрены в этой главе.
Следует отметить, что имеет смысл подробно изучать только фильтры нижних частот, т. к. другие типы фильтров (верхних частот, полосовые и заграждающие) могут быть легко получены из ФНЧ с помощью замены переменной (частоты). Для этого во всех выражениях, содержащих переменную ![]() , нужно произвести замену переменной таким образом, чтобы характеристики ФНЧ Ар(
, нужно произвести замену переменной таким образом, чтобы характеристики ФНЧ Ар(![]() ) и |Hр(j
) и |Hр(j![]() )|2 преобразовались в характеристики соответствующего фильтра. Подобная замена переменной
)|2 преобразовались в характеристики соответствующего фильтра. Подобная замена переменной ![]() называется преобразованием частоты, а исходный ФНЧ – фильтром НЧ-прототипа.
называется преобразованием частоты, а исходный ФНЧ – фильтром НЧ-прототипа.
Преобразование частоты позволяет установить соответствие между частотами полос пропускания и непропускания НЧ-прототипа и частотами фильтров верхних частот, полосового или заграждающего, а также преобразовать схему ФНЧ в схемы ФВЧ, ПФ или ЗФ. Более подробно вопросы, связанные с преобразованием частоты, будут рассматриваться в § 17.5.
Фильтры Баттерворта. Если в выражениях, описывающих квадрат АЧХ фильтра (17.4) и его рабочее ослабление (17.5), в качестве функции фильтрации используются полиномы Баттерворта ![]() = Bm(
= Bm(![]() ) =
) = ![]() m (по имени автора, предложившего использовать их для “конструирования” частотных характеристик фильтра), то такие фильтры называются фильтрами Баттерворта.
m (по имени автора, предложившего использовать их для “конструирования” частотных характеристик фильтра), то такие фильтры называются фильтрами Баттерворта.
Из формул (17.4) и (17.5) следует, что для фильтров Баттерворта на частоте ![]() = 0 значение квадрата АЧХ равно единице, а рабочего ослабления – нулю. С ростом частоты квадрат АЧХ фильтра Баттерворта уменьшается и падает до нуля на бесконечно большой частоте. Рабочее ослабление плавно растет до бесконечно большого значения. Таким образом, выражения (17.4) и (17.5) приближенно воспроизводят характеристики идеального фильтра.
= 0 значение квадрата АЧХ равно единице, а рабочего ослабления – нулю. С ростом частоты квадрат АЧХ фильтра Баттерворта уменьшается и падает до нуля на бесконечно большой частоте. Рабочее ослабление плавно растет до бесконечно большого значения. Таким образом, выражения (17.4) и (17.5) приближенно воспроизводят характеристики идеального фильтра.
Чтобы эти характеристики “вписывались” в предъявляемые к фильтру требования (см. рис. 17.3), необходимо иметь рабочее ослабление (17.5) в полосе пропускания меньшее Арmax, а в полосе непропускания большее Арmin. Первому условию можно удовлетворить, если потребовать на граничной частоте полосы пропускания (![]() = 1) выполнения равенства Ар(
= 1) выполнения равенства Ар(![]() )
)![]() =1 = Арmax или |Hр(j
=1 = Арmax или |Hр(j![]() )|
)|![]() =
= ![]() . Отсюда с учетом (17.5) или (17.4) имеем 1 +
. Отсюда с учетом (17.5) или (17.4) имеем 1 + ![]() 2 =
2 = ![]() и
и ![]() 2 =
2 = ![]() – 1. Вычисленный таким способом коэффициент
– 1. Вычисленный таким способом коэффициент ![]() :
:
![]() (17.6)
(17.6)
называется коэффициентом неравномерности ослабления в полосе пропускания фильтра.
В формуле (17.6) величина Арmax имеет размерность непер. Если воспользоваться значениями Арmax в децибелах, то
![]() (17.7)
(17.7)
С учетом введенных обозначений квадрат АЧХ фильтра Баттерворта запишется в виде
![]() (17.8)
(17.8)
Эта функция удовлетворяет свойствам квадрата АЧХ реальных четырехполюсников, и поэтому ей можно сопоставить физически осуществимый электрический фильтр.
Рабочее ослабление фильтра Баттерворта:
![]() (17.9)
(17.9)
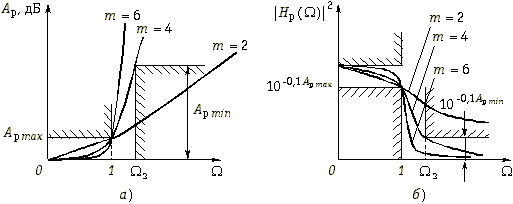 |
|
| Рис. 17.4 |
Крутизна частотных характеристик (17.8) и (17.9) зависит от степени m (порядка фильтра). Чем больше степень m, тем выше крутизна характеристик. На рис. 17.4, а, и б показаны графики рабочего ослабления и квадрата АЧХ фильтра Баттерворта для различных m. Таким образом, для удовлетворения требований в полосе непропускания необходимо выбрать соответствующий порядок фильтра m. Его легко определить из условия: на граничной частоте полосы непропускания: ![]() з Ар(
з Ар(![]() з)
з) ![]() Арmin или |Hр (j
Арmin или |Hр (j![]() )|
)|![]()
![]()
![]() . С учетом этого условия получим 1 +
. С учетом этого условия получим 1 + ![]() 2
2![]()
![]() >
> ![]() , откуда
, откуда ![]()
![]()
![]() . Логарифмируя обе части неравенства, придем к выражению
. Логарифмируя обе части неравенства, придем к выражению
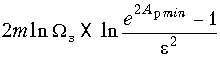
Из него находим окончательно
m ![]()
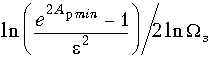 (17.10)
(17.10)
Величина Арmin входит в формулу в неперах. Если вычислять ее в децибелах, то:
m ![]()
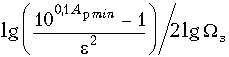 (17.11)
(17.11)
Передаточную функцию фильтра Баттерворта можно получить из (17.8), если положить j![]() = p:
= p:
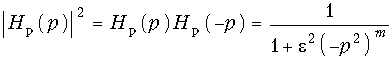 (17.12)
(17.12)
и разложить знаменатель полученной функции на произведение сомножителей.
Вычислим корни знаменателя, т. е. полюсы функции Hр(p) X Hр(–p), отдельно для четных и нечетных значений m. Для четных значений m:
![]() и
и 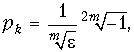 k = 1, 2, …, 2m.
k = 1, 2, …, 2m.
Так как:
![]() ,
,
имеем:
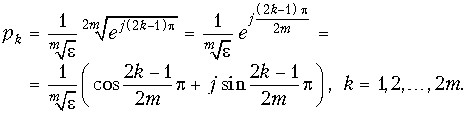 (17.13)
(17.13)
Для нечетных значений m:
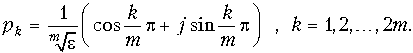
Выражение (17.12) примет вид:
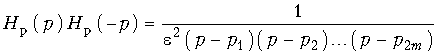 .
.
Половина полюсов функции Hр(p)Hр(–p) лежит в левой полуплоскости комплексной переменной p и может быть отнесена к передаточной функции реализуемого фильтра Hр(p). Другая половина полюсов, являясь зеркальным отражением первой, располагается в правой полуплоскости и относится к Hр(–p).
Построенная из полюсов, лежащих в левой полуплоскости, передаточная функция фильтра Баттерворта является полиномиальной передаточной функцией типа (17.1):
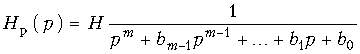 ,
,
где H = 1/![]() .
.
Пример. Найти выражения для частотной характеристики и передаточной функции фильтра нижних частот Баттерворта, удовлетворяющего следующим требованиям: Арmax = 3 дБ; Арmin = 12,2 дБ; fп = 159 кГц; fз = 318 кГц.
Определим нормированную частоту ![]() з = fз/fn = 2 и по формуле (17.7) коэффициент неравномерности ослабления
з = fз/fn = 2 и по формуле (17.7) коэффициент неравномерности ослабления ![]() 2 = 100,1×3 – 1 = 1. Порядок фильтра найдем согласно (17.11):
2 = 100,1×3 – 1 = 1. Порядок фильтра найдем согласно (17.11):
![]() .
.
Выберем m = 2. Тогда в соответствии с (17.8) и (17.9):
![]() .
.
Найдем передаточную функцию фильтра Hр(p). Значения полюсов функции |Hр(p)|2 = Hр(p)Hр(–p) = 1/
(1 + р4) вычислим из формулы (17.13): p1 = 0,707 + j0,707; p2 = – 0,707 + j0,707; p3 = – 0,707 – j0,707; p4 = 0,707 – j0,707. Расположение полюсов в комплексной плоскости показано на рис. 17.5, а.
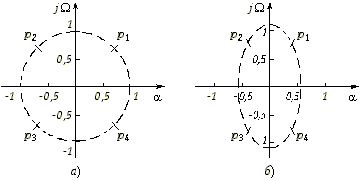 |
|
| Рис. 17.5 |
По теореме Виета из полюсов в левой полуплоскости p2 и p3 формируем передаточную функцию:
![]() .
.
Используя введенное ранее обозначение Bm(![]() ) =
) = ![]() m полинома Баттерворта, можно представить частотные характеристики (17.8) и (17.9) фильтра Баттерворта в следующей форме:
m полинома Баттерворта, можно представить частотные характеристики (17.8) и (17.9) фильтра Баттерворта в следующей форме:
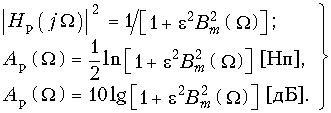 (17.14)
(17.14)
Фильтры Баттерворта называют также фильтрами с максимально плоским ослаблением в полосе пропускания (см. рис. 17.4, а).
Полиномиальные фильтры Чебышева. Если в качестве функции фильтрации в (17.4) и (17.5) использовать полином Чебышева, обозначаемый ![]() (
(![]()
) = Tm(![]()
), то формулы (17.14) примут вид:
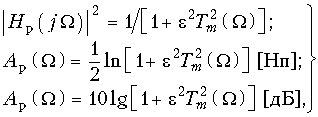 (17.15)
(17.15)
где Tm(![]() ) – полином Чебышева степени (порядка) m;
) – полином Чебышева степени (порядка) m; ![]() – коэффициент неравномерности, определяемый (17.6) или (17.7).
– коэффициент неравномерности, определяемый (17.6) или (17.7).
Фильтры с частотными характеристиками (17.15) называются фильтрами Чебышева. Проанализируем частотные характеристики фильтра Чебышева. Для этого вначале рассмотрим свойства полиномов Tm(![]() ). Ниже приведены шесть первых полиномов Чебышева:
). Ниже приведены шесть первых полиномов Чебышева:
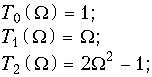
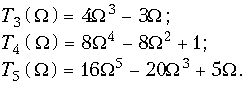 (17.16 а)
(17.16 а)
Любой полином Чебышева при m ![]() 2 может быть вычислен по рекуррентной формуле Tm(
2 может быть вычислен по рекуррентной формуле Tm(![]()
) = 2![]()
Tm–1(![]()
) – Tm–2(![]()
). Таким образом, выражения (17.15) удовлетворяют общим выражениям (17.1) – (17.3) характеристик полиномиальных фильтров.
Существует единая тригонометрическая форма записи полиномов Чебышева в интервале –1 ![]()
![]()
![]()
1:
![]() (17.16)
(17.16)
Действительно, T0(![]()
) = cos0arccos![]()
= 1; T1(![]()
) = cos1arccos![]()
= = ![]()
; T2(![]()
) = cos2arccos![]()
= 2cos2arccos![]()
– 1 = 2![]()
2 – 1. Вне интервала –1 ![]()
![]()
![]()
1 полиномы Tm(![]()
) также представляются в тригонометрической форме:
![]() (17.16 в)
(17.16 в)
Анализ поведения полиномов Чебышева показывает, что в интервале –1 ![]()
![]()
![]()
1 угол ![]() = arccos
= arccos![]()
изменяется от –![]() (при
(при ![]()
= –1) до 0 (при ![]()
= 1), поэтому полином Tm(![]() ) = cosm
) = cosm![]() ровно m раз принимает значения, равные нулю, и m + 1 раз достигает значений, равных +1 или –1 и чередующихся друг с другом. Вне интервала –1
ровно m раз принимает значения, равные нулю, и m + 1 раз достигает значений, равных +1 или –1 и чередующихся друг с другом. Вне интервала –1 ![]()
![]()
![]()
1 полином Tm(![]()
) согласно формуле (17.16 в) монотонно возрастает. В качестве примера на рис. 17.6, а изображен график полинома Чебышева T4(![]() ), т. е. полинома четвертого порядка.
), т. е. полинома четвертого порядка.
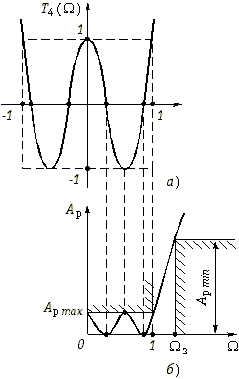 |
|
| Рис. 17.6 |
В соответствии с (17.15) рабочее ослабление Ap(![]() ) фильтра Чебышева на тех частотах
) фильтра Чебышева на тех частотах ![]() , где полином Tm(
, где полином Tm(![]() ) обращается в нуль, также обращается в нуль. На частотах, на которых Tm(
) обращается в нуль, также обращается в нуль. На частотах, на которых Tm(![]() ) равен
) равен ![]() 1, рабочее ослабление достигает величины:
1, рабочее ослабление достигает величины:
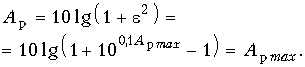
С ростом значений полинома Tm(![]() ) на частотах
) на частотах ![]() > 1 рабочее ослабление Ap(
> 1 рабочее ослабление Ap(![]() ) также монотонно растет. На рис. 17.6, б приведен график рабочего ослабления фильтра Чебышева четвертого порядка.
) также монотонно растет. На рис. 17.6, б приведен график рабочего ослабления фильтра Чебышева четвертого порядка.
Фильтры Чебышева называют также фильтрами с равноволновой характеристикой ослабления в полосе пропускания.
На рис. 17.7 показаны частотные зависимости квадрата АЧХ фильтра Чебышева для различных значений m, полученные для |Hр(j![]() )|2 из (17.15). Подобные зависимости могут быть построены для рабочего ослабления фильтра.
)|2 из (17.15). Подобные зависимости могут быть построены для рабочего ослабления фильтра.
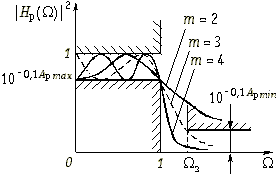 |
|
| Рис. 17.7 |
Чтобы характеристики фильтра отвечали требованиям в полосе непропускания, необходимо выбрать порядок фильтра m из условия |Hр(j![]() )|
)|![]()
![]()
![]() . Для полосы непропускания Tm(
. Для полосы непропускания Tm(![]()
) определяется формулой (17.16 в), следовательно, 1 + ![]() 2сh2m X Arch
2сh2m X Arch![]() з
з ![]()
![]() . Отсюда сhmArch
. Отсюда сhmArch![]() з
з![]()
![]() . Далее mArch
. Далее mArch![]()
з ![]()
![]() и m
и m ![]()
![]() .
.
В этой формуле величина Apmin измеряется в неперах. При использовании единицы децибел порядок фильтра вычисляется из выражения:
m ![]()
 (17.17 a)
(17.17 a)
Сравнивая частотные характеристики фильтров Баттерворта и Чебышева, следует указать, что полиномы Чебышева являются полиномами наилучшего приближения. Это означает, что при одинаковом значении m из всех полиномиальных фильтров, ослабления которых в полосе пропускания не превышают Apmax, наибольшие значения ослабления в полосе непропускания имеет фильтр Чебышева. В частности, рабочее ослабление фильтра Чебышева в полосе непропускания может превышать (и весьма значительно) рабочее ослабление фильтра Баттерворта при равных значениях m и Apmax. Однако характеристика рабочего ослабления фильтра Баттерворта имеет в полосе пропускания монотонный характер и легче поддается корректированию для устранения искажений передаваемых сигналов.
Выбор типа полиномиальных фильтров определяется конкретными условиями их применения в аппаратуре связи и радиотехнических устройствах.
Для получения передаточной функции фильтра Чебышева поступим аналогично тому, как делали это для фильтров Баттерворта. Заменим оператор j![]()
на оператор р и перейдем от функции |Hр(j![]()
)|2 к функции:
![]() .
.
Представим полином Tm(![]() ) в виде (17.16 б) и найдем полюсы функции |Hр(p)|2, решив уравнение:
) в виде (17.16 б) и найдем полюсы функции |Hр(p)|2, решив уравнение:
![]() (17.17 б)
(17.17 б)
Поскольку согласно (17.16 а) коэффициент при старшем члене полинома Чебышева Tm(![]()
) равен 2m–1, то коэффициент при старшем члене полинома в левой части приведенного выше уравнения равен ![]()
222(m–1).
Корни уравнения (17.17 б), как можно доказать, определяются аналитически следующим выражением:
![]() (17.18)
(17.18)
где ![]() .
.
Из корней в левой полуплоскости составляются сомножители (p – pi), и по теореме Виета строится передаточная функция фильтра:
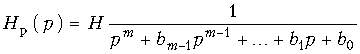 ,
,
где ![]() .
.
Пример. Построить передаточную функцию фильтра Чебышева второго порядка (m = 2), рабочее ослабление в полосе пропускания (от 0 до 159 кГц) которого не превышает величину Apmax = 3 дБ. Граничная частота полосы непропускания 318 кГц.
Коэффициент неравномерности ![]() такого фильтра согласно (17.7) равен 1. Рабочее ослабление на частоте
такого фильтра согласно (17.7) равен 1. Рабочее ослабление на частоте ![]() з = 318/159 = 2 составляет Ap(
з = 318/159 = 2 составляет Ap(![]()
)![]() =2 = 10lg(1 + ch22Arch2) = 17 дБ, что почти на 5 дБ превышает рабочее ослабление на этой же частоте фильтра Баттерворта второго порядка (см. предыдущий пример).
=2 = 10lg(1 + ch22Arch2) = 17 дБ, что почти на 5 дБ превышает рабочее ослабление на этой же частоте фильтра Баттерворта второго порядка (см. предыдущий пример).
Расчет полюсов функции Hp(p)Hp(–p) по формулам (17.18) дает величины: p1 = 0,322 + j0,777; p2 = 0,322 – j0,777; p3 = –0,322 – j0,777; p4 = –0,322 + j0,777. Расположение полюсов в комплексной плоскости показано на рис. 17.5, б.
Передаточная функция фильтра:
![]() .
.
В заключение отметим, что для полиномиальных фильтров в справочниках составлены весьма полные таблицы полюсов и коэффициентов передаточных функций для различных величин Apmax и m. Порядок же фильтров m определяется по специальным графикам, исходя из заданных величин Apmax, Apmin и ![]()
з.
Фильтры со всплесками ослабления (на основе дробей Чебышева и Золотарева). Частотные характеристики полиномиальных фильтров, описываемые выражениями (17.1)—(17.3), имеют монотонный характер в полосе непропускания. В частности, рабочее ослабление таких фильтров монотонно возрастает по мере удаления от полосы пропускания (рис. 17.4, а и 17.6, б).
При “жестких” требованиях к частотным характеристикам (малая переходная область между полосами пропускания и непропускания и большая величина рабочего ослабления в полосе непропускания) порядок фильтра m может получиться очень большим даже в случае применения полинома Чебышева. Это приведет к существенному усложнению фильтра и к излишнему “расходу” элементов.
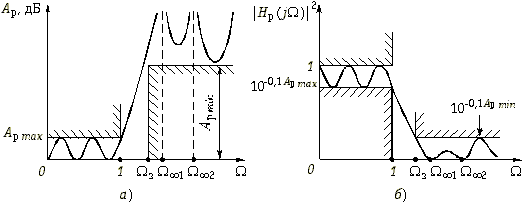 |
|
| Рис. 17.8 |
В таких случаях целесообразно применять фильтры со всплесками рабочего ослабления в полосе непропускания (рис. 17.8, а). На частотах всплеска ![]()
![]() 1,
1, ![]()
![]() 2 и т. д. рабочее ослабление фильтра стремится к бесконечности; за счет этого возрастает крутизна характеристики ослабления в переходной области. Соответственно АЧХ фильтра на частотах
2 и т. д. рабочее ослабление фильтра стремится к бесконечности; за счет этого возрастает крутизна характеристики ослабления в переходной области. Соответственно АЧХ фильтра на частотах ![]()
![]() 1,
1, ![]()
![]() 2 и т. д. будет обращаться в нуль (рис. 17.8, б).
2 и т. д. будет обращаться в нуль (рис. 17.8, б).
Для выполнения указанных условий в выражениях (17.2)—(17.3) используют рациональные дроби вида:
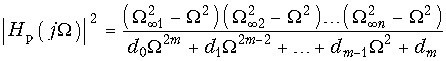 (17.19)
(17.19)
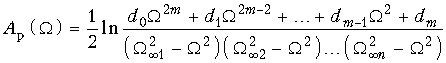 (17.20)
(17.20)
Действительно, когда ![]() принимает значения
принимает значения ![]()
![]() 1,
1, ![]()
![]() 2, …,
2, …, ![]()
![]() n, |Hр(j
n, |Hр(j![]()
)|2 = 0 и Aр(![]() )
) ![]()
![]() .
.
Передаточная функция таких фильтров является дробно-рациональной:
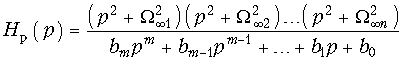 (17.21)
(17.21)
и кроме полюсов p1, p2, …, pm имеет нули:
![]() .
.
Фильтры со всплесками рабочего ослабления называют еще фильтрами с нулями передачи.
Среди фильтров со всплесками ослабления наиболее широкое распространение получили фильтры, построенные на основе дробей Чебышева и Золотарева. Чтобы получить частотные характеристики фильтра на основе дробей Чебышева, нужно в формулах (17.14) или (17.15) использовать в качестве функции фильтрации дробь Чебышева. Обозначая ее Фm(![]()
), получим:
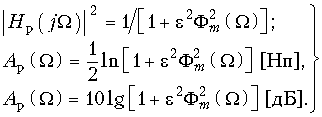 (17.22)
(17.22)
В качестве примера укажем дробь Чебышева пятого порядка, для которой построены графики Aр(![]() ) и |Hр(j
) и |Hр(j![]() )|2 на рис. 17.8, а и б:
)|2 на рис. 17.8, а и б:
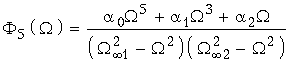 ,
,
где a0, a1 и a2 – коэффициенты, связанные с частотами всплеска ![]()
![]() 1 и
1 и ![]()
![]() 2.
2.
Очевидно, что подстановка этой дроби в (17.22) приведет после некоторых преобразований к выражениям общего вида (17.19) и (17.20).
В полосе пропускания дробь Чебышева ведет себя так же, как и полином Чебышева, т. е. рабочее ослабление фильтра носит равноволновый характер. На частотах всплеска ![]()
![]()
1 и ![]()
![]()
2 дробь Чебышева обращается в бесконечность, что приводит к бесконечно большому рабочему ослаблению.
Следует отметить, что дробь Чебышева является дробью наилучшего приближения. Это означает, что фильтр на основе дроби Чебышева на любой частоте полосы непропускания имеет большее значение рабочего ослабления по сравнению с фильтрами на основе других дробей (и полиномов, как частных случаев дробей) при прочих равных условиях (при одинаковых порядках m, при таком же количестве и расположении частот всплеска и тех же величинах Apmax).
Частным случаем дробей Чебышева являются дроби Золотарева:
![]() (17.23)
(17.23)
где ![]() ,
, ![]() , значение S равно 0 для четных m и равно 1 для нечетных m; m – порядок дроби;
, значение S равно 0 для четных m и равно 1 для нечетных m; m – порядок дроби; ![]() 0V,
0V, ![]()
![]() V – нули и полюсы дроби, связанные соотношением
V – нули и полюсы дроби, связанные соотношением ![]()
![]() V =
V = ![]()
з/![]()
0V.
Используя в качестве функции фильтрации в (17.14) и (17.15) дроби Золотарева, получим:
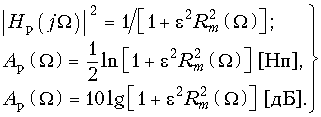 (17.24)
(17.24)
Из формул (17.23) и (17.24) следует, что нули функции Aр(![]()
) совпадают с нулями дроби Золотарева, а всплески функции Aр(![]()
) – с полюсами этой же дроби. Нули и полюсы дроби Золотарева можно рассчитывать, однако обычно их определяют по каталогам для операторных передаточных функций ФНЧ. На рис. 17.9 показан график Aр(![]()
) для фильтра Золотарева пятого порядка.
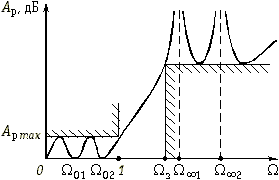 |
|
| Рис. 16.8 |
Дроби Золотарева так же, как и полиномы Чебышева, дают равноволновую характеристику рабочего ослабления фильтра в полосе пропускания. Однако в полосе непропускания у фильтров Золотарева значения всех минимумов рабочего ослабления оказываются одинаковыми и равными значению рабочего ослабления на частоте ![]() з. Такие фильтры называются также фильтрами с изоэкстремальными характеристиками рабочего ослабления.
з. Такие фильтры называются также фильтрами с изоэкстремальными характеристиками рабочего ослабления.
Фильтры с характеристиками Золотарева можно рассматривать как частный случай фильтров с характеристиками Чебышева, когда значения минимумов ослабления фильтра в полосе непропускания выравнены, а число всплесков – максимально возможное при выбранном значении m.