Как найти передаточную функцию системы по возмущению - Сайт, где вы сможете решить свои вопросы

Большинство
структурных схем САУ с помощью
рассмотренных ранее преобразований
можно привести к виду, приведенному на
рисунке 2.52.

Рисунок
2.52

Введем обозначения:

(2.124)

–
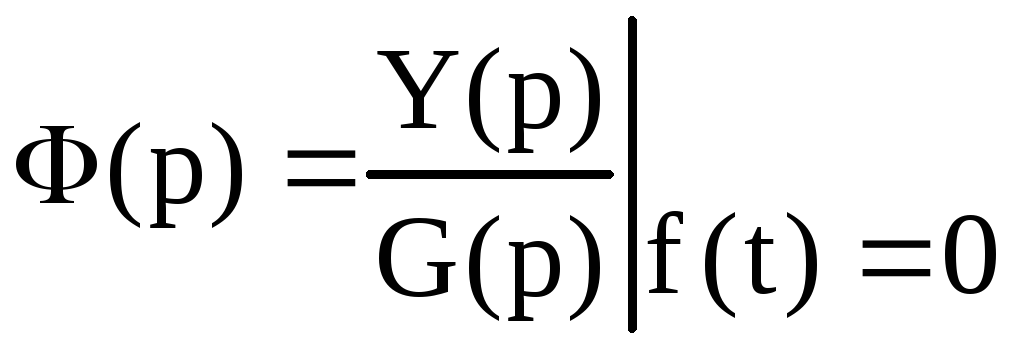
передаточная
функция замкнутой системы
по задающему
воздействию.

Определяет
связь между выходной величиной
и задающим воздействиемпри возмущении;

–передаточная
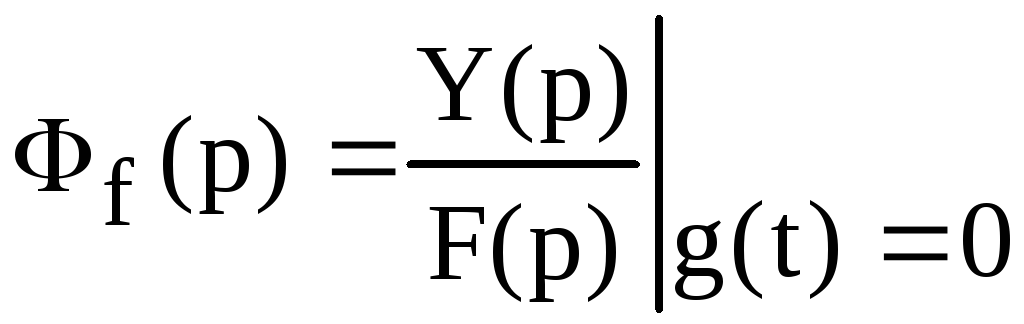
функция замкнутой системы (2.125)

по возмущающему
воздействию.

Определяет
связь между выходной величиной
и возмущениемпри задающем воздействии;

–передаточная
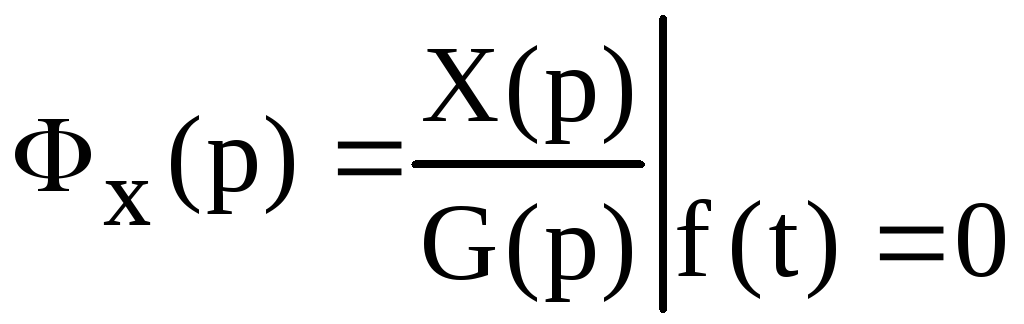
функция замкнутой системы
(2.126)

относительно
ошибки по задающему воздействию.

Определяет
связь между ошибкой регулирования
и задающим воздействиемпри возмущении;

–передаточная
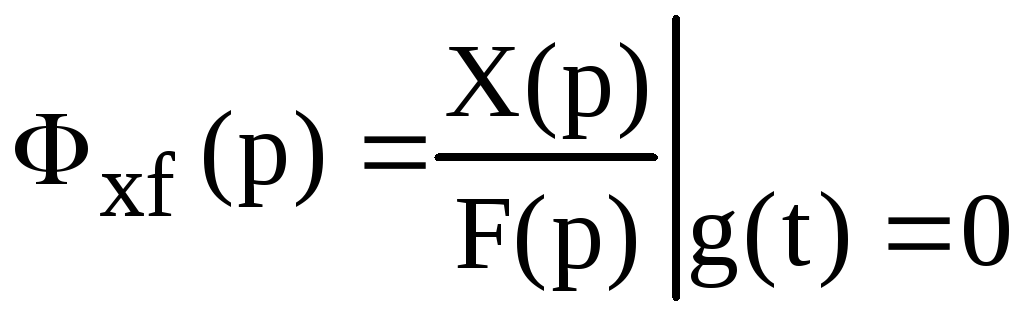
функция замкнутой системы относительно
ошибки по возмущающему воздействию.
(2.127)

Определяет
связь между ошибкой регулирования
и возмущениемпри задающем воздействии.

Сформируем
передаточные функции (2.124) – (2.127) с
помощью правила (2.122). Очевидно, что
передаточная функция разомкнутой цепи
будет одинаковой для всех формул (2.124)
– (2.127):

.
(2.128)

С
этим результатом совпадает передаточная
функция прямой цепи от точки приложения
до выходной величины(составляющая формулы (2.124)):

.
(2.129)

Тогда
передаточная функция замкнутой системы
по управляющему воздействию (2.124)
принимает вид

.
(2.130)

Передаточная
функция прямой цепи от точки приложения
возмущения
до выходной величины(составляющая формулы (2.125)):

.
(2.131)

В
результате передаточная функция
замкнутой системы по возмущающему
воздействию (2.125) принимает вид

.
(2.132)

Передаточная
функция прямой цепи от точки приложения
до ошибки регулирования(составляющая формулы (2.126)):

.
(2.133)

Тогда передаточная
функция замкнутой системы относительно
ошибки по задающему воздействию (2.126)
принимает вид

.
(2.134)

Передаточная
функция прямой цепи от точки приложения
возмущения
до ошибки регулирования(составляющая формулы (2.127)):

.
(2.135)

В
результате передаточная функция
замкнутой системы относительно ошибки
по возмущающему воздействию (2.127)
принимает вид

.
(2.136)

Полученные
четыре передаточные функции (2.130),
(2.132), (2.134), (2.136) содержат всю информацию
о качестве функционирования системы,
например, изображение управляемой
координаты определяется как

,
(2.137)

а
ошибки регулирования

.
(2.138)

Формулы
(2.137) и (2.138) позволяют рассчитать переходные
процессы в замкнутой САУ, определить
время регулирования, перерегулирование
и величину установившейся ошибки.

Запишем передаточную
функцию прямой цепи (2.129) в виде

.
(2.139)

Тогда
передаточная функция замкнутой системы
по управляющему воздействию (2.130)

,
(2.140)

где
–характеристический
полином замкнутой САУ.

(2.141)

Передаточная
функция замкнутой системы относительно
ошибки по задающему воздействию (2.134) с
учетом формулы (2.139) будет

.
(2.142)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Макеты страниц

Передаточная функция замкнутой системы по возмущению

Представляет собой отношение изображения по Лапласу регулируемой величины к изображению возмущения при нулевых начальных значениях функций и их соответствующих производных:

где

При вычислении передаточной функции (3.47) задающее воздействие и все другие возмущающие воздействия (если они есть) не учитываются. В результате общая структурная схема САР (см.

рис. 3.3, б) приводится к виду, показанному на рис. 3.5, а, где обведенная штриховой линией часть может быть в соответствии с формулой (2.111) при заменена одним звеном с передаточной функцией Поэтому (рис. 3.5, б)

Из рис. 3.3, б следует, что передаточная функция объекта регулирования по возмущению представляет собой просто передаточную функцию разомкнутой системы по возмущающему воздействию При такой трактовке на основании выражения (3.48) можно сформулировать следующую общую рекомендацию. Для определения передаточной функции САР по некоторому возмущению приложенному в любой точке системы, следует найти передаточную функцию разомкнутой системы по этому возмущению и разделить ее на передаточную функцию разомкнутой системы (3.26), увеличенную на единицу. Размыкание САР, как обычно, производится в цепи главной обратной связи.

Рис. 3.5. Структурная схема САР для вычисления передаточной функции замкнутой системы по возмущению: а — исходная; б — преобразованная

Пользуясь формулами (3.25) и (3.32) и учитывая, что выражение (3.48) нетрудно привести к следующему виду:

где многочлен

Обычно т. е. передаточная функция САР по возмущению, как и главный оператор, представляет собой правильную рациональную дробь. Знаменатели у передаточных функций (3.43) и (3. 49) одинаковы, что характерно для всех передаточных функций замкнутой системы.

Для САР скорости вращения и для следящей системы основным возмущающим воздействием является изменение момента нагрузки. Воспользовавшись формулами (3.22), (3.28) и (3.48), для САР скорости вращения получим

где

Для следящей системы (см. рис. 3.2, б), разомкнув цепь обратной связи, найдем

Воспользовавшись соотношениями (3.30) и (3.48), будем иметь

где

Формулы (3.50) и (3.52) могут быть получены и непосредственно из уравнений (3.8) и (3.15).

Если на САР действуют несколько возмущений то для каждого из этих возмущений передаточная функция САР

Здесь — передаточная функция разомкнутой системы относительно возмущения — многочлен относительно степень которого не превосходит

Если передаточные функции известны, то разыскание дифференциального уравнения САР относительно регулируемой величины не представляет труда. На самом деле, из соотношения (3.41) вытекает уравнение САР в изображениях при отсутствии возмущающих воздействий:

Из соотношения (3.47) получается уравнение САР в изображениях при отсутствии задающего воздействия:

Так как система линейна, то при одновременном наличии задающего и возмущающего воздействий по принципу наложения

откуда

Следовательно, дифференциальное уравнение САР имеет вид

или

Для случая нескольких возмущений по принципу наложения

откуда

что приводит к дифференциальному уравнению

Воспользовавшись этой методикой, для САР скорости вращения при помощи передаточных функций (3.45) и (3.50) получим, естественно, дифференциальное уравнение (3.8) относительно напряжения Уравнение САР относительно регулируемой величины [см. (3.5)] можно найти, разделив все члены уравнения (3.8) на крутизну тахогенератора так как

Положив в формуле нетрудно получить общее дифференциальное уравнение САР относительно ошибки:

Это уравнение может быть получено и непосредственно по структурной схеме САР, если вычислить предварительно передаточные функции замкнутой системы, связывающие сигнал ошибки х с каждым из внешних воздействий К ним относятся передаточная функция системы для ошибки

и передаточные функции замкнутой системы для ошибки по возмущениям

В этих формулах Нетрудно показать, что

Источник

Время на прочтение
7 мин

Количество просмотров 13K

Продолжаем публикацию лекций по курсу “Управление в Технических Системах” автор – Олег Степанович Козлов на кафедре Э7 МГТУ им. Н.Э. Баумана.

Данные лекции готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется. В предыдущих сериях:

1. Введение в теорию автоматического управления.
2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ.
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности. 4 Структурные преобразования систем автоматического регулирования.

Будет как всегда позновательной увлекательно и жестко

5.1. Главная передаточная функция. Передаточные функции по возмущающему воздействию и для ошибки (рассогласования)

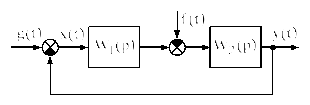
Используя структурные преобразования (см. раздел 4), структурную схему практически любой линейной или линеаризованной САР (САУ) можно привести к виду:

Рисунок 5.1.1 Типовая струкутура САР

Где функции по времени:

– управляющее воздействие;

– регулируемая величина (выходное воздействие);

– возмущающее воздействие;

Или в изображениях:

$left { begin{align}x(t)&rightarrow X(s)\y(t)&rightarrow Y(s)\ f(t)& rightarrow F(s) \ epsilon(t)&rightarrow E(s) end{align} right.$

Определение: Если единичная обратная связь охватывает все элементы (звенья) САР – она называется главной.

Определение: Если главная обратная связь отсутствует – САР считается разомкнутой.

Передаточная функция может быть любой сложности (т.е. содержать местные обратные связи, параллельные и последовательные цепи и т.д.).

Возмущающих воздействий может быть несколько и приложены они могут быть в любом месте структурной схемы.

Передаточную функцию которую в Теории Управления называют передаточной функцией разомкнутой САР, будем представлять в следующем виде (для единообразия):

$W(s)=frac{Kcdot N(s)}{L(s)} mathbf{(5.1)}$

где – общий коэффициент усиления; – полиномы по степеням переменной , причем свободные члены в них равны 1 (единице).

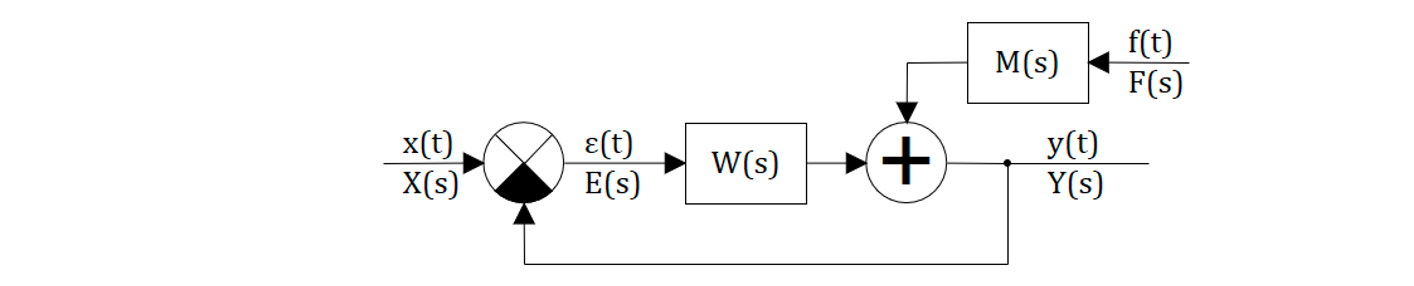
Учитывая, что САР линейна или линеаризована, разделим на структурной схеме каналы прохождения управляющего и возмущающего воздействий. Выделим в отдельное звено (может быть и очень сложное) ту часть системы, через которую проходит возмущающее воздействие обозначим ее через Структурная схема САР принимает вид:

Рисунок 5.1.2 Структурная схема общего вида с передаточной функцией и внешним воздействием

где:

В Теории Управления используют 3 основных передаточных функций замкнутой САР:

главная передаточная функция ;
передаточная функция по возмущающему воздействию ;
передаточная функция для ошибки (рассогласования)

Рассмотрим более подробно вышеупомянутые передаточные функции.

Главная передаточная функция

Главная передаточная функция -передаточная функция по управляющему воздействию математическое определение этой передаточной функции:

$Phi(s) =frac{Y(s)}{X(s)} mathbf{(5.2)}$

выведем формулу при условии если возмущеющие воздействие равно . “Обойдем” структурную схемв по контуру:

$Y(s)= E(s)cdot W(s)=left[ X(s)-Y(s)right]cdot W(s)Rightarrow\Y(s)=X(s)cdot W(s)-Y(s)cdot W (s) Rightarrow\Y(s)+Y(s)cdot W(s)=X(s)cdot W(s)Rightarrow\ frac{Y(s)}{X(s)}=frac{W(s)}{1+W(s)};$ $Phi(s)=frac{W(s)}{1+W(s)} mathbf{(5.3)}$

Примечание. Формула (5.3) совпадает с формулой для передаточной функции цепи с местной единичной обратной связью (см. раздел 4 – «Структурные преобразования»).

Подставляя вместо ее выражение через полиномы и

$Phi(s)=frac{Kcdot N(s)/L(s)}{1+Kcdot N(s)/L(s)}=frac{Kcdot N(s)}{L(s)+Kcdot N(s)}=frac{Kcdot N(s)}{D(s)} mathbf{(5.4)}$

где:

Анализ выражения (5.4) показывает, что свойства главной передаточной функции замкнутой САР однозначно определяются свойствами разомкнутой САР, т.е. через полиномы и .

Передаточная функция замкнутой САР по внешнему возмущающему воздействию

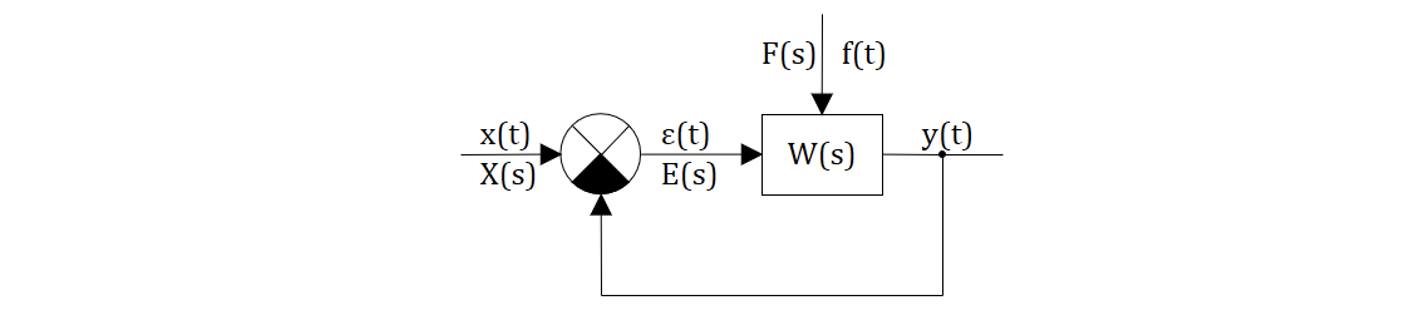
Дадим математическое определение рассматриваемой передаточной функции если управляющие воздействи , а возмущеющие воздействие отличное от нуля . В этом случае (см. рисунок 5.1.2) получается:

$y(t)=y_1(t)+y_2(t)\ x(t)=0Rightarrow varepsilon(t)=0-y(t)=-y(t);$

Перрейдем к изображением и “обойдем” схему (см. рис. 5.1.2) по контуру

$Y(s)=Y_1(s)+Y_2(s) =E(s)cdot W(s)+F(s)cdot M(s)=\=-Y(s)cdot W(s)+F(s)cdot M(s) Rightarrow\Y(s)cdot[1+W(s)]=F(s)cdot M(s)Rightarrow frac{Y(s)}{F(s)}=frac{M(s)}{1+W(s)};$ $Phi_f=frac{Y(s)}{F(s)} =frac{M(s)}{1+W(s)}$

Подставляя вместо ее выражение через полиномы и получаем:

$Phi_f=frac{M(s)}{1+Kcdot N(s)/L(s)}=frac{M(s)cdot L(s)}{L(s)+K(s)cdot N(s)}=frac{R(s)}{D(s)} mathbf{(5.6)}$

где: – вид данного полинома зависит от места приложения возмущающего воздействия;

Формулы 5.4 и 5.6 имеют общий занаменатель

Передаточная функция замкнутой САР для ошибки (рассогласования)

Дадим математическое определение рассматриваемой передаточной функции если управляющие воздействиt отлично от 0 , а возмущеющие воздействие равно 0 . В этом случае для передаточной функции получается (см. рис. 5.1.2):

$Phi_varepsilon(s)=frac{E(s)}{X(s)}$

Сделаем вывод соответствующих формул, выполнив «обход» по контуру схемы (см. рис. 5.1.2)

$E(s)=X(s)-Y(s)=X(s)-E(s)cdot W(s)Rightarrow \ E(s)cdot(1+W(s))=X(s) Rightarrow frac{E(s)}{X(s)}=frac{1}{1+W(s)}$ $Phi_varepsilon(s)=frac{1}{1+W(s)} mathbf{(5.7)}$

Учитывая формулу для главной передаточной функции $Phi(s)=frac{W(s)}{1+W(s)}$ можно записать выражения для передаточной функции рассоглаосвания:

$Phi_varepsilon(s)=1-Phi(s) mathbf{(5.8)}$

Подставляя вместо ее выражение через полиномы и получаем:

$Phi_varepsilon(s)=frac{1}{1+Kcdot N(s)/L(s)}=frac{L(s)}{L(s)+Kcdot N(s)}=frac{L(s)}{D(s)} mathbf{(5.9)}$

где:

Опять замечаем, что знаменатель передаточной функции равен полиному следовательно, характерным признаком передаточных функций замкнутой САР является общность знаменателей ! ! !

В Теории Управления выражение имеет «собственное» название: характеристический полином замкнутой САР.

5.2 Уравнения динамики замкнутой САР

Как указывалось в подразделе 5.1, любую замкнутую САР можно привести к виду представленному на рисунке 5.2.1:

Рисунок 5.2.1 Общая схема замкнутой САР с возмущающим воздействием

Выведены соотношения для 3-х основных передаточных функций замкнутой САР позволяют записать выражения для регулируемой величины в изображениях:

$Y(s)=underbrace{Phi(s)cdot X(s)}_{Y_x(s)}+underbrace{Phi_f(s)cdot F(s)}_{Y_f(s)} mathbf{(5.2.1)}$

Подставляя значения и через полиномы и разомкнутой САР получаем:

$Y(s)=frac{Kcdot N(s)}{L(s)+Kcdot N(s)}cdot X(s)+frac{R(s)}{L(s)+Kcdot N(s)}cdot F(s)$

подставим значения для характеристического полинома получим выражение для динамического уравнения замкнутой САР в изображениях:

Переходя к оригиналам получаем символическую форму записи обыкновенного дифференциального уравнения замкнутой САР:

Решение диференциального уравнения состоит из двух частей:

$y(t)= y_{соб.}(t)+y_{вын.}(t)$

где: $y_{соб.}(t)$ – собственная часть, решение однородного дифференциального уравнения ;

$y_{вын.}$ – вынужденная часть решения (частное решение), определяемая правой частью уравнения ( 5.2.3 ).

Решения однородного уравнения замкнутой САР:

$D(p)y(t)=0 Rightarrow a_ncdot y^{(n)}+a_{n-1}cdot y^{n-1}+...+a_1cdot y^1+a_0cdot y=0$

записываем соответствующее характеристическое уравнение:

$D(lambda)=0 Rightarrow a_ncdotlambda^n+a_{n-1}cdot lambda^{n-1}+...+a_1cdot lambda+a_0=0 Rightarrow$

находим корни степенного уравнения если все корни уравнения разные:

$Y_{соб}(t)=sum_{j=1}^nC_jcdot e^{lambdacdot j},$

Если есть совпадающие корни характеристического уравнения, то формула для $Y_{соб}(t)$ изменится (см. Математическое описание систем автоматического управления).

Обычно $y_{вын.}$ находят по виду правой части уравнения (5.2.3) или, используя другие методы (например, метод вариаций постоянных).

Необходимо отметить, что порядок дифференциального уравнения (5.2.3) равен «n», т.е. такой же, как и у разомкнутой САР

если нет возмущающего воздействия, т.к. порядок дифференциального оператора L(p) обычно значительно выше, чем N(p).

По аналогии с выводом уравнения (5.2.3) можно получить уравнение динамики для рассогласования :

$E(s)=Phi_varepsilon(s)cdot X(s)-Phi_f(s)cdot F(s) mathbf{(5.2.4)}$

подставляя значения и (см. 5.6 и 5.9) получаем:

$E(s)=frac{L(s)}{D(s)}cdot X(s)-frac{R(s)}{D(s)}cdot F(s) Rightarrow$

Уравнение (5.2.5)- уравнение динамики замкнутой САР в ихображениях для рассогласования (ошибки) при наличии управляющего и возмущающего воздействий.

Особенностью данного уравнения (5.2.5) является то, что левая часть его практически совпадает с левой частью (5.2.2), в то время, как порядок правой части заметно выше , т.к. порядок многочленов D (s) и L (s) – одинаков, а порядок N(s) меньше L(s).

Это означает, что внешние воздействия и влияют на более сильным образом.

Дифференциальное уравнение замкнутой САР для ошибки:

Способы решения уравнения ( 5.2.6 ) такие же, как и для уравнения ( 5.2.3 ) .

5.3. Частотные характеристики замкнутой САР.

Наибольший интерес при анализе замкнутых САР имеет АФЧХ замкнутой САР по управляющему воздействию:

$Phi(s)_{s=icdotomega}=Phi(icdotomega)=frac{W(icdotomega)}{1+W(icdot omega)} mathbf{(5.3.1)}$

где передаточная функция:

$W(icdotomega)=frac{Kcdot N(icdotomega)}{L(icdot omega)}$

Учитывая, что – комплексное число, по аналогии имеем:

Где – вещественная часть функции, – мнимая часть функиции.

Рисунок 5.3.1 Пример зависмостей P и Q

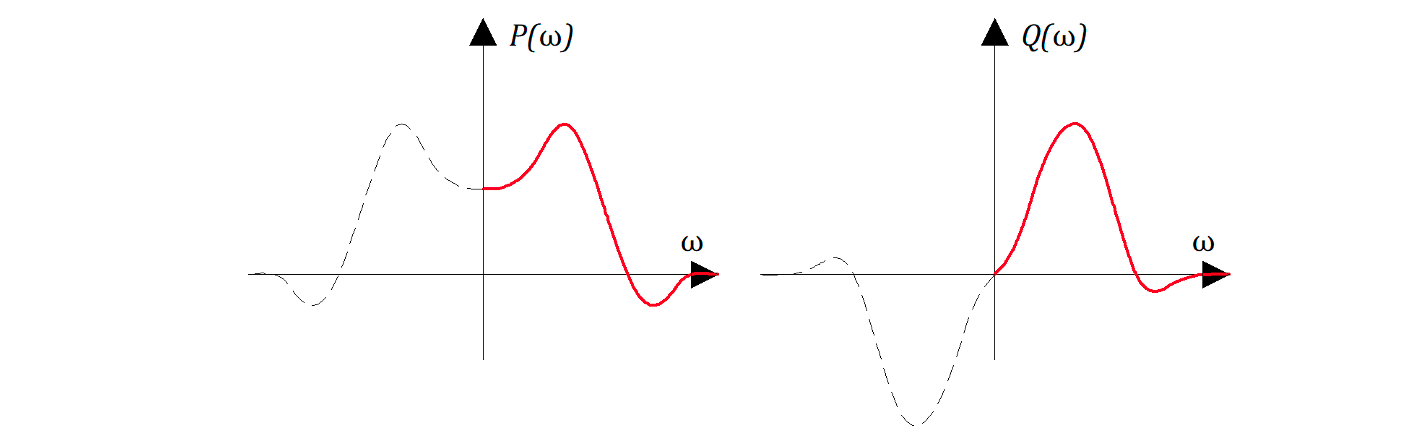
На этих рисунках представлен «примерный» вид зависимостей P (w)и Q(w) для «какой-то» замкнутой САР причем P(w) – четная функция, т.е. P(w) = P(-w); Q(w) – нечетная функция, т.е. Q(w) = – Q(-w).

Если известны частотные свойства разомкнутой САР, то можно определить частотные свойства замкнутой САР. Воспользуемся показательной формой для АФЧХ

$W(icdotomega) = A(omega)cdot e^{icdot varphi(omega)}$

Где – амплитуда (модуль), – сдвиг фазы (фаза). Подставляя это в (5.3.1), имеем получаем:

$Phi(icdotomega) = A_{з}(omega)cdot e^{icdotvarphi_з(omega)}=frac{A(omega)cdot e^{icdot varphi(omega)}}{1+A(omega)cdot e^{icdot varphi(omega)}}Rightarrow$ $Rightarrow 1+A(omega)cdot e^{icdotvarphi(omega)}=frac{A(omega)cdot e^{icdot varphi(omega)}}{A_{з}cdot e^{icdot varphi_з(omega)}}Rightarrow$ $Rightarrow frac{e^{-icdot varphi_3(omega)}}{A_з(omega)}=1+frac{e^{-icdot varphi(omega)}}{A(omega)} mathbf{(5.3.3)}$

Учитывая, что $e^{-icdot varphi}=cos(varphi)-icdot sin(varphi) Rightarrow$

$frac{cos[varphi_з(omega)]}{A_з(omega)}-icdotfrac{sin[varphi_З(omega)]}{A_з(omega)}=1+frac{cos[varphi(omega)]}{A(omega)}-icdotfrac{sin[varphi(omega)]}{A(omega)} mathbf{(5.3.4)}$

Приравнивая чисто вещественные и чисто мнимые части, имеем

$left { begin {align}frac{cos[varphi_з(omega)]}{A_з(omega)}&=1+frac{cos[varphi(omega)]}{A(omega)} (1)\ frac{sin[varphi_з(omega)]}{A_з(omega)}&=frac{sin[varphi(omega)]}{A(omega)} (2). end{align} right. mathbf{(5.3.5)}$

Для нахождения амплитуды и сдвига фазы замкнутой передаточной функции как функции от амплитуды и сдвига фазы разомкнутой системы. Разделив (2) на (1) получим:

$tg[varphi_з(omega)]=frac{sin[varphi(omega)]}{A(omega)+cos[varphi(omega)]} Rightarrow$

Сдвиг фазы замкнутой системы через характеристики разомкнутой системы:

$varphi_з(omega) = arctg left[ frac{sin[varphi(omega)]}{A(omega)+cos[varphi(omega)]}right] - picdot j mathbf{(5.3.6)}$

Для получения амплитуды замкнутоей системы возведем оба уравнения системы (5.3.5) в квадрат:

$left { begin {align}frac{cos^2[varphi_з(omega)]}{A^2_з(omega)}&=1+frac{cos^2[varphi(omega)]}{A^2(omega)}+2 cdotfrac{cos[varphi(omega)]}{A(omega)} ;\ frac{sin^2[varphi_з(omega)]}{A_з^2(omega)}&=frac{sin^2[varphi(omega)]}{A^2(omega)} . end{align} right.$

складываем эти два уравнения:

$frac{1}{A^2_з(omega)}left[underbrace{cos^2varphi_з(omega)+sin^2varphi_з(omega)}_1right]=1+frac{1}{A^2(omega)}left[underbrace{cos^2varphi(omega)+sin^2varphi(omega)}_1right]+dots\dots+2frac{cos[varphi(omega]}{A(omega)}$ $frac{1}{A^2_з(omega)}=frac{A^2(omega)+2cdot Acdot cos[varphi(omega)]+1}{A^2(omega)}Rightarrow$ $A_з(omega)=frac{A(omega)}{sqrt{A^2(omega)+2cdot A(omega)cdot cos[varphi(omega)]+1}} mathbf{(5.3.7)}$

Аналогичным образом можно выразить, например, P(w) и Q(w) – характеристики замкнутой САР через u(w) и u(w) – характеристики разомкнутой САР.

Пример

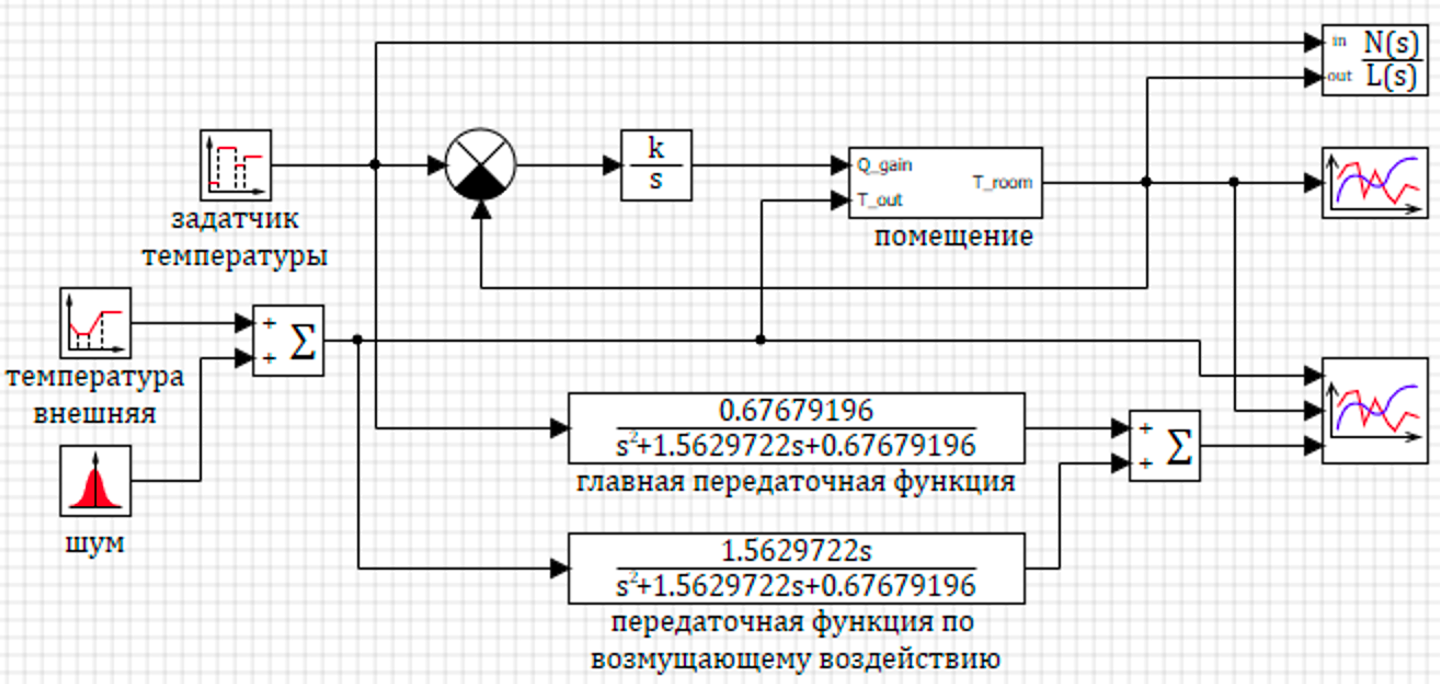
В качестве примера на рисунке 5.4.1 приведена модель помещения, в котором с помощью интегрирующего звена обеспечивается подвод тепла для поддержания температуры. Температура задается в виде ступенчатой функции. В качестве внешнего воздействия используется внешняя температура.

5.4.1 Рисунок сравнение физической модели и передаточных функций

Передаточные функции построены средтвами автоматического анализа. Видно, что знаменатель главной передаточной функции и знаменатель передаточной функции по возмущающиму воздействию одинаковы.

5.4.2 Результаты моделирования.

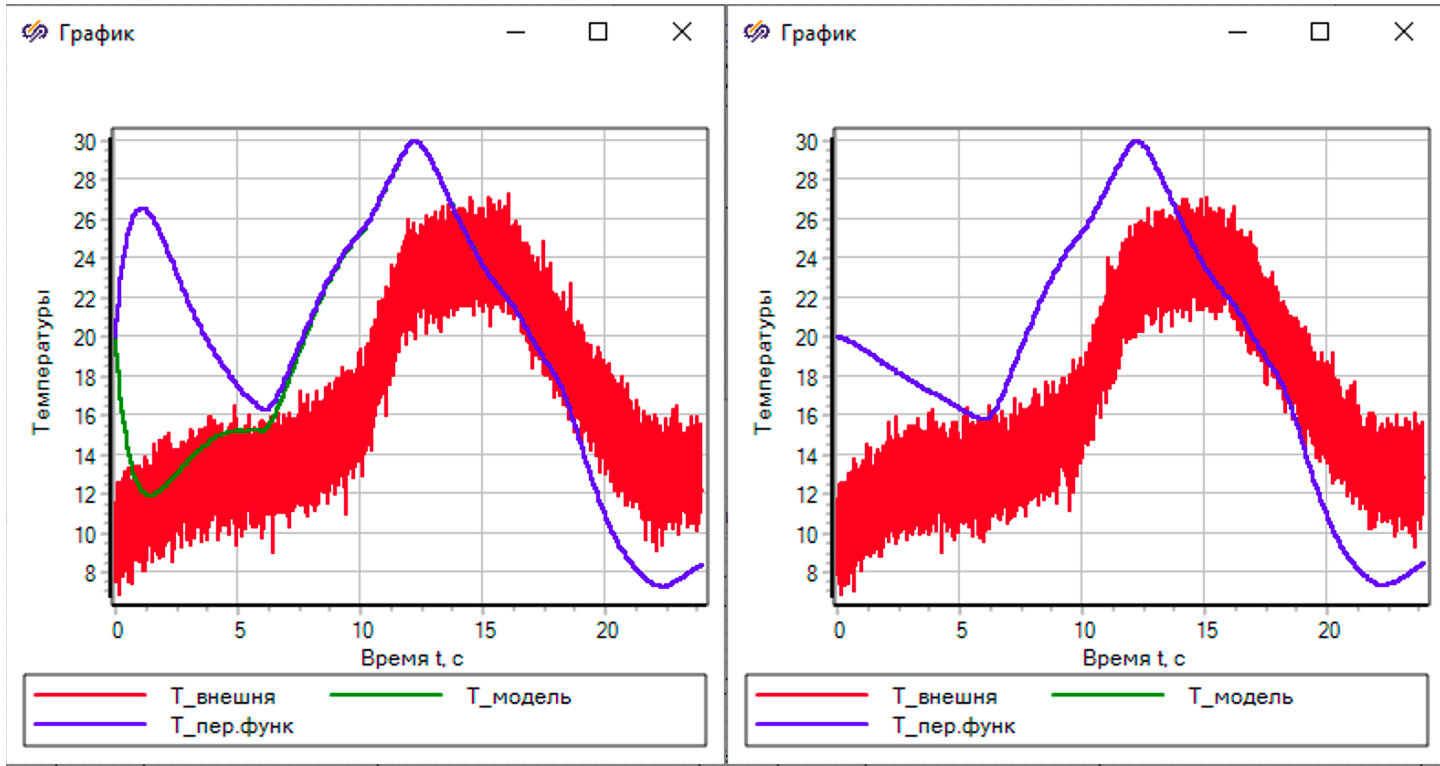
График справа показывает расхождение результаты модели (зеленая линия) и передаточных функций (синит линя) в начале расчета, но потом функции сходятся. Расхождение объясняются разными начальными условиями по производным. Слева тот же самый график, но в это случае начальное состояние определено с помощю загрузки стационарного состояния, полученного предварительным моделированием. В этом случае совпадение модели и передаточных функций полное.

Ссылку на модель примера можено взять здесь…

Источник

ГЛАВА 2

Передаточные функции и частотные характеристики

2.1. Передаточная функция

Помимо дифференциального уравнения, динамические свойства звена могут быть описаны также при помощи передаточной функции, которая представляет собой отношение операторного полинома воздействия к собственному операторному полиному, т.е. в общем виде передаточная функция звена определяется выражением

, (39)

а передаточная функция объекта, динамика которого описывается уравнением (13), выражением

. (40)

Рекомендуемые материалы

2.2. Частотная характеристика

В ряде случаев системы автоматического регулирования и входящие в состав их звенья работают под воздействием периодических и, в частности, гармонических возмущений. В связи с этим возникает необходимость исследовать работу систем также в режиме вынужденных колебаний с помощью, так называемого частотного метода. Отличительной особенностью частотного метода является также возможность применения его для экспериментального исследования динамических свойств реальных систем, аналитическое исследование которых невозможно.

Если на вход линейного звена подать гармоническое возмущение с амплитудой A₁ и частотой w, при этом , то по прошествии некоторого времени выходная координата также будет изменяться по гармоническому закону с той же частотой w, но с другой амплитудой А₂ и сдвигом колебаний по фазе j. Графически это показано на рис. 25.

Частотной характеристикой звена или амплитудно-фазовой частотной характеристикой называется зависимость амплитуды и фазы вынужденных гармонических колебаний от амплитуды и частоты входного возмущения.

Рис. 25. Вынужденные колебания САР

Для получения частотной функции, называемой также комплексной передаточной функцией, необходимо в выражение передаточной функции вместо р подставить iw, где , а w — круговая частота, т.е.

. (41)

Рис. 26. Амплитудно-фазовая характеристика

Последнее выражение в общем виде можно представить в прямоугольной системе координат:

, (42)

либо в полярной системе в виде показательной функции:

(43)

где — модуль, определяющий амплитуду колебаний;

— фаза.

Если изобразить частотную функцию (43) в виде вектора в комплексной плоскости , то при изменении частоты w от 0 до ∞ конец вектора опишет кривую, называемую амплитудно-фазовой характеристикой. Пример такой кривой приведен на рис. 26. Амплитудно-фазовые характеристики широко используются при исследовании динамических свойств систем.

2.3. Типовые динамические звенья

Несмотря на то, что звенья, входящие в состав различных САР, отличаются во многих случаях друг от друга как по конструктивному выполнению, так и по функциональному назначению, представляется возможным свести их к сравнительно небольшой группе звеньев, отличающихся одинаковыми динамическими свойствами. При такой классификации по динамическим свойствам звенья, переходные процессы в которых описываются одинаковыми уравнениями, относят к одному типу динамического эвена.

В теории автоматического регулирования принято различать следующие основные динамические звенья: пропорциональное или безынерционное, апериодическое или инерционное, колебательное, дифференцирующее, интегрирующее, с чистым запаздыванием.

Динамические свойства пропорционального или безынерционного звена описываются уравнением вида:

, (44)

а переходный процесс имеет вид, изображенный на рис. 27.

Рис. 27. Переходный процесс безынерционного звена

Передаточная и частотная функции этого звена описываются следующими выражениями:

; (45)

. (46)

Динамика апериодического звена описывается уравнением

. (47)

При ступенчатом возмущении и нулевых начальных условиях переходная функция имеет вид (см. рис. 22):

. (48)

Передаточная и частотная функции этого звена имеют следующие выражения:

;

(49)

Амплитудно-фазовая характеристика этого звена представлена на рис. 28.

Рис. 28. Амплитудно-фазовая характеристика

апериодического звена 1-го порядка

Динамика колебательного звена описывается уравнением

. (50)

При ступенчатом возмущении и нулевых начальных условиях переходная функция имеет вид (рис. 29):

, (51)

где — постоянная времени огибающей экспоненты;

Передаточная и частотная функции колебательного звена будут иметь выражения:

; (52)

. (53)

Рис. 29. График переходного процесса колебательного звена

Амплитудно-фазовая характеристика колебательного звена представлена на рис. 26.

В том случае, если в уравнении будет иметь место неравенство , то звено превращается в апериодическое 2-го порядка с переходной функцией

, (54)

где

;

Переходный процесс в этом случае будет иметь вид, представленный на рис. 30.

Рис. 30. График переходного процесса

апериодического звена 2-го порядка

Идеальным дифференцирующим называется звено, динамика которого описывается уравнением вида:

. (55)

График переходной функции этого звена показан на рис. 31 и представляет собой мгновенный импульс, который возникает только в момент подачи ступенчатого входного возмущения. Передаточная и частотная функции идеального дифференцирующего звена:

; . (56)

Рис. 31. Переходный процесс идеального

дифференцирующего звена

Большинство реальных систем обладают определенной инерционностью. Динамика инерционного дифференцирующего звена может быть описана уравнением вида:

. (57)

Рис. 32. Переходный процесс идеального интегрирующего звена

Динамика идеального интегрирующего звена описывается уравнением вида

(58)

или

, (59)

а в операторной форме

. (60)

Из уравнения (58) следует, что если на вход интегрирующего звена подать ступенчатое возмущение, то выходная величина будет со временем беспрерывно увеличиваться.

Графики переходного процесса такого звена показаны на рис. 32. Передаточная и частотная функции определяются по уравнениям:

(61)

Уравнение динамики реального интегрирующего звена будет:

. (62)

Дифференцируя обе части уравнения, можно получить другое выражение:

. (63)

В ряде случаев изменение выходной величины начинается не одновременно с изменением входной, а спустя некоторый промежуток времени, называемый запаздыванием.

Различают звенья с чистым или транспортным запаздыванием, примером которого может служить ленточный питатель (рис. 33). Если входной координатой считать положение шибера на питающем бункере 1 (х), а выходной координатой — количество материала, поступающего в бункер (Q), то переходная характеристика этого звена может быть описана уравнением

, (64)

где t — время;

— время чистого или транспортного запаздывания.

Рис. 33. Схема звена с чистым запаздыванием:

1, 3 – бункера; 2 – шибер

В общем случае любое звено с запаздыванием можно рассматривать состоящим из обыкновенного звена без запаздывания и идеального звена с чистым запаздыванием. Передаточная функция звена с запаздыванием в общем случае будет иметь выражение

, (65)

где W₀(p) — передаточная функция звена без запаздывания.

Рис. 34. Переходные процессы:

а – идеальное звено с чистым запаздыванием;

б – инерционное звено с чистым запаздыванием

Переходные процессы для идеального звена с запаздыванием и для инерционного звена при наличии чистого запаздывания приведены на рис. 34.

2.4. Соединение звеньев, алгебра передаточных функций

Выше была рассмотрена динамика отдельных звеньев, которые входят в состав САР и взаимодействуют между собой. В реальных САР встречаются разнообразные схемы соединения звеньев, которые можно свести к последовательному и параллельному соединению, а также их комбинации. В свою очередь при параллельном соединении может иметь место одинаковое направление входа и выхода либо противоположное. Рассмотрим выражения передаточных функций комплекса элементарных звеньев при различных способах их включения.

Рис. 35. Схема последовательного соединения звеньев

Последовательное соединение. Рассмотрим цепочку, состоящую из трех последовательно соединенных звеньев (рис. 35). На вход первого звена поступает величина х, а на выход последнего — у. Результирующая передаточная функция при последовательном соединении звеньев равна произведению передаточных функций отдельных звеньев:

. (66)

Параллельное соединение. Случай одинакового направления входа и выхода представлен на рис. 36.

Рис. 36. Схема параллельного соединения звеньев

Передаточная функция параллельно соединенных звеньев равна сумме передаточных функций отдельных звеньев:

. (67)

Случай противоположного направления сигналов (охват звена обратной связью) представлен на рис. 37. При включении обратной связи входной сигнал х алгебраически суммируется с сигналом, прошедшим через звено обратной связи, и при отрицательной обратной связи он равен:

В этом случае передаточная функция будет иметь вид:

. (68)

Рис. 37. Схема охвата звена обратной связью

При комбинированном соединении звеньев в САР необходимо контур разбить на отдельные цепи, в которых будут четко выражены последовательное и параллельное соединения, составить передаточные функции для этих цепей, а затем и для всего контура в целом. Таким образом, используя указанные зависимости, можно составить передаточную функцию сложной схемы, из которой при необходимости можно получить дифференциальное уравнение динамики системы.

Из выражения (68) для передаточной функции звена, охваченного обратной связью, принимая , можно легко получить выражение для передаточной функции замкнутой системы, схема которой показана на рис. 38.

Рис. 38. Схема замыкания звена

Передаточная функция замкнутой системы может быть представлена следующим образом:

, (69)

где — передаточная функция разомкнутой системы.

2.5. Уравнение динамики замкнутой системы

Система автоматического регулирования состоит из ряда звеньев, динамика которых в общем случае описывается дифференциальными уравнениями. Так как элементы САР находятся во взаимодействии друг с другом, а сама система является замкнутой, то математическим описанием САР будет являться система дифференциальных уравнений динамики звеньев, входящих в систему и их связей. Путем исключения промежуточных координат систему дифференциальных уравнений можно привести к одному дифференциальному уравнению, которое включает в себя только входные воздействия и выходную, регулируемую величину.

В качестве примера рассмотрим систему автоматического регулирования частоты вращения вала теплового двигателя, принципиальная схема которой приведена на рис. 39.

Структурная схема этой САР изображена на рис. 40. Динамику звеньев, входящих в состав системы, запишем в операторной форме: