Содержание
- Куб — свойства, виды и формулы
- Элементы куба
- Грань
- Ребро
- Вершина
- Центр грани
- Центр куба
- Ось куба
- Диагональ куба
- Диагональ грани куба
- Объем куба
- Периметр куба
- Площадь поверхности
- Сфера, вписанная в куб
- Сфера, описанная вокруг куба
- Координаты вершин куба
- Свойства куба
- Как нарисовать куб: правильное построение куба в перспективе, распределение теней, штриховка
- Введение
- Почему важно уметь рисовать куб в перспективе
- Основные правила перспективы
- Как нарисовать куб в перспективе
- Как нарисовать 3D куб
Куб — свойства, виды и формулы
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
прямая призма, все грани которой есть квадраты;
прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.
Диагональ куба — одна из осей симметрии.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.
Объем куба
Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Периметр куба
Сумма длин всех рёбер равна:

Площадь поверхности
Сумма площадей всех граней называется площадью поверхности куба. Она равна:

Сфера, вписанная в куб
Такая сфера имеет центр, совпадающий с центром куба.

Радиус равен половине ребра:

Сфера, описанная вокруг куба
Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:


Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
Свойства куба
Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.
у куба все грани равны, являются квадратами;
один центр и несколько осей симметрии.
Источник
Как нарисовать куб: правильное построение куба в перспективе, распределение теней, штриховка
Как правильно нарисовать куб карандашом? Правильное построение куба в перспективе, светотени, штриховка. Поэтапный урок – 10 фото.
Введение
Такая, казалось бы, простая геометрическая фигура, как куб, очень много значит в рисовании. В этой статье будем разбираться, зачем художнику учиться рисовать кубы с разных ракурсов карандашом, а также, на примере двух мастер-классов, создадим изображение куба поэтапно и расскажем, как штриховать куб.
Почему важно уметь рисовать куб в перспективе
Научившись рисовать куб, вы сможете рисовать практически любые предметы и фигуры – людей, машины, здания.
Куб – это простая фигура в геометрии и графике, а построение куба в перспективе, поможет вам мыслить объемно. У куба есть 6 поверхностей: верхняя и нижняя, передняя и задняя, и две боковых.
Освоив построение куба, вам будет проще понять, как рисовать, и, что главное, нарисовать другие предметы, например, стул или шкаф, или любой другой объект, который содержит форму куба.
Основные правила перспективы
Если переводить дословно, то перспектива означает смотреть сквозь. Умение рисовать в перспективе – это целое учение, как правильно изображать, передавать объемные предметы на плоскости в академическом рисунке.
Прежде всего, давайте закрепим то, что перспективу не придумали художники, она появилась исходя из законов физики, связанных с оптикой и светом.
Перспектива – это изображение настоящего мира на листе бумаги, с некоторыми искажениями в пропорциях, сделанных для того, чтобы изобразить их в пространстве.
Когда художник рисует какой-либо предмет, он его из мира объема переносит в мир плоскости, то есть на листок бумаги (холст). И для того, чтобы этот объект на рисунке выглядел также живо и объемно, как и в жизни, художник должен передать этот объем, учитывая правила перспективы.
У перспективы есть также несколько своих терминов и правил:
- Рисовать нужно с учетом линии горизонта
Это такая воображаемая линия, которая находится на уровне глаз. Предмет, который вы хотите нарисовать (в нашем случае это будет куб), должен быть выше такой линии, ниже или чуть-чуть выше или ниже.
- Есть определенная точка схода
Это такая точка (воображаемая), в которой сходятся все параллельные линии предмета.
- Воздушная перспектива – чем дальше от нас предмет, тем хуже его будет видно.
- Световая перспектива – чем ближе к нам предмет, чем ярче светотень.
Как нарисовать куб в перспективе
1 этап – намечаем куб, его высоту и ширину

Карандашом НВ намечаем высоту и ширину нашего куба. Обращаем внимание на то, чтобы справа у нас было немного больше расстояние, чем слева. Высота и ширина у куба должны быть примерно равны. Также обозначаем переднюю грань нашего куба, где левая сторона у нас чуть-чуть больше, чем правая. Правая сторона куба должна вмещаться в левую сторону по ширине, примерно в полтора раза. Также, намечаем, условно, где у нас будет располагаться крышка нашего куба.
В данном случае, высота крышки куба будет равняться, примерно почтив два раза должна вкладываться она в правую сторону нашего куба, чуть-чуть меньше, чем в два раза.
2 этап – рисуем стороны наклона куба

Далее, мы показываем наклоны сторон у куба. Обращаем внимание на то, что правая сторона куба меньше, и уходит в перспективу, поэтому, углы наклона будут гораздо более резкими и линии направлены больше вверх, чем слева.
Также, обращаем внимание на то, чтобы все линии у нас сходились в одну точку. То есть, линии, которые у нас направлены вправо, они должны в итоге в конце, если их дальше и дальше проводить, они должны сойтись в одной точке. Точно также и с левой стороны. Также обращаем внимание на то, что нижняя плоскость от основания куба имеет более резкие наклоны, чем верхняя часть.
3 этап – рисуем линии куба и крышку в перспективе

Куб мы должны видеть насквозь, поэтому мы рисуем дно нашего куба. Таким образом, мы из левого нижнего угла и из правого нижнего угла выводим линии. Они точно также должны уходить в перспективу. То есть, линии, которые у нас направлены влево, они уходят в левую точку, и линии, которые у нас направлены вправо, они уходят в правую точку.
Таким образом, мы находим самую дальнюю грань нашего куба, которую мы не видим. Она нужна нам для того, чтобы увидеть, где у нас заканчивается угол на крышке куба сверху.
После этого, мы, когда нашли эту точку, мы поднимаем вверх вертикальную линию и находим дальнюю невидимую нам грань куба. Точно также, опираясь на эту грань и имея размер нашей крышки, мы намечаем нашу крышку.
Точно также обращаем внимание на то, чтобы все линии уходили в перспективу.

Далее, подтираем все лишние линии. Затем, карандашом НВ, либо 2В мы делаем штриховку. Правую сторону мы делаем самой темной. На нее мы накладываем штриховку сначала диагональными штрихами, а затем вертикальными. Обращаем внимание на то, что тон у нас расположен именно в левом углу верхнем. То есть, сторона нашего тона сверху темнее, снизу становится чуть-чуть светлее.
Точно также, просто диагональной штриховкой мы проходимся по левой стороне куба, а крышку мы оставляем полностью белой. Далее, карандашом 2В, либо 4В мы еще сильнее уточняем переднюю грань нашего куба. То есть, мы делаем ее самой яркой. Далее, точно также подчеркиваем основание и верхнюю сторону куба. А дальние линии крышки мы оставляем светлыми.
Таким образом, получаем заштрихованный рисунок куба карандашом поэтапно для начинающих.
Как нарисовать 3D куб
В этом мастер-классе мы покажем, как нарисовать куб с тенью, а сначала как начертить линии построения.
1 этап – намечаем высота и ширину куба

Карандашом НВ намечаем высоту куба. Далее, делим куб по вертикали пополам и серединку немного смещаем вниз. Таким образом, крышка куба будет чуть-чуть больше по высоте, чем высота самой передней грани, которая находится ближе к нам.
Далее, определяем ширину куба. Она должна быть чуть-чуть меньше, чем высота и определяем место, где у нас находится передняя грань. Она будет находиться ровно посередине.
2 этап – рисуем грани куба

Далее, начинаем уводить наши стороны в перспективу. Для этого мы проводим из нижней части грани куба линии, которые уходят у нас под резким углом. Точно также мы из верхней части грани мы проводим тоже длинные линии. Обращаем внимание на то, чтобы линии, которые идут на лево, они, в дальнейшем, где-то далеко, должны сойтись.
Они должны не расходиться и не быть параллельными. Они должны в итоге где-то далеко-далеко сойтись.
Точно также и с линиями, которые идут в правую сторону. Точно также мы рисуем основание нашего куба. Оно нужно для того, чтобы найти верхнюю дальнюю грань, которую мы не видим. Для этого, из углов слева и справа, нижних углов, мы выводим точно также длинные линии, которые точно также сходятся.
После этого, линии перекрещиваются, и там же и будет находиться наша дальняя грань куба, которую мы не видим.
3 этап – рисуем падающую тень

Таким же образом, как мы рисовали дно нашего куба, точно также мы рисуем крышку куба, точно также линии должны быть в перспективе, то есть сходиться в одной точке. Также мы выравниваем все стороны куба для того, чтобы он у нас был ровным, и мы могли стереть все линии построения, которые нам не нужны.
Также мы строим падающую тень. Она у нас в данном случае, находится немного под наклоном. То есть наклон падающей тени – передний край, он должен быть чуть менее острым и более горизонтальным, чем плоскость основания справа у куба. Линия сверху, которая у тени идет, она должна заходить немного за куб, потому что куб у нас объемный, соответственно, там линия тени падает от дальней грани, поэтому она и заходит за куб.
Обращайте внимание на то, чтобы размер тени у нас был в данном случае не больше, чем высота передней грани. Также мы параллельно край тени делаем параллельным линии основания куба.

Далее, стираем все лишние линии, все линии построения, и еще раз выравниваем наш кубик. Далее, карандашом НВ, либо 2В, начинаем накладывать нашу штриховку. Штриховку мы сначала накладываем по диагонали, штрихуем и левую, и правую сторону куба. Также не забываем штриховать тень. Далее, накладываем вертикальную штриховку на стороны куба. Обращаем внимание на то, что левая сторона куба у нас должна быть немного темнее, чем правая сторона.
Также, и на падающую тень мы накладываем 2 вида штриховки. Первую штриховку мы кладем по направлению нижней линии тени, а второе направление штриховки мы делаем чуть более горизонтально, то есть меняем направление штриховки.
Обращаем внимание на то, чтобы при штриховке, когда у нас соединяется одно направление штриховки с другим, чтобы у нас не образовывались ровные квадратики. То есть должно образовываться что-то похожее на параллелепипеды или на ромбики.
5 этап – усиливаем штриховку

Далее, карандашом 4В мы начинаем еще сильнее усиливать штриховку. Обращаем внимание на то, что левая сторона куба темнее, чем правая. Также обращаем внимание на то, что тень на сторонах у нас расположена неравномерно. То есть, на левой стороне куба тень сильнее от внутреннего правого верхнего угла, и она начинает растворяться как влево, так и вниз, начинает высветляться.
Также обращаем внимание на то, что падающая тень еще темнее, чем все стороны куба. Но также имеет растяжку — у основания куба она темнее, чем дальше от куба, тем она светлее.
Источник
Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:
- многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;
- прямая призма, все грани которой есть квадраты;
- прямоугольный параллелепипед, все рёбра которого равны.
Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.
Элементы куба
Основными элементами многогранника считаются грани, рёбра, вершины.
Грань
Плоскости, образующие поверхность куба, называются гранями.
Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть.
Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.
Грани куба попарно перпендикулярны, являются квадратами, равны между собой.
Ребро
Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать.
Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.
Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.
Вершина
Точки пересечения рёбер называются вершинами. Их число равно восьми.
Центр грани
Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.
Центр куба
Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.
Ось куба
Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.
Диагональ куба
Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:
Формула доказывается с помощью дважды применённой теоремы Пифагора.
Диагональ куба — одна из осей симметрии.
Все диагонали куба равны между собой и точкой пересечения делятся пополам.
Диагональ грани куба
Длина диагонали грани в √2 раз больше ребра, то есть:
Эта формула доказывается также с помощью теоремы Пифагора.
Перспективный рисунок куба

ЦЕЛЬ И ПОСТАНОВКА ЗАДАНИЯ. Чтобы научиться рисовать куб в перспективе, сначала изобразите куб в произвольном положении на основе горизонтального квадрата. Проанализируйте перспективные закономерности построения куба на примере вашего рисунка. Затем изобразите кубы в произвольном и заданном повороте, выше и ниже линии горизонта.
РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ
Приступая к работе над рисунком, продумайте композицию листа. На нем должны разместиться 7 – 8 кубов (рис. 3.2). В верхней части листа изображайте кубы, на которые вы смотрите снизу, в нижней части листа – кубы, на которые вы смотрите сверху -так, как будто примерно посередине листа проходит линия горизонта. При желании можно действительно провести ее на рисунке, тогда раскрытие квадратов в основании кубов будет задано более точно. Обозначьте на листе место и приблизительный размер каждого куба легкими линиями.

Наилучшее представление о геометрическом теле дает анализ его ортогональных проекций. Рассмотрите перспективный рисунок куба на рис. 3.3 и его ортогональные проекции на рис. 3.4. Перспектива куба строится на перспективе квадратов, его образующих. Чувство перспективы квадрата, а также куба, должно быть развито у архитектора особенно хорошо, так как квадрат и куб являются основными модулями площади и объема для других плоских и пространственных форм.

Для выполнения задания внимательно изучите схемы построения куба в угловой и фронтальной перспективах. Сначала изобразите куб ниже линии горизонта в угловой перспективе. Рисунок куба начните с горизонтального квадрата верхнего основания. Квадрат постройте на основе эллипса (рис. 3.5). Проведите из вершин квадрата вертикальные ребра куба и отложите на ближнем вертикальном ребре высоту куба. Она, примерно, равна большой оси эллипса, вписанного в квадрат основания куба. Определив высоту куба, последовательно достраивайте недостающие ребра, сводя параллельные линии в точки схода на горизонте. Эти построения лучше совершать в определенной последовательности – в той, которая позволит вам постоянно контролировать ход работы и своевременно исправлять замеченные ошибки. Сначала из полученной точки в нижнем основании куба проведите горизонтальное ребро, достроив до квадрата ту вертикальную грань, которая имеет большее раскрытие (рис. 3.6). Визуально проверьте правильность этого квадрата и, если это необходимо, исправьте его, увеличив или уменьшив выбранную высоту куба. Направление второго горизонтального ребра легко определить, продлив его линию на рисунке и проверив, насколько она сходится в перспективе с горизонтальными ребрами верхнего основания куба (рис. 3.7). Третье ребро также проведите, ориентируясь на уже существующие линии параллельного направления (рис. 3.8). Последнее ребро нижнего основания соединяет две вершины, место которых на рисунке уже определено предыдущим построением (рис. 3.9). Изображенный куб должен выглядеть убедительно и правдиво – каждая его грань, вне зависимости от того, видим мы ее или нет, должна по ощущению быть похожа именно на квадрат. Проверьте это визуально, а затем графически, вписав в видимые нам вертикальные грани куба окружности (рис. 3.10).

Закончив рисунок, еще раз проанализируйте закономерности раскрытия граней куба и перспективных сокращений его ребер:
• горизонтальные параллельные линии, на которых лежат ребра куба, равномерно сходятся в точки схода на линии горизонта, а вертикальные ребра куба сохраняют на листе свое вертикальное направление (рис. 3.11);
• те горизонтальные ребра, что идут в точку схода, расположенную ближе к кубу, сходятся быстрее, чем те, что идут в точку схода, расположенную дальше (рис. 3.12);
• те ребра, которые расположены ближе к зрителю, на рисунке имеют больший размер по сравнению с ребрами, которые расположены дальше. Заметьте, что подобным образом можно сравнивать только те ребра, которые лежат на параллельных прямых. Так, например, из четырех вертикальных ребер куба наибольший размер имеет ближнее к нам ребро, а по мере удаления от зрителя размер ребер на рисунке уменьшается (рис. 3.13);

• верхняя горизонтальная грань куба, расположенная ближе к линии горизонта, раскрыта меньше, чем нижняя горизонтальная грань (рис. 3.14). Из двух параллельных вертикальных граней больше раскрыта та грань, которая расположена дальше от зрителя (рис. 3.15 и 3.16);
• из двух видимых вертикальных граней куба больше раскрыта та грань, точки схода горизонтальных ребер которой находятся дальше от куба, таким образом, больший угол при основании а соответствует менее раскрытой вертикальной грани куба, меньший угол р – более раскрытой грани (рис. 3.17);
• параллельные диагонали, проведенные в горизонтальных гранях куба, сходятся на линии горизонта (рис. 3.18).

Если вы обнаружили ошибки в своем рисунке, исправьте их. В следующих кубах старайтесь отслеживать перспективные закономерности в процессе рисунка, а не в конце, когда построение уже закончено.
На рисунке куба во фронтальной перспективе фронтальные грани куба изображаются как квадраты различного размера – в зависимости от того, ближе или дальше от зрителя они расположены. Ребра, ограничивающие фронтальные грани, имеют вертикальное и горизонтальное направления. Горизонтальные ребра куба, уходящие от зрителя, сходятся в точке схода на линии горизонта. Сначала изобразите верхнее основание куба – горизонтальный квадрат во фронтальной перспективе на основе эллипса (рис. 3.19). Опустите из вершин основания вертикальные ребра куба и достройте до квадрата переднюю вертикальную грань (рис. 3.20). Из нижних точек фронтальной грани проведите прямые в точку схода на линии горизонта. Точки пересечения этих прямых с дальними вертикальными ребрами определят на вашем рисунке размеры остальных граней куба (рис. 3.21). Завершите рисунок, вписав окружности во фронтальные грани куба (рис. 3.22).

Для того, чтобы нарисовать куб в определенном повороте, сначала необходимо изобразить в соответствующем повороте его горизонтальное основание. Вы можете самостоятельно задать этот поворот, определяя его как отношение проекций боковых граней куба на горизонтальную прямую (рис. 3.23). Выберите простые отношения – 1:2, 1:3, 1:4. Изображая куб в заданном положении, сначала, как обычно, изобразите эллипс, а затем опишите вокруг него квадрат, добиваясь заданного положения квадрата путем последовательных приближений. На основе квадрата постройте куб.

Координаты вершин куба
В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:
Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).
рисуем куб
Все окружающие нас вещи, которые мы хотели бы нарисовать, какими бы сложными по форме они нам не казались, всегда можно схематически представить с помощью простых геометрических фигур, таких как куб, цилиндр, шар. Поэтому, нужно понять, как правильно рисовать эти простейшие фигуры, и потом в рисовании более сложных фигур у вас будет гораздо меньше сложностей.
Для начала нужно построить куб. Чтобы понять, как будут изменяться пропорции куба в перспективе, рассмотрим рисунок, на котором изображен непрозрачный и прозрачный куб. Точка F на рисунке – точка схода.
Тут показано фронтальное положение куба в трех возможных случаях:
1) когда линия горизонта пересекает куб – значит, мы смотрим на прямо куб, находящийся на уровне наших глаз;
2) когда куб находится ниже линии горизонта – мы смотрим на куб прямо и немного сверху и
3) когда куб находится над линией горизонта – мы смотрим прямо и снизу. Вот всех этих случаях вся передняя грань куба находится на одинаковом расстоянии от наших глаз, поэтому она не изменится в перспективе. Чтобы построить куб во всех этих положениях, достаточно построить переднюю грань, провести линии из четырех углов в точку схода, отложить на этих линиях верхние и нижние ребра и соединить их между собой.

На рисунке 1 видно, что когда куб расположен на линии горизонта, его передние боковые ребра не подвергаются перспективным изменениям, а задние ребра кажутся короче передних, из-за этого верхние и нижние ребра, уходящие в глубину, кажутся не параллельными, и продлив их до линии горизонта, мы получим точку схода.
Если куб поставить ниже или выше линии горизонта (рис 2 и 3), то ребра, уходящие в глубину, поднимутся вверх или, соответственно, опустятся вниз, сходясь на линии горизонта.
Возможны еще случаи, когда линия горизонта проходит через верхнюю или нижнюю грани куба, такие положения построить тоже достаточно легко. Теперь рассмотрим вариант, если куб развернут к нам одним из своих боковых ребер, так же в трех положениях: на линии горизонта, ниже и выше линии горизонта. В этом случае точек схода будет две.

В первом случае, нам будут видны только две грани, расположенные под углом. Ближе всего к зрителю будет находиться переднее боковое ребро, и только оно не подвергнется перспективным сокращениям. Из углов куба проводим вправо и влево прямые, сходящиеся на линии горизонта, на них будут лежать верхние и нижние ребра куба.
Если поставить куб выше или ниже линии горизонта, то нам будет видна верхняя или нижняя грань. В этом упражнении мы будем рисовать куб, развернутый к нам одним из боковых ребер, расположенный ниже линии горизонта.
Вам нужно будет нарисовать линейный рисунок прозрачного куба, прорисовывая задние ребра. Во время рисования можно использовать линейку. Если вы выполняли упражнения на развитие моторики кисти, то, скорее всего, у вас вполне получится сделать это и без линейки, во всяком случае, хотя бы попробуйте. Вполне можно наметить все линии от руки, а потом нарисовать окончательный контур с помощью линейки. Пусть размен нашего куба будет 5х5 см. Наверняка вам придется вытирать черновые линии, поэтому возьмите лист ватмана. Карандаш подойдет любой от Н до 2В.
Начните с переднего бокового ребра, которое мы видим без перспективных искажений, и только это ребро будет иметь реальный размер 5 см. На уровне нижнего угла ребра проведите вспомогательную горизонтальную прямую, потом ее можно будет вытереть, она нужна нам, чтобы определить углы, под которыми мы будем строить боковые грани куба. Если они равны, обе боковые грани мы видим одинаково, но в нашем варианте это разные углы.
Чем больше угол, тем меньше открыта соответствующая боковая грань. Определившись с углами, проведите прямые, содержащие горизонтальные ребра. Для тренировки глазомера на листе бумаги желательно не располагать точки схода, и если вы разместите ваш рисунок на вертикально развернутом листе, то они просто не поместятся, главное, чтобы из рисунка было понятно, что эти прямые сойдутся, Но вполне можно довести прямые до точек схода и указать их на линии горизонта, так нарисовать куб будет проще. Теперь, помня о том ,что исходя из законов перспективы, чем дальше от нас что-то тем оно меньше, откладываем на прямых нижние и верхнее горизонтальные ребра.
Здесь можно проверить себя с помощью линейки. Все ребра, кроме переднего бокового должны быть меньше 5 см. Например, дальнее ребро, будет меньше противоположному ему ближнему, так как более удалено от зрителя.

После того, как куб будет построен, попробуйте придать линиям разную толщину, чтобы подчеркнуть этим перспективу. Самым тонким будет дальнее вертикальное ребро, а самым толстым – ближнее. На горизонтальных ребрах нужно сделать плавный переход от более тонкого (дальнего) угла к более толстому (ближнему). Так будет выглядеть ваш куб.
Градации светотени. Тоновый рисунок куба
Теперь, зная, как правильно построить куб, мы будем разбираться, как его нарисовать тоном. Чтобы правильно нарисовать даже простейшие геометрические фигуры, нам понадобится немного теории. Мы видим предметы, если они освещены. Лучи света по-разному попадают на разные участки поверхности предметов и вы видим его форму, сам предмет закрывает собой доступ для лучей света на какую-нибудь поверхность и образуется падающая тень. Светотеневые участки на любом предмете можно представить в виде нескольких градаций:
Свет – это участок поверхности предмета, получающий наибольший поток прямых лучей света.
Полутон – участок поверхности предмета, освещенных скользящими лучами света. Полутон делится на полутон света и полутон тени.
Тень (собственная тень) – участок поверхности предмета, куда прямые и скользящие лучи света не попадают. Это самый темный участок на поверхности предмета. Блик – бывает на блестящих или лакированных поверхностях, чаще всего на территории света.
Рефлекс – участок теневой поверхности предмета, получающий поток отраженных лучей света от окружающих предметов или от поверхности, на которой предмет расположен.
Цвет рефлекса зависит от цвета окружающих предметов, а яркость или светлота зависит от характера поверхности предмета: на блестящих объектах рефлексы более светлые и ярче выражены, чем на матовых. Падающая тень – это тень, отбрасываемая объектом на какую-нибудь поверхность. Падающая тень темнее, чем собственная, а наиболее темный участок падающей тени ближе всего к источнику света. Позже я сделаю дополнение к этому уроку о том, как правильно построить падающую тень. Источников света может быть несколько, мы рассмотрим вариант с одним источником света, расположенным вверху слева относительно объекта.

На стыках по-разному освещенных граней можно наблюдать так называемый краевой контраст. На границе светлого и темного светлое кажется светлее, а темное – темнее.
Для того, чтобы выполнить это упражнение, вам потребуется настольная лампа и гипсовый куб. Гипсовые геометрический фигуры продаются в магазинах для художников, но в домашних условиях вполне можно обойтись, сделав, например, бумажный кубик, вырезанный из белого листа ватмана или картона по такой схеме:

После того, как вы сделаете куб из бумаги, поставьте его на ровную горизонтальную поверхность справа от настольной лампы так, чтобы свет от нее был направлен на куб немного сверху и слева. Желательно, чтобы поверхность стола и фон сзади куба были однотонными, чтобы не отвлекать ваше внимание. Рассмотрите куб в различных положениях, о которых мы говорили в первой части этого урока, И подробнее остановимся на том положении, которой нам предстоит нарисовать. Обратите внимание, как распределяются светотеневые участки на гранях, как ведет себя падающая тень, если приближать или удалять куб от источника света, постарайтесь увидеть краевой контраст и рефлекс.

Дальше можно выполнять это упражнение по-разному. Более простой вариант – снова начертить линейный куб и раскрасить его тоном, а более сложный – сделать рисунок куба с натуры. При рисовании с натуры тоже начинаем с переднего бокового ребра, строим сходящиеся линии, необязательно доводить их до точки схода. После определяем углы. Можно применять визирование, этот метод помогает определять углы и расстояния. Прищурив один глаз, держа на вытянутой руке карандаш, используют его, для измерения. Например, замерив одну из граней куба карандашом, смотрим, на сколько процентов или частей другая грань больше или меньше. Чтобы измерить углы, держим карандаш горизонтально на вытянутой руке как бы образуя им вспомогательную линию, параллельную линии горизонта и проходящую через нижний угол передней грани куба.
При визировании обязательно рука всегда должна быть вытянутой, иначе все время будут получаться разные результаты. Визирование тормозит развитие глазомера, поэтому не стоит им пользоваться постоянно.
Старайтесь штриховать параллельно ребрам куба, плотно и аккуратно. В результате у вас получится примерно такой куб как на рисунке выше или ниже.

Как найти площадь грани куба
Под кубом подразумевается правильный многогранник, у которого все грани образованы правильными четырехугольниками – квадратами. Для того, чтобы найти площадь грани любого куба, не потребуется тяжелых расчетов.

Инструкция
Для начала стоит заострить внимание на само определение куба. Из него видно, что любая из граней куба представляет собой квадрат. Таким образом, задача по нахождению площади грани куба сводится к задаче по нахождению площади любого из квадратов (граней куба). Можно взять именно любую из граней куба, так как длины всех его ребер равны между собой.
Для того, чтобы найти площадь грани куба, требуется перемножить между собой пару любых из его сторон, ведь все они между собой равны. Формулой это можно выразить так:
S = a², где а – сторона квадрата (ребро куба).
Пример: Длина ребра куба 11 см, требуется найти ее площадь.
Решение: зная длину грани, можно найти ее площадь:
S = 11² = 121 см²
Ответ: площадь грани куба с ребром 11 см равна 121 см²
Обратите внимание
Любой куб имеет 8 вершин, 12 ребер, 6 граней и 3 грани при вершине.
Куб – это такая фигура, которая встречается в быту невероятно часто. Достаточно вспомнить игровые кубики, игральные кости, кубики в различны детских и подростковых конструкторах.
Многие элементы архитектуры имеют кубическую форму.
Кубическими метрами принято измерять объемы различных веществ в различных сферах жизни общества.
Говоря научным языком, кубический метр – это мера измерения объема вещества, которое способно поместиться в куб с длиной ребра 1 м
Таким образом, можно ввести и иные единицы измерения объема: кубические миллиметры, сантиметры, дециметры и т.п.
Помимо различных кубических единиц измерения объема, в нефтяной и газовой промышленности возможно применение иной единицы – баррель (1м³ = 6.29 баррелей)
Полезный совет
Если у куба известна длина ее ребра, то, помимо площади грани можно найти и другие параметры данного куба, например:
Площадь поверхности куба: S = 6*a²;
Объем: V = 6*a³;
Радиус вписанной сферы: r = a/2;
Радиус сферы, описанной вокруг куба: R = ((√3)*a))/2;
Диагональ куба (отрезок, соединяющие две противоположные вершины куба, который проходит через его центр): d = a*√3
Источники:
- площадь куба если ребра равны 11 см
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Содержание:
- § 1 Куб и элементы куба
- § 2 Изображение куба на плоскости
§ 1 Куб и элементы куба
В этом уроке познакомимся с геометрическим телом «куб» и научимся его изображать на плоскости.

Одна из первых детских игр – «кубики».
Возьмем один из кубиков.
В математике его называют «куб».
Рассмотрим это геометрическое тело.
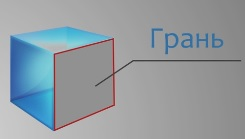
Поверхность куба состоит из квадратов.
У квадрата все стороны равны.
Все квадраты, из которых состоит поверхность куба, одинаковы.
Их называют гранями.
Поэтому куб называют многогранником.
У куба 6 граней.
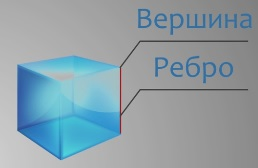
У каждой грани есть стороны.
Стороны называют ребрами.
У куба 12 ребер.
Каждое ребро относится к двум граням куба.
Так как у квадрата все стороны равны, то и все грани куба имеют одинаковую длину.
Концы ребер называются вершинами.
Каждое ребро соединяет две вершины.
Вершин у куба – 8.
Грань, ребро, вершина – это элементы куба.
В одной вершине сходится 3 ребра, каждая грань имеет 4 соседних грани, у каждой грани – 4 ребра.
§ 2 Изображение куба на плоскости
Возьмем куб, выполненный из бумаги. Попробуем его развернуть. Получится развертка куба.

Развертка – это выкройка куба.
Она состоит из 6 квадратов, расположенных в таком порядке, что из них можно сложить или склеить модель куба.
Перейдем к практической части.
Как изобразить куб на плоскости, например, на листе бумаги?
Куб – объемный предмет. Если обвести основание куба – получится квадрат. Это не является изображением куба.
Для наглядного изображения куба достаточно показать три его грани, например, верхняя, правая и передняя. Также можно сделать чертеж куба.
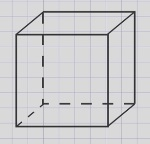
Для выполнения чертежа построим сначала переднюю грань, сзади выше и правее – заднюю грань, проведем нижние и верхние ребра боковых граней.
Ребра, которые не видны, изображают пунктирной линией, остальные сплошной линией.
Отметим, что на рисунке и чертеже мы не можем передать реальные размеры всех ребер куба.
Итак, в этом уроке Вы познакомились с геометрическим телом «куб», а также научились его изображать на плоскости.
Список использованной литературы:
- Чекин А.Л. Математика: 3 кл.: Учебник: В 2 ч./А.Л. Чекин; под ред. Р.Г. Чураковой.- М.: Академкнига / Учебник, 2013.
- Чуракова Р.Г. Математика. Поурочное планирование методов и приемов индивидуального подхода к учащимся в условиях формирования УУД.3 кл.: В 4 ч. Ч. 1/Р.Г. Чуракова, Г.В. Янычева. — М.: Академкнига /Учебник, 2014.
Использованные изображения:
Нахождение площади поверхности куба: формула и задачи
В данной публикации мы рассмотрим, как можно найти площадь поверхности куба и разберем примеры решения задач для закрепления материала.
- Формула вычисления площади куба
- 1. Через длину ребра
- 2. Через длину диагонали грани
Формула вычисления площади куба
1. Через длину ребра
Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате.
S = 6 ⋅ a 2

Данная формула получена следующим образом:
-
Куб – это правильная геометрическая фигура, все грани которого являются равными квадратами с длиной стороны a (одновременно является ребром куба).
2. Через длину диагонали грани
Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√ 2 .

Это значит, что вычислить площадь поверхности фигуры можно так:
S = 6 ⋅ (d/√ 2 ) 2
Примеры задач
Задание 1
Найдите площадь поверхности куба, если длина его ребра составляет 12 см.Решение:
Используем первую формулу выше и получаем:
S = 6 ⋅ (12 см) 2 = 864 см 2 .Задание 2
Площадь поверхности куба равняется 294 см 2 . Вычислите длину его ребра.Решение:
Примем ребро куба за a. Из формулы расчета площади следует:
Задание 3
Вычислите площадь поверхности куба, если диагональ его грани равняется 5 см.Решение:
Воспользуемся формулой, в которой задействована длина диагонали:
S = 6 ⋅ (5 см : √ 2 ) 2 = 75 см 2 .Объём куба равен 128√2. Как найти площадь грани куба?

Вот что тут писать? Когда данная задача решается в одну строчку? Предположим ребро равно скольким-то единицам (ед). Чтобы найти площадь грани. Это действие вычисляется квадратом из этого ребра, запись такая:
А чтобы найти объём куба, то это действие вычисляется возведением в третью степень или в куб из этого ребра, запись такая:
Но здесь уже известно, что:
Требуется всего лишь обратное преобразование:
(128*2^(1/2))^(2/3) = 32 ед^2. Получится 32 единицы в квадрате.
Вычислю длину ребра:
Чему равен корень из 2? Вычислю:
чему равна эта запись 128√2? Вычислю:
Проверка завершилась успешно!
Мой ответ: Чтобы найти площадь грани куба нужно из этого числа 128√2 извлечь кубический корень и полученный результат возвести в квадрат и получится 32.
Как найти площадь грани куба

Для того, чтобы найти площадь грани куба, требуется перемножить между собой пару любых из его сторон, ведь все они между собой равны. Формулой это можно выразить так:
S = a², где а — сторона квадрата (ребро куба).
Пример: Длина ребра куба 11 см, требуется найти ее площадь.
Решение: зная длину грани, можно найти ее площадь:
Ответ: площадь грани куба с ребром 11 см равна 121 см²
- площадь куба если ребра равны 11 см
- Как найти сторону куба
- Как вычислить площадь грани
- Как найти сумму длин рёбер куба
