Как найти перегрузку формула

В данной статье репетитор по физике и математике рассказывает о том, как рассчитать перегрузку, которую испытывает тело в момент разгона или торможения. Данный материал очень плохо рассматривается в школе, поэтому школьники очень часто не знают, как осуществлять расчёт перегрузки, а ведь соответствующие задания встречаются на ЕГЭ и ОГЭ по физике. Так что дочитайте эту статью до конца или посмотрите прилагающийся видеоурок. Знания, которые вы получите, пригодятся вам на экзамене.

Начнём с определений. Перегрузкой называется отношение веса тела к величине силы тяжести, действующей на это тело у поверхности земли. Вес тела — это сила, которая действует со стороны тела на опору или подвес. Обратите внимание, вес — это именно сила! Поэтому измеряется вес в ньютонах, а не в килограммах, как некоторые считают.

Таком образом, перегрузка — это безразмерная величина (ньютоны делятся на ньютоны, в результате ничего не остаётся). Однако, иногда эту величину выражают в ускорениях свободного падения. Говорят, к примеру, что перегрузка равна , имея ввиду, что вес тела вдвое больше силы тяжести.

Примеры расчёта перегрузки

Покажем, как осуществлять расчёт перегрузки на конкретных примерах. Начнём с самых простых примеров и перейдём далее к более сложным.

Пример 1. Чему равна перегрузка человека, стоящего на земле? Чему равна перегрузка человека, свободно падающего с некоторой высоты?

Очевидно, что человек, стоящий на земле, не испытывает никаких перегрузок. Поэтому хочется сказать, что его перегрузка равна нулю. Но не будем делать поспешных выводов. Нарисуем силы, действующие на этого человека:

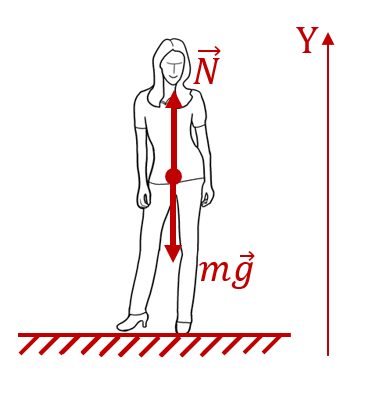
К человеку приложены две силы: сила тяжести , притягивающая тело к земле, и противодействующая ей со стороны земной поверхности сила реакции , направленная  вверх. На самом деле, если быть точным, то эта сила приложена к подошвам ног человека. Но в данном конкретном случае, это не имеет значения, поэтому её можно отложить от любой точки тела. На рисунке она отложена от центра масс человека.

Вес человека приложен к опоре (к поверхности земли), в ответ в соответствии с 3-м законом Ньютона со стороны опоры на человека действует равная по величине и противоположно направленная сила . Значит для нахождения веса тела, нам нужно найти величину силы реакции опоры.

Поскольку человек стоит на месте и не проваливается сквозь землю, то силы, которые на него действуют скомпенсированы. То есть , и, соответственно, . То есть расчёт перегрузки в этом случае даёт следующий результат:

   

Запомните это! При отсутствии перегрузок перегрузка равна 1, а не 0. Как бы странно это не звучало.

Определим теперь, чему равна перегрузка человека, который находится в свободном падении.

Если человек пребывает в состоянии свободного падения, то на него действует только сила тяжести, которая ничем не уравновешивается. Силы реакции опоры нет, как нет и веса тела. Человек находится в так называемом состоянии невесомости. В этом случае перегрузка равна 0.

Пример 2. Определите перегрузку космонавтов, находящихся в ракете, движущейся на небольшой высоте вверх с ускорением 40 м/с².

Космонавты находятся в горизонтальном положении в ракете во время её старта. Только так они могут выдержать перегрузки, которые они испытывают, не потеряв при этом сознания. Изобразим это на рисунке:

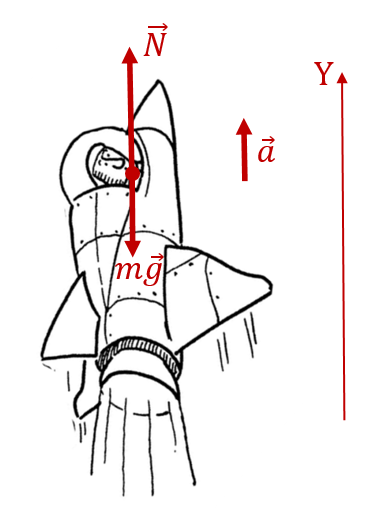
В этом состоянии на них действует две силы: сила реакции опоры и сила тяжести . Как и в прошлом примере, модуль веса космонавтов равен величине силы реакции опоры: . Отличие будет состоять в том, что сила реакции опоры уже не равна силе тяжести, как в прошлый раз, поскольку ракета движется вверх с ускорением . С этим же ускорением синхронно с ракетой ускоряются и космонавты.

Тогда в соответствии со 2-м законом Ньютона в проекции на ось Y (см. рисунок), получаем следующее выражение: , откуда . То есть искомая перегрузка равна:

   

Надо сказать, что это не самая большая перегрузка, которую приходится испытывать космонавтам во время старта ракеты. Перегрузка может доходить до 7. Длительное воздействие таких перегрузок на тело человека неминуемо приводит к летальному исходу.

Пример 3. Рассчитайте перегрузку, которую испытывает пилот самолёта, выполняющего «мёртвую петлю» в нижней точке траектории. Скорость самолёта в этой точке составляет 360 км/ч. Радиус «мёртвой петли» составляет 200 м.

В нижней точке «мёртвой петли» на пилота будут действовать две силы: вниз — сила , вверх, к центру «мёртвой петли», — сила (со стороны кресла, в котором сидит пилот):

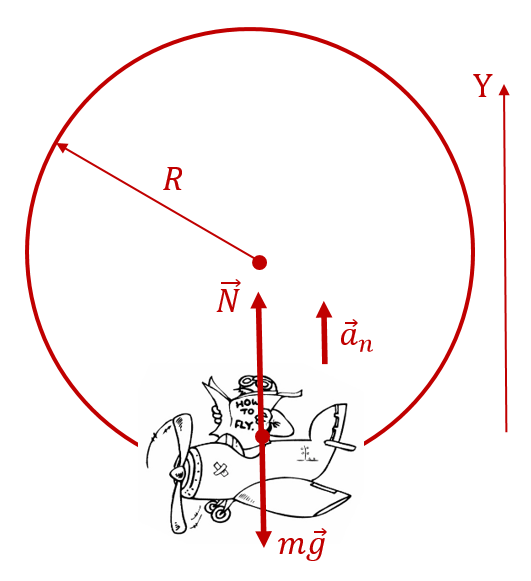
Туда же будет направлено центростремительное ускорение пилота , где км/ч м/с — скорость самолёта, — радиус «мёртвой петли». Тогда вновь в соответствии со 2-м законом Ньютона в проекции на ось, направленную вертикально вверх, получаем следующее уравнение:

   

Тогда вес равен . Итак, расчёт перегрузки даёт следующий результат:

   

Весьма существенная перегрузка. Спасает жизнь пилота только то, что действует она не очень длительно.

Ну и напоследок, рассчитаем перегрузку, которую испытывает водитель автомобиля при разгоне.

Пример 4. Рассчитайте перегрузку, которую испытывает водитель автомобиля, разгоняющегося с места до скорости 180 км/ч за 10 с.

Итак, конечная скорость автомобиля равна км/ч м/с. Если автомобиль ускоряется до этой скорости из состояния покоя за c, то его ускорение равно м/с².

На водителя в процессе ускорения действуют две составляющие силы реакции опоры: со стороны седушки кресла (вертикальная составляющая) и со стороны спинки кресла (горизонатльная составляющая) :

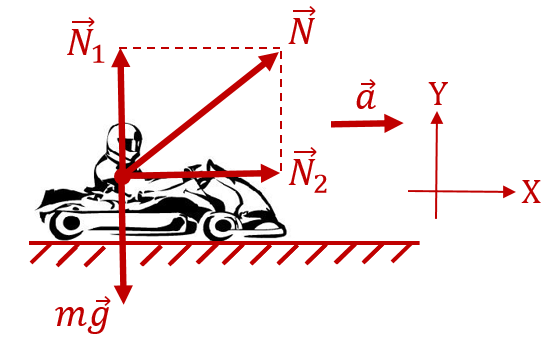
Автомобиль движется горизонтально, следовательно, вертикальная составляющая силы реакции опоры уравновешена силой тяжести, то есть . В горизонтальном направлении водитель ускоряется вместе с автомобилем. Следовательно, по 2-закону Ньютона в проекции на ось, сонаправленную с ускорением, горизонтальная составляющая силы реакции опоры равна .

Величину общей силы реакции опоры найдём по теореме Пифагора: . Она будет равна модулю веса. То есть искомая перегрузка будет равна:

   

Сегодня мы научились рассчитывать перегрузку. Запомните этот материал, он может пригодиться при решении заданий из ЕГЭ или ОГЭ по физике, а также на различных вступительных экзаменах и олимпиадах.

Материал подготовил репетитор по физике в Москве, Сергей Валерьевич

Смотрите также:

• Как рассчитать скорость спутника, вращающегося вокруг земли
• Как легко решить сложную задачу на относительность движения

Давайте разберёмся, что называют перегрузкой в физике, в каких единицах она измеряется и научимся рассчитывать её.

Итак, Перегрузка – отношение веса тела к силе тяжести, действующей на это тело   (1*).

Как известно (см. статью блога «Консультация онлайн репетитора по физике. Сила тяжести. Вес тела. Невесомость.» от 22 декабря 2011), сила тяжести (F = mg) – сила, с которой планета действует на тело, а вес тела (/P/ = /N/) – сила с которой тело, под действием силы тяжести, действует на опору (или подвес), удерживающие это тело от свободного падения.

И исходя из определения (1*), перегрузка рассчитывается по формуле  N/mg         (2*).

Задача 1.

Тело массой m = 100 г. падает с высоты h₁ = 1,25 м и после упругого удара о пол подскакивает на высоту h₂ = 0,8 м. Рассчитать перегрузку, которую испытывает тело во время удара, если удар длится  Δt = 0,1 с.

Решение.

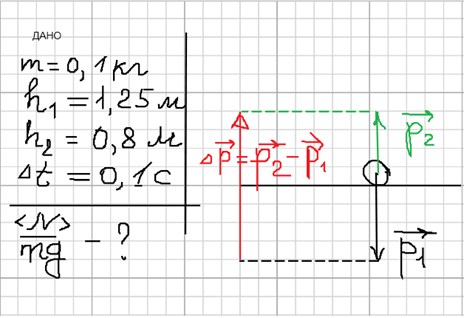
Найдём <N> при ударе тела о пол, написав предварительно формулу для изменения импульса тела:

/Δp^–/ = /p₂^-> – p₁^->/ = mϑ₂ + mϑ₁ = m(√(2gh₂) + √(2gh₁))        (3*)

Во время удара на тело со стороны Земли действует сила тяжести F = mg и со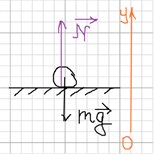 стороны пола сила реакции опоры <N>.

Учитывая это, запишем II закон Ньютона в векторном виде: ma^-> = N^-> + mg^->

В проекции на ось ОУ это уравнение будет иметь вид:
<F> = <N> – mg.

Умножим левую и правую часть уравнения на Δt, получаем:
<F> Δt = <N>Δt – mg · Δt.

Так как импульс силы равен импульсу тела
<F^->> · Δt = Δp^->, то Δp = <N> · Δt – mg · Δt.

Выразим <N>: <N> = (Δp/Δt) + mg.

Используя выражения (2*) и (3*), запишем решение нашей задачи в общем виде:

N/mg = ((Δp/Δt) + mg)/mg = (Δp/Δt · mg) + 1 = (m[√(2gh₂) + √(2gh₁)] / Δtmg) + 1 =

= (√(2gh₂) + √(2gh₁) / Δt · g) + 1                (4*).

Обратите внимание, что в конечном виде формулы (4*) не присутствует масса тела. И поэтому можем сделать вывод о том, что при расчёте перегрузки, которую может испытывать тело, масса тела значения не имеет.

Подставим в выражение (4*) числовые значения и рассчитаем его, приняв g = 10 м/с²

N/mg = ([√(2 · 10 м/с² · 0,8м) + √(2 · 10 м/с² · 1,25 м)] / 0,1 с · 10 м/с²) + 1 = ([√16 м²/с² + √25 м²/с²)] / 1с · м/с²) + 1 =

=([4 м/с + 5 м/с] / 1м/с) + 1 = 10.

Говорят так: «Перегрузка равна 10 g (десять жэ)». Это и есть единицы измерения перегрузки.

Ответ: 10 g.

Зная выражение (2*), можно легко рассчитать перегрузку, которую испытывает космонавт при старте корабля. Попробуйте и у Вас всё получится 🙂

Остались вопросы? Не знаете, как рассчитать перегрузку, которую испытывает тело?
Чтобы получить помощь репетитора – зарегистрируйтесь.

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Остались вопросы?

Задайте свой вопрос и получите ответ от профессионального преподавателя.

Перегрузка в динамике.

Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называется перегрузкой.

При перегрузке не только тело начинает сильнее давить на опору, но и его отдельные части начинают сильнее давить друг на друга.

Если тело движется с ускорением, направленным вертикально вверх, вес тела увеличивается. Такое состояние тела называется перегрузкой. По второму закону Ньютона

.

Будучи отношением двух сил, перегрузка – безразмерная величина, однако, часто она выражается в единицах ускорения свободного падения g. Перегрузка в одну единицу (1 g) численно равна весу тела, покоящемуся в поле тяжести Земли.

Перегрузки испытывают космонавты при взлете и торможении космического корабля, летчики при выполнении фигур высшего пилотажа, пассажиры лифта при его подъеме или торможении и т. д.

В состоянии перегрузки у человека затрудняется дыхание, ухудшается сердечная деятельность, перераспределяется кровь – приливает к голове или отливает и т. д.

Перегрузка – векторная величина. Для живого организма важно направление ее действия. При перегрузке органы человека стремятся остаться в прежнем состоянии. При перегрузке голова-ноги (положительная перегрузка) кровь отливает от головы в ноги, желудок опускается вниз. При отрицательной перегрузке кровь приливает к голове. Положение тела человека, при котором он может выдерживать наибольшие перегрузки – лежа на спине, лицом к направлению ускорения движения.

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Равномерное движение по окружности

Равномерное движение по окружности – это простейший пример криволинейного движения. Например, по окружности движется конец стрелки часов по циферблату. Скорость движения тела по окружности носит название линейная скорость.

При равномерном движении тела по окружности модуль скорости тела с течением времени не изменяется, то есть v = const, а изменяется только направление вектора скорости Тангенциальное ускорение в этом случае отсутствует (a_r = 0), а изменение вектора скорости по направлению характеризуется величиной, которая называется центростремительное ускорение (нормальное ускорение) a_n или а_ЦС. В каждой точке траектории вектор центростремительного ускорения направлен к центру окружности по радиусу.

Модуль центростремительного ускорения равен

Где v – линейная скорость, R – радиус окружности

Рис. 1.22. Движение тела по окружности.

Когда описывается движение тела по окружности, используется угол поворота радиуса – угол φ, на который за время t поворачивается радиус, проведённый из центра окружности до точки, в которой в этот момент находится движущееся тело. Угол поворота измеряется в радианах. Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу окружности (рис. 1.23). То есть если l = R, то

Так как длина окружности равна

360 о = 2πR / R = 2π рад.

1 рад. = 57,2958 о = 57 о 18’

Угловая скорость равномерного движения тела по окружности – это величина ω, равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершён этот поворот:

Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени t:

Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина l дуги окружности, пройденной точкой, связана с углом поворота φ выражением

где R – радиус окружности.

Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:

v = l / t = Rφ / t = Rω или v = Rω

Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.Частота обращения – это величина, обратная периоду обращения – число оборотов в единицу времени (в секунду). Частота обращения обозначается буквой n.

За один период угол поворота φ точки равен 2π рад, поэтому 2π = ωT, откуда

То есть угловая скорость равна

Центростремительное ускорение можно выразить через период Т и частоту обращения n:

a_ЦС = (4π 2 R) / T 2 = 4π 2 Rn 2

[spoiler title=”источники:”]

http://fizmat.by/kursy/kinematika/okruzhnost

[/spoiler]

Нормальная
перегрузка

вычисляется по формуле:

,

где

кН
– сила тяги двигателя летательного
аппарата;

– нормальная
аэродинамическая сила;

–
угол
поворота двигателя;

m=11483,3
кг

– масса летательного аппарата на
расчётный момент времени;

м/с²
– ускорение свободного падения.

Полная
нормальная аэродинамическая сила
рассчитывается по формуле

,

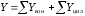где

– суммарное значение всех полных
нормальных аэродинамических сил на
конических участках;

– суммарное
значение всех полных нормальных
аэродинамических сил на цилиндрических
участках.

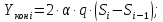
где

– удлинение цилиндра;

–
площади основания конуса.

На
рисунке 1.8 изображена схема ЛА с
обозначением необходимых для определения
нормальной аэродинамической силы
участков и расположение оснований,
необходимых для расчета и приведенных
для наглядности.

Рисунок
1.8 – Схема ЛА с обозначением расположения
участков и оснований конусов

Н,

где


– площади основания конуса.

Н,

где

–
площади основания конуса.

Н,

где

– удлинение цилиндрического участка
1-5,

–
площадь
основания цилиндрического участка 1-5.

Н,

где

– удлинение цилиндрического участка
7-12,

–
площадь
основания цилиндрического участка
7-12.

Полная
нормальная аэродинамическая сила:

Нормальная
перегрузка

в этом случае:

Угловое
ускорение

можно найти из уравнения вращательного
движения летательного аппарата вокруг
оси z

,

где

– момент всех внешних сил;

кгм²
– массовый
момент инерции летательного аппарата
относительно оси z.

Момент
всех внешних сил определяется по формуле:

,

где
м
– расстояние от носка до центра масс
летательного аппарата для расчётного
момента времени;

=
12,4 м
– координата точки приложения тяги
двигательной установки;

–
координата
точки приложения равнодействующей
нормальной аэродинамической силы.

Координата
точки приложения равнодействующей
нормальной аэродинамической силы
определяется по формуле:

где
–
координата центра давления i-го
конического
участка от носка аппарата;

где
–
координата центра давления i-го
цилиндрического
участка от носка аппарата.

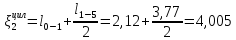м;

м;

м;

м,

где

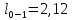
м
– длина участка 0-1,

=
3,77 м
– длина участка 1-5,

=
1,8 м
– длина
участка 5-7,

=
5,29 м
– длина
участка 7-12,

м,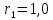
м
– радиусы
оснований конусов.

Получаем
координату приложения
:

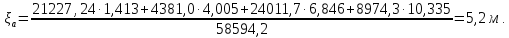
_{Момент
внешних сил}

Угловое
ускорение:

Значения
эпюр M
и Q
по длине летательного аппарата находим
с помощью программы QM.exe.
Распечатка результатов работы программы
приведена на странице 18. Эпюры представлены
на рисунке 1.9 и рисунке 1.10.

Рисунок
1.9 — Эпюра перерезывающей силы Q

Рисунок
1.10 — Эпюра изгибающего момента М

Suhov

KУPCOBOЙ
ПPOEKT ПO PACЧETУ

Л.A.
HA ПPOЧHOCTЬ

PACЧET
HAГPУЗOK

ЗHAЧEHИE
CEKУHДЫ ПOЛETA 56.00000

CKOPOCTЬ
ПOЛETA, M/C 600.0000

CKOPOCTЬ
BETPA, M/C 60.00000

УГOЛ
OTKЛOHEHИЯ TЯГИ, ГPAД 4.800000

ПЛOTHOCTЬ
BOЗДУXA, KГ/M**3 .4000000

ЧИCЛO
MAXA 2.004000

ЗHAЧEHИE
ПEPEPEЗЫB. CИЛЫ, KH .0000000

ИЗГИБAЮЩИЙ
MOMEHT, KH*M .0000000

KOHTPOЛЬHOE
CEЧEHИE 0

HOMEP
BAPИAHTA 7

MACCA
ЛETATEЛЬHOГO AППAPATA, KГ 11483.260

KOOPДИHATA
ЦEHTPA MACC, M 8.770

MACCOBЫЙ
MOMEHT ИHEPЦИИ, KГ*M**2 9.8636E+04

ПOПEPEЧHAЯ
AЭPOДИHAMИЧECKAЯ CИЛA, KH 58.59

KOOPДИHATA
ЦEHTPA ДABЛEHИЯ, M 5.200

ПOПEPEЧHAЯ
ПEPEГPУЗKA .6852

УГЛOBOE
УCKOPEHИE, 1 / C**2 1.4366

**********************************************************************************************

*
* * *
*

*
* * ПEPEPEЗЫBAЮЩAЯ CИЛA Q, KH *
ИЗГИБAЮЩИЙ MOMEHT M, KH*M *

*
HOMEPA * ДЛИHA * *
*

*
CEЧ. * УЧ.,M * CЛEBA * B CEPEДИHE* CПPABA *
CЛEBA * B CEPEДИHE* CПPABA *

*
* * * * * *
* *

**********************************************************************************************

*
* * * * * *
* *

*
0, 1 * 2.120E+00 * 0.000E+00 * 5.045E+00 * 2.024E+01 * 0.000E+00
*-1.777E+00 *-1.428E+01 *

*
1, 2 * 1.650E+00 * 1.352E+01 * 1.409E+01 * 1.469E+01 *-1.428E+01
*-2.566E+01 *-3.753E+01 *

*
2, 3 * 5.300E-01 * 9.221E+00 * 9.420E+00 * 9.622E+00 *-3.753E+01
*-4.000E+01 *-4.252E+01 *

*
3, 4 * 5.300E-01 * 8.926E+00 * 9.131E+00 * 9.339E+00 *-4.252E+01
*-4.491E+01 *-4.736E+01 *

*
4, 5 * 1.060E+00 * 9.128E+00 *-3.135E+00 *-1.458E+01 *-4.736E+01
*-4.891E+01 *-4.418E+01 *

*
5, 6 * 1.120E+00 *-1.945E+01 *-1.313E+01 *-5.950E+00 *-4.545E+01
*-3.628E+01 *-3.090E+01 *

*
6, 7 * 6.800E-01 *-5.950E+00 *-1.169E+00 * 3.931E+00 *-3.090E+01
*-2.968E+01 *-3.014E+01 *

*
7, 8 * 2.163E-01 * 3.559E+00 * 3.682E+00 * 3.806E+00 *-3.014E+01
*-3.053E+01 *-3.094E+01 *

*
8, 9 * 1.370E-02 * 3.806E+00 * 3.670E+00 * 3.535E+00 *-3.094E+01
*-3.096E+01 *-3.099E+01 *

*
9,10 * 1.050E+00 * 1.290E-02 * 6.334E-01 * 1.281E+00 *-3.126E+01
*-3.143E+01 *-3.193E+01 *

*
10,11 * 1.102E+00 *-8.023E-02 * 7.383E-01 * 1.572E+00 *-3.144E+01
*-3.162E+01 *-3.225E+01 *

*
11,12 * 1.328E+00 * 1.572E+00 *-9.811E+00 *-1.847E+01 *-3.225E+01
*-2.937E+01 *-1.983E+01 *

*
12,13 * 1.580E+00 *-2.482E+00 *-1.272E+00 *-4.929E-06 *-1.993E+00
*-5.065E-01 * 5.721E-05 *

*
* * * * * *
* *

**********************************************************************************************