Рассмотрим
упрощеннуюсхему полета, а именно: полет
вертикально вверх без учета аэродинамических
сисл. Схема сил, действующих на ракету,
приведена на рис. 5.7.
Исходные данные
=100
[т];
=90
[т];
Т=100 с – время работы
двигателей;
=1,5
– начальная перегрузка.
Рис. 5.7. Схема сил,
действующих на ракету, при полете
вертикально вверх без учета аэродинамических
сил
Решение
В общем виде
значение перегрузки подсчитывается по
следующей зависимости:
.
(5.6)
Алгоритм
определения перегрузки
1. Находится сила
тяги двигателей ракеты:
[kH].
2. Определяется
расход топлива в единицу времени:
[т/с].
3. Определяется
текущее значение массы ракеты (вполете):
.
4. Выводится формула
для расчета перегрузки во время полета
ракеты (см. формулу (5.6)):

5. Строится график
продольной перегрузки ракеты с помощью
системы Mathcad (см. рис. 5.8).
6. Определяется
максимальное значение перегрузки (в
конце активного участка полета ракеты):

Рис. 5.8. Зависимость
продольной перегрузки ракеты
от
времени работы двигателей
5.2.9. Типовые задачи по определению перегрузок
П
1. Определить продольную перегрузку
ракеты, стоящую на старте. Схема сил
приведена на рис. 5.9. На этой схеме
– реакция опоры;
– сила тяжести.
Расчетные формул
следующие:
;
.
Рис. 5.9. Схема для
определения продольной
перегрузки
к примеру 1
П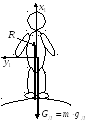
2. Определить перегрузку космонавта,
стоящего на поверхности Луны, если
приближенно принять, что ускорение
тяготения на поверхности Луны в 6 раз
меньше Земного.
Схема сил приведена
на рис. 510.
На этой схеме
– реакция опоры;
– сила тяжести космонавта на Луне;
– ускорение свободного падения на Луне.
Рис. 5.10. Схема для
определения продольной
перегрузки к
примеру 2
Расчетн производим
в следующей последовательности:
;
,
где
– ускорение свободного падения тела на
Земле.
.
,
где
– Сила веса космонавта на Земле;
.
Пример 3. Чему
равна перегрузка
самолета при прямолинейном наборе
высоты под углом
?
С
сил, действующих на самолет представлена
на рис. 5.11. Здесь учтены только силы,
имеющие проекции на ось
.
Для прямолинейного
полета (безискривления траектории)
необходимо, чтобы проекция аэродинамической
силы на ось
(подъемная сила
)
равнялась проекции
силы тяжести
на туже ось, то
есть
.
Тогда перегрузка
определяется следующим образом:
Рис. 5.11.Схема сил
для определения поперечной перегрузки
самолета
Пример 4. Определите
полную перегрузку
самолета на установившемся вираже
(вираж без снижения самолета) с углом
крена
?
. Схема сил приведена на рис. 5.12.
Д
полета самолета по кругу без снижения
высоты необходимо, что бы проекция
подъемной силы на вертикальную ось
равнялась силе тяжести, то есь:
.
Подъемную силу
самолета
,
действующую по оси
,
найдем по следующей зависимости:
.
Теперьможно
определить искомую перегрузку
Рис. 5.12. Схема для
определения поперечной перегрузки
самолета при выполнении виража без
скольжения
Пример 5. Какие
силы действуют на космический аппарат
в орбитальном полете?
Схема сил, действующих
на КА при орбитальном полете, показана
на рис. 5.13.
Сила
выполняет роль центростремительной
силы и искривляет траекторию полета
КА.
С
и другое, упрощенное объяснение: почему
космический аппарат не падает на Землю.
Дело в том, что под действием силы
притяжения КА постоянно падает на Землю
и постоянно двжется по касательной к
орбите со скоростью
.
На рисунке показаны расстояния
и
,
пройденные космическим аппаратом за
время
по касательнойк орбите и к центру Земли
соответственно, где
;
.
В результате КА
оказывается на круговой орбите.
Рис. 5.13. Схема сил,
действующих на КА при орбитальном полете
Пример 6. Определить
перегрузку, действующую на космонавта,
находящегося в центрифуге.
С
силы, действующих на косонавта в
центрифуге показана нп рис.5.14.
Расчет производитя
в следующей последовательности:
,
где
– угловая скорость вращения ротора
центрифуги.
Рис. 5.14. Схема сил,
действующих на косонавта в центрифуге
Следует отметить,
что в данном случае рассчитывается
средняя перегрузка. На самом же деле на
отдельные части человеческого могут
дествовать различные перегрузки и в
различных направлениях. Многое зависит,
в частности от формы кресла. На рис.
5.15. приведена схема сил. действующих на
отдельные части человека при наклоне
стула, на котором сидит человек.
Рис. 5.15. Схема сил,
действующих на на отдельные части
человеческого тела
при определении
перегрузок
Задачи
1. Чему равна
перегрузка
самолета при вертикальном пикировании,
когда лобовое сопротивление равно тяге
двигателя?
2. Как изменится
перегрузка
самолета в момент сброса бомбы, вес
которой составляет 10% от веса самолета?
(Первоначальное направление полета
самолета горизонтальное).
3. Чему равна
перегрузка
самолета при прямолинейном наборе
высоты под углом 45?
4. Определите
перегрузку
самолета
при посадке, если в момент приземления
подъемная сила самолета равна 0,75G,
а вертикальная реакция Земли 3G
. Здесь G – вес
самолета.
5. Определите полную
перегрузку n и перегрузку
самолета
на установившемся вираже (вираж без
снижения самолета) с углом крена 60?
(см. рис. 7).
Рис. 7. Схема,
иллюстрирующая установившийся вираж
6. Определите
перегрузку самолета
,
если подъемная сила крыла RY1 = 80 т, сила
от горизонтального оперения
=
– 10 т и вес самолета 10 т.
7. Определите
внешнюю силу, действующую на подвешенную
внутри самолета бомбу весом 2 т при
правильном установившемся вираже, если
угол крена 60. (См.
рис.).
8. Определите
перегрузку
самолета при посадке с торможением,
если вертикальная реакция Земли равна
3G, коэффициент трения колес о землю 0,3,
а лобовое сопротивление самолета
составляет 0,2G.
9. Определите
горизонтальную реакцию Земли, если
боковая перегрузка при посадке самолета
со скольжением
.
Вес самолета G.
10. Каким образом
можно осуществить состояние невесомости
на самолете во время полета.
11. Чему равна
подъемная сила самолета, вес которого10
т, а перегрузка
=8?
Направление полета принять горизонтальным.
12. Чему равна
перегрузка
самолета при вертикальном пикировании,
когда тяга двигателя равна нулю, а
лобовое сопротивление самолета равно
его весу?
13. Чему равна
перегрузка
самолета
в горизонтально установившемся полете?
14. Чему равна
перегрузка
самолета
в горизонтальном установившемся полете?
15. Чему равна
перегрузка
головной части ракеты на стартовой
установке в вертикальном положении,
если двигатели не работают?
16. Чему равна
перегрузка
ракеты
в полете, если тяга двигателей
,
где G – вес ракеты в рассматриваемое
время, а аэродинамическая нагрузка
?
17. Как изменяется
в полете одноступенчатой ракеты?
18. Определить
максимальное значениеодноступенчатой
ракеты, если масса конструкции равна
,
масса топлива в момент заправки mт и
тяга двигателей равна (m0 + mт)g2 , где g –
ускорение Земного тяготения.
19. Определить
ракеты, если аэродинамическая сила
,
где G – вес ракеты в рассматриваемый
момент времени.
20. Определить
перегрузку космонавта, стоящего на
поверхности Луны, если приближенно
принять, что ускорение тяготения на
поверхности Луны в 6 раз меньше Земного.
21. Определить
перегрузку
самолета при выходе из пикирования,
если скорость полета в этой точке равна
V, а радиус кривизны траектории равен
r.
22. Определить
перегрузку
самолета
при полете по траектории, изображенной
на рис., если скорость равна V и радиус
кривизны r.
23. Какие
уравновешивающие силы действуют на
космический аппарат в орбитальном
полете?
24. Определить
внешнюю силу, действующую на подвешенную
внутри самолета бомбу при вираже со
скольжением, если угол крена 60,
а перегрузка
,
вес бомбы 2 т (см. рис.).
25. Каковы принципы
создания искусственного гравитационного
поля (или имитации силы тяжести) в
космосе?
26. Определите
перегрузку спускаемого аппарата
,
если сила сопротивления атмосферы равна
3G , где G – вес спускаемого аппарата (см.
рис.).
Контрольные
вопросы
1. Для каких целей
необходимо знать нагрузки, действующие
на ЛА?
2. Назовите основные
этапы эксплуатации летательных аппаратов.
3. На каких этапах
возникают, как правило, наибольшие
нагрузки?
4. Какие основные
сила действуют на ЛА в полете?
5. Составьте схему
сил, действующих на ЛА на активном
участке траектории.
6. Приведите схему
сил, действующих на спускаемый аппарат
при баллистическом спуске.
7. Расскажите о
классификации нагрузок (объемные,
поверхностные; статические, динамические;
распределенные, сосредоточенные) и
дайте их определение.
8. Дайте определение
коэффициента перегрузки (через отношение
ускорений и через действия сил).
9. Какие перегрузки,
сколько времени и в каких позах выдерживает
человек?
10. Какого порядка
перегрузки возникают при полете
пилотируемых и беспилотных ЛА?
11. Для каких типов
летательных аппаратов характерны
большие значения
,
а для каких
?
12. Приведите
расчетную схему для определения
перегрузок, действующих на самолет при
выполнении мертвой петли. Получите или
приведите расчетные зависимости.
9. Расскажите о
типовых фигурах высшего пилотажа и
перегрузках, возникающие при их
выполнении.
10. Приведите
расчетную схему и зависимости для
определения перегрузок, действующих
на РН при вертикальном полете.
11. Приведите схему
сил, действующих на на отдельные части
человеческого тела, если человек сидит
на стуле в наклонном положении.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
|
Макеты страниц
Как мы видели выше, характерной чертой пассивного полета под действием одних лишь гравитационных сил является состояние невесомости, господствующее на борту космического корабля. Предположим теперь, что пассивный полет внезапно прерван включением бортового ракетного двигателя. Состояние невесомости принтом исчезнет, так как появится внешняя поверхностная сила — сила тяги. Как было выявлено выше (§ 3 гл. 2), при пассивном полете в безвоздушном пространствегравитационные силы никак себя не проявляют в относительномперемещении предметов на борту космического корабля и не вызывают вних никаких напряжений. Теперь, после включения двигателя, гравитационные силы, естественно, остаются по-прежнему? неощутимыми и проявляется лишь сила тяги. Как она проявляется?
С точки зрения неподвижного наблюдателя, находящегося вне корабля, сила тяги заставляет корабль ускорить свое движение. Если в кабине корабля находится незакрепленный предмет (например, карандаш, который космонавт выпустил из пальцев), то этот предмет, не получая ускорения, начнет отставать от корабля (это увидел бы неподвижный наблюдатель, скажем, через прозрачную стенку кабины). Космонавт же, находящийся в кабине, воспримет это отставание как падение предметав сторону, противоположную направлению силы тяги (в сторону истечения газов из сопла). В этой же стороне космонавт ощутит опору (у кабины появится пол), в эту же сторону будет направлен отвес, указывающий кажущуюся вертикаль, свободная поверхность жидкости в сосуде окажется перпендикулярной к направлению отвеса. На борту корабля появятся все обычные проявления тяжести. Необычно только название этой тяжести — перегрузка, носящее во многих случаях совершенно условный характер.
В обычных, земных, условиях характеристикой силы тяжести является ускорение свободного падения тел 


На участке разгона ракеты-носителя (рис. 21) перегрузка вполне определяется равнодействующей негравитационных сил — силы тяги и силы аэродинамического сопротивления (рис. 21, б). В общем случае последняя сила состоит из силы лобового сопротивления, направленной противоположно скорости, и перпендикулярной к ней подъемной силы (рис. 21, а). Указанная равнодействующая создает негравитационное ускорение, определяющее перегрузку (рис. 21, в).

Рис. 21. Перегрузка на участке разгона ракеты.
Коэффициент перегрузки на участке разгона составляет несколько единиц. На рис. 21, б показана равнодействующая всех сил, действующих на ракету-носитель; эта сила определяет полное ускорение (рис. 21, в), характеризующее движение ракеты, но не проявляющееся в полной мере на явлениях в кабине корабля. Все явления в кабине при разгоне определяются величиной именно не “гравитационного ускорения. Поэтому негравитационное ускорение иногда называют ощутимым или кажущимся.
Это ускорение может быть измерено специальными приборами — акселерометрами. Простейший акселерометр представляет собой, по существу, динамометр, градуированный в единицах ускорения.
В заключение заметим, что «обычное» ощущение силы тяжести, весомости (в земных условиях) имеет ту же природу, что и перегрузка в космическом полете. Как это ни может показаться парадоксальным, весомость любого предмета в обычных условиях также определяется полностью величиной внешней поверхностной силы — силы реакции опоры (предмет сжат) или подвеса (предмет растянут). Тот факт, что сила реакции «пассивна», а сила тяги ракеты «активна», совершенно несуществен. Натяжение троса, на котором неподвижно висит кабина лифта, из пассивного может стать активным, когда лифт начнет подниматься, но во всех случаях ускорение падения предметов, наблюдаемое внутри кабины, полностью определяется внешней поверхностной силой — натяжением троса — и равно по величине сообщаемому этим натяжением ускорению (т. е. равно этой силе, деленной на массу лифта). В частности, это верно и в случае, когда лифт неподвижен (коэффициент перегрузки равен единице). Нет разницы между действиями натяжения троса и силы тяги ракетного двигателя, а сила притяжения лифта к Земле никакой роли в наших рассуждениях не играла.
Оглавление
- ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
- ВВЕДЕНИЕ
- § 1. Космодинамика — теория космических полетов
- § 2. Основные законы механики
- § 3. О единицах силы и массы
- § 4. О системах отсчета
- Часть первая. ОСНОВЫ РАКЕТО- И КОСМОДИНАМИКИ
- § 1. Законы ракетного движения
- § 2. Структура ракеты
- § 3. Составная ракета
- § 4. Термохимические ракетные двигатели
- § 5. Ядерные тепловые двигатели
- § 6. Тепловые двигатели с внешним источником энергии
- § 7. Электрические ракетные двигатели (ЭРД)
- § 8. Парусные системы
- § 9. Фотонный (квантовый) ракетный двигатель
- § 10. Классификации двигательных систем
- Глава 2. СВОБОДНЫЙ ПОЛЕТ В ПОЛЯХ ТЯГОТЕНИЯ
- § 1. Силы, действующие на космический аппарат в полете
- § 2. Задача n тел и метод численного интегрирования
- § 3. Невесомость
- § 4. Центральное поле тяготения
- § 5. Траектории в центральном поле тяготения
- § 6. Неограниченная задача двух тел
- § 7. Сфера действия и приближенный метод расчета траекторий
- Глава 3. АКТИВНОЕ ДВИЖЕНИЕ КОСМИЧЕСКОГО АППАРАТА
- § 1. Выход на траекторию свободного полета
- § 2. Активное движение в космическом пространстве
- § 3. Перегрузка
- § 4. Управление движением космического аппарата
- § 5. Движение космического аппарата относительно центра масс и управление им
- Часть вторая. ОКОЛОЗЕМНЫЕ ПОЛЕТЫ
- Глава 4. ДВИЖЕНИЕ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ
- § 2. Возмущенное движение спутника
- § 3. Влияние несферичности Земли
- § 4. Эволюция орбиты в земной атмосфере
- § 5. Влияние притяжений Луны и Солнца
- § 6. Спутники в точках либрации
- § 7. Влияние давления солнечного света
- § 8. Движение спутника относительно земной поверхности
- Глава 5. АКТИВНОЕ ДВИЖЕНИЕ В ОКОЛОЗЕМНОМ ПРОСТРАНСТВЕ
- § 1. Выведение спутника на орбиту с низким перигеем
- § 2. Многоимпульсное выведение
- § 3. Изменение плоскости орбиты
- § 4. Спуск с орбиты
- § 5. Относительное движение в окрестности спутника
- § 6. Встреча на орбите
- § 7. Конечное сближение и стыковка
- § 8. Разгон с малой тягой до параболической скорости
- § 9. Изменения орбит и их коррекция с помощью малых тяг
- § 10. Разгон с помощью солнечного паруса
- § 11. Ориентация и стабилизация спутников
- Глава 6. ИСПОЛЬЗОВАНИЕ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ
- § 1. Космические объекты в околоземном пространстве
- § 2. Исследовательские спутники
- § 3. Метеорологические спутники и спутники для исследования природных ресурсов Земли
- § 4. Спутники связи
- § 5. Навигационные и геодезические спутники
- § 6. Орбитальные энергостанции
- Глава 7. ПИЛОТИРУЕМЫЕ ОРБИТАЛЬНЫЕ ОБЪЕКТЫ
- § 1. Корабли-спутники и орбитальные станции
- § 2. Роль орбитальных станций
- § 3. Искусственная тяжесть
- § 4. Многоразовый транспортный космический корабль (МТКК)
- § 5. Межорбитальный транспортный аппарат
- § 6. Эксплуатация многоразовых транспортных аппаратов
- Часть третья. ПОЛЕТЫ К ЛУНЕ
- § 1. Плоская задача достижения Луны
- § 2. Пространственная задача достижения Луны
- § 3. Учет эллиптичности лунной орбиты, притяжения Луны и ее размеров
- § 4. Влияние гравитационных возмущений от сжатия Земли и от Солнца
- § 5. Точность наведения
- § 6. Коррекция траектории
- § 7. Посадка на Луну
- § 8. Научное значение автоматических лунных станций
- Глава 9. ПРОЛЕТНЫЕ ОПЕРАЦИИ
- § 1. Пролетная траектория
- § 2. Сближение с возвращением к Земле
- § 3. Периодический облет Луны
- § 4. Разгонные траектории
- § 5. Маневрирование на пролетных траекториях
- § 6. Научное значение пролетных операций
- Глава 10. Искусственный Спутник луны
- § 1. О возможности захвата Луной космического аппарата
- § 2. Запуск искусственного спутника Луны
- § 3. Орбиты спутников Луны и их эволюция
- § 4. Движение спутника относительно лунной поверхности
- § 5. Маневрирование спутников Луны
- § 6. Научное значение спутников Луны
- Глава 11. ВОЗВРАЩЕНИЕ НА ЗЕМЛЮ
- § 1. Траектории возвращения
- § 2. Вход в земную атмосферу и спуск
- § 3. Возвращение на Землю космических аппаратов, облетевших Луну
- § 4. Возвращение на Землю станций, совершивших посадки на Луне
- Глава 12. ЭКСПЕДИЦИЯ НА ЛУНУ
- § 1. Особенности траекторий полета человека
- § 2. Прямой полет Земля — Луна — Земля (первый вариант лунной экспедиции)
- § 3. Встреча в космосе и монтаж корабля (второй вариант лунной экспедиции)
- § 4. Разъединение и сближение на окололунной орбите (третий вариант лунной экспедиции)
- § 5. Экспедиции по программе «Аполлон»
- § 6. Лунная транспортная космическая система
- § 7. Лунные грузовые корабли с малой тягой
- § 8. Окололунная орбитальная станция
- § 9. Перспективы использования Луны
- Часть четвертая. МЕЖПЛАНЕТНЫЕ ПОЛЕТЫ
- § 1. Главные особенности межпланетного полета
- § 2. Движение внутри сферы действия Земли
- § 3. Гелиоцентрическое движение вне сферы действия Земли
- § 4. Гомановские и параболические перелеты
- § 5. Движение внутри сферы действия планеты-цели
- § 6. Межпланетный пертурбационный маневр
- § 7. Искусственные спутники планет
- § 8. Возмущения межпланетных траекторий
- § 9. Коррекция межпланетных траекторий
- Глава 14. МЕЖПЛАНЕТНЫЕ ПОЛЕТЫ С МАЛОЙ ТЯГОЙ
- § 1. Траектории достижения планет
- § 2. Перелеты на орбиты искусственных спутников планет
- § 3. Солнечный парус
- § 4. Разработки космических аппаратов с двигателями малой тяги
- Глава 15. ЗОНДИРОВАНИЕ МЕЖПЛАНЕТНОГО ПРОСТРАНСТВА
- § 1. Одноимпульсные орбиты искусственных планет
- § 2. Полеты вне плоскости эклиптики
- § 3. Поворот плоскости орбиты с помощью солнечной ЭРДУ
- § 4. Двухимпульсные орбиты искусственных планет
- § 5. Переход через бесконечность
- § 6. Выведение искусственной планеты в точку либрации
- § 7. Научное значение искусственных планет
- Глава 16. ПОЛЕТЫ К МАРСУ
- § 1. Траектории в случае упрощенной модели планетных орбит
- § 2. Влияние эксцентриситета и наклона орбиты Марса
- § 3. Географические условия старта к Марсу
- § 4. Посадка на Марс
- § 5. Искусственные спутники Марса
- § 6. Полеты на спутники Марса — Фобос и Деймос
- § 7. Облет Марса с возвращением к Земле
- § 8. Автоматические станции исследуют Марс
- § 9. Результаты исследований Марса
- Глава 17. ПОЛЕТЫ К ВЕНЕРЕ
- § 1. Достижение Венеры
- § 2. Посадка и искусственный спутник Венеры
- § 3. Облет Венеры
- § 4. Автоматические станции исследуют Венеру
- § 5. Результаты исследований Венеры
- Глава 18. ПОЛЕТЫ К МЕРКУРИЮ
- § 1. Достижение Меркурия
- § 2. Посадка и искусственный спутник Меркурия
- § 3. Полет к Меркурию при попутном облете Венеры
- § 4. Полет с солнечно-электрическим двигателем
- Глава 19. ПОЛЕТЫ К ЮПИТЕРИАНСКИМ ПЛАНЕТАМ
- § 1. Планеты, совсем не похожие на нашу
- § 2. Прямые перелеты
- § 3. Полеты к Юпитеру и Сатурну через планеты земной группы
- § 4. Пертурбационные маневры в сферах действия планет группы Юпитера
- § 5. Через Юпитер — к Солнцу и подальше от плоскости эклиптики
- § 6. Искусственный спутник Юпитера
- § 7. Искусственные спутники других планет группы Юпитера
- § 8. Посадки на естественные спутники
- § 9. Зондирование атмосфер юпитерианских планет. Посадка на Плутон
- § 10. Полеты с малой тягой
- § 11. Исследования Юпитера и Сатурна
- § 12. Результаты исследований в системах Юпитера и Сатурна
- Глава 20. ПОЛЕТЫ К АСТЕРОИДАМ
- § 1. Пролет астероида
- § 2. Встреча с астероидом
- § 3. Выход на орбиту вокруг астероида
- § 4. Посадка на астероид и возвращение на Землю
- Глава 21. ПОЛЕТЫ К КОМЕТАМ
- § 1. Импульсные полеты
- § 2. Полеты с малой тягой
- § 3. Операции вблизи ядра кометы
- Глава 22. МЕЖПЛАНЕТНЫЕ ЭКСПЕДИЦИИ
- § 2. Особенности межпланетных экспедиций
- § 3. Спуск на Землю при возвращении из экспедиции
- § 4. Безостановочные пилотируемые облеты планет
- § 5. Экспедиции с остановками при прямых симметричных перелетах
- § 6. Экспедиции с траекториями возвращения, несимметричными траекториям прибытия
- § 7. Операции на околопланетных орбитах, пролетных траекториях и поверхностях
- § 8. Экспедиции на астероиды
- § 9. Использование кораблей с малой тягой
- § 10. Немного о будущем
- Часть пятая. ПОЛЕТЫ ЗА ПРЕДЕЛЫ СОЛНЕЧНОЙ СИСТЕМЫ
- Глава 23. ПРЕДДВЕРИЕ ПОЛЕТА К ЗВЕЗДАМ
- § 2. Полеты с большой тягой
- § 3. Полеты с малой тягой
- Глава 24. МЕЖЗВЕЗДНЫЕ ПОЛЕТЫ
- § 1. Астронавтика — составная часть космонавтики
- § 2. Фотонная ракета — средство осуществления межзвездных полетов
- § 3. Обобщенная формула Циолковского
- § 4. Продолжительности полетов
- § 5. О «собственных» скоростях звездолета
- § 6. Мечта или реальность?
- ПОСЛЕСЛОВИЕ
- Дополнение при корректуре
- КОСМИЧЕСКИЙ ЛИФТ
- Приложение I. ПЕРЕЧЕНЬ ТАБЛИЦ В ТЕКСТЕ КНИГИ
- Приложение II. К ВЫЧИСЛЕНИЮ НАЧАЛЬНЫХ МАСС РАКЕТНЫХ СИСТЕМ
Такие предположения позволяют рассматривать полёт ракеты как
движение материальной точки, подчинённое некоторым идеальным связям. Эти связи
определяются методом наведения. Методом наведения называется заданный закон
сближения ракеты с целью, который в зависимости от координат и параметров
движения цели определяет требуемое движение ракеты, обеспечивающее попадание
ракеты в цель. Траектория ракеты, определяемая методом наведения, называется
кинематической или идеальной траекторией, поэтому метод наведения можно
определить как способ задания кинематической траектории наведения ракеты на
цель, движение которой (цели) задано.
Классификация
методов наведения. Основные требования, предъявляемые к методам наведения
Методы наведения делятся на две группы (Ф.К.
Неупокоев «Стрельба зенитными ракетами» 1970 год):
1. Двухточечного типа, идеальная траектория при которых
определяется положением двух точек: ракеты и цели.
2. Трёхточечного типа, идеальная траектория при которых
определяется положением трёх точек: ракеты, цели и пульта управления.
Двухточечные методы реализуются при
самонаведении, а трёхточечные – при телеуправлении.
Из методов наведения первой группы можно
назвать: метод погони, метод прямого наведения, метод параллельного сближения,
метод пропорционального движения и т.д.
Наиболее известными методами второй группы
являются: метод накрытия цели (метод трёх точек) и группа спрямляющих методов
(методы «полного» и «половинного» спрямления).
Рассмотрим требования к методам наведения.
Основным требованием к методу
наведения является прохождение траектории ракеты, представленной как точка,
через точку цели. Этому требованию в принципе удовлетворяет значительное число
возможных методов наведения, однако, на практике нашло применение сравнительно
небольшое число методов наведения. Это объясняется теми требованиями, которые
предъявляются к методам наведения реальных ракет. Рассмотрим основные из них.
1. Метод наведения должен обеспечивать наименьшую кривизну
кинематической траектории на всех участках и особенно в районе точки встречи.
Управляемая ракета имеет ограниченную манёвренность, которая определяется
нормальными перегрузками, которые может создать ракета при максимальном отклонении
управляющих органов (рулей).
R – тяга, – угол атаки
Располагаемые перегрузки определяют в заданных
условиях полёта и при заданной скорости ракеты минимальный радиус кривизны траектории,
который способна осуществить ракета.
Характер кинематической траектории определяют
так называемые потребные перегрузки ракеты , т.е.
перегрузки, которыми должна обладать ракета для полёта по этой траектории.
Величина потребных перегрузок при заданных параметрах движения цели и скорости
ракеты является функцией метода наведения. Таким образом, метод наведения
определяет требования к маневренности ЛА.
– потребная перегрузка для движения
по кинематической траектории
– запас перегрузки для отработки
случайных (флуктуационных) отклонений от кинематической траектории
– запас перегрузки для
парирования силы веса
Скорость на пассивном участке с подъёмом на
высоту также уменьшается, т.е. в результате располагаемая перегрузка убывает.
Если ЛА представляет зенитную ракету и если метод наведения приводит к
возрастанию кривизны кинематической траектории ракеты по мере её приближения к
цели, то для обеспечения заданных боевых возможностей зенитного ракетного
комплекса потребуется создать более маневренную ракету. Всякое увеличение
маневренности ракеты () приводит к увеличению веса,
габаритов и усложнению конструкции. Кроме того, кривизна кинематической
траектории в районе встречи с целью влияет на величину ошибок наведения ракеты
на цель. Следовательно, уменьшение кривизны кинематической траектории по мере
приближения ракеты к цели – одно из существенных требований к методу наведения.
Спрямление кинематической траектории также приводит к уменьшению пути и
полётного времени ракеты до цели, что позволяет повысить пропускную способность
комплекса, улучшить характеристики ракеты.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Слайд 1Тема № 2. «Зенитная управляемая ракета 9М39.»
Занятие
№ 3. «Силы и моменты, действующие на
ракету в полёте».

Слайд 2Вопросы занятия:
1-ый вопрос: Аэродинамическая компоновка ЗУР.
2
– ой вопрос: Аэродинамические моменты, действующие на
ракету в полете.
3 – ий вопрос: Перегрузки, создаваемые на ракете.
4-ый вопрос: Силы, действующие на ракету в полёте.

Слайд 31-ый вопрос: Аэродинамическая компоновка ЗУР.
Под аэродинамической компоновкой ЗУР понимается взаимное размещение
основных частей ракеты.
Аэродинамическая схема ЗУР в общем случае включает в себя корпус, крылья, органы управления и стабилизации.
Аэродинамически симметричной называется ракета, при вращении которой вокруг продольной оси, при заданной ориентации её относительно набегающего воздушного потока, аэродинамические силы и моменты не меняются как по величине, так и по направлению.
В зависимости от взаимного расположения рулей и крыльев на корпусе ракеты, аэродинамическая компоновка её может быть выполнена:
– по нормальной схеме;
– по схеме «безхвостка»;
– по схеме «утка»;
– по схеме с поворотным крылом.

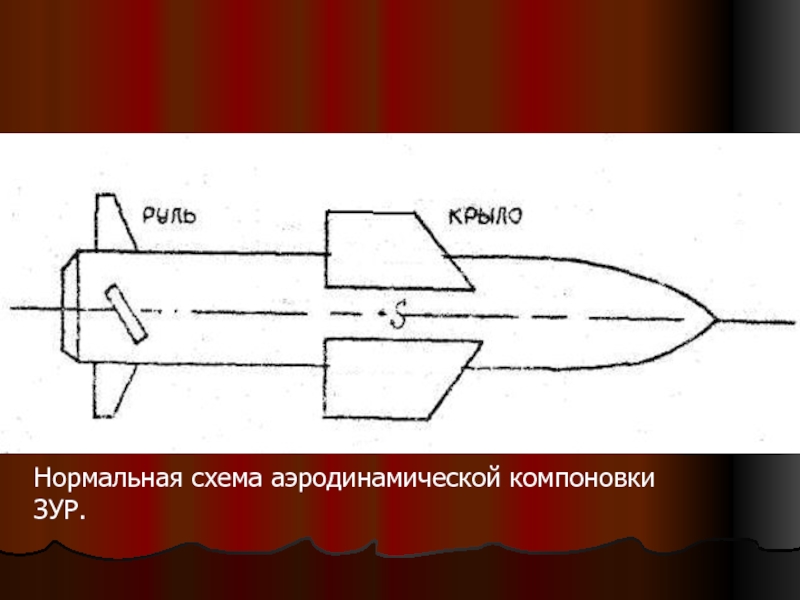
Слайд 4Нормальная схема аэродинамической компоновки ЗУР.
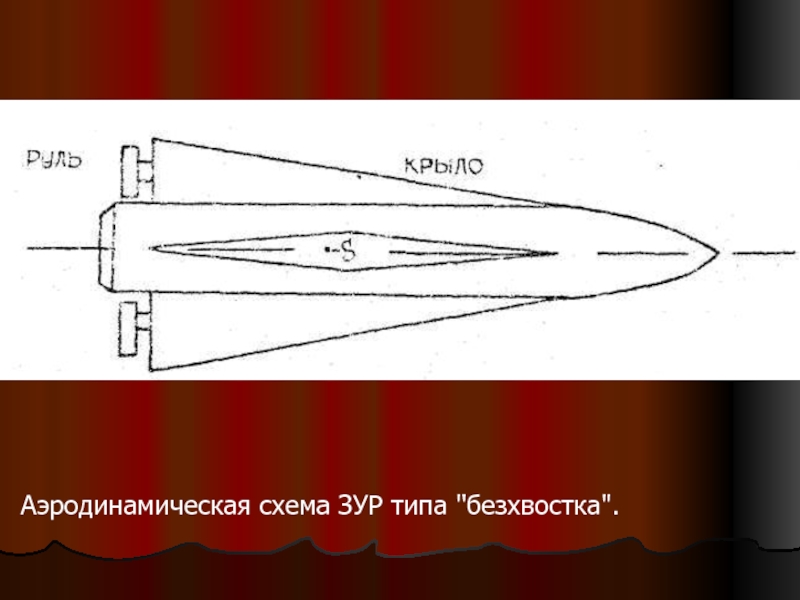
Слайд 5Аэродинамическая схема ЗУР типа “безхвостка”.
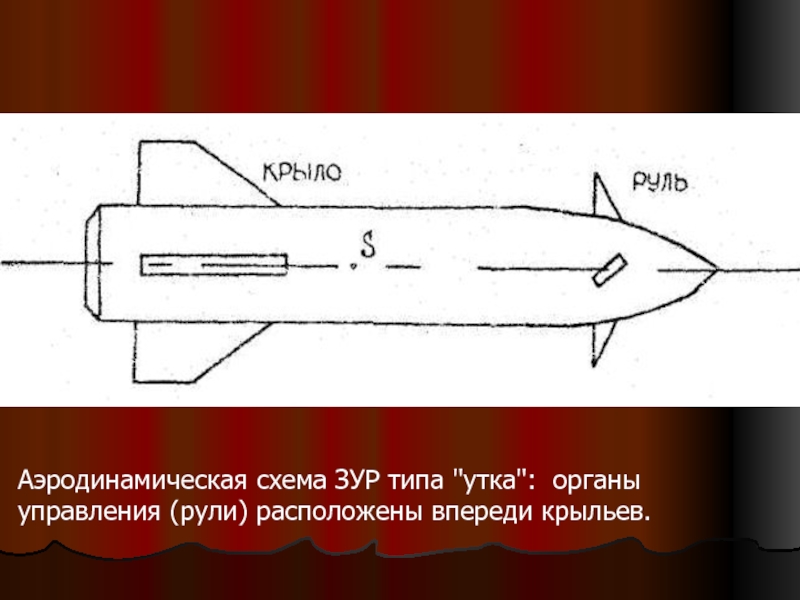
Слайд 6Аэродинамическая схема ЗУР типа “утка”: органы управления
(рули) расположены впереди крыльев.
Слайд 7 Аэродинамическая схема “поворотное крыло”: увеличенная
площадь крыльев и перемещение их ближе к
центру масс ракеты.
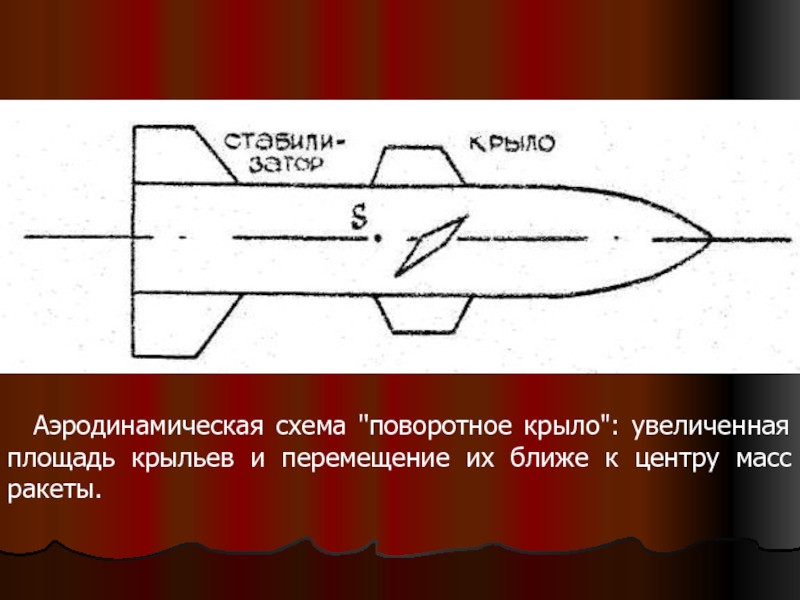
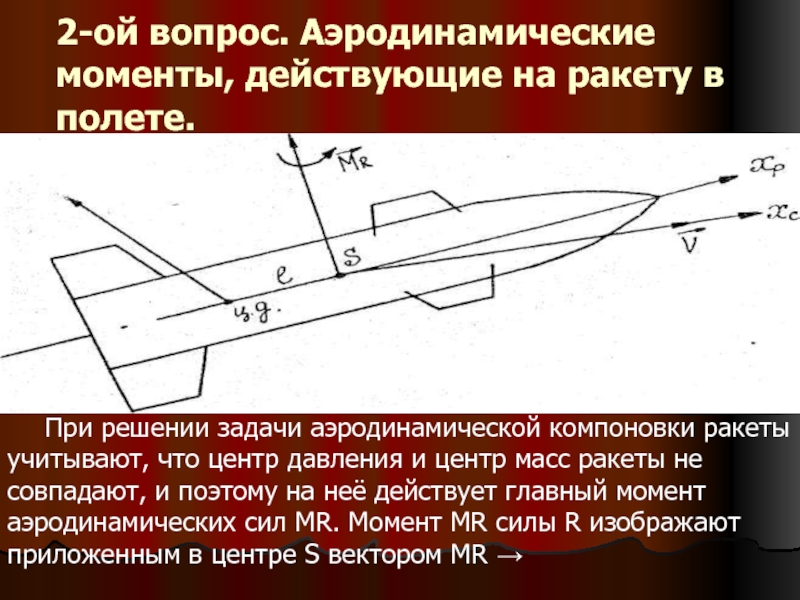
Слайд 82-ой вопрос. Аэродинамические моменты, действующие на ракету
в полете.
При решении задачи
аэродинамической компоновки ракеты учитывают, что центр давления и центр масс ракеты не совпадают, и поэтому на неё действует главный момент аэродинамических сил МR. Момент МR силы R изображают приложенным в центре S вектором МR →
Слайд 9 mR – безразмерный аэродинамический коэффициент,
зависящий от формы ракеты, её положения на
траектории, скорости и; других условий полета).
ba – средняя аэродинамическая хорда крыла.
q – величина скоростного напора.
Главный момент аэродинамических сил поворачивает ракету вокруг её центра масс.
При изучении вращения ракеты вокруг центра масс главный момент аэродинамических сил принято раскладывать на три составляющие по осям связанной системы координат SXpYpZp (см.рис)

Слайд 10где Мхр – момент крена
Мyр – момент рыскания
Мzр – момент тангажа .
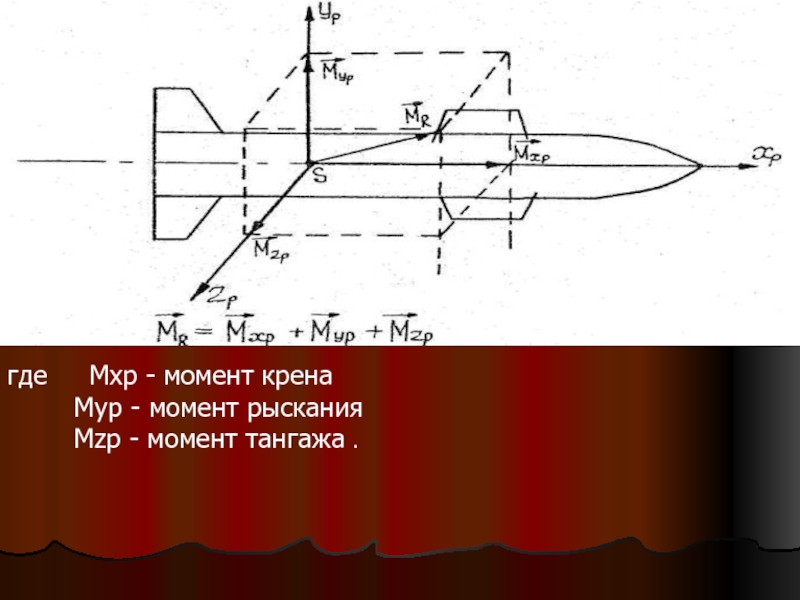
Слайд 11 Управляющие, стабилизирующие, и тушащие
моменты крена, рыскания и тангажа образуют систему
аэродинамических моментов.
Стабилизирующий момент тангажа Мzpcт возникает при отклонении продольной оси ракеты в вертикальной плоскости от направления вектора скорости V , т.е. при возникновении угла атаки α (см. рис.) Он создается составляющей подъемной силы Уα α.

Слайд 12 Ракеты, которые под действием
стабилизирующего момента возвращаются в первоначальное положение, называются
статически устойчивыми.
Величина стабилизирующего момента тангажа пропорциональна углу атаки α.

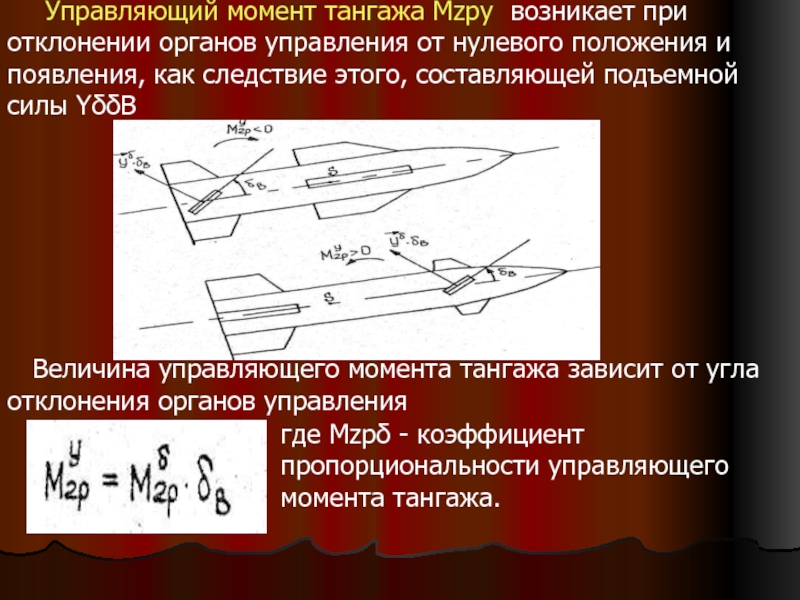
Слайд 13 Управляющий момент тангажа Mzpу
возникает при отклонении органов управления от нулевого
положения и появления, как следствие этого, составляющей подъемной силы YδδB
Величина управляющего момента тангажа зависит от угла отклонения органов управления
где Mzpδ – коэффициент пропорциональности управляющего момента тангажа.
Слайд 14 Под воздействием управляющего момента
тангажа ракета поворачивается вокруг поперечной оси SZp
и изменяет свое положение относительно набегающего потока. Если бы при этом не возникал стабилизирующий момент Мzpст,
который действует в противоположном направлении, то ракета непрерывно вращалась бы вокруг оси SZp. При условии равенства стабилизирующего момента управляющему моменту (Мzpст = Мzpу), вращение ракеты прекратится и установится угол атаки, который будет зависеть от угла поворота органов управления.

Слайд 15 Тушащий (демпфирующий) момент тангажа
МzрT обусловлен возникновением дополнительных аэродинамических сил при
вращении летящей ракеты вокруг своей поперечной оси SZp.
При вращении ракеты дополнительные аэродинамические силы в её передней части будут направлены вниз, а в хвостовой части вверх. Поэтому момент, обусловленный угловой скоростью вращения ракеты вокруг оси SZp, будет иметь направление противоположное направлению угловой скорости ωzр, Этот момент препятствует вращению ракеты и поэтому называется тушащим (или демпфирующим) моментом тангажа, знаки тушащего момента и угловой скорости противоположны.

Слайд 16Величина тушащего момента пропорциональна угловой скорости ωzр
=V.
– аэродинамический коэффициент тушащего момента тангажа.
ωzp – угловая скорость вращения ракеты относительно поперечной оси SZp
Величины аэродинамических моментов тангажа зависят от скоростного напора, а следовательно, с увеличением высоты они уменьшаются. То же относится и к аэродинамическим моментам крена и рыскания.

Слайд 173-ий вопрос: Перегрузки, создаваемые на ракете.
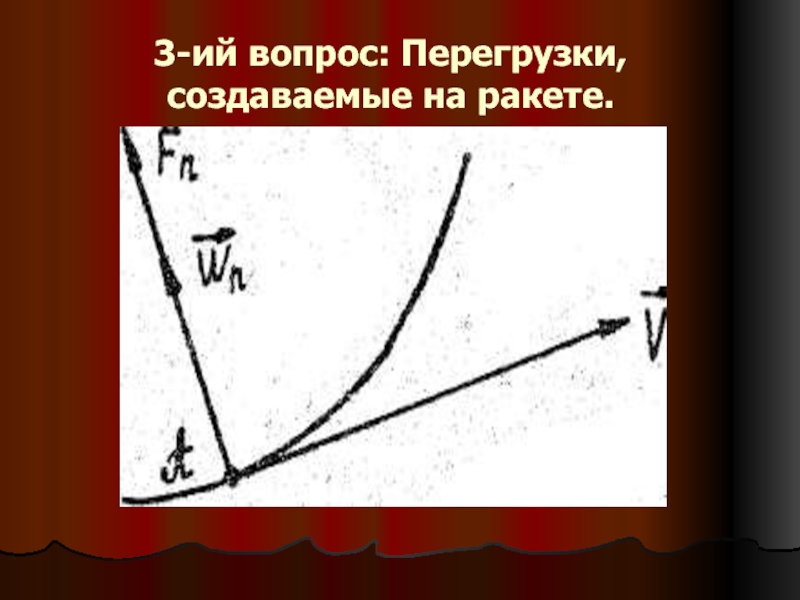
Слайд 18 Кинематическая траектория ракеты представляет
собой некоторую кривую линию, каждую точку которой
можно характеризовать некоторым радиусом кривизны Rк. Этому радиусу кривизны при данной скорости ракеты соответствует определенное значение потребных нормальных сил, способных соответствующим образом изменить кривизну траектории полета ЗУР.
Согласно третьему закону Ньютона
, где
– масса ракеты,
Fn – сумма проекций всех сил на ось Yc
Wn- нормальное ускорение ракеты.
Силы составляющие Fn можно измерять не в Ньютонах, а принять за единицу измерения вес ракеты G, т.е. силу, эффект действия которой – ускорение g – известен. В таком случае, разделив значение, силы Fn, на вес ракеты G, можно сказать, сколько единиц веса содержится в ней и какое ускорение в величинах g она создает.
Fn/G = m ⋅ Wn / m ⋅ g = Wn/g = n

Слайд 19 Число, полученное от деления
величины силы, действующей на ракету, на вес
ракеты, принято называть перегрузкой n.
Т.о. перегрузка есть число, показывающее во сколько раз сила, действующая на ракету в полете больше веса ракеты. Перегрузки, действующие вдоль осей SУс и SZс характеризуют быстроту изменения направления полета ракеты в вертикальной или горизонтальной (наклонной) плоскостях и являются нормальными по отношению к траектории полета ракеты перегрузками. Они зависят в основном от величины подъемной и боковой сил.
Отношение переменной силы, необходимой для движения ракеты по кинематической траектории к весу ракеты принято называть нормальной кинематической перегрузкой, nк.
Нормальные кинематические перегрузки, которые должна развивать ракета для движения по траектории метода наведения с заданной точностью называются потребными перегрузками, nтр.
Потребные перегрузки определят требования к маневренным свойствам ракеты, т.е. к её способности осуществлять криволинейные траектории.

Слайд 20nтр= nk +nb + nф
nk – кинематические перегрузки, определяемые реализуемым
методом наведения
nb – перегрузки веса
nф – флюктуационные, случайные перегрузки.
Реальная ракета обладает ограниченной маневренностью. Нормальные силы, изменяющие направление движения ракеты, являются аэродинамическими силами. При данной аэродинамической компановке ракеты, наибольшая нормальная аэродинамическая сила может быть получена при выдаче на рули ракеты максимальной команды управления.
Параметры перегрузки, возникающие на ракете при максимальной команде управления, называются располагаемыми перегрузками, np.
Для наведения ракеты на цель с заданной точностью, располагаемые перегрузки всегда должны быть больше требуемых (потребных):

Слайд 214-ый вопрос: Силы, действующие на ракету в
полёте.
При полёте ракеты в
атмосфере на неё действуют: сила тяжести G, сила тяги двигателя P, полная аэродинамическая сила R.

Слайд 22 Сила тяжести G представляет равнодействующую
силы земного притяжения F и центробежной силы
инерции Fе, возникающей в результате вращательного движения Земли вокруг своей оси с угловой скоростью Ω.
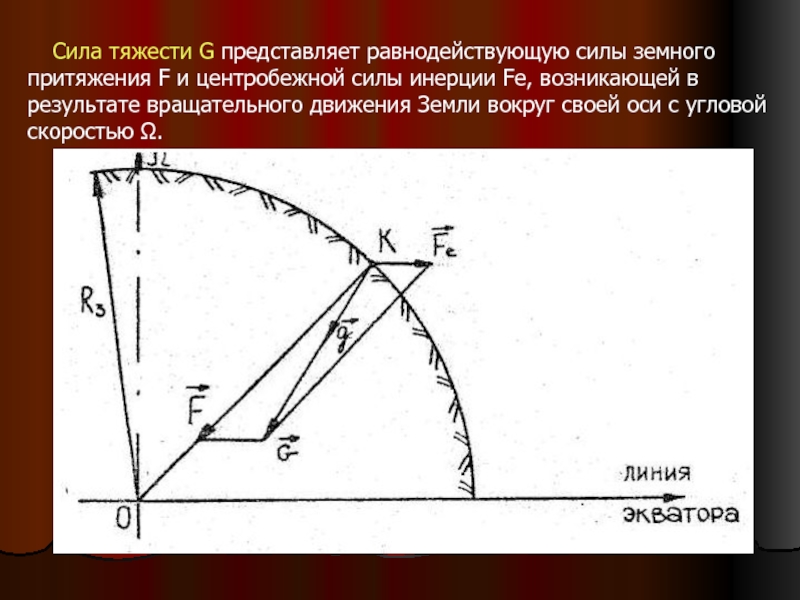
Слайд 23 При условии Fе
G = mg. Масса ракеты меняется во
времени. поэтому G(t) =m(t)g. При изучении движения ЗУР ускорение силы тяжести g – const. по величине и направлена вертикально вниз к центру Земли. В процессе полета ракеты сила тяжести изменяется только по величине, вследствие изменения массы ракеты из-за выгорания топлива, т.е. ракета является телом переменной массы.
Сила тяжести G рассчитывается по формуле
где
G0 – все ракеты перед стартом,
G1 – вес стартовых ускорителей,
Gc(t) – секундный весовой расход топлива,
t – текущее время.

Слайд 24Сила тяги двигателя P – представляет
собой равнодействующую сил реакций газовой струи, истекающей
из сопла двигателя, на внутренние поверхности камеры сгорания двигателя.
В зенитных ракетах наиболее широко используются два типа двигателей – воздушно-реактивные и ракетные.
В воздушно-реактивных двигателях для создания газовой струи в качестве окислителя используется атмосферный воздух, поступающий в камеру сгорания через воздухозаборник.
В ракетных двигателях сгорание топлива происходит без участия воздуха.
Величина силы тяги воздушно-реактивного двигателя может быть рассчитана по формуле:
где
Gт – секундный расход топлива, кг/сек,
Gb – секундный расход воздуха, кг/сек
Sа – площадь сечения сопла двигателя, м2,
Wa – относительная скорость истечения газов из сопла двигателя, м/сек,
V – скорость ракеты, м/сек,
Pa – давление газов на срезе сопла, (кг*см)/м2
Po – атмосферное давление на высоте полёта ракеты, кг*сек/м2.

Слайд 25Для ракетного двигателя сила тяги P определяется
по формуле :
Сила тяги ракетного
двигателя возрастает с увеличением относительной скорости истечения газов Wа и секундного весового расхода топлива Gt. Современные зенитные управляемые ракеты имеют либо стартовый и маршевый двигатели, либо двухрежимный двигатель. Разгон ракеты осуществляется большой силой тяги, во много раз превосходящей вес ракеты. После сброса ускорителей или окончания первого режима работы двухрежимного двигателя полет ракеты происходит под действием значительно меньшей силы тяги.
При изучении движения ЗУР принято, что сила тяги приложена к центру масс и направлена вдоль продольной оси ракеты, хотя в действительности имеют место отклонения линии действия силы Р от продольной оси ракеты.

Слайд 26 Полная аэродинамическая сила R –
это сила, возникающая в результате взаимодействия воздуха
с поверхностью движущейся ракеты. Создается из-за неодинакового разряжения и сжатия воздушного потока около различных частей ЗУР и вследствие вязкости воздуха, приводящей к трению его частиц о поверхность планера ракеты. Полную аэродинамическую силу R можно представить как равнодействующую элементарных сил давления ΔRgi→, направленных по нормали к поверхности ракеты, и сил трения ΔRtpi→, воздуха об эту поверхность и касательных к ней. Эта равнодействующая сила R→ приложена к ракете в точке, которую называют центром давления.

Слайд 27 Величина полной аэродинамической силы R
зависит от формы и размеров ракеты, скорости
её полета, свойств атмосферы и положения корпуса ракеты относительно набегающего потока воздуха. Перечисленные выше факторы в процессе полета ЗУР изменяются, что приводит к изменению величины и направления полной аэродинамической силы R→,а также точки её приложения.
Величина полной аэродинамической силы определяется известной из аэродинамики формулой
R=Cr× q× Skp
Cr- безразмерный аэродинамический коэффициент,
q- скоростной напор, равный q =ρV2/2 (кг/м2 )
ρ – массовая плотность воздуха кг*сек2/м4
Skp – характерная площадь крыла, м2.
С увеличением высоты полета уменьшается и величина полной аэродинамической силы.
Так как величина, направление и точка приведения полной аэродинамической сипы в процессе полёта изменяются, то с целью удобства изучения влияния этой силы на движение ракеты её переносят в центр масс и раскладывают на составляющие по осям скоростной системы координат.

Слайд 28Приведенную к центру масс полную аэродинамическую силу
разлагают на три составляющие – проекции на
оси скоростной системы координат.
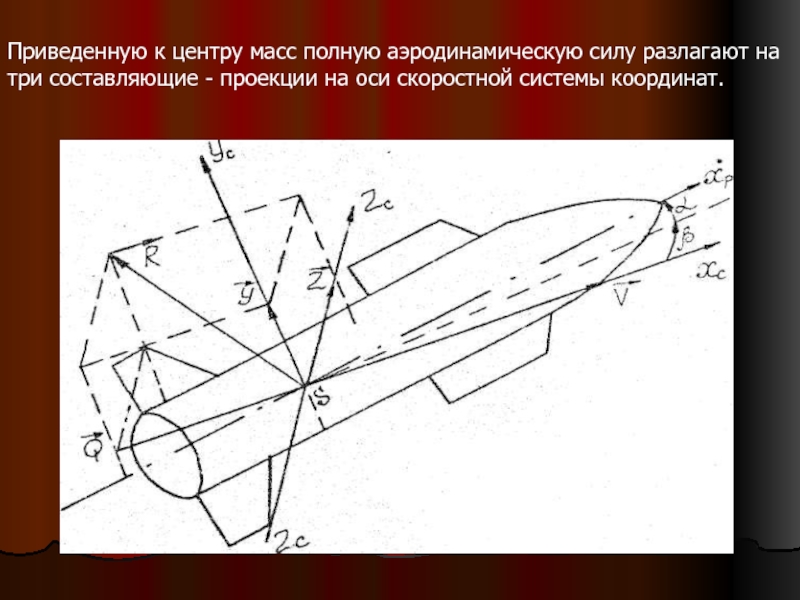
Слайд 29 Проекция полной аэродинамической силы на
ось SXc направлена в сторону, противоположную вектору
скорости ракеты Т, и называется лобовым сопротивлением Q→. Проекция на ось SУс называется подъемной силой У→, а проекция на ось SZc – боковой силой Z→.
R = Q + Y + Z
где: Cx, Сy, Cz – коэффициенты аэродинамических сил лобового сопротивления, подъемной силы и боковой силы.

Слайд 30 Лобовое сопротивление Q→ действует в
направлении уменьшения скорости ракеты. Для его преодоления
расходуется анергия двигательной установки. Чем меньше Q→, тем больше при прочих одинаковых условиях дальность полета ЗУР, которая в значительной степени определяет положение дальней границы зоны поражения. Поэтому всегда при создании ракет, путем выбора формы и других конструктивных характеристик ЗУР, стремятся уменьшить величину их лобового сопротивления.
Величина силы лобового сопротивления существенно зависит от коэффициента Сx,который в свою очередь зависит, в основном, от форм и размеров ракеты, числа М =V/a, углов атаки α и скольжения β и углов отклонения органов управления δ, и определяется экспериментально.
С увеличением высоты полета величина лобового сопротивления падает.

Слайд 31 Подъемная Y и
боковая Z силы лежат в плоскости, перпендикулярной
вектору скорости ракеты, и представляет собой нормальные силы. Они не изменяют величины вектора V→, а влияют только на его направление. Подъемная сила Y→ влияет на направление полета ракеты в вертикальной плоскости, а боковая сила Z→ – на направление полета в горизонтальной плоскости. Чем больше они по величине, тем больше возможности ракеты изменять направление полета. Значит, эти силы могут быть использованы для управления движением ракеты. Изменяя величины сил Y→ и Z→, представляется возможным наводить ракету на цель. Величина подъемной силы Y существенно зависит от коэффициента Су→.
Су=Суα α + Cyσ δв
где Суα , Cyσ – коэффициенты пропорциональности, характеризующие приращение коэффициента подъемной силы Су, при изменении соответственно угла атаки α и угла отклонения органа управления δв по высоте на единицу и зависящие от числа М.
Формулу для подъемной силы можно записать в виде:

Слайд 32 Вводя обозначение, где Уα α –
составляющая подъемной силы от α
Yδ δв – составляющая подъемной силы от δв.
При одинаковых условиях полёта ракеты типа “утка” и “поворотное крыло”, у которых органы управления расположены впереди центра масс, при одном и том же угле поворота органов управления δв могут создать большую величину подъемной силы Y, чем ракета нормальной аэродинамической схемы.

В данной статье репетитор по физике и математике рассказывает о том, как рассчитать перегрузку, которую испытывает тело в момент разгона или торможения. Данный материал очень плохо рассматривается в школе, поэтому школьники очень часто не знают, как осуществлять расчёт перегрузки, а ведь соответствующие задания встречаются на ЕГЭ и ОГЭ по физике. Так что дочитайте эту статью до конца или посмотрите прилагающийся видеоурок. Знания, которые вы получите, пригодятся вам на экзамене.
Начнём с определений. Перегрузкой называется отношение веса тела к величине силы тяжести, действующей на это тело у поверхности земли. Вес тела — это сила, которая действует со стороны тела на опору или подвес. Обратите внимание, вес — это именно сила! Поэтому измеряется вес в ньютонах, а не в килограммах, как некоторые считают.
Таком образом, перегрузка — это безразмерная величина (ньютоны делятся на ньютоны, в результате ничего не остаётся). Однако, иногда эту величину выражают в ускорениях свободного падения. Говорят, к примеру, что перегрузка равна , имея ввиду, что вес тела вдвое больше силы тяжести.
Примеры расчёта перегрузки
Покажем, как осуществлять расчёт перегрузки на конкретных примерах. Начнём с самых простых примеров и перейдём далее к более сложным.
Пример 1. Чему равна перегрузка человека, стоящего на земле? Чему равна перегрузка человека, свободно падающего с некоторой высоты?
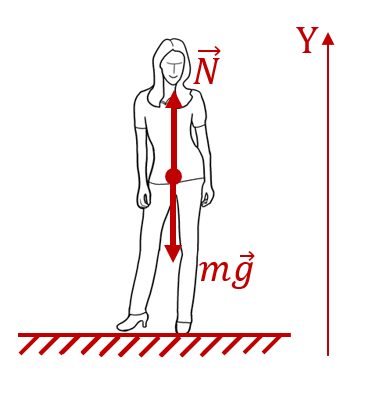
Очевидно, что человек, стоящий на земле, не испытывает никаких перегрузок. Поэтому хочется сказать, что его перегрузка равна нулю. Но не будем делать поспешных выводов. Нарисуем силы, действующие на этого человека:
К человеку приложены две силы: сила тяжести , притягивающая тело к земле, и противодействующая ей со стороны земной поверхности сила реакции
, направленная вверх. На самом деле, если быть точным, то эта сила приложена к подошвам ног человека. Но в данном конкретном случае, это не имеет значения, поэтому её можно отложить от любой точки тела. На рисунке она отложена от центра масс человека.
Вес человека приложен к опоре (к поверхности земли), в ответ в соответствии с 3-м законом Ньютона со стороны опоры на человека действует равная по величине и противоположно направленная сила
. Значит для нахождения веса тела, нам нужно найти величину силы реакции опоры.
Поскольку человек стоит на месте и не проваливается сквозь землю, то силы, которые на него действуют скомпенсированы. То есть , и, соответственно,
. То есть расчёт перегрузки в этом случае даёт следующий результат:
Запомните это! При отсутствии перегрузок перегрузка равна 1, а не 0. Как бы странно это не звучало.
Определим теперь, чему равна перегрузка человека, который находится в свободном падении.
Если человек пребывает в состоянии свободного падения, то на него действует только сила тяжести, которая ничем не уравновешивается. Силы реакции опоры нет, как нет и веса тела. Человек находится в так называемом состоянии невесомости. В этом случае перегрузка равна 0.
Пример 2. Определите перегрузку космонавтов, находящихся в ракете, движущейся на небольшой высоте вверх с ускорением 40 м/с2.
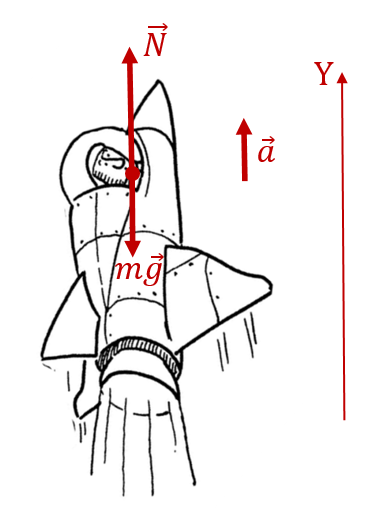
Космонавты находятся в горизонтальном положении в ракете во время её старта. Только так они могут выдержать перегрузки, которые они испытывают, не потеряв при этом сознания. Изобразим это на рисунке:
В этом состоянии на них действует две силы: сила реакции опоры и сила тяжести
. Как и в прошлом примере, модуль веса космонавтов равен величине силы реакции опоры:
. Отличие будет состоять в том, что сила реакции опоры уже не равна силе тяжести, как в прошлый раз, поскольку ракета движется вверх с ускорением
. С этим же ускорением синхронно с ракетой ускоряются и космонавты.
Тогда в соответствии со 2-м законом Ньютона в проекции на ось Y (см. рисунок), получаем следующее выражение: , откуда
. То есть искомая перегрузка равна:
Надо сказать, что это не самая большая перегрузка, которую приходится испытывать космонавтам во время старта ракеты. Перегрузка может доходить до 7. Длительное воздействие таких перегрузок на тело человека неминуемо приводит к летальному исходу.
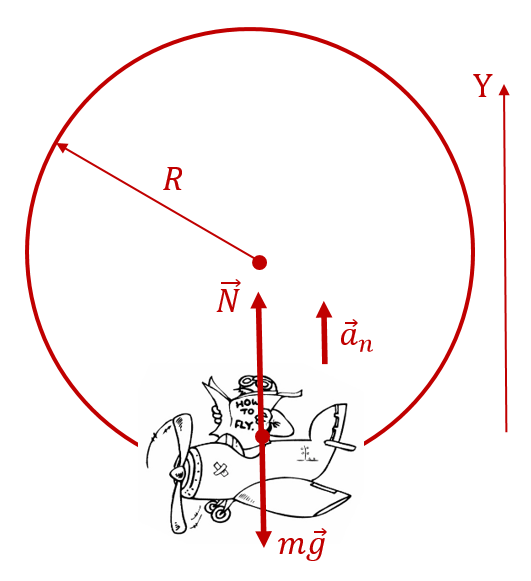
Пример 3. Рассчитайте перегрузку, которую испытывает пилот самолёта, выполняющего «мёртвую петлю» в нижней точке траектории. Скорость самолёта в этой точке составляет 360 км/ч. Радиус «мёртвой петли» составляет 200 м.
В нижней точке «мёртвой петли» на пилота будут действовать две силы: вниз — сила , вверх, к центру «мёртвой петли», — сила
(со стороны кресла, в котором сидит пилот):
Туда же будет направлено центростремительное ускорение пилота , где
км/ч
м/с — скорость самолёта,
— радиус «мёртвой петли». Тогда вновь в соответствии со 2-м законом Ньютона в проекции на ось, направленную вертикально вверх, получаем следующее уравнение:
Тогда вес равен . Итак, расчёт перегрузки даёт следующий результат:
Весьма существенная перегрузка. Спасает жизнь пилота только то, что действует она не очень длительно.
Ну и напоследок, рассчитаем перегрузку, которую испытывает водитель автомобиля при разгоне.
Пример 4. Рассчитайте перегрузку, которую испытывает водитель автомобиля, разгоняющегося с места до скорости 180 км/ч за 10 с.
Итак, конечная скорость автомобиля равна км/ч
м/с. Если автомобиль ускоряется до этой скорости из состояния покоя за
c, то его ускорение равно
м/с2.
На водителя в процессе ускорения действуют две составляющие силы реакции опоры: со стороны седушки кресла (вертикальная составляющая) и со стороны спинки кресла (горизонатльная составляющая)
:
Автомобиль движется горизонтально, следовательно, вертикальная составляющая силы реакции опоры уравновешена силой тяжести, то есть . В горизонтальном направлении водитель ускоряется вместе с автомобилем. Следовательно, по 2-закону Ньютона в проекции на ось, сонаправленную с ускорением, горизонтальная составляющая силы реакции опоры равна
.
Величину общей силы реакции опоры найдём по теореме Пифагора: . Она будет равна модулю веса. То есть искомая перегрузка будет равна:
Сегодня мы научились рассчитывать перегрузку. Запомните этот материал, он может пригодиться при решении заданий из ЕГЭ или ОГЭ по физике, а также на различных вступительных экзаменах и олимпиадах.
Материал подготовил репетитор по физике в Москве, Сергей Валерьевич
Смотрите также:
- Как рассчитать скорость спутника, вращающегося вокруг земли
- Как легко решить сложную задачу на относительность движения









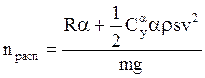
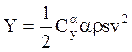

![Rendered by QuickLaTeX.com [ frac{mleft(g+frac{upsilon^2}{R}right)}{mg} = 1+frac{upsilon^2}{gR} = 1+frac{100^2}{10cdot 200} = 6. ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-bd0d66979d42352b265faec5a2a13b2e_l3.png)
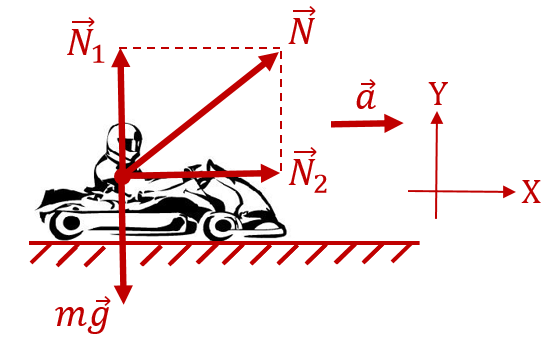
![Rendered by QuickLaTeX.com [ frac{P}{mg} = frac{N}{mg} = frac{msqrt{g^2+a^2}}{mg} = sqrt{1+frac{a^2}{g^2}} approx 1.12. ]](https://yourtutor.info/wp-content/ql-cache/quicklatex.com-57f6de2348b1dde4ac2ab7c3c900e407_l3.png)
