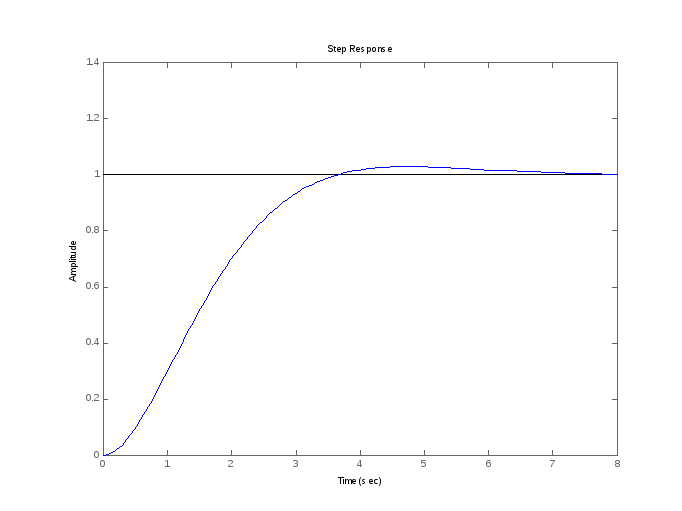
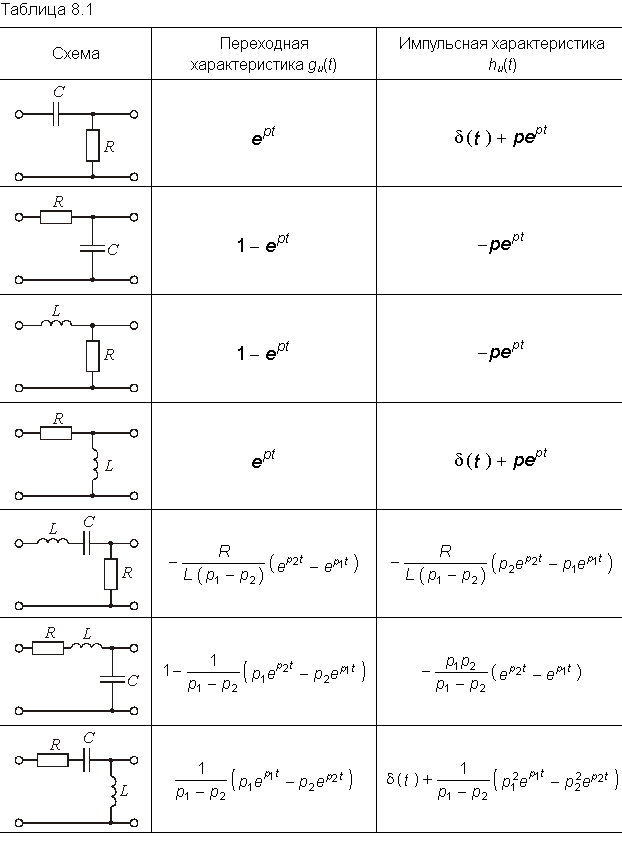
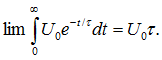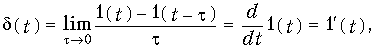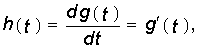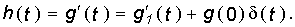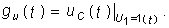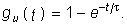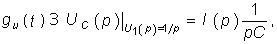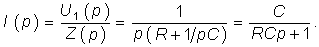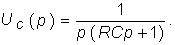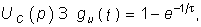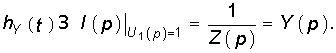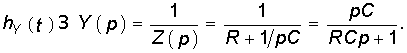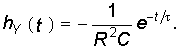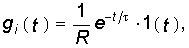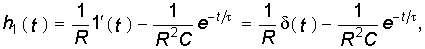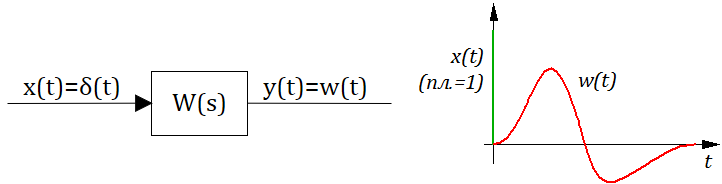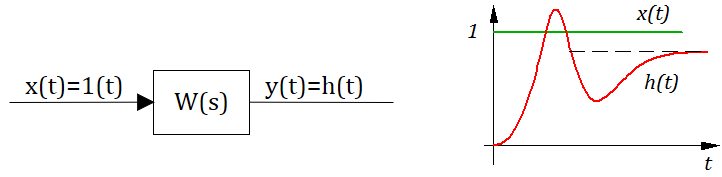Как найти переходную характеристику системы

Как найти переходную характеристику системы

Переходная характеристика

Переходной характеристикой (переходной
функцией)называется реакция системы (при нулевых
начальных условиях) на единичный
ступенчатый сигнал (единичный скачок)


.

Импульсная и переходная функции связаны
выражениями

,.

Для систем без интеграторов переходная
характеристика стремится к постоянному
значению. Переходная характеристика
системы с дифференцирующим звеном
(числитель передаточной функции имеет
нуль в точке
)
стремится к нулю. Если система содержит
интегрирующие звенья, переходная
характеристика асимптотически стремится
к прямой, параболе и т.д., в зависимости
от количества интеграторов.

По определению предельное значение
переходной функции
приесть статический коэффициент усиления:

.

Эта величина имеет смысл только для
устойчивых систем, поскольку при
неустойчивости переходный процесс не
сходится к конечному значению.

Е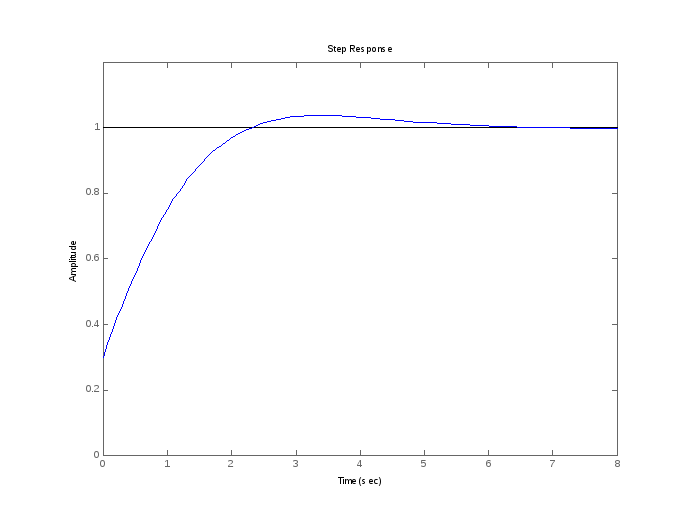сли
передаточная функция правильная, но не
строго правильная (матрицамодели в пространстве состояний не
равна нулю), скачкообразное изменение
входного сигнала мгновенно приводит к
скачкообразному изменению выхода.
Величина этого скачка равна отношению
коэффициентов при старших степенях
числителя и знаменателя передаточной
функции (или матрицемодели в пространстве состояний).

П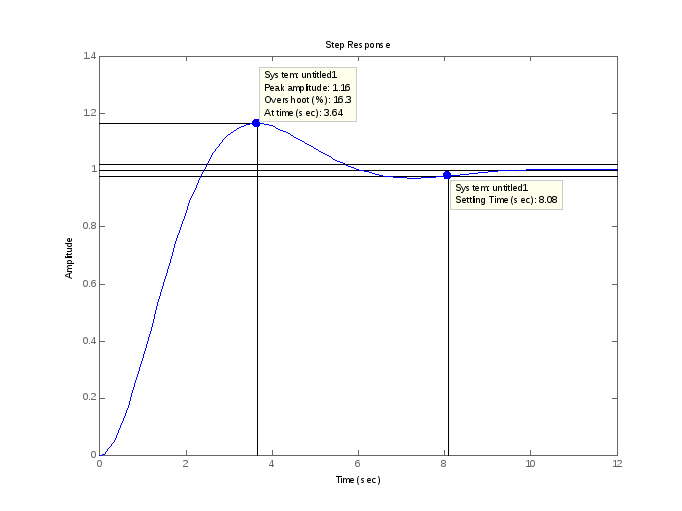о
переходной характеристике можно найти
важнейшие показатели качества системы
– перерегулирование (overshoot)
и время переходного процесса (settling
time).

Перерегулирование определяется
как

,

где
– максимальное значение функции,
а– установившееся значение выхода.

Время переходного процесса– это
время, после которого сигнал выхода
отличается от установившегося значения
не более, чем на заданную малую величину
(в средеMatlab
по умолчанию используется точность
2%).

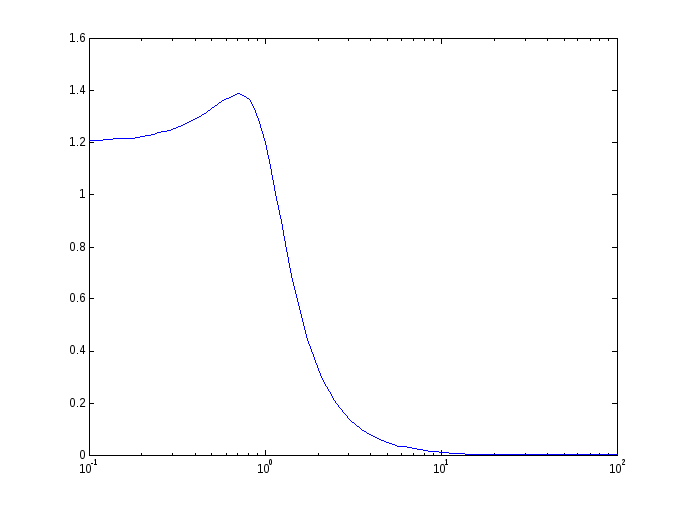
Частотная характеристика

При подаче на вход линейной системы
гармонического (синусоидального) сигнала
с
частотой(она измеряется в радианах в секунду),
на выходе будет также гармонический
сигнал той же частоты, но другой амплитуды
и фазы4,
где– амплитуда и– сдвиг фазы.

Частотная характеристика определяется
как реакция системы на комплексный
экспоненциальный сигнал
.
Для ее построения надо использовать
подстановкув передаточной функции.
Выражениеназываетсячастотной передаточной
функциейилиамплитудно-фазовой
частотной характеристикой системы(АФЧХ).

Зависимость модуля величины
от частоты называетсяамплитудной
частотной характеристикой(АЧХ), а
зависимость аргумента комплексного
числа (фазы)от частоты ­–фазовой частотной
характеристикой(ФЧХ):

.

АЧХ показывает, насколько усиливается
амплитуда сигналов разных частот после
прохождения через систему, а ФЧХ
характеризует сдвиг фазы сигнала.


Реальные объекты имеют строго правильную
передаточную функцию, поэтому их АЧХ
убывает с ростом частоты и асимптотически
стремится к нулю. Говорят, что такой
объект обладает свойством фильтра– фильтрует (не пропускает) высокочастотные
сигналы (помехи, шумы измерений). Это
свойство служит основой для использования
метода гармонического баланса.

Частота, после которой значение АЧХ
уменьшается ниже 0 дБ (коэффициент
усиления меньше 1, сигнал ослабляется),
называется частотой срезасистемы.Частота,
после которой значение АЧХ падает ниже
-3 дБ (коэффициент усиления меньше,
чем 0.708), называетсяполосой пропусканиясистемы.
Для ее вычисления используют команду

>>
b = bandwidth ( f )

Максимум АЧХ соответствует частоте, на
которой усиление наибольшее. Значение
АЧХ при
равно усилению при постоянном сигнале,
то есть, статическому коэффициенту
усиления.
Это следует и из равенства

.

Для систем с интегрирующими звеньями
частотная характеристика стремится к
бесконечности при
.
Это значит, что их выход бесконечно
увеличивается или уменьшается при
постоянном входном сигнале.

Чтобы построить частотные характеристики
в Matlab,надо сначала создать массив частот в
нужном диапазоне. Для этого можно
использовать функцииlinspace(равномерное распределение точек по
линейной шкале) иlogspace(равномерное распределение точек по
логарифмической шкале). Команда

>>
w
= linspace
(0, 10, 100);

строит массив из 100 точек с равномерным
шагом в интервале от 0 до 10, а команда

>>
w
= logspace
(-1, 2, 100);

– массив из 100 точек с равномерным шагом
по логарифмической шкале в интервале
от
до.

Частотная характеристика на сетке wдля линейной моделиf
(заданной как передаточная функция,
модель в пространстве состояний или в
форме «нули-полюса») вычисляется с
помощью функцииfreqresp:

>>
r
= freqresp(f,
w);

Функция freqresp
возвращает трехмерный массив.
Это связано с тем, что она применима и
для многомерных моделей (с несколькими
входами и выходами), передаточная функция
которых представляет собой матрицу.
Первые два индекса обозначают строку
и столбец в этой матрице, а третий –
номер точки частотной характеристики.
Для системы с одним входом и одним
выходом удобно преобразовать трехмерный
массив в одномерный командой

>>
r
= r(:);

Для вывода графика АЧХ на экран можно
использовать команды Matlab

>>
plot ( w, abs(r) );

>>
semilogx ( w, abs(r) );

>>
loglog
( w,
abs(r)
);

В первом случае масштаб обеих осей
координат – линейный, во втором случае
используется логарифмический масштаб
по оси абсцисс (частот), в последнем ­–
логарифмический масштаб по обеим осям.
Для вычисления фазы (в градусах)
используется команда

>>
phi
= angle(r)*180/pi;

после чего можно строить ФЧХ, например:

>>
semilogx
( w,
phi
);

Источник

В линейной теории цепей автоматического управления и в других дисциплинах часто пользуются понятиями переходной характеристики и импульсной переходной характеристики какой-либо системы или цепи.
Аналогично вводят понятие переходной характеристики любой цепи или системы, например для четырехполюсника переходной характеристикой называется реакция (напряжение или ток) на выходе при единичном ступенчатом воздействии на входе.
Понятие переходной характеристики h(t) как реакции (отклика) системы (или как выходной величины, за которую может быть принята любая из функций системы) на единичное ступенчатое воздействие, приложенное к ее входу (причем, за вход системы может быть принята любая ветвь или два вывода), применимо не только к электрическим цепям, но и к любым физическим системам — механическим, пневматическим, гидравлическим, электромеханическим и т. д. Так, переходные характеристики rL-, rС- и rLC-цепей, если, например, в качестве выходной величины выбраны токи, даются формулами (14.14), (14.26), (14.60), (14.63) при U = 1, а если выбраны напряжения на емкостных элементах, то формулами (14.25), (14.59), (14.62) также при U = 1.

Переходная характеристика введена в основном по двум причинам.
1. Единичное ступенчатое воздействие 1(t) — скачкообразное, и поэтому довольно тяжелое для любой системы внешнее воздействие. Следовательно, важно знать реакцию системы именно при таком воздействии. Иные, например, всевозможные плавные воздействия будут для системы легче.
2. Если определена характеристика h(t), то при помощи интеграла Дюамеля (см. раздел и раздел) можно определить реакцию системы при любой форме внешних воздействий.

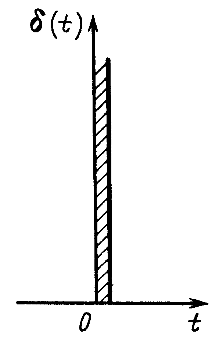
Существует еще один вид внешнего воздействия, называемый единичным импульсом, дельта-функцией d(t) или функцией Дирака, которое определяется как производная
по времени единичной функции



и представляет собой предельный случай импульса очень большого значения и очень малой продолжительности (рис. 14.39), когда его длительность стремится к нулю, но площадь сохраняется равной единице.
Действительно, оставляя сейчас в стороне вопрос о законности операций дифференцирования разрывной функции 1(t), но отметив, что в теории обобщенных функций эти операции достаточно строго обоснованы, найдем площадь единичного импульса:

Рис. 14.39

Импульсной переходной функцией или характеристикой (весовой функцией) системы (например, четырехполюсника) k(t) называется реакция на выходе, если на входе действует внешнее возмущение в виде единичного импульса δ(t). Поскольку внешние возмущения 1(t) и δ(t) связаны равенством (14.83), то при h(0+)=0 получаем, что подобным же равенством связаны и их реакции на выходе системы, т. е.

В справедливости (14.84) можно убедиться непосредственно, вычислив h(t), k(t) и dh(t)/dt для любой цепи.
Если же , то соотношение (14.84) обобщается:

Например, если при включении rС-цепи на единичный импульс напряжения в качестве выходной величины рассматривается ток, то



Так как при t — 0 в составе приложенного напряжения имеется дельта-функция и в этот момент по второму закону коммутации , то дельта-функция должна быть и в составе тока, что и объясняет наличие второго слагаемого в правой части (14.85).

Импульсная переходная характеристика k(t) введена по тем же двум причинам, что и h(t).
1. Единичный импульс — скачкообразное и поэтому довольно тяжелое возмущение для системы или цепи; оно тяжелее, чем плавное возмущение. Следовательно, важно знать реакцию системы или цепи на это возмущение.
2. При помощи некоторого видоизменения интеграла Дюамеля можно, зная k(t), вычислить реакцию системы или цепи на любое внешнее возмущение (см. раздел).
Реализацию внешнего воздействия в виде единичного импульса напряжения δ(t) обычно представляют как экспоненциальное воздействие с очень большой начальной ординатой и очень малой постоянной времени t, так что



где — площадь, ограничиваемая экспоненциальным импульсом, т. е.


Источник

В основе временного метода лежит понятие переходной и импульсной характеристик цепи. Переходной характеристикой цепи называют реакцию цепи на воздействие в форме единичной функции (7.19). Обозначается переходная характеристика цепи g(t). Импульсной характеристикой цепи называют реакцию цепи на воздействие единичной импульсной функции (d-функции) (7.21). Обозначается импульсная характеристика h(t). Причем, g(t) и h(t) определяются при нулевых начальных условиях в цепи. В зависимости от типа реакции и типа воздействия (ток или напряжение) переходные и импульсные характеристики могут быть безразмерными величинами, либо имеют размерность А/В или В/А.

Использование понятий переходной и импульсной характеристик цепи позволяет свести расчет реакции цепи от действия непериодического сигнала произвольной формы к определению реакции цепи на простейшее воздействие типа единичной 1(t) или импульсной функции d(t), с помощью которых аппроксимируется исходный сигнал. При этом результирующая реакция линейной цепи находится (с использованием принципа наложения) как сумма реакций цепи на элементарные воздействия 1(t) или d(t).

Между переходной g(t) и импульсной h(t) характеристиками линейной пассивной цепи существует определенная связь. Ее можно установить, если представить единичную импульсную функцию через предельный переход разности двух единичных функций величины 1/t, сдвинутых друг относительно друга на время t (см. рис. 7.4):

т. е. единичная импульсная функция равна производной единичной функции. Так как рассматриваемая цепь предполагается линейной, то соотношение (8.1) сохраняется и для импульсных и переходных реакций цепи

т. е. импульсная характеристика является производной от переходной характеристики цепи.

Уравнение (8.2) справедливо для случая, когда g(0) = 0 (нулевые начальны е условия для цепи). Если же g(0) ¹ 0, то представив g(t) в виде g(t) = 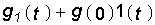, где = 0, получим уравнение связи для этого случая:

Для нахождения переходных и импульсных характеристик цепи можно использовать как классический, так и операторный методы. Сущность классического метода состоит в определении временной реакции цепи (в форме напряжения или тока в отдельных ветвях цепи) на воздействие единичной 1(t) или импульсной d(t) функции. Обычно классическим методом удобно определять переходную характеристику g(t), а импульсную характеристику h(t) находить с помощью уравнений связи (8.2), (8.3) или операторным методом.

Пример. Найдем классическим методом переходную характеристику по напряжению для цепи, изображенной на рис. 8.1. Численно gu(t) для данной цепи совпадает с напряжением на емкости при подключении ее в момент t= 0 к источнику напряжения U1 = l В:

Закон изменения напряжения uC(t) определяется уравнением (6.27), где необходимо положить U= l В:

При нахождении характеристик g(t) и h(t) операторным методом пользуются изображениями функций 1(t), d(t) и методикой расчета переходных процессов, изложенных в гл. 7.

Пример. Определим операторным методом переходную характеристику gu(t) RС-цепи (см. рис. 8.1). Для данной цепи в соответствии с законом Ома в операторной форме (7.35) можем записать:

где

Окончательно получаем

Отсюда по теореме разложения (7.31) находим

т. е. то же значение, что и полученное классическим методом.

Следует отметить, что величина I(р) в уравнении (8.4) численно равна изображению переходной проводимости. Аналогичное изображение импульсной характеристики численно равно операторной проводимости цепи

Например, для RС-цепи (см. рис. 8.1) имеем:

Применив к Y(p) теорему разложения (7.30), получим:

Следует отметить, что формула (8.5) определяет свободную составляющую реакции цепи при единичном импульсном воздействии. В общем случае в реакции цепи, кроме экспоненциальных составляющих свободного режима при t > 0 присутствует импульсное слагаемое, отображающее воздействие при t = 0 единичного импульса. Действительно, если учесть, что для RС-контура (см. рис. 8.1) переходная характеристика по току при U= 1(t) согласно (6.28) будет

то после дифференцирования (8.6) согласно (8.2) получаем импульсную характеристику RС-цепи hi(t) в виде

т. е. реакция hi(t) содержит два слагаемых — импульсное и экспоненциальное.

Физический смысл первого слагаемого в (8.7) означает, что при t = 0 в результате воздействия на цепь импульсного напряжения d(t) зарядный ток мгновенно достигает бесконечно большого значения, при этом за время от 0– до 0+ элементу емкости передается конечный заряд и она скачком заряжается до напряжения I/RC. Второе слагаемое определяет свободный процесс в цепи при t> 0 и обусловлено разрядом конденсатора через короткозамкнутый вход (так как при t> 0 d(t) = 0, что равносильно КЗ входа) с постоянной времени t = RC. Из этого следует, что при d(t)-импульсном воздействии на RС-цепь нарушается непрерывность заряда на емкости (второй закон коммутации). Аналогично нарушается и условие непрерывности тока в индуктивности (первый закон коммутации), если к цепи, содержащей элемент индуктивности воздействовать напряжением в виде d(t).

В табл. 8.1 сведены значения переходной и импульсных характеристик по току и напряжению для некоторых цепей первого и второго порядка.

Источник

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

В это части будут рассмотрены:

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции.
2.12. Mетод переменных состояния.
2.13. Переход от описания переменных «вход-выход» к переменным состояния.

Попробуем применить, полученные знания на практике, создавая и сравнивая расчетные модели в разных видах. Будет интересно познавательно и жестко.

2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)

Рассмотрим динамическое звено САР изображенное на рисунке 2.9.1

Рис. 2.9.1 — Звено САР

Предположим, что уравнение динамики имеет вид:

$T_2^2cdot y''(t)+T_1cdot y'(t)+y(t)=kcdot[tau cdot x'(t)+x(t)];$

где:

$T_2,T_1, tau$ — постоянные времени;

$k$ — коэффициент усиления.

Пусть известны отображения:

$x(t) to X(t)\ y(t) to Y(t)$

Найдем изображения для производных:

$x',y',y'':$

$x'(t) to s cdot X(s) + добавка\ y'(t) to s cdot Y(s) + добавка\ y''(t) to s^2 cdot Y(s) + добавка$

Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:

$T_2^2 cdot s^2cdot Y(s) + T_1 cdot s cdot Y(s) + Y(s) + sum добавок = k cdot[s cdot tau cdot X(s) +X(s)] +k cdot добавки\ (T_2^2 cdot s^2 + T_1 cdot s + 1) cdot Y(s)+ sum добавок =k cdot(s cdot tau +1)cdot X(s) +k cdot добавки\ Y(s) = underbrace{frac{k cdot(s cdot tau +1)}{T_2^2 cdot s^2 + T_1 cdot s + 1}}_{W(s)}cdot X(s) + underbrace{frac{k cdot добавки-sum добавок}{T_2^2 cdot s^2 + T_1 cdot s + 1}}_{B(s)} $

B(s) — слагаемое, которое определяется начальными условиями, при нулевых начальных условиях B(s)=0.
W(s) — передаточная функция.

$Y(s) = W(s) cdot X(s); W(s) = frac{Y(s) - изображение выходного сигнала} {X(s)- изображение входного воздействия}$

Передаточной функцией САР (звена) называется отношение изображений выходного сигнала к входному воздействию при нулевых н.у.

После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.

Пример

Построить выходной сигнал звена САР при единичном входном воздействии и нулевых начальных условиях, если уравнение динамики звена имеет следующий вид:

$T cdot y'(t)+y(t) = k cdot x(t) $

начальные условия:

$ при t le0: x(0)=0,y(0)=0. $

входное воздействие:

$x(t) = 1(t)$ — единичное ступенчатое воздействие.

Выполним преобразование Лапласа:

$x(t) to X(s) = frac{1}{s} \ y(t) to Y(s) \ y' to s cdot Y(s)$

Подставим в уравнение динамики и получим уравнение динамики в изображениях:

$(T cdot s+1) cdot Y(s) = k cdot X(s) \ Y(s) = frac{k}{Tcdot s+1} cdot X(s) = frac{k}{Tcdot s+1} cdot frac{1}{s}\ Y(s) = frac{k}{s(Tcdot s+1)}$

Для получения выходного сигнала из уравнения в изображениях выполним обратное преобразования Лапласа:

$y(t) = L^{-1}[Y(s)] = L^{-1}left[frac{k}{s(Tcdot s+1)}right] =frac{1}{T}k cdot L^{-1}left[frac{1}{s(s+frac{1}{T})}right] Longrightarrow \ y(t) = frac{k}{T}(1-e^{-frac{t}{T}}) cdot T = k cdot(1-e^{-frac{t}{T}}).$

Рисунок 2.9.2 График переходного процесса.

2.10. Весовая и переходная функции звена (системы).

Определение: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.

Рисунок 2.10.1 Весовая функция.

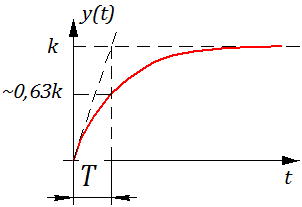
Определение: Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.

Рисунок 2.10.2 Переходная функция.

Рисунок 2.10.3 Пример весовой функции.

Рисунок 2.10.4 Пример перходной функции.

На этом месте можно вспомнить, что преобразование Лапласа это интеграл от 0 до бесконечности по времени (см. предыдущий текст), а импульсное воздействие при таком интегрировании превращается в 1 $L[delta(t)] =1$ тогда в изображениях получаем что:

$Y(s) =W(s) cdot underbrace{X_{имп}(s)}_1 Rightarrow Y(s) = W(s)$

Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.

Рисунок 2.10.5 Весовая функция как передаточная в изображениях.

Рисунок 2.10.6 Ступенчатое воздействие.

Для единичного ступенчатого воздействия преобразование Лапласа тоже известно (см. предыдущий текст):

$L[1(t)] = frac{1}{s}$

тогда в изображениях получаем, что реакция системы $Н(s)$ на ступенчатое воздействие, рассчитывается так:

$Н(s) =W(s) cdot underbrace{X_{ступ}(s)}_{1/s} Rightarrow Н(s) = frac {W(s)}{s},$

Реакция системы на единичное ступенчатое воздействие рассчитывается обратным преобразованием Лапласа:

$h(t) = L^{-1}left[frac{W(s)}{s}right]$

2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона

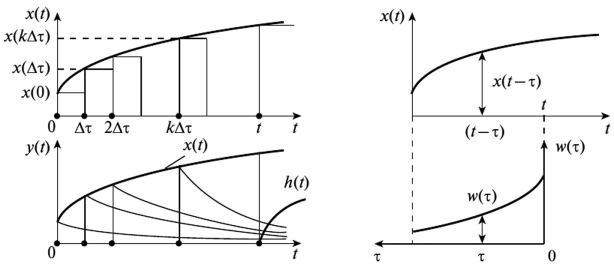
Предположим, что на вход системы поступает произвольное воздействие x(t), заранее известное. Найти реакцию системы y(t), если известны входное воздействие x(t) и весовая функция w(t).

Рисунок 2.11 Демонстрация расчета по формуле Дюамеля-Карсона

Решение.

Представим, что входное воздействие представляет собой последовательность прямоугольных импульсов до времени t и ступеньки высотой x(t) в момент времени t. см.рис. 2.11 Для каждого импульса мы можем записать реакцию системы через весовую функциию:

$Y_k approx Y_{k-1}+x(t) cdot w(t-Deltatau) cdotDeltatau$

где:

$Y_{k-1} $ — значение отклика по завершению предыущего импульса;

$t= k cdot Deltatau$ — время завершения текущего импульса;

$w(t-Deltatau) $ — значение весовой функции в начале текущего импульса.

Тогда для определения занчения отклика в произвольный момент времени необходимо сложить все импульсы и ступенчатое воздействие в момент времени t:

$Y(t) = h(0)x(t)+ sum_{k=0}^{n}x(kcdot Deltatau)cdot w(t-kcdot Deltatau) cdot Deltatau;$

Переходя к пределам

$n to infty, Deltatau to0$

получаем интеграл:

$y(t) = h(0)x(t)+int_0^t x(tau)cdot w(t-tau)dtau$

если перейти от t к бесконечности мы получим формулу интеграла Дюамеля-Карсона, или по другому «интеграла свертки» который обеспечивает вычисление оригинала функции по произвдению изображения двух функций:

$Y(s) = L[y(t)];\ W(s) =L[w(t)];\ X(s) = L[x(t)];\ если Y(s) = W(s)cdot X(s), то\ y(t) =int_0^infty x(tau)cdot w(t-tau)dtau $

где $tau$ — вспомогательное время

Для вывода аналогичной зависмости от переходной функции вспомним что изображение весовой и переходной функции связаны соотношением: $H(s) =frac{W(s)}{s} $ запишем выражение изображения для отклика в операторной форме:

$y(t) = L^{-1} [W(s) cdot Y(s)]=L^{-1} left[s cdot frac{W(s)}{s} cdot Y(s) right] \ свойства преобразований Лапласа x(t) to X(s), frac {d}{dt}x(t) to s cdot X(s) to \ y(t)= frac {d}{dt}L^{-1} left[ H(s) cdot Y(s)right]$

Используя интеграл свертки получаем, что при известной переходной функции (h(t)) и известному входному воздействию х(t) выходное воздействие рассчитывается как:

$y(t) = frac{d}{dt} int_0^infty x(t)cdot h(t-tau)dtau$

2.12. Mетод переменных состояния.

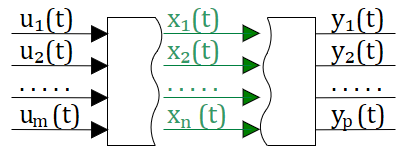
До этого мы рассматривали системы с одной передаточной функцией, но жизнь всегда сложнее и как правило в системах есть несколько передаточных функций несколько входных воздейстий и несколько реакций системы. (см. рис. 2.12.1)

Рисунок 2.12.1 Моногомерная система автоматического управления.

В этом случае наиболее удобной формой пердставления систем для их анализа и расчета оказался метод переменных состояния. Для этого метода, вместо передаточных функций связывающих вход с выходом используются дополнительные переменные состояния, которые описывают систему. В этом случае можно говорить, что состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно. см. рис. 2.12.2

Рисунок 2.12.2 Перменные состояния в многомерной системе.

В методе состояний, производные всех переменных состояния, в общем случае зависит от всех переменных и всех входных воздействия, и могут быть записаны в представленной ниже системы обыкновенных дифференциальных уравнений (ОДУ) первой степени. Эта система уравнений называю системой ОДУ в форме Коши:

$left { begin{gathered} x_1'(t) = a_{11}cdot x_1(t)+ a_{12}cdot x_1(t)+..+a_{1n}cdot x_n(t)+b_{11}cdot u_1(t)+..b_{1m}u_m(t)\ x_2'(t) = a_{21}cdot x_1(t)+ a_{22}cdot x_2(t)+..+a_{2n}cdot x_n(t)+b_{21}cdot u_1(t)+..b_{2m}u_m(t)\ ...................................................................\ x_n'(t) = a_{n1}cdot x_1(t)+ a_{n2}cdot x_n(t)+..+a_{nn}cdot x_n(t)+b_{21}cdot u_1(t)+..b_{nm}u_m(t)\ end{gathered} right. $

Выход из системы зависит от переменных состояния и, в общем случае от входных воздействий и описывается следующей системой уравнений:

$left { begin{gathered} y_1(t) = c_{11}cdot x_1(t)+ c_{12}cdot x_1(t)+..+c_{1n}cdot x_n(t)+d_{11}cdot u_1(t)+..d_{1m}u_m(t)\ y_2(t) = c_{21}cdot x_1(t)+ c_{22}cdot x_2(t)+..+c_{2n}cdot x_n(t)+d_{21}cdot u_1(t)+..d_{2m}u_m(t)\ ...................................................................\ y_p(t) = c_{p1}cdot x_1(t)+ c_{p2}cdot x_n(t)+..+cp_{pn}cdot x_n(t)+d_{p1}cdot u_1(t)+..d_{pm}u_m(t)\ end{gathered} right.$

где:
n — количество перемнных состояния,
m — количество входных воздействий,
p — количество выходных переменных;

Данная система уравнений может быть записана в матричной форме:

$left { begin{gathered} x'= Acdot x+Bcdot u\ y= Ccdot x+Dcdot u end{gathered} right. $

где:
$u=left[ begin{gathered} u_1(t)\ u_2(t)\ ..\ u_m(t)\ end{gathered} right]$ — вектор входа (или вектор управления);
$x'=left[ begin{gathered} x'_1(t)\ x'_2(t)\ ..\ x'_n(t)\ end{gathered} right]$ — вектор столбец производных переменных состояния;
$x=left[ begin{gathered} x_1(t)\ x_2(t)\ ..\ x_n(t)\ end{gathered} right]$ — вектор столбец переменных состояния;
$y=left[ begin{gathered} y_1(t)\ y_2(t)\ ..\ y_p(t)\ end{gathered} right]$ — вектор выхода;
$А=left[ begin{gathered} а_{11} а_{12} ... a_{1n}\ а_{21} а_{22} ... a_{2n}\ .. .. .. ........ \ а_{n1} а_{n2} ... a_{nn}\ end{gathered} right]$ — собственная матрица системы [n x n],
$a_{ij} $ — постоянные коэффициенты;
$B=left[ begin{gathered} b_{11} b_{12} ... b_{1m}\ b_{21} b_{22} ... b_{2m}\ .. .. .. ........ \ b_{n1} b_{n2} ... b_{nm}\ end{gathered} right]$ — матрица входа [n x m],
$b_{ij} $ — постоянные коэффициенты;
$C=left[ begin{gathered} c_{11} c_{12} ... c_{1n}\ c_{21} c_{22} ... c_{2n}\ .. .. .. ........ \ c_{p1} c_{p2} ... c_{pn}\ end{gathered} right]$ — матрица выхода а [p x n],
$c_{ij} $ — постоянные коэффициенты;
$D=left[ begin{gathered} d_{11} d_{12} ... d_{1m}\ d_{21} d_{22} ... d_{2m}\ .. .. .. ........ \ d_{p1} d_{p2} ... d_{pm}\ end{gathered} right]$ — матрица обхода [p x m],
$d_{ij} $ — постоянные коэффициенты;

В нашем случае почти всегда все элементы матрицы D будут нулевыми: D = 0.

Такое описание системы позволяет с одной стороны стандартным образом описывать различные технические системы. Явная формула для расчета производных позволяет достаточно просто осуществлять численное интегрирование по времени. И это используется в различных программах моделирования

Другое использование данного представления для простых систем, описанных в переменных «вход-выход», зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.

Еще одним преимуществом данного описания, является то, что уравнения в форме Коши можно получить из законов физики

Пример решения задачи в форме коши.

Рассмотрим задачу моделирования гидравлического привода, при следующих условиях:

Дано:
Цилиндрический плунжер диаметром 10 мм, с приведенной массой 100 кг, работает на пружину жесткостью 200 Н/мм и демпфер с коэффициентом вязкого трения — 1000 Н/(м/с). Полость начальным объемом 20 см3 соединяется с источником давлния дросселем диаметром диаметр которого 0,2 мм. Коэффициент расхода дросселя 0.62. Плотность рабочей жидкости ρ = 850 кг/м3.
Определить:
Перемещение дросселя, если в источнике давление происходит скачек 200 бар. см. рис. 2.12.13

Рисунок 2.12.3 Гидравлическая система.

Уравенение движение плунжера:

$m cdot frac{d^2x}{dt}=p cdot Ap - c_{pr} - b_{tr} cdot frac{dx}{dt}$

Где:

$A_p$ – площадь плунжера,

$c_{pr}$ – жесткость пружины,

$b_{tr}$ – коэффициент вязкого трения, p – давление в камере.

Поскольку дифференциальное движения это уравнение второго порядка, превратим его в систему из двух уравнений первого порядка, добавив новую переменную — скорость $v = frac{dx}{dt}v = $, тогда $frac{d^2x}{dt} = v'$

$left { begin{align} x' &= v \ v' &=frac{A_p}{m}cdot p-frac{c_{pr}}{m}cdot x-frac{b_{tr}}{m}cdot v) end{align} right.$

Уравнение давления в камере, для упрощения принимаем что изменениям объема камеры из-за перемещения плунжера можно пренебречь:

$p'=frac{E}{V}(Q - A_p cdot x')$

Где: Q – расход в камеру, V — объем камеры.

Расход через дроссель:

$Q = mucdot f sqrt{frac{2}{rho}(p_n-p)}$

Где: f– площадь дросселя,

$p_n$– давление в источнике, p – давление в камере.
Уравнение дросселя не линейное, по условию задачи, давление входное изменяется скачком, от 0 до 200 бар, проведем линеаризацию в окрестности точки давления 100 бар тогда:

$Q_{100} = mucdot f sqrt{frac{2}{rho}(p_{100}-0)} K_{100} =frac{Q_{100}}{p_{100}} \ Qapprox frac{Q_{100}}{p_{100}}(p_n-p) = K_{100}(p_n-p), где: K_{100} =frac{Q_{100}}{p_{100}}$

Подставляем линеаризованную формул расхода в формулу давления:

$p'=frac{E}{V}(K_{100} (p_n-p)- A_p cdot v)\ p' = - frac{E}{V}A_p cdot v - frac{E}{V}K_{100} cdot p + frac{E}{V}K_{100} cdot p_n$

Таким образом общая система уравнений в форме Коши, для рис 2.12.3 привода принимает вид:

$left { begin{align} x' &= v \ v' &=-frac{c_{pr}}{m}cdot x-frac{b_{tr}}{m}cdot v+frac{A_p}{m}cdot p\ p' &= - frac{E}{V}A_p cdot v - frac{E}{V}K_{100} cdot p + frac{E}{V}K_{100} cdot p_n end{align} right.$

Матрицы A, B, С, В для матричной формы системы уравнений принимают вид:

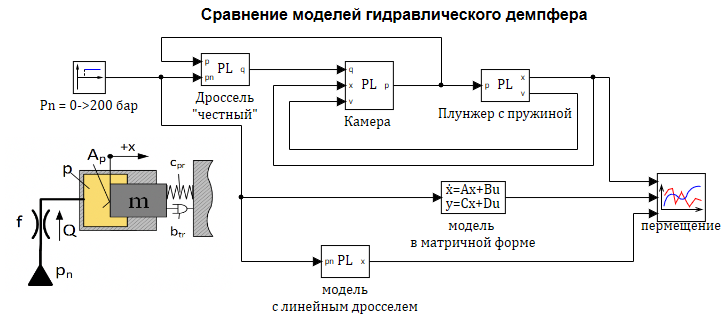
$left { begin{align} x' &= v \ v' &=-frac{c_{pr}}{m}cdot x-frac{b_{tr}}{m}cdot v+frac{A_p}{m}cdot p\ p' &= - frac{E}{V}A_p cdot v - frac{E}{V}K_{100} cdot p + frac{E}{V}K_{100} cdot p_n end{align} right.\ A =left[ begin{array}{cccc} 0& 1 & 0\ -frac{c_{pr}}{m}& -frac{b_{tr}}{m} &frac{A_p}{m}\ 0& - frac{E}{V}A_p & - frac{E}{V}K_{100} end{array} right]; B = left[ begin{array}{cccc} &0 \ &0\ & frac{E}{V}K_{100} end{array} right]; C= left[ 1,0,0 right]; D =[0].$

Проверим моделированием в SimInTech составленную модель. На рисунке 2.12.13 представлена расчетная схема содержащая три модели:
1 — «Честная» модель со всеми уравнениями без упрощений.
2 — Модель в блоке «Переменные состояние» (в матричной форме).
3 — Модель в динамическом блоке с линеаризованным дросселем.

Рисунок 2.12.4 Расчетная схема .

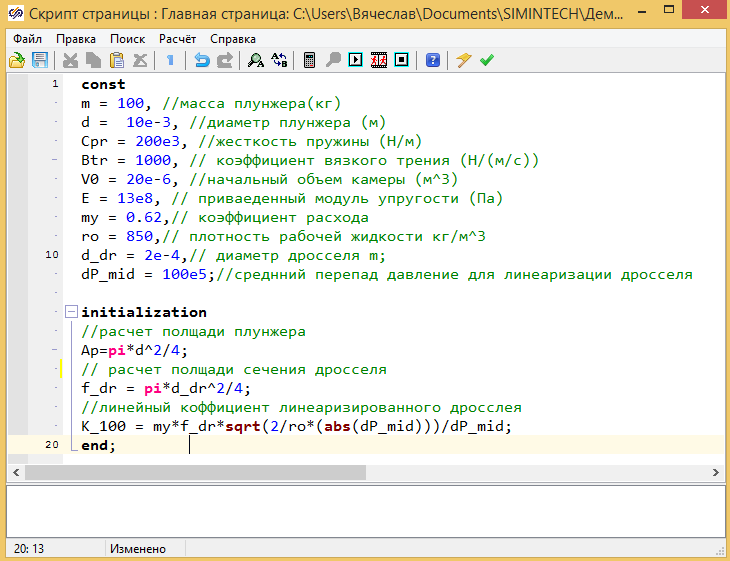
Все условия задачи задаются как глобальные константы проекта, в главном скрипте проекта, там же расчитываются на этапе инициализации расчета, площади плунжера и проходного сечения дросселя см. рис. 2.12.5:

Рисунок 2.12.5 Глобальный скрипт проекта.

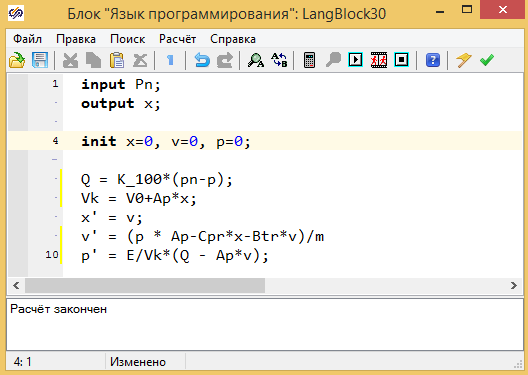
Модель на внутреннем языке программирования представлена на рис. 2.12.6. В данной модели используется описание модели в форме Коши. Так же выполняется учет изменения объема дросселя на каждом шаге расчета, за счет перемещения плунжера (Vk = V0+Ap*x.)

Рисунок 2.12.6 Скрипт расчета модели в форме Коши.

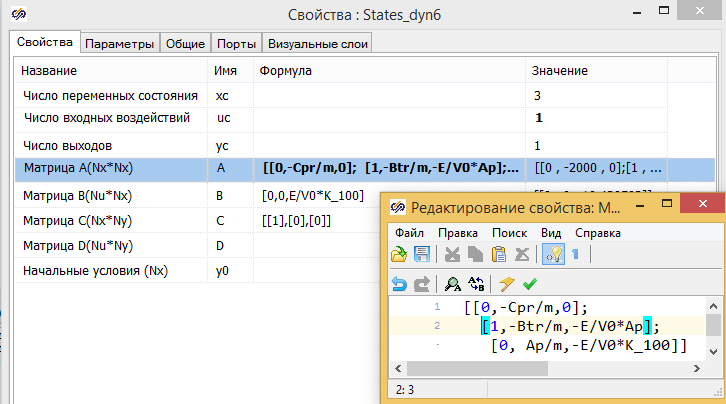
Модель в матричном форме задается с использованием глобальных констант в виде формул. (Матрица в SimInTech задается в виде последовательности из ее столбцов) см. рис. 2.12.7

Рисунок 2.12.7 Настройка блока расчета системы уравнений в пременных состояния в матричной форме.

Результаты расчета показывают, что модель в матричной форме и модель на скриптовом языке в форме Коши, практически полностью совпадают, это означает, что учет изменения объема полости практически не влияют на результаты. Кривые 2 и З совпадают.
Процедура линеаризация расхода через дроссель вызывает заметное отличие в результатах. 1-й график c «честной» моделью дросселя, отличается от графиков 2 и 3. (см. рис. 2.12.8)

Рисунок 2.12.8 Результаты расчета трех моделей гидравлического плунжера.

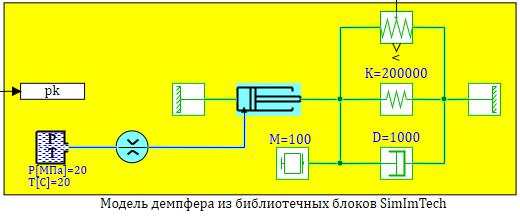
Сравним полученные модели, с моделью созданной из библиотечных блоков SimInTech, в которых учитываются так же изменение свойств реальной рабочей жидкости — масла АМГ-10. Сама модель представлена на рис. 2.12.9, набор графиков на рисунке 2.12.10

Рисунок 2.12.9 Модель демпфера из библиотечных блоков.

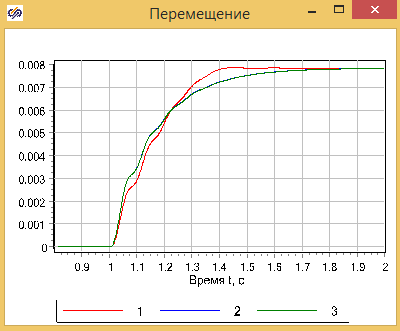
Рисунок 2.12.10 Результаты рассчета моделей демпфера. График 4 — модель из библиотечных блоков.

На графиках видно, что уточненная модель отличается от предыдущих, однако погрешность модели составлят наших упрощенных моделей составляют примерно 10%, в лишь в некоторые моменты времени.

2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно

Рассмотрим несколько вариантов перехода от описания «вход-выход», к переменным состояния:

$L(p)cdot y(t)=N(p)cdot u(t)$

Вариант прехода зависит от правой части уравнения с переменными «вход-выход»:

$a_ncdot y^{(n)}(t)+...+a_1cdot y'(t)+a_0cdot y(t)=b_mcdot u^{(m)}(t)+...b_1cdot u'(t)+b_0cdot u(t)$

2.13.1. Правая часть содержит только b0*u(t)

В этом варианте, в уравнениях в правой части отсутствуют члены с производными входной величины u(t). Пример с плунжером выше так же относится к этому варианту.

Что бы продемонстрировать технологию перехода рассмотрим следующее уровнение:

$a_3 cdot y'''(t)+ a_2 cdot y''(t)+a_1 cdot y'(t)+a_0 cdot y(t) = b_0 cdot u(t)$

Для перехода к форме Коши ведем новые переменные:

$x_1(t) = y(t);\ x_2(t) =y'(t) = x_1'(t);\ x_3(t) = y''(t) =x_2'(t);$

И перепишем уравнение относительно y”'(t):

$ y'''(t) = x_3'=- frac{a_2}{a_3} cdot underbrace{y''(t)}_{x_3} - frac{a_1}{a_3} cdot underbrace{y'(t)}_{x_2} - frac{a_0}{a_3} cdot underbrace{y(t)}_{x_1}+ frac{b_0}{a_3} cdot u(t) $

Используя эти переменные можно перейти от дифференциального уравнения 3-го прядка, к системе из 3-х уравнений первого порядка в форме Коши:

$left { begin{align} x_1' &= x_2 \ x_2' &= x_3\ x_3' &=-frac{a_0}{a_3}cdot x_1-frac{a_{1}}{a_3}cdot x_2-frac{a_2}{a_3}cdot x_3+ frac{b_0}{a_3}cdot u(t)\ end{align} right.$

Соотвественно матрицы для матричного вида уравнений в переменных сосотяния:

$A =left[ begin{array}{cccc} 0& 1 & 0\ 0& 0 &1\ -frac{a_0}{a_3}& -frac{a_1}{a_3} & -frac{a_2}{a_3} end{array} right]_{[3 times 3]}; B = left[ begin{array} {}&0 \ &0\ & frac{b_0}{a_3} end{array} right]_{[3 times 1]}; C= left[ 1,0,0 right]_{[1 times 3]}; D =[0].$

2.13.2. Правая часть общего вида

Более сложный случай, когда в уравнениях есть производные от входных воздействий и уравнение в общем случае выглядит так:

$a_ncdot y^{(n)}(t)+...+a_1cdot y'(t)+a_0cdot y(t)=b_mcdot u^{(m)}(t)+...b_1cdot u'(t)+b_0cdot u(t)$

Сделаем преобразования: перейдем к уравнениям динамики в изображениях:

$left[ begin{gathered} y(t) to Y(s)\ y'(t) to s cdot Y(s)\ y''(t) to s^2cdot Y(s)\ ..\ y^{n}(t) to s^{n} cdot Y(s)\ end{gathered} right] ; left[ begin{gathered} u(t) to U(s)\ u'(t) to s cdot U(s)\ u''(t) to s^2cdot U(s)\ ..\ u^{m}(t) to s^{m} cdot U(s)\ end{gathered} right]$

Тогда можно представить уравнение в изображениях в виде:

$L(s) cdot Y(s) =N(s) cdot U(s)$

где:

$L(s) = a_ncdot s^{n}+a_{n-1}cdot s^{n-1}_....+a_1cdot s+a_0;\ N(s)=b_mcdot s^{m}(t)+b_{m-1}cdot s^{m-1}+...b_1cdot s+b_0;$

Разделим уравнение в изображениях на произведение полиномов $L(s) cdot N(s)$, получим:

$frac{Y(s)}{N(s)} = frac{U(s)}{L(s)} =X_1(s)$

Где: $X_1(s) $ — некоторая комплексная величина (отношение двух комплексных величин). Можно считать, что $X_1(s) $ отображение величины $x_1(t) to X_1(s) $. Тогда входная величина может быть в изображениях представлена как:

$frac{U(s)}{L(s)} = X_1(s) Rightarrow U(s) = X_1(s) cdot L(s);$

Вренемся к оригиналу от изображений получим: $u(t) = alpha (p) x_1(t)$,
где: $alpha (p) $ — дифференциальный оператор.

$u(t) = a_n cdotunderbrace{ x_1^{(n)}}_{x_n'}+ a_{n-1} cdot underbrace{x_1^{(n-1)}}_{x_n}+...+a_2 cdot underbrace{ x_1''}_{x_3}+a_1 cdot underbrace{x_1'}_{x_2}+ a_0 cdot x_1$

А это дифференциальное уравнение n-го порядка мы можем преобразовать к системе из n дифференциальных уравнений первого порядка, как это мы делали выше:

$left { begin{eqnarray} x_1'&=& x_2\ x_2'&= &x_3\ &.....\ x_n'&=&-frac{1}{a_n}[a_0 cdot x_1+a_1 cdot x_2+a_2cdot x_3+..+a_{n-1}cdot x_n]+frac{u(t)}{a_n} end{eqnarray} right.$

Таким образом, мы получили систему уравнение в форе Коши, относительно переменных состояния $X_1$:

$ X_1=left[ begin{gathered} x_1(t)\ x_2(t)\ ..\ x_n(t)\ end{gathered} right]$

А регулируемую величину (выход системы) мы так же можем выразить через эти переменные, в изображениях:

$frac{Y(s)}{N(s)} = X_1(s) Rightarrow Y(s) =N(s) cdot X_1(s);$

Перейдем от изображения к оригиналам:

$y(t)=N(p) cdot X_1(t)\ y(t) = b_m cdotunderbrace{ x_1^{(m)}}_{x_{m+1}}+ b_{m-1} cdot underbrace{x_1^{(m-1)}}_{x_m}+...+b_2 cdot underbrace{ x_1''}_{x_3}+b_1 cdot underbrace{x_1'}_{x_2}+ b_0 cdot x_1\ y(t) = b_m cdot x_{m+1}+ b_{m-1} cdot x_{m}+...+b_2 cdot x_3+b_1 cdot x_1+ b_0 cdot x_1\$

Если обозначить вектор $С = [b_{m+1},b_m, ..b_2,b_1,b_0]$, то мы получим уравнения переменных состояниях в матричной форме, где D = 0:

$left { begin{eqnarray} x'&=& Acdot x+Bcdot u\ y&=& Ccdot x +D cdot uend{eqnarray} right. $

Пример:


Рисунок 2.13.1 Передаточная функция.

Имеется передаточная функция (рис. 2.13.1) в изображениях :

$W(s) = frac{s+1}{2 cdot s^3+s^2+3 cdot s+1}$

Необходимо преобразовать передаточную функцию к системе уравнений в форме Коши

В изображения реакция системы связана с входным воздействие соотношением:

$Y(s) = W(s) cdot U(s); Rightarrow Y(s) = frac{N(s)}{L(s)} cdot U(s) Rightarrow \ Rightarrow Y(s) cdot L(s) = U(s) cdot N(s)$

Разделим в последнем правую и левую часть на произведения $L(s) cdot N(s)L $, и введем новую перменную $Х_1$:

$X_1(s) = frac {Y(s)}{N(s)} = frac{U(s)}{L(s)} Rightarrow \ Rightarrow U(s) = X_1(s) cdot L(s)$

Полиномы N(s) и L(s) равны:

$ N(s)= s+1\ L(s)=2 cdot s^3+s^2+3 cdot s+1 \ Rightarrow U(s) = X_1(s) cdot (2 cdot s^3+s^2+3 cdot s+1) $

Перейдем в последнем выражении от изображения к оригиналам и ведем новые переменные (состояния):

$u(t) = 2 cdot underbrace{x_1'''(t)}_{x'_3} + underbrace{x_1''(t)}_{x_3} +3 cdot underbrace{x_1'(t)}_{x_2}+underbrace{x_1(t)}_{x_1}$

Переходим от уравнения третьего порядка к системе трех уравнений первого порядка:

$left { begin{eqnarray} x_1'&=&x_2\ x_2'&=&x_3\ x_3'&=&- frac{1}{2} left[ x_1+3 cdot x_2+x_3 right]+frac {1}{2} cdot u(t) end{eqnarray} right. $

Или в матричной форме:

$x' = A cdot x+ B cdot u\ А=left[ begin{gathered} 0& 1& 0\ 0& 0& 1\ - frac{1}{2}& - frac{3}{2}& - frac{1}{2}\ end{gathered} right]; B = left[ begin{gathered} 0 \ 0\ frac{1}{2} \ end{gathered} right];\ $

Для получения второго матричного уравнения воспользуемся соотношением для новых переменных в отображениях:

$X_1(s) = frac {Y(s)}{N(s)} = frac{U(s)}{L(s)} Rightarrow \ Rightarrow Y(s) = X_1(s) cdot N(s) = X_1(s) cdot (s+1)$

Перейдем от изображений к оригиналу:

$y(t) = underbrace {x_1'(t)}_{x_2}+underbrace {x_1(t)}_{x_1} = x_1(t)+x_2(t)$

Таким образом второе уравнение матричной системы выглядит так:

$y =C cdot x+ D cdot u;\ C=[1 1 0]; D = 0;$

Проверим в SimInTech сравнив передаточную функцию и блок переменных состояния, и убедимся, что графики совпадают см. рис. 2.13.2


Рисунок 2.13.2 Сравнение переходного процеса у блока передаточной функции и блока переменных состояния.

Продолжение лекций находится здесь:
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ (РЕГУЛИРОВАНИЯ).
3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ.
3.2. Типовые звенья систем автоматического управления (регулирования). Классификация типовых звеньев. Простейшие типовые звенья.
3.3. Апериодическое звено 1–го порядка (инерционное звено). На примере входной камеры ядерного реактора.
3.4. Апериодическое звено 2-го порядка.
3.5. Колебательное звено.
3.6. Инерционно-дифференцирующее звено.
3.7. Форсирующее звено.
3.8. Инерционно-интегрирующее (звено интегрирующее звено с замедлением).
3.9 Изодромное звено (изодром).

Полезные ссылки:

Модель демпфера из лекции можно взять здесь…
Волченко Ю.М. Теоремы операционного исчисления.
Интеграл Дюамеля и физический смысл функции веса
Лекция. «Векторно-матричные модели систем управления в непрерывном времени»
Л. С. Шихобалов. Учебное пособие «МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ»
Характеристическое уравнение матрицы
Подробное описание моделирования гидравлического демпфера.

Источник

Добавить комментарий