3.1. Переходная характеристика цепи.
Переходная
характеристика используется при расчете
реакции
линейной электрической цепи, когда на
ее вход подается импульспроизвольной формы. При этом входной
импульсаппроксимируют множеством ступенек и
определяют реакцию цепи на каждую
ступеньку, а затем находят интегральную
цепи,
как сумму реакций на каждую составляющую
входного импульса.
Переходная
характеристика или переходная функция
цепи
–это ее
обобщенная характеристика, являющаяся
временной функцией, численно равной
реакции цепи на единичный скачок
напряжения или тока на ее входе, при
нулевых начальных условиях (рис. 13.11);
|
|
|
Рис. |
другими словами,
это отклик цепи, свободной от начального
запаса энергии на функцию
на входе.
Выражение переходной
характеристики
зависит только от внутренней структуры
и значения параметров элементов цепи.
Из определения
переходной характеристики цепи следует,
что при входном воздействии
реакция цепи
(рис. 13.11).
Пример.
Пусть цепь подключается к источнику
постоянного напряжения
.
Тогда входное воздействие будет иметь
вид,
реакция цепи –
,
а переходная характеристика цепи по
напряжению –
.
При.
Умножение реакции
цепи
на функцию
или
означает, что переходная функция
при
и
при
,
что отражаетпринцип
причинности
в линейных электрических цепях, т.е.
отклик (на
выходе цепи) не может появиться раньше
момента приложения сигнала к входу
цепи.
Виды переходной характеристик.
Различают следующие
виды переходной характеристики:
|
|
– переходная |
|
|
– переходная |
|
|
– переходное |
|
|
– переходная |
где
– уровни входного ступенчатого сигнала.
Переходную функцию
для любого пассивного двухполюсника
можно найти классическим или операторным
методом.
Расчет переходной
характеристики классическим методом.
Пример.
Пример.
Рассчитаем переходную характеристику
по напряжению для цепи (рис. 13.12, а)
с параметрами
.
|
|
|
Рис. |
Решение
Воспользуемся
результатом, полученном в п.11.4. Согласно
выражению (11.20) напряжение на индуктивности
где
.
Проведем
масштабирование согласно выражению
(13.5) и построение функции
(рис. 13.12,б):
.
Расчет переходной характеристики операторным методом
Комплексная схема
замещения исходной цепи примет вид на
рис. 13.13.
|
|
|
Рис. |
Передаточная
функция этой цепи по напряжению:
где
.
При
,
т.е. при ,
изображение ,
а изображение напряжения на катушке .
В этом случае
оригинал
изображения
есть переходная функция цепи по
напряжению, т.е.
или в общем виде:
,
(13.6)
т.е. переходная
функция
цепи равна
обратному преобразованию Лапласа ее
передаточной функции
,
умноженной на изображение единичного
скачка
.
В рассматриваемом
примере (см. рис. 13.12) передаточная функция
по напряжению:
,
где ,
а функция
имеет вид .
Примечание.
Если на вход цепи подано напряжение ,
то в формуле переходной функции
время
необходимо заменить на выражение .
В рассмотренном примере запаздывающая
передаточная функция по напряжению
имеет вид:
.
(13.7)
Выводы
Переходная
характеристика введена, в основном, по
двум причинам.
1. Единичное
ступенчатое воздействие
– скачкообразное, и потому довольно
тяжелое для любой системы или цепи
внешнее воздействие. Следовательно,
важно знать реакцию системы или цепи
именно при таком воздействии, т.е.
переходную характеристику .
2. При известной
переходной характеристике
с помощью интеграла Дюамеля (см. далее
пп.13.4, 13.5) можно определить реакцию
системы или цепи при любой форме внешних
воздействий.
Соседние файлы в папке ДРТЦ дляЗАО
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В основе временного метода лежит понятие переходной и импульсной характеристик цепи. Переходной характеристикой цепи называют реакцию цепи на воздействие в форме единичной функции (7.19). Обозначается переходная характеристика цепи g(t). Импульсной характеристикой цепи называют реакцию цепи на воздействие единичной импульсной функции (d-функции) (7.21). Обозначается импульсная характеристика h(t). Причем, g(t) и h(t) определяются при нулевых начальных условиях в цепи. В зависимости от типа реакции и типа воздействия (ток или напряжение) переходные и импульсные характеристики могут быть безразмерными величинами, либо имеют размерность А/В или В/А.
Использование понятий переходной и импульсной характеристик цепи позволяет свести расчет реакции цепи от действия непериодического сигнала произвольной формы к определению реакции цепи на простейшее воздействие типа единичной 1(t) или импульсной функции d(t), с помощью которых аппроксимируется исходный сигнал. При этом результирующая реакция линейной цепи находится (с использованием принципа наложения) как сумма реакций цепи на элементарные воздействия 1(t) или d(t).
Между переходной g(t) и импульсной h(t) характеристиками линейной пассивной цепи существует определенная связь. Ее можно установить, если представить единичную импульсную функцию через предельный переход разности двух единичных функций величины 1/t, сдвинутых друг относительно друга на время t (см. рис. 7.4):
т. е. единичная импульсная функция равна производной единичной функции. Так как рассматриваемая цепь предполагается линейной, то соотношение (8.1) сохраняется и для импульсных и переходных реакций цепи
т. е. импульсная характеристика является производной от переходной характеристики цепи.
Уравнение (8.2) справедливо для случая, когда g(0) = 0 (нулевые начальны е условия для цепи). Если же g(0) ¹ 0, то представив g(t) в виде g(t) = 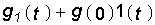
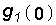
Для нахождения переходных и импульсных характеристик цепи можно использовать как классический, так и операторный методы. Сущность классического метода состоит в определении временной реакции цепи (в форме напряжения или тока в отдельных ветвях цепи) на воздействие единичной 1(t) или импульсной d(t) функции. Обычно классическим методом удобно определять переходную характеристику g(t), а импульсную характеристику h(t) находить с помощью уравнений связи (8.2), (8.3) или операторным методом.
Пример. Найдем классическим методом переходную характеристику по напряжению для цепи, изображенной на рис. 8.1. Численно gu(t) для данной цепи совпадает с напряжением на емкости при подключении ее в момент t= 0 к источнику напряжения U1 = l В:
Закон изменения напряжения uC(t) определяется уравнением (6.27), где необходимо положить U= l В:
При нахождении характеристик g(t) и h(t) операторным методом пользуются изображениями функций 1(t), d(t) и методикой расчета переходных процессов, изложенных в гл. 7.
Пример. Определим операторным методом переходную характеристику gu(t) RС-цепи (см. рис. 8.1). Для данной цепи в соответствии с законом Ома в операторной форме (7.35) можем записать:
где
Окончательно получаем
Отсюда по теореме разложения (7.31) находим
т. е. то же значение, что и полученное классическим методом.
Следует отметить, что величина I(р) в уравнении (8.4) численно равна изображению переходной проводимости. Аналогичное изображение импульсной характеристики численно равно операторной проводимости цепи
Например, для RС-цепи (см. рис. 8.1) имеем:
Применив к Y(p) теорему разложения (7.30), получим:
Следует отметить, что формула (8.5) определяет свободную составляющую реакции цепи при единичном импульсном воздействии. В общем случае в реакции цепи, кроме экспоненциальных составляющих свободного режима при t > 0 присутствует импульсное слагаемое, отображающее воздействие при t = 0 единичного импульса. Действительно, если учесть, что для RС-контура (см. рис. 8.1) переходная характеристика по току при U= 1(t) согласно (6.28) будет
то после дифференцирования (8.6) согласно (8.2) получаем импульсную характеристику RС-цепи hi(t) в виде
т. е. реакция hi(t) содержит два слагаемых — импульсное и экспоненциальное.
Физический смысл первого слагаемого в (8.7) означает, что при t = 0 в результате воздействия на цепь импульсного напряжения d(t) зарядный ток мгновенно достигает бесконечно большого значения, при этом за время от 0– до 0+ элементу емкости передается конечный заряд и она скачком заряжается до напряжения I/RC. Второе слагаемое определяет свободный процесс в цепи при t> 0 и обусловлено разрядом конденсатора через короткозамкнутый вход (так как при t> 0 d(t) = 0, что равносильно КЗ входа) с постоянной времени t = RC. Из этого следует, что при d(t)-импульсном воздействии на RС-цепь нарушается непрерывность заряда на емкости (второй закон коммутации). Аналогично нарушается и условие непрерывности тока в индуктивности (первый закон коммутации), если к цепи, содержащей элемент индуктивности воздействовать напряжением в виде d(t).
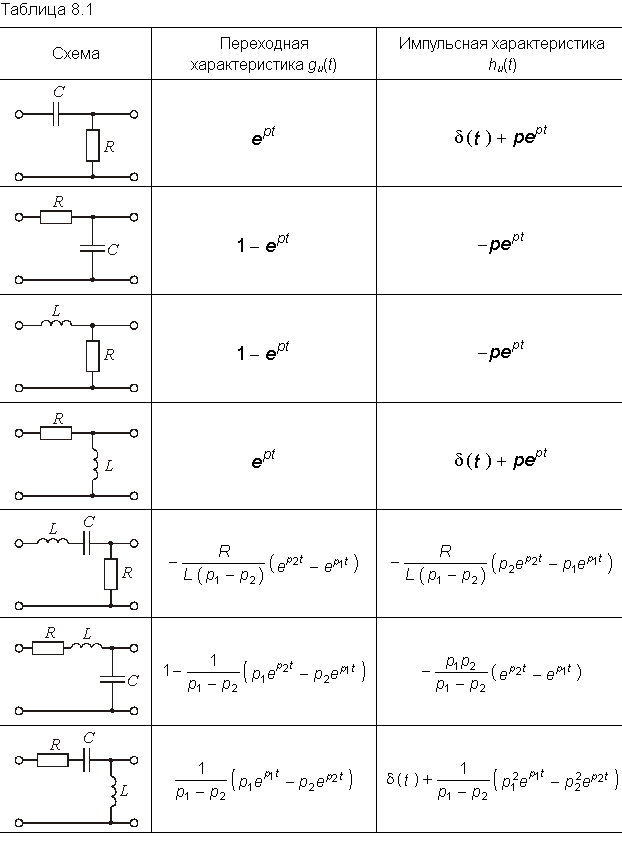
В табл. 8.1 сведены значения переходной и импульсных характеристик по току и напряжению для некоторых цепей первого и второго порядка.
Переходные характеристики цепи
В этой статье рассматривается несколько примеров отыскания переходных функций цепей.
Переходная характеристика цепи 
Чтобы определить переходную характеристику, цепь надо рассчитать так или иначе, например, классическим или операторным методом. В случае использования операторного метода надо не забыть определить оригинал переходной характеристики.
Начнем с простых цепей и попробуем записать для них переходные и импульсные характеристики.
Цепь для расчета
Пример 1. Дана цепь, в которой 

Определяем ток в индуктивности до коммутации (ключ открыт). 
Определяем ток в индуктивности после коммутации (ключ закрыт, переходной процесс завершен) 
Расчет сопротивления
Записываем характеристическое уравнение и находим его корень, для этого исключаем источник из цепи (закорачиваем), разрываем цепь в любом месте, относительно получившихся точек разрыва записываем комплексное сопротивление цепи, где производим замену 



Ток в индуктивности тогда 




Записываем ток в индуктивности: 

Заметим, что пока при расчете мы не акцентировали внимания на том, какой формы напряжение на источнике. Теперь предполагаем, что это единичный источник: E=1 B. Тогда определяем переходные характеристики для тока: 


Вторая схема
Пример 2. Рассчитать переходную характеристику (переходную проводимость) для расчета тока 




Рассчитаем цепь классическим методом. При этом придется сначала определить напряжение на емкости, так как оно подчиняется закону коммутации.
Определяем состояние цепи до коммутации (до подключения источника). В этом случае токи во всех ветвях отсутствуют, конденсатор разряжен: 
После подключения источника и окончания переходного процесса в цепи конденсатор заряжен, ток протекает в контуре 



Запишем теперь характеристическое уравнение цепи. Для этого исключим источник энергии из цепи, и заменим конденсатор его комплексным сопротивлением, при этом заменяем 
Определение сопротивления схемы

откуда 

Напряжение на емкости найдем как сумму свободной и принужденной составляющей:



Тогда можем записать: 
А при подстановке известных чисел получим: 
Определяем постоянную интегрирования, пользуясь законом коммутации:



Тогда напряжение на емкости:

Определим ток в емкости через производную:
Разделив напряжение на емкости на сопротивление 


Осталось определить 
Теперь, предполагая, что источник напряжения – единичный, запишем переходную проводимость:

Схема 3
Пример 3. В данной цепи найти переходные характеристики для отыскания токов 
Составляем операторную схему замещения. Для этой схемы записываем систему уравнений Кирхгофа:
Из этой системы можно выразить по очереди нужные токи, а затем отыскать их оригиналы. Однако эта схема – схема с двумя узлами, а такую схему проще рассчитать методом двух узлов.
Операторная схема замещения
По методу двух узлов записываем напряжение между точками а и b:
Так как 
Найдем сразу корни знаменателя:
Записанное нами напряжение – это уже готовое напряжение на емкости 

Определим оригиналы. Для этого воспользуемся теоремой разложения. Числитель:
Нам понадобится также производная знаменателя:
Определяем оригинал напряжения на емкости:
Для упрощения решения можем определить оригинал тока не по его изображению, а разделив оригинал напряжения на сопротивление резистора 
Зная оригинал напряжения на емкости, можем найти ток в емкости, взяв производную:
Ток 
Если теперь во всех полученных нами выше уравнениях заменить источник на единичный, получим переходные характеристики:
Схема 4
Пример 4. Найти переходную проводимость последовательного RLC контура, параметры которого 


Определяем ток в индуктивности и напряжение на емкости до коммутации (ключ открыт). 
Определяем ток в индуктивности после коммутации (ключ закрыт, переходной процесс завершен) 
Определение сопротивления
Записываем характеристическое уравнение и находим его корень, для этого исключаем источник из цепи (закорачиваем), разрываем цепь в любом месте, относительно получившихся точек разрыва записываем комплексное сопротивление цепи, где производим замену 



Корни: 

Отсюда 

Напряжение на емкости 



откуда

Снова воспользуемся граничными условиями при t=0:

Осталось решить систему:
Выражаем 

Записываем напряжение на емкости: 

тогда ток
Первым слагаемым можно пренебречь по сравнению со вторым, поэтому
Теперь предполагаем, что это единичный источник: E=1 B. Тогда определяем переходную характеристику для тока: 
Демьян Бондарь
Эксперт по предмету «Электроника, электротехника, радиотехника»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Назначение и виды электрических цепей
Определение 1
Частотная характеристика электрической цепи — это зависимость параметров электрической цепи от частоты гармонического воздействия.
Большинство электрических цепей предназначены для передачи сигналов в нагрузку от источника. Электрические колебания, которые создаются на входе цепи называются входным воздействием — x(t). Сигнал, которые образуется на выходе электрической сети называют откликом или выходным сигналом — y (t). Связь между выходным и входным сигналами можно выразить следующим выражением:
$y(t) = Fx((t)a, b, c, …)$
Получается, что отклик зависит от воздействия, параметров элементов цепи (a,b,c), а также ее схемы. При гармоническом воздействии используются комплексные амплитуды, вместо значений сигналов, то есть x(t) – Xm, y(t) – Ym, а уравнение будет иметь следующий вид:
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
$Ym = H(a, b, c) Xm$
где, Н (a, b, c) – параметр электрической цепи, который зависит от элементов цепи и схемы их соединения, представляющий собой комплексную величину.
В зависимости от числа полюсов (выводов) все электрические цепи делятся на двухполюсники, четырехполюсники или многополюсники. Основными параметрами двухполюсников являются комплексное сопротивление и комплексная проводимость. Параметры четырехполюсника делятся на четыре группы: входные (комплексные входные сопротивление и проводимость), передаточные (характеризуют передачу сигналов четырехполюсника в прямом направлении), выходные (выходные сопротивление и проводимость), параметры обратной передачи (характеризуют передачу сигналов в обратном направлении).
Расчет частотных характеристик
В основе расчета частотной характеристики электрической цепи лежит метод комплексных амплитуд. Для простых электрических цепей частотная характеристика может быть найдена по законам Кирхгофа и Ома. Для сложных цепей применяются методы узловых потенциалов, контурных токов, эквивалентных преобразований и другие. Порядок применения метода комплексных амплитуд следующий.
«Расчет частотной и переходной характеристик электрической цепи» 👇
Гармонические напряжения токи (x(t) = Xm cos(wt-фх) всех ветвей меняют на их комплексные амплитуды:
Рисунок 1. Формула. Автор24 — интернет-биржа студенческих работ
От исходной схемы элементов цепи (R, L, C) переходят к комплексной схеме замещения, то есть:
ZR = R; ZL = jwL; ZC = 1 / (jwC).
Затем составляется уравнение электрического равновесия цепи для комплексных изображений напряжений и токов при помощи законов Кирхгофа и Ома, а также другими способами.
Затем уравнение решается относительно комплексных амплитуд искомых напряжений и токов.
Для того, чтобы найти комплексную частотную характеристику цепи записывают отношение комплексной амплитуды отклика к комплексной амплитуде воздействия.
Далее переходят от комплексных амплитуд к гармоническим функциям времени.
Например, для цепи второго порядка комплексную частотную характеристику можно записать в следующем виде:
Рисунок 2. Формула. Автор24 — интернет-биржа студенческих работ
где, H(jw) – амплитудно-частотная характеристика.
Если в числителе и знаменателе выделить мнимые и действительные части и привести подобные члены, то амплитудно-частотная характеристика записывается в показательной форме
Рисунок 3. Формула. Автор24 — интернет-биржа студенческих работ
Откуда получают выражения для расчета фазо-частотной и амплитудно- частотной характеристик.
Рисунок 4. Формулы. Автор24 — интернет-биржа студенческих работ
Методы расчета переходной характеристики. Расчет переходной характеристики по передаточной функции
Определение 2
Передаточная характеристика — это функция времени численно равная реакции электрической цепи на единичное ступенчатое воздействие, которая определяется при нулевых независимых условиях для линейных цепей.
Переходные характеристики в зависимости от типа реакции и воздействия могут быть следующих видов:
- По сопротивлению.
- По току.
- По проводимости.
- По напряжению.
Размерность переходной характеристики зависит от отношения размерности реакции к размерности воздействия. Таким образом по сопротивлению размерность переходной характеристики будет измеряться в Омах, по проводимости в Сименсах, а по току и напряжения будет являться безразмерной величиной. Для расчет переходной характеристики могут применяться следующие методы: практический метод, заключающийся в наблюдении за импульсом на осциллографе; классический метод, который заключается в подключении соответствующего источника через ключ и определении реакции напряжения или тока; операторный метод, заключающийся в определении операторной реакции и нахождении функции времени по операторному коэффициенту передачи.
Допустим, что задана передаточная функция динамического звена, имеющая следующий вид:
Рисунок 5. Функция. Автор24 — интернет-биржа студенческих работ
В этом случае переходную характеристику можно рассчитать по формуле:
Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ
Для определения переходной характеристики в этом случае используется разложение передаточной функции W(p) на сумму простых дробей, то есть:
Рисунок 7. Уравнение. Автор24 — интернет-биржа студенческих работ
Корни уравнения равны:
р1 = -1; р2 = -4; р3 = 0
А коэффициенты К1, К2 и К3:
Рисунок 8. Коэффициенты. Автор24 — интернет-биржа студенческих работ
Затем в формулу для нахождения переходной характеристики подставляем значения К1, К2, К3, р1 и р2 и получаем:
Рисунок 9. Формула. Автор24 — интернет-биржа студенческих работ
Для того, чтобы найти обратное преобразование Лапласа для данной функции используется следующее выражение:
Рисунок 10. Формула. Автор24 — интернет-биржа студенческих работ
где, а и b — некоторые константы.
Получается, что:
Рисунок 11. Формула. Автор24 — интернет-биржа студенческих работ
График найденной переходной характеристики будет выглядеть следующим образом:
Рисунок 12. График. Автор24 — интернет-биржа студенческих работ
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Домашнее задание № 3.2
-
Определить переходную и импульсную характеристику цепи. Входное напряжение
подключено к зажимам 1-1’. Выходное напряжение
снимается с зажимов 2-2’.
-
Пользуясь любой из найденных характеристик, определить реакцию цепи
на заданное входное воздействие
.
: длительность импульса
следует выбрать равной постоянной времени цепи,
-
Построить временную зависимость
. Рассчитать значения
,
,
,
|
R1 |
R2 |
C2 |
|
10 Ом |
10 Ом |
20 мкФ |
-
Определим переходную и импульсную характеристики цепи.
Входное сопротивление цепи:
Ток равняется:
Выходное напряжение найдём по второму закону Кирхгофа:
Тогда передаточная функция цепи:
Подставляя числовые значения, получим:
Переходная характеристика цепи – это реакция цепи на единичное входное воздействие:
Изображение единичной функции , поэтому мы можем найти изображение выходного напряжение при таком воздействии на входе цепи:
Теперь найдём оригинал этого изображения выходного напряжения – это и будет переходная характеристика цепи. Изображение имеет вид дроби , где корни уравнения
равняются
и
. Повторяющихся корней нет. Производная знаменателя:
Так как дробь мы можем представить в виде дроби:
То в нашем случае:
Таким образом:
Оригинал , который и будет переходной функцией, имеет вид:
Импульсная характеристика четырёхполюсника определяется как реакция на входное воздействие, представляющее собой дельта-функцию . Изображение дельта-функции равняется 1, поэтому изображение выходного напряжения имеет вид:
Оригинал этого напряжения будет импульсной характеристикой цепи:
Импульсная характеристика – это производная от переходной характеристики:
-
Определим реакцию цепи
на заданное входное воздействие.
Входное воздействие имеет вид:
Где – постоянная времени цепи. Постоянная времени цепи определяет время, в течении которого напряжение на выходе уменьшается в
раз. В нашем случае
Это входное воздействие можно рассматривать как 3 следующих друг за другом этапа:
– скачок входного напряжения в момент времени от 0 до
– постоянное значение при
– скачок входного напряжения в момент времени от
до 0
Воспользуемся для определения реакции цепи (нахождения ) интегралом Дюамеля:
при :
Первое слагаемое обусловлено скачком в момент времени , второе слагаемое – постоянным значением напряжения на входе цепи в период времени
, равняется 0, так как
.
при
Третье слагаемое обусловлено скачком напряжения в момент . Воспользовавшись единичной функцией
, можем записать для
:
Входной сигнал имеет вид:
Найдём изображение входного напряжения :
Определим реакцию цепи на такое входное воздействие. Изображение выходного напряжения :
Рассмотрим дробь:
Корни уравнения , откуда
и
. Первая производная
. Таким образом:
Таким образом:
Оригинал выходного напряжения имеет вид:
Что совпадает с выходным напряжением, полученным с использованием переходной характеристики цепи.
-
Построим графически зависимость
. Рассчитаем значения
,
,
,
График напряжения :
Рассчитаем значения в моменты времени
. Для этого воспользуемся аналитическим выражением для
.
Для :
Так как выходное напряжение – это напряжение на конденсаторе, поэтому согласно законам коммутации оно не может измениться скачком, а для оно было равно нулю, так как входное напряжение было равно нулю. Таким образом,
.
Для моментов времени и
также
, потому что выходное напряжение – это напряжение на конденсаторе, и оно не может измениться скачком, согласно законам коммутации.
Заметим, что, если бы входное напряжение представляло собой единичный скачок амплитудой бесконечной длительности, то напряжение на конденсаторе для
равнялось бы напряжению на резисторе
в установившемся процессе:
. Но так как длительность единичного импульса ограниченно временем
, равным постоянной времени цепи, то конденсатор не успевает зарядиться до этого значения, и успевает зарядиться только до значения, на
меньшее, а при
разряжается через резистор
.
Для :
При входное напряжение равняется нулю, поэтому при
конденсатор разряжается через резистор
и напряжение на нем, которое равняется выходному, стремится к нулю.
Ответ:
Переходная характеристика цепи:
Импульсная характеристика цепи:
Реакция цепи на заданное входное воздействие:
Сайт управляется системой uCoz



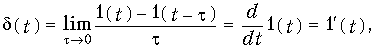
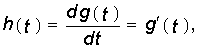
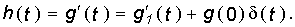
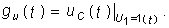
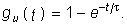
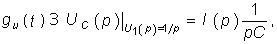
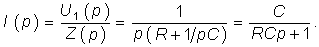
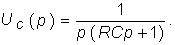
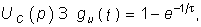
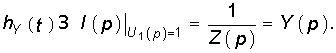
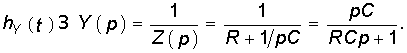
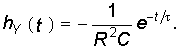
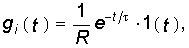
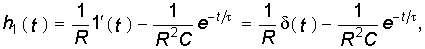























































![toe3_2-12.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-12.jpg)
![toe3_2-13.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-13.jpg)
![toe3_2-14.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-14.jpg)
![toe3_2-17.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-17.jpg)
![toe3_2-31.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-31.jpg)
![toe3_2-40.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-40.jpg)
![toe3_2-52.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-52.jpg)
![toe3_2-57.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-57.jpg)
![toe3_2-62.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-62.jpg)
![toe3_2-67.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-67.jpg)
![toe3_2-76.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-76.jpg)
![toe3_2-77.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-77.jpg)
![toe3_2-85.jpg [image]](http://www.sanish1.narod.ru/toe/toe3.2/toe3_2-85.jpg)
