Здравствуйте!
Извините за вери изи, не догоняю
Как в Си получить значения синуса(допустим 30, 60, 90 градусов). Т.е. я подставляю я sin(30), а он мне 0,5.
Запутался с этими радианами.
Спасибо.
задан 17 дек 2013 в 12:16
ВладиславМСКВладиславМСК
1,51311 золотых знаков37 серебряных знаков59 бронзовых знаков
1
1 ответ
Упс, наоборот сначала написал, градусы в радианы 🙂
sin(grad*(PI/180));
ответ дан 17 дек 2013 в 12:20
3
Функция sin() в C++ возвращает синус угла (аргумента) в радианах.
Эта функция определена в заголовочном файле <cmath>.
[Mathematics] sin x = sin(x) [In C++ Programming]
прототип sin() (в соответствии со стандартом C ++ 11)
double sin(double x); float sin(float x); long double sin(long double x); double sin (T x); // For integral type
Параметры
Функция sin() принимает единственный обязательный аргумент в радианах.
Возвращаемое значение
Функция sin() возвращает значение в диапазоне [-1, 1]. Возвращаемое значение может быть в формате double, float или long double.
Пример 1. Как sin() работает в C ++?
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
double x = 0.439203, result;
result = sin(x);
cout << "sin(x) = " << result << endl;
double xDegrees = 90.0;
// converting degrees to radians
x = xDegrees*3.14159/180;
result = sin(x);
cout << "sin(x) = " << result << endl;
return 0;
}
Когда вы запустите программу, вывод будет:
sin(x) = 0.425218 sin(x) = 1
Пример 2: функция с целым типом
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
int x = -1;
double result;
result = sin(x);
cout << "sin(x) = " << result << endl;
return 0;
}
Когда вы запустите программу, вывод будет:
sin(x) = -0.841471
Читайте также
- 👉 Функция iscntrl() в C++
- 👉 Функция isdigit() в С++
- 👉 Функция isblank() в C++
На чтение 5 мин Просмотров 1.4к. Опубликовано 21.10.2021
В математике функция синуса входит в число трех основных функций, другие включают косинус и тангенс. Методы выполнения основных математических операций, таких как элементарные экспоненциальные, логарифмические, квадратные и математические операции, включены в заголовок <math.h>. Вы должны включить файл заголовка <math.h>, чтобы использовать эти функции. Функция sin принимает угол в радианах и выдает его значение синуса, которое может быть подтверждено с помощью кривой синуса.
Вы можете использовать закон синуса, чтобы найти любой произвольный угол в треугольнике, а также длину определенной стороны треугольника. Это фундаментальное тригонометрическое понятие. Функция sin используется в версиях языка C. ANSI / ISO 9899-1990. Sin () возвращает результат от 1 до -1.
Теперь давайте начнем с нескольких примеров функции sin () на языке программирования C.
Предварительные условия
- Установка компилятора GCC в Windows / Linux
Примечание: мы используем компилятор GCC в Windows 10.
Содержание
- Пример 1
- Пример 2
- Пример 3
- Заключение
Пример 1
В нашей первой иллюстрации мы собираемся использовать функцию sin () в нашей программе. Изначально вам нужно открыть компилятор GCC и создать новый файл с любым требуемым именем. После этого вставьте в него следующий код.

Мы добавили несколько библиотек: <stdio.h> и <math.h>. После добавления перейдите к основной функции. В функции main () мы объявили две переменные, «a» и «result» с типом данных double. Одной из переменных мы присвоили ей значение «7.1» и вычислили ее значение sin; вывод будет сохранен в переменной «результат». Затем мы присвоили отрицательное значение переменной «a» и вычислили ее значение sin. После этого переменной «а» будет присвоен ноль, и результат ее вычисления будет сохранен в переменной «результат». Теперь мы готовы к выполнению программы. В строке меню компилятора GCC вы должны нажать на опцию «Скомпилировать и запустить», чтобы получить результат. Эта опция присутствует в меню «Сборка».

Как только вы нажмете на эту опцию, на вашем экране появится черный экран с названием «Консоль». Вы получите следующий прикрепленный результат, как показано на скриншоте ниже.

Пример 2
Во втором примере мы будем использовать функцию sin () в нашей программе немного сложнее. Изначально вам нужно открыть компилятор GCC и создать новый файл с любым требуемым именем. Также можно использовать предыдущий файл. После этого вставьте в него следующий код.

Мы добавили несколько библиотек: <stdio.h> и <math.h>. Мы добавили значение PI, как видно на скриншоте. После добавления перейдите к основной функции. В функции main () мы объявили три переменные «a», «retu» и «value» с типом данных double. Одной из переменных мы присвоили ей значение «79.0». Мы применили формулу, сохранили ее значение в переменной «retu» и вычислили ее значение sin; затем мы распечатали результат с помощью функции printf (). Теперь мы готовы к выполнению программы. В строке меню компилятора GCC вы должны нажать на опцию «Скомпилировать и запустить», чтобы получить результат. Эта опция присутствует в меню «Сборка».
Как только вы нажмете на эту опцию, на вашем экране появится черный экран с названием «Консоль». Вы получите следующий прикрепленный результат, как показано на прилагаемом ниже снимке экрана.

Пример 3
В нашем третьем и последнем примере мы будем использовать функцию sin () в нашей программе немного по-другому. Этот пользователь должен ввести число во время выполнения, чтобы вычислить значение sin (). Изначально вам нужно открыть компилятор GCC и создать новый файл с любым требуемым именем. Также можно использовать предыдущий файл. После этого вставьте в него следующий код.

Мы добавили несколько библиотек: <stdio.h> и <math.h>. После добавления перейдите к основной функции. В функции main () мы объявили две переменные «Sineval» и «num» с типом данных double. Мы использовали функции printf () и scanf (). После этого мы вычислим sin () введенного пользователем значения и отобразим его результат.
Теперь мы готовы выполнить программу. В строке меню компилятора GCC вы должны нажать на опцию «Скомпилировать и запустить», чтобы получить результат. Эта опция присутствует в меню «Сборка». Как только вы нажмете на эту опцию, на вашем экране появится черный экран с названием «Консоль». Вы получите следующий прикрепленный результат, как показано на скриншоте ниже.

Как видите, мы ввели число «19» и тоже получили его результат. Номер можно выбрать в соответствии с вашими потребностями.

Заключение
Эта статья представляет собой краткое введение в функцию sin () в языке программирования C. Мы разработали три различных примера для понимания пользователями. Все примеры разные по реализации. Теперь я надеюсь, что всякий раз, когда вы пытаетесь реализовать эти примеры в своей системе, вы легко поймете основную концепцию функции sin () в языке программирования C.
Постановка задачи. Вычислить значение тригонометрической функции sin(x) от произвольного значения аргумента x.
Вариант решения 1. Поищем готовый вариант решения. Тригонометрия – раздел математики. Предположим, что в библиотеке System реализован класс, связанный с математическими функциями (в библиотеках прежних языков всегда была функция извлечения квадратного корня из числа – sqrt()). Как же узнать название класса?
Воспользуемся интеллектуальной подсказкой. Внутри метода Main() консольного приложения наберем одну букву M в английской раскладке. В выпадающем меню выберем класс Math (по-английски математика – Mathematics или maths). Наведя мышкой на это слово, прочитаем:
«class System.Math. Предоставляет константы и статические методы для тригонометрических, логарифмических и иных общих математических функций».
Мы почти у цели.
После слова Math ставим точку и снова выбираем что-либо, например метод Sin. Прочтем подсказку:
« double Math.Sin(double a). Возвращает синус указанного угла».
Выбрав Sin, откроем скобку « ( ». Снова появится подсказка:
«double Math.Sin(double a) Возвращает синус указанного угла. a: — Угол, измеряемый в радианах)».
Итак, если нам необходимо вычислить y=sin(x), где переменные x и y должны быть объявлены типом double, то это можно сделать одним оператором:
y = Math.Sin(x);
Если вы обратили внимание на третью подсказку, то вы знаете, или хотите узнать, что за единица измерения угла 1 радиан. В школе чаще всего вас приучили к измерению углов в градусах (прямой угол — 90°, развернутый — 180°, и т.д.), а при необходимости еще и в минутах и секундах.
Разработчики библиотеки не стали вводить еще один новый тип данных («градусный»), но обеспечили возможность для перевода градусов в радианы, добавив константу – число π (double Math.PI).
По определению, 1 радиан — центральный угол, длина дуги которого равна радиусу окружности, 2π радиан = 360°. Вспомните, что длина окружности радиусом R равна 2πR.
Составив пропорцию, вы сможете переводить угол a, заданный в градусах, в угол x, заданный в радианах: x = a· π /180.
Проверка: a=360°, x=2π; a=30°, x=0,523598775598299.
Программа, реализующая вычисление sin(a), угол а задан в градусах, представлена ниже:
using System;
namespace sin_x_ЧерезРяд
{
class Program
{
static void Main(string[] args)
{
Console.Write("Вычисление sin(x)nУгол в градусах = ");
double a = Convert.ToDouble(Console.ReadLine());
double x, y;
x = a * Math.PI / 180;
Console.WriteLine("Угол в радианах = {0}",x);
y = Math.Sin(x);
Console.WriteLine("sin({0})={1}",x,y);
Console.ReadKey();
}
}
}
Результат выполнения программы:
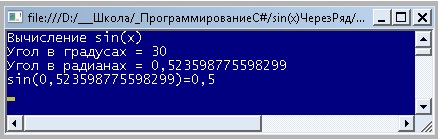
Вариант решения 2.
Понятно, что метод Sin( ) есть некоторая подпрограмма класса Math, которая вызывается по имени. Однако может быть вам будет интересно узнать, как она устроена. Для этого мы дополним наш проект методом Sin2(x), в котором самостоятельно реализуем некоторый алгоритм вычисления sin(x). Тогда библиотечную функцию Sin(x) мы сможем использовать для задания ожидаемого результата при тестировании, а обсуждая алгоритм вычисления Sin2(x), мы освоим элементы языка C# и приобретем некоторые навыки программирования.
Заглянем в справочник по высшей математике, раздел «Ряды». Из него мы узнаем, что функция sin(x) может быть представлена бесконечным рядом:

В теории, вы скажете все красиво, но бесконечный ряд – это бесконечное время вычислений, кроме того, возможно переполнение при возведении в степень и вычислении знаменателя.
Справка. Через n! обозначается функция ФАКТОРИАЛ — произведение целых чисел от 1 до n. По определению 0!=1. Например, 3!=1·2·3; 7!=1·2·…·6·7.
Отметим, что ряд знакопеременный: + , — , + , — , …
Предположим, что |x|<=1. Тогда отношение двух соседних членов ряда rn+2 и rn будет равно:
|rn+2 / rn | = x2 / ((n+2)(n+1)) <= 1/((n+2)(n+1).
То есть каждый следующий член ряда будет вносить в сумму все меньший и меньший вклад, поэтому можно использовать столько членов ряда, сколько нужно для достижения заданной точности вычислений. Например, если n=9, то | r11 / r9 | <=1/110 (более чем в 100 раз).
Что следует предпринять, если |x| >> 1 (много больше 1), ведь в этом случае наш критерий работать не будет? Тут пригодится знание такого свойства функции sin(x) как периодичность. Для угла x, заданного в радианах:
sin(x+2πk) = sin(x), где k – любое целое число, 0, ±1, ±2, ±3, … .
Для угла а, заданного в градусах:
sin(a+360°·k) = sin(a), где k – любое целое число.
Таким образом, если угол х по модулю не будет больше 2π, |x|<=2π, то тогда оценка отношения двух соседних членов ряда не превысит:
|rn+2 / rn | = 4π2 / ((n+2)(n+1))
т.е., начиная с n=7 убывание гарантировано.
Перейдем к программированию функции Sin2(x). Используем принцип 7 – проектирование сверху-вниз. Объявим в классе Program метод:
static double Sin2(double x) { }
а перед оператором Console.ReadKey(); в методе Main() вставим:
y = Sin2(x);
Console.WriteLine(«sin({0})={1}», x, y);
Наша функция, также как и библиотечная, получает на вход значение угла в радианах и возвращает значение sin(x). Тип аргумента и самой функции задан как double. Приступим к разработке начинки метода Sin2() – блока в фигурных скобках.
Реализация 2.
Очевидный, но не лучший алгоритм состоит в непосредственной реализации формулы ряда: начальное значение суммы ряда s = x, затем в цикле for добавлять каждый вычисленный член ряда с чередованием знака rn=xn/n!, для чего будет необходимо написать еще две функции: возведение в степень и вычисление факториала.
Не совсем понятно, сколько раз выполнять цикл. Хотелось бы увязать необходимое число членов ряда с требуемой точностью вычислений eps.
Добавим в метод Sin2() локальную константу double eps = 1E-15.
Вместо цикла for применим цикл while (условие) { }.
Введем две переменные: double r – активный член ряда, int n – степень.
Для учета смены знака используем функцию модуля числа – Math.Abs( ).
Тогда метод Sin2() может быть записан так:
static double Sin2(double x)
{
const double eps = 1e-15; // погрешность вычислений
double s = 0; // начальная сумма
double r = x; // первый член ряда
int n = 1; // показатель степени
while (Math.Abs(r) > eps) // условие выполнения цикла
{
s=s+r; // добавление члена ряда
n = n + 2; // наращивание n: 1,3,5,7,...
r=-r*x*x/(n*(n-1)); // новый член ряда
}
return s; // возврат результата
}
Выполним тестирование программы:
| Угол a, градусы | Угол x, радианы | Sin(x) | Sin2(x) |
| 0 | 0 | 0 | 0 |
| 30 | 0,523598775598299 | 0,5 | 0,5 |
| 60 | 1,0471975511966 | 0,8660254037844439 | 0,8660254037844438 |
| 90 | 1,5707963267949 | 1 | 1 |
| 270 | 4,71238898038469 | -1 | -1 |
| 360 | 6,28318530717959 | -2,45E-16 | -4,16E-15 |
| 10000 | 174,532925199433 | -0,984807753012209 | -3,07952784012437E+58 |
При углах, не превышающих 360°, оба метода дают практически одинаковый результат, погрешность почти не превышает eps=1E-15. При больших значениях углов Sin2() иногда выдает неверный результат (|sin(x)|<=1).
Учтем замечание о периодичности функции sin(x). Для этого вставим сразу после { один оператор, позволяющий учесть периодичность функции:
x = x — 2 * Math.PI * Math.Truncate(x/(2*Math.PI));
Примечание. Функция Truncate( ) класса Math вычисляет целую часть числа двойной точности с плавающей запятой.
Протестируйте результирующую программу sin_x_ЧерезРяд для произвольных углов. В частности, Sin2(10000°)=-0,984807753012207.
Следующая учебная задача «Бином Ньютона».
NEW: Наш Чат, в котором вы можете обсудить любые вопросы, идеи, поделиться опытом или связаться с администраторами.
Помощь проекту:
Прототип функции sin:
double sin ( double agl ); float sin ( float agl ); long double sin( long double agl );
Заголовочный файл
| Название | Язык |
|---|---|
| math.h | С |
| cmath | С++ |
Описание
Вычисление синуса, функция sin возвращает синус угла agl, переведенного в радианы. В C++, эта функция перегружена в заголовочных файлах <complex> и <valarray> (смотреть sin комплексных чисел и sin в библиотеке массивов числовых значений).
В Си, определён только один прототип этой функции, с типом данных double.
Параметры:
- agl
Значение с плавающей точкой, представляющее угол в радианах.
Возвращаемое значение
Синус угла agl.
Пример: исходный код программы
// пример использования функции синуса: sin
#include <iostream> // для оператора cout
#include <cmath> // для функции sin
#define PI 3.14159265 // число ПИ
int main()
{
double param = 30.0; // угол 30 градусов
std::cout << "Cинус угла " << param
<< " градусов = " << sin(param * PI / 180) // вычисляем синус угла, переведённого в радианы
<< std::endl;
return 0;
}
Пример работы программы
CppStudio.com
Cинус угла 30 градусов = 0.5
