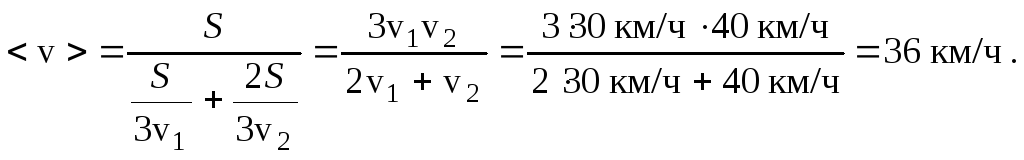Как найти перемещение решение задач - Сайт, где вы сможете решить свои вопросы

Пример №1

Допустим, из точки ( displaystyle A) и из точки ( displaystyle B) навстречу друг другу выехали две машины. Скорость одной машины – ( displaystyle 60) км/ч, а скорость ( displaystyle 2) машины – ( displaystyle 40) км/ч. Они встретились через ( displaystyle 1,2) часа.

Какое расстояние между пунктами ( displaystyle A) и ( displaystyle B)?

1 вариант решения

Можно рассуждать так: машины встретились, значит расстояние между городами – это сумма расстояния, которая прошла первая машина, и расстояния, которое прошла вторая.

( displaystyle 60cdot 1,2text{ }=text{ }72) (км) – путь, который проехала первая машина

( displaystyle 40cdot 1,2text{ }=text{ }48) (км) – путь, который проехала вторая машина

( displaystyle 72 + 48 = 120) (км) – расстояние, которое проехали обе машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).

2 вариант решения (более рациональный)

А можно просто воспользоваться очень логичной формулой о сложении скоростей.

Проверим, работает ли она:

( displaystyle 60 + 40 = 100) (км/ч) – скорость сближения машин

( displaystyle 100cdot 1,2text{ }=text{ }120) (км) – расстояние, которые проехали машины, то есть, расстояние между пунктами ( displaystyle A) и ( displaystyle B).

Оба решения являются верными. Второе просто более рациональное.

Пример №3

Итак, задача:

Из пункта ( displaystyle A) и пункта ( displaystyle B) машины движутся навстречу друг другу со скоростями ( displaystyle 50) км/ч и ( displaystyle 80) км/ч. Расстояние между пунктами – ( displaystyle 195) км.

Через сколько времени машины встретятся?

1 вариант решения

Пусть ( displaystyle x) – время, которое едут машины, тогда путь первой машины – ( displaystyle 50x), а путь второй машины – ( displaystyle 80x).

Их сумма и будет равна расстоянию между пунктами ( A) и ( B) – ( displaystyle 50x+80x=195).

Решим уравнение:

( displaystyle 50x+80x=195)

( displaystyle 130x=195)

( displaystyle x=1,5) (ч) – время, через которое встретились машины.

2 вариант решения (более рациональный)

( displaystyle 50 + 80 = 130) (км/ч) – скорость сближения машин;

( displaystyle 195:130 = 1,5) (ч) – время, которое машины были в пути.

Задача решена.

Пример №4

Из пунктов A и B одновременно навстречу друг другу выехали два автомобиля со скоростями ( displaystyle 60) км/ч и ( displaystyle 40) км/ч. Через сколько минут они встретятся. Если расстояние между пунктами ( displaystyle 100) км?

2 способа решения:

I способ

Относительная скорость автомобилей ( displaystyle 60+40=100) км/ч. Это значит, что если мы сидим в первом автомобиле, то он нам кажется неподвижным, но второй автомобиль приближается к нам со скоростью ( displaystyle 100) км/ч. Так как между автомобилями изначально расстояние ( displaystyle 100) км, время, через которое второй автомобиль проедет мимо первого:

( displaystyle t=frac{100}{100}=1 час=60 минут).

II способ

Время от начала движения до встречи у автомобилей, очевидно, одинаковое. Обозначим его ( displaystyle t). Тогда первый автомобиль проехал путь ( displaystyle 60t), а второй – ( displaystyle 40t).

В сумме они проехали все ( displaystyle 100) км. Значит,

( displaystyle 60t+40t=100Rightarrow t=1 час=60 минут).

Из пункта ( displaystyle A) в пункт ( displaystyle B), расстояние между которыми ( displaystyle 30) км, одновременно выехал велосипедист и мотоциклист. Известно, что в час мотоциклист проезжает на ( displaystyle 65) км больше, чем велосипедист.

Определите скорость велосипедиста, если известно, что он прибыл в пункт ( displaystyle B) на ( displaystyle 156) минут позже, чем мотоциклист.

Вот такая вот задача. Соберись, и прочитай ее несколько раз. Прочитал? Начинай рисовать – прямая, пункт ( displaystyle A), пункт ( displaystyle B), две стрелочки…

В общем рисуй, и сейчас сравним, что у тебя получилось.

Пустовато как-то, правда? Рисуем таблицу.

Как ты помнишь, все задачи на движения состоят из ( displaystyle 3) компонентов: скорость, время и путь. Именно из этих граф и будет состоять любая таблица в подобных задачах.

Правда, мы добавим еще один столбец – имя, про кого мы пишем информацию – мотоциклист и велосипедист.

Так же в шапке укажи размерность, в какой ты будешь вписывать туда величины. Ты же помнишь, как это важно, правда?

У тебя получилась вот такая таблица?

	Скорость, км/ч	Время t, часов	Путь S, км
велосипедист
мотоциклист

Теперь давай анализировать все, что у нас есть, и параллельно заносить данные в таблицу и на рисунок.

Первое, что мы имеем – это путь, который проделали велосипедист и мотоциклист. Он одинаков и равен ( displaystyle 30) км. Вносим!

	Скорость, км/ч	Время t, часов	Путь S, км
велосипедист			( displaystyle 30)
мотоциклист			( displaystyle 30)

Рассуждаем дальше. Мы знаем, что мотоциклист проезжает на ( displaystyle 65) км/ч больше, чем велосипедист, да и в задаче нужно найти скорость велосипедиста…

Возьмем скорость велосипедиста за ( displaystyle x), тогда скорость мотоциклиста будет ( displaystyle x+65)…

Если с такой переменной решение задачи не пойдет – ничего страшного, возьмем другую, пока не дойдем до победного. Такое бывает, главное не нервничать!

	Скорость, км/ч	Время t, часов	Путь S, км
велосипедист	( displaystyle x)		( displaystyle 30)
мотоциклист	( displaystyle x+65)		( displaystyle 30)

Таблица преобразилась. У нас осталась не заполнена только одна графа – время. Как найти время, когда есть путь и скорость?

Правильно, разделить путь на скорость. Вноси это в таблицу.

	Скорость, км/ч	Время t, часов	Путь S, км
велосипедист	( displaystyle x)	( displaystyle frac{30}{x})	( displaystyle 30)
мотоциклист	( displaystyle x+65)	( displaystyle frac{30}{65+x})	( displaystyle 30)

Вот и заполнилась наша таблица, теперь можно внести данные на рисунок.

Что мы можем на нем отразить?

Молодец. Скорость передвижения мотоциклиста и велосипедиста.

Еще раз перечитаем задачу, посмотрим на рисунок и заполненную таблицу.

Какие данные не отражены ни в таблице, ни на рисунке?

Верно. Время, на которое мотоциклист приехал раньше, чем велосипедист. Мы знаем, что разница во времени – ( displaystyle 156) минут.

Что мы должны сделать следующим шагом? Правильно, перевести данное нам время из минут в часы, ведь скорость дана нам в км/ч.

( displaystyle 156) минут / ( displaystyle 60) минут = ( displaystyle 2,6) часа.

И что дальше, спросишь ты? А дальше числовая магия!

Взгляни на свою таблицу, на последнее условие, которое в нее не вошло и подумай, зависимость между чем и чем мы можем вынести в уравнение?

Правильно. Мы можем составить уравнение, основываясь на разнице во времени!

( displaystyle frac{30}{x}-frac{30}{65+x}=2,6)

Логично? Велосипедист ехал больше, если мы из его времени вычтем время движения мотоциклиста, мы как раз получим данную нам разницу.

Это уравнение – рациональное. Если не знаешь, что это такое, прочти тему «Рациональные уравнения».

Приводим слагаемые к общему знаменателю:

( displaystyle frac{30cdot left( 65+x right)}{xcdot left( 65+x right)}-frac{30x}{xcdot left( 65+x right)}=2,6)

Раскроем скобки и приведем подобные слагаемые: Уф! Усвоил? Попробуй свои силы на следующей задаче.

( displaystyle frac{1950}{xcdot left( 65+x right)}=2,6)

Из этого уравнения мы получаем следующее:

( displaystyle 2,6cdot xcdot left( 65+x right)=1950)

( displaystyle xcdot left( 65+x right)=frac{1950}{2,6})

( displaystyle xcdot left( 65+x right)=750)

Раскроем скобки и перенесем все в левую часть уравнения:

( displaystyle {{x}^{2}}+65{x}-750=0)

Вуаля! У нас простое квадратное уравнение. Решаем!

( displaystyle {{x}^{2}}+65{x}-750=0)

( displaystyle D={{b}^{2}}-4ac)

( displaystyle D={{65}^{2}}-4cdot 1cdot left( -750 right)=4225+3000=7225)

( displaystyle sqrt{D}=sqrt{7225}=85)

( displaystyle {{x}_{1,2}}=frac{-bpm sqrt{D}}{2a})

( displaystyle {{x}_{1}}=frac{-65+85}{2}=10)

( displaystyle {{x}_{2}}=frac{-65-85}{2}=-75)

Мы получили два варианта ответа. Смотрим, что мы взяли за ( displaystyle x)? Правильно, скорость велосипедиста.

Вспоминаем правило «3Р», конкретнее «разумность». Понимаешь, о чем я? Именно! Скорость не может быть отрицательной, следовательно, наш ответ – ( displaystyle 10) км/ч.

Пример №9

Два велосипедиста одновременно отправились в ( displaystyle 165)-километровый пробег. Первый ехал со скоростью, на ( displaystyle 5) км/ч большей, чем скорость второго, и прибыл к финишу на ( displaystyle 5,5) часов раньше второго.

Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.

Напоминаю:

Прочитай задачу пару раз – усвой все-все детали. Усвоил?
Начинай рисовать рисунок – в каком направлении они двигаются? какое расстояние они прошли? Нарисовал?
Проверь, все ли величины у тебя одинаковой размерности, и начинай выписывать кратко условие задачи, составляя табличку (ты же помнишь, какие там графы?).
Пока все это пишешь, думай, что взять за ( displaystyle x)? Выбрал? Записывай в таблицу!
Ну а теперь просто: составляем уравнение и решаем. Да, и напоследок – помни о «3Р»!

Все сделал? Молодец! У меня получилось, что скорость велосипедиста – ( displaystyle 10) км/ч.

Пример №10

Из пункта ( displaystyle A) круговой трассы выехал велосипедист. Через ( displaystyle 40) минут он еще не вернулся в пункт ( displaystyle A) и из пункта ( displaystyle A) следом за ним отправился мотоциклист.

Через ( displaystyle 20) минут после отправления он догнал велосипедиста в первый раз, а еще через ( displaystyle 40) минут после этого догнал его во второй раз.

Найдите скорость велосипедиста, если длина трассы равна ( displaystyle 50) км. Ответ дайте в км/ч.

Попробуй нарисовать рисунок к этой задаче и заполнить для нее таблицу. Вот что получилось у меня:

Пусть скорость велосипедиста будет ( displaystyle x), а мотоциклиста – ( displaystyle y). До момента первой встречи велосипедист был в пути ( displaystyle 60) минут, а мотоциклист – ( displaystyle 20).

При этом они проехали равные расстояния:

( displaystyle 60x=20y (1))

Между встречами велосипедист проехал расстояние ( displaystyle 40x), а мотоциклист – ( displaystyle 40y).

Но при этом мотоциклист проехал ровно на один круг больше, это видно из рисунка:

(Надеюсь, ты понимаешь, что по спирали они на самом деле не ездили – спираль просто схематически показывает, что они ездят по кругу, несколько раз проезжая одни и те же точки трассы.)

Значит,

( displaystyle 40x+50=40y (2))

Полученные уравнения решаем в системе:

( displaystyle left{ begin{array}{l}60x=20y\40x+50=40yend{array} right.Leftrightarrow left{ begin{array}{l}y=3x\4x+5=4yend{array} right.Rightarrow text{4}x+5=12xRightarrow )

( displaystyle Rightarrow x=frac{5}{8}=0,625frac{text{км}}{мин}=0,625cdot 60frac{text{км}}{text{ч}}=37,5frac{text{км}}{text{ч}})

Ответ: ( displaystyle 37,5).

Разобрался? Попробуй решить самостоятельно следующие задачи:

Представь, что у тебя есть плот, и ты спустил его в озеро. Что с ним происходит? Правильно. Он стоит, потому что озеро, пруд, лужа, в конце концов, – это стоячая вода.

Скорость течения в озере равна ( displaystyle 0).

Плот поедет, только если ты сам начнешь грести. Та скорость, которую он приобретет, будет собственной скоростью плота. Неважно куда ты поплывешь – налево, направо, плот будет двигаться с той скоростью, с которой ты будешь грести.

Это понятно? Логично же.

А сейчас представь, что ты спускаешь плот на реку, отворачиваешься, чтобы взять веревку…, поворачиваешься, а он … уплыл…

Это происходит потому что у реки есть скорость течения, которая относит твой плот по направлению течения.

Его скорость при этом равна нулю (ты же стоишь в шоке на берегу и не гребешь) – он движется со скоростью течения.

Разобрался? Тогда ответь вот на какой вопрос – «С какой скоростью будет плыть плот по реке, если ты сидишь и гребешь?» Задумался?

Здесь возможно два случая:

1 случай – ты плывешь по течению, и тогда ты плывешь с собственной скоростью + скорость течения. Течение как бы помогает тебе двигаться вперед.

2 случай – ты плывешь против течения. Тяжело? Правильно, потому что течение пытается «откинуть» тебя назад. Ты прилагаешь все больше усилий, чтобы проплыть хотя бы ( displaystyle 100) метров, соответственно скорость, с которой ты передвигаешься, равна собственная скорость – скорость течения.

Источник

Достаточно большой класс задач физики связан с исследованием траектории движения тела. Классическими вопросами таких задач являются вопросы о пути и перемещении тела. Рациональней всего в этом случае просто увидеть параметры, необходимые для нахождения в задаче, т.е. нарисовать рисунок и посмотреть на форму траектории движения тела.

Чаще всего для нахождения искомых параметров достаточно помнить изречение моего учителя: «Ваша траектория является или частью чего-то геометрического (окружности, треугольника, трапеции и т.д.) или состоит из чего-то геометрического (несколько отрезков, дуги окружностей и т.д.)». Определив составные части и зная математические формулы нахождения каждой из них, вы получаете ответ.

Мяч упал с высоты отскочил от пола и был пойман на высоте…
Спортсмен на тренировке пробежал N кругов радиусом R…
Строительный кран поднимает груз на высоту h. Одновременно кран передвигается на расстояние l…
Определить путь и модуль перемещения конца часовой стрелки длиной l за промежуток времени…
Человек прошел по проспекту 240 м, затем повернул на перекрестке и прошел в перпендикулярном направлении еще 70 м…
Часовой охраняет объект, огороженный квадратным забором ABCD, обходя его по периметру. Чему будут равны его путь…

Источник

Задача. Для балки определить перемещения в т. А, В, С, D, подобрать сечение из двух швеллеров из условия прочности, проверить жесткость, показать изогнутую ось балки. Материал — сталь Ст3, допускаемое перемещение .

Определим опорные реакции.

Наносим значение опорных реакций на расчетную схему

2. Строим эпюру моментов от заданной нагрузки – грузовую эпюру М_F.

Т.к. под равномерно распределенной нагрузкой линия параболическая кривая, то для её проведения потребуется дополнительная точка – поставим т.К в середине нагрузки.

Строим эпюру М_F от заданной нагрузки.

3. Подберем сечение из двух швеллеров:

Подбираем 2 швеллера №33 см³.

Проверим прочность подобранного сечения.

Прочность обеспечена.

4. Определим перемещения в заданных точках. Снимаем с балки всю нагрузку. Для определения линейных перемещений (прогибов) прикладываем единичную силу (F=1), а для определения угловых перемещений — единичный момент .

Точки А и В – это опоры, и по граничным условиям в шарнирных опорах прогиб невозможен, а угловое перемещение присутствует. В точках С и D будут и линейные (прогибы), и угловые (углы поворота) перемещения.

Определим угловое перемещение в т.А. Прикладываем в А единичный момент (рис. б). Строим эп , определяем в ней необходимые ординаты. (рис. в).

Ординаты эп.М_F – все положительные, эп. – тоже.

Перемещения будем определять методом Мора по формуле Симпсона.

Определим момент инерции I_х для сечения.

Модуль продольной упругости Е для Ст3 Е = 2·10⁵МПа = 2·10⁸кПа. Тогда:

Угол поворота φ_А получился положительным, это значит, что угол поворота сечения совпадает с направлением единичного момента.

Определим угол поворота φ_В. (рис.г,д )

Теперь определим перемещения в т. С (линейное и угловое). Прикладываем единичную силу (рис. е), определяем опорные реакции и строим эп. от единичной силы (рис.ж).

Рассмотрим рис. е.

Строим эп. :

Определим прогиб в т. С.

Для определения угла поворота в т. С приложим единичный момент (рис. з), определим опорные реакции и построим эпюру единичных моментов (рис. и).

(знак “— “ говорит о том, что реакция R_А направлена в обратную сторону. Показываем это на расчетной схеме – рис.з).

Строим эп. ,

Поскольку m=1 приложен в т. С пролета балки, то момент в т. С определим как от левых, так и от правых сил.

Определим прогиб в точке С.

(знак «-» говорит о том, что угол поворота направлен противоположно направлению единичного момента)

Аналогично определим линейное и угловое перемещения в т. D.

Определим у_D. (рис. к).

Строим эп. (рис.л) :

Определим φ_D (рис. м):

Строим эп. — (рис.н).

Определим угол поворота:

(угол поворота направлен в сторону, противоположную единичному моменту).

Теперь покажем изогнутую ось балки (упругую линию), которой стала прямолинейная ось под действием нагрузки. Для этого зарисуем первоначальное положение оси и в масштабе отложим вычисленные перемещения (рис.о).

Проверим жесткость балки , где f – максимальный прогиб.

Максимальный прогиб — жесткость не обеспечена.

Т.о. в данной задаче мы убедились в том, что не всегда сечения, подобранные из условия прочности (в данном случае – сечение из двух швеллеров) удовлетворяют условиям жесткости.

Задача. Определить горизонтальное перемещение свободного конца рамы по интегралу Мора

1. Составляем выражение изгибающего момента M_F от действующей нагрузки.

2. Снимаем с балки все нагрузки, и в точке, где необходимо определить перемещение, прикладываем единичную силу (если определяем линейное перемещение) либо единичный момент (если определяем угловое перемещение) по направлению искомого перемещения. В нашей задаче прикладываем горизонтальную единичную силу. Составляем выражение изгибающего момента.

Определяем моменты от единичной нагрузки F=1

По интегралу Мора вычисляем горизонтальное перемещение:

Перемещение имеет положительное значение. Это значит, что оно соответствует направлению единичной силы.

Интеграл Мора, формула Мора. В криволинейном брусе определить горизонтальное перемещение точки А. Жесткость в пределах всей длины бруса постоянна.

Ось бруса очерчена по параболе, уравнение которой:

Учитывая, что брус безраспорный и достаточно пологий (f/ι = 3/15 = 0,2), влиянием продольных и поперечных сил пренебрегаем. Поэтому для определения перемещения воспользуемся формулой:

Так как жесткость EJ постоянна, то:

Составим выражение M₁ для действительного состояния бруса (1-го состояния) (рис. а):

Снимаем с бруса все нагрузки и прикладываем в точке А горизонтальную единичную силу (2-е состояние) (рис. б). Составляем выражение для :

Вычисляем искомое перемещение в точке А:

Знак минус указывает на то, что перемещение точки А противоположно направлению единичной силы, т.е. это точка смещается по горизонтали влево.

Интеграл Мора, формула Мора.Определить угол поворота шарнирной опоры D для рамы с определенными опорными реакциями, Жесткости элементов указаны на расчетной схеме.

Составим выражение М₁, используя схему системы в 1-м состоянии. М₁ – функция внутреннего изгибающего момента на силовом участке для заданной балки или рамы от действия заданных нагрузок 1-го состояния.

Освобождаем раму от нагрузок, прикладываем единичный момент на опоре D, получаем систему второго состояния.

Составляем выражения – это функция внутреннего изгибающего момента на силовом участке для вспомогательной системы 2- го состояния, нагруженной единичным усилием:Находим искомое перемещение — угол поворота по формуле (интегралу) Мора:Значение угла поворота положительно, значит направление соответствует выбранному направлению единичного момента.

Интеграл Мора (формула Мора). Для рамы определить горизонтальное перемещение точки C. Жесткости элементов указаны на рисунке. Назовем заданную систему системой первого состояния. . Составляем для каждого элемента выражение М₁, пользуясь схемой 1-го состояния системы:

Снимаем с рамы все нагрузки и получим 2-е состояние рамы, приложив по направлению искомого перемещения горизонтальную единичную силу. Составляем выражение единичных моментов : . Вычисляем по формуле (интегралу) Мора искомое перемещение:

Тогда получим:

Знак минус указывает, что направление перемещения противоположно направлению единичной силы.

Для стальной балки подобрать размеры поперечного сечения, состоящего из двух двутавров, на основе условия прочности по нормальным напряжениям, построить эпюры линейных и угловых перемещений. Дано:

Расчет опорных реакций и значений грузовой эпюры (эпюры изгибающих моментов) приводить не будем, покажем без расчетов. Итак, грузовая эпюра моментов:

При этом на эпюре М у значений изгибающих моментов отсутствуют знаки, указываются волокна, испытывающие сжатие. Как видно из эпюры, в опасном сечении: М_С=М_max=86,7кНм.

Подберем сечение из двух двутавров. Из условия прочности:

Согласно сортаменту прокатной стали выбираем двутавр №27а, у которого I_x₁=5500см³, h=27см. Фактическое значение осевого момента сопротивления всего сечения W_x=2I_x₁/(h/2)=2·5500/(27/2)=815см^3.

Вычисляем линейные и угловые перемещения сечения балки методом О.Мора, применяя формулу Симпсона. Выбор количества сечений, необходимого для построения эпюр линейных и угловых перемещений в балке, зависит от числа участков и характера эпюры изгибающих моментов. В рассматриваемой балке к таким можно отнести сечения А, B, C, D (принадлежат границам силовых участков) и сечения 1, 2, 3 – в середине участков (определение перемещений в этих сечениях повышает точность построения эпюр).

Сечение А. Как известно, линейное перемещение сечения в шарнирной опоре y_A=0.

Для вычисления углового перемещения θ_а загружаем вспомогательную систему единичной парой сил -моментом, равным единицеУравнения равновесия

Решая уравнения равновесия, получим:

Определяем значения моментов в характерных сечениях

Участок АD:

В середине участка АВ значение изгибающего момента грузовой эпюры M_F равно f=73,3·1- 80·1²/2=33,3кНм

Определяем угловое перемещение сечения А по формуле Симпсона:

Угловое перемещение сечения А направлено против часовой стрелки (противоположно действию единичного момента).

Сечение В

Прикладываем в сечении В силу, равную единице, для определения линейного перемещения, и строим единичную эпюру моментов

Уравнения равновесия:

Из решения уравнений равновесия следует:

Определяем значения моментов в характерных сечениях:

Определяем линейное перемещение y_В.

Линейное перемещение y_В=3,65×10^-3м направлено вверх (противоположно действию единичной силы).

Для определения углового перемещения в сечении В прикладываем единичный момент и строим единичную эпюру моментов.

В результате «перемножения» единичной эпюры и грузовой эпюры получим угловое перемещение:

Угловое перемещение направлено против часовой стрелки.

Сечение С.

Линейное перемещение:

Линейное перемещение y_С=5,4 ×10^{-3 м} направлено вверх.

Угловое перемещение:

Угловое перемещение направлено по часовой стрелке.

Сечение D. Линейное перемещение в данном сечении равно нулю.

Угловое перемещение:

Угловое перемещение направлено по часовой стрелке.

Дополнительные сечения:

Сечение 1 (z=0,5ℓ)

Линейное перемещение y₁=1,34×10^-3м направлено вверх;

Угловое перемещение:

Угловое перемещение направлено против часовой стрелки.

Аналогично строим единичные эпюры для сечения 2 (z=1,5ℓ) и сечения 3 (z=2,5ℓ),находим перемещения.

Применяя правило знаков для линейных перемещений вверх — плюс, вниз — минус, а для угловых перемещений против часовой стрелки — плюс, по часовой стрелке – минус, строим эпюры линейных и угловых перемещений y и θ.

Для балки определить максимальный прогиб и максимальный угол поворота.

Ввиду симметрии нагрузки опорные реакции А=В=ql/2

Дифференциальное уравнение изогнутой оси балки:

Интегрируем данное уравнение дважды. После первого интегрирования получаем уравнение углов поворота:

(а)

После второго интегрирования получаем уравнение прогибов:

(б)

Необходимо определить значение постоянных интегрирования — С и Д. Определим их из граничных условий. В сечениях А и В балка имеет шарнирные опоры, значит прогибы в них равны нулю. Следовательно, имеем граничные условия:

1) z = 0, y = 0.

2) z = l, y = 0.

Используем первое граничное условие: z = 0, y = 0.

Тогда из (б) имеем:

Второе граничное условие при z =l дает:

, откуда:

Окончательно получаем.

Уравнение углов поворота:

Уравнение прогибов:

При угол поворота равен нулю, а прогиб будет максимальным:

Знак минус говорит о том, что при принятом положительном направлении оси вверх, прогиб будет направлен вниз.

Наибольшее значение угол поворота имеет на опорных сечениях, например, при

z = 0:

Знак минус говорит о том, что угол поворота при z = 0 направлен по часовой стрелке.

Для рамы требуется определить угол поворота сечения 1 и горизонтальное перемещение сечения 2.

Дано: L=8 м, F=2 кН, q=1 кН/м, h=6 м, моменты инерции I₁=I, I₂=2I

1. Определяем опорные реакции и строим грузовую эпюру:

а) Определяем опорные реакции:

Проверка сошлась. Вертикальные реакции определены верно. Для определения горизонтальных реакций нужно использовать свойство шарнира, а именно — записать уравнение моментов относительно шарнира от всех сил, расположенных с одной стороны рамы.

Проверка сошлась, значит, горизонтальные реакции определены верно.

б) Строим грузовую эпюру — эпюру от заданной нагрузки. Грузовую эпюру будем строить на растянутых волокнах.

Разбиваем раму на участки. На каждом участке намечаем сечения в начале и конце участка, а на участках с распределенной нагрузкой дополнительное сечение в середине. В каждом сечении определяем значение внутреннего изгибающего момента по правилу: изгибающий момент равен алгебраической сумме моментов всех внешних сил, расположенных с одной стороны от сечения, относительно центра этого сечения. Правило знаков для изгибающего момента: момент считается положительным, если он растягивает нижние волокна.

Строим грузовую эпюру.

2.Определяем угол поворота сечения (1)

а) Для того, чтобы определить угол поворота указанного сечения, нужно зарисовать исходную раму без внешней нагрузки и к заданному сечению приложить единичный момент.

Сначала определяем реакции:

Строим единичную эпюру моментов.

б) Определяем угол поворота по формуле Симпсона, подставив I₁=I, I₂=2I:

Знак « — » означает, что поворот сечения происходит против направления единичного момента, т.е. по часовой стрелке.

3. Определяем горизонтальное перемещение сечения (2).

а) Для того, чтобы определить горизонтальное перемещение в указанном сечении, нужно зарисовать исходную раму без внешней нагрузки и к заданному сечению приложить в горизонтальном направлении единичную силу.

Определяем реакции:

Строим единичную эпюру моментов

б) Определяем горизонтальное перемещение сечения (2) по формуле Симпсона:

Результат получился с «+», значит точка (2) перемещается по направлению единичной силы, т.е. вправо.

Для балки определить линейные и угловые перемещения в точках A, B, C, предварительно подобрав сечение двутавра из условия прочности.

Дано: a=2 м, b=4 м, с=3 м, F=20 кН, М=18 кНм, q=6 кН/м, σ_adm=160 МПа, Е=2 10⁵ МПа

1) Вычерчиваем схему балки, определяем опорные реакции. В жёсткой заделке возникает 3 реакции — вертикальная и горизонтальная, а так же опорный момент. Поскольку горизонтальных нагрузок нет – соответствующая реакция равна нулю. Для того, чтобы найти реакции в точке E, составим уравнения равновесия.

∑F_y= 0 q7-F+R_E=0

R_E=-q7+F=-67+20=-22кН (знак говорит о том, что реакция направлена в обратную сторону, показываем это на схеме)

Найдем опорный момент в жесткой заделке, для чего решим уравнение моментов относительно любой выбранной точки.

∑M_C: -M_E-R_E9-F6-q77/2-M=0

M_E=-18-229+649/2=-18-198+147=-69кНм (знак говорит о том, что реакция направлена в обратную сторону, показываем это на схеме)

Далее требуется выполнить проверку правильности определения реакций, составив уравнение равновесия относительно любой точки, к примеру, точки Е, ∑M_Е= 0.

2) Строим грузовую эпюру M^F– эпюру моментов от заданной нагрузки.

Для построения эпюр моментов найдем моменты в характерных точках. В точке В определяем моменты как от правых, так и от левых сил, поскольку в этой точке приложен момент.

Для построения эпюры момента на линии действия распределенной нагрузки (участки АВ и ВС) нам нужны дополнительные точки для построения кривой. Определим моменты в серединах этих участков. Это моменты в серединах участков АВ и ВС 15,34 кНм и 23,25кНм. Строим грузовую эпюру.

3) Для определения линейных и угловых перемещений в точке необходимо приложить в этой точке, в первом случае, единичную силу (F=1) и построить эпюру моментов, во втором случае, единичный момент (M=1) и построить эпюру моментов. Строим эпюры от единичных нагрузок для каждой точки – А, В и С.

4) Для нахождения перемещений мы используем формулу Симпсона.

где l_i– длина участка;

EI_i– жесткость балки на участке;

M_F – значения изгибающих моментов с грузовой эпюры, соответственно в начале, в середине и в конце участка;

– значения изгибающих моментов с единичной эпюры, соответственно в начале, в середине и в конце участка.

Если ординаты эпюр расположены с одной стороны от оси балки, то при перемножении учитывается знак «+», если с разных, то знак «-».

Если результат получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением соответствующего единичного силового фактора.

Рассмотрим применение формулы Симпсона на примере определения перемещений в точке А.

Определим прогиб, перемножив грузовую эпюру на эпюру от единичной силы.

Прогиб получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением единичной силы (направлено вверх).

Определим угол поворота, перемножив грузовую эпюру на эпюру от единичного момента.

Угол поворота получился со знаком «-», значит искомое перемещение по направлению не совпадает с направлением соответствующего единичного момента (направлен против часовой стрелки).

5) Для определения конкретных значений перемещений требуется подобрать сечение. Подберем сечение двутавра

где M_max – это максимальный момент на грузовой эпюре моментов

Подбираем по сортаменту двутавр №30 с W_x=472см³ и I_x= 7080см⁴

6) Определяем перемещения в точках, раскрывая жесткость сечения: E – модуль продольной упругости материала или модуль Юнга (2 10⁵МПа), J_x – осевой момент инерции сечения

Прогиб в точке А (вверх)

Угол поворота (против часовой стрелки)

Если требуется построить изогнутую ось балки, то балка вычерчивается без нагрузки, и в точках откладываются прогибы в соответствующие стороны — строится плавная кривая – изогнутая ось балки.

Определить прогиб и угол поворота в сечении В

Сначала построим грузовую эпюру от заданной нагрузки. Площадь грузовой эпюры имеет криволинейное очертание и равна:

Теперь снимем с балки нагрузку и приложим в точке, где необходимо определить перемещение единичную силу для определения прогиба и единичный момент для определения угла поворота. Строим эпюры от единичных нагрузок.

Центр тяжести грузовой эпюры находится на расстоянии одной четверти (см. эпюру)

Ординаты единичных эпюр напротив центра тяжести грузовой эпюры :

Теперь по формуле правила Верещагина определяем:

сначала прогиб

затем угол поворота:

В знаменателе формулы – жесткость сечения.

Источник

Для решения задач на движение по прямой используется одна основная формула:

где:

Скорость (V) — расстояние, пройденное за единицу времени.
Время (t) — время в пути.
Расстояние (S) — пройденный путь, или расстояние.

Зная эту формулу (для расстояния), вы можете легко вывести из неё формулу для скорости, или времени.

Если вы запомните эту формулу, то сможете решить любую задачу на движение, так как все задачи на движение по прямой — это применение данной формулы к одному или нескольким взаимосвязанным объектам.

Рассмотрим, как решать разные задачи на движение в зависимости от условий и уровня сложности.

Все задачи на движение делятся на следующие типы:

простые задачи на скорость, время и расстояние;
задачи на движение в разных направлениях: сближение и удаление;
задачи на движение в одном направлении: сближение и удаление;
решение задач на движение по реке.

Решение простых задач на движение: скорость, время и расстояние

В простых задачах на движение, как правило, есть один движущийся объект, для которого нужно найти неизвестную величину: скорость, время или расстояние. В данном случае применяется формула в ее первоначальном виде:

Задача 1. Автомобиль ехал 2ч со скоростью 85 км/ч. Определите расстояние.
Решение: Вычислим путь по формуле: S=V × t= 2 ч * 85 км/ч = 170 км.

Задача 2. Велосипедист проехал 60 км за 5ч. Определите скорость.
Решение: Вычислим скорость велосипедиста по формуле: V = S:t = 60 км : 5 ч = 12 км/ч.

Задача 3. Мотоциклист проехал 30 км со скоростью 15км/ч. Сколько времени он затратил на этот путь?
Решение: Вычислим время движения мотоциклиста по формуле: t = S:V = 30 км : 15 км/ч = 2 ч.

В таких задачах нужно также следить, чтобы были одинаковыми единицы измерения. Например, если расстояние измеряется в километрах, а время — в часах, то скорость буде измеряться в км/час. Но если единицы измерения скорости — метр/час, а время дано в минутах, то в этом случае скорость и время нужно привести к одинаковым единица измерения, иначе ответ будет неверным.

Задача 4. Мотоциклист ехал 30 минут со скоростью 60 км/ч. Какое расстояние он проехал?
Решение: для того, чтобы вычислить расстояние, нужно время и скорость привести к одинаковым единицам измерения. При этом есть 2 способа:
1) Переведем время: 30 минут = 30/60 = 0,5 часа.
Найдем расстояние: 60 км/ч * 0,5 ч = 30 км.
2) Переведем скорость: 60 км/ч = 60км / 1час = 60км / 60 мин = 1км/мин.
Найдем расстояние: 1км/мин*30минут = 30 км.

Решение задач на движение в разных направлениях: сближение (встречное движение) и удаление (противоположное движение)

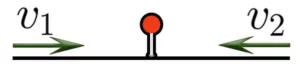
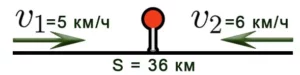
При встречном движении расстояние между объектами уменьшается. Объекты приближаются друг к другу со скоростью сближения.
Скорость сближения находится по формуле:

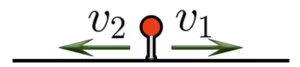
При движении в противоположных направлениях скорости объектов направлены в разные стороны. Объекты удаляются друг от друга со скоростью удаления.
Скорость удаления находится по формуле:

При решении подобных задач лучше нарисовать схему движения, чтобы было легче решать.

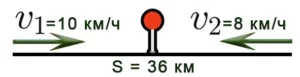
Задача 5. Два велосипедиста выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого велосипедиста 10 км/ч, второго — 8 км/ч. Через сколько часов они встретятся?
Решение: 1) Найдем скорость сближения: V=10+8 = 18 км/ч.
2) Найдем время: t = S:V = 36 : 18 = 2 ч.

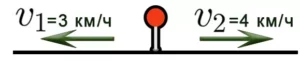
Задача 6. Два пешехода вышли одновременно из одного и того же пункта в противоположных направлениях. Скорость первого пешехода 3км/ч, второго — 4км/ч. Какое расстояние между ними будет через 30 минут?
Решение: 1) Найдем скорость удаления пешеходов: V = 3+4=7 км/час.
2) Переведем в соответствие единицы измерения: t=30 мин = 0,5 ч.
3) Найдем расстояние: S=V × t = 7 × 0,5 = 3,5 км.

Задача 7. Два автобуса выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 300 км. Через 2 часа они встретились. Найдите второго второго автобуса, если первый ехал со скоростью 70 км/ч.
Решение. 1) Нам известно расстояние и скорость, поэтому найдем скорость по формуле: V = S:t = 300:2=150км/ч. Это скорость сближения.
2) Найдем скорость второго автобуса: 150-70 = 80км/ч.

Решение задач на движение в одном направлении: сближение и удаление

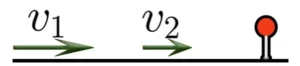
Если два объекта движутся в одном направлении и один объект “догоняет” второй, то расстояние между объектами уменьшается.
Скорость сближения при таком движении определяют по формуле:

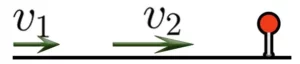
Если два объекта движутся в одном направлении и один объект “отстает” от второго, то расстояние между объектами увеличивается.
Скорость удаления при таком движении определяют по формуле:

Если объект движется в стоячей воде (озере), то его скорость называют собственной скоростью объекта. То есть, скорость объекта равная собственной скорости объекта.

Заметим, что плот — это тело, у которого собственная скорость равна нулю (V=0). Значит, плот может плыть только по течению и со скоростью течения.

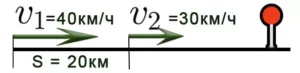
Задача 8. Расстояние между двумя автомобилями, движущимися в одном направлении, составляет 20 км. Первый автомобиль едет со скоростью 40км/ч, второй — со скоростью 30км/ч. Через сколько часов первый автомобиль догонит второй?
Решение. 1) Найдем скорость сближения автомобилей: V=40-30=10км/ч.

2) Зная расстояние (20км) и скорость сближения (10км/ч) найдем время: 20:10=2 часа.

Задача 9. Из одного населенного пункта выехали автомобиль и автобус. скорость автомобиля 70 км/ч, скорость автобуса — 50 км/ч. Какое расстояние будет между ними через 3 часа?
Решение. 1) Найдем скорость удаления : V=70-50=20км/ч.
2) Зная скорость удаления и время, найдем расстояние: S = 20*3 =60 км.

Решение задач на движение по реке

Особенностью задач на движение реке является то, что у объекта появляется дополнительная скорость — скорость течения реки. При этом возможно два варианта:

по течению реки → скорость увеличивается;
против течения реки → скорость уменьшается.

Таким образом, в задачах рассматривают 2 скорости:

Скорость собственная — Vs;
Скорость течения реки — Vt.

Задача 9. Собственная скорость лодки составляет 12 км/ч. Скорость течения реки равна 3 км/ч. Какое расстояние проплывёт лодка через 3 часа, если она плывёт по течению реки?
Решение. 1) Найдем скорость лодки. Так как она плывет по течению реки, ее скорость увеличивается.
V = Vs+ Vt = 12+3 =15км/ч.
2) Найдем расстояние: S=V×t = 15×3=45км.

Задача 10. Собственная скорость катера составляет 30 км/ч. Скорость течения реки равна 4 км/ч. Какое расстояние преодолеет катер через 4 часа, если он плывёт против течения реки?
Решение. 1) Найдем скорость. Так как катер плывет против течения реки, его скорость уменьшится.
V = Vs- Vt = 30-4 =26 км/ч.
2) Найдем расстояние: S=V×t = 26 * 4 = 104 км.

Задача 10. Скорость лодки равна 10 км/ч. При этом надо успеть проплыть 25 км за 2 часа по течению реки. Какой должна быть скорость течения реки, чтобы успеть в срок?
Решение. 1) Найдем нужную скорость: V=S:t = 25:2=12,5 км/ч.
2) Найдем скорость, которую нужно прибавить до нужно (скорость течения реки): 12,5-10=2,5км/ч.

Задача 11. Уровень ЕГЭ.
Катер прошёл по течению реки 120 км и вернулся обратно. Известно, что обратный путь занял на 1 час больше времени, а скорость катера в неподвижной воде равна 27 км/ч. Найдите скорость течения.
Решение: Пусть Vt — cкорость течения реки, тогда:
1) В одну сторону: 27+Vt – скорость перемещения катера по течению, S=120км.
2) В обратную сторону: 27-Vt – скорость перемещения катера против течения, S=120км.
Выразим время:
1) В одну сторону: t=S:V = 120:(27+Vt) – время, затраченное катером на перемещение по течению,
2) В обратную сторону: t=S:V = 120:(27-Vt) – время, затраченное катером на перемещение против течения.
Так как время перемещения против течения на час больше, чем время по течению, то:
120:(27+Vt) +1 = 120:(27-Vt).
Далее решаем уравнение и получаем ответ 3 км/ч.

Больше задач на движение Ваш ребёнок может решить, скачав программы:

Правильность решения задач вы можете проверить на сайте intmag24.ru с помощью калькулятора решения задач на движение.

Полезные советы для решения задач на движения

В процессе решения задач на движение может быть составлена формула квадратного уравнения, которое будет иметь два корня. В этом случае нужно взять тот ответ, который будет логичен для задачи (положительный). Отрицательный корень не берется во внимание.
Внимательно следите, чтобы в задаче все данные измерялись одними величинами. Если это не так, нужно се привести к единым единицам измерения.
При решении задач на движение рисуйте картинки. Особенно, когда текст задачи большой и сразу в голове не укладывается. Чаще всего это нужно делать в задачах, где кто-то кого-то догоняет, встречается, или перемещается между пунктами А и В туда и обратно. На картинке сразу видно, какие отрезки пути можно просчитать. Картинка облегчает составление математической модели.

Для решения более сложных задач на движение посмотрите, как составлять схемы и таблицы данных для наглядного представления и структурирования данных.

Источник

Перемещение, путь, средняя скорость Примеры решения задач

1.Материальная точка прошла
половину окружности. Найти отношение
средней путевой скорости <v> к модулю
средней векторной скорости.

Решение. Из определения средних
значений путевой и векторной скоростей
с учетом того, что путь, пройденный
материальной точкой за время движенияt, равенR, а
величина перемещения 2R, гдеR–
радиус окружности, получим:

2.Автомобиль проехал первую треть
пути со скоростью v₁= 30 км/ч,
а оставшуюся часть пути – со скоростью
v₂= 40 км/ч. Найти среднюю
скорость <v> на всем пройденном пути.

Решение. По определению <v> =гдеS– путь, пройденный за времяt.
Очевидно, чтоПоэтому искомая средняя скорость равна

3.Студент проехал половину пути
на велосипеде со скоростьюv₁= 12 км/ч.
Далее половину оставшегося времени он
ехал со скоростьюv₂= 10 км/ч,
а оставшуюся часть пути шел пешком со
скоростьюv₃= 6 км/ч.
Определить среднюю скорость движения
студента <v> на всем
пути.

Решение. По определениюгдеS –путь, аt– время движения.
Ясно, чтоt=t₁+t₂+t₃.
Здесь–
время движения на первой половине пути,t₂– время движения на втором
участке пути иt₃– на третьем.
По условию задачиt₂=t₃.
Кроме того,S/2 =v₂t₂+ v₃t₃= (v₂+v₃)t₂.
Отсюда следует:

Подставив t₁
и t₂+t₃ = 2t₂
в выражение для средней скорости,
получим:

4.Расстояние между двумя станциями
поезд прошел за времяt₁= 30 мин.
Разгон и торможение длилисьt₂= 8 мин,
а остальное время
поезд двигался
равномерно со скоростью v = 90 км/ч.
Определить среднюю скорость поезда
<v>, считая, что при разгоне скорость
увеличивалась с течением времени по
линейному закону, а при торможении
уменьшалась тоже по линейному закону.

ешение. Построим график
зависимости скорости поезда от времени
(см. рис.). Этот график
описывает трапецию с длинами оснований,
равнымиt₁иt₁–t₂и высотой, равной v. Площадь этой трапеции
численно равна пути, пройденному поездом
от начала движения до остановки. Поэтому
средняя скорость равна:

Задачи и упражнения

1.1.Мяч упал с высотыh₁= 4 м,
отскочил от пола и был пойман на
высотеh₂= 1 м. Чему равен путьSи величина перемещения?

1.2.Материальная точка переместилась
на плоскости из точки с координатамиx₁= 1 см иy₁= 4cм
в точку с координатамиx₂= 5 см
иy₂= 1 см. Построить
вектор перемещения и с помощью линейки
определить модуль вектора перемещения
и проекции вектора перемещения на осиxиy. Найти эти же величины
аналитически и сравнить результаты.

1.3.Первую половину пути поезд
шел со скоростью вn= 1,5 раза
большей, чем вторую половину пути.
Средняя скорость поезда на всем
пути
<v> = 43,2 км/ч. Каковы скорости
поезда на первой и второй половинах
пути ?

1.4.Первую половину времени своего
движения велосипедист проехал со
скоростью v₁= 18 км/ч, а
вторую половину времени – со скоростью
v₂= 12 км/ч. Определить
среднюю скорость движения велосипедиста.

1.5. Движение двух автомобилей
описывается уравнениямии,
где все величины измеряются в системе
СИ. Запишите закон изменения расстояниямежду автомобилями от времени и найдитечерез времяс.
после начала движения.