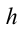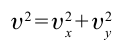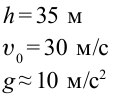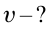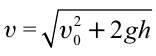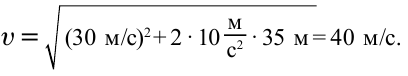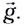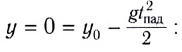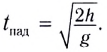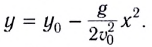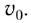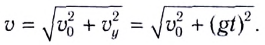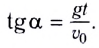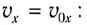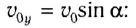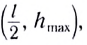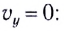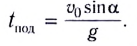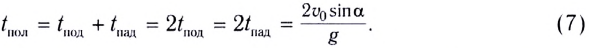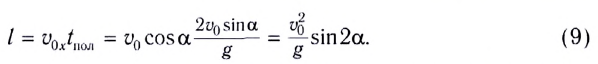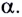Движение по окружности
Движение по окружности – простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории – предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости – радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → – v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → – v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → – радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
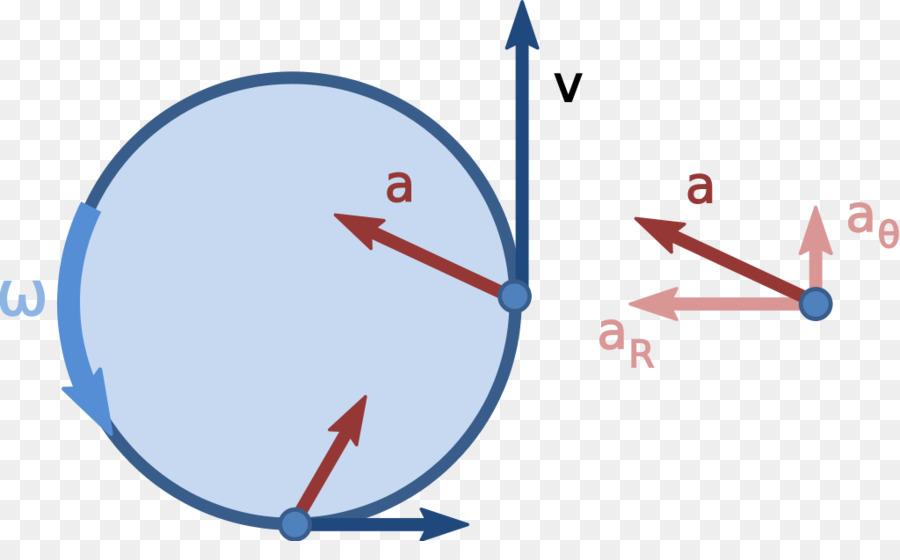
В общем случае ускорение при движении по окружности состоит из двух компонентов – нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 – v 1 – изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
Движение по окружности: формулы и расчеты
Перемещение тел по окружности достаточно распространено в нашей жизни и в природе. Яркими примерами этого типа перемещения являются вращения ветровых мельниц, планет вокруг своих звезд и колес транспортных средств. В данной статье рассмотрим, какими формулами движение по окружности тел описывается.
Перемещение по окружности и по прямой линии в физике
В физике вопросами движения занимается кинематика. Она устанавливает связь между величинами, описывающими этот процесс. В динамике также уделяется внимание движению, однако она ориентирована на описание причин его возникновения. Другими словами, если для кинематики главными физическими величинами являются путь и скорость, то для динамики – это действующие на тела силы.

В физике принято выделять два идеальных типа траекторий движения:
Математический аппарат для описания движения по обоим типам траекторий развит настолько хорошо, что понимание формул, например для прямолинейного движения, автоматически приводит к пониманию выражений для движения по окружности. Единственная принципиальная разница между формулами указанных типов перемещения заключается в том, что для движения по окружности удобно использовать угловые характеристики, а не линейные.

Далее в статье будем рассматривать исключительно кинематические формулы движения по окружности тел, не вдаваясь в подробности динамики.
Угловые характеристики движения: угол поворота
Прежде чем записывать формулы движения по окружности в физике, следует ввести величины, которые будут фигурировать в этих формулах.
Начнем с угла поворота. Будем обозначать его греческой буквой θ (тета). Поскольку вращение предполагает движение точки вдоль одной и той же окружности, то значение угла поворота θ за определенный промежуток времени можно использовать для определения количества оборотов, которое сделала эта точка. Напомним, что вся окружность равна 2*pi радиан, или 360o. Тогда формула для числа оборотов n через угол θ примет вид:

Здесь и далее во всех формулах угол выражается в радианах.
Пользуясь известным углом θ, также можно определить линейное расстояние, которое точка прошла вдоль окружности. Это расстояние будет равно:
Здесь r – радиус рассматриваемой окружности.
Угловая скорость и ускорение
Кинематические формулы движения по окружности точки предполагают также использование понятий угловой скорости и углового ускорения. Обозначим первую буквой ω (омега), а вторую буквой α (альфа).
Физический смысл угловой скорости ω прост: эта величина показывает, на какой угол в радианах поворачивается точка за каждую секунду времени. Данное определение имеет следующее математическое представление:
Эта формула скорости движения по окружности записана в дифференциальной форме. Полученная с ее помощью величина ω называется мгновенной скоростью. Ее удобно использовать, если движение не является равномерным, то есть происходит с переменной скоростью.
Угловое ускорение α – это величина, которая описывает быстроту изменения скорости ω, то есть:
Угловое ускорение измеряется в радианах в секунду квадратную (рад/с2). Так, 1 рад/с2 означает, что тело увеличивает за каждую секунду времени скорость на 1 рад/с.
Учитывая выражение для ω, записанное выше, равенство можно представить в такой форме:
В зависимости от особенностей движения по окружности величина α может быть постоянной, переменной или нулевой.
Равномерное движение
Когда на вращающееся тело не действует никакая внешняя сила, то угловая скорость будет оставаться постоянной сколь угодно длительное время. Такое движение получило название равномерного вращения. Оно описывается следующей формулой:
В этом выражении переменными являются всего две величины: t и θ. Скорость ω = const.
Следует отметить один важный момент: нулю равна лишь равнодействующая внешних сил на тело, внутренние же силы, действующие в системе, нулю не равны. Так, внутренняя сила заставляет вращающееся тело изменять свою прямолинейную траекторию на криволинейную (окружность). Эта сила приводит к появлению центростремительного ускорения. Последнее не изменяет ни скорость ω, ни линейную скорость v, оно лишь изменяет направление движения.
Равноускоренное движение по окружности
Формулы для этого типа перемещения можно получить непосредственно из приведенных математических выражений для величин ω и α. Равноускоренное движение предполагает, что за более-менее длительный промежуток времени модуль и направление ускорения α не изменяются. Благодаря этому можно проинтегрировать дифференциальное выражение для α и получить следующие две формулы:
Очевидно, что в первом случае движение будет равноускоренным, во втором – равнозамедленным. Величина ω0 здесь – это некоторая начальная скорость, которой вращающееся тело обладало до появления ускорения.
Для равноускоренного движения не существует конечной скорости, поскольку она может возрастать сколь угодно долго. Для равнозамедленного движения конечным состоянием будет прекращение вращения, то есть ω = 0.
Теперь запишем формулы для определения угла θ при движении с постоянным ускорением. Эти формулы получаются, если произвести двойное интегрирование по времени для выражения α через θ. Получаются следующие выражения:
То есть центральный угол θ, на который тело повернется за время t, будет равен сумме двух слагаемых. Первое слагаемое – это вклад в θ равномерного движения, второе – равноускоренного (равнозамедленного).
Связь между угловыми и линейными величинами
При рассмотрении понятия угла поворота θ уже была приведена формула, которая его связывает с линейным расстоянием L. Здесь же рассмотрим аналогичные выражения для скорости ω и ускорения α.
Линейная скорость v при равномерном движении определяется как расстояние L, пройденное за время t, то есть:
Подставляя сюда выражение для L через θ, получаем:
Мы получили связь между линейной и угловой скоростью. Важно отметить, что удобство использования угловой скорости связано с тем, что она не зависит от радиуса окружности. В свою очередь, линейная скорость v возрастает линейно с увеличением r.
Остается записать связь между линейным ускорением a и его угловым аналогом α. Чтобы это сделать, запишем выражение для скорости v при равноускоренном движении без начальной скорости v0. Получаем:
Подставляем сюда полученное выражение связи между v и ω:
Как и скорость, линейное ускорение, направленное по касательной к окружности, зависит от радиуса.
Ускорение центростремительное
Выше уже было сказано несколько слов об этой величине. Здесь приведем формулы, которые можно использовать для ее вычисления. Через скорость v выражение для центростремительного ускорения ac имеет вид:
Через угловую скорость его можно записать так:
Величина ac не имеет никакого отношения к тангенциальному ускорению a. Центростремительное ускорение обеспечивает поддержание вращающегося тела на одной окружности.
Задача на определение угловой скорости вращения планеты
Известно, что ближе всего к солнцу находится Меркурий. Полагая, что он вращается по окружности вокруг светила, мы можем определить его угловую скорость ω.
Для решения задачи следует обратиться к справочным данным. Из них известно, что планета делает полный оборот вокруг светила за 87 дней 23,23 часа земных. Это время называется периодом обращения. Учитывая, что движение происходит с постоянной угловой скоростью, запишем рабочую формулу:
Остается перевести время в секунды, подставить значение угла θ, соответствующее полному обороту (2*pi), и записать ответ: ω = 8,26*10-7 рад/c.
I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
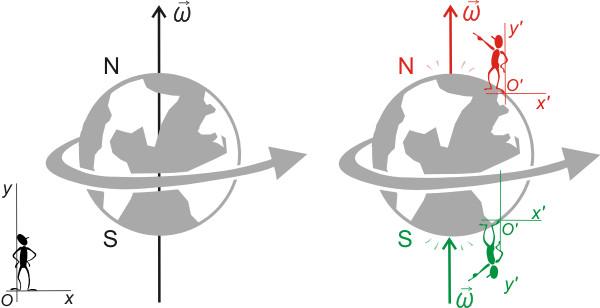
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
[spoiler title=”источники:”]
http://1ku.ru/obrazovanie/45948-dvizhenie-po-okruzhnosti-formuly-i-raschety/
http://fizmat.by/kursy/kinematika/okruzhnost
[/spoiler]
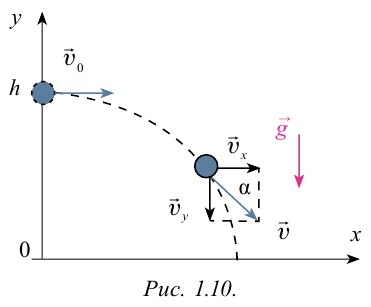
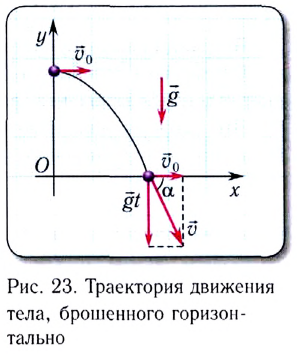
Движение горизонтально брошенного тела:
Рассмотрим движение шара, движущегося прямолинейно по поверхности стола с высотой
При достаточно малом сопротивлении воздуха, которым можно пренебречь, тело будет двигаться в горизонтальном направлении равномерно со скоростью 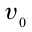
в горизонтальном направлении в любой момент времени 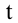
Проекции скорости тела на оси 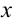
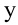
В вертикальном же направлении, двигаясь равноускоренно без начальной скорости, тело будет свободно падать с высоты 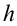
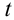
Из соотношений (1.21) и (1.22) уравнение траектории движения горизонтально брошенного тела на плоскости 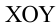
Выражение (1.24) является уравнением параболы. Значит, горизонтально брошенное тело будет двигаться по параболической линии. Время полета тела, брошенного горизонтально с высоты 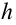
В этом случае формула для расчета длины полета тела будет иметь вид:
Горизонтально брошенное тело, одновременно двигаясь в горизонтальном направлении равномерно и в вертикальном направлении равноускоренно, свободно падает. К концу движения (после истечения времени 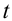
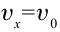
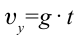
или
Перемещение и траектория тела при криволинейном движении неравны между собой. Модуль вектора и направление движения горизонтально брошенного тела на протяжении движения меняются непрерывно.
Образец решения задачи:
Тело брошено горизонтально на высоте 35 м со скоростью 30м/с. Найти скорость тела при падении на землю.
Дано:
Найти:
Формула:
Решение:
Ответ: 40 м/c.
Движение тела, брошенного горизонтально и под углом к горизонту
Если материальная точка участвует одновременно в нескольких движениях, то такое движение называют сложным.
Примером сложного движения является движение под действием силы тяжести в том случае, если падающему телу сообщена начальная скорость, непараллельная вектору ускорения свободного падения.
Рассмотрим движение тела, брошенного горизонтально со скоростью 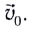
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного с постоянной скоростью 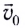
Движение тела в горизонтальном направлении будет описываться уравнением
а в вертикальном — уравнением
Здесь 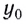
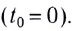
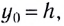
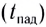
условия
Для получения уравнения траектории движения у(х) необходимо исключить время из уравнений движения (1) и (2). Из уравнения (1) выражаем время t и подставляем в уравнение (2). Получаем
Это уравнение параболы, ветви которой направлены вниз, так как коэффициент перед множителем 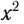
Скорость вдоль направления оси Ох остается неизменной и равной
Вдоль оси Оу движение равноускоренное. В начальный момент времени вертикальная составляющая скорости равна нулю 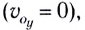
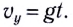
Угол между начальной скоростью 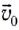
В приведенных формулах сопротивление воздуха не учитывается.
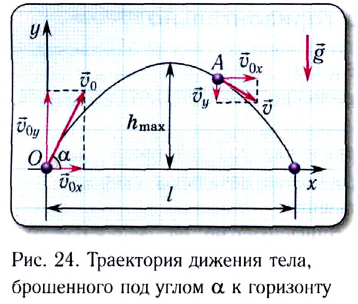
Рассмотрим теперь движение тела, брошенного со скоростью 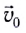
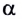
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного в горизонтальном направлении со скоростью
и равноускоренного в вертикальном направлении с ускорением 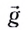
скоростью
В том случае, если система координат выбрана так, что начальные координаты 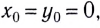
Как и при движении тела, брошенного горизонтально, траектория представляет собой параболу, ветви которой направлены вниз, поскольку коэффициент перед 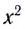
где l — дальность полета тела, 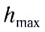
Модули горизонтальной 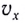
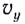
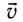
Мгновенную скорость 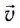
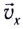
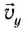
Время подъема тела можно найти из условия
Если сопротивление воздуха при движении не учитывается, то время подъема равно времени падения: 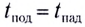
Таким образом, время полета тела можно найти как
Определив вертикальную составляющую скорости 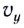
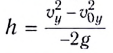
Максимальная высота подъема тела 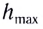
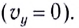
Дальность полета l — расстояние, пройденное телом за время полета 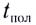
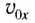
Таким образом, дальность полета определяется модулем начальной скорости 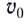
Заметим, что согласно формуле (9) при неизменном модуле начальной скорости тела максимальная дальность 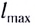
- Движение тела, брошенного под углом к горизонту
- Принцип относительности Галилея
- Движение в гравитационном поле
- Зависимость веса тела от вида движения
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
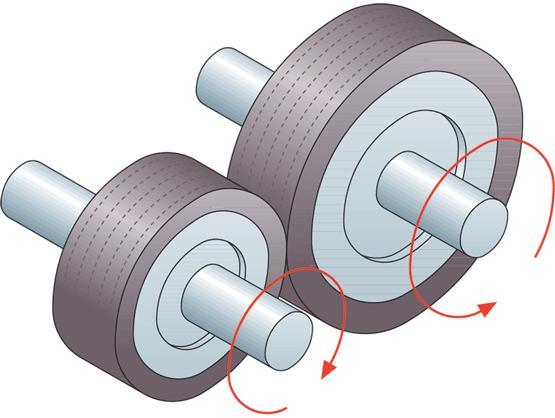
- Взаимная передача вращательного и поступательного движения
Как найти путь и модуль вектора перемещения тела по окружности?
Знаток
(298),
закрыт
15 лет назад
Prowling Tiger
Мастер
(1897)
15 лет назад
Перемещение будет равно нулю,если тело закончило движение в начальной точке,если нет,то перемещение будет равно длине хорды,соединяющий начальную и конечную точки.путь рассчитывается как длина окружности тело совершило полный оборот (длина рассчитывается по формуле 2*пи*радиус,а радиус – это расстояние между начальной точкой и центром окружности,рассчитывается по формуле d=кв.корень из ((x2-x1)^2+(y2-y1)^2) )если не полный оборот,то как длина дуги=радиус*угол (в радианах) или (радиус*пи*угол (в градусах))/180 град
Как физически и математически описать и смоделировать движение шарика, учитывая возможность его вращения, трение и потери энергии?
Достаточно давно, участвуя в турнире юных физиков, я описал движение упругих и жестких мячиков. Задача заключалась в том, чтобы определить параметры, влияющие на угол отскока, угловую и линейную скорость после удара и потери энергии при деформациях.
Это первая из цикла статей, посвящённых описанию удара.
Кстати, у меня есть замечательная школа математики для программистов – Академия вектозавров. Первую, бесплатную, главу пройти обязательно всем! 🙂
В этой статье я расскажу, как можно описать удар о жесткую поверхность жёсткого мяча, используя законы ньютона и сохранения импульса. Также я покажу, как можно сделать компьютерную симуляцию мяча, используя полученные результаты. То есть использовать это можно будет и для создания компьютерных игр, где нужно точно описать удар.
Вторая статья будет про движение упругих мячей.
Чтобы представлять себе, что мы получим в итоге, я покажу конечный результат:
Описание движения жесткого шара
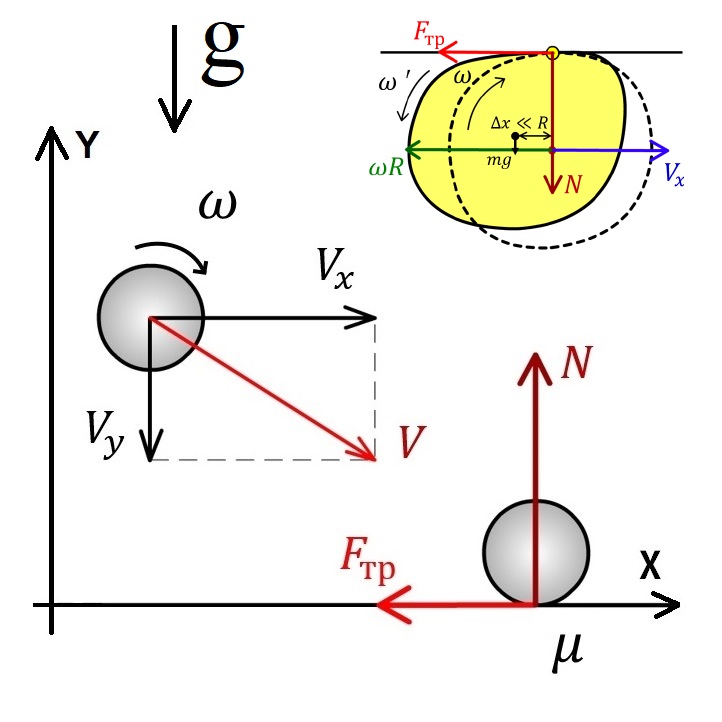
Рассмотрим случай, когда абсолютно жесткий шар (нет деформаций во время удара) массы (m) налетает на жесткую плоскость с горизонтальной и вертикальной скоростями (V_x) и (V_y), угловой скоростью (omega), радиусом (R) и коэффициентом трения между поверхностью шара и плоскостью (mu):
Положительное направление угловой скорости показано на рисунке. Ясно, что если мы опишем первый удар, то легко сможем описать и второй.
На рисунке не указана сила тяжести, но её присутствие никак не повлияет, ведь сила реакции опоры во время удара намного больше силы тяжести (сила реакции опоры меняет направление вертикальной скорости, а значит именно она определяющая).
Удар происходит не мгновенно, а длится какое-то конечное время. В это время (когда есть проскальзывание) на шар действует сила трения-скольжения. Она может быть направлена влево или вправо (в зависимости от направления скорости нижней точки шара).
При (V_x > omega R):
$$
F = -mu N qquad (1)
$$
При (V_x < omega R):
$$
F = mu N
$$
Эта сила изменяет горизонтальную составляющую импульса шара:
$$
Delta{P_x} = -mu int{Ndt} qquad (2)
$$
Возможны два варианта:
1) Проскальзывание длится все время удара.
2) В некоторый момент проскальзывание прекращается, но удар ещё может продолжаться.
Пусть проскальзывание длится все время удара.
Сила реакции опоры изменяет вертикальную составляющую импульса:
$$
Delta{P_y} = int{Ndt} qquad (3)
$$
Отсюда выразим интеграл и подставим его в выражение (2):
$$
Delta{P_x} = -mu Delta{P_y} qquad (4)
$$
Некоторое количество энергии, естественно, теряется при вертикальных деформациях мяча во время удара, и в выражении для вертикальной скорости после удара должен появиться некоторый безразмерный коэффициент восстановления, который зависел бы от свойств материала шарика:
$$
V_y^{‘} = -gamma V_y
$$
Путем не сложных преобразований, в итоге, получаем горизонтальную и вертикальную скорости после удара:
$$
V_x^{‘} = V_x + mu V_y (1 + gamma) qquad (при ; V_x > omega R)
$$
$$
V_x^{‘} = V_x – mu V_y (1 + gamma) qquad (при ; V_x < omega R) qquad (5)
$$
$$
V_y^{‘} = -gamma V_y
$$
Когда (V_x = omega R) проскальзывания нет и (V_x^{‘} = V_x).
При проверке формул учитывайте, что (V_y) всегда отрицательна.
Помимо того, что сила трения изменяет горизонтальную скорость, она ещё меняет угловую. Запишем 2-й закон Ньютона для вращательного движения:
$$
int{Idomega} = mu R int{Ndt} qquad (при ; V_x > omega R)
$$
$$
int{Idomega} = -mu R int{Ndt} qquad (при ; V_x < omega R) qquad (6)
$$
То есть момент определяет сила трения, плечо которой (=R). Момент силы реакции опоры равен нулю из-за нулевого плеча.
В (6) (I) – это момент инерции шара, который удобнее записывать как (I = alpha mR^2). Пользуясь этой заменой, уравнением (3) и (6) находим угловую скорость после удара:
$$
omega^{‘} = omega – frac{mu V_y (1 + gamma)}{R alpha} qquad (при ; V_x > omega R)
$$
$$
omega^{‘} = omega + frac{mu V_y (1 + gamma)}{R alpha} qquad (при ; V_x < omega R) qquad (7)
$$
При (V_x = omega R) проскальзывания нет и (omega^{‘} = omega).
Легко получить, что для полного шара (alpha = 2/5), для сферы (alpha = 2/3), для обруча (alpha = 1). (см. Момент инерции)
Мы рассмотрели случай, когда проскальзывание длится все время удара, но как было сказано ранее, возможна такая ситуация, когда проскальзывание прекратилось, но удар ещё продолжается. Рассмотрим и этот случай.
Пусть в некоторый момент устанавливается режим не проскальзывания.
Теперь нельзя как раньше связать (2) и (3), ведь пределы интегрирования будут разными: горизонтальная и угловая скорости остаются постоянными, когда нет проскальзывания (считаем, что нет силы трения-качения), а вертикальная скорость продолжает изменяться!
Если проскальзывание прекратилось, то скорость нижней точки шара равна нулю. В скалярном виде получаем условие движения без проскальзывания: (V_x^{‘} – omega^{‘} R = 0)
Это условие дает возможность разрешить систему.
Используя это условие и уравнения (2) и (6), получаем угловую и поступательную скорости после удара:
$$
V_x^{‘} = frac{alpha omega R + V_x}{1 + alpha}
$$
$$
V_y^{‘} = -gamma V_y qquad (8)
$$
$$
omega^{‘} = frac{alpha omega R + V_x}{R(1 + alpha)}
$$
Легко убедится, что такое решение будет верным и при (V_x > omega R), и при (V_x < omega R) (В первом случае сила трения создаёт положительный момент и в уравнение (6) войдёт со знаком плюс, но эта сила будет уменьшать импульс тела (2), а значит изменение импульса войдет в уравнение со знаком минус. В итоге в правой части получим знак минус. Во втором случае сила трения создаёт уже отрицательный момент, но увеличивает импульс, т.е знак тоже отрицательный.
Из этого решения мы видим, что при (V_x = omega R) угловая и горизонтальная скорости не изменяются, что и следовало ожидать.
Теперь объединим (5), (7) и (8), рассмотрев критический случай, при котором будет выполнятся и первое, и второе решение и получим условие на (mu):
$$
mu = -frac{alpha (V_x – omega R)}{V_y(1 + gamma)(1 + alpha)} qquad (при ; V_x > omega R)
$$
$$
mu = -frac{alpha (omega R – V_x)}{V_y(1 + gamma)(1 + alpha)} qquad(при ; V_x < omega R) qquad (9)
$$
Не нужно смущаться минуса перед дробью. Он происходит оттого, что (V_y) всегда отрицательна (Шар налетает на плоскость, а значит его скорость направлена против нормали к поверхности)
Очевидно, что при меньшем значении (mu) будет выполнятся первое решение, а при большем – второе. Маленькая сила трения не сможет остановить шарик и проскальзывание будет происходить весь удар. Бóльшая же сила трения быстро остановит шар и мы попадём в режим не проскальзывания.
Видно, что если скорость ((V_x – omega R)) точки контакта большая, то скольжение будет происходить весь удар. При малой же скорости условие на (mu) легко выполняется и происходит зацеп.
Обозначим переходную силу трения за (mu_{e}):
$$
mu_{e} = -frac{alpha |V_x – omega R|}{V_y(1 + gamma)(1 + alpha)} qquad (10)
$$
В случае, когда (mu = mu_{e}) проскальзывание заканчивается ровно в момент отскока шарика. То есть выполняются оба решения.
Для удобства введем функцию (xi(V_x, omega)) следующим образом:
$$
xi(V_x, omega) =
begin{bmatrix}
1 ; при ; V_x > omega R\
-1 ; при ; V_x < omega R\
end{bmatrix}
$$
В конечном итоге получаем решение:
При (mu leq mu_{e}):
$$
V_x^{‘} = V_x + xi(V_x, omega)mu V_y (1 + gamma)
$$
$$
V_y^{‘} = -gamma V_y
$$
$$
omega^{‘} = omega – xi(V_x, omega)frac{mu V_y (1 + gamma)}{R alpha}
$$
При (mu geq mu_{e}):
$$
V_x^{‘} = frac{alpha omega R + V_x}{1 + alpha}
$$
$$
V_y^{‘} = -gamma V_y
$$
$$
omega^{‘} = frac{alpha omega R + V_x}{R(1 + alpha)}
$$
Угол отскока легко найти зная горизонтальную и вертикальную скорость после удара:
$$
tan phi = frac{V_x^{‘}}{V_y^{‘}}
$$
Где (phi) – угол между вектором скорости после удара и вертикалью.
Как видно, ответ получился достаточно громоздким. Но это только из-за того, что помимо двух случаев проскальзывания возможны два направления силы трения, каждое из которых мы учли при решении.
Удар как линейное преобразование.
Теперь моя любимая часть 🙂
Представим себе, что шар налетает не на горизонтальную поверхность, а на наклонённую под углом (varphi) плоскость. В этом случае нам нужно просто спроецировать скорости (V_x) и (V_y) на новые оси (совершить поворот координат на угол (varphi)):
Записывается такое преобразование очень просто:
$$
begin{pmatrix}
v_x \
v_y \
Omega
end{pmatrix}
=
begin{bmatrix}
cosvarphi & sinvarphi & 0 \
-sinvarphi & cosvarphi & 0 \
0 & 0 & 1 \
end{bmatrix}
begin{pmatrix}
V_x \
V_y \
omega
end{pmatrix}
=
T^{-1}
begin{pmatrix}
V_x \
V_y \
omega
end{pmatrix}
qquad (11)
$$
После перехода (11) нужно найти скорости после удара и вернуться в старую систему координат.
Заметим, что наше решение (для скоростей после удара) является линейным преобразованием скоростей (когда я это заметил у меня пошли мурашки по коже. Такое бывает и это нормально). То есть удар является линейным преобразованием!
$$
begin{pmatrix}
V_x^{‘} \
V_y^{‘} \
omega^{‘}
end{pmatrix}
=
TPT^{-1}
begin{pmatrix}
V_x \
V_y \
omega
end{pmatrix} qquad (12)
$$
Единственное, что немного портит картину, так это условие на (mu_e) и функция (xi(V_x, omega)), ведь для нахождения линейного преобразования (P) нужно проверить выполнимость всех условий и выбрать подходящий ответ:
В случае (mu leq mu_{e}):
$$
P
=
begin{bmatrix}
1 & ximu (1+gamma) & 0 \
0 & -gamma & 0\
0 & -xifrac{mu(1 + gamma)}{R alpha} & 1
end{bmatrix}
$$
В случае (mu geq mu_{e}):
$$
P
=
begin{bmatrix}
frac{1}{1+alpha} & 0 & frac{alpha R}{1+alpha} \
0 & -gamma & 0\
frac{1}{R(1+alpha)} & 0 & frac{alpha}{1+alpha}
end{bmatrix}
$$
Компьютерное моделирование движения
Ну а теперь самое интересное – результат работы алгоритма!
Имея угловую и поступательную скорость до удара, можно предсказать что будет после. Для визуализации движения и проверки полученных результатов неплохо бы сделать моделирование. О том, как численно решать задачи я уже упоминал в одной из моих статей. Я накидал простой алгоритм для лучшего понимания того, как это все можно реализовать:
Ну и, наконец, результат работы программы!
В данном случае мы запускаем шар между двумя горизонтальными пластинами:
Данная постановка легко повторяется в реальной жизни. Для проверки я собрал вот такую установку:
Траекторию мячика я брал из видео с помощью специальной программы для трассировки.
Как видно модель хорошо согласуется с экспериментом!
А вот что будет если бросить шарик на наклонную поверхность:
Алгоритм работает и в сложных случаях, какой был показан в самом начале:
Если трение не велико, то возможно прокручивание и изменение направления скорости:
В следующей статье я расскажу, как можно описывать движение не жёстких шариков, а упругих мячей. С упругими мячиками можно получить много интересных траекторий. Например вот такую:
Друзья! Я очень благодарен вам за то, что вы интересуетесь моими работами, ведь каждый пост на сайте даётся очень непросто. Я буду рад любому отклику и поддержке с вашей стороны.
Если у вас остались вопросы или пожелания, то вы можете оставить комментарий (регистрироваться не нужно)
Гость из Новосибирска:
Сижу с телефона, верстка плывет дичайше.
Мурашки таки пишутся через ш, алсо вставлять предложение в скобки тоже не очень хорошо.
Анимашки покороче плиз, не очень так долго ждать, когда заново запустятся.
Годно, ждем вторую часть.
——————————————-
Отображение сайта на разных платформах только что починил.
Орфографическую ошибку исправил, спасибо С:
Дата: 23-10-2018 в 19:42
Гость:
Я ничего не понял.
——————————————-
Бывает
Дата: 17-11-2018 в 20:40
Cтарый новый Гость:
Я человек простой: вижу интегралы-ставлю лойс
————————————————————————-
Автор – добавь систему лойсов ((
Дата: 30-03-2020 в 12:33
Анонимно:
Очень интересный пост. Хотелось бы взглянуть на исходный код алгоритма.
Дата: 07-06-2020 в 08:48
План урока:
Механическое движение. Система отсчёта. Закон относительности движения
Уравнения движения. Радиус-вектор. Проекция вектора
Траектория. Путь. Перемещение
Равномерное прямолинейное движение: скорость и уравнение движения
Механическое движение. Система отсчёта. Закон относительности движения
Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.
То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).
Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.
Рисунок 1 – Иллюстрация к примеру
Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение.
Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета. То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение.
Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)
Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.
Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку.
Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.
Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.
Уравнения движения. Радиус-вектор. Проекция вектора
Для описания движения тела необходимо уметь рассчитывать его положение в каждый момент времени. Как это сделать?
Самый очевидный способ – координатный. Если вернуться к примеру на рисунке 2, можно увидеть, что летящий мяч в каждый момент времени имеет три координаты по осям OX, OY и OZ. Эти координаты являются функциями времени (т.е. они зависят от времени), а значит, их можно записать в виде системы:
Вид этих уравнений будет зависеть от многих вещей: от того, с какой силой бросили мяч в начале, от массы мяча, под каким углом его бросили и так далее. В любом случае, если эти уравнения заданы, можно найти координаты (то есть положение) тела в любой момент времени. Поиск этих уравнений – основная задача кинематики.
Эта система является кинематическими уравнениями движения тела или материальной точки, записанными в координатной форме. Повторим: если вид уравнений движения задан, можно узнать координату движущейся точки в любой момент времени.
В общем случае, координат три, но иногда можно обойтись двумя или даже одной координатой. Например, для описания движения бильярдного шара достаточно двух координат (так как шар не может двигаться вверх и вниз), а для описания движения шарика, катящегося по прямому горизонтальному желобку достаточно одной координаты (шарик не может двигаться вверх-вниз и вправо-влево).
Еще один способ описания движения – векторный.
*Перед дальнейшим прочтением данной статьи желательно вспомнить основную теорию по теме «Векторы» и «Метод координат»
Вектор, проведенный из начала координат к материальной точке, называется радиус-вектором (см. рисунок 3).
Рисунок 3 – Радиус-вектор (серой линией изображены траектория движения материальной точки, r1 и r2* радиус-векторы, проведенные к этой материальной точке в разные моменты времени)
Радиус-вектор проведенный к материальной точке в разные моменты времени будет разным. Значит, его тоже можно представить, как функцию времени:
r = r(t)
Такая функция и будет уравнением движения в векторной форме. Если ее вид задан, можно описать движение тела с той же полнотой, как и при координатной записи.
Еще раз обозначим отличия: при записи уравнения движения в координатной форме в каждый момент времени наблюдающий будет знать три координаты тела; при записи в векторной форме в каждый момент времени известен радиус-вектор (его модуль и направление). Обе записи равносильны.
*На письме векторы обычно обозначаются стрелкой сверху, над величиной. Однако в печатном тексте не всегда удобно нагромождать формулы дополнительными знаками, поэтому в печати векторные величины пишут просто жирным шрифтом. В данной статье далее жирным шрифтом будут написаны только векторные величины.
Покажем, что векторная и координатная записи равносильны. Для этого необходимо вспомнить, как построить проекцию вектора на ось (см. рисунок 4).
Рисунок 4 – Построение проекции вектора на ось
Чтобы построить проекцию вектора на ось, необходимо опустить перпендикуляра из начала и конца вектора на эту ось. Длина получившегося отрезка между проекциями начала и конца вектора, взятая со знаком «+», если вектор а сонаправлен с осью Х, или со знаком «-», если вектор а противонаправлен оси Х, – это и есть искомая проекция.
Если вектор выходит из начала координат, задача облегчается – необходимо опустить перпендикуляр только из конца вектора.
Напоминания из геометрии:
-
два вектора равны, если они параллельны или лежат на одной прямой, сонаправлены, а их модули равны;
-
проекции равных векторов равны.
Рассмотрим пример (см. рисунок 5)
Рисунок 5 – Задача на нахождение проекции векторов
Предлагаем читателю самому подумать, а затем сравнить свои рассуждения с приведенными ниже.
Итак, вектор а: его начала соответствует координате хн=1, а конец хк = 4. Значит ax = хк – хн = 4-1 = 3. Вектор b: его начало лежит в точке хн=2, а конец хк =0. Значит bx = хк – хн = 0-2 = -2.
В двумерном случае, проецировать нужно на две оси, но принцип остается тем же.
Иногда еще нужно находить составляющие компоненты вектора ах и ау. Рассмотрим пример, для простоты возьмем вектор, выходящий из начал координат (см. рисунок 6).
Сумма векторов ах и ау равна а. Модули векторов ах и ау численно равны координатам точек, куда попали перпендикуляры, опущенные из конца вектора а на оси ОХ и ОУ.
Еще следует отметить, что, если известен угол β между вектором а и осью ОХ, воспользовавшись основами тригонометрии, можно найти величины проекций:
ах = а*cos(β);
аy = а*sin(β).
Если бы вектор а совпадал с радиус-вектором какой-нибудь точки, то величины ах и ау совпадали бы с координатами тела по осям ОХ и ОY.
Способ с использованием тригонометрических функций удобен, когда координата конца вектора попадает в нецелое число и опустив перпендикуляр на ось его трудно найти точно. В физических задачах такое часто случается.
Рисунок 6 – Нахождение компонент вектора а
Рассмотрим пример (см. рисунок 7). Модуль вектора r равен 2. Сам вектор направлен под углом в 45 градусов к оси ОХ. Необходимо найти величины проекций (они же координаты) этого вектора на оси ОХ и ОУ.
Рисунок 7 – Задача на нахождение проекций вектора в двумерном пространстве
В общем случае радиус-вектор находится в трехмерном пространстве (см. рисунок 8). Построение проекции осуществляется по тому же принципу, что и в рассмотренных выше примерах. Когда строятся проекции на оси ОХ и ОУ, перпендикуляр сначала опускается на плоскость, в которой лежат оси ОХ и ОУ, а затем точка, в которую упал перпендикуляр к плоскости, проецируется на оси ОХ и ОУ.
Точки, в которые попал перпендикуляры к осям – rx, ry, rz – это и есть координаты x, y, z тела в текущий момент времени.
Следует оговориться, что большинство задач 10-го класса будут ограничиваться двумерным пространством.
Рисунок 8 – Построение проекций радиус-вектора
Траектория. Путь. Перемещение
Траектория – это линия, вдоль которой движется тело.
Траектория движения может быть прямолинейной, если тело движется по прямой линии, и криволинейной, если тело движется по кривой.
Путь (S), пройденный телом, равен длине траектории.
Перемещение (r)* – это вектор, проведенный из начала пути в конец.
В случае прямолинейного движения путь и модуль перемещения тела совпадают (см. рисунок 9а). В случае криволинейного – путь и перемещение различаются (см. рисунок 9б), так как длина линии движения тела больше длины вектора, соединяющего начало и конец траектории.
Рисунок 9 – Путь (S) и перемещение (r) при прямолинейном (а) и криволинейном (б) движении
*Иногда перемещение так же, как и путь, называют буквой S – (на письме с вектором над ней, при печати – жирным шрифтом, так как это векторная величина). В данной статье, чтобы не путаться, перемещение называется только буквой r. В целом, обозначения равноправны, поэтому при решении задач можно использовать то, которое удобнее. Однако не стоит забывать отмечать, что именно обозначено под той или иной буквой.
Равномерное прямолинейное движение: скорость и уравнение движения
Путь и перемещение при равномерном прямолинейном движении
Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.
Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:
- равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.
Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.
Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см. рисунок 8). Радиус-вектор, проведенный в точку A обозначим r0, а радиус-вектор в точку Б обозначим r1. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.
Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении
Тогда скорость движения (v) будет вычисляться по формуле:
Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.
Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r1 – r0. Тогда выражение для скорости можно переписать в виде:
Из этого выражения следует:
r1 = r0 + v*t.
Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:
r = r0 + v*t.
Данное уравнение является уравнением движения при прямолинейном равномерном движении.
*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t1, где t – конечный момент времени, t1 – начальный. Если же начальный момент времени совпадает с началом отсчета t1 = 0, то △t = t – 0 = t.
Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.
Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.
rx = r0x + vx*t;
ry = r0y + vy*t;
rz = r0z + vz*t.
В этих выражениях r0x, r0y, r0z и vx, vy, vz – это компоненты изначальных векторов r0 и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:
rx = r0x + vx*t;
ry = r0y + vy*t;
rz = r0z + vz*t.
Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.
В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х0) и конечной (х1) точки на ось ОХ.
Рисунок 9 – Перемещение тела в координатном представлении
Уравнение координаты (х) движения будет выглядеть:
x(t) = x0 + v*t.
А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:
S(t) = S0 + v*t.
Если точка начала двигаться из начала отсчета S0 = 0, можно переписать эту формулу в виде:
S(t) = v*t.
Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:
Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x0 = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.
Итак, для начала приведем все единицы измерения к СИ:
x0 = 3 см = 0,03 м.
Теперь можно записывать уравнение для координаты х:
x(t) = x0 + v*t = 0,03 + 5*t.
Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:
x(2) = 0,03 + 5*2 = 10, 03.
А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2) = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:
S = x(2) – x0 = 10, 03 – 0,03 = 10 м.
А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?
Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный:
x(t) = x0 – v*t = 0,03 – 5*t.