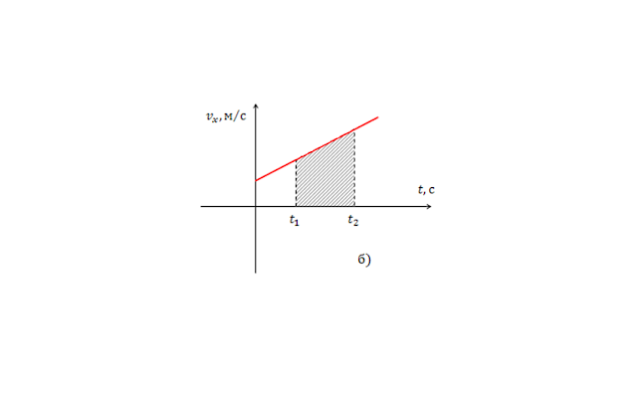
Как найти перемещение тела с ускорением - Сайт, где вы сможете решить свои вопросы

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Формула перемещения

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

v = v₀± at

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀= 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают (а↑↑v). Если векторы имеют противоположное направление (а↑↓v), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

t₁ = t – t₂

Когда тело тормозит, через некоторое время t₁ оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

0 = v₀₁ – at₁

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

t₂ = t – t₁

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂равна:

v = at₂

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

s = |s₁ – s₂|

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

l = s₁ + s₂

Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с². Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

v₀₂ = v₀₁ + a₁t₁ = a₁t₁ (так как v₀₁= 0)

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с^2.Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с². Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения сонаправлены (v↑↑a), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно (v↓↑a), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

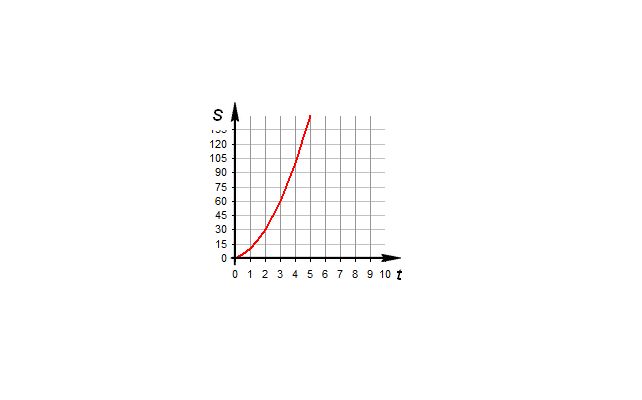
Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Задание EF18553

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t– 3t²(все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

1.Записать исходные данные и перевести их единицы измерения величин в СИ.

2.Записать уравнение движения тела при прямолинейном равноускоренном движении в общем виде.

3.Сравнить формулу из условия задачи с этим уравнением движения и выделить кинематические характеристики движения.

4.Определить перемещение тела и его кинетическую энергию.

5.Выбрать для физических величин соответствующую позицию из второго столбца таблицы и записать ответ.

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет вид:

x(t)=x0+v0t+at22

Теперь мы можем выделить кинематические характеристики движения тела:

• a/2 = –3 (м/с2), следовательно, a = –6 (м/с2).

Перемещение тела определяется формулой:

s=v0t+at22

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

x(t)=v0t+at22=5t−3t2

Кинетическая энергия тела определяется формулой:

Ek=mv22

Скорость при прямолинейном равноускоренном движении равна:

v=v0+at=5−6t

Поэтому кинетическая энергия тела равна:

Ek=m(5−6t)22=0,22(5−6t)2=0,1(5−6t)2

Следовательно, правильная последовательность цифр в ответе будет: 34.

Ответ: 34

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

Определить, какому типу движения соответствует график зависимости координаты тела от времени.
Определить величины, которые характеризуют такое движение.
Определить характер изменения величин, характеризующих это движение.
Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

перемещение и путь;
скорость;
ускорение.

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

Ответ: 24

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18831

На рисунке представлен график зависимости модуля скорости υ автомобиля от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от t₁=20 с до t₂=50 с.

Алгоритм решения

Охарактеризовать движение тела на различных участках графика.
Выделить участки движения, над которыми нужно работать по условию задачи.
Записать исходные данные.
Записать формулу определения искомой величины.
Произвести вычисления.

Решение

Весь график можно поделить на 3 участка:

От t₁ = 0 c до t₂ = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
От t₁ = 10 c до t₂ = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
От t₁ = 30 c до t₂ = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

От t₁ = 20 c до t₂ = 30 с — с равномерным движением.
От t₁ = 30 c до t₂ = 50 с — с равнозамедленным движением.

Исходные данные:

Для первого участка. Начальный момент времени t₁ = 20 c. Конечный момент времени t₂ = 30 с. Скорость (определяем по графику) — 10 м/с.
Для второго участка. Начальный момент времени t₁ = 30 c. Конечный момент времени t₂ = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.

Записываем формулу искомой величины:

s = s₁ + s₂

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁ и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁ и s₂, а затем сложим их:

s₁ + s₂ = 100 + 100 = 200 (м)

Ответ: 200

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 25.3k

Источник

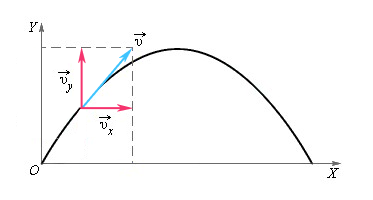
Равноускоренное движение в поле тяжести Земли. На рисунке видно, что перемещение складывается из прямолинейного равномерного движения и свободного падения

Равноуско́ренное движе́ние — движение тела, при котором его ускорение постоянно по модулю и направлению^[1].

Скорость при этом определяется формулой

${displaystyle {vec {v}}(t)={vec {v}}_{0}+{vec {a}}t}$

где ${displaystyle {vec {v}}_{0}}$ — начальная скорость тела, — время. Траектория имеет вид участка параболы или прямой.

Примером такого движения является полёт камня, брошенного под углом alpha к горизонту в однородном поле силы тяжести: камень летит с постоянным ускорением , направленным вертикально вниз.

Частным случаем равноускоренного движения является равнозамедленное, когда векторы vec{v} и противонаправлены, а модуль скорости равномерно уменьшается со временем (в примере с камнем реализуется для ${displaystyle alpha =90^{0}}$ при подъёме).

Характер равноускоренного движения[править | править код]

Равноускоренное движение происходит в плоскости, содержащей векторы ускорения и начальной скорости ${displaystyle {vec {v}}_{0}}$ . С учётом того, что (здесь — радиус-вектор), траектория описывается выражением

${displaystyle {vec {r}}(t)={vec {r}}_{0}+{vec {v}}_{0}t+{frac {{vec {a}}t^{2}}{2}}}$

На заданном интервале времени она представляет собой участок параболы, который при параллельности (то есть со или противо- направленности) векторов и ${displaystyle {vec {v}}_{0}}$ превращается в отрезок прямой.

Для каждой из координат, скажем , могут быть записаны аналогичные по структуре выражения:

${displaystyle y(t)=y_{0}+v_{0y}t+{frac {a_{y}t^{2}}{2}}}$

где ${displaystyle a_{y}}$ — составляющая ускорения вдоль оси , а ${displaystyle {vec {r}}_{0}=x_{0}{vec {i}}+y_{0}{vec {j}}+z_{0}{vec {k}}}$ — радиус-вектор материальной точки в момент ( vec{i} , vec{j} , vec{k} — орты).

В примере с камнем ${displaystyle x_{0}=y_{0}=z_{0}=0}$ , компоненты ускорения ${displaystyle a_{x}=a_{z}=0}$ , ${displaystyle a_{y}=-g}$ , начальной скорости ${displaystyle v_{x0}=v_{0}cos alpha }$ , ${displaystyle v_{y0}=v_{0}sin alpha }$ , ${displaystyle v_{z0}=0}$ , при этом ${displaystyle x(t)=v_{0x}t}$ , а значит, ${displaystyle y=operatorname {tg} alpha cdot x-g/2v_{0}^{2}cos ^{2}alpha cdot x^{2}}$ .

Перемещение и скорость[править | править код]

В случае равноускоренного движения любая из компонент скорости, например ${displaystyle v_{x}}$ , зависит от времени линейно:

${displaystyle v_{x}=v_{0x}+a_{x}t}$

При этом имеет место следующая связь между перемещением ( ${displaystyle Delta x=x-x_{0}}$ ) вдоль координаты и скоростью вдоль той же координаты:

$Delta x={frac {v_{x}^{2}-v_{{0x}}^{2}}{2a_{x}}}$

Отсюда можно получить выражение для -составляющей конечной скорости тела при известных -составляющих начальной скорости и ускорения:

$v_{x}=pm {sqrt {v_{{0x}}^{2}+2a_{x}Delta x}}$

Если ${displaystyle a_{x}=0}$ , то ${displaystyle v_{x}=v_{ox}}$ , а ${displaystyle Delta x=v_{0x}t}$ .

Выражения для смещений Delta y , Delta z и компонент скорости вдоль координат и принимают точно такой же вид, как для Delta x и $v_{x}$ , но символ всюду заменяется на или .

Суммарно, по теореме Пифагора, перемещение составит

${displaystyle |Delta {vec {r}}|={sqrt {(Delta x)^{2}+(Delta y)^{2}+(Delta z)^{2}}}}$

а модуль конечной скорости находится как

$|{vec v}|={sqrt {v_{{x}}^{2}+v_{{y}}^{2}+v_{{z}}^{2}}}$

Равноускоренное движение не может происходить неограниченно долго: это означало бы, что, начиная с какого-то момента времени , модуль скорости тела превысит величину скорости света в вакууме , что исключается теорией относительности.

Условие осуществления[править | править код]

Равноускоренное движение реализуется при действии на тело (материальную точку) постоянной силы vec{F} , обычно в однородном гравитационном или электростатическом поле, если величина скорости тела значительно меньше, чем скорость света . Тогда, по второму закону Ньютона, ускорение составит

${vec {a}}={frac {{vec {F}}}{m}},$

где через обозначена масса тела. В примере с камнем роль vec{F} играет сила тяжести.

Если же скорость тела сопоставима со скоростью света, то закон Ньютона в выписанном виде неприменим. При этом, в случае действия постоянной силы, происходит так называемое релятивистски равноускоренное движение, при котором постоянно только собственное ускорение, а ускорение в фиксированной ИСО приближается к нулю со временем по мере приближения величины скорости к её пределу .

Теорема о кинетической энергии точки[править | править код]

Формула перемещения при равноускоренном движении используется при доказательстве теоремы о кинетической энергии. Для этого необходимо перенести ускорение в левую часть и домножить обе части на массу тела:

$ma_{x}Delta x={frac {mv_{x}^{2}}{2}}-{frac {mv_{{0x}}^{2}}{2}}$

Записав аналогичные соотношения для координат и и просуммировав все три равенства, получим соотношение:

${displaystyle {vec {F}}cdot Delta {vec {r}}={frac {mv^{2}}{2}}-{frac {mv_{0}^{2}}{2}}}$

Слева стоит работа постоянной равнодействующей силы vec F , а справа — разность кинетических энергий в конечный и начальный моменты движения. Полученная формула представляет собой математическое выражение теоремы о кинетической энергии точки для случая равноускоренного движения^[2].

Равнопеременное движение[править | править код]

Равнопеременным называется движение, при котором тангенциальная (параллельная скорости) составляющая ускорения постоянна^[3]. Такое движение не является равноускоренным, кроме ситуации, когда оно происходит по прямой, но в математическом плане может быть рассмотрено аналогично.

В этом случае вводится обобщённая координата , часто называемая путём, соответствущая длине пройденной траектории (длине дуги кривой). Таким образом, формула приобретает вид:

$Delta S={frac {v^{2}-v_{{0}}^{2}}{2a_{tau }}}$

где $a_{tau }$ — тангенциальное ускорение, «отвечающее» за изменение модуля скорости тела. Для скорости получаем:

$v=pm {sqrt {v_{{0}}^{2}+2a_{tau }Delta S}}$

При ${displaystyle a_{tau }=0}$ имеем движение с постоянной по модулю скоростью.

Иногда прилагательное равнопеременное заменяют на криволинейное равноускоренное, что вносит путаницу, так как, скажем, равноускоренное движение камня по кривой (параболе) в поле тяжести не равнопеременное.

См. также[править | править код]

Релятивистски равноускоренное движение

Примечания[править | править код]

↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 37. — 560 с. — ISBN 5-9221-0225-7.
↑ Тарг С. М. Краткий курс теоретической механики. — 11-е изд. — М.: «Высшая школа», 1995. — С. 214. — 416 с. — ISBN 5-06-003117-9.
↑ См. Физический энциклопедический словарь — М.: Советская энциклопедия, под. ред. А. М. Прохорова (1983), статья «Равнопеременное движение», стр. 602.

Источник

Равноускоренное движение

Равноускоренное движение – это движение, при котором вектор ускорения не меняется по модулю и направлению (в случае равнозамедленного движения модуль скорости равномерно меняется). Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту. Равномерное движение, в отличие от неравномерного, – частный случай ускоренного в равной степени движения с ускорением, равным нулю.

Рассмотрим случай свободного падения (тело брошено под углом к горизонту) более подробно с вычислением. Такое движение можно рассчитать и представить в виде суммы движений относительно вертикальной и горизонтальной осей.

Как найти ускорение в физике? Нахождение ускорения в физике происходит с учетом того, что в любой точке траектории на тело действует ускорение свободного падения g→, которое не меняется по величине и всегда направлено в одну сторону.

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y – движение равноускоренное и прямолинейное. Будем рассматривать определенные проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости (формула ускорения) при равноускоренном движении:

v=v0+at.

Здесь v0 – начальная скорость тела, a=const – ускорение.

Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии. Вот небольшой тест.

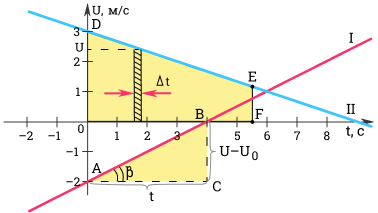
Как найти ускорение? Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC. Вот как выглядит формула ускорения в физике.

a=v-v0t=BCAC

Чем больше угол β, тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v0=-2 мс; a=0,5 мс2.

Для второго графика: v0=3 мс; a=-13 мс2.

По данному графику физик может также вычислить (произвести определение) перемещение тела за время t. Как это сделать?

Выделим на графике малый отрезок времени ∆t. Будем считать, что он настолько мал, что движение за время ∆t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆t. Тогда, перемещение ∆s за время ∆t будет равно ∆s=v∆t.

Разобьем все время t на бесконечно малые промежутки ∆t. Перемещение s за время t равно площади трапеции ODEF.

s=OD+EF2OF=v0+v2t=2v0+(v-v0)2t.

Мы знаем, что v-v0=at, поэтому окончательная формула или расчет для перемещения тела примет вид:

s=v0t+at22

Для того чтобы найти координату тела в данный момент времени, нужно к начальной координате тела добавить перемещение (расстояние). Изменение координаты в зависимости от времени выражает закон равноускоренного движения.

Какова будет формула пути при равноускоренном движении? В этом случае путь изменяется согласно квадратной зависимости: 8=v0t + at²/2.

Закон равноускоренного движения

y=y0+v0t+at22.

Еще одна распространенная задача кинематики, которая возникает при анализе равноускоренного движения – находить координаты при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s=v2-v022a.

По известным начальной скорости, ускорению и перемещению может находиться конечная скорость тела:

v=v02+2as.

При v0=0 s=v22a и v=2as

Важно!

Величины v, v0, a, y0, s, входящие в выражения, являются алгебраическими величинами. Они могут принимать как положительные, так и отрицательные значения – это будет зависеть от характера движения и направления координатных осей в условиях конкретной задачи.

Источник

Прямолинейным равноускоренным движением называется движение, при котором скорость тела за любые равные
промежутки времени изменялась на одинаковую величину. И основной
характеристикой такого движения являлось ускорение — это физическая
векторная величина, характеризующая быстроту изменения скорости.

Как определить координату тела, пройденный путь и перемещение
при прямолинейном равноускоренном движении?

Это можно сделать, если рассмотреть прямолинейное равноускоренное движение
как набор большого количества очень малых равномерных перемещений тела.

Первым решил задачу местоположения тела
в определённый момент времени при ускоренном движении итальянский учёный
Галилео Галилей. Галилей использовал
наклонную плоскость с гладкой канавкой посередине, по которой скатывались
латунные шары. По водным часам он засекал определённый интервал времени и
фиксировал расстояния, которые за это время преодолевали шары. Галилей выяснил,
что если время увеличить в два раза, то шары прокатятся в четыре раза дальше
(т.е. зависимость квадратичная). Это опровергало мнение Аристотеля, что
скорость шаров будет постоянной.

Получим формулу для определения перемещения при
равноускоренном движении графическим методом.

Известно, что при равноускоренном движении тела,
происходящем вдоль координатной оси X,
скорость
с течением времени не остается постоянной, а меняется со временем согласно
формуле

Т.
е. скорость является линейной функцией, и поэтому графики скорости имеют вид
прямой.

Прямая
1 соответствует движению с положительным ускорением (скорость
увеличивается), прямая 2 — движению с отрицательным ускорением
(скорость убывает).

График скорости разобьем на маленькие прямоугольные участки.
Каждый участок будет соответствовать определённой постоянной скорости.

Необходимо определить пройденный путь за первый промежуток
времени. Запишем формулу

Теперь посчитаем суммарную площадь всех имеющихся у нас фигур. А
сумма площадей при равномерном движении – это полный пройденный путь.

Обратите внимание, от точки к точке скорость будет изменяться, тем
самым можно получить путь, пройденный телом именно при прямолинейном
равноускоренном движении.

Заметим, что при прямолинейном равноускоренном движении тела,
когда скорость и ускорение направлены в одну сторону, модуль перемещения равен
пройденному пути, поэтому, когда определяется модуль перемещения, то определяется
и пройденный путь.

В данном случае можно говорить, что модуль перемещения будет
равен площади фигуры, ограниченной графиком скорости и осью времени.

Фигура, ограниченная графиком скорости и осью
времени есть не что иное, как прямоугольная трапеция. Из математики известна
формула для нахождения площади трапеции. Площадь трапеции равна произведению
половины суммы её оснований на высоту.

Следовательно, перемещение за все время tчисленно
равно площади трапеции ОАВС. В
нашем случае длина одного из оснований численно равна υ_o_х, длина другого
— υ_х. Высота же ее численно равна t. Отсюда следует, что перемещение равно:

Подставим в эту формулу вместо υ
равную
ей величину υ₀
+ at.Тогда

Разделив почленно числитель на знаменатель, получим

Это есть уравнение перемещения в проекциях на ось
координат.

При пользовании этой формулой нужно помнить, что s,
υ₀и
а могут быть как положительными, так и отрицательными — ведь это проекции векторов пути, начальной скорости
и ускорения на ось X.

Теперь вспомним, что пройденный путь, равный в нашем случае модулю
перемещения, выражается разностью: s = x – x₀

Если в уравнение подставить полученное нами выражение для S,
то запишем закон, по которому движется тело при прямолинейном равноускоренном
движении:

Это уравнение называется основным кинематическим уравнением
равноускоренного движения.

Если тело движется из
состояния покоя, график проходит через начало координат, фигура под графиком –
прямоугольный треугольник, площадь которого равна половине произведения
катетов.

Тогда формула для определения перемещения принимает
вид:

Это уравнение перемещения при равноускоренном
движении без начальной скорости.

Тогда

x = x₀ + at²/2

Это
кинематическое уравнение равноускоренного движения , без начальной
скорости.

Рассмотрим некоторые важные зависимости между величинами
равноускоренного движения. Для равноускоренного движения без начальной скорости
путь, пройденный телом, пропорционален квадрату времени. Значит, пути,
пройденные телом за 1 с, 2 с, 3 с, 4 с будут относиться как
квадраты последовательных натуральных чисел.

Для любого равноускоренного движения, пути, пройденные телом за
любые равные промежутки времени, будут относиться как последовательный ряд
нечетных чисел.

Основные выводы:

–
Перемещение тела за все время t численно равно площади трапеции,
ограниченной графиком скорости и осью времени.

—
уравнениеперемещения

—
кинематическое
уравнение
равноускоренного движения

– Для равноускоренного движения без начальной скорости путь, пройденный телом,
пропорционален квадрату времени.

– Для любого равноускоренного движения,
пути, пройденныетеломза любые равные промежутки времени,
будутотноситьсякакпоследовательный ряд нечетных чисел.

Источник

Перемещение при прямолинейном равноускоренном движении

Средняя оценка: 4

Всего получено оценок: 156.

Средняя оценка: 4

Всего получено оценок: 156.

Движение, при котором траектория представляет собой прямую линию, называется прямолинейным. Если при таком движении скорость равномерно изменяется, то изменение скорости за единицу времени называется ускорением, а такое движение называется равноускоренным. Рассмотрим перемещение при прямолинейном равноускоренном движении.

Прямолинейное равноускоренное движение

Наиболее удобным для изучения примером равноускоренного прямолинейного движения является свободное падение тел в первые секунды полета, когда сопротивление воздуха пренебрежительно мало. Скорость падения тела при этом равномерно увеличивается, и за одинаковые промежутки времени изменение составляет одну и ту же величину.

Рис. 1. Свободное падение тел.

Для Земли на средних широтах каждую секунду скорость падения увеличится приблизительно на 9.81 м/с. Данная величина называется ускорением свободного падения.

Если бы движение было равномерным, то материальная точка каждую секунду проходила бы одно и то же расстояние. Однако для равноускоренного движения это не так.

Найдем формулу перемещения тела при прямолинейном равноускоренном движении.

Вывод формулы перемещения

Наиболее просто найти формулу перемещения из графика скорости. Перемещение материальной точки равно площади фигуры, лежащей под графиком скорости.

Например, для равномерного движения график скорости представляет горизонтальную прямую, а значит, площадь под этим графиком является прямоугольником, высота которого равна скорости, а ширина – времени. Для нахождения его площади необходимо перемножить эти величины, получив известную формулу «расстояние равно произведению скорости на время пути».

При равноускоренном движении скорость равномерно меняется, а значит, ее график представляет собой наклонную прямую:

Рис. 2. График скорости при равноускоренном движении.

Найдем площадь фигуры под этой прямой.

Фигура является четырехугольником, одна сторона является отрезком оси абсцисс длинной $Δt=t_2-t_1$, две соседние стороны – вертикальные отрезки, длина каждого равна значению скорости в соответствующий момент времени: $v_1$ и $v_2$. То есть, фигура является трапецией, площадь которой, как известно из геометрии, равна произведению полусуммы оснований на высоту. Высота равна промежутку времени, основания – скоростям вначале и в конце пути. То есть, если начальный момент времени нулевой ($t_1=0$), а скорость в начальный момент обозначить $v_0$ то рассматриваемое перемещение равно:

$$x(t)={v+ v_0over 2}t$$

Поскольку при равноускоренном движении скорость за единицу времени увеличивается на величину ускорения, то скорость в момент $t$ будет равна сумме начальной скорости и произведению ускорения на время пути:

$$v(t)= v_0 + at$$

Подставив значение скорости в предыдущую формулу, и приняв, что перемещение в начальный момент времени было равно $x_0$, получим окончательную формулу перемещения тела при прямолинейном равноускоренном движении:

$$x(t)=x_0+v_0t+{at^2over 2}$$

Из вида формулы можно заключить, что график перемещения при равноускоренном движении является параболой.

Рис. 3. График перемещения при равноускоренном движении.

При решении задач время движения зачастую неизвестно, в этом случае удобно выразить его из предыдущей формулы, получив соотношение:

$$x(t)=x_0+{v^2-v_0^2over 2a}$$

Парабола имеет, как правило, два корня. А значит, задачи о перемещении тела при равноускоренном движении могут иметь не одно, а два правильных решения. Например, если найти время, когда предмет, брошенный вверх со скоростью 20м/с достигнет высоты 9 м, мы получим два ответа: через 0.52 с и 3.56 с. Оба эти ответы правильны. Предмет будет на высоте 9 м дважды – первый раз при полете вверх, второй раз в момент падения.

Что мы узнали?

Наиболее частый пример прямолинейного равноускоренного движения – это свободное падение тел, пока сопротивление воздуха пренебрежительно мало. Перемещение при равноускоренном прямолинейном движении является квадратичной функцией, ее график является параболой.

Тест по теме

Доска почёта

Чтобы попасть сюда – пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

Средняя оценка: 4

Всего получено оценок: 156.

А какая ваша оценка?

Источник

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://spadilo.ru/wp-content/uploads/2020/07/word-image-149.png" width="430" height="61" />

Перемещение при разгоне и торможении тела

Этап торможения

Этап разгона

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Проекция и график перемещения

График пути

Характер равноускоренного движения[править | править код]

Перемещение и скорость[править | править код]

Условие осуществления[править | править код]

Теорема о кинетической энергии точки[править | править код]

Равнопеременное движение[править | править код]

См. также[править | править код]

Примечания[править | править код]

Равноускоренное движение

Формулы для равноускоренного движения

Закон равноускоренного движения

Перемещение при прямолинейном равноускоренном движении

Прямолинейное равноускоренное движение

Вывод формулы перемещения

Что мы узнали?

Тест по теме

Оценка доклада

Вам также может понравиться

Hosts как найти эту папку

Как найти суммарный импульс до взаимодействия

Как найти фулл по гиф

Добавить комментарий Отменить ответ