Как найти перемещение треугольник

Плоскопараллельное перемещение треугольника

Плоскопараллельное перемещение треугольника ΔABC используемое для преобразования его ортогональных проекций, соответствующих плоскости общего положения δ, в проекции δ₂ // H для получения натуральной величины сторон и углов треугольника ΔABC требует выполнения следующих построений: – горизонтали (или фронтали) плоскости AD;

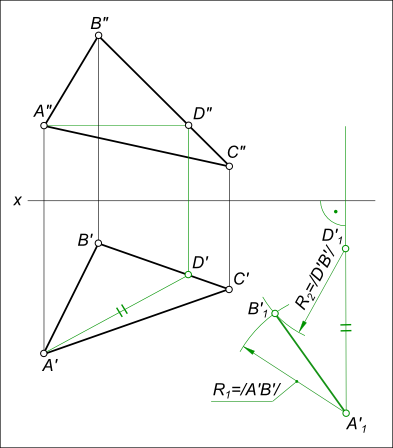
– перевода горизонтали плоскости в положение A₁D₁ ⊥ V: – на направлении перпендикуляра к плоскости V проведенном на свободном месте чертежа откладываем величину A`D` = A`<sub>1</sub>D`₁ – перестроение других точек проекции ΔA`B`C` на новое положение ΔA`₁B`<sub>1</sub>C`₁: – точку B`<sub>1</sub> дает пересечение дуг R<sub>1</sub> = /A`B`/ и R<sub>2</sub> = /D`B`/; – сторону B`D` продолжим до пересечения

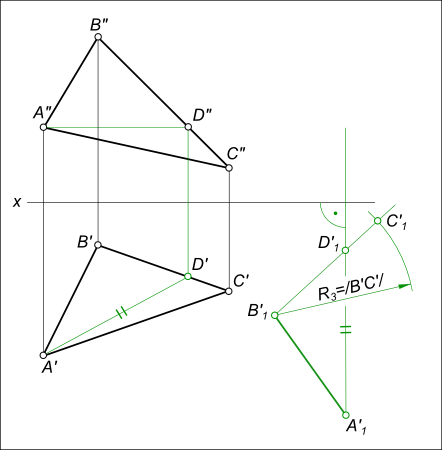
с дугой радиуса R₃ = /B`C`/; – проекции вершин треугольника в новом положении соединяем прямыми линиями;

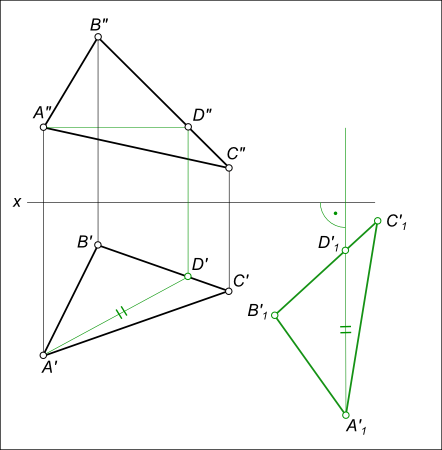
– перемещения фронтальных проекций ΔA”B”C” к новому положению ΔA”₁B”₁C”₁, происходящего в плоскостях уровня β1_V, β2_V и β3_V параллельных плоскости H;

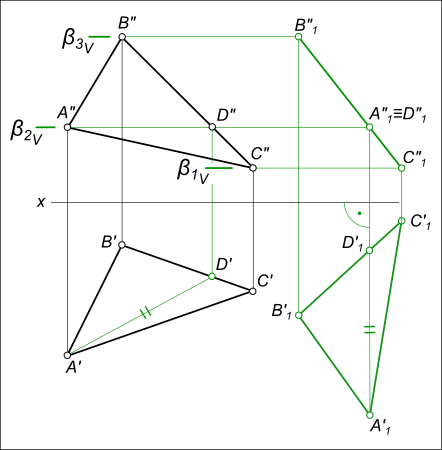
– новое положение проекций определится на пересечении траекторий их движения в плоскостях уровня с вертикальными линиями проекционной связи; – перемещения фронтальной проекции ΔA”₁B”₁C”₁ в положение параллельное H,

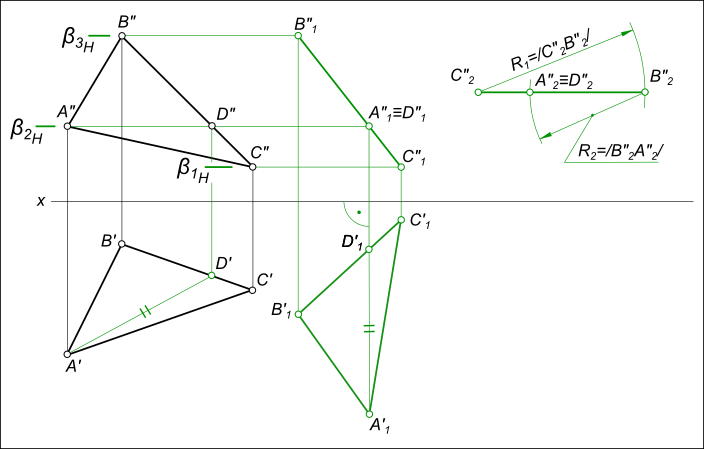
которое выполняем переводом прямой В”₁С”₁ – фронтальной проекции ΔA₁B₁C₁ в положение параллельное оси x: В”₂С”₂ // x; – перемещения горизонтальных проекций ΔA`<sub>1</sub>B`₁C`<sub>1</sub> к новому положению ΔA`₂B`<sub>2</sub>C`₂, происходящего в плоскостях уровня α1_H, α2_H и α3_H параллельных плоскости V;

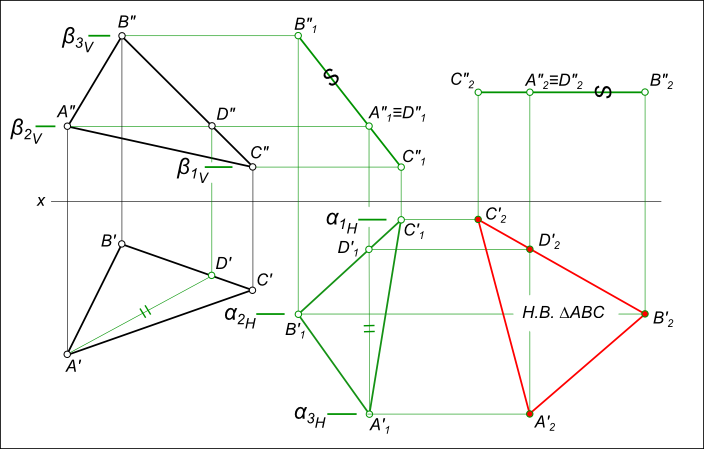
– новое положение проекций определится на пересечении траекторий их движения в плоскостях уровня с вертикальными линиями проекционной связи: проекция ΔA`<sub>2</sub>B`₂C`₂ соответствует натуральной величине треугольника ΔABC.

Метод плоскопараллельного перемещения

В начертательной геометрии метод плоскопараллельного перемещения используется, как правило, для определения натуральных величин плоских фигур, отрезков и углов.

Свойства плоскопараллельного перемещения:

1. При перемещении любой фигуры параллельно плоскости проекции, проекция фигуры на эту плоскость остается неизменной.
2. При перемещении точки параллельно горизонтальной плоскости проекции, её фронтальная проекция движется по прямой, параллельной оси X. На рисунке ниже точки C” и D”, следуя этому свойству, заняли положение C”₁ и D”₁.
3. При перемещении точки параллельно фронтальной плоскости проекции, её горизонтальная проекция движется по прямой, параллельной оси X.

Рассмотрим перевод произвольно расположенного отрезка CD в положение, параллельное горизонтальной плоскости проекций П₂.

• Используя первое свойство параллельного перемещения, на любом свободном месте чертежа строим отрезок C’₁D’₁ = C’D’.
• По линиям связи определяем недостающие проекции C”₁ и D”₁. Стрелками показано перемещение точек C” и D” параллельно оси X в соответствии со вторым свойством рассматриваемого метода.

Следующий рисунок иллюстрирует перевод отрезка MN в проецирующее положение по отношению к фронтальной плоскости проекций П₂. В общем случае для решения подобной задачи необходимо дважды воспользоваться методом плоскопараллельного перемещения.

• После первого преобразования отрезок MN займет положение параллельно плоскости П₁. Сначала строится M”₁N”₁ = M”N” на произвольном месте чертежа, после чего по линиям связи находятся недостающие проекции M’₁ и N’₁.
• Второе преобразование заключается в параллельном переносе горизонтальной проекции отрезка M’₁N’₁ в положение M’₂N’₂, перпендикулярное оси X. После этого точки M”₂ = N”₂ определяются по линиям связи.

Определение натуральной величины треугольника

Рассмотрим порядок плоскопараллельного перемещения треугольника ABC с целью определения его натуральной величины.

1. Через точку С треугольника ABC проводим горизонталь CD. Находим её недостающие проекции.
2. Переводим ABC в положение, перпендикулярное фронтальной плоскости проекций. Для этого строим C’₁D’₁ = C’D’ перпендикулярно оси X. В соответствии с первым свойством плоскопараллельного перемещения достраиваем треугольник A’₁B’₁C’₁ = A’B’C’. По линиям связи определяем точки A”₁, B”₁, C”₁.
3. Перемещаем проекцию A”₁B”₁C”₁ треугольника ABC в положение A”₂B”₂C”₂, параллельное оси X, соблюдая равенство A”₂B”₂C”₂ = A”₁B”₁C”₁. По линиям связи определяем точки A’₂, B’₂, C’₂. Теперь треугольник ABC расположен параллельно горизонтальной плоскости проекций и проецируется на неё в натуральную величину A’₂B’₂C’₂.

Определение расстояния между параллельными прямыми

Расстояние между двумя параллельными прямыми равно длине перпендикуляра, опущенного из произвольной точки первой прямой на вторую прямую. Рассмотрим, как указанное расстояние определяется на практике с помощью метода плоскопараллельного перемещения.

Путем двух последовательных преобразований прямые a и b переводятся в положение, перпендикулярное горизонтальной плоскости. Таким образом, они проецируются на неё в точки A’₂ и B’₂, расстояние между которыми является искомым. Показанные на рисунке величины d₁ и d₂ являются вспомогательными для выполнения построений согласно свойствам плоскопараллельного перемещения.

Секержицкий В.С. О векторных способах решения избранных задач кинематики

Секержицкий В.С. О векторных способах решения избранных задач кинематики // Фізіка: праблемы выкладання. – Вып. 6. – С. 111-116.

В ряде случаев векторный способ имеет преимущество перед координатным, не только упрощая решение конкретной задачи, но и превращая иногда сложные, на первый взгляд, задачи в подстановочные, решаемые практически устно. В данной статье мы рассмотрим возможность применения векторных способов к решению задач кинематики, большинство из которых предлагались в различные годы на олимпиадах школьников по физике.

1. Некоторые методы теоретической механики предполагают применение достаточно простого математического аппарата, вполне доступного студентам младших курсов вузов и учащимся старших классов (особенно с углубленным изучением физики). К таким методам относится, в частности, использование векторных способов решения задач кинематики. При изучении механики в школе предполагается знакомство с векторным способом кинематического описания движения (вводятся понятия векторов перемещения, скорости и ускорения), но значительно больше внимания уделяется координатному и естественному способам. Вместе с тем в ряде случаев векторный способ имеет преимущество перед координатным, не только упрощая решение конкретной задачи, но и превращая иногда сложные, на первый взгляд, задачи в подстановочные, решаемые практически устно.

В данной статье мы рассмотрим возможность применения векторных способов к решению задач кинематики, большинство из которых предлагались в различные годы на олимпиадах школьников по физике, т е считаются в школьном курсе физики задачами повышенной трудности.

2. При движении тела (материальной точки) его перемещение можно рассматривать как геометрическую сумму нескольких последовательных перемещений, например,

(1)

Соответствующий уравнению (1) многоугольник перемещений (треугольник в данном случае) представлен на рис. 1. Изменение скорости тела

(2)

Этому выражению соответствует треугольник скоростей (рис. 2).

При движении тела с постоянным по величине и направлению ускорением выражение для скорости в любой момент времени t имеет вид:

(3)

где при t = 0.

В общем случае направления векторов начальной скорости и ускорения могут не совпадать. Треугольник скоростей, соответствующий выражению (3), приведен на рис. 3.

Вектор перемещения при этом определяется следующим образом:

(4)

Треугольники перемещений представлены на рис. 4, а–в.

Наиболее эффективно применение векторного способа, основанного на построении треугольников скоростей и перемещений в тех случаях, когда известны направления векторов ускорения и одной из скоростей (например, начальной). Это относится, в частности, к задачам о движении тела под действием силы тяжести. Рассмотрим примеры.

Задача 1. Тело брошено вверх перпендикулярно плоскости, наклоненной под углом a к горизонту. На каком расстоянии от места броска тело упадет на эту наклонную плоскость? Сопротивлением движения пренебречь.

Решение. На рис. 5 изображен треугольник перемещений, соответствующий условию задачи и соотношению . Легко видеть, что , откуда время движения . Тогда искомое расстояние .

Задача 2. На наклонную плоскость с углом a свободно падает мяч без начальной скорости. Пролетев расстояние h , он упруго отразился от плоскости. На каком расстоянии от места удара мяч упадет на плоскость вторично? Определите величину и направление его скорости в этот момент. Сопротивлением движению пренебречь.

Решение. При упругом ударе угол падения равен углу отражения, и скорость u ₀ отскока мяча равна конечной скорости его падения с высоты h : . Треугольник перемещений BCD (рис. 6), соответствующий соотношению , равнобедренный. Тогда и искомое расстояние

Соотношению соответствует треугольник перемещений BED (рис. 6), из которого по теореме синусов находим:

Величину скорости u можно определить по теореме косинусов из треугольника ECD:

Итак, мяч вторично падает на наклонную плоскость со скоростью , вектор которой направлен к плоскости под углом .

Заметим, что основанные на принципе независимости движений координатные способы решения данных задач более трудоемкие, чем предложенные выше. Другие примеры решения задач кинематики с использованием треугольников перемещений и скоростей приведены в [1].

При движении двух материальных точек относительно некоторой систему отсчета, зная их перемещения , можно вычислить перемещение второго тела относительно первого:

(5)

Разность скоростей тел (относительная скорость) определяется выражением:

(6)

соответствующим закону сложения скоростей Галилея:

(7)

где – скорости первого и второго тел в неподвижной системе отсчета (естественно, «неподвижность» системы относительна), – скорость второго тела относительно первого. Треугольник и параллелограммы скоростей, соответствующие формулам (6) и (7), представлены на рис. 7, а-в.

Применим формулы (6) и (7) к решению задач

Задача 3. Две частицы брошены одновременно из одной точки с одинаковыми по модулю скоростями u : первая – вертикально вверх, вторая – горизонтально. Найдите расстояние между ними спустя время t . Сопротивлением движению пренебречь.

Решение. Ускорения частиц одинаковы и равны g (движение под действием силы тяжести). Следовательно, относительное движение равномерное и прямолинейное, т.е. вторая частица движется относительно первой с постоянной скоростью (рис. 8). Тогда искомое расстояние .

Задача 4. Две частицы находятся на одной высоте на расстоянии l друг от друга. Им одновременно сообщили одинаковые по величине скорости, направления которых показаны на рис. 9. Найдите минимальное расстояние между частицами в процессе их движения. Частицы движутся в одной вертикальной плоскости, сопротивление отсутствует.

Решение. Свяжем систему отсчета с телом А. Тогда (рис 10)

Ускорения обеих частиц одинаковы и равны g в системе отсчета, связанной с землей. Следовательно, относительная скорость постоянна по величине и направлению, траектория относительного движения – прямая. Искомое наименьшее расстояние между частицами (между точкой А и траекторией относительного движения на рис. 10) .

Задача 5. Собственная скорость пловца в п раз ( n > 1) меньше скорости течения. Под каким углом к течению он должен стараться плыть, чтобы при переправе через реку снос был минимальным?

Решение. Воспользуемся формулой (7) и треугольником скоростей, представленным на рис 7, а. Здесь – скорость течения, – собственная скорость пловца (относительно воды), – скорость пловца относительно неподвижной системы отсчета (берега). Так как u ₁ > u ₂₁, го снос будет иметь место при любом направлении вектора (при движении пловца по течению или против течения снос максимальный). Геометрическое место концов вектора для всевозможных его направлений представляет собой полуокружность (рис. 11). Легко видеть, что снос будет минимальным, если вектор направлен по касательной к этой полуокружности, т.е. . Тогда . Искомый угол .

Задача 6. Жесткий стержень АВ движется в плоскости рисунка 12, на котором показаны направления скоростей точек А и В. Найдите величину скорости u _B, если u _A = 5,0 м/с.

Решение. Так как расстояние между точками A и В неизменно (стержень жесткий), то скорость точки В относительно точки А может быть направлена только перпендикулярно стержню. Учитывая, что , строим параллелограмм скоростей (рис. 13), который в данное случае является прямоугольником. Тогда

Примеры решения аналогичных задач приведены в [2]. Очевидно, что применение векторных способов для решения ряда задач кинематики весьма эффективно, но в IX классе общеобразовательной школы для этого нет достаточной математической (тригонометрической) базы. В классах же с углубленным изучением физики, в курсах по выбору, при подготовке к олимпиадам изучение векторных способов решения задач вполне целесообразно. Опыт преподавания автором на протяжении нескольких лет факультативного спецкурса “Избранные задачи по физике и методы их решения” в лицее №1 г. Бреста показывает, что учащиеся XI класса достаточно легко воспринимают и усваивают векторные способы решения задач.

1. Койфман Ю.Г., Секержицкий В.С. Кинематика: о векторном cnocoбе решения избранных задач // Фокус. – 1993. – №4. – С. 61-68.

2. Секержицкий В.С. Кинематика: относительность движения // Фокус. – 1995. – №2. – С. 77-80.

[spoiler title=”источники:”]

http://ngeometry.ru/metod-ploskoparallelnogo-peremeshcheniya.html

http://alsak.ru/item/26-7.html

[/spoiler]

По графику скорости от времени v(t) можно найти перемещение тела. Для этого нужно уметь рассчитывать площади плоских фигур.

По-английски «Square» – значит «площадь». Первая буква этого слова – буква «S». Перемещение обозначают буквой S потому, что S – это площадь фигуры, заключенной между линией скорости и горизонтальной осью времени.

Как вычислить площади плоских фигур

Площадь прямоугольника

Площадь прямоугольника (рис. 1а) можно найти, перемножив две его перпендикулярные стороны:

[ large boxed{ S_{text{прямоуг}}  = a cdot b }]

Площадь трапеции

 Примечание: Трапеция – это четырехугольник, две его стороны параллельные, а две другие – не параллельные. Параллельные стороны называются основаниями трапеции.

Умножив полусумму оснований трапеции на ее высоту, получим площадь (рис. 1б) трапеции:

[ large boxed{ S_{text{трапец}}  = frac{1}{2} (a + b) cdot h }]

Площадь прямоугольного треугольника

Для прямоугольного треугольника (рис. 1в) площадь можно вычислить, перемножив два его катета и взяв половину от получившегося произведения:

[ large boxed{ S_{text{треуг}}  = frac{1}{2} cdot a cdot b }]

Скорость не меняется

Пусть тело движется по прямой и при этом его скорость не изменяется (остается одной и той же). На языке математики «скорость не изменяется» можно записать так:

[v=const]

На графике для скорости v(t) такая скорость обозначается горизонтальной линией. На рисунке 2 эта линия обозначена синим цветом.

Примечание: Движение с постоянной (т. е. с одной и той же) скоростью называют равномерным движением.

Если скорость направлена по оси движения – линия лежит выше оси t времени (рис. 2а).

А когда скорость направлена против оси движения – линия скорости располагается ниже оси t времени (рис. 2б). Математики в таком случае говорят: «Скорость имеет отрицательную проекцию на ось».

Какую бы проекцию не имела скорость – положительную, или отрицательную, длина вектора скорости остается положительной. Поэтому, когда мы вычисляем площадь фигуры, то не учитываем знак «минус» для скорости (рис. 2б).

В обоих случаях перемещение тела можно вычислить по формуле:

[ large S  = v_{0} cdot (t_{2} — t_{1}) ]

Примечание: Перемещение тела – это всегда либо нулевая, либо положительная величина S. Математики словосочетание «либо нулевая, либо положительная» заменят одним словом «не отрицательная».

Скорость увеличивается

Когда скорость тела увеличивается, то линия скорости на графике v(t) всегда располагается так, чтобы с ростом времени удаляться от оси времени. Чем больше времени пройдет, тем дальше от горизонтали располагаются точки, лежащие на линии скорости (рис. 3).

Примечание: Движение с возрастающей скоростью называют равноускоренным движением.

Когда тело движется по направлению оси, линия скорости расположена выше горизонтальной оси времени (рис 3а).

А если тело движется против оси, линия скорости располагается ниже горизонтальной оси времени (рис. 3б).

Вычислим перемещение тела, движущегося в положительном направлении оси Ox. Для тела, движущегося противоположно оси, перемещение рассчитывается аналогично.

Выбор интервала времени влияет на то, будем ли мы вычислять площадь трапеции (рис. 4а), или прямоугольного треугольника (рис. 4б).

На графике скорости v(t) для рисунка 4а перемещение с помощью трапеции вычисляется так:

[ large S  = frac{1}{2} cdot (v_{1} + v_{2}) cdot (t_{2} — t_{1}) ]

А для рисунка 4б перемещение тела найдем с помощью площади треугольника:

[ large S  = frac{1}{2} cdot v_{2} cdot (t_{2} — 0) ]

Скорость уменьшается

Когда тело замедляется и его скорость уменьшается, с ростом времени линия скорости приближается к горизонтальной оси t

• сверху – если тело движется по оси (рис. 5а),
• или снизу – когда тело движется против оси (рис. 5б).

Примечание: Движение с уменьшающейся по модулю скоростью называют равнозамедленным движением.

Будем вычислять перемещение тела, движущегося в положительном направлении оси Ox. Аналогичным способом рассчитывается перемещение тела, движущегося противоположно оси.

От того, какой интервал времени нас интересует, зависит, будем ли мы вычислять площадь трапеции (рис. 6а), или треугольника (рис. 6б).

Найдем на графике v(t) перемещение с помощью площади трапеции для рисунка 6а:

[ large S  = frac{1}{2} cdot (v_{1} + v_{2}) cdot (t_{2} — t_{1}) ]

А для рисунка 6б перемещение тела найдем с помощью площади треугольника:

[ large S  = frac{1}{2} cdot v_{1} cdot (t_{2} — t_{1}) ]

Выводы

На графике v(t) перемещение – это:

1. площадь прямоугольника, когда скорость не изменяется;
2. площадь треугольника, или трапеции, когда скорость изменяется — падает, или растет.

С понятием пути вы уже неоднократно сталкивались. Познакомимся теперь с новым для вас понятием – перемещением, которое более информативно и полезно в физике, чем понятие пути.

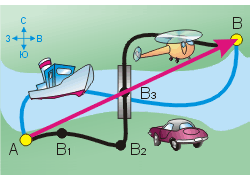
Допустим, из пункта А в пункт В на другом берегу реки нужно переправить груз. Это можно сделать на автомобиле через мост, на катере по реке или на вертолёте. В каждом из этих случаев путь, пройденный грузом, будет разным, но перемещение будет неизменным: из точки А в точку В.

Перемещением называют вектор, проведённый из начального положения тела в его конечное положение. Вектор перемещения показывает расстояние, на которое переместилось тело, и направление перемещения. Обратите внимание, что направление перемещения и направление движения – два разных понятия. Поясним это.

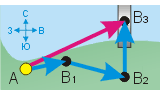
Рассмотрим, например, траекторию движения автомобиля от пункта А до середины моста. Обозначим промежуточные точки – В1, В2, В3 (см. рисунок). Вы видите, что на отрезке АВ1 автомобиль ехал на северо-восток (первая синяя стрелка), на отрезке В1В2 – на юго-восток (вторая синяя стрелка), а на отрезке В2В3 – на север (третья синяя стрелка). Итак, в момент проезда моста (точки В3) направление движения характеризовалось синим вектором В2В3, а направление перемещения – красным вектором АВ3.

Итак, перемещение тела – векторная величина, то есть имеющая пространственное направление и числовое значение (модуль). В отличие от перемещения, путь – скалярная величина, то есть имеющая только числовое значение (и не имеющая пространственного направления). Путь обозначают символом l, перемещение обозначают символом 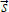(важно: со стрелочкой). Символом s без стрелочки обозначают модуль перемещения. Примечание: изображение любого вектора на чертеже (в виде стрелки) или упоминание его в тексте (в виде слова) делает необязательным наличие стрелочки над обозначением.

Почему в физике не ограничились понятием пути, а ввели более сложное (векторное) понятие перемещения? Зная модуль и направление перемещения, всегда можно сказать, где будет находиться тело (по отношению к своему начальному положению). Зная путь, положение тела определить нельзя. Например, зная лишь, что турист прошёл путь 7 км, мы ничего не можем сказать о том, где он сейчас находится.

Задача. В походе по равнине турист прошёл на север 3 км, затем повернул на восток и прошел ещё 4 км. На каком расстоянии от начальной точки маршрута он оказался? Начертите его перемещение.

Решение 1 – с измерениями линейкой и транспортиром.

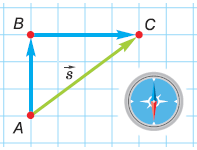
Перемещение – это вектор, соединяющий начальное и конечное положения тела. Начертим его на клетчатой бумаге в масштабе: 1 км – 1 см (чертёж справа). Измерив линейкой модуль построенного вектора, получим: 5 см. Согласно выбранному нами масштабу, модуль перемещения туриста равен 5 км. Но напомним: знать вектор – значит знать его модуль и направление. Поэтому, применив транспортир, определим: направление перемещения туриста составляет 53° с направлением на север (проверьте сами).

Решение 2 – без использования линейки и транспортира.

Поскольку угол между перемещениями туриста на север и на восток составляет 90°, применим теорему Пифагора и найдём длину гипотенузы, так как она одновременно является и модулем перемещения туриста:

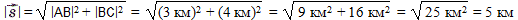
Как видите, это значение совпадает с полученным в первом решении. Теперь определим угол α между перемещением (гипотенузой) и направлением на север (прилежащим катетом треугольника):

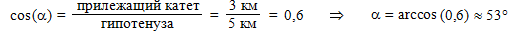
Итак, задача решена двумя способами с совпадающими ответами.

Плоскопараллельное перемещение треугольника

Плоскопараллельное перемещение треугольника ΔABC используемое для преобразования его ортогональных проекций, соответствующих плоскости общего положения δ, в проекции δ₂ // H для получения натуральной величины сторон и углов треугольника ΔABC требует выполнения следующих построений:
– горизонтали (или фронтали) плоскости AD;

– перевода горизонтали плоскости в положение A₁D₁ ⊥ V:
– на направлении перпендикуляра к плоскости V проведенном на свободном месте чертежа откладываем величину A`D` = A`<sub>1</sub>D`₁

– перестроение других точек проекции ΔA`B`C` на новое положение ΔA`₁B`<sub>1</sub>C`₁:
– точку B`<sub>1</sub> дает пересечение дуг R<sub>1</sub> = /A`B`/ и R<sub>2</sub> = /D`B`/;
– сторону B`D` продолжим до пересечения

с дугой радиуса R₃ = /B`C`/;
– проекции вершин треугольника в новом положении соединяем прямыми линиями;

– перемещения фронтальных проекций ΔA”B”C” к новому положению ΔA”₁B”₁C”₁, происходящего в плоскостях уровня β1_V, β2_V и β3_V параллельных плоскости H;

– новое положение проекций определится на пересечении траекторий их движения в плоскостях уровня с вертикальными линиями проекционной связи;
– перемещения фронтальной проекции ΔA”₁B”₁C”₁ в положение параллельное H,

которое выполняем переводом прямой В”₁С”₁ – фронтальной проекции ΔA₁B₁C₁ в положение параллельное оси x: В”₂С”₂ // x;
– перемещения горизонтальных проекций ΔA`<sub>1</sub>B`₁C`<sub>1</sub> к новому положению ΔA`₂B`<sub>2</sub>C`₂, происходящего в плоскостях уровня α1_H, α2_H и α3_H параллельных плоскости V;

– новое положение проекций определится на пересечении траекторий их движения в плоскостях уровня с вертикальными линиями проекционной связи: проекция ΔA`<sub>2</sub>B`₂C`₂ соответствует натуральной величине треугольника ΔABC.

+