Выбирайте формулу в зависимости от известных величин.
1. Как найти периметр треугольника, зная три стороны
Просто посчитайте сумму всех сторон.
- P — искомый периметр;
- a, b, c — стороны треугольника.
2. Как найти периметр треугольника, зная его площадь и радиус вписанной окружности
Умножьте площадь треугольника на 2.
Разделите результат на радиус вписанной окружности.
- P — искомый периметр;
- S — площадь треугольника;
- r — радиус вписанной окружности.
3. Как вычислить периметр треугольника, зная две стороны и угол между ними
Сначала найдите неизвестную сторону треугольника с помощью теоремы косинусов:
- Умножьте одну сторону на вторую, на косинус угла между ними и на 2.
- Посчитайте сумму квадратов известных сторон и отнимите от неё число, полученное в предыдущем действии.
- Найдите корень из результата.
Теперь прибавьте к найденной стороне две ранее известные стороны.
- P — искомый периметр;
- b, c — известные стороны треугольника;
- ɑ — угол между известными сторонами;
- a — неизвестная сторона треугольника.
4. Как найти периметр равностороннего треугольника, зная одну сторону
Умножьте сторону на 3.
- P — искомый периметр;
- a — любая сторона треугольника (напомним, в равностороннем треугольнике все стороны равны).
5. Как вычислить периметр равнобедренного треугольника, зная боковую сторону и основание
Умножьте боковую сторону на 2.
Прибавьте к результату основание.
- P — искомый периметр;
- a — боковая сторона треугольника (в равнобедренном треугольнике боковые стороны равны);
- b — основание треугольника (это сторона, которая отличается длиной от остальных).
6. Как найти периметр равнобедренного треугольника, зная боковую сторону и высоту
Найдите квадраты боковой стороны и высоты.
Отнимите от первого числа второе.
Найдите корень из результата и умножьте его на 2.
Прибавьте к полученному числу две боковые стороны.
- P — искомый периметр;
- a — боковая сторона треугольника;
- h — высота (перпендикуляр, опущенный на основание треугольника со стороны противоположной вершины; в равнобедренном треугольнике высота делит основание пополам).
7. Как вычислить периметр прямоугольного треугольника, зная катеты
Найдите квадраты катетов и посчитайте их сумму.
Извлеките корень из полученного числа.
Прибавьте к результату оба катета.
- P — искомый периметр;
- a, b — катеты треугольника (стороны, которые образуют прямой угол).
8. Как найти периметр прямоугольного треугольника, зная катет и гипотенузу
Посчитайте квадраты гипотенузы и катета.
Отнимите от первого числа второе.
Найдите корень из результата.
Прибавьте катет и гипотенузу.
- P — искомый периметр;
- a — любой катет прямоугольника;
- c — гипотенуза (сторона, которая лежит напротив прямого угла).
Основные определения
Наверное, каждый из нас сталкивался с треугольником. Это могло быть в школе, вузах, колледжах, на работе, во время помощи детям. Треугольник – это одна из самых простых геометрических фигур, но в то же время она выполняет очень важную роль. Множество свойств хранит треугольник. Но сегодня не будем вдаваться в подробности, а поговорим про периметр и порешаем задачи по нахождению его.
Если мы отметим на плоскости 3 точки и проведём к ним линии, то как раз получим треугольник.
Понятия
Треугольник – это геометрическая фигура, состоящая из трёх точек, которые соединены отрезками – сторонами. В зависимости от отношений между сторонами фигуры, то они бывают равносторонними, разносторонними и равнобедренными (р/б – равнобедренный, р/с – равносторонний).
Вершины треугольника – это точки, где соединяются 2 стороны фигуры.
Р/б треугольник – это треугольник у которого две стороны равны, но не равны третьей.
Р/с треугольник – это треугольник, у которого все стороны равны между собой.
Разносторонний треугольник – это треугольник, у которого все стороны не равны между собой.
Прямоугольный треугольник — это треугольник, у у которого один угол равен 90о. Самая длинная сторона называется гипотенузой, а две другие катетами.
Формула нахождения периметра
Из определения следует, что периметр геометрической фигуры – это сумма длин всех сторон, и треугольник не стал исключением. Общая формула имеет вид: Р = а + b + с. Периметр будет обозначаться Р. а, b и с — стороны треугольника. Решим задачу №1.
Задача 1
Пусть нам дан треугольник со сторонами 13 см, 15 см, 12 см. Нужно найти периметр данного треугольника.
Решение: [P=13+15+12=40] см.
Ответ: 40 см.
Периметр разностороннего треугольника
В прошлой задаче мы как раз нашли периметр разностороннего треугольника. Решим похожую задачу №2
Задача 2
Дан треугольник со сторонами 25 дм, 30 дм, 15 дм. Найдите периметр треугольника. Ответ выразите в метрах.
Решение:
P = 30 + 25 + 15 = 70 дм
70 : 10 = 7 м
Ответ: 7 м.
Периметр равнобедренного треугольника
Так как в р/б треугольнике 2 стороны равны (боковые), то формулу нахождения можно представить как: P = 2a + b. Решим 2 задачи.
Задачи 3 — 4
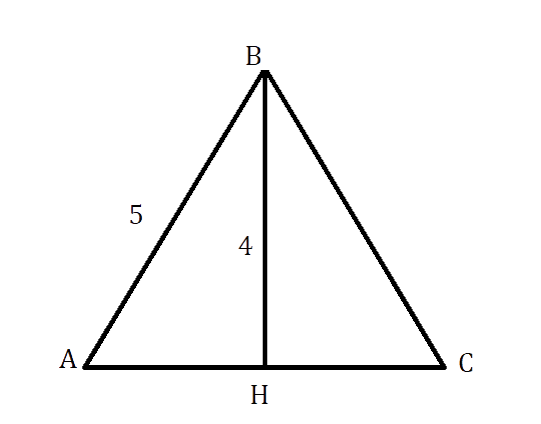
Дан равнобедренный треугольник АВС с биссектрисой, проведённой к основанию и равной 4 см, а также с боковой
стороной, равной 5 см. Найдите периметр данного треугольника.
Решение:
Так как ВН – биссектриса р/б треугольника АВС, то она является как высотой, так и медианой. Следовательно, ΔАВН прямоугольный и АН = НС.
В ΔАВН по теореме Пифагора [A H^{2}=A B^{2}-B H^{2}=25-16=9]см
АН = НС = √9 = 3 см
АС = АН + НС = 3 + 3 = 6 см
Р = 6 + 2*5 = 16 см
Ответ: 16 см.
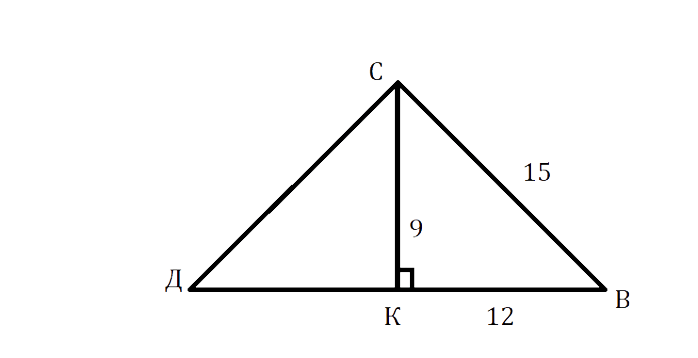
В треугольнике ДСВ ДС = СВ = 15 см, высота СК = 9 см. Найдите периметр этого треугольника.
Решение:
В ΔСКД по теореме Пифагора:
[text { ДК² }=text { ДС }^{2}-mathrm{CK}^{2}=225-81=144]см
ДК = √144 = 12 см.
Так как СК — высота в р/б треугольнике, проведённая к основанию, то она является медианой, следовательно, ДВ = ДК + КВ = 12 + 12 = 24 см.
Р = ДС + СВ + ДВ = 15 + 15 + 24 = 54 см.
Ответ: 54 см.
Нет времени решать самому?
Наши эксперты помогут!
Периметр равностороннего треугольника
А это один из самых “хороших” треугольников, его ещё называют правильным, так как все стороны и углы равны между собой. Формула нахождения периметра будет иметь вид: P = 3a.
Задачи 5 — 6
Дан равносторонний треугольник со стороной а = 13. Найдите периметр этого треугольника.
Решение:
Р = 3а = 3 * 13 = 39
Ответ: 39.
В равностороннем треугольнике АВС есть стороны: АВ = АС = СВ = 15 см, Найдите периметр данного треугольника.
Решение:
Р = 3АВ = 15 * 3 = 45 см.
Ответ: 45 см.
Периметр прямоугольного треугольника
Вычисляем по стандартной формуле: Р = а + в + с. Но у такого вида треугольников есть огромное преимущество – применение теоремы Пифагора.
Задачи 7 — 8
Дан прямоугольный треугольник с катетами а = 6 и в = 8. Найдите периметр.
Решение:
По теореме Пифагора: [c^{2}=в^{2}+a^{2}=64+36=100]
с = √100 = 10
Р = а + в + с = 6 + 8 + 10 = 24
Ответ: 24.
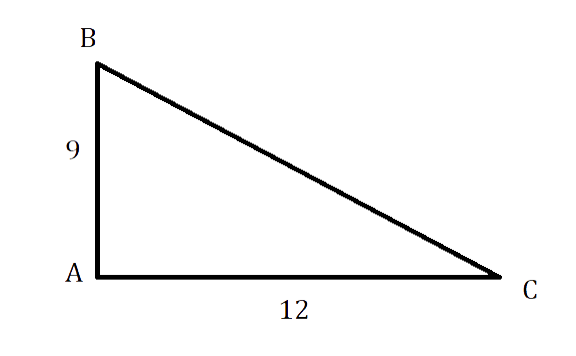
В прямоугольном треугольнике АВС, [angle mathrm{A}=90^{circ}, mathrm{AB}=9 mathrm{~см}, mathrm{AC} = 12см]. Надо найти периметр и площадь АВС.
Решение
По теореме Пифагора в ΔАВС:
[mathrm{CB}^{2}=mathrm{AC}^{2}+A mathrm{C}^{2}=144+81=225 mathrm{~см}]
СВ = √225 = 15 см
S = (АС * АВ) : 2 = (9 * 12) : 2 = 54 см
P = 15 + 9 + 12 = 36 см
Ответ: 36 см; 54 см.
Треугольник — это геометрическая фигура, состоящая из трех точек, последовательно соединенных между собой.
Треугольник имеет три стороны и три угла.
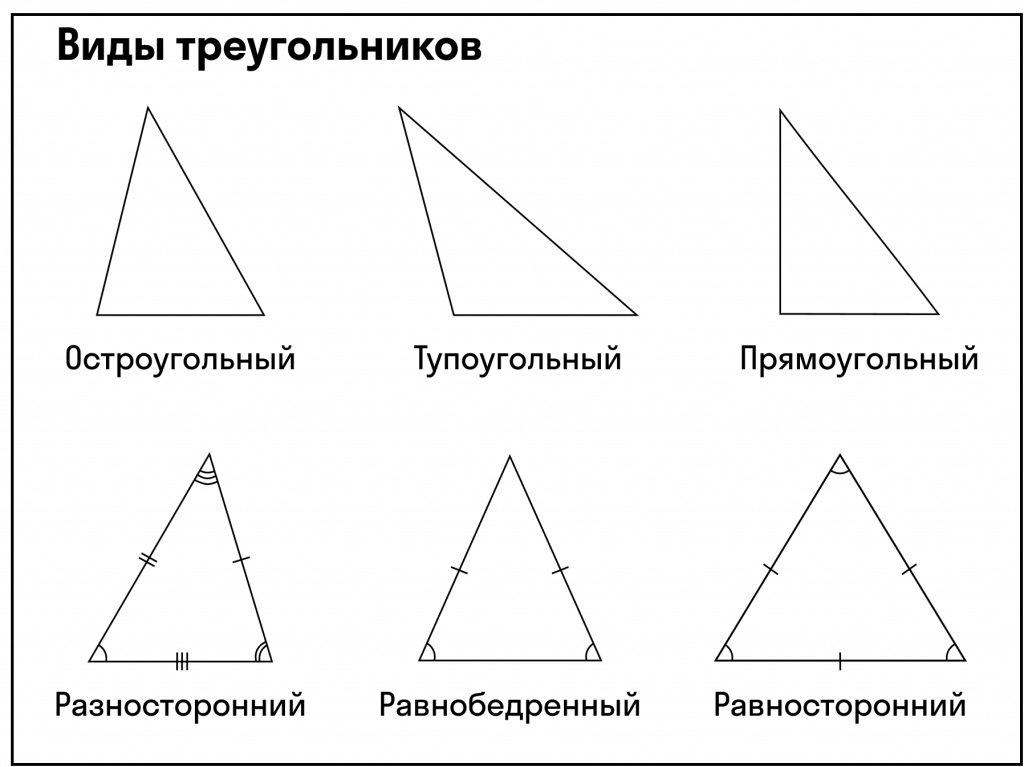
Существует множество видов треугольников, и все они обладают разными свойствами. Перечислим основные виды треугольников:
- Разносторонний (все стороны разной длины);
- Равнобедренный (две стороны равны, два угла при основании равны);
- Равносторонний (все стороны и все углы равны).
Однако для всех видов треугольников действует одна универсальная формула нахождения периметра треугольника – это сумма длин всех сторон треугольника.
Онлайн-калькулятор периметра треугольника
Формула периметра треугольника
P=a+b+cP = a + b + c
a,b,ca, b, c — длины сторон треугольника.
Разберем задачи на нахождение периметра треугольника.
Треугольник имеет стороны: a = 28 см, b = 46 см, c = 51 см. Чему равен периметр треугольника?
Решение
Воспользуемся формулой нахождения периметра треугольника и подставим вместо aa, bb и cc их численные значения:
P=a+b+cP = a + b + c
P=28+46+51=125 смP = 28 + 46 + 51 = 125text{ см}
Ответ:
P=125 см.P = 125 text{ см.}
Треугольник является равносторонним со стороной 23 см. Чему равен периметр треугольника?
Решение
Воспользуемся формулой нахождения периметра треугольника:
P=a+b+cP = a + b + c
Но по условию у нас равносторонний треугольник, то есть все стороны у него равны. В этом случае формула примет следующий вид:
P=a+a+a=3aP = a + a + a = 3a
Подставляем в формулу численное значение и находим периметр треугольника:
P=3⋅23=69 смP = 3cdot23 = 69text{ см}
Ответ
P=69 см.P = 69 text{ см.}
В равнобедренном треугольнике боковая сторона b равна 14 см, а основание a – 9 см. Найти периметр треугольника.
Решение
Воспользуемся формулой нахождения периметра треугольника:
P=a+b+cP = a + b + c
Но по условию у нас равнобедренный треугольник, то есть боковые стороны у него равны. В этом случае формула примет следующий вид:
P=a+b+b=2b+aP = a + b + b = 2b + a
Подставляем в формулу численные значения и находим периметр треугольника:
P=2⋅14+9=28+9=37 смP = 2 cdot 14 + 9 = 28 + 9 = 37 text{ см}
Ответ
P=37 см.P = 37text{ см.}
Учитесь на заочной форме обучения? Возникли трудности с работой? На нашем сервисе предусмотрено написание контрольных работ на заказ для заочников, скорее обращайтесь к экспертам!
Download Article
Download Article
Finding the perimeter of a triangle means finding the distance around the triangle.[1]
The simplest way to find the perimeter of a triangle is to add up the length of all of its sides, but if you don’t know all of the side lengths you will need to calculate them first. This article will first teach you to find the perimeter of a triangle when you do know all three side lengths; this is the easiest and most common way. It will then teach you to find the perimeter of a right triangle when only two of the side lengths are known. Finally, it will teach you to find the perimeter of any triangle for which you know two side lengths and the angle measure between them (an “SAS Triangle”), using the Law of Cosines.
-
1
Remember the formula for finding the perimeter of a triangle. For a triangle with sides a, b and c, the perimeter P is defined as: P = a + b + c.[2]
- What this formula means in simpler terms is that to find the perimeter of a triangle, you just add together the lengths of each of its 3 sides.
-
2
Look at your triangle and determine the lengths of the three sides. In this example, the length of side a = 5, the length of side b = 5, and the length of side c = 5.
- This particular example is called an equilateral triangle, because all three sides are of equal length. But remember that the perimeter formula is the same for any kind of triangle.
Advertisement
-
3
Add the three side lengths together to find the perimeter. In this example, 5 + 5 + 5 = 15. Therefore, P = 15.
- In another example, where a = 4, b = 3, and c=5, the perimeter would be: P = 3 + 4 + 5, or 12.
-
4
Remember to include the units in your final answer. If the sides of the triangle are measured in centimeters, then your answer should also be in centimeters. If the sides are measured in terms of a variable like x, your answer should also be in terms of x.[3]
- In this example, the side lengths are each 5cm, so the correct value for the perimeter is 15cm.
Advertisement
-
1
Remember what a right triangle is. A right triangle is a triangle that has one right (90 degree) angle. The side of the triangle opposite the right angle is always the longest side, and it is called the hypotenuse. Right triangles show up frequently on math tests, and fortunately there is a very handy formula for finding the length of unknown sides!
-
2
Recall the Pythagorean Theorem. The Pythagorean Theorem tells us that for any right triangle with sides of length a and b, and hypotenuse of length c, a2 + b2 = c2.[4]
-
3
Look at your triangle, and label the sides “a,” “b,” and “c”. Remember that the longest side of the triangle is called the hypotenuse. It will be opposite the right angle and must be labeled c. Label the two shorter sides a and b. It doesn’t really matter which is which, the math will turn out the same!
-
4
Enter the side lengths that you know into the Pythagorean Theorem. Remember that a2 + b2 = c2. Substitute the side lengths in for the corresponding letters in the equation.[5]
- If, for example, you know that side a = 3 and side b = 4, then plug those values into the formula as follows: 32 + 42 = c2.
- If you know the length of side a = 6, and the hypotenuse c = 10, then you should set the equation up like so: 62 + b2 = 102.
-
5
Solve the equation to find the missing side length. You will first need to square the known side lengths which means multiplying each value by itself (for example 32 = 3 * 3 = 9). If you are looking for the hypotenuse, simply add the two values together and find the square root of this number to find the length. If it is a side length you are missing, you must do a bit of easy subtraction, and then take the square root to get your side length.[6]
- In the first example, square the values in 32 + 42 = c2 and find that 25= c2. Then calculate the square root of 25 to find that c = 5.
- In the second example, square the values in 62 + b2 = 102 to find that 36 + b2 = 100. Subtract 36 from each side to find that b2 = 64, then take the square root of 64 to find that b = 8.
-
6
Add up the lengths of the three side lengths to find the perimeter. Recall that the perimeter P = a + b + c. Now that you know the lengths of sides a, b and c, you simply need to add the lengths together to find the perimeter.[7]
- In our first example,P = 3 + 4 + 5, or 12.
- In our second example, P = 6 + 8 + 10, or 24.
Do you have the perimeter and are missing one side? Then you should subtract the sum of the two sides from the perimeter. This number equals the length of the missing side.
Advertisement
-
1
Learn the Law of Cosines. The Law of Cosines allows you to solve any triangle when you know two side lengths and measurement of the angle between them. It works on any triangle, and is a very useful formula. The Law of Cosines states that for any triangle with sides a, b, and c, with opposite angles A, B, and C: c2 = a2 + b2 – 2ab cos(C).[8]
[9]
-
2
Look at your triangle and assign variable letters to its components. The first side that you know should be labeled a, and the angle opposite it is A. The second side that you know should be labeled b; the angle opposite it is B. The angle that you know should be labeled C, and the third side, the one you need to solve in order to find the perimeter of the triangle, is side c.[10]
- For example, imagine a triangle with side lengths 10 and 12, and an angle between them of 97°. We will assign variables as follows: a = 10, b = 12, C = 97°.
-
3
Plug your information into the equation and solve for side c. You will first need to find the squares of a and b, and add them together. Then find the cosine of C using the cos function on your calculator, or an online cosine calculator.[11]
Multiply cos(C) by 2ab and subtract the product from the sum of a2 + b2. The result is c2. Find the square root of this value and you have the length of side c.[12]
Using our example triangle:- c2 = 102 + 122 – 2 × 10 × 12 × cos(97).
- c2 = 100 + 144 – (240 × -0.12187) (Round the cosine to 5 decimal places.)
- c2 = 244 – (-29.25)
- c2 = 244 + 29.25 (Carry the minus symbol through when cos(C) is negative!)
- c2 = 273.25
- c = 16.53
-
4
Use side length c to find the perimeter of the triangle. Recall that Perimeter P = a + b + c, so all you need to do is add the length you just calculated for side c to the values you already had for a and b.
- In our example: 10 + 12 + 16.53 = 38.53, the perimeter of our triangle!
Advertisement
Triangle Perimeter Calculator, Practice Problems, and Answers
Add New Question
-
Question
Can you find the perimeter if only one side is given?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
If you know only 1 side but all 3 angles, you can use the rule of sines to find the remaining sides, then calculate the perimeter. If you know 1 side and 1 angle, you won’t be able to find the perimeter unless you’re dealing with a right triangle. For right triangles, you know that 1 angle is always 90°, so if you know another angle, you can use the sum of angles (180°) to figure out the third one. From there, you can use the laws of sine and cosine to figure out the other sides.
-
Question
How can you find the perimeter of a triangle if one side is missing?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
If it’s a right triangle, you can use the Pythagorean theorem (a2 + b2 = c2) to find the length of the missing side. From there, you can easily calculate the perimeter. For other types of triangles, you can use the law of cosines to find the perimeter if you know 2 sides and at least 1 of the angles.
-
Question
How can you find the missing side of a triangle given the perimeter?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
Since the perimeter is the sum of the lengths of all sides, you can solve for the missing side by subtracting the lengths of the other 2 sides from the perimeter.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
References
About This Article
Article SummaryX
To find the perimeter of a triangle, use the formula perimeter = a + b + c, where a, b, and c are the lengths of the sides of the triangle. For example, if the length of each side of the triangle is 5, you would just add 5 + 5 + 5 and get 15. Therefore, the perimeter of the triangle is 15. If you only know the length of 2 of the triangle’s sides, you can still find the perimeter if it’s a right triangle, which means the triangle has one 90-degree angle. Just use the Pythagorean theorem, which is a^2+ b^2 = c^2, where a and b are the lengths of the known sides and c is the length of the unknown hypotenuse. For example, if the length of the known sides are 3 and 4, you would just add 3^2+ 4^2, or 9 + 16, and get 25. Then, you would take the square root of 25 to find c, which is 5. Therefore, the length of the unknown side is 5. Finally, add all of the side lengths together to find the perimeter. In this case you would add 3 + 4 + 5 and get 12. Therefore, the perimeter of the triangle is 12. If you want to learn how to solve the perimeter of your triangle if you only know 2 sides and an angle, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,728,629 times.
Reader Success Stories
-
“This was really helpful for me. It was easy to understand, and it gives a lot of information. I really appreciated…” more
Did this article help you?
Загрузить PDF
Загрузить PDF
Периметр треугольника — это общая длина всех его сторон.[1]
Самый простой способ найти периметр треугольника заключается в том, чтобы сложить длины всех его сторон, однако если вы не знаете длину хотя бы одной стороны треугольника, необходимо сначала найти ее. В первом разделе данной статьи рассказано, как вычислить периметр треугольника по трем известным сторонам — это наиболее простой и распространенный метод. Затем показано, как найти периметр прямоугольного треугольника, если известны длины двух сторон. И наконец, описано, как с помощью теоремы косинусов рассчитать периметр любого треугольника, если даны две стороны и угол между ними.
-
1
Запомните формулу, которая позволяет вычислить периметр треугольника. Если треугольник имеет стороны a, b и c, его периметр P равен: P = a + b + c.
- Таким образом, чтобы найти периметр треугольника, следует сложить длины всех трех его сторон.
-
2
Посмотрите на треугольник и узнайте длины всех трех сторон. Предположим, треугольник имеет следующие стороны: a = 5, b = 5 и c = 5.
- Рассматриваемый треугольник называется равносторонним, так как все три его стороны имеют одинаковую длину. Тем не менее формула для расчета периметра справедлива для любого треугольника.
-
3
Сложите длины всех трех сторон, чтобы найти периметр. В нашем примере 5 + 5 + 5 = 15, то есть P = 15.
- Рассмотрим другой пример: a = 4, b = 3 и c=5. В этом случае периметр равен: P = 3 + 4 + 5 = 12.
-
4
В ответе не забывайте указывать единицу измерения. Если стороны измеряются в сантиметрах, окончательный ответ также должен быть приведен в сантиметрах. Ответ должен быть в тех же единицах, в которых приведены длины сторон в условии задачи.
- В приведенном примере длина каждой стороны составляет 5 сантиметров, поэтому периметр равен 15 сантиметрам.
Реклама
-
1
Запомните, что такое прямоугольный треугольник. Прямоугольным называется такой треугольник, один из углов которого является прямым, то есть равен 90 градусам. Самая длинная сторона такого треугольника всегда лежит напротив прямого угла и называется гипотенузой. Две другие стороны, образующие прямой угол, называются катетами. Прямоугольные треугольники очень часто встречаются в задачах по математике. К счастью, есть формула, с помощью которой всегда можно рассчитать длину неизвестной стороны!
-
2
Вспомните теорему Пифагора. Эта теорема гласит, что в любом прямоугольном треугольнике с катетами a и b и гипотенузой c стороны связаны следующим соотношением: a2 + b2 = c2.[2]
-
3
Нарисуйте прямоугольный треугольник и обозначьте стороны как a, b и c. Самая длинная сторона прямоугольного треугольника — это гипотенуза. Она лежит напротив прямого угла. Обозначьте гипотенузу как c, а более короткие стороны — как a и b. Неважно, какой катет вы обозначите буквой a, а какой — буквой b, так как это не повлияет на конечный результат.
-
4
Подставьте в формулу значения известных сторон. Помните, что a2 + b2 = c2. Вместо букв подставьте числа, данные в условии задачи.
- Предположим, в условии дано, что a = 3 и b = 4, тогда получаем: 32 + 42 = c2.
- Если катет a = 6 и гипотенуза c = 10, тогда можно записать: 62 + b2 = 102.
-
5
Решите полученное уравнение, чтобы найти неизвестную сторону. Для этого сначала возведите в квадрат известные длины сторон (просто умножьте данное число само на себя, например 32 = 3 * 3 = 9). Если вы ищете гипотенузу, сложите квадраты двух сторон и из полученной суммы извлеките квадратный корень. Если необходимо найти катет, вычтите квадрат известного катета из квадрата гипотенузы и из полученного числа извлеките квадратный корень.
- В первом примере складываем квадраты сторон 32 + 42 = c2 и получаем 25= c2. После этого извлекаем квадратный корень из 25 и находим c = 5.
- Во втором примере складываем квадраты сторон 62 + b2 = 102 и получаем 36 + b2 = 100. Переносим 36 в правую сторону уравнения: b2 = 64. Извлекаем квадратный корень из 64 и находим b = 8.
-
6
Сложите длины трех сторон, чтобы найти периметр. Как мы помним, периметр вычисляется по формуле: P = a + b + c. После того как мы нашли длины сторон a, b и c, необходимо сложить их, чтобы определить периметр.
- В первом примере: P = 3 + 4 + 5 = 12.
- Во втором примере: P = 6 + 8 + 10 = 24.
Реклама
-
1
Выучите теорему косинусов. Эта теорема позволяет вычислить неизвестную сторону треугольника, если даны длины двух других сторон и величина угла между ними. Теорема косинусов очень полезна, она справедлива для всех треугольников. Эта теорема гласит, что для любого треугольника со сторонами a, b и c и противолежащими им углами A, B и C справедлива следующая формула: c2 = a2 + b2 – 2ab cos(C).[3]
[4]
-
2
Дайте обозначения сторонам и углам треугольника. Обозначьте первую известную сторону как a, а противоположный ей угол — как A. Вторую известную сторону и противолежащий ей угол обозначьте соответственно b и B. Известный угол между этими сторонами обозначьте как C, а противолежащую ему сторону, длину которой необходимо найти, — как c.
- Предположим, дан треугольник со сторонами 10 и 12 и углом между ними 97°. В этом случае имеем: a = 10, b = 12, C = 97°.
-
3
Подставьте известные значения в формулу и найдите неизвестную сторону с. Сначала возведите в квадрат длины известных сторон и сложите полученные значения. Затем найдите косинус угла С с помощью обычного или онлайн-калькулятора.[5]
Умножьте cos(C) на 2ab и вычтите полученное число из суммы a2 + b2. В результате вы получите c2. Извлеките квадратный корень, чтобы найти длину неизвестной стороны c. В нашем примере имеем:- c2 = 102 + 122 – 2 × 10 × 12 × cos(97°).
- c2 = 100 + 144 – (240 × -0,12187) (мы округлили значение косинуса до 5 знаков после запятой).
- c2 = 244 – (-29,25).
- c2 = 244 + 29,25 (два минуса дают плюс!).
- c2 = 273,25.
- c = 16,53.
-
4
Используйте вычисленную длину стороны c, чтобы найти периметр треугольника. Напомним, что периметр вычисляется по формуле: P = a + b + c, то есть следует прибавить к известным величинам сторон a и b найденную длину стороны c.
- В нашем примере получаем: 10 + 12 + 16,53 = 38,53. Итак, периметр треугольника равен 38,53!
Реклама
Об этой статье
Эту страницу просматривали 269 839 раз.