Как найти переплату по кредиту егэ

Дифференцированный платеж – это такая система выплат, при которой сама сумма долга уменьшается равномерно, то есть на одну и ту же величину каждый год (месяц).
При этом платежи каждый год разные.

Таким образом, если кредит взят на (n) лет, то это значит, что сумму кредита (A) разделили на (n) равных частей и что каждый год после платежа сумма долга уменьшается на (dfrac1n A) по сравнению с долгом на начало года.

Пример 1. Клиент взял в банке кредит на (2) года под (15%) годовых. Выплачивать кредит он должен ежегодными платежами так, чтобы сумма долга уменьшалась равномерно. Какую сумму он взял в банке, если оказалось, что в итоге он заплатил банку (490,000) рублей?

Пусть кредит составил (A) рублей. Т.к. кредит взят на (2) года, значит после первой выплаты долг должен составлять (A-frac12
A=frac12 A) рублей, после второй выплаты (frac12 A-frac12 A=0) рублей. Составим таблицу: [begin{array}{|l|c|c|c|c|}
hline text{Год}&text{Сумма долга}&text{Сумма долга}&text{Сумма долга}&
text{Выплата}\
&text{до начисления} %&text{после начисления }%&text{после выплаты}&\
hline 1&A&A+0,15A&frac12 A&0,15A+frac12A\
hline 2&frac12A&frac12A+0,15cdotfrac12A&0&0,15cdotfrac12A+frac12A\
hline
end{array}] То, что клиент в итоге заплатил банку, есть не что иное, как сумма всех выплат по кредиту.

Т.е. (0,15A+frac12A+0,15cdotfrac12A+frac12A=490,000 Rightarrow
A=dfrac{490,000cdot 2}{2,45}=400,000) рублей.

Пример 2. Александр взял в банке кредит на (50,000) рублей на (3) месяца, причем выплачивать кредит он должен ежемесячными выплатами так, чтобы сумма долга каждый месяц уменьшалась на одну и ту же величину. Сколько рублей составит переплата Александра по кредиту, если процентная ставка в банке (10%)?

Т.к. кредит взят на (3) месяца, то после первой выплаты долг должен составить (A-frac13A=frac23 A), после второй (frac23A-frac13A=frac13A), а после третьей — (0) рублей. Составим таблицу, производя все вычисления в тыс. рублей: [begin{array}{|l|c|c|c|c|}
hline text{Месяц}&text{Сумма долга}&text{Сумма долга}&text{Сумма долга}&
text{Выплата}\
&text{до начисления} %&text{после начисления }%&text{после выплаты}&\
hline 1&50&50+0,1cdot 50&frac23cdot 50&0,1cdot 50+frac13cdot 50\
hline 2&frac23cdot 50&frac23cdot 50+0,1cdotfrac23cdot 50&frac13cdot
50&0,1cdot frac23cdot 50+frac13cdot50\
hline 3&frac13cdot 50&frac13cdot 50+0,1cdot frac13cdot
50&0&0,1cdot frac13cdot 50+frac13cdot 50\
hline
end{array}]

Таким образом, всего Александр заплатил банку (big(0,1cdot
50+dfrac13cdot 50big)+big(0,1cdot dfrac23cdot
50+dfrac13cdot50big)+big(0,1cdot dfrac13cdot 50+dfrac13cdot
50big)) тыс.рублей.

Перегруппируем слагаемые и вынесем за скобки общие множители:

(0,1cdot 50 left(1+dfrac23+dfrac13right)+3cdot dfrac13cdot
50=0,1cdot 50cdot 2+50)

Для того, чтобы найти переплату по кредиту, необходимо из того, что он в итоге заплатил банку, отнять сумму кредита:

(big(0,1cdot 50cdot 2+50big)-50=10) тыс. рублей.
Таким образом, его переплата составила (10,000) рублей.
 

Заметим,

I. что каждая выплата состоит из двух частей:
первая часть — это сумма “набежавших” процентов на текущий долг (в первый год это (0,1cdot 50), во второй — (0,1cdot big(frac23cdot
50big)) и т.д.)
вторая часть всегда фиксирована — это та часть, на которую должен уменьшаться долг каждый год (в нашем примере это (frac13cdot 50)).

Действительно, когда клиент выплачивает “набежавшие” проценты, сумма его долга становится равна той, которая была до начисления процентов (например, в первый год становится равна (A)). А далее он еще вносит (frac 1n) часть от этого долга. И таким образом сумма долга уменьшается на (frac 1n) часть, что и подразумевает дифференцированная система платежей.

II. переплата по кредиту всегда равна сумме “набежавших” процентов на долг в первый год, во второй год, в третий год и т.д.

В нашем примере переплата как раз равна (0,1cdot 50+0,1cdot
frac23cdot 50+0,1cdot frac13cdot 50).

Пример 3. Банк предлагает клиентам кредит на (1) млн рублей на следующих условиях:
– каждый год банк начисляет на оставшуюся часть долга (10%);
– после начисления процентов клиент обязан внести платеж;
– через (5) лет кредит должен быть выплачен полностью;
– система выплат дифференцированная.

Сколько процентов от первоначального долга составит переплата по такому кредиту?

Т.к. кредит выдается на (5) лет, это значит, что долг должен уменьшаться каждый год на (frac15cdot 1) млн рублей, то есть после первой выплаты долг составит (1-frac15cdot 1=frac45) млн рублей, после второй (frac45-frac15=frac35) млн рублей и т.д.

Составим таблицу, причем все вычисления будем производить в млн рублей: [begin{array}{|l|c|c|c|c|}
hline text{Год}&text{Сумма долга}&text{Сумма долга}&text{Сумма долга}&
text{Выплата}\
&text{до начисления} %&text{после начисления }%&text{после
выплаты}&\
hline 1&1&1+0,1&frac45&0,1+frac15\
hline 2&frac45&frac45+0,1cdotfrac45&frac35&0,1cdot
frac45+frac15\
hline 3&frac35&frac35+0,1cdotfrac35&frac25&0,1cdot
frac35+frac15\
hline 4&frac25&frac25+0,1cdotfrac25&frac15&0,1cdot
frac25+frac15\
hline 5&frac15&frac15+0,1cdotfrac15&0&0,1cdot
frac15+frac15\
hline
end{array}]

Для того, чтобы посчитать, сколько процентов составила переплата относительно кредита, необходимо переплату разделить на сумму кредита и умножить на (100%):

(dfrac{frac3{10}}{1}cdot 100%=30%)
 

Выведем несколько формул:

Вывод формулы для выплаты по кредиту:

Пусть взят кредит на (A) рублей, на (n) лет, годовая ставка (r%).

Значит, каждый год долг должен уменьшаться на (frac1n A) рублей. К тому же, например, в первый год после начисления процентов долг составит (A+frac r{100}A), поэтому обозначим для удобства (frac
r{100}=y) и составим таблицу: [begin{array}{|l|c|c|c|c|}
hline text{Год}&text{Сумма долга}&text{Сумма долга}&text{Сумма долга}&
text{Выплата}\
&text{до начисления} %&text{после начисления }%&text{после
выплаты}&\[1ex]
hline 1&A&A+yA&frac {n-1}n A& yA+frac 1n
A\[1ex]
hline 2&frac{n-1}n A&frac{n-1}n A+ycdot frac{n-1}n A&
frac{n-2}n A&ycdot frac{n-1}n A+frac 1n A\[1ex]
hline 3&frac{n-2}n A&frac{n-2}n A+ycdot frac{n-2}n
A&frac{n-3}n A&ycdot frac{n-2}n A+frac 1nA\[1ex]
hline 4&frac{n-3}n A&frac{n-3}n A+ycdot frac{n-3}n
A&frac{n-4}n A&ycdot frac{n-3}n A+frac 1nA\[1ex]
hline dots&dots&dots&dots&dots\[1ex]
hline n-1& frac 2nA&frac 2nA+ycdot frac 2nA&frac
1nA&ycdot frac 2nA+frac 1nA\[1ex]
hline n&frac 1nA&frac 1nA+ycdot frac 1nA&0&ycdot frac
1nA+frac 1nA\[1ex]
hline
end{array}]

Таким образом, если (i) — номер года, то выплата в (i)-ый год будет равна:
(x_i=ycdot frac{n-(i-1)}nA+dfrac 1nA), или: [{large{x_i=dfrac{r}{100}cdot dfrac{n-i+1}{n}A+dfrac1n A}}]

Вывод формулы для переплаты по кредиту:

В скобках находится арифметическая прогрессия, первый член которой (a_1=1), последний (a_n=dfrac 1n), разность (d=-dfrac 1n), а количество членов равно (n). Сумма такой прогрессии равна:

(S_n=dfrac{a_1+a_n}{2}cdot n=dfrac{1+frac1n}{2}cdot
n=dfrac{n+1}2)

Значит, вся переплата равна (yAcdot dfrac{n+1}2),  или [{large{P=dfrac r{100}cdot dfrac{n+1}2A}}]

Размещённые в настоящем разделе сайта публикации носят исключительно ознакомительный характер, представленная в них информация не является гарантией и/или обещанием эффективности деятельности (доходности вложений) в будущем. Информация в статьях выражает лишь мнение автора (коллектива авторов) по тому или иному вопросу и не может рассматриваться как прямое руководство к действию или как официальная позиция/рекомендация АО «Открытие Брокер». АО «Открытие Брокер» не несёт ответственности за использование информации, содержащейся в публикациях, а также за возможные убытки от любых сделок с активами, совершённых на основании данных, содержащихся в публикациях. 18+

АО «Открытие Брокер» (бренд «Открытие Инвестиции»), лицензия профессионального участника рынка ценных бумаг на осуществление брокерской деятельности № 045-06097-100000, выдана ФКЦБ России 28.06.2002 (без ограничения срока действия).

ООО УК «ОТКРЫТИЕ». Лицензия № 21-000-1-00048 от 11 апреля 2001 г. на осуществление деятельности по управлению инвестиционными фондами, паевыми инвестиционными фондами и негосударственными пенсионными фондами, выданная ФКЦБ России, без ограничения срока действия. Лицензия профессионального участника рынка ценных бумаг №045-07524-001000 от 23 марта 2004 г. на осуществление деятельности по управлению ценными бумагами, выданная ФКЦБ России, без ограничения срока действия.

25 ноября 2013

Кредиты — это вообще больная тема для многих наших соотечественников. А в задаче B2 из ЕГЭ по математике — тем более. Будьте внимательны и следите за тем, что спрашивают в условии задачи.

В сегодняшнем кратком видеоуроке мы разберем нестандартную задачу на проценты. Тем не менее, такие задачи могут вам встретиться как на самостоятельных задачах, так и на пробнике, а также на настоящем ЕГЭ по математике. Итак, задача:

Задача B2. Клиент взял в банке кредит на сумму 36 000 рублей с годовой процентной ставкой 140%. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?

Расчет общей величины процентов

Как решать такую задачу? В первую очередь, нужно понять, что сумму, которую должен вернуть клиент за год, нужно рассчитать по исходной сумме и ставке кредита. При этом очевидно, что возвращаемая сумма будет намного больше, чем 36 000 рублей, которые клиент взял изначально. Как найти ту сумму, которую теперь клиент должен вернуть?

Воспользуемся нашей основной формулой, а именно — формулой простых процентов. Пусть х — исходная величина (в нашем случае это 36 000 рублей). Пусть также k — это процент, на который исходная величина изменяется. Наконец, y — это итоговое значение величины, полученное после изменения на k%. Тогда все три величины связаны следующей формулой:

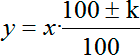
Плюс или минус ставится в зависимости от того, увеличивается или уменьшается исходная величина. Очевидно, что в нашем случае в формуле будет стоять плюс, потому что клиент брал кредит, и возвращать ему нужно будет больше, чем он взял.

Давайте посмотрим, сколько всего денег задолжал клиент нашему банку. Подставляем в формулу:

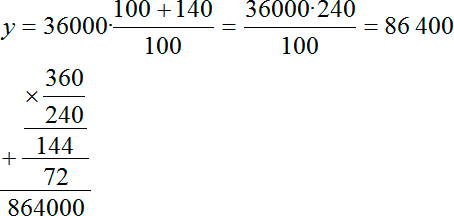
Получились довольно большие числа. Поэтому считать пришлось столбиком. Итого клиент взял 36 000 рублей, а должен вернуть 86 400 рублей. Нормально, в следующий раз будет думать, прежде чем брать кредит.

Никогда не берите кредиты. Особенно потребительские и особенно в торговых центрах. Потому что вы купите ненужную вещь и потеряете много денег.

Расчет ежемесячного платежа

Однако в задаче требуется найти, сколько рублей он должен вносить в банк ежемесячно. По условию полученную нами сумму он должен выплатить за год, т. е. за 12 месяцев. Тогда каждый месяц он должен выплачивать по 1/12 этой суммы. Следовательно, чтобы найти сумму ежемесячного платежа нам нужно разделить всю сумму на 12:

S = 86 400 : 12 = 360 · 240 : 12 = 7200

Итак, клиент должен ежемесячно отдавать в банк 7200 рублей. Как видите, переплата по кредиту оказалась даже больше, чем исходная сумма 36 000 рублей. Причем это совсем не выдумка: когда берете кредит, обязательно читайте условия, написанные мелким шрифтом в договоре, иначе можете залететь вот на такие бешенные ставки — 140% годовых. А лучше вообще не берите кредиты — никогда и ни на что.

Надеюсь, этот урок поможет вам при подготовке к ЕГЭ по математике, а также отобьет желание брать кредиты на всякое барахло, типа iPhone, iPad и прочие ненужные девайсы. А у меня на этом все. С вами был Павел Бердов. До новых встреч!

Смотрите также:

1. Нестандартная задача B2: студенты, гонорары и налоги
2. Задача B2 про комиссию в терминале
3. Тест к уроку «Сложные выражения с дробями» (легкий)
4. Тест: простейшие показательные уравнения (2 вариант)
5. Быстрое возведение чисел в квадрат без калькулятора
6. ЕГЭ 2022, задание 6. Касательная и квадратичная функция с параметром

Как самостоятельно рассчитывают переплату по кредиту

Разобраться, как рассчитать сумму переплаты по кредиту, реально. Работать можно в Excel или вручную. Если формула расчета переплаты по кредиту покажется сложной, используют онлайн-калькулятор.

Что такое переплата

Переплата представляет собой сумму, что платит заемщик кредитору сверх величины займа. Ее размер напрямую зависит от типа процентов. Они могут быть дифференцированными или аннуитетными. Определяя, как рассчитать процент переплаты по кредиту, следует учитывать, какие именно ставки применяет банк.

Аннуитет

Как рассчитать переплату по кредиту – формула при аннуитетных процентах выглядит так:

Переплата = Ежемесячный платеж х Число периодов – Сумма займа

Число периодов определяется как количество месяцев кредитования. Если договор заключен на 1 год, то считаем исходя из 12 месяцев. Если срок кредитования 3 года, то 3 х 12 = 36.

Ежемесячный платеж (Пм), если процент аннуитетный, считают так:

Пм = (С х (Пр / (12 х 100%)) / (1 – (1 + Пр / (12 х 100%)) ^ (-Т))

С – размер кредита, используемый при определении платежа за 1-ый месяц. При расчетах за 2-ой и последующие периоды подставляют сумму, соответствующую остатку займа;

Пр – годовая процентная ставка, %;

12 – число месяцев в году;

T – количество периодов, оставшихся до окончательного расчета.

При аннуитете заемщик расплачивается по кредиту равными суммами. Структура платежа такова, что в первой половине срока действия договора большая часть взноса состоит из процентов. Сам долг гасится очень медленно, что существенно увеличивает переплату, поскольку процентные начисления идут на остаток.

Пример при аннуитете

Наример, потребительский займ 60 000 рублей предоставлен на срок 3 года под 15% годовых. Здесь число периодов равно 3 х 12 = 36. Ежемесячный платеж составит:

Пм = (60 000 х (15% / (12 х 100%)) / (1 – (1 + 15% / (12 х 100%)) ^ (-36)) = 2 080 рублей

Итого за весь период кредитования нужно внести: 36 х 2 080 = 74 880 рублей

Переплата: 74 880 – 60 000 = 14 880 рублей

Дифференцированные платежи

При дифференцированных платежах сумма основного долга погашается равномерными взносами. Первые выплаты будут больше последних. Так получается, потому что процент начисляется на остаток, а он при такой схеме уменьшается равномерно.

Как посчитать, сколько составит переплата по кредиту, если процент дифференцированный – сначала также считают месячный платеж. Он будет равен:

Пм = С / n + С х (Пр / (12 х 100%))

Здесь n – число месяцев кредитования. Соотношение С / n показывает, какая сумма ежемесячно будет направляться на погашение займа. Вторая часть формулы – это расчет процентов. После погашения части долга база для начислений (С) будет уменьшаться, соответственно, снизятся и затраты на обслуживание договора. Сумма этих процентов за все периоды кредитования и составит переплату.

Пример по дифференцированным платежам

При дифференцированных процентах как посчитать переплату по кредиту по указанной формуле – пример, его условия, оставим те же, что были при аннуитете, тогда в первый месяц нужно будет заплатить:

Пм = 60 000 / 36 + 60 000 х (15% / 12 х 100%) = 1 666,67 + 750 = 2 416,67 рубля

Во второй месяц, при условии соблюдения графика, банку нужно отдать:

Пм = 60 000 / 36 + (60 000 – 1 666,67) х (15% / 12 х 100%) = 1 666,67 + 729,17 = 2 395,84 рубля

По итогам вычислений согласно приведенному примеру по каждому из 36 месяцев получим переплату в размере 13 875 рублей.

Уточнения

Как рассчитать переплату по кредиту и проверить корректность начислений банка по действующим договорам:

• при определении числа периодов следует считать в днях, а не в месяцах, учитывая високосные годы, когда дней будет не 365, а 366;
• кредиторы указывают годовой процент. При реальных вычислениях используют дневной. Его получают путем деления годовой ставки на число дней в году;
• следует учитывать суммы плановых и досрочных погашений, что уменьшают остаток долга, на величину которого и начисляют процент, и впоследствии снижают переплату. Следует вносить корректировки уже на следующий день после внесения платежа.

Кредитный калькулятор

Самостоятельно вычислить аннутитет сложно. Калькулятор кредита быстро выдаст все необходимые данные. Сервис работает с аннуитетными процентами, как с наиболее часто используемыми.

Для начала вводят параметры кредитного договора, то есть указывают:

• сумму займа;
• срок;
• стоимость кредитования.

Если прожать кнопку «Рассчитать», то программа покажет:

• размер месячного платежа;
• задолженность за весь период кредитования;
• график платежей: какие суммы направляются на расчет по займу, какие на уплату процентов, каков остаток по состоянию на каждый отдельный платежный период.

Чтобы посчитать переплату, от суммы, что нужно внести за все время действия договора кредитования, отнимают размер займа.

Резюме

С точки зрения влияния инфляционных процессов, аннуитет выгоднее, поскольку при дифференцированных платежах изначально банку отдаются деньги, примерно равные по покупательской способности тем, что были получены в долг. При аннуитетных платежах по средним и долгосрочным договорам средства успевают обесцениться.

При равных условиях предоставления кредита при аннуитете переплата будет больше на 7-15%, нежели при дифференцированных платежах. Чем больше срок кредитования, тем больше заметна разница.