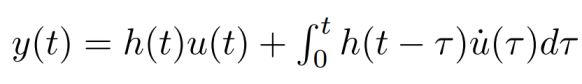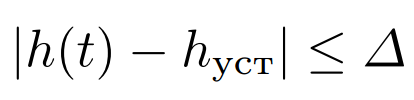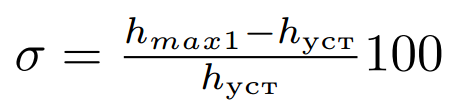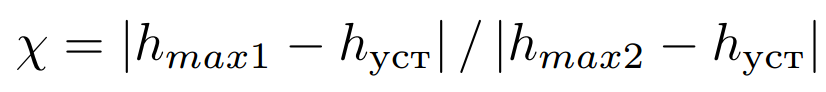Как найти перерегулирование переходного процесса

6

ЛЕКЦИЯ 9

КАЧЕСТВО ПЕРЕХОДНЫХ
ПРОЦЕССОВ В ЛИНЕЙНЫХ СИСТЕМАХ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Понятие о качестве
переходных процессов.

Из предыдущей
лекции мы узнали, что автоматическая
система прежде всего должна быть
устойчива. В устойчивой системе переходный
процесс затухает. Однако для практики
вовсе не безразличен характер затухания
переходного процесса. Так, например,
если переходный процесс затухает
медленно, и система долго входит в новый
установившийся режим, то она обладает
недостаточным быстродействием, и,
следовательно, ее применение будет
ограничено. Поэтому устойчивость
является необходимым, но недостаточным
условием работоспособности автоматических
систем. Достаточным условием является
качество
процессов регулирования,
которое оценивается качеством
переходных процессов и ошибками в
установившихся режимах.

Качество переходных
процессов обычно оценивают по переходной
функции h(t),
которая представляет собой реакцию
системы на внешнее воздействие типа
единичной ступенчатой функции 1(t).
Для следящих систем и систем управления
рассматривают переходную функцию по
отношению к задающему воздействию h(t),
а для систем стабилизации – по отношению
к возмущению h_f
(t).

На примере переходной
функции h(t)
(рис. 9.1) познакомимся с основными
показателями качества переходного
процесса: временем регулирования,
перерегулированием, основной частотой
колебаний, количеством колебаний,
максимальной скоростью и максимальным
ускорением регулируемой величины.

Время регулирования
t_р
определяется длительностью переходного
процесса. теоретически переходный
процесс длится бесконечно долго, однако
практически считают, что он заканчивается,
как только отклонения регулируемой
величины от нового ее установившегося
значения не будут превышать допустимых
пределов ε.
Обычно принимают ε
= (3 – 5)% от h_уст.
Временем регулирования характеризуют
быстродействие системы. однако иногда
быстродействие характеризуют также
временем t_у
достижения переходной функцией первый
раз нового установившегося значения
или временем t_max
достижения максимального значения
h_max.

Перерегулирование
Δ h_max,
или выброс, представляет собой максимальное
отклонение регулируемой величины от
нового установившегося значения. Обычно
первый максимум является наибольшим.
Относительное перерегулирование
вычисляют по формуле

.

Время регулирования
и перерегулирование, основные показатели
переходного процесса, тесно связаны
между собой. На первый взгляд может
показаться, что перерегулирование
недопустимо, так как оно увеличивает
время регулирования. Однако это не так.
Действительно, перерегулирование
появляется вследствие того, что система
к новому установившемуся состоянию
подходит с определенной скоростью,
которая графически отображается
тангенсом угла наклона касательной в
точке А (рис. 9.1):

.

Чем больше эта
скорость, тем дальше за новое установившееся
положение пройдет система по инерции.
Значит, для уменьшения перерегулирования
необходимо уменьшить скорость, с которой
система подходит к новому установившемуся
состоянию. Это, в конце концов, приведет
к увеличению времени регулирования.
Если система подходит к установившемуся
состоянию с нулевой скоростью, то
перерегулирования вообще не будет, но
время регулирования значительно
увеличится (рис. 9.2,б).

Так как время
регулирования характеризует быстродействие
системы, то стремятся, там где это
необходимо, свести его к минимуму. Это
значит, что система должна отрабатывать
задающее воздействие с большой скоростью,
что в итоге приводит к большому
перерегулированию. Кроме того, поскольку
переходный процесс колебательный, то
будут иметь место большие ускорения
регулируемой величины, что может вызвать
недопустимо большие динамические
нагрузки на элементы системы. Таким
образом, как отсутствие, так и слишком
большое перерегулирование нежелательно.
Поэтому в качестве оптимального допускают
перерегулирование в пределах 20 – 30%.
При этом число полуколебаний переходной
функции равно 2 – 3.

Числовые значения
времени регулирования и перерегулирования
часто задают в качестве исходных данных
для синтеза корректирующих устройств,
поскольку правильным выбором и настройкой
последних обеспечивается подавление
нежелательных колебаний регулируемой
величины в переходном процессе.

Для некоторых
систем перерегулирование вообще
недопустимо, например, для систем
автоматического регулирования химических
процессов, где перерегулирование может
испортить выпускаемый продукт. Необходимо
также иметь в виду, что стремление
уменьшить время регулирования приводит
к увеличению мощности исполнительного
устройства.

Коррекция
динамических свойств линейных САУ.

Коррекция
динамических свойств САУ осуществляется
для выполнения требований по точности,
устойчивости и качеству переходных
процессов.

С точки зрения
требований к точности САУ в установившихся
режимах коррекция динамических свойств
САУ может понадобиться для увеличения
коэффициента передачи или порядка
астатизма при сохранении устойчивости
и определенного качества переходных
процессов.

Коррекция применяется
также как средство обеспечения
устойчивости неустойчивой системы или
расширения области устойчивости и
повышения качества переходных процессов.

Осуществляется
коррекция с помощью введения в систему
специальных корректирующих
звеньев с
особо подобранной передаточной функцией.

Различают 4 основных
вида корректирующих устройств.

1. Последовательные
корректирующие устройства
или, как их еще называют, корректирующие
фильтры,
которые могут описываться различными
передаточными функциями W_к(s)
(рис. 9.3).

Здесь
–
передаточная функция основных звеньев
системы;
–
передаточная функция корректирующих
звеньев.

В первом случае
(рис. 9.3,а) общая передаточная функция
разомкнутой цепи системы будет

.

Во втором случае
(рис. 9.3, б) имеем

,

где нулями отмечены
передаточные функции заданных частей
системы.

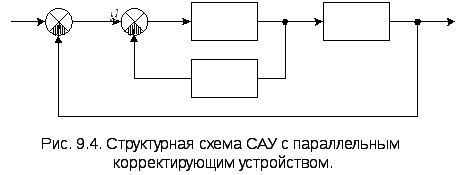
2. Параллельные
корректирующие устройства.
Выполняются в виде дополнительных
местных обратных связей

(рис. 9.4), когда

.

3. Корректирующие
устройства по внешнему воздействию.

4. Неединичная
главная обратная связь.

Передаточная
функция корректирующего устройства

или

может иметь, вообще говоря, произвольный
вид. Но наиболее часто применяются
определенные типы корректирующих
устройств, которые мы и рассмотрим.

Типовые
последовательные корректирующие
устройства.

Введение
производной от ошибки
– простейший метод улучшения качества
переходного процесса. Структурно
введение производной представлено на
рис. 9.5.

Технически это
может быть осуществлено различными
устройствами, причем производная может
осуществляться не в чистом виде, а с
инерционностью, например, в виде

.

Передаточная
функция разомкнутой цепи (рис. 9.5) с
идеальной производной будет

.

Заменив s=jω,
получим амплитуду и фазу в виде:

.

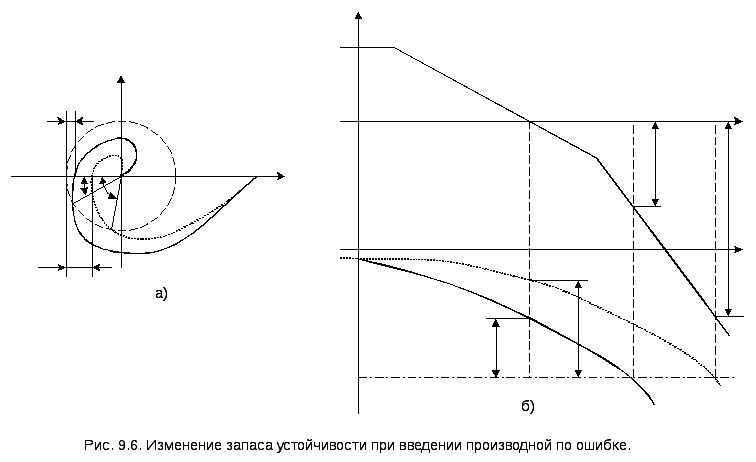
Существенным
здесь является то, что при введении
воздействия по производной добавляется
положительная фаза.

Вследствие этого
радиус-векторы амплитудно-фазовой
характеристики (рис. 9.6, а) поворачиваются
против часовой стрелки, увеличивая
запас устойчивости и улучшая качество
переходного процесса. То же самое легко
проследить и на логарифмических
характеристиках (рис. 9.6,б).

В случае неидеального
дифференцирования (с инерционностью)
этот эффект несколько уменьшается
количественно, но качественно он
сохраняется.

Заметим, что
введение производной от ошибки может
служить и стабилизирующим средством,
т.е. превращать неустойчивую замкнутую
систему в устойчивую, например, если на
рис. 9.6,а
точка (-1,j0)
лежала бы внутри характеристики
,
то новая характеристика

уже могла бы не охватывать точку (-1,j0).

Перерегулирование и время переходного процесса являются показателями качества системы, процессы которой устойчивы и имеют конечную длительность.

Определение перерегулирования и времени переходного процесса в продукте Acsocad

В режиме просмотра графика необходимо щелкнуть на режим “=” для показа на графике перерегулирования и времени переходного процесса. При подведении к линии графика дополнительно выводится в числовом виде значение перерегулирования (O, %) и времени переходного процесса (Tp, с).

Определение перерегулирования и времени переходного процесса в продукте MATLAB Simulink

В MATLAB Simulink необходимо задать вход и выход исследуемой системы и запустить инструмент линейного анализа. Эта процедура подробно рассмотрена на странице “Анализ: годограф Найквиста и Михайлова, ЛАЧХ и ЛФЧХ”.
После запуска линеаризации выбирается режим графика “Step” и далее на рисунке вызывается меню путем нажатия правой кнопки мыши. В меню “Characteristics” выбираются подпункты меню “Peak Response” и “Setting Time”.

Для вывода текстовой информации о значениях показателей необходимо щелкнуть левой кнопкой мыши по отмеченным на графике точкам.

Перехо́дный проце́сс — в теории систем представляет изменения во времени координат динамической системы, до некоторого установившегося состояния; возникает под влиянием возмущающих воздействий, изменяющих её состояние, структуру или параметры, а также вследствие ненулевых начальных условий^{[B: 1]}.

Характеристики[править | править код]

Изучение переходных процессов — важный шаг в процессе анализа динамических свойств и качества рассматриваемой системы. Широкое применение нашло экспериментальное и аналитическое определение и построение переходных процессов для наиболее неблагоприятных условий работы динамической системы при внешних возмущениях типа дельта-функции, ступенчатом или синусоидальных воздействиях^{[B: 1][B: 2]}.

Оценка качества САУ по виду кривой переходного процесса производится при помощи так называемых прямых показателей качества — перерегулирования, допустимого числа колебаний и времени переходного процесса. Обычно рассматривают переходный процесс, возникающий в системе при воздействии единичной ступенчатой функции, т. е. переходная функция замкнутой системы^[1].

Время переходного процесса[править | править код]

Длительность переходного процесса в системе характеризует её быстродействие, а его характер определяет качество системы. За количественную характеристику длительности переходного процесса принимают время, необходимое выходному сигналу системы для того, чтобы приблизиться к своему установившемуся значению, т. е. время, по истечении которого выполняется равенство:

где  — установившееся значение;

 — наперёд заданное положительное число^[1].

В линейных непрерывных динамических системах принято рассматривать переходной процесс, вызванный единичным ступенчатым возмущением, но в этом случае установившееся значение достигается за бесконечно большое время. Если же ограничить точность достижения установившегося значения некоторой малой величиной , то тогда длительность переходного процесса будет конечной величиной^{[B: 1]}.

В приложениях теории управления обычно в САУ принимают равной 0,01—0,05 от , т. е. переходный процесс считают закончившимся, когда переходная функция отличается не более, чем на 1–5 % от своего установившегося (стационарного) значения^[1].

Перерегулирование[править | править код]

Перерегулирование (определяется величиной первого выброса) — отношение разности максимального значения переходной характеристики и её установившегося значения к величине установившегося значения. Измеряется обычно в процентах.

Степень затухания переходного процесса[править | править код]

Степень затухания переходного процесса определяется относительным уменьшением соседних амплитуд переходной характеристики^{[B: 3]}.

Числителем является амплитуда первого колебания. Степень затухания показывает во сколько раз уменьшается амплитуда второго колебания по сравнению с первым.

Степень затухания системы зависит от показателя колебательности (см. ниже).

Логарифмический декремент колебания[править | править код]

Логарифмический декремент колебания — натуральный логарифм отношения амплитуд двух соседних перерегулирований. Обратная ему величина показывает, за какое число колебаний их амплитуда уменьшается в раз ( — основание натуральных логарифмов). Уместен лишь для характеристики линейных систем^{[B: 4]}.

Колебательность[править | править код]

Характеризует склонность системы к колебаниям и определяется как модуль отношения амплитуд второго колебания к амплитудам первого колебания. Колебательность системы характеризуют при помощи показателя колебательности , который представляет собой отношение резонансного пика при резонансной частоте к значению АЧХ при нулевой частоте^[2].

Показатель колебательности связан со степенью колебательности формулой:

При увеличении , уменьшается показатель колебательности и соответственно происходит уменьшение степени колебательности.

Установившаяся ошибка[править | править код]

Установившаяся ошибка системы — разница между предполагаемым и реальным значением выходного сигнала при времени, стремящемся к бесконечности. В идеальных астатических системах установившаяся ошибка равна нулю.

Примеры[править | править код]

Электрические цепи[править | править код]

В электрической цепи переходный процесс характеризуется плавным инерционным изменением тока и напряжения в цепи в ответ на приложенное внешнее воздействие^{[B: 5]}.

Формула, описывающие протекание простейших переходных процессов (разряд конденсатора через резистор):

где  — значение напряжения на конденсаторе в момент перед началом переходного процесса,

 — постоянная времени переходного процесса, С — ёмкость, R — сопротивление элементов цепей.

Для цепей, содержащих индуктивность, если можно пренебречь активным сопротивлением, постоянная времени равна:

См. также[править | править код]

• Бифуркационная память
• Время изодрома
• Зона нечувствительности
• Коэффициент демпфирования
• Переходные процессы в электрических цепях

Примечания[править | править код]

Литература[править | править код]

Книги

В следующей части (2) расскажем о теории регулирования ПИД, применяемой в преобразователях частоты. Во всех моделях частотных преобразователей, которые можно у нас купить: Lenze, INNOVERT и Advanced Control присутствует эта функция.

Переходный процесс

Переходный процесс – процесс изменения во времени координат динамической системы, возникающий при переходе из одного установившегося режима работы в другой. В динамической системе переходный процесс возникает под влиянием возмущающих воздействий, изменяющих ее состояние, структуру или параметры, а также вследствие ненулевых начальных условий. Широкое применение нашло экспериментальное и аналитическое определение и построение переходного процесса для наиболее неблагоприятных условий работы динамической системы при внешних возмущениях типа дельта-функции, ступенчатом и синусоидальном воздействиях и т.д.

В линейных непрерывных динамических системах принято рассматривать переходный процесс, вызванный единичным ступенчатым возмущением. Установившееся значение достигается за бесконечно большое время. Если ограничить точность достижения установившегося значения некоторой величиной Δ, то тогда длительность переходного процесса tр будет конечной величиной (см. рис. ниже: Виды переходных процессов). При этом длительность переходного процесса в системе характеризует ее быстродействие, а его характер определяет качество системы.

Поскольку характер изменения во времени координат системы зависит в общем случае от начального состояния системы, ее свойств, вида и интенсивности действующих возмущений и т. д., в ряде случаев можно выбрать структуру и параметры динамической системы так, что переходный процесс, вызываемый действиями определенных возмущений, будет иметь минимальную длительность либо его не будет вообще. В зависимости от характера различают переходные процессы (см. рис. выше: Виды переходных процессов): колебательные (1), слабоколебательные (2) и неколебательные (4). Кроме того, различают монотонные колебательные (3) и немонотонные колебательные (1) переходные процессы.

В линейных импульсных системах управления при соответствующем выборе параметров системы переходный процесс может совершаться за конечное число периодов регулирования — длительность переходного процесса конечна.

Оценка качества переходного процесса при воздействии ступенчатой функции

Переходный процесс в системе зависит не только от свойств САУ, но и от характера внешнего воздействия, которое в общем случае может быть сложной функцией времени. Поведение системы рассматривают при следующих типовых воздействиях: единичной ступенчатой функции 1(t), импульсной δ(t) и гармонической функций. Прямые оценки качества получают по кривой переходной характеристики h(t)

Переходной характеристикой (переходной функцией) h(t) называется реакция системы на единичное ступенчатое входное воздействие u(t – τ) = 1(t – τ) при нулевых начальных условиях (то есть объект в начальный момент находится в состоянии покоя).

Отметим, что единичная ступенчатая функция – это функция, которая обладает свойством:

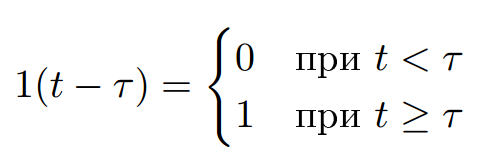
Для аналитического определения переходной функции следует решить дифференциальное уравнение при нулевых начальных условиях и единичном входном воздействии.

При исследовании реального объекта переходную характеристику можно получить экспериментальным путем, подавая на его вход ступенчатое воздействие и фиксируя реакцию на выходе. Если входное воздействие представляет собой неединичную ступенчатую функцию u(t)=k·1(t), то выходная величина будет равна y(t)=k·h(t), т. е. представляет собой переходную характеристику с коэффициентом пропорциональности k.

Зная переходную характеристику, можно вычислить реакцию системы на произвольное входное воздействие с помощью интеграла свертки:

Эту характеристику можно построить для выходной величины (см. рис. ниже).

К прямым оценкам качества относят:

1. Время регулирования tр — минимальное время, по истечении которого регулируемая величина будет оставаться близкой к установившемуся значению с заданной точностью:

   

   где Δ — постоянная величина, значение которой нужно оговаривать (задается величина Δ в процентах от установившегося значения выходной величины tуст).

2. Перерегулирование σ — максимальное отклонение переходной характеристики от установившегося значения выходной величины, выраженное в относительных единицах или процентах:

   

   где hmax1 — значение первого максимума.

   Допустимое значение перерегулирования в каждом конкретном случае будет подсказано опытом эксплуатации системы, обычно σ = 10 ÷ 30 % но в некоторых случаях допускается и до 70 %. Иногда перерегулирование недопустимо совсем.

3. Частоту колебаний ω = 2π/T где Т — период колебаний для колебательных переходных характеристик.
4. Число колебаний n, которое имеет переходная характеристика h(t) за время регулирования tр.

   При проектировании систем чаще всего допускают n = 1 ÷ 2, а иногда и до 3 – 4, но в некоторых случаях колебания в системе недопустимы.

5. Время достижения первого максимума tmax1.
6. Время нарастания переходного процесса tн — абсциссу первой точки пересечения кривой переходной характеристики h(t) с уровнем установившегося значения hуст.
7. Декремент затухания χ, равный отношению модулей двух смежных перерегулирований:

   

Перечисленные показатели качества могут быть дополнены другими, но это обусловлено спецификой конкретной системы.

Переходной процесс

Полезное