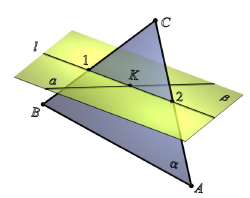
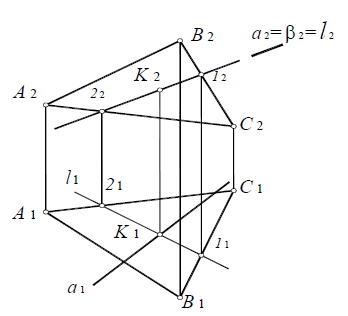
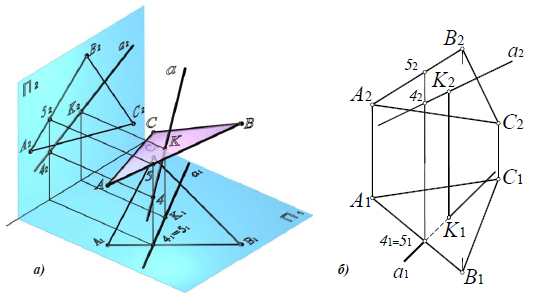
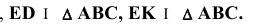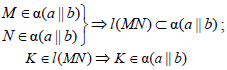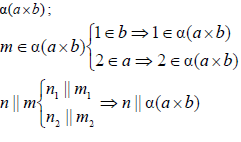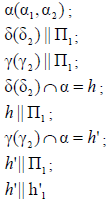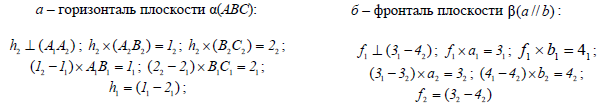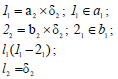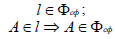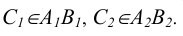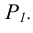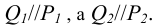Пересечение двух плоскостей
Пересечение двух плоскостей общего положения представляет собой прямую линию, поэтому для ее определения достаточно найти две
точки, принадлежащие одновременно каждой из двух заданных плоскостей – так называемые общие точки.
Чтобы найти общие точки, достаточно ввести одну или две вспомогательные секущие плоскости γ1
и γ2.
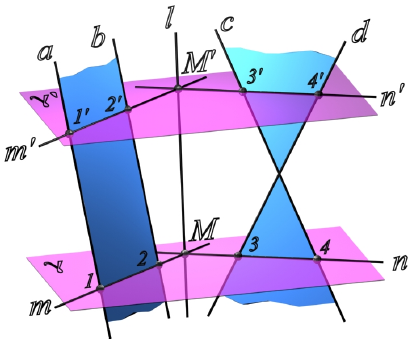
Найти пересечение двух плоскостей общего положения линию l, если плоскости заданны пересекающимися прямыми b c и
параллельными прямыми d e.
Пересечение двух плоскостей
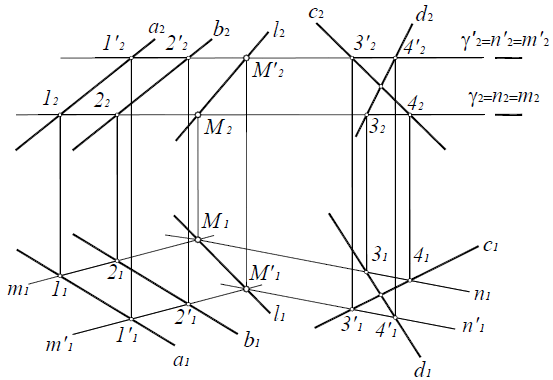
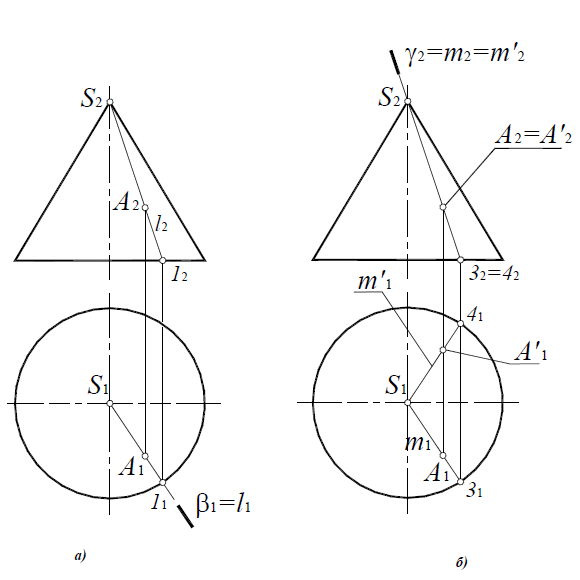
Вспомогательная плоскость γ1 пересекает заданные плоскости по прямым n1 и n2, которые пересекаясь между собой дают первую точку искомой линии.
Вспомогательная плоскость γ2 пересекает заданные плоскости по прямым m1 и m2, которые пересекаясь между собой дают вторую точку искомой линии.
Проведя через найденные точки L1 и L2 прямую линию получаем искомое, пересечение двух плоскостей – линию l.
Определить линию пересечения l плоскостей заданных следами αH,
αV и βH, βV.
Пересечение двух плоскостей
Задача на пересечение плоскостей заданных следами αH,
αV и βH, βV.
Пересечение двух плоскостей
Задача на пересечение плоскостей заданных следами αH,
αV и βH, βV причем αV ║ βV.
Пересечение двух плоскостей
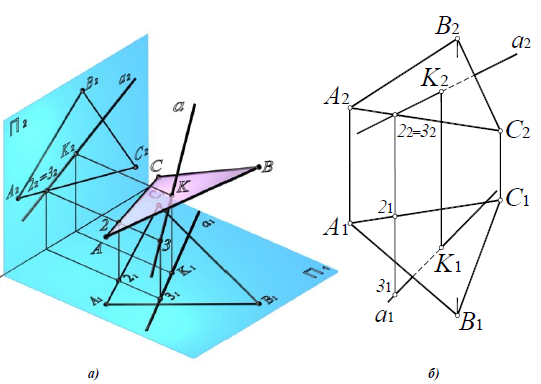
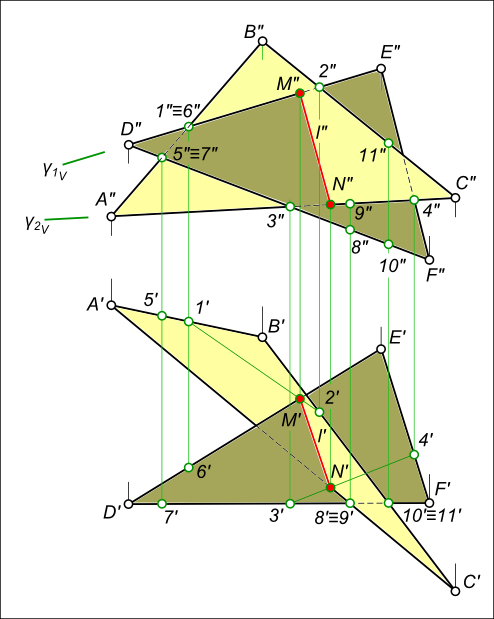
Пересечение двух плоскостей, заданных треугольниками ABC и DEF.
Пересечение двух плоскостей
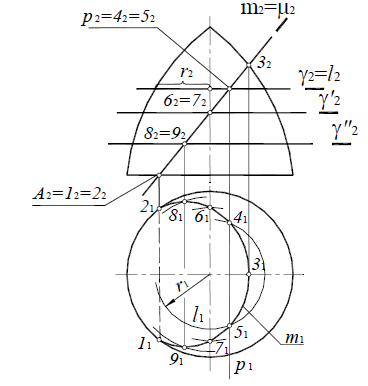
Вспомогательная плоскость γ1 пересекает заданные плоскости по прямым 1-2 и DE, которые пересекаясь между собой дают первую точку искомой линии – точка M.
Вспомогательная плоскость γ2 пересекает заданные плоскости по прямым 3-4 и AC, которые пересекаясь между собой дают вторую точку искомой линии – точка N.
Соединяем точки MN прямой линией получаем искомую линию l пересечения двух плоскостей.
Определение видимости пересекающихся плоскостей на плоскостях проекций выполняем, используя Конкурирующие точки:
на фронтальной плоскости проекций – 1″≡6″; 1`, 6` и 5″≡ 7″; 5`, 7` – будет видна вершина D с прилегающими сторонами до линии пересечения.
на горизонтальной плоскости проекций – 8`≡9`; 8″, 9″ и 10`≡ 11`; 10″, 11″ – будет видна вершина C с прилегающими сторонами до линии пересечения.
Построить линию пересечения двух плоскостей треугольник ABC и α(αH, αV)
Пересечение двух плоскостей
Графическая работа 1 представляет задачу на пересечение двух плоскостей заданных треугольником и ромбом
+
Линия пересечения плоскостей онлайн
С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Линия пересечения плоскостей − теория, примеры и решения
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α1 и α2:
| α1: A1x+B1y+C1z+D1=0, | (1) |
| α2: A2x+B2y+C2z+D2=0, | (2) |
где n1={A1, B1, C1} и n2={A2, B2, C2} − нормальные векторы плоскостей α1 и α2, соответственно.
Найдем уравнение линии пересеченя плоскостей α1 и α2. Для этого рассмотрим следующие случаи:
1. Нормальные векторы n1 и n2 плоскостей α1 и α2 коллинеарны (Рис.1).
Поскольку векторы n1 и n2 коллинеарны, то существует такое число λ≠0, что выполнено равенство n1=λn2, т.е. A1=λA2, B1=λB2, C1=λC2.
Умножив уравнение (2) на λ, получим:
| α2: A1x+B1y+C1z+λD2=0, | (3) |
Если выполненио равенство D1=λD2, то плоскости α1 и α2 совпадают, если же D1≠λD2то плоскости α1 и α2 параллельны, то есть не пересекаются.
2. Нормальные векторы n1 и n2 плоскостей α1 и α2 не коллинеарны (Рис.2).
Если векторы n1 и n2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.
Так как в системе линейных уравнений (4) векторы n1={A1, B1, C1} и n2={A2, B2, C2} не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:
где x0, y0, z0, m, p, l действительные числа, а t − переменная.
Равенство (5) можно записать в следующем виде:
Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α1 и α2. Полученное уравнение прямой можно записать в каноническом виде:
Пример 1. Найти линию пересечения плоскостей α1 и α2:
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α1 имеет нормальный вектор n1={A1, B1, C1}={1, 2, 1}. Плоскость α2 имеет нормальный вектор n2={A2, B2, C2}={2, 9, −5}.
Поскольку направляющие векторы n1 и n2 неколлинеарны, то плолскости α1 и α2 пересекаются.
Для нахождения линии пересечения влоскостей α1 и α2 нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:
Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 2 со строкой 1, умноженной на −2:
Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
Получим решение:
где t− произвольное действительное число.
Запишем (11) в следующем виде:
Получили уравнение линии пересечения плоскостей α1 и α2 в параметрическом виде. Запишем ее в каноническом виде.
Из равентсв выше получим каноническое уравнение прямой:
Ответ. Уравнение линии пересечения плоскостей α1 и α2имеет вид:
Пример 2. Найти линию пересечения плоскостей α1 и α2:
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α1 имеет нормальный вектор n1={A1, B1, C1}={1, 2, 7}. Плоскость α2 имеет нормальный вектор n2={A2, B2, C2}={2, 4, 14}.
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/2), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/2:
Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α1 и α2 не совпадают. Следовательно они параллельны, т.е. не пересекаются.
Пример 3. Найти линию пересечения плоскостей α1 и α2:
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α1 имеет нормальный вектор n1={A1, B1, C1}={5, −2, 3}. Плоскость α2 имеет нормальный вектор n2={A2, B2, C2}={15, −6, 9}.
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/3), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/3:
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α1 и α2 совпадают.
Л
пересечения двух плоскостей – прямая
линия. Рассмотрим сначала частный случай
(рис. 3.9), когда одна из пересекающихся
плоскостей параллельна горизонтальной
плоскости проекций (α ׀׀
π1,
f0α
׀׀Х).
В этом случае линия пересечения а,
принадлежащая плоскости α,
будет также параллельна плоскости π1,
(рис. 3.9. а) т.
е. будет совпадать с горизонталью
пересекающихся плоскостей (а ≡ h).
Если одна из
плоскостей параллельна фронтальной
плоскости проекций (рис. 3.9. б), то линия
пересечения а, принадлежащая этой
плоскости, будет параллельна плоскости
π2
и будет совпадать с фронталью
пересекающихся
плоскостей (а ≡ f).
а)
б)
Рис. 3.9. Частный
случай пересечения плоскости общего
положения с плоскостями: а) горизонтального
уровня; б) фронтального уровня
Пример построения
точки пересечения (К) прямой а (АВ) с
плоскостью α (DEF)
показан на рис. 3.10. Для этого прямая а
заключена в произвольную плоскость β
и определена линия пересечения плоскостей
α и β.
В рассматриваемом
примере прямые АВ и MN
принадлежат одной плоскости β и
пересекаются в точке К, а т. к. прямая MN
принадлежит заданной плоскости α (DEF),
то точка К является и точкой пересечения
прямой а (АВ) с плоскостью α. (рис. 11).
Рис. 3.10. Построение
точки пересечения прямой с плоскостью
Для решения подобной
задачи на комплексном чертеже необходимо
уметь находить точку пересечения прямой
общего положения с плоскостью общего
положения.
Рассмотрим пример
нахождения точки пересечения прямой
АВ c
плоскостью треугольника DEF
представленный на рис. 3.11.
Для нахождения
точки пересечения через фронтальную
проекцию прямой А2В2
проведена фронтально-проецирующая
плоскость β которая пересекла треугольник
в точках M
и N.
На фронтальной плоскости проекций (π2)
эти точки представлены проекциями M2,
N2.
Из условия принадлежности прямой
плоскости на горизонтальной плоскости
проекций (π1)
находятся горизонтальные проекции
полученных точек M1
N1.
В пересечении горизонтальных проекций
прямых А1В1
и M1N1
образуется горизонтальная проекция
точки их пересечения (К1).
По линии связи и условиям принадлежности
на фронтальной плоскости проекций
находится фронтальная проекция точки
пересечения (К2).
В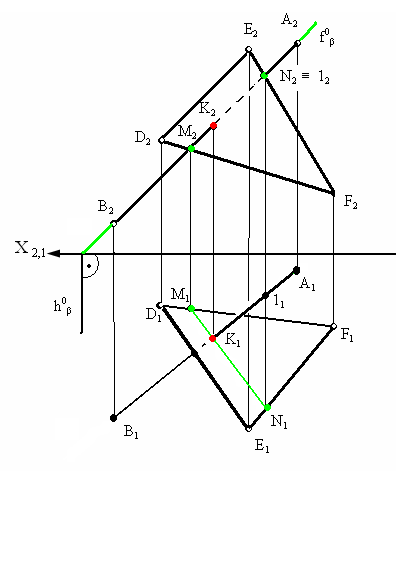
отрезка АВ относительно треугольника
DEF
определена методом конкурирующих
точек.
На плоскости π2
рассмо- трены две точки NEF
и
Рис. 3.11. Пример
определения точки
пересечения прямой
и плоскости
1АВ.
По горизонтальным проекциям этих
точек можно установить, что точка N
рас- положена ближе к наблюда-
телю (YN>Y1
), чем точка 1 (направление луча
зрения параллельно S).
Следовательно, прямая АВ, т. е. часть
прямой АВ (К1)
закрыта плоскостью DEF
на плоскости π2
(ее проекция К212
показана штриховой линией). Аналогично
установлена видимость на плоскости
π1.
Вопросы для
самоконтроля
-
В чем заключается
сущность метода конкурирующих точек
? -
Свойства прямой.
-
Каков алгоритм
определения точки пересечения прямой
и плоскости ? -
Каков алгоритм
определения линии пересечения плоскостей
? -
Какие задачи
называются позиционными ? -
Сформулируйте
условия принадлежности прямой плоскости.
Соседние файлы в папке Лекции нг
- #
- #
- #
- #
- #
- #
- #
- #
Построение линии пересечения плоскостей, заданных различными способами
Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.
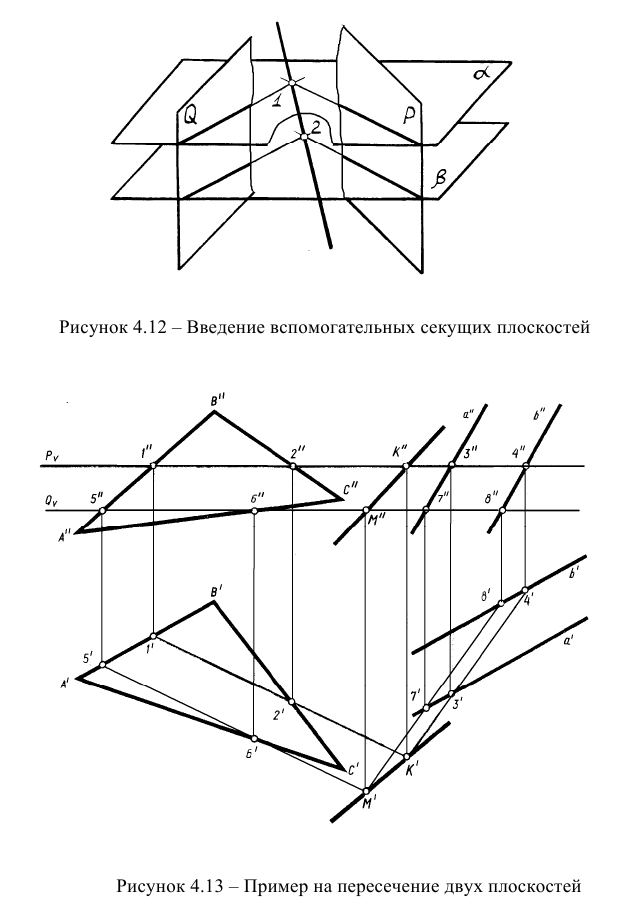
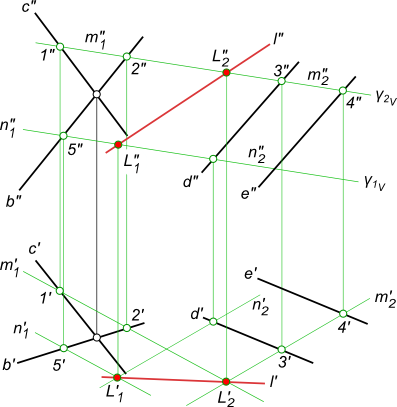
Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L1 и L2, принадлежащих линии пересечения.
- Вводим вспомогательную горизонтальную плоскость γ1. Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1”C” и 2”3”, совпадают с фронтальным следом пл. γ1. Он обозначен на рисунке как f0γ1 и расположен параллельно оси x.
- Определяем горизонтальные проекции 1’C’ и 2’3′ по линиям связи.
- Находим горизонтальную проекцию точки L1 на пересечении прямых 1’C’ и 2’3′. Фронтальная проекция точки L1 лежит на фронтальном следе плоскости γ.
- Вводим вспомогательную горизонтальную плоскость γ2. С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L2.
- Через L1 и L2 проводим искомую прямую l.
Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.
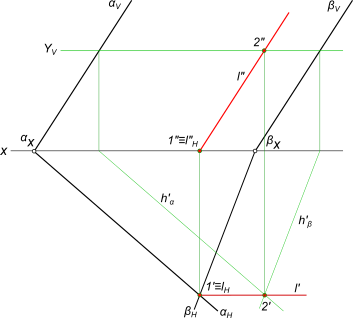
Пересечение плоскостей, заданных следами
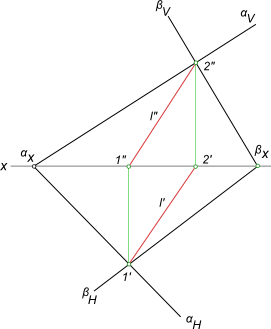
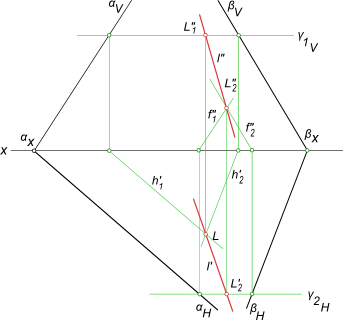
Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П1 и П2.
- Находим точку L’1, расположенную на пересечении горизонтальных следов h0α и h0β. Точка L”1 лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L’1.
- Находим точку L”2 на пересечении фронтальных следов пл. α и β. Точка L’2 лежит на оси x. Её положение определяется по линии связи, проведенной из L”2.
- Проводим прямые l’ и l” через соответствующие проекции точек L1 и L2, как это показано на рисунке.
Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.
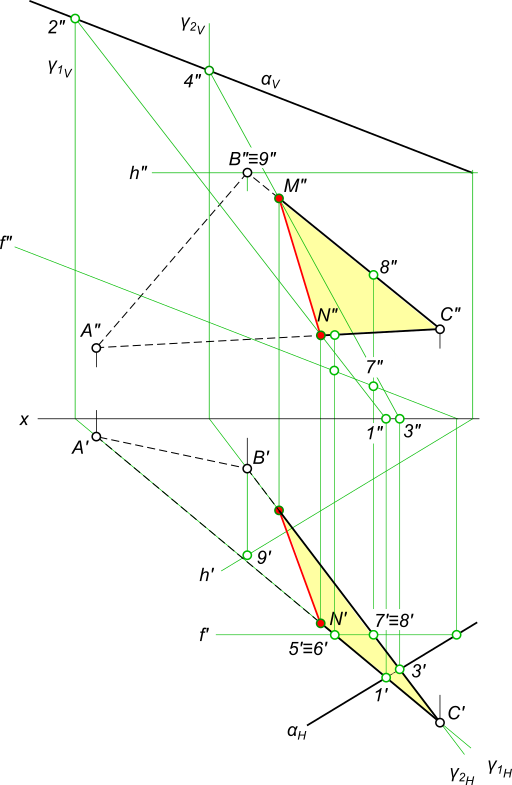
Пересечение плоскостей треугольников
Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.
- Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f0σ. Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3”=A”B”∩f0σ и 5”=A”С”∩f0σ, определяем положение (∙)3′ и (∙)5′ по линиям связи на ΔA’B’C’.
- Находим горизонтальную проекцию N’=D’E’∩3’5′ точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ. Проекция N” расположена на фронтальном следе f0σ на одной линии связи с N’.
Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.
Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π2. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π2. С противоположной стороны от линии N”K” видимость треугольников меняется.
Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π1. Так как (∙)6” находится выше, чем (∙)7”, то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π1. С противоположной стороны от линии N’K’ видимость треугольников меняется.
Позиционные задачи в начертательной геометрии с примерами
Содержание:
Позиционными задачами называются задачи на построение элементов, общих для взаимодействующих объектов, и задачи на взаимное положение геометрических объектов. Первая группа задач включает задачи на принадлежность и задачи на пересечение. Ко второй группе задач относятся задачи на параллельность геометрических объектов.
Задачи на перпендикулярность объектов относят к метрическим задачам, которые будут рассмотрены в следующем разделе. Позиционные задачи, в которых участвуют поверхности, будут рассмотрены в главе “Поверхности”.
Классификация позиционных задач, относящихся к элементарным геометрическим объектам (точка, прямая, плоскость), представлена на рисунке 4.1.
Позиционные задачи
Задачи, связанные с определением взаимного расположения геометрических объектов в пространстве, традиционно называют позиционными.
Поскольку Начертательная геометрия изучает объекты расширенного Евклидова пространства
В линейной алгебре утверждается, что для всех объектов пространства справедливо выражение (в соответствии с рисунком 4.1) 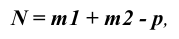
где N— размерность рассматриваемого пространства,
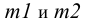
Очевидно, все позиционные задачи, с точки зрения линейной алгебры, можно свести к определению вида и размерности пересечения.
Полагая, что рассматриваемое
пространство трехмерно, при вычислении размерности пересечения исходное выражение примет вид
Заметим, что этот подход позволяет определить только и только размерность
Рассмотрим вопрос о принадлежности точки прямой, точки и прямой -плоскости. Особенность решения этих вопросов заключается в том, что прямая и точка на чертеже задаются проекциями, а плоскость – соответствием трех пар точек.
Задачи на принадлежность
Эта группа задач содержит три типовые задачи – точка принадлежит прямой, точка принадлежит плоскости, прямая принадлежит плоскости, суть решения которых основана на свойствах проецирования. Если точка принадлежит прямой, то проекции этой точки принадлежат одноименным проекциям прямой.
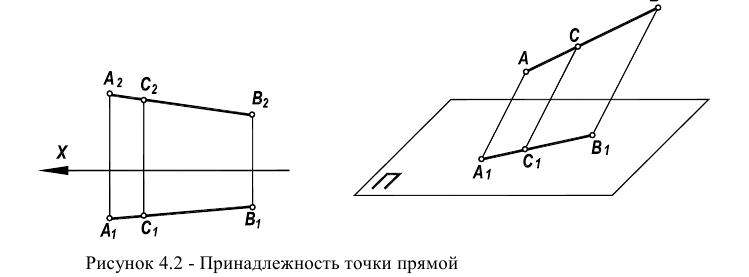
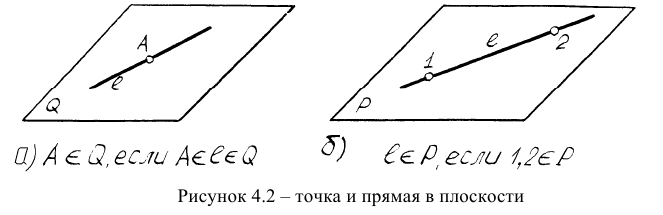
Точка принадлежит плоскости, если она принадлежит прямой, находящейся в этой плоскости (рисунок 4.2а). Прямая принадлежит плоскости, если она проходит через две точки, принадлежащих плоскости. Поэтому для того, чтобы указать в плоскости какую-либо точку, необходимо сначала указать в плоскости прямую, а затем на этой прямой указать положение точки.
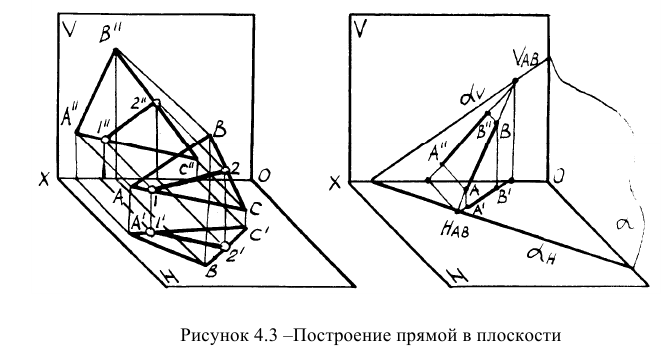
На рисунках 4.3 показано построение прямой в плоскостях, заданных треугольником и следами. Если плоскость задана треугольником, то целесообразно упомянутые точки взять на сторонах треугольника. Если плоскость задана следами, то в качестве двух точек целесообразно взять следы прямой. Это основано на следующем свойстве: если плоскость задана следами и в ней находится прямая, то следы прямой лежат на одноименных следах плоскости.
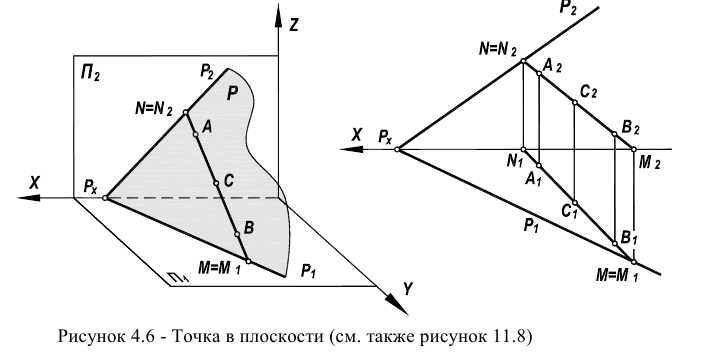
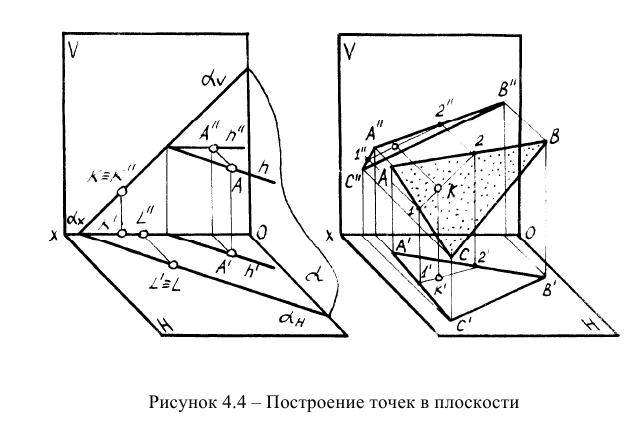
На рисунке 4.4 представлено построение точек в плоскости, заданной следами и точки в плоскости, заданной треугольником. В первом случае точка А построена с помощью горизонтали. На этом же рисунке показано построение точек (К и L), находящихся на следах плоскости. Во втором случае точка К построена с помощью прямой 1-2.
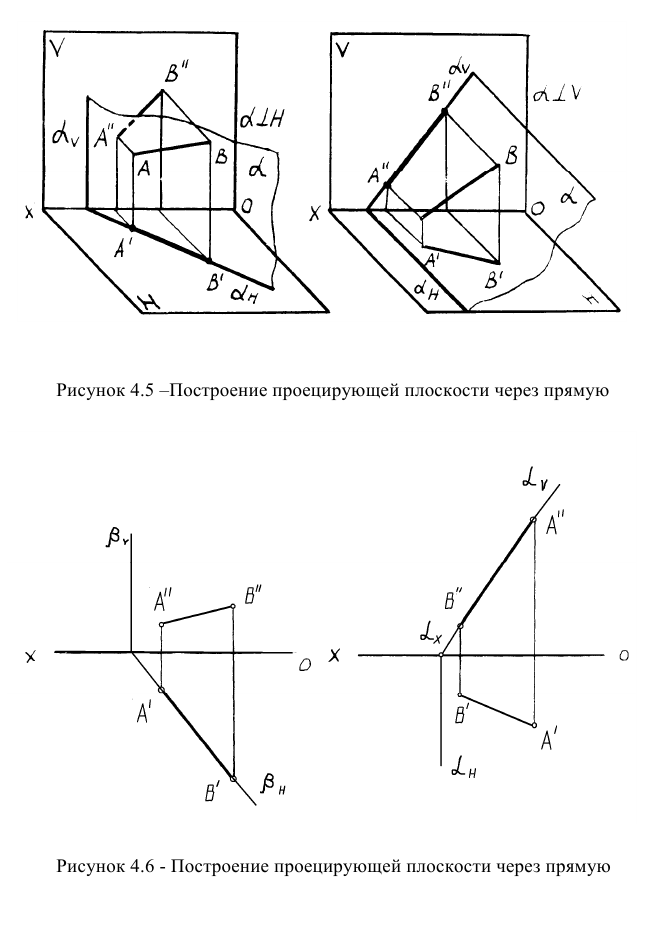
С рассматриваемым вопросом тесно связан вопрос о проведении плоскости частного положения (например, проецирующих плоскостей) через прямую.
Если прямая принадлежит плоскости частного положения и плоскость задается следами, то одна из проекций прямой будет совпадать с собирательным следом плоскости в соответствие с рисунком 4.5.
На рисунке 4.6 в эпюрной форме показано проведение через прямую фронтально проецирующей плоскости а и горизонтально проецирующей плоскости
Задачи на пересечение
Задача на пересечение двух прямых рассмотрена ранее в разделе “Пересекающиеся прямые”.
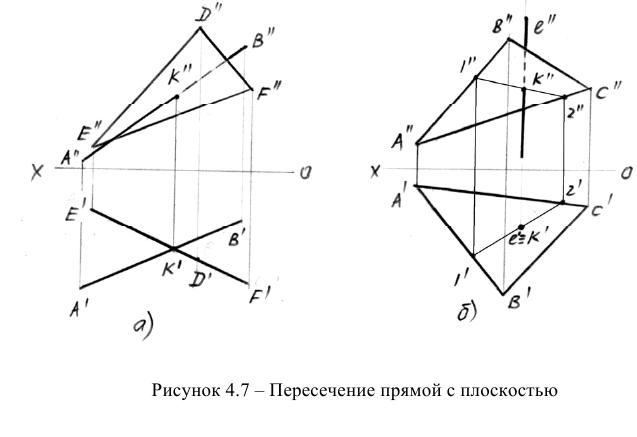
Наиболее важной позиционной задачей является задача о пересечении прямой с плоскостью. При решении задачи могут встретиться следующие случаи пересечения:
- Прямая общего положения пересекается с плоскостью частного положения;
- Прямая частного положения (например, проецирующая) пересекается с плоскостью общего положения;
- Прямая общего положения пересекается с плоскостью общего положения.
Решение первых двух задач не представляет особых трудностей (рисунок 4.7). На рисунке 4.7а дано построение точки встречи прямой общего положения с горизонтально-проецирующей плоскостью, а на рисунке 4.76 – горизонтально-проецирующей прямой с плоскостью общего положения. Последняя задача решена с помощью вспомогательной прямой 1-2.
Для решения задачи о пересечении прямой с плоскостью в общем положении разработана следующая методика (рисунок 4.8а):
- Через прямую проводят вспомогательную плоскость частного положения
(чаще всего проецирующую плоскость, заданную следами);
- Находят линию пересечения заданной а и вспомогательной плоскостей
(линия 1-2);
- Находят точку пересечения заданной прямой и найденной линии пересечения плоскостей. Полученная точка К – искомая.
Рисунок 4.8 – Пересечение прямой общего положения с плоскостью общего положения
На рисунке 4.86 дана пространственная схема решения задачи, в которой прямая пересекается с плоскостью, заданной следами. В качестве вспомогательной плоскости взята горизонтально-проецирующая плоскость.
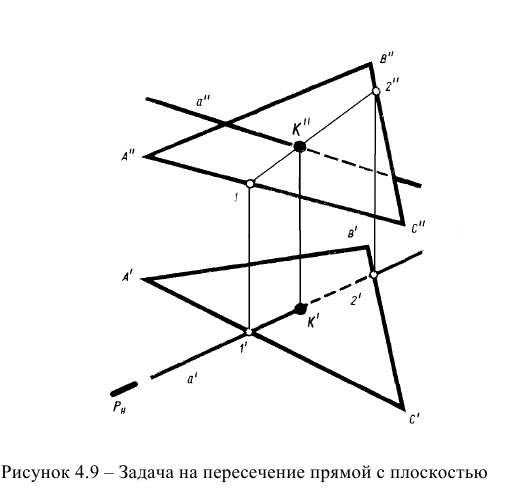
На рисунке 4.9 дано решение задачи на пересечение прямой общего положения с плоскостью общего положения, заданной треугольником. В качестве вспомогательной плоскости использована горизонтально-проецирующая плоскость.
Видимость проекций определена методом конкурирующих точек (прямых).
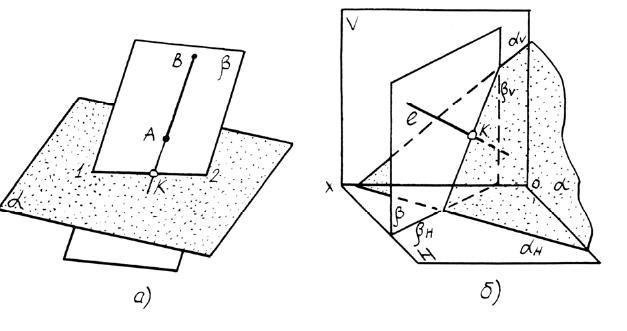
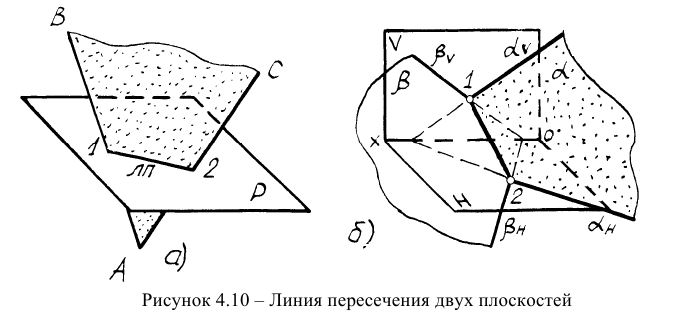
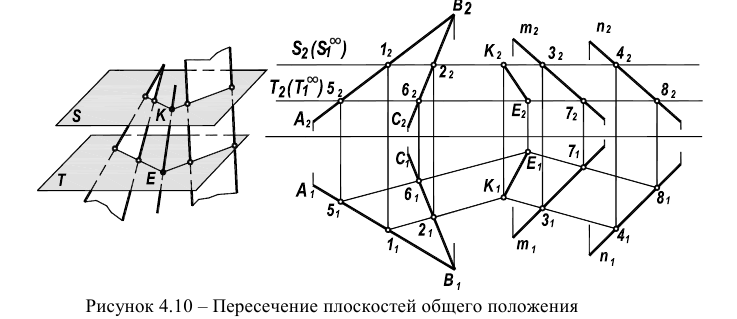
К главным задачам на пересечение относится также задача о пересечении двух плоскостей. Линия пересечения двух плоскостей – это прямая, принадлежащая как одной, так и другой плоскости. Следовательно, для построения линии пересечения двух плоскостей надо найти какие-либо две точки, каждая из которых принадлежит обеим плоскостям (рисунок 4.10).
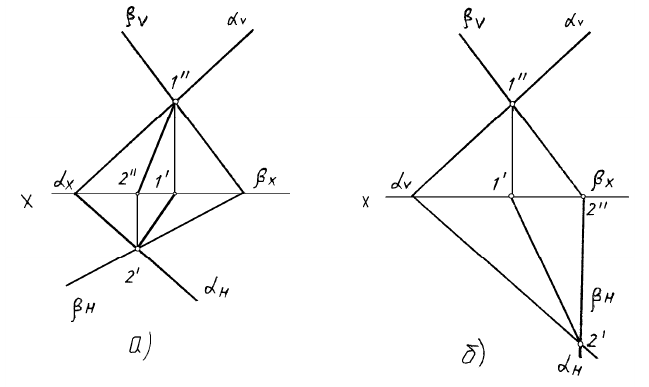
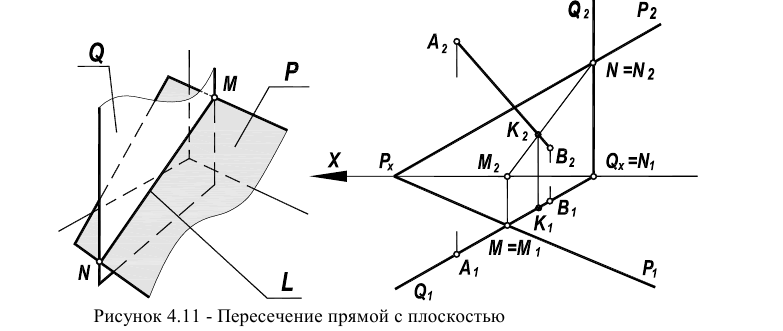
Если плоскости заданы следами, то исходя из рисунка 4.106 линия пересечения таких плоскостей определяется точками пересечения одноименных следов. На рисунке 4.11 представлены решения задач о пересечении двух плоскостей, заданных следами. Во втором случае одна из плоскостей является плоскостью общего положения, а другая -фронтально-проецирующей.
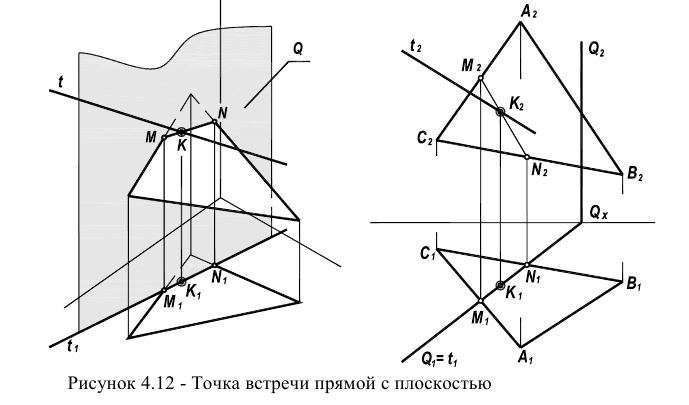
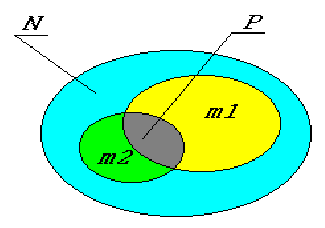
Рисунок 4.11 – Пересечение плоскостей, заданных следами В случаях, если плоскости заданы разными способами, применяют общий метод построения линии пересечения, основанный на введении вспомогательных плоскостей (рисунок 4.12).
Сущность метода заключается в том, что заданные плоскости Q и Р дважды пересекают вспомогательными плоскостями а и 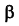
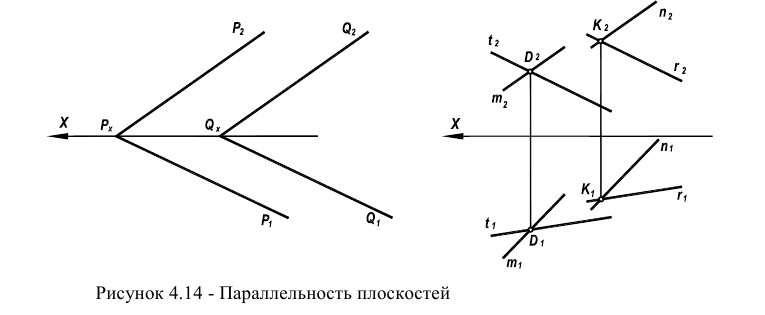
Если пересекающиеся плоскости являются плоскостями частного положения, или если одна из пересекающихся плоскостей является плоскостью частного положения, то задача упрощается. На рисунке 4.14 представлены примеры решения задач на пересечение упомянутых плоскостей. И более трудоемкой задачей является задача на пересечение двух плоскостей общего положения, заданных плоскими фигурами, например, треугольниками, многоугольниками и т.д.
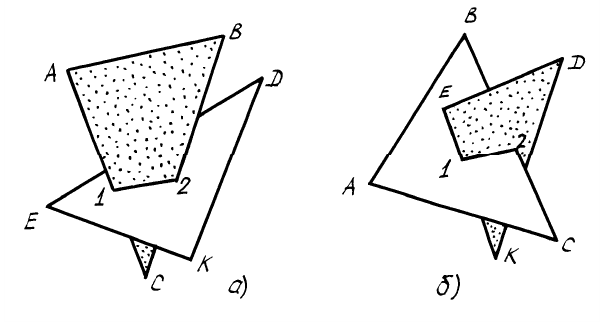
При пересечении плоских фигур возможны два случая пересечения (рисунок 4.15): полное пересечение (а) и неполное пересечение (б).
Рисунок 4.15 – Полное и неполное пересечение плоских фигур
В обоих случаях линия пересечения треугольников определяется двумя точками 1 и 2, каждая из которых определяется как точка пересечения стороны одного треугольника с плоскостью другого. Отсюда следует вывод: для того, чтобы построить линию пересечения
треугольников, необходимо дважды решить задачу о пересечении стороны одного треугольника с плоскостью другого треугольника (типовая задача о пересечении прямой с плоскостью). При этом пару пересекающихся объектов можно подбирать произвольно. В любом случае линия пересечения будет построена.
Задачи на параллельность
Задача на параллельность двух прямых была рассмотрена ранее в разделе “Параллельные прямые”.
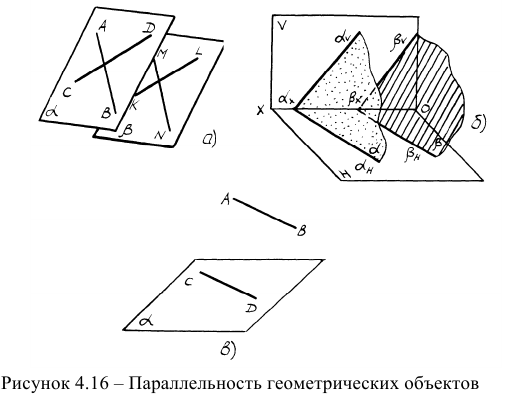
Задачи на параллельность плоскостей основываются на положениях элементарной геометрии. Две плоскости параллельны, если две пересекающиеся прямые одной плоскости взаимно параллельны двум пересекающимся прямым другой плоскости (рисунок 4.16а).
Если две параллельные плоскости заданы следами, то одноименные следы таких плоскостей параллельны друг другу (рисунок 4.166).
Прямая будет параллельна плоскости в том случае, если она параллельна любой прямой, находящейся в этой плоскости.
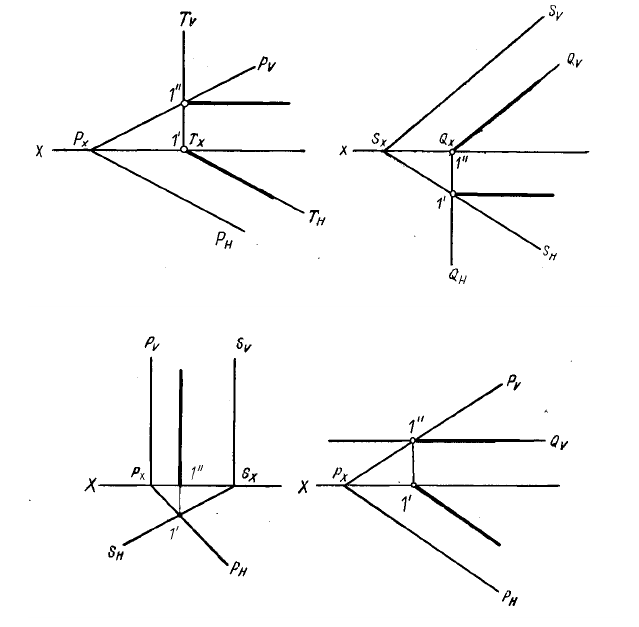
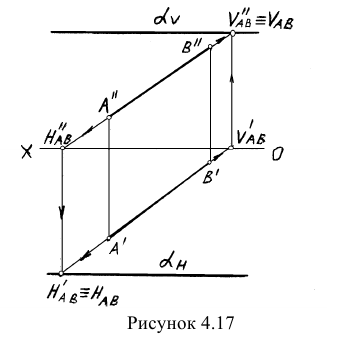
Пример: Через прямую АВ провести профильно-проецирующую плоскость (рисунок 4.17).
Решение: Как было показано ранее горизонтальный и фронтальный следы профильно-проецирующей плоскости располагаются параллельно оси ОХ. Было также показано, что если прямая принадлежит плоскости, заданной следами, то следы прямой находятся на одноименных следах плоскости. Сказанное позволяет разработать план решения задачи:
- Найдем горизонтальный и фронтальный следы прямой;
- Через найденные следы прямой проведем одноименные следы плоскости.
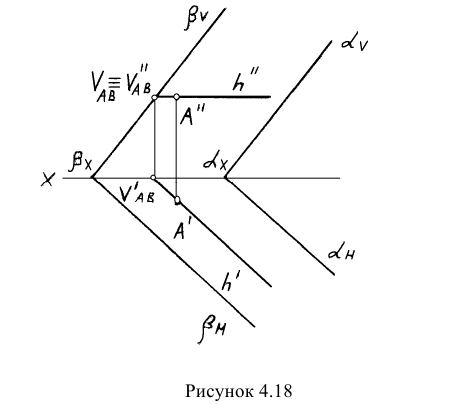
Пример: Через точку провести плоскость, параллельную заданной (рисунок 4.18).
Решение: Плоскость задана следами. Искомую плоскость целесообразно тоже задать следами. Чтобы обеспечить параллельность плоскостей, необходимо следы искомой плоскости провести параллельно одноименным следам заданной плоскости.
Для того чтобы искомая плоскость проходила через заданную точку, необходимо через точку провести прямую (например, горизонталь), которая принадлежала бы искомой плоскости. Исходя из изложенного, определяется следующий план решения задачи:
- Проводим через заданную точку горизонталь h;
- Через фронтальный след горизонтали проводим фронтальный след искомой плоскости параллельно фронтальному следу заданной плоскости;
- Горизонтальный след искомой плоскости проводим параллельно горизонтальному следу заданной плоскости.
- Через фронтальный след горизонтали проводим фронтальный след искомой плоскости параллельно фронтальному следу заданной плоскости;
- Горизонтальный след искомой плоскости проводим параллельно горизонтальному следу заданной плоскости.
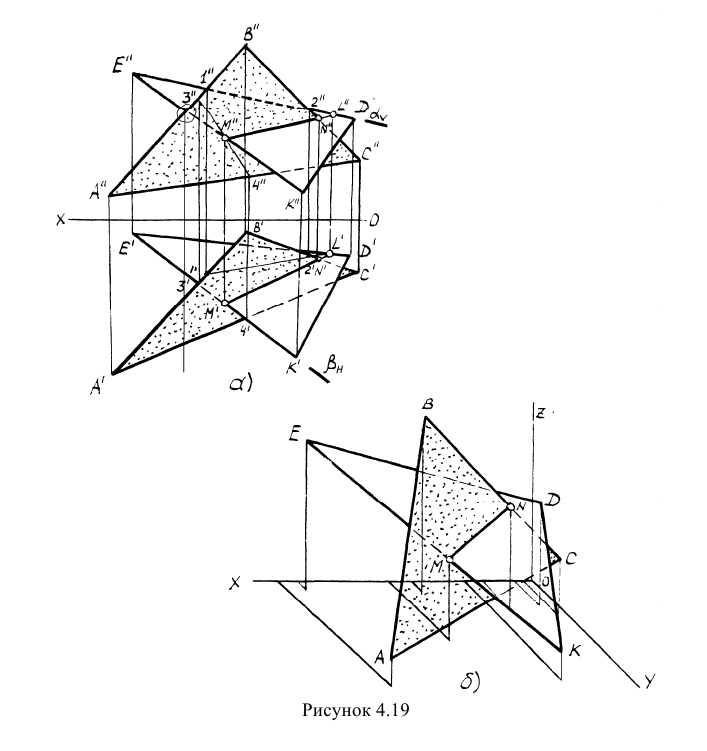
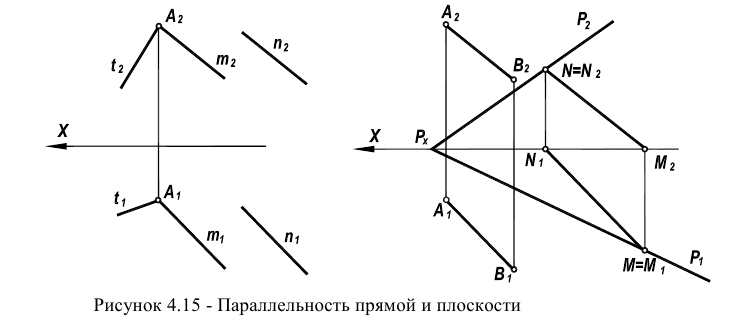
Пример: Построить линию пересечения треугольников АВС и EDK, определить видимость проекций (рисунок 4.19).
Построить линию пересечения треугольников АВС и EDK, определить видимость проекций (рисунок 4.19).
Решение: Предварительно намечаем две произвольные задачи на пересечение стороны одного треугольника с плоскостью другого (произвольно). Например,
Решаем первую задачу. Через ED проводим вспомогательную фронтально-проецирующую плоскость а (след плоскости 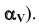
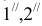
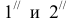
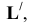
Аналогично решаем вторую задачу. В качестве вспомогательной плоскости берем горизонтально-проецирующую плоскость 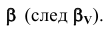
Далее соединяем полученные точки L и М. Однако не вся эта линия будет являться линией пересечения треугольников, а лишь участок MN, который принадлежит обоим треугольникам. Таким образом, в результате решения двух произвольно выбранных задач получили линию MN пересечения заданных треугольников.
Определяем видимость проекций треугольников. При определении видимости проекций методом конкурирующих точек (прямых) необходимо учитывать следующие особенности:
- Плоскости треугольников считаются геометрически непрозрачными;
- В точках М и N линии пересечения видимость сторон треугольников меняется;
- Если при вершине какого-либо треугольника одна сторона видна (не видна), то и другая сторона будет видна (не видна).
Учет перечисленных особенностей позволяет определить видимость проекций треугольников по анализу одного конкурирующего места на каждой проекции, что значительно ускоряет решение задачи.
Отметим на фронтальной проекции любое конкурирующее место из шести (отмечено кружочком). Проведем через него линию связи и вдоль линии связи сравним ординаты конкурирующих прямых ЕК и АВ. Наибольшую ординату имеет прямая АВ. Она и будет видна на рассматриваемой фронтальной проекции. Видимость остальных сторон треугольников определяется с учетом особенностей, отмеченных выше.
На горизонтальной проекции отметим конкурирующее место, в котором конкурируют прямые АВ и ED. Аналогично описанному определяем, что на горизонтальной проекции будет видна прямая АВ, так как у ней наибольшая аппликата. Видимость остальных сторон треугольников определим аналогично рассмотренному выше.
Для усиления эффекта видимости треугольников на проекциях целесообразно один их треугольников заштриховать с учетом видимости или раскрасить оба треугольника.
На рисунке 4.196 представлено наглядное аксонометрическое изображение пересекающихся треугольников в косоугольной фронтальной изометрии. Вершины треугольников строятся по заданным координатам точек, линия пересечения MN – по координатам, взятым с проекционного чертежа.
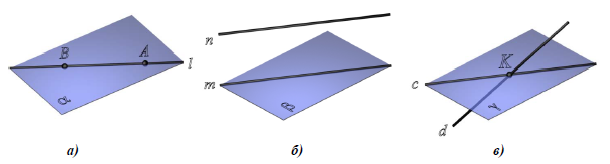
Относительное положение прямой и плоскости
Прямая по отношению к плоскости может занимать три различных
положения:
- • прямая l лежит в плоскости (рис. 8.1,а);
- • прямая n параллельна плоскости (рис. 8.1, б);
- • прямая d пересекается с плоскостью (рис. 8.1,в).
Рис. 8.1. Относительное положение прямой и плоскости:
а – l ⊂ α ; б – n || β ; в – d х γ
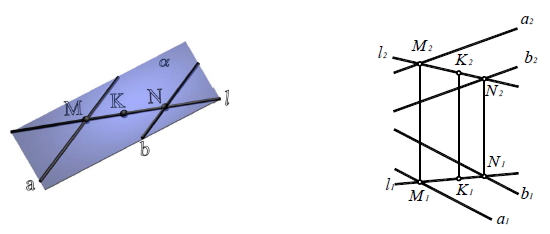
Принадлежность точки и прямой линии плоскости
Прямая линия принадлежит плоскости, если две точки этой прямой принадлежат плоскости (рис. 8.2).
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости (см. рис. 8.2).
Рис. 8.2. Принадлежность точки и прямой линии плоскости:
Параллельность прямой и плоскости
Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости (рис. 8.3).
Рис. 8.3. Параллельность прямой и плоскости:
Линии уровня плоскости
Прямые, лежащие в данной плоскости и параллельные одной из плоскостей проекций, называются линиями уровня плоскости.
Прямая, лежащая в данной плоскости и параллельная горизонтальной плоскости проекций П1, называется горизонталью плоскости (рис. 8.4). Все горизонтали плоскости параллельны между собой, поскольку каждая из них может быть получена как линия пересечения данной плоскости общего положения и горизонтальной плоскости уровня.
Рис. 8.4. Горизонтали плоскости:
Рассмотрим построение горизонтали плоскости общего положения α(ABC) (рис. 8.5,а).
Рис. 8.5. Линии уровня плоскости:
Фронтальная проекция любой горизонтали всегда перпендикулярна линиям связи, поэтому построение горизонтали начинается с построения ее фронтальной проекции h2 
Фронталь плоскости β( a||b )строится аналогично, но построение фронтали начинается с построения ее горизонтальной проекции (рис. 8.5,б). Все фронтали плоскости также параллельны между собой, поскольку каждая из них может быть получена как линия пересечения данной плоскости общего положения и фронтальной плоскости уровня.
Таким образом, любую плоскость общего положения можно представить как совокупность параллельных линий уровня – горизонталей, фронталей или профильных прямых. Иными словами, плоскость общего положения, заданную любым способом, можно также задать параллельными линиями уровня или пересекающимися горизонталью и фронталью. Такой способ задания плоскостей наиболее удобен для решения ряда метрических задач.
Пересечение прямой общего положения и плоскости частного положения
Рассмотрим построение точки пересечения K фронтально-проецирующей плоскости γ(γ2)
Рис. 8.6. Пересечение прямой общего положения и плоскости частного положения:
а- наглядное изображение;
б – комплексный чертеж
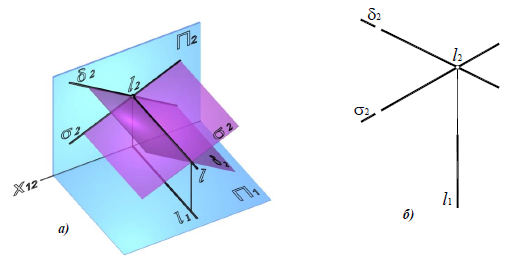
Пересечение двух плоскостей частного положения
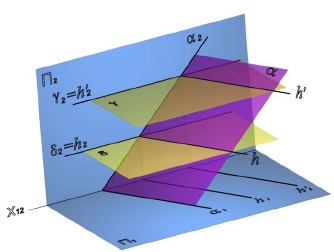
Линией пересечения двух фронтально-проецирующих плоскостей δ(δ2) и σ(σ2) является фронтально-проецирующая прямая l (рис. 8.7).
Рис. 8.7. Пересечение плоскостей частного положения:
а-наглядное изображение; б – комплексная проекция
линии пересечения двух фронтально-проецирующих плоскостей δ(δ2)и σ(σ2)определяется как точка пересечения фронтальных следов плоскостей δ2 и σ2: l2=δ2×σ2, а горизонтальная проекция строится по линии связи, перпендикулярно направлению оси x12.
Пересечение плоскости общего положения и плоскости частного положения
Линией пересечения двух плоскостей (рис. 8.8) является прямая, для построения которой достаточно определить две точки, принадлежащие обеим плоскостям одновременно.
Рис. 8.8. Пересечение плоскости общего положения с проецирующей плоскостью
а – наглядное изображение; б – комплексный чертеж
Рассмотрим построение линии пересечения l плоскости общего положения α(a×b) и фронтально-проецирующей плоскости δ(δ2)(рис. 8.8, б). Линия, по которой пересекаются две плоскости, принадлежит обеим плоскостям одновременно, следовательно, для ее построения достаточно определить две точки, общие для пересекающихся плоскостей, или одну точку и направление линии пересечения.
В данном случае, достаточно определить точки пересечения прямых а и b с плоскостью δ(δ2). Они однозначно определят линию пересечения l.
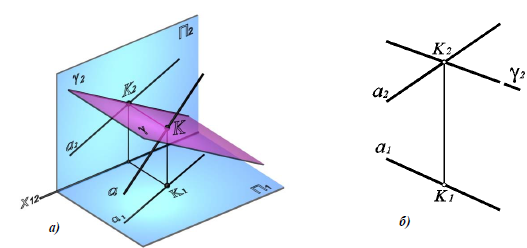
Пересечение прямой общего положения и плоскости общего положения. Первая позиционная задача
Задача об определении точки пересечения прямой общего положения с плоскостью общего положения называется первой позиционной задачей. На рис. 8.9 представлено наглядное изображение решения первой позиционной задачи.
Рис. 8.9. Пересечение прямой общего положения и плоскости общего положения
Дано: а(ABC) – плоскость общего положения;
a (a 1, a2) – прямая общего положения.
Определить: K=a×α(ABC).
Решение:
1. Прямую заключить во вспомогательную плоскость частного положения: αeβ.
2. Определить линию l как линию пересечения вспомогательной и заданной плоскостей l=α (ABC) 
3. Определить взаимное положение заданной прямой a и полученной прямой l.
Поскольку прямые a и l лежат в одной плоскости, они могут пересекаться или быть параллельными. Точка пересечения K=a×l и является искомой точкой пересечения прямой а с плоскостью α(ABC). Если прямые a и l параллельны, то прямая а параллельна плоскости α(ABC).
Определение точки пересечения прямой a(a1,a2) и плоскости α(ABC) на комплексном чертеже:
1. Заключить прямую a(a 1 ,а 2) во вспомогательную проецирующую плоскость β(β2) (рис. 8.10).
2. Определить линию пересечения l(1-2) вспомогательной плоскости β(β2) и заданной плоскости α(ABC):
l = α(ABC) 
Рис. 8.10. Пересечение прямой a(a1,a2 )и плоскости α( ABC)
3. Определить взаимное положение заданной прямой a и полученной прямой l. В данном случае, прямые а и lпересекаются в точке K, которая и является искомой точкой пересечения прямой a(a1,a2) и плоскости α(ABC):
11×a 1=K1; K2∈a2; K= a(a1,a2)×α(ABC).
4. Считая плоскость непрозрачной, определить видимость прямой a(a1 ,a2) относительно плоскости α(ABC)
Рис. 8.11. Определение видимости относительно горизонтальной плоскости проекций:
а – наглядное изображение;
б – комплексный чертеж
Для определения видимости относительно горизонтальной плоскости проекций необходимо найти конкурирующие точки – точки, горизонтальные проекции которых совпадают.
Прямые a и (AB) в пространстве являются скрещивающимися (точки пересечения проекций не лежат на одной линии связи), поэтому для определения видимости прямой относительно плоскости достаточно определить видимость прямой a относительно прямой (AB) (8.11). Для этого рассмотрим две конкурирующие точки: 4 – на прямой a и 5 – на прямой (AB). Высота точки 5 больше, следовательно, на П1 видима прямая (AB), то есть плоскость, а прямая a – невидима.
Рис. 8.12. Определение видимости относительно фронтальной плоскости проекций:
а – наглядное изображение; б – комплексный чертеж
Видимость прямой а по отношению к плоскости α(ABC) на фронтальной плоскости проекций (рис. 8.12) определяется с помощью конкурирующих точек 2на прямой (AC) и 3-на прямой а. Глубина точки 3 больше, следовательно, видима будет прямая а.
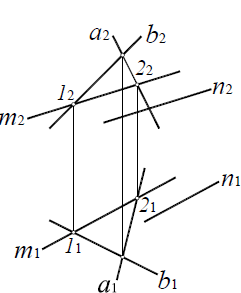
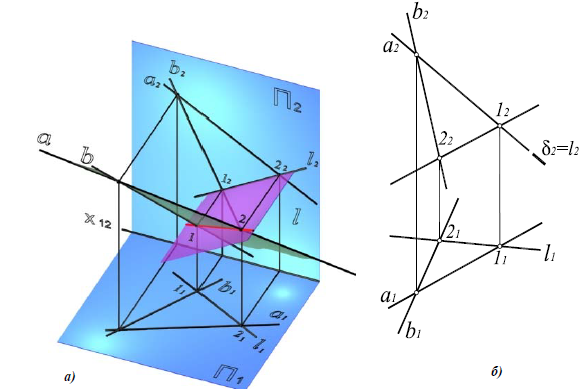
Пересечение двух плоскостей общего положения. Вторая основная позиционная задача
Вторая позиционная задача – это задача об определении линии пересечения двух плоскостей. Наглядное изображение решения второй позиционной задачи показано на рис. 8.13.
Рис. 8.13. Пересечение двух плоскостей общего положения
Алгоритм решения второй позиционной задачи состоит в следующем:
1. Заданные плоскости α(a||b) и β(c×d) пересечь вспомогательной плоскостью частного положения γ.
2. Определить линии пересечения m и n вспомогательной плоскости с каждой из заданных плоскостей:
γ 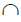
γ 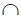
3. Определить точку M пересечения линий m и n. Точка M принадлежит прямой m, а, следовательно, и плоскости α (a||b). Точка M принадлежит прямой n, следовательно, и плоскости β(c×d). Таким образом, точка M принадлежит обеим плоскостям, то есть является одной из точек линии пересечения.
4. Вторую точку линии пересечения определяют аналогично, рассекая плоскости α(a||b) и β(c×d) вспомогательной плоскостью частного положения γ’.
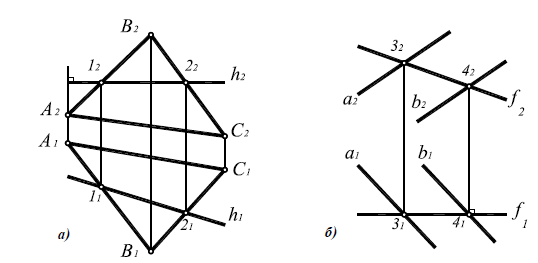
Определение линии пересечения двух плоскостей общего положения α(a||b) и β(c×d) на комплексном чертеже:
1. Пересечь данные плоскости вспомогательной фронтально-проецирующей плоскостью γ(γ2)
2. Определить линии пересечения вспомогательной плоскости с каждой из заданных плоскостей:
m =γ(γ2)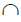
n =γ(γ2)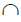
3. Определить точку пересечения прямых n и m:M=n× m.
4. Точка M ⊂ m 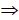
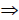
5. Точка M’ определяется аналогично, вспомогательной плоскости γ / (γ / 2).
Рис. 8.14. Вторая позиционная задача
6. Через полученные точки M и M’ провести прямую l. Прямая l -искомая линия пересечения плоскостей α( a || b) и β( c × d).
Сечение поверхности плоскостью
В сечении поверхности плоскостью получается плоская кривая линия, которую строят по отдельным точкам. Сначала строят опорные точки – точки смены видимости и экстремальные (крайние). Точки смены видимости принадлежат очерковым образующим поверхности. Экстремальными точками являются: самая близкая и самая удаленная, высшая и низшая и т. д. относительно плоскостей проекций.
Если проекция линии пересечения этими точками не определяется полностью, то строят дополнительные, промежуточные между опорными, точки. При построении сечений секущая плоскость обычно считается прозрачной и определяется только видимость поверхности и линии сечения.
Точка на поверхности
Точка принадлежит поверхности, если она принадлежит какой-либо линии на этой поверхности. Для построения точек на поверхности или определения недостающих проекций строится сечение поверхности вспомогательной плоскостью. Вспомогательная плоскость выбирается таким образом, чтобы в сечении получались простые линии – прямые или окружности. Кроме того, окружность в сечении должна проецироваться на одну из плоскостей проекций без искажения.
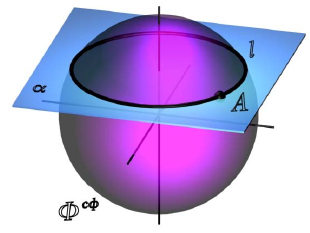
Рис. 8.15. Точка на поверхности сферы:
Любая плоскость рассекает поверхность сферы по окружности (рис. 8.15), но без искажения на соответствующую плоскость проекций проецируются только окружности, лежащие в плоскостях уровня. Таким образом, для построения точки на поверхности сферы в качестве вспомогательных плоскостей используются только плоскости уровня.
На поверхности конуса можно получить как окружности, так и прямые линии.
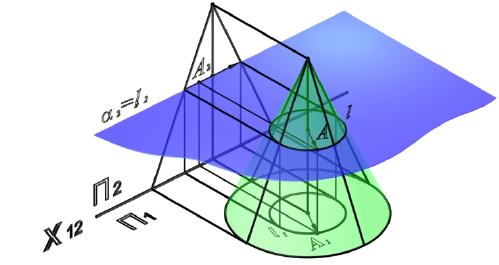
Для построения горизонтальной проекции точки A на поверхности конуса (рис. 8.16, 8.17), конус рассекается горизонтальной плоскостью уровня α(α2), проходящей через точку A.
В сечении конуса получается окружность радиуса r, которая проецируется на П1 без искажения – как окружность 11 с центром в точке 01 радиусом r1=r. Фронтальная проекция окружности -12 представляет собой отрезок [ 11 2 1].
Рис. 8.16. Точка на поверхности конуса
Рис. 8.17. Построение точки на поверхности конуса
Горизонтальная проекция точки A строится на пересечении вертикальной линии связи (A2A1) и окружности l1. При этом фронтальной проекции A2 могут соответствовать две точки – A и A’.
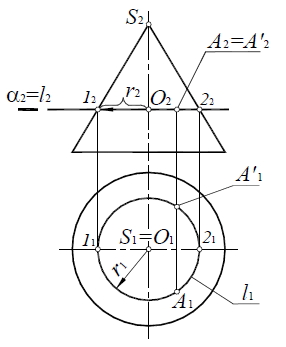
Поскольку любая плоскость, проходящая через вершину конуса, рассекает его по двум пересекающимся прямым, вспомогательную плоскость можно задать точкой A и осью вращения конуса (рис. 8.18).
Рис. 8.18. Точка на поверхности конуса
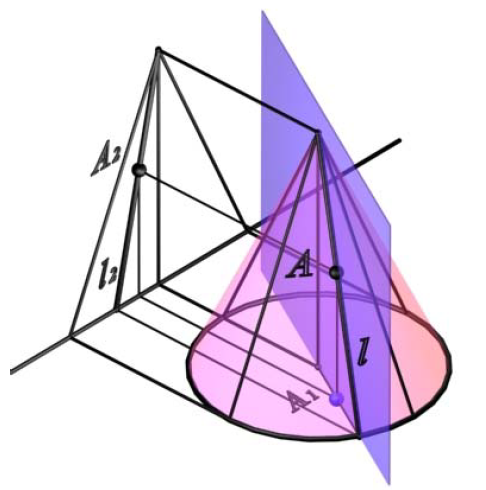
Если необходимо определить фронтальную проекцию точки A, принадлежащей поверхности конуса (рис. 8.19,а), конус рассекается вспомогательной горизонтально-проецирующей плоскостью β(A, i), проходящей через ось вращения конуса и искомую точку. Плоскость β(A, i) пересекает основание конуса в точке 1. Вершина конуса S и точка 1 определят образующую конуса l, проходящую через точку A:
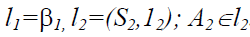
Рис. 8.19. Построение точки на поверхности конуса:
а – определение фронтальной проекции;
б – определение горизонтальной проекции
Если необходимо определить горизонтальную проекцию точки A, принадлежащей поверхности конуса (рис. 8.19,б), конус рассекается вспомогательной фронтально-проецирующей плоскостью γ(γ2) eS. Плоскость γ(γ2) пересекает основание конуса в точках 3 и 4. Вершина конуса S и точка 3 определят образующую конуса m, проходящую через точку A:
m2= γ2, m1=(S1,31); A1 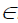
m’2=γ2, m’1=(S1,31); A’1βm , 1.
Таким образом, данной фронтальной проекции точки A2 могут соответствовать две точки – A и A / .
Сечение поверхности вращения плоскостью частного положения
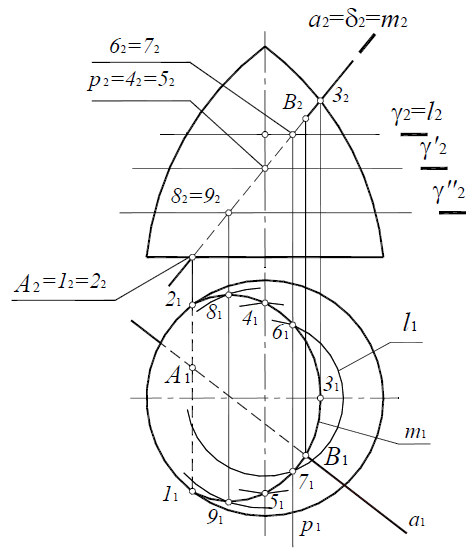
Рассмотрим построение линии пересечения поверхности закрытого тора с фронтально-проецирующей плоскостью μ(μ2) (рис. 8.20). Сначала определяются опорные точки: 1 и 2 – точки пересечения плоскости μ(μ2) с плоскостью основания тора, точка 3 – точка пересечения плоскости μ(μ2) с очерковой образующей тора.
Промежуточные точки 4 и 5 строятся при помощи вспомогательной плоскости уровня γ(γ2), которая рассекает поверхность тора по линии:
l=Ф m 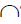
P=μ(μ2)nγ(γ2); p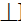
Точки 4 и 5 пересечения полученных линий принадлежат секущей плоскости μ(μ 2 ) и линии l поверхности тора, то есть принадлежат плоскости и поверхности одновременно, а следовательно, являются точками искомой линии пересечения m.
Точки 6, 7, 8 и 9 определяются аналогично. Полученные точки соединяют плавной лекальной кривой и определяют видимость линии пересечения m относительно поверхности.
Рис. 8.20. Сечение поверхности вращения плоскостью частного положения
При построении сечений поверхности плоскостью общего положения выполняют такое преобразование комплексного чертежа, при котором плоскость займет частное положение.
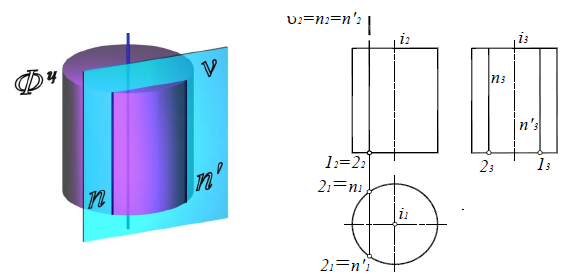
Цилиндрические сечения
В сечении цилиндрической поверхности вращения плоскостью могут быть получены следующие линии:
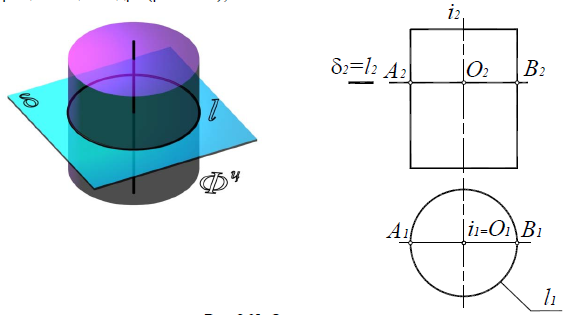
Окружность, если секущая плоскость δ(δ2) перпендикулярна оси вращения цилиндра (рис. 8.21);
Рис. 8.21. Окружность
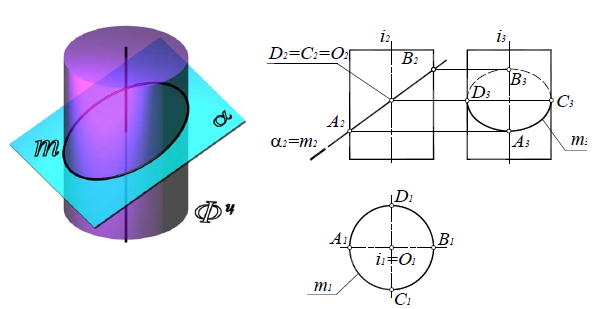
Эллипс, если секущая плоскость α(α2) наклонена под произвольным углом к оси цилиндра (рис. 8.22);
Рис. 8.22. Эллипс
Две параллельные прямые (образующие), если секущая плоскость ν(ν2)
параллельна оси цилиндра (рис. 8.23)
Рис. 8.23. Параллельные прямые
На плоскость, перпендикулярную оси вращения поверхности, окружность и эллипс на поверхности цилиндра проецируются в окружность, совпадающую с проекцией всей поверхности.
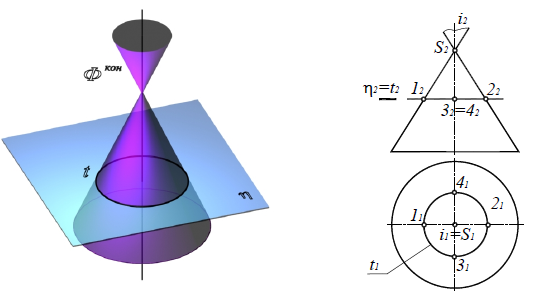
Конические сечения
Кривые линии, которые получаются в сечении прямого кругового конуса плоскостью, называются коническими сечениями. В зависимости от положения секущей плоскости по отношению к конической поверхности образуются
следующие линии:
Окружность, если секущая плоскость η(η2) перпендикулярна оси вращения конуса i (рис. 8.24).
Рис. 8.24. Окружность
Две пересекающиеся прямые, если секущая плоскость β(β2) проходит через вершину поверхности конуса (рис. 8.25).
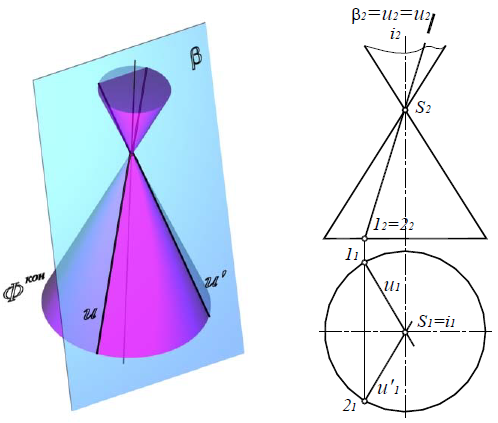
Рис. 8.25. Пересекающиеся прямые
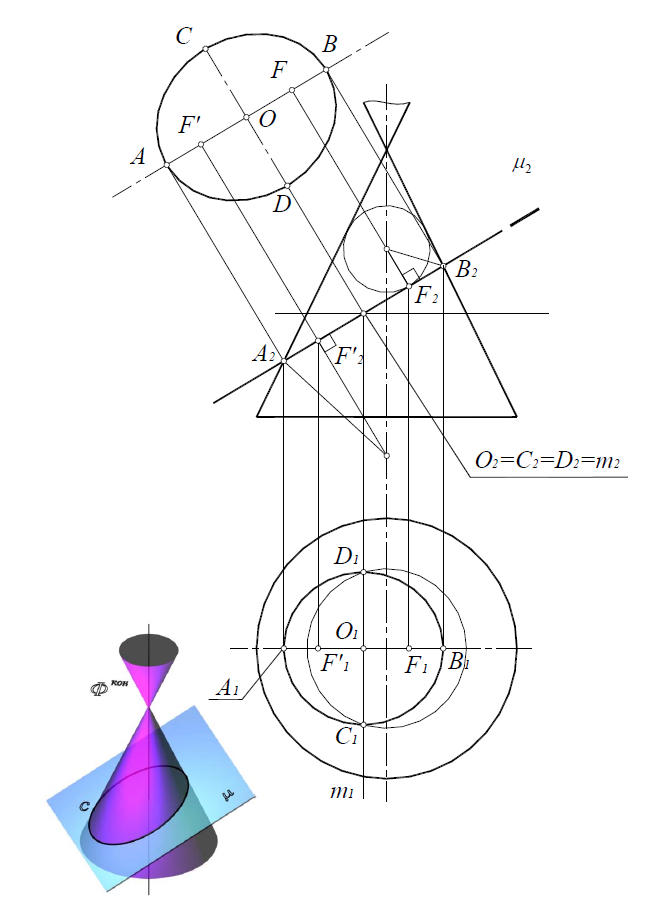
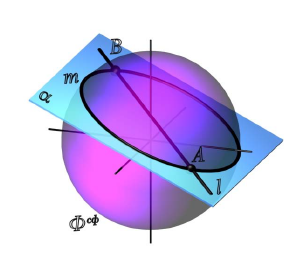
Эллипс (рис. 8.26), если секущая плоскость μ(μ2) пересекает все образующие, расположенные по одну сторону от вершины конуса.
Точки A и B являются опорными и не требуют дополнительных построений (см. рис. 95.). Отрезок [AB] определяет большую ось эллипса. Для определения малой оси отрезок [A2B2] делят пополам. Так получается центр эллипса – точка O. Затем через точку O проводят вспомогательную плоскость σ(σ2), которая пересекает поверхность конуса по окружности:
σ(σ2)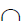
σ(σ2) 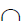
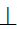
m1×l1=C1D1; [C1D1] – малая ось эллипса.
Для построения фокуса проводят биссектрису угла 
Свойство эллипса: сумма расстояний от любой точки эллипса до его фокусов есть величина постоянная и равна большой оси эллипса АВ=FP+F’P.
Рис. 8.26. Эллипс
Парабола (рис. 8.27), если секущая плоскость λ(λ2) параллельна одной из образующих поверхности конуса.
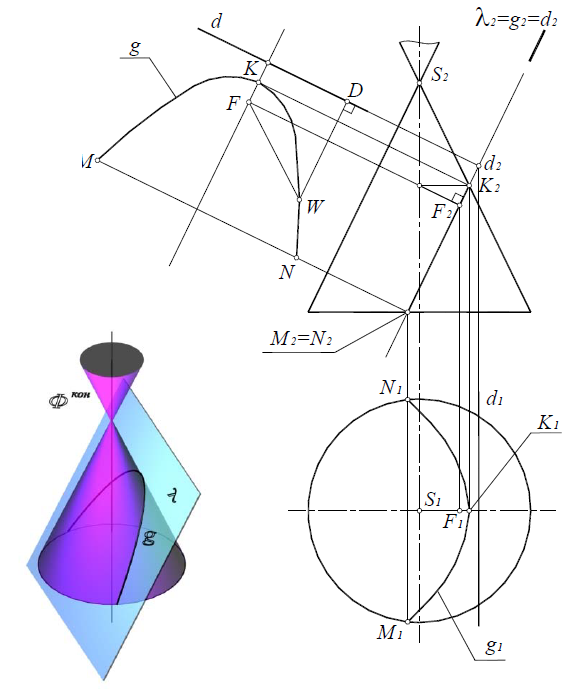
Рис. 8.27. Парабола
Точка К – вершина параболы (см. рис. 96). Точки N и Mлежат на основании. Фокус параболы строится при проведении биссектрисы угла 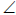

Свойство параболы: расстояние от любой точки параболы до ее фокуса равно расстоянию от этой точки до директрисы WD=WF.
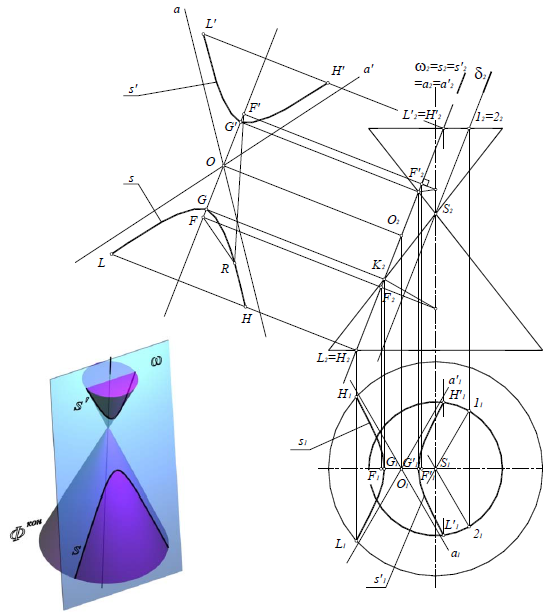
Гипербола (рис. 8.28), если секущая плоскость ω(ω2) пересекает обе половины поверхности конуса.
Рис. 8.28. Гипербола
При пересечении конуса образуются две части гиперболы 5 и 5′. G и G’ -вершины гиперболы, F(F 1, F2) и F'(F 1‘, F2) – фокусы гиперболы, O(O 1, O2) -центр гиперболы, а и a′ – асимптоты гиперболы, получающиеся как прямые, параллельные образующим конуса S1 и S2, полученным при рассечении его плоскостью δ(δ2),параллельной плоскостиω(ω2).
Свойство гиперболы: разность расстояний от любой точки гиперболы до ее фокусов есть величина постоянная, равная расстоянию между вершинами гиперболы RF-RF’=GG’.
Пересечение прямой с поверхностью
Прямая по отношению к поверхности может занимать следующие положения:
- прямая касается поверхности (одна общая точка);
- прямая пересекает поверхность (две и более общих точек);
- прямая не пересекает и не касается поверхности (общих точек нет).
Алгоритм решения задач об определении взаимного положения поверхности и прямой аналогичен решению первой позиционной задачи (рис. 8.29):
- Прямая заключается во вспомогательную плоскость частного положения.
- Определяется линия пересечения вспомогательной плоскости и заданной поверхности, то есть, строится сечение поверхности вспомогательной плоскостью.
- Определяется взаимное положение полученной линии (сечения) и заданной прямой. Точки пересечения являются искомыми точками пересечения прямой с поверхностью.
- Определяется видимость прямой относительно поверхности.
Рис. 8.29. Пересечение прямой с поверхностью
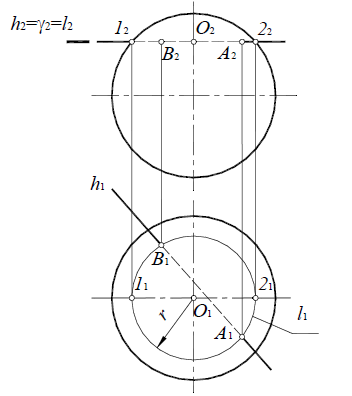
Для построения точки пересечения поверхности сферы с горизонталью (рис. 8.30), горизонталь заключают во вспомогательную горизонтальную плоскость уровня γ(γ2).
Сечение сферы горизонтальной плоскостью уровня представляет собой окружность l с центром в точке O2 и радиусом r=O2l2, которая проецируется на П1 без искажения. Затем определяются точки пересечения окружности l1 и заданной горизонтали h1 :
h 1×11=A1, B1; A2, B2∈h2.
Далее следует определить видимость прямой: между точками A и B прямая невидима на обеих проекциях, поскольку находится внутри сферы, фронтальная проекция горизонтали находится выше фронтальной проекции очерковой образующей сферы, поэтому горизонталь на П1 видима; точка A имеет большую глубину, чем очерковая образующая сферы, поэтому на фронтальной проекции горизонталь видима до точки A, а за точкой B – невидима.
Рис. 8.30. Пересечение прямой с поверхностью сферы
Для построения точки пересечения поверхности закрытого тора с прямой общего положения (рис. 8.31), прямую заключают во вспомогательную фронтально-проецирующую плоскость δ(δ2). Далее строится сечение тора плоскостью δ(δ2):
Точки 1 и 2 – точки пересечения с основанием и точка 3 – опорные точки на очерковой образующей определяются без дополнительных построений;
Точки 4 и 5 также опорные (лежат на образующих, проекции которых совпадают с осью тора). Точки 4 и 5 определяются как точки на поверхности тора с помощью вспомогательной плоскости γ’.
Промежуточные точки 6,7,8,9 определяются аналогично.
Полученные точки соединяются плавной лекальной кривой m. Линия m -сечение тора плоскостью δ(δ2). Затем определяют точки A и B пересечения полученной линии m с прямой a и определяют видимость. Точки A и B -искомые точки пересечения прямой с поверхностью тора.
Рис. 8.31. Пересечение прямой общего положения с поверхностью тора
2. m = δ(δ2)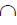
γ(γ2) – вспомогательная плоскость;
γ(γ2) 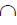
γ(γ2) 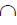
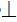
l×p = 6, 7 – промежуточные точки сечения m;
m×a = A, B – искомые точки пересечения прямой с поверхностью тора;
3. Определить видимость прямой относительно поверхности тора.
Принадлежность точки и прямой
Вопрос о принадлежности точки прямой решается на основе свойств (особенностей) метода проецирования. Точка С лежит на прямой АВ, если ее проекции, в соответствии с рисунком 4.2, лежат на одноименных проекциях Прямой
В геометрии принято считать, что прямая принадлежит плоскости, если две ее точки (действительные или несобственные) принадлежат этой плоскости (рисунки 4.3, 11.8)
В соответствии с рисунком 4.3 прямая AВ лежит в плоскости Р. Это обуславливается тем, что точка A лежит на следе 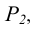
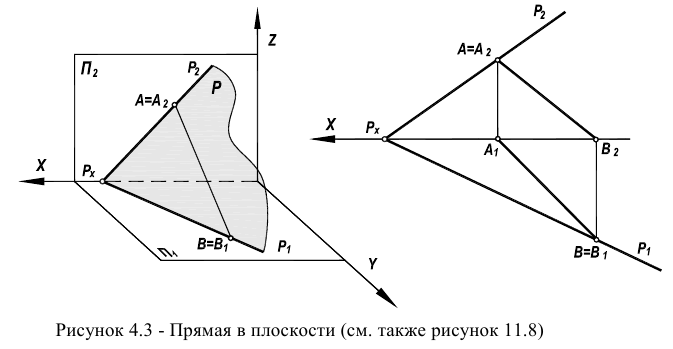
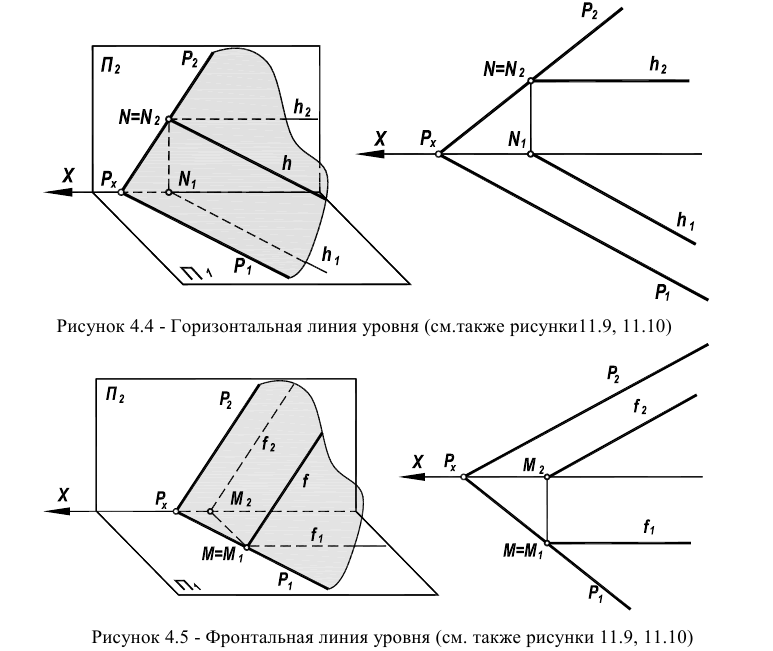
При условии, что одна из точек плоскости, через которые проходит прямая, лежит на следе и является несобственной (в соответствии с рисунками 4.4 и 4.5), прямая общего положения переходит в прямую частного положения (линию уровня).
В плоскости различают горизонтальную линию уровня h (рисунки 4.4, 11.9) и фронтальную линию уровня 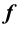
В силу специального расположения следов 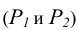
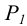
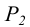
Фронтали и горизонтали плоскости получили название главных линии плоскости.
Вопрос о принадлежности точки плоскости можно свести к предыдущей задаче. Достаточно добиться того, чтобы точка лежала на одной из прямых плоскости (рисунки 4.6, 11.8)
Точка С лежит на прямой АВ (ее проекции, в соответствии с рисунком 4.2, лежат на одноименных проекциях прямой 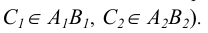
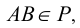
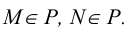
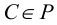
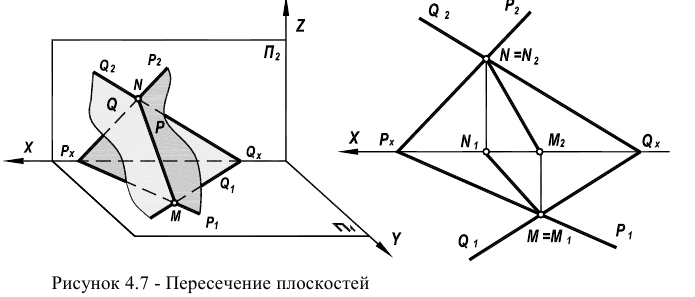
Пересечение плоскостей
В соответствии с формулой р=2+2-3=1 пересечение двух плоскостей должно привести к появлению одномерного объекта, т.е. прямой линии. Для построения линии пересечения двух плоскостей общего положения (Р и 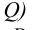
Пересечение горизонтальных следов 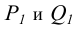
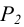
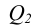
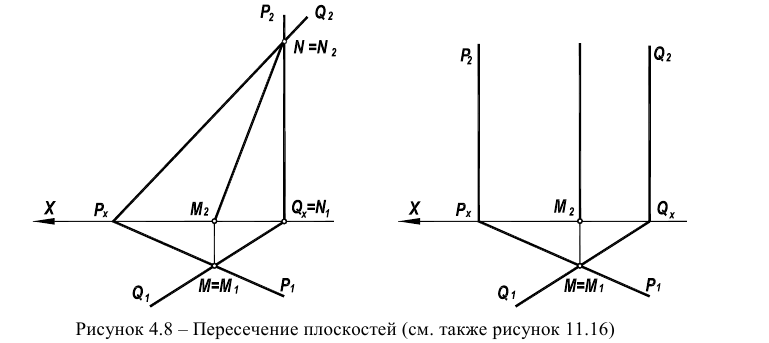
Если одна из плоскостей проецирующая (например, горизонтально-проецирующая, в соответствии с рисунком 4.8, 4.12), то линия пересечения 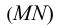
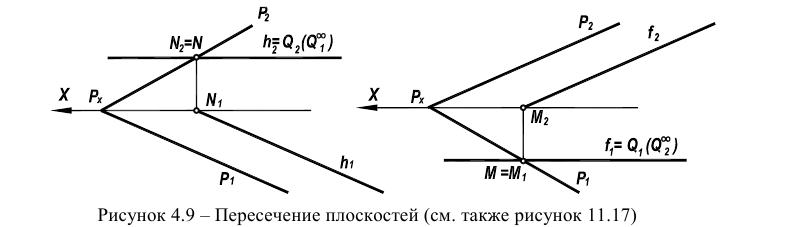
При пересечении плоскости общего положения плоскостью уровня в сечении получается соответствующая линия уровня (рисунок 4.9).
Определение линии пересечения двух плоскостей для других случаев, например, при задании плоскостей треугольником (симплексом) и параллельными прямыми, базируется на следующей идее. Три плоскости всегда пересекаются в одной точке. Следовательно, введение дополнительной плоскости к двум, уже имеющимся, позволит определить точку, одновременно принадлежащую заданным плоскостям. Проиллюстрируем это на рисунке 4.10.
Две плоскости, заданные параллельными и пересекающимися прямыми, пересекаются по прямой ЕК, найденной с помощью секущих плоскостей уровня S и Т. Плоскость S пересекает 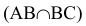
Пересечение прямой и плоскости
Пересечением прямой и плоскости в пространстве является точка, что подтверждается и вычислением по формуле р=1 +2-3=0.
Прямая L в пространстве (в соответствии с рисунком 4.11) может рассматриваться как результат пересечения проецирующих плоскостей 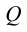
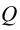
Восстановление одной из проецирующих плоскостей, например 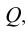
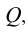
Аналогичное решение этой задачи и в случае задания плоскости Р треугольником (симплексом). Восстановление одной из проецирующих плоскостей (например, 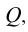
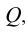
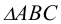
Параллельность
Частным случаем пересечения прямых и плоскостей является взаимная параллельность. В трехмерном пространстве отсутствует полная параллельность. Понятие параллельности вводится с помощью признаков (условий).
При параллельности пересечением является несобственный элемент.
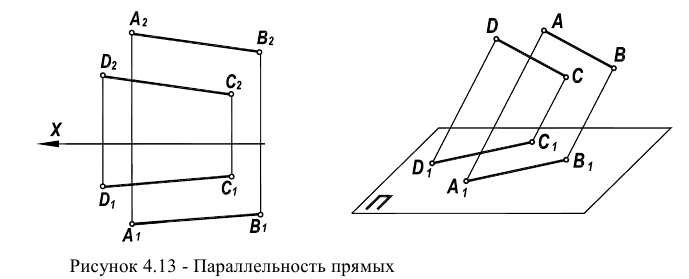
Признак параллельности прямых следует непосредственно из определения пересечения прямых (раздел 2.1). В соответствии с рисунком 4.13 одноименные проекции параллельных прямых попарно параллельны (параллельные прямые пересекаются в несобственной точке).
Признаком параллельности плоскостей является то, что две пересекающиеся прямые одной плоскости должны быть параллельны двум пересекающимся прямым другой плоскости (рисунок 4.14).
Такими прямыми могут быть следы. В этом случае одноименные следы должны быть параллельны между собой
В любом другом случае (в соответствии с рисунком 4.14) должна соблюдаться параллельность пересекающихся прямых, образующих плоскости, 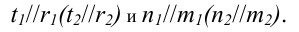
Параллельность прямой и плоскости должны отвечать следующему условию: прямая параллельна плоскости, если она параллельна одной из прямых этой плоскости. В соответствии с вышесказанным и рисунком 4.15 проекции
пространственной прямой должны быть параллельны соответствующим проекциям прямой, лежащей в плоскости.
Прямая n параллельна прямой m, лежащей в плоскости 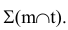
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Методы преобразования эпюра Монжа
- Касательные плоскости
- Пересечение поверхностей вращения плоскостью
- Виды, разрезы, сечения
- Метод замены плоскостей проекций
- Проецирование прямой линии
- Проецирование плоскости
- Плоскость на эпюре Монжа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Консультации по отчетам к практике, контрольные, курсовые
Линейная алгебра
http://www.tochkalubvi.ru купить вибратор – недорогие глубинные вибраторы купить.
Начертательная геометрия. Расчетно-графическая работа
Треугольник следов и его свойства. Теорема Польке.
Треугольник следов и его свойства.
В общем случае плоскость картины пересекает координатные плоскости по линиям, которые своими отрезками образуют так называемый треугольник следов (рисунок 11.3, 11.3а)
Рисунок 11.3 Рисунок 11.3а Проекции точки на три плоскости проекций. Октанты пространства В начертательной геометрии принято от пространственного изображения точки и ее проекций переходить к плоскому, или комплексному, чертежу, образованному вращением плоскости проекций вокруг осей проекций
Изображение имеет главную и вторичную проекции. Главной называется изображение А´ самой точки А; вторичной – изображение первичной проекции точки на какой – либо плоскости координат П1 П2 П3. Вторичных проекций может быть три, но преимущественно используется вторичная проекции на горизонтальной плоскости. При необходимости по главной и вторичной проекции могут быть построены и другие вторичные проекции на П2 и П3.
Таким образом, в аксонометрии имеется два поля проекций: поле главной и поле вторичной проекций. Обычно в начале строится вторичная проекция, а затем главная.
В этом плане аксонометрия не имеет принципиального отличия от ортогональных проекций, о чем свидетельствует решение задачи определения точки пересечения прямой АВ с плоскостью, заданной отсеком, аналогично решению в ортогональных проекциях (рисунок 11.4)
Аксонометрическое изображение (главная и вторичная проекции оригинала) с осями и масштабами являются обратимой проекцией и позволяет восстановить объект в пространстве.
При построении параллельной проекции можно произвольно выбрать плоскость проекций П´ и направление проецирования.
Очевидно, любое изменение взаимного положения осей координат и плоскости проекций и всякое изменение направления вызовет как изменение положения аксонометрических осей, так и коэффициентов искажения по ним.
Геометр прошлого века К. Польке в 1853г., изучая вопрос о том, в какой зависимости находятся направление аксонометрических осей и коэффициенты искажения по ним от направления проецирования и положения плоскости проекций, пришел к следующему выводу.
Три произвольно выбранные отрезка О´x´, O´y´, O´z´ (рисунок 11.1) на плоскости П´, выходящие из одной точки, представляют параллельную проекцию трех равных и взаимно перпендикулярных отрезков Ox, Oy, Oz, выходящих из некоторой точки пространства. Доказательство теоремы Польке приведено в курсе Е.А. Глазунова и Н.Ф. Четверухина «Аксонометрия» (Гостехиздат, 1953).
Эта теорема К. Польке имеет существенное значение как для аксонометрии, так и для многих ее приложений. На основании теоремы Польке системы аксонометрических осей, а так же отношение коэффициентов искажения по ним могут быть заданны совершенно произвольно.
Коэффициенты искажения пропорциональны соответственно отрезкам, изображающим аксонометрические оси. Действительно, отрезки О´x´, О´y´, О´z´, которые являются числителями дробей, определяющих коэффициенты искажений u, v, w, могут быть согласно теореме Польке выбраны произвольно. Но все эти три произвольно выбранных отрезка служат параллельной проекцией трех равных и взаимно перпендикулярных отрезков пространства. Пусть длина каждого из них равна m. Составив отношение u : v : w = : : и, заменяем Ох, Оу, Оz через m, получим: u : v : w = O´x : O´y´ : O´z´, что и доказывает пропорциональность коэффициентов искажения соответствующим отрезкам.
11.4. Прямоугольная аксонометрия и ее свойства.
Для того чтобы направление проецирования было перпендикулярно картине, ее плоскость должно быть расположена под какими – то углами к пространственным осям координат. В этом случае треугольник следов в прямоугольной аксонометрии всегда остроугольный, аксонометрические оси являются высотами этого треугольника и образуют между собой тупые углы (рисунок 11.5)
При решении ряда задач приходится определять натуральные размеры отдельных элементов изображенного объекта (длины отрезков, величины углов и пр.) или, наоборот, строить эти элементы по заданным условиям.
Метрические задачи в аксонометрии проще решать в том случае, если элемент тем или иным способом приведен в плоскость картины или в плоскость, параллельную ей. После операций, проделанных в плоскости картины, элемент надо привести в исходное положение. Наиболее распространенным и практически удобным способом является способ вращение до совпадения элемента с плоскостью картины или до положения, перпендикулярного к картине.
В первую очередь этот способ применяется для определения натуральных масштабов по произвольно выбраны аксонометрическим или, наоборот, для установления аксонометрических масштабов по натуральным точкам. Он так же используется для определения положения картины и направления проецирования по отношению к координатным плоскостям, если это требуется по ходу работы.
На рисунке 11.5 видно, что плоскость картины отсекает от координатных плоскостей треугольники, ограниченные двумя отрезками осей координат и стороной треугольника следов. Эти треугольники на картине проецируются искаженно, но сохраняют сторону треугольника следов.
Для нахождения натуральной величины этих треугольников, а следовательно, и отсеченных отрезков осей надо их совместить с плоскостью картине вращением вокруг следа картины; при этом точка О´ – проекция начала координат – будет перемещаться по перпендикуляру к стороне треугольника следов (следу плоскости Р) и расположится на дуге окружности, построенной на стороне треугольника следов, как на диаметре (рисунок 11.6 а).
На совмещенных треугольниках будут определяться истинные величины отрезков координатных осей, а следовательно, и натуральные масштабы, что позволит установить показатели искажения, т.е. отношения аксонометрических масштабов к натуральным.
Но может быть выполнен и обратный процесс – определение положения осей аксонометрии по данным натуральным масштабам и выбранным показателям искажения.
Для определения натуральной величины отрезка только одной оси аксонометрии Z и натурального масштаба по ней вращение производится вокруг этой оси Z (рисунок 11.6 б), и совмещенное положение точки О´ будет так же на окружности, построенной на отрезке В´1´ как на диаметре. Здесь, как и в первом совмещении, будут установлены натуральный размер отрезка оси Z, натуральный масштаб и величина «сжатия» фигур, лежащих в горизонтальной плоскости, а следовательно, и «коэффициент сжатия» в направлении, параллельном оси Z, т.е. высоты объекта. Коэффициент сжатия – отношение О´1´ : O´31´ в дальнейшем будет использована для решения позиционных и метрических задач, а так же для преобразования кривых 2-го порядка в более простые (окружности).
На изображения, выполняемые в аксонометрических проекциях, имеются ГОСТы (ГОСТ 2.317 – 69), которые рекомендую следующие виды аксонометрических изображений:
1. Два вида прямоугольных аксонометрических проекций (изометрию и диметрию).
2. Три вида косоугольных (фронтальную изометрию, горизонтальную изометрию, фронтальную диметрию).
[spoiler title=”источники:”]
http://www.evkova.org/pozitsionnyie-zadachi
http://arthis.ru/giperbol/piramida54.htm
[/spoiler]
§11. Построение линии пересечения двух плоскостей. (Вторая позиционная задача).
Результатом пересечения двух плоскостей является прямая . Для построения этой прямой достаточно найти две точки, принадлежащие обеим плоскостям и провести через них прямую линию.
Если мы возьмем прямую, принадлежащую одной плоскости и найдем точку ее пересечения с другой плоскостью, то эта точка будет общей для обеих плоскостей. Таким образом, построение линии пересечения двух плоскостей сводится к решению первой позиционной задачи, повторенному дважды.
Задача 11.1. Построить линию пересечения плоскости α, заданной треугольником АВС, и плоскости β, заданной двумя пересекающимися прямыми МЕ и МК (рисунок 11.1). Определить видимость плоскостей.
Решение.
1. Возьмем прямую АВ, принадлежащую плоскости α, и найдем точку ее пересечения с плоскостью β. Для этого заключим ее в проецирующую плоскость и найдем точку пересечения, используя алгоритм для решения первой позиционной задачи (см. §7).
На рисунке 11.2 продемонстрирован этот этап решения – точка N является точкой пересечения прямой АВ и плоскости β(МК, МЕ). В данном случае мы заключили прямую в фронтально-проецирующую плоскость ФП, прямая 1-2 является результатом пересечения плоскости ФП и плоскостиβ.
Не нужно забывать о том, что все точки на чертеже отображены в проекциях. Так, например, на рисунке 11.2. точка N представлена проекциями N1 и N2.
2. Возьмем прямую МК, принадлежащую плоскости β, и найдем точку ее пересечения с плоскостью α. Заключив ее в горизонтально-проецирующую плоскость, и проведя аналогичные построения, найдем точку L (рисунок 11.3).
3. Проведем прямую NL, являющуюся линией пересечения плоскостей α и β (рисунок 11.4).
4. Определяем видимость плоскостей (рисунок 11.5).
Применяем метод конкурирующих точек – для определения видимости на фронтальной проекции берем конкурирующие точки, проекции которых совпадают с точкой 22, для определения видимости на горизонтальной проекции берем точки с проекцией в 41. Конкурирующие точки 22 принадлежат фронтальной проекции АВ и МК. Пройдя по стрелке взгляда вниз, видим, что точка, лежащая на прямой АВ находится ближе к наблюдателю, так как у нее координата у больше, поэтому в районе проекции прямая АВ видимая, а МК – невидимая. Следовательно, проекция М2К2 в точке 22 меняет свой вид с видимой на невидимую.
Точка 41 лежит на горизонтальной проекции ВС и МК. Видимой будет та прямая, которая по стрелке взгляда находится выше на фронтальной проекции, в данном случае это прямая ВС.
Нужно обратить внимание на то, что прямые АВ и ВС меняют видимость в точках пересечения с прямой NL. Линия пересечения плоскостей всегда видимая.
На рисунке 11.6 показано окончательное решение задачи, для наглядности плоскости затонированы.
Задача 11.2. Построить линию пересечения плоскостей α и β, заданных следами (рисунок 11.7). Определить видимость плоскостей.
Решение.
Поскольку следы плоскости – это прямые, принадлежащие этой плоскости, а точки пересечения 1 и 2 одноименных проекций следов являются общими для обеих плоскостей, то очевидно, что результат пересечения плоскостей – это прямая, проходящая через эти точки. На эпюре Монжа определяем фронтальные и горизонтальные проекции точек 1 и 2 (рисунок 11.8).
Как видно на рисунке 11.8, горизонтальная проекция точки 1, являющейся точкой пересечения фронтальных следов α и β, а также фронтальная проекция точки 2 – лежат она оси х, поскольку сами прямые принадлежат плоскостям проекций. Соединив одноименные проекции точек 1 и 2, получим линию пересечения плоскостей (рисунок 11.9).
Определив видимость плоскостей в проекциях, получим окончательное решение задачи (рисунок 11.10)






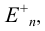
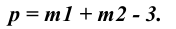
 (чаще всего проецирующую плоскость, заданную следами);
(чаще всего проецирующую плоскость, заданную следами);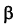 (линия 1-2);
(линия 1-2);