Вычисление пересекающихся интервалов в линейных и замкнутых пространствах имен
Время на прочтение
5 мин
Количество просмотров 44K
Здравствуйте! И сразу прошу прощение, за слишком мудрёное название, но оно наиболее полно отражает излагаемый ниже материал.
Я думаю многие из вас сталкивались с необходимостью вычисления пересекающихся интервалов. Но задача с которой я столкнулся на днях — оказалась не столь тривиальной. Но, обо всем по порядку.
Вычисление пересекающихся интервалов в линейном пространстве имен
Если у вас уже есть представление о пересечении интервалов, то пройдите сразу сюда.
Вычисление пересечений временных интервалов (отрезков времени) на прямой линии времени не составляет особого труда. Мы можем условно иметь пять видов временных пересечений.
Обозначим один отрезок времени как ” “, а другой “/ /”
- Смещение вперед по оси времени “/ / “
- Смещение назад по оси времени ” / /”
- Вхождение ” / / “
- Поглощение ” / / “
- Совпадение «X X»
Таким образом, мы можем выразить каждое конкретное пересечение с помощью знаков <, > и =. А имея в арсенале знаки <= и >= мы можем сократить количество шаблонов для вычисления до четырех (срастив, таким образом, «вхождение» и «совпадение» либо «поглощение» и «совпадение» или даже «смещние» и «совпадение»). Кроме того, либо «вхождение» либо «поглощение»(но не то и другое вместе) можно также упразднить, считая его частным случаем «смещения».
Итак, имея таблицу вида:
| user | start | end |
| user1 | 2 | 7 |
| user2 | 5 | 9 |
| user3 | 8 | 11 |
| user4 | 1 | 12 |
Для выборки из таблицы всех пользователей пересекающих заданный интервал (допустим 4-8), используем запрос:
SET @start:=4;
SET @end:=8;
SELECT * FROM `table`
WHERE
(`start` >= @start AND `start` < @end) /*смещение вперед*/
OR
(`end` <= @end AND `end` > @start) /*смещение назад*/
OR
(`start` < @end AND `end` > @start) /*вхождение - на самом деле здесь не обязательно оно обработается одним из предыдущих выражений*/
OR
(`start` >= @start AND `end` <= @end)/*поглощение и совпадение*/
Данный запрос вернет первого, второго и третьего пользователей. Всё довольно просто.
Хм. А что если нужно выбрать непересекающиеся интервалы?
На самом деле всё еще проще: в отличии от пересечения, случаев НЕпересечения всего два:
- Смещение назад ” / /”
- Смещение вперед “/ / “
а на непрерывной линии времени нам нужно лишь проверить меньше ли конец одного интервала, чем начало другого.
А занчит SQL запрос сводится к
SET @start:=4;
SET @end:=8;
SELECT * FROM `table`
WHERE
`start` >= @end OR `end` <= @start /*оба случая смещения*/
И вот тут мы вспоминаем про отрицания выражений. Если вычислять непересечения намного проще чем пересечения, то почему бы просто не отбросить все непересечения?
WHERE
NOT ( `start` >= @end OR `end` <= @start )
Раскрываем скобки (спасибо Yggaz ):
WHERE `start` < @end AND `end` > @start
Вуа-ля! Все намного лаконичнее!
Всё это очень прекрасно, и замечательно работает… пока линия времени прямая.
Вычисление пересекающихся интервалов в замкнутых пространствах имен
С вычислениями на линии времени мы разобрались. Так что же такое «замкнутое» пространство имен?
Это такое пространство имен, которое, при исчерпании имён первого порядка, не переходит на новый порядок а возвращается к своему началу.
Линейное пространство имен:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14,…
Замкнутое пространство имен:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3, 4,…
Предположим, что у нас есть таблица с расписанием графика работы (пусть это будет круглосуточный колл-центр):
*минуты «00» опущены для простоты выражений
| usrer | start | end |
| usrer1 | 0 | 6 |
| usrer2 | 6 | 12 |
| usrer3 | 12 | 18 |
| usrer4 | 18 | 23 |
Я работаю с 10 до 19 и хочу знать какие именно работники будут пересекать мой график работы.
Делаем выборку, заданной ранее схеме:
SET @start:=10;
SET @end:=19;
SELECT * FROM `table`
WHERE
NOT ( `start` >= @end OR `end` <= @start )
Все отлично! Я получил данные трёх работников, чей интервал пересекается с моим.
Ок, а если я работаю в ночь? Допустим с 20 до 6? То есть начало моего интервала больше его конца. Выборка из таблицы по этим условиям вернет полную ахинею. То есть крах случается, когда мой временной интервал пересекает «нулевую» отметку суток. Но ведь и в базе могут хранится интервалы пересекающие «нулевую» отметку.
С подобной проблемой я столкнулся два дня назад.
Проблема выборки интервалов по линейной методике из таблицы с данными нелинейной структуры была на лицо.
Первое, что мне пришло в голову — это расширить пространство суток до 48 часов, тем самым избавляясь от «нулевой» отметки. Но эта попытка потерпела крах — потому что интервалы между 1 и 3 никак не могли попасть в выборку между 22 и 27(3). Эх! Вот если бы у меня была двадцати-четыричная система счисления, я бы просто убирал знак второго порядка и все дела.
Я предпринял попытку найти решение этой проблемы в интернете. Информации по пересечению интервалов на «линейном» времени было сколько угодно. Но то ли этот вопрос не имел широкого обсуждения, то ли гуру SQL держали решение «для себя» — решения по замкнутой системе нигде небыло.
В общем, поспрашивав на форумах советов от гуру, я получил решение: нужно было разбить пересекающие «ноль» интервалы на две части, тем самым получив два линейных интервала, и сравнивать их оба с интервалами в таблице (которые тоже нужно было разбить на две части, если они пересекают ноль). Решение работало и вполне стабильно, хоть и было громоздким. Однако меня не покидало ощущение, что всё «намного проще».
И вот, выделив пару часов для этого вопроса, я взял тетрадь и карандаш… Привожу то, что у меня получилось:
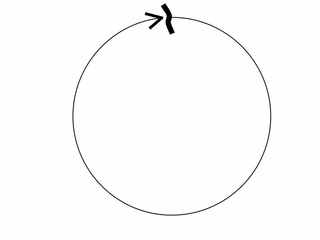
Суть в том, что сутки — есть замкнутая линия времени — окружность.
А временные интервалы — суть дуги этой окружности.
Таким образом, мы для отрицания непересечений (см. первую часть поста), можем построить пару схем непересечения:
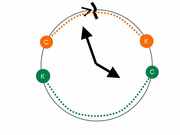
В первом случае мы имеем обычную линейную схему для отрицания непересечений. Во втором одна из дуг пресекает «нулевую» отметку. Есть и третий случай, который можно сразу принять как пересечение ( без отрицаний непересечения ):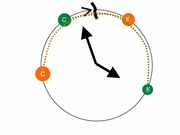
Оба интервала пересекают «нулевую» отметку, а значит пересекаются по определению. Кроме того, есть еще два случая, когда интервалы (вводимый и взятый из таблицы) «меняются» местами.
Немного наколдовав с базой (где-то даже методом высоконаучного тыка), мне удалось собрать вот такой запрос:
SET @start:= X ;
SET @end:= Y;
SELECT * FROM `lparty_ads`
WHERE
((`prime_start` < `prime_end` AND @start < @end)
AND NOT (`prime_end`<= @start OR @end <=`prime_start` )
OR
(( (`prime_start` < `prime_end` AND @start > @end) OR (`prime_start` > `prime_end` AND @start < @end))
AND NOT
( `prime_end` <= @start AND @end <= `prime_start` ))
OR (`prime_start` > `prime_end` AND @start > @end))
И упрощенный вариант из комментария от kirillzorin:
set @start := X;
set @end := Y;
select * from tab
where greatest(start, @start) <= least(end, @end)
or ((end > @start or @end > start) and sign(start - end) <> sign(@start - @end))
or (end < start and @end < @start);
Запрос вполне работоспособен и, что самое забавное, справедлив для любых замкнутых систем счисления — будь то час, сутки, неделя, месяц, год. А еще, этот метод не использует «костылей», вроде дополнительных полей.
Скорее всего, я изобрёл велосипед. Но ввиду того, что сам я не нашел подобной информации, когда она мне понадобилась — предполагаю, что этот метод не слишком широко освещен. На этом моё повествование заканчивается.
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given N intervals of the form of [l, r], the task is to find the intersection of all the intervals. An intersection is an interval that lies within all of the given intervals. If no such intersection exists then print -1.
Examples:
Input: arr[] = {{1, 6}, {2, 8}, {3, 10}, {5, 8}}
Output: [5, 6]
[5, 6] is the common interval that lies in all the given intervals.Input: arr[] = {{1, 6}, {8, 18}}
Output: -1
No intersection exists between the two given ranges.
Approach:
- Start by considering first interval as the required answer.
- Now, starting from the second interval, try searching for the intersection. Two cases can arise:
- There exists no intersection between [l1, r1] and [l2, r2]. Possible only when r1 < l2 or r2 < l1. In such a case answer will be 0 i.e. no intersection exists.
- There exists an intersection between [l1, r1] and [l2, r2]. Then the required intersection will be [max(l1, l2), min(r1, r2)].
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void findIntersection(int intervals[][2], int N)
{
int l = intervals[0][0];
int r = intervals[0][1];
for (int i = 1; i < N; i++) {
if (intervals[i][0] > r || intervals[i][1] < l) {
cout << -1;
return;
}
else {
l = max(l, intervals[i][0]);
r = min(r, intervals[i][1]);
}
}
cout << "[" << l << ", " << r << "]";
}
int main()
{
int intervals[][2] = {
{ 1, 6 },
{ 2, 8 },
{ 3, 10 },
{ 5, 8 }
};
int N = sizeof(intervals) / sizeof(intervals[0]);
findIntersection(intervals, N);
}
Java
import java.io.*;
class GFG
{
static void findIntersection(int intervals[][], int N)
{
int l = intervals[0][0];
int r = intervals[0][1];
for (int i = 1; i < N; i++)
{
if (intervals[i][0] > r ||
intervals[i][1] < l)
{
System.out.println(-1);
return;
}
else
{
l = Math.max(l, intervals[i][0]);
r = Math.min(r, intervals[i][1]);
}
}
System.out.println ("[" + l +", " + r + "]");
}
public static void main (String[] args)
{
int intervals[][] = {{ 1, 6 },
{ 2, 8 },
{ 3, 10 },
{ 5, 8 }};
int N = intervals.length;
findIntersection(intervals, N);
}
}
Python
def findIntersection(intervals,N):
l = intervals[0][0]
r = intervals[0][1]
for i in range(1,N):
if (intervals[i][0] > r or intervals[i][1] < l):
print(-1)
else:
l = max(l, intervals[i][0])
r = min(r, intervals[i][1])
print("[",l,", ",r,"]")
intervals= [
[ 1, 6 ],
[ 2, 8 ],
[ 3, 10 ],
[ 5, 8 ]
]
N =len(intervals)
findIntersection(intervals, N)
C#
using System;
class GFG
{
static void findIntersection(int [,]intervals, int N)
{
int l = intervals[0, 0];
int r = intervals[0, 1];
for (int i = 1; i < N; i++)
{
if (intervals[i, 0] > r ||
intervals[i, 1] < l)
{
Console.WriteLine(-1);
return;
}
else
{
l = Math.Max(l, intervals[i, 0]);
r = Math.Min(r, intervals[i, 1]);
}
}
Console.WriteLine("[" + l + ", " + r + "]");
}
public static void Main()
{
int [,]intervals = {{ 1, 6 }, { 2, 8 },
{ 3, 10 }, { 5, 8 }};
int N = intervals.GetLength(0);
findIntersection(intervals, N);
}
}
PHP
<?php
function findIntersection($intervals, $N)
{
$l = $intervals[0][0];
$r = $intervals[0][1];
for ($i = 1; $i < $N; $i++)
{
if ($intervals[$i][0] > $r ||
$intervals[$i][1] < $l)
{
echo -1;
return;
}
else
{
$l = max($l, $intervals[$i][0]);
$r = min($r, $intervals[$i][1]);
}
}
echo "[" . $l . ", " . $r . "]";
}
$intervals = array(array(1, 6), array(2, 8),
array(3, 10), array(5, 8));
$N = sizeof($intervals);
findIntersection($intervals, $N);
?>
Javascript
<script>
function findIntersection(intervals, N)
{
let l = intervals[0][0];
let r = intervals[0][1];
for (let i = 1; i < N; i++)
{
if (intervals[i][0] > r ||
intervals[i][1] < l)
{
document.write(-1 + "</br>");
return;
}
else
{
l = Math.max(l, intervals[i][0]);
r = Math.min(r, intervals[i][1]);
}
}
document.write("[" + l +", " + r + "]" + "</br>");
}
let intervals = [[ 1, 6 ],
[ 2, 8 ],
[ 3, 10],
[ 5, 8 ]];
let N = intervals.length;
findIntersection(intervals, N);
</script>
Time Complexity: O(N), where N is the size of the given 2D-array
Auxiliary Space: O(1), no extra space is required, so it is a constant.
Last Updated :
15 Nov, 2022
Like Article
Save Article
Операции над числовыми промежутками.
Операций над промежутками совсем немного. Всего две. Это пересечение и объединение. При решении серьёзных заданий с неравенствами эти две операции над промежутками необходимо проделывать постоянно. В самых разных сочетаниях. По своей сути это очень простые операции. Но, справедливости ради, эти самые операции являются вторым источником досадных ошибок при решении неравенств после тождественных преобразований. Разберёмся?
Пересекать и объединять числовые промежутки, проще всего при помощи числовой оси. Начнём с пересечения, оно хоть и проще в визуальном восприятии, но простора для ошибок даёт больше…
Как пересекать промежутки?
Сама по себе операция пересечения промежутков совсем простая. Тем не менее, именно пересечение промежутков — самая богатая на сюрпризы операция, которая столько людей ушибла! И очень больно ушибла. Но мы-то с вами — люди думающие и осторожные! С сюрпризами разберёмся, да и под ноги смотреть будем.) И не споткнёмся на ровном месте.
Итак, для начала запоминаем:
Пересечением двух числовых промежутков называется их общая часть.
И всё! Смутить могут только слова “общая часть”. Всё просто. Общая часть — это те точки (или кусочки оси), которые одновременно входят в каждый из промежутков. Слова “общая часть” и “одновременно” здесь синонимы. Если раз и навсегда разобраться в этих нехитрых словах, то при ответе на любой вопрос о пересечении любых промежутков вы даже не заметите проблем! Намёк понятен?)
Возможно, вы до сих пор в сомнениях, но картинка с числовой осью, наш главный помощник, всё сразу же прояснит! Это только на конкретных примерах показать можно.
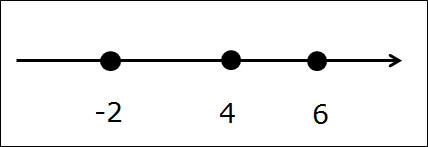
Начнём с совсем простенького, безо всяких подводных камней в виде выколотых точек. Допустим, нам надо пересечь два промежутка:
[-2; 6]
и
[4; +∞)
Первым делом рисуем числовую ось, отмечаем все граничные точки правильными кружочками. Они здесь — чёрные:
Вот так. Следующим шагом подштриховываем оба промежутка на одной оси. Чтобы не запутаться, для отличия пользуемся штриховкой с разных сторон оси в разных направлениях. Не нужно ювелирно штриховать по линеечке, мы не на черчении. Штрихуем грубо, брутально, но — разборчиво. Где-то штриховки будут встречаться одна под другой, образуя “ёлочку”, но ничего не смущаемся, это — именно то, что нам и нужно! Получим такую картинку:
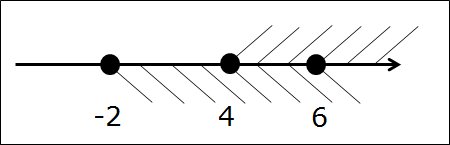
А теперь смотрим и соображаем: какой кусочек числовой оси подштрихован обоими видами штриховки одновременно? Верно! Кусочек между точками 4 и 6. Или — промежуток [4; 6]. Этот промежуток и будет пересечением промежутков [-2; 6] и [4; +∞). И все дела.)
Математически результат пересечения оформляют вот так:
[-2; 6] ⋂ [4; +∞) = [4; 6]
Значок “⋂” означает “пересечение”.
Разбираем следующий пример. Пример совсем безобидный, но ступор у некоторых случается, да…)
Пересечём, например, промежутки:
[-2; +∞)
и
[4; 6]
Как видим, граничные точки (те, что будем рисовать на оси) остались прежними — это -2, 4 и 6. Кружочки также не поменялись, так и остались чёрными. Только сами промежутки — другие.
Рисуем. В этот раз я буду использовать второй способ рисования — дужки. Получим такую картинку:
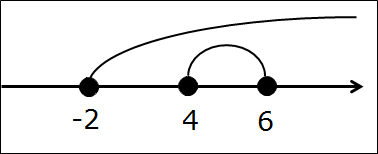
И опять соображаем: какой кусок оси содержит точки обоих промежутков одновременно?
Не догадались? Тогда снова штрихуем промежутки в разных направлениях, прямо под дужками. И смотрим, где штриховки накладываются:
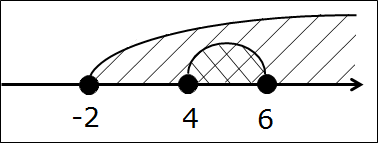
Ну и как, осенило? Да! Второй промежуток [4; 6] — и есть наше пересечение (т.е. общая часть)! Да, весь целиком. Дело всё в том, что второй промежуток, [4; 6], целиком содержится в первом [-2; +∞). Ничего страшного, так бывает.
В математической форме:
[-2; +∞) ⋂ [4; 6] = [4; 6]
Уловили идею? Ну-ка, быстренько закрепим успех!
Найдите пересечения следующих числовых промежутков:
(-∞; -3] ⋂ [-4; +∞) =
[1; 7] ⋂ [5; 10] =
[0; 8] ⋂ [1; 4] =
(-∞; 0] ⋂ [-1; 0] =
Ответы (в беспорядке):
[1; 4]
[-4; -3]
[-1; 0]
[5; 7]
Что, примитив? Ну да, проще некуда. А вот сейчас начинаются первые сюрпризы! Я же обещал…)
Сюрприз первый — пустое множество
Попробуем пересечь, скажем, такие два промежутка:
(-∞; 1] ⋂ [2; +∞)
Дело нехитрое. Рисуем ось, точки-кружочки, помечаем дужками каждый промежуток, штрихуем, всё чин-чинарём…
Получаем картинку:
И? Где здесь общая часть? А нигде! Нету такого кусочка оси, который был бы закрашен разными штриховками одновременно. На нет и суда нет. В таких случаях говорят, что данные промежутки не пересекаются.
Математически эта фишка записывается вот как:
(-∞; 1] ⋂ [2; +∞) = Ø
Этот перечёркнутый кружочек означает “пустое множество”. Множество, в котором нет ни одного элемента. Ни одного числа… Очень частое явление. Особенно — при решении систем неравенств.
Сюрприз второй — изолированная точка
Всё то же самое, что и в предыдущем примере, только двойку во втором промежутке заменю на единичку. Вот так:
(-∞; 1] ⋂ [1; +∞)
Делать нечего, опять рисуем ось. В этот раз рисуем одну единственную точку 1. Закрашенную.
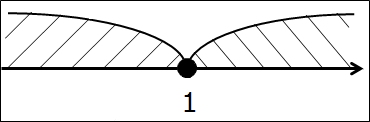
А здесь какие мысли насчёт пересечения? Да! Единственная общая часть — точка 1. Одна точка. Любая другая точка — правее ли единички, левее ли — попадает лишь в один из пересекаемых промежутков. Либо только в левый, либо только в правый. И только лишь единичка попадает в оба промежутка сразу.
В таких случаях результат пересечения (одна точка) оформляют так:
(-∞; 1] ⋂ [1; +∞) = {1}
Фигурные скобочки в такой записи означают множество. Числовое множество. Единичка внутри фигурных скобок — элемент этого множества. Один-единственный. Или — изолированная точка.
Не следует думать, что пустое множество и изолированная точка –такая уж экзотика при решении неравенств. Такие сюрпризы попадаются в системах неравенств, в методе интервалов, в нахождении области определения функции, в уравнениях/неравенствах с модулем и прочих серьёзных темах. В соответствующих уроках убедимся.)
Кто читает вдумчиво, тот заметил, что слово “множество” я употребил в этом уроке уже не один раз. И это неспроста. Дело в том, что числовые промежутки и операции над ними — это знакомство с ещё одним новым разделом математики, помимо неравенств. Раздел называется “Теория множеств” и работает именно с множествами объектов самой разной природы. Числовыми промежутками, в том числе. Но множества — отдельная большая тема. Не в этот раз…
Полдела сделано. Можно заниматься наскальной живописью. Что-то типа такого:
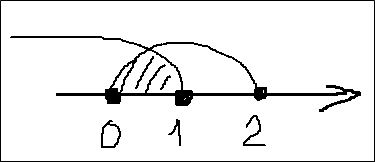
Несведущий человек отшатнётся в ужасе. А сведущий сразу твёрдой рукой напишет:
(-∞; 1] ⋂ [0; 2] = [0; 1].
Так обычно оформляют пересечение промежутков в большинстве школ. Рисуют ось, штрихуют промежутки, ищут общую часть, да и записывают ответ. Такой способ хорош только в самых простых случаях. Пока точки — чёрные.
Проблемы начинаются с появлением выколотых точек.
Как работать с выколотыми точками?
Как только в игру вступают выколотые (т.е. незакрашенные) точки, вся простота куда-то испаряется напрочь… Особенно, если одна и та же точка в разные промежутки входит по-разному. Где-то она выколота, где-то закрашена… И в каком виде рисовать её на одной оси? Закрашивать её или нет?! Вот и путается народ…
Более того, обратите внимание! Во всех примерах этого урока мы пересекаем лишь два промежутка. Для простоты и понимания сути. А в более продвинутых заданиях (системы неравенств, нахождение ОДЗ и прочие крутые штучки) приходится пересекать и три, и пять… И все с разными кружочками и скобочками… Как не запутаться?
Есть, есть один секретный способ не запутаться! Но о нём — в конце урока.
А пока фиксируем в памяти одну простую вещь:
Операция пересечения — штука жёсткая. Если точка НЕ входит хотя бы в ОДИН из пересекаемых промежутков, то она автоматически НЕ входит и в окончательный результат пересечения.
Поясняю. Если какая-то точка хотя бы в одном из промежутков является выколотой, то нас уже не волнует, что там у неё с остальными промежутками (вторым, третьим, пятым…) — входит она в них или нет: в окончательный ответ такая точка УЖЕ не войдёт. Типа, даже если вы положили в борщ картошку, морковку, свёклу, лук, но в конце посолили стиральным порошком, кушать такой борщ вы уже не будете, да…) Уловили?
Разберём ценные зелёные слова на практике. Был у нас в самом начале урока примерчик:
[-2; 6] ⋂ [4; +∞)
А теперь я немного видоизменю в нём один из промежутков. Сделаю во втором промежутке точку 4 выколотой. Т.е. скобочка перед четвёркой станет круглой. Вот такое пересечение теперь рассмотрим:
[-2; 6] ⋂ (4; +∞)
Рисуем, штрихуем, получаем картинку:
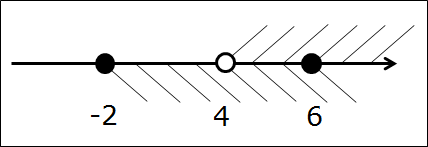
Ищем общую часть, записываем ответ:
[-2; 6] ⋂ (4; +∞) = (4; 6]
Стоп! Внимание!
Задаю вам ключевой вопрос: Почему четвёрка не вошла в окончательный ответ (4; 6], а шестёрка – вошла?
Кто в теме и врубился в слова “общая часть” и “одновременно”, тот сразу всё понял. А кто не в теме, то… начинаем рассуждать. Примерно так:
“Так, берём первый промежуток (-2; 6]. Входит туда четвёрка? Разумеется! Раз уж она строго между -2 и 6. А во второй (4; +∞)? Э-э-э-э… нет! Скобочка там — круглая! Входит ли в таком случае четвёрка одновременно в оба промежутка? Нет! Во второй не вошла. Пересечение — штука жёсткая… Стало быть, и в результат пересечения четвёрка также не входит. Рисуем круглую скобочку: (4; …
А шестёрка? Тут без вопросов: в первый промежуток число 6 попадает на границу, но в закрашенном виде, а во второй (4; +∞) входит явно. Входит одновременно в оба? Да! Рисуем квадратную скобку: …6].
Итого: (4; 6].“
Вот так. Я же говорил, что ключевое слово здесь — одновременно!
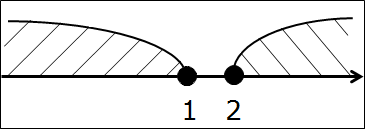
Здесь-то ещё просто. А бывает куда злее! Когда неясно, как даже рисовать картинку-то… Например:
(-∞; 1) ⋂ [1; +∞)
Всё как обычно, рисуем прямую и отмечаем одну единственную граничную точку 1.
И… что-то не рисуется… В первом промежутке единичка с круглой скобкой, во втором — с квадратной. А ось — одна… Каким именно кружочком — пустым или закрашенным — рисовать единицу на оси? Непонятно…
Непонятно, если не понимать сути операции пересечения. А если понимать, то проблем — никаких. Наша граничная точка 1 в первый промежуток (-∞; 1) не входит. Выколота. Стало быть, при пересечении нам уже без разницы, закрашена ли единица во втором промежутке [1; +∞): в окончательный ответ она УЖЕ не войдёт!
Вывод: на оси точка 1 изображается выколотой. Т.е. незакрашенной.
Вот так:
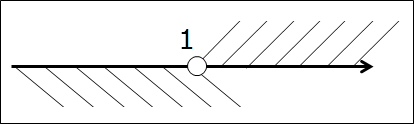
Штриховки нигде не накладываются, а единственная разделяющая точка 1 — выколота. Ответ очевиден — пустое множество:
(-∞; 1) ⋂ [1; +∞) = Ø
Обычно именно так и поступают со всеми подозрительными точками. Берут конкретную точку, поочерёдно подставляют её в каждый из промежутков, анализируют, входит/не входит, и если хоть куда-то не входит — вычёркивают отовсюду. Так рисуются все белые точки. Потом собирают все точки, которые входят одновременно во все промежутки. И рисуют чёрными… И только потом рисуют окончательную картинку… Кошмар? Согласен, кошмар. Когда ось только одна, а точек разной раскраски — много.
Поэтому сейчас мы отдохнём от писанины и тягостных раздумий. А вместо этого — порисуем. Рисовать будем много, но зато результат окупится с лихвой. А количество ошибок резко сократится.)
Обещанный секретный способ!
Пересекаем промежутки без ошибок! Метод параллельных осей.
Итак, снова пересекаем те же самые промежутки: [-2; 6] ⋂ (4; +∞).
Сейчас берём в руки карандаш и рисуем… три параллельные оси! Всё правильно, именно три, я не обсчитался. На первых двух осях отдельно рисуем и штрихуем те промежутки, которые будем пересекать. Т.е. [-2; 6] и (4; +∞). На каждой из осей — свой. Соблюдаем одинаковый масштаб по всем трём осям! Это важно. Зачем нужна третья ось? Сейчас узнаем.) Получим такую картинку:
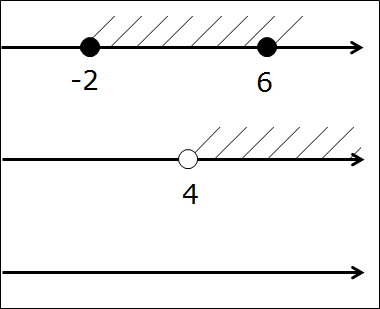
А вот теперь — самое интересное! Настал черёд третьей, пустой (пока) оси. Сейчас делаем вот что. Все граничные точки начинаем проецировать на третью ось. Как? Через все граничные точки всех промежутков проводим вертикальные прямые. Прямо насквозь. А на третьей оси — делаем засечки в виде соответствующих точек. Представьте себе, что первые две оси мы просвечиваем рентгеном, а на третьей оси у нас снимок в виде всех “засветившихся” точек.) А это -2, 4 и 6. Других точек нет.
Представили? Вот так:
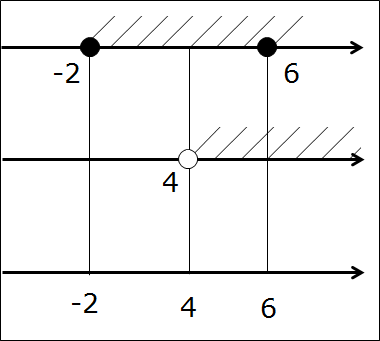
Следующим этапом фиксируем все точки соответствующими кружочками на первых двух осях. Принцип простой. Попала точка в промежуток (заштрихованную область) — значит, чёрная. Не попала — выколотая. Получаем ещё три кружочка — один белый (точка -2 на второй оси) и два чёрных (точка 4 на первой оси и точка 6 на второй). Вот так:
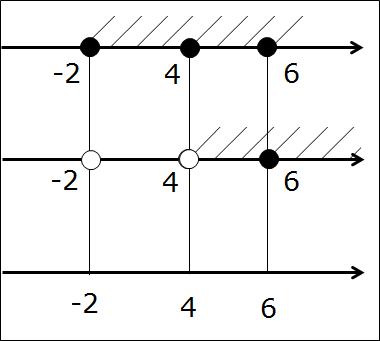
А нужны они нам — эти кружочки-то?! Ещё как! Самый ответственный, третий этап — рисуем нужные кружочки на третьей оси. Для этого рассуждаем так же, как и при прикидке в уме: если на первых двух осях обе точки чёрные, то и на третьей оси точка также чёрная. Если же хоть одна из двух точек выколота — на третьей оси точка также выколота!
Картинка станет вот такой:
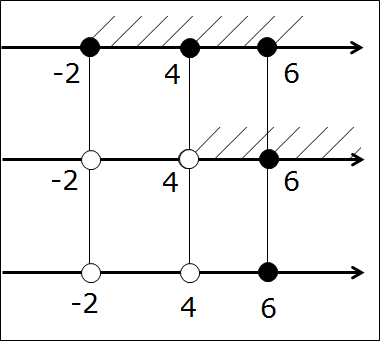
Остались пустяки. Четвёртым этапом штрихуем на третьей прямой тот её кусочек, который заштрихован на первых двух прямых одновременно. Вот так:
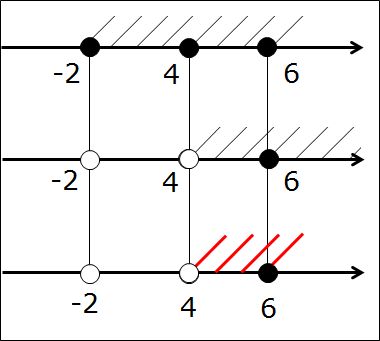
Ответ: (4; 6]
Решаем тот самый злой пример с единичкой и пустым множеством: (-∞; 1) ⋂ [1; +∞)
Рисуем картинку с тремя осями и сразу видим всю необходимую информацию:
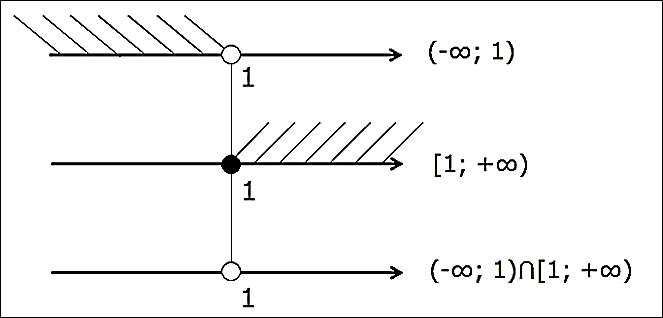
Безо всяких сомнений ясно, что единичка — выколота, а штриховать на третьей оси и вовсе нечего…
Ответ: Ø
Казалось бы, и зачем целый урок разжёвывать очевидные вещи, мог бы и в пару-тройку примеров уложиться. Но… Если бы вы знали, сколько учеников косячит при решении неравенств именно на этом этапе — какие точки включаются в ответ, а какие – нет! И не самых слабых учеников, между прочим.
Переходим к следующей важной операции — к объединению промежутков. В следующем уроке…
Нажмите вышеСинее словоУстановить звезду
Брат Донг берет тебя за пряжку ~
Автор: labuladong
Публичный номер: labuladong
Вышеуказанная исходная информация также должна быть сохранена, если белый список разрешен.
Эта статья является третьей частью серии задач с интервалом. В первых двух соответственно говорилось о наибольшем непересекающемся подмножестве интервалов и слиянии перекрывающихся интервалов. Сегодня я напишу алгоритм, который может быстро найти пересечение двух наборов интервалов.
Давайте сначала рассмотрим вопрос, вопрос 986 LeetCode – это следующий вопрос:
Проблема проста для понимания, она состоит в том, чтобы позволить вам найти пересечение и отметить, что все интервалы являются закрытыми интервалами.
Анализ мышления
Идея решения проблемы интервалов обычно состоит в том, чтобы сначала выполнить сортировку, чтобы облегчить работу., Но в названии написано, что он отсортирован, поэтому вы можете использовать два указателя индексаAсBПройдите посередине, найдите перекресток, код, наверное, такой:
# A, B Как [[0,2], [5,10] ...]
def intervalInterp(A, B):
i, j = 0, 0
res = []
while i < len(A) and j < len(B):
# ...
j += 1
i += 1
return res
Это несложно, давайте честно разберем различные ситуации.
Прежде всего,На два антракта,мы используем[a1,a2]с[b1,b2]Выраженный вAсBВ двух интервалах, при каких обстоятельствах эти два интервалаНет пересеченияЧто о:
Только в этих двух случаях условное суждение о написании кода выглядит так:
if b2 < a1 or a2 < b1:
[A1, a2] и [b1, b2] без пересечения
Итак, при каких обстоятельствах эти два интервала пересекаются? Согласно отрицанию предложения, отрицание приведенной выше логики является условием существования пересечения:
# Измените знак неравенства или измените его на и
if b2 >= a1 and a2 >= b1:
Есть пересечение между [a1, a2] и [b1, b2]
Далее, каковы ситуации, когда два интервала пересекаются? Исчерпаны:
Это очень просто, всего эти четыре ситуации.Итак, затем подумайте, есть ли у перекрестков что-нибудь общее в этих ситуациях?
Мы с удивлением обнаруживаем, что интервал пересечения регулярный!Если интервал пересечения равен[c1,c2], Потомc1=max(a1,b1)，c2=min(a2,b2)！Это суть поиска пересечения, мы продвигаем код еще на один шаг:
while i < len(A) and j < len(B):
a1, a2 = A[i][0], A[i][1]
b1, b2 = B[j][0], B[j][1]
if b2 >= a1 and a2 >= b1:
res.append([max(a1, b1), min(a2, b2)])
# ...
Последний шаг, наш указательiсjОпределенно идем вперед (инкрементально), когдаСтоит ли двигаться вперед?
В сочетании с примером анимации легко понять, двигаться ли вперед зависит только отa2сb2Соотношение размеров:
while i < len(A) and j < len(B):
# ...
if b2 < a2:
j += 1
else:
i += 1
Код
# A, B Как [[0,2], [5,10] ...]
def intervalInterp(A, B):
I, j = 0, 0 # Двойной указатель
res = []
while i < len(A) and j < len(B):
a1, a2 = A[i][0], A[i][1]
b1, b2 = B[j][0], B[j][1]
Между двумя интервалами есть пересечение
if b2 >= a1 and a2 >= b1:
Рассчитайте пересечение и добавьте разрешение
res.append([max(a1, b1), min(a2, b2)])
# Указатель перемещается вперед
if b2 < a2: j += 1
else: i += 1
return res
Подводя итог, можно сказать, что задачи с интервалом кажутся более сложными, и со многими ситуациями трудно справиться, но на самом деле, наблюдая общие черты между разными ситуациями, вы можете найти закономерности, и с ними можно справиться с помощью краткого кода.
Кроме того, в проблеме дальности нет ничего особенного, и работа с ней проста и неприхотлива, а вот применение очень широко.。
Рекомендовано в прошлом????
Классическое динамическое программирование: задача о рюкзаке 0-1
Руководство по изучению структуры данных и алгоритмов
Фреймворк для решения задач динамического программирования
Структура решения проблем алгоритма обратного отслеживания
Чтобы научиться бинарному поиску, я написал стихотворение
———————–
Публичный номер: labuladong
Станция B: лабуладонг
Знай: labuladong
Автор открыл на Github склад под названием fucking-algorithm и за две недели получил 10к звезд.。Нажмите и удерживайте QR-код, чтобы следовать, оторвите LeetCode руками и почувствуйте удовольствие от доминирования над алгоритмом, Ах ~
Backstage reply [добавить группу] Вы можете присоединиться к группе вопросов LeetCode, и все могут вместе обмениваться вопросами.
Есть список с различными промежутками времени. Например:
time_list = ['9:00 - 15:00', '13:00 - 17:00', '16:00 - 20:00']
Как мне из этого списка выбрать только ‘9:00 – 15:00′ и ’16:00 – 20:00’? То есть, нужно выбрать только те промежутки времени, которые не пересекаются между собой (напр. 9:00 – 15:00 и 13:00 – 17:00 пересекаются, так как 13:00 входит в промежуток 9:00 – 15:00).
Уже три дня не могу решить эту задачу, и кажется что ответ на поверхности, а понять не могу.
Пробовал в циклах сравнивать каждый элемент списка с каждым элементом этого же списка, но ничего нормального так и не получилось.
Буду благодарен, если кто-то поможет.
задан 7 сен 2022 в 14:36
3
Жадный метод – отсортировать по началу интервалов.
Взять первый интервал, далее найти тот, который первым идёт после его конца, и так далее.
ответ дан 7 сен 2022 в 15:11
MBoMBo
47.8k1 золотой знак17 серебряных знаков40 бронзовых знаков
1
Как и обещал, реализовал функцию, выполняющую бòльшую часть работы (даже дебаг-вывод есть). Почитай код, поймешь. Но, чтобы ты не терял интерес к задаче, эта функция имеет баг – если указать сначала вечерний промежуток времени, а потом утренний, то система будет выводить противоположное значение. Она возвращает только булево значение. Много переменных тут ради удобства чтения, а так это можно и в однострочник всунуть
Функция-парсер, выводит True, если промежутки пересекаются
def parse_time(first_time: str, second_time: str, debug=False):
"""
Возвращает True, если указанные промежутки времени пересекаются. Вводятся
они в формате ЧЧ:ММ - ЧЧ:ММ
"""
first_time = first_time.split()
second_time = second_time.split()
first_time.pop(1)
second_time.pop(1)
first_time_start = first_time[0].split()[0]
first_time_stop = first_time[1].split()[0]
first_time_start_hours = eval(first_time_start.split(':')[0])
first_time_start_minutes = eval(first_time_start.split(':')[1])
first_time_stop_hours = eval(first_time_stop.split(':')[0])
first_time_stop_minutes = eval(first_time_stop.split(':')[1])
first_time_start_all_minutes = first_time_start_hours * 60 + first_time_start_minutes
first_time_stop_all_minutes = first_time_stop_hours * 60 + first_time_stop_minutes
second_time_start = second_time[0].split()[0]
second_time_stop = second_time[1].split()[0]
second_time_start_hours = eval(second_time_start.split(':')[0])
second_time_start_minutes = eval(second_time_start.split(':')[1])
second_time_stop_hours = eval(second_time_stop.split(':')[0])
second_time_stop_minutes = eval(second_time_stop.split(':')[1])
second_time_start_all_minutes = second_time_start_hours * 60 + second_time_start_minutes
second_time_stop_all_minutes = second_time_stop_hours * 60 + second_time_stop_minutes
if debug:
print(first_time)
print(f"{first_time_start} + {first_time_stop}")
print(f"{first_time_start_hours}-{first_time_start_minutes} {first_time_stop_hours}-{first_time_stop_minutes}")
print(second_time)
print(f"{second_time_start} + {second_time_stop}")
print(f"{second_time_start_hours}-{second_time_start_minutes} {second_time_stop_hours}-{second_time_stop_minutes}")
print(first_time_start_all_minutes)
print(first_time_stop_all_minutes)
print(second_time_start_all_minutes)
print(second_time_stop_all_minutes)
if first_time_stop_all_minutes > second_time_start_all_minutes:
return True
У этой функции баг – если указать сначала поздний, а затем ранний промежуток времени, то система будет говорить противоположное истине
time = ['9:00 - 15:00', '13:00 - 18:00', '17:00 - 21:00']
# Вот здесь
if parse_time(time[2], time[0]):
print('Yes')
else:
print('No')
Yes
insolor
45.7k16 золотых знаков54 серебряных знака95 бронзовых знаков
ответ дан 7 сен 2022 в 18:01
3
не очень понятно какие промежутки считать пересекающимися, а какие не пересекающимися, поэтому сделал так:
from datetime import time
time_list = ['7:00 - 11:00', '9:00 - 15:00', '13:00 - 17:00', '16:00 - 20:00', '10:00 - 12:00']
res = {}
time_type = [list(map(lambda x: time.fromisoformat(x.zfill(5)), p.split(' - '))) for p in time_list]
for i in range(len(time_type)):
interv = time_type.pop(0)
intervs = [' - '.join(map(lambda x: x.strftime('%H:%M'),j)) for j in time_type if interv[1]<j[0] or j[1]<interv[0]]
if intervs: res.update({' - '.join(map(lambda x: x.strftime('%H:%M'),interv)):intervs})
time_type.append(interv)
на выходе имеем словарь где ключ это промежуток, а значение это промежутки с которыми он не пересекается
>>> res
'''
{'07:00 - 11:00': ['13:00 - 17:00', '16:00 - 20:00'],
'09:00 - 15:00': ['16:00 - 20:00'],
'13:00 - 17:00': ['10:00 - 12:00', '07:00 - 11:00'],
'16:00 - 20:00': ['10:00 - 12:00', '07:00 - 11:00', '09:00 - 15:00'],
'10:00 - 12:00': ['13:00 - 17:00', '16:00 - 20:00']}
ответ дан 8 сен 2022 в 13:58
SergFSMSergFSM
5,6501 золотой знак6 серебряных знаков17 бронзовых знаков
Еще один вариант поиска непрекращающихся интервалов
Алгоритм:
- создаем отсортированный список в минутах включающий все метки начала и окончания интервалов [t0, t1, t2, t3, …]
- создаем список интервалов в минутах ([[a0, b0], [a1, b1], … ])
- проходим по первому списку беря текущее и следующее значения и ищем такой интервал во втором списке, при совпадении выводим.
Объяснение:
Первый список содержит полную временную шкалу точек времени начала и окончания. Между двумя ближайшими точками не может быть другой с точки зрения логики, но не все из этого является указанными интервалами, так как две точки могут обозначать конец одного интервала и начало другого, или два конца/начала интервалов. По этой причине мы ищем в интервалах есть ли там интервал заданный двумя соседними точками времени.
На предоставленном графике видно, что только t[7] и t[8] две соседние точки совпадающие с имеющимися интервалами.
Реализация:
from datetime import time
time_list = ['8:00 - 9:00', '9:00 - 15:00', '13:00 - 17:00', '16:00 - 20:00']
def time_to_minutes(t):
t = time.fromisoformat(t.zfill(5))
return t.hour * 60 * 60 + t.minute * 60
time_intervals = [list(map(lambda x: time_to_minutes(x), item.split(' - '))) for item in time_list ]
time_minutes = [time_to_minutes(item) for sublist in time_list for item in sublist.split(' - ')]
time_minutes.sort()
for n in range(0, len(time_minutes) - 1):
if [time_minutes[n], time_minutes[n + 1]] in time_intervals:
print(time_list[n])
Вывод:
8:00 - 9:00 так как это единственный не пересекающийся интервал.
Пояснения к коду:
Строчки в коде
time_intervals = [list(map(lambda x: time_to_minutes(x), item.split(' - '))) for item in time_list ]
time_minutes = [time_to_minutes(item) for sublist in time_list for item in sublist.split(' - ')]
аналогичны коду
time_intervals = []
time_minutes = []
for n in time_list:
[start, end] = n.split(' - ')
[start_m, end_m] = [time_to_minutes(start), time_to_minutes(end)]
time_intervals.append([start_m, end_m])
time_minutes += [start_m, end_m]
ответ дан 10 сен 2022 в 13:21
Daniil LobanDaniil Loban
10.6k2 золотых знака8 серебряных знаков18 бронзовых знаков
