Как найти пересечение матрицы

Как найти пересечение матрицы

Given two matrix A[][] and B[][] of same order m*n. The task is to find the intersection of both matrix as C, where: 

  • Cij = Aij if Aij = Bij
  • C = “*”, otherwise.

Examples:  

Input : 
A[N][N] = {{2, 4, 6, 8},
           {1, 3, 5, 7},
           {8, 6, 4, 2},
           {7, 5, 3, 1}};

B[N][N] = {{0, 4, 3, 8},
           {1, 3, 5, 7},
           {8, 3, 6, 2},
           {4, 5, 3, 4}};
Output :
* 4 * 8 
1 3 5 7 
8 * * 2 
* 5 3 *

As intersection of two set is a set which includes common elements to both set, similarly intersection of two matrix will include only corresponding common element and place “*” at the position of rest unmatching elements. 

For finding the intersection of both matrix simply iterate over their size and print * if element at particular position in both matrix are not equal else print the element.

Below is the implementation of the above approach: 

C++

#include <bits/stdc++.h>

#define N 4

#define M 4

using namespace std;

void printIntersection(int A[][N], int B[][N])

{

    for (int i = 0; i < M; i++) {

        for (int j = 0; j < N; j++) {

            if (A[i][j] == B[i][j])

                cout << A[i][j] << " ";

            else

                cout << "* ";

        }

        cout << "n";

    }

}

int main()

{

    int A[M][N] = { { 2, 4, 6, 8 },

                    { 1, 3, 5, 7 },

                    { 8, 6, 4, 2 },

                    { 7, 5, 3, 1 } };

    int B[M][N] = { { 2, 3, 6, 8 },

                    { 1, 3, 5, 2 },

                    { 8, 1, 4, 2 },

                    { 3, 5, 4, 1 } };

    printIntersection(A, B);

    return 0;

}

Java

import java.io.*;

class GFG {

  static int N = 4;

static int M = 4;

static void printIntersection(int A[][], int B[][])

{

    for (int i = 0; i < M; i++) {

        for (int j = 0; j < N; j++) {

            if (A[i][j] == B[i][j])

                System.out.print(A[i][j] +" ");

            else

                System.out.print( "* ");

        }

        System.out.println( " ");

    }

}

    public static void main (String[] args) {

           int A[][] = { { 2, 4, 6, 8 },

                    { 1, 3, 5, 7 },

                    { 8, 6, 4, 2 },

                    { 7, 5, 3, 1 } };

    int B[][] = { { 2, 3, 6, 8 },

                    { 1, 3, 5, 2 },

                    { 8, 1, 4, 2 },

                    { 3, 5, 4, 1 } };

    printIntersection(A, B);

    }

}

Python3

N, M = 4, 4

def printIntersection(A, B) :

    for i in range(M) :

        for j in range(N) :

            if (A[i][j] == B[i][j]) :

                print(A[i][j], end = " ")

            else :

                print("* ", end = " ")

        print()

if __name__ == "__main__" :

    A = [ [2, 4, 6, 8 ],

        [ 1, 3, 5, 7 ],

        [ 8, 6, 4, 2 ],

        [ 7, 5, 3, 1 ] ]

    B = [ [ 2, 3, 6, 8 ],

        [ 1, 3, 5, 2 ],

        [ 8, 1, 4, 2 ],

        [ 3, 5, 4, 1 ] ]

    printIntersection(A, B)

C#

using System;

class GFG {

static int N = 4;

static int M = 4;

static void printIntersection(int [,]A, int [,]B)

{

    for (int i = 0; i < M; i++) {

        for (int j = 0; j < N; j++) {

            if (A[i,j] == B[i,j])

                Console.Write(A[i,j] +" ");

            else

                Console.Write( "* ");

        }

        Console.WriteLine( " ");

    }

}

    public static void Main () {

        int [,]A = { { 2, 4, 6, 8 },

                    { 1, 3, 5, 7 },

                    { 8, 6, 4, 2 },

                    { 7, 5, 3, 1 } };

    int [,]B = { { 2, 3, 6, 8 },

                    { 1, 3, 5, 2 },

                    { 8, 1, 4, 2 },

                    { 3, 5, 4, 1 } };

    printIntersection(A, B);

    }

}

PHP

<?php

function printIntersection($A, $B)

{

    $N = 4; $M = 4;

    for ($i = 0; $i < $M; $i++)

    {

        for ($j = 0; $j < $N; $j++)

        {

            if ($A[$i][$j] == $B[$i][$j])

                echo $A[$i][$j] . " ";

            else

                echo "* ";

        }

        echo "n";

    }

}

$A = array(array(2, 4, 6, 8 ),

        array(1, 3, 5, 7 ),

        array(8, 6, 4, 2 ),

        array(7, 5, 3, 1 ) );

$B = array(array(2, 3, 6, 8 ),

        array(1, 3, 5, 2 ),

        array(8, 1, 4, 2 ),

        array(3, 5, 4, 1 ) );

printIntersection($A, $B);

?>

Javascript

<script>

var N = 4

var M = 4

function printIntersection( A, B)

{

    for (var i = 0; i < M; i++) {

        for (var j = 0; j < N; j++) {

            if (A[i][j] == B[i][j])

                document.write( A[i][j] + " ");

            else

                document.write( "* ");

        }

        document.write( "<br>");

    }

}

var A = [ [ 2, 4, 6, 8 ],

                [ 1, 3, 5, 7 ],

                [ 8, 6, 4, 2 ],

                [ 7, 5, 3, 1 ] ];

var B = [ [ 2, 3, 6, 8 ],

                [ 1, 3, 5, 2 ],

                [ 8, 1, 4, 2 ],

                [ 3, 5, 4, 1 ] ];

printIntersection(A, B);

</script>

Output

2 * 6 8 
1 3 5 * 
8 * 4 2 
* 5 * 1

Complexity Analysis:

  • Time Complexity: O(M * N)
  • Auxiliary Space: O(1)

Last Updated :
09 Sep, 2022

Like Article

Save Article

Источник

Нахождение дополнения, суммы и пересечения подпространств

Нахождение алгебраического дополнения подпространства

Для заданного подпространства Ltriangleleft mathbb{R}^n требуется найти алгебраическое дополнение подпространства L^{+}, т.е. такое подпространство L^{+} triangleleftmathbb{R}^n, что mathbb{R}^n=Loplus L^{+}.

В зависимости от способа описания подпространства L, используем одно из следующих двух утверждений.

1. Если подпространство Ltriangleleft mathbb{R}^n задано как линейная оболочка L=operatorname{Lin}(a_1,ldots,a_k) столбцов матрицы A=begin{pmatrix} a_1&cdots&a_kend{pmatrix}, то множество решений однородной системы A^Tx=o является его алгебраическим дополнением L^{+}triangleleft mathbb{R}^n, т.е.

L=operatorname{Lin}(a_1,a_2,ldots,a_k)quad Rightarrowquad L^{+}= Bigl{A^Tx=oBigr}.

(8.16)

2. Если подпространство Ltriangleleft mathbb{R}^n задано как множество решений однородной системы Ax=o m уравнений с n неизвестными, то линейная оболочка столбцов a_1^{tau},ldots, a_m^{tau} транспонированной матрицы A^T=begin{pmatrix}a_1^{tau}&cdots& a_m^{tau}end{pmatrix} является его алгебраическим дополнением L^{+}triangleleft mathbb{R}^n, т.е.

L={Ax=o}quad Rightarrowquad L^{+}=operatorname{Lin} (a_1^{tau},ldots,a_m^{tau}),

(8.17)

где a_i^{tau} — i-й столбец матрицы A^T.

Разумеется, в (8.16) и (8.17) указано одно из возможных алгебраических дополнений подпространства L^{+} (см. свойство 3 алгебраических дополнений подпространств).

Докажем сначала справедливость (8.16) в одномерном случае (k=1), а потом в общем. Пусть L=operatorname{Lin}(a) — одномерное подпространство R^n, a=begin{pmatrix}alpha_1&cdots&alpha_nend{pmatrix}^T — ненулевой столбец. Найдем алгебраическое дополнение подпространства L. Рассмотрим уравнение a^Tx=o в координатной форме: alpha_1x_1+ldots+ alpha_nx_n=0. Множество {a^Tx=o} решений однородной системы, состоящей из одного уравнения, образует подпространство L' размерности (n-1). Найдем пересечение Lcap L'. Подставляя элемент x=lambda a линейной оболочки L в уравнение a^Tx=o, получаем lambda[(alpha_1)^2+ (alpha_2)^2+ldots+(alpha_n)^2]=0, что возможно только при lambda=0, так как ane o. Следовательно, элемент x из L принадлежит подпространству L' только тогда, когда x — нулевой столбец, т.е. Lcap L'={o}. Учитывая, что dim{L}+dim{L'}=n, заключаем, что L' — алгебраическое дополнение подпространства L в mathbb{R}^ncolon, Loplus L'=mathbb{R}^n.Таким образом,

operatorname{Lin}(a)oplus{a^Tx=o}=mathbb{R}^n.

(8.18)

Учитывая (8.18), докажем (8.16) в общем случае (kgeqslant1). Представим L=operatorname{Lin}(a_1,ldots,a_k) в виде суммы L=L_1+ldots+L_k, где L_i=operatorname{Lin}(a_i), i=1,ldots,k. Из (8.15) следует, что (L_1+ldots+L_k)oplus (L_1^{+}+ldots+L_k^{+})= mathbb{R}^n. Согласно (8.18), множество L_1^{+}={(a_i)^Tx=o} решений однородной системы, состоящей из одного уравнения, дополняет L_i до всего пространства mathbb{R}^n. Пересечение множеств решений отдельных уравнений дает, разумеется, множество L_1^{+} capldotscap L_k^{+}={A^Tx=o} решений системы этих уравнений. Поэтому (L_1+ ldots+L_k)oplus{A^Tx=o}=mathbb{R}^n, что и требовалось доказать. Утверждение (8.17) доказывается аналогично, используя (8.18).

Пример 8.10. Найти алгебраическое дополнение подпространства L=operatorname{Lin}[(t-1)^2,(t+1)^3] в пространстве P_3(mathbb{R}) многочленов не более, чем 3-й степени.

Решение. Сначала нужно переформулировать задачу для арифметического пространства (см. следствие теоремы 8.3 об изоморфизме конечномерных пространств). Для этого возьмем в P_3(mathbb{R}) стандартный базис mathbf{e}_1(t)=1, mathbf{e}_2(t)=t, mathbf{e}_3(t)=t^2, mathbf{e}_4(t)=t^3. Пространство P_3(mathbb{R}) изоморфно mathbb{R}^4. Найдем координаты многочленов mathbf{a}_1(t)=(t-1)^2 и mathbf{a}_2(t)=(t+1)^3 в стандартном базисе. Раскладывая mathbf{a}_1(t) по базису, получаем:

mathbf{a}_1(t)= (t-1)^2= 1-2t+t^2=1cdot mathbf{e}_1(t)+(-2)cdot mathbf{e}_2(t)+ 1cdot mathbf{e}_3(t)+0cdot mathbf{e}_4(t),

т.е. многочлену mathbf{a}_1(t) соответствует координатный столбец a_1= begin{pmatrix}1&-2&1&0end{pmatrix}^T — элемент пространства mathbb{R}^4. Аналогично получаем координатный столбец a_2= begin{pmatrix} 1&3&3&1end{pmatrix}^T для многочлена mathbf{a}_2(t).

Таким образом, исходная задача сводится к следующей: требуется найти алгебраическое дополнение подпространства L=operatorname{Lin}(a_1,a_2) в пространстве mathbb{R}^4. Используя правило (8.16), получаем, что L^{+} — это множество решений системы A^Tx=o, где A^T=begin{pmatrix} a_1&a_2 end{pmatrix}^T= begin{pmatrix}1&-2&1&0\ 1&3&3&1end{pmatrix}, т.е. системы begin{cases} x_1-2x_2+x_3=0,\ x_1+3x_2+3x_3+x_4=0. end{cases}

Решаем ее методом Гаусса. Приводим матрицу системы к упрощенному виду, прибавляя ко второй строке первую, умноженную на (-1), поделив вторую строку на 5, а затем прибавив ее, умноженную на 2, к первой:

A^T=begin{pmatrix}1&-2&1&0\ 1&3&3&1end{pmatrix}sim begin{pmatrix}1&-2&1&0\ 0&5&2&1 end{pmatrix}sim begin{pmatrix}1&0&9/5&2/5\ 0&1&2/5&1/5 end{pmatrix}!.

Базисные переменные x_1,,x_2, свободные — x_3,,x_4. Выражаем базисные переменные через свободные: x_1=-frac{9}{5}x_3-frac{2}{5}x_4; x_2=-frac{2}{5}x_3-frac{1}{5}x_4. Находим фундаментальную систему решений. Подставляя стандартные наборы свободных переменных (x_3=1,,x_4=0 и x_3= 0,,x_4=1), получаем решения: varphi_1=begin{pmatrix}-dfrac{9}{5}&-dfrac{2}{5}& 1&0end{pmatrix}^T, varphi_2=begin{pmatrix}-dfrac{2}{5}&-dfrac{1}{5}&0&1 end{pmatrix}^T, которые образуют фундаментальную систему решений и являются базисом алгебраического дополнения L^{+}=operatorname{Lin}(varphi_1,varphi_2) Полученный результат переносим в пространство многочленов. По координатному столбцу varphi_1 находим многочлен

varphi_1(t)=-frac{9}{9}cdot mathbf{e}_1(t)-frac{2}{5}cdot mathbf{e}_2(t)+ 1cdot mathbf{e}_3(t)+0cdot mathbf{e}_4(t)= -frac{9}{5}-frac{2}{5},t+t^2.

Аналогично получаем varphi_2(t)= -frac{2}{5}-frac{1}{5}t+t^3. Искомое алгебраическое дополнение имеет вид

L^{+}=operatorname{Lin}!left[left( -frac{9}{5}-frac{2}{5},t+t^2 right)!,,left( -frac{2}{5} -frac{1}{5}t+ t^3right)right]!,

Проверим равенство Lcap L^{+}={mathbf{o}}. Для этого приравняем между собой линейные комбинации многочленов mathbf{a}_1(t),,mathbf{a}_2(t) и varphi_1(t),,varphi_2(t):

alpha(1-t)^2+beta(1+t)^3= gamma!left(-frac{9}{5}-frac{2}{5},t+t^2 right)+delta! left(-frac{2}{5} -frac{1}{5}t+ t^3right)!.

Преобразовывая, получаем

(alpha+beta)cdot t^3+(alpha+3beta-gamma)cdot t^2+left(-2alpha+ 3beta+ frac{2}{5},gamma+frac{1}{5},deltaright)!cdot t+alpha+beta+ frac{9}{5},gamma+ frac{2}{5},delta=0.

Чтобы это равенство выполнялось тождественно, все его коэффициенты должны быть равны нулю:

begin{cases}beta-delta=0,\ alpha+3beta-gamma=0,\ -2alpha+3beta+ frac{2}{5} gamma+ frac{1}{5}delta=0,\ alpha+beta+ frac{9}{5}gamma+ frac{2}{5}delta=0, end{cases} Leftrightarrowquad underbrace{begin{pmatrix}0&1&0&-1\ 1&3&-1&0\ -2&3&2/5&1/5\ 1&1&9/5&2/5 end{pmatrix}}_{B}!cdot! begin{pmatrix}alpha\ beta\ gamma\ delta end{pmatrix}= begin{pmatrix} 0\0\0\0 end{pmatrix}!.

Ранг матрицы B этой системы равен 4 (находится, например, методом Гаусса). Поэтому однородная система имеет только нулевое решение alpha=beta= gamma= delta=0. Таким образом, равенство Lcap L^{+}={mathbf{o}} выполняется.

Нахождение алгебраической суммы подпространств

Для заданных подпространств A и B пространства mathbb{R}^n требуется найти размерность и базис их алгебраической суммы A+B. Рассмотрим методику решения этой задачи для двух случаев описания подпространств.

Пусть подпространства заданы линейными оболочками своих образующих (внутреннее описание): mathbf{A} =operatorname{Lin}(mathbf{a}_1,ldots, mathbf{a}_{k_1}) и mathbf{B} =operatorname{Lin} (mathbf{b}_1,ldots, mathbf{b}_{k_2}). Тогда, приписывая к образующим mathbf{a}_1,ldots, mathbf{a}_{k_1} одного подпространства образующие mathbf{b}_1,ldots, mathbf{b}_{k_2} другого подпространства, получаем образующие суммы подпространств mathbf{A} и mathbf{B}:

left.{begin{gathered}mathbf{A} =operatorname{Lin}(mathbf{a}_1,ldots, mathbf{a}_{k_1}),hfill\ mathbf{B}=operatorname{Lin}(mathbf{b}_1,ldots, mathbf{b}_{k_2}) end{gathered}}!right}quad Rightarrowquad mathbf{A}+mathbf{B}=operatorname{Lin} (mathbf{a}_1,ldots, mathbf{a}_{k_1},mathbf{b}_1,ldots, mathbf{b}_{k_2}),

(8.19)

поскольку любой вектор mathbf{v}in(mathbf{A}+mathbf{B}) имеет вид mathbf{v}= underbrace{alpha_1 mathbf{a}_1+ldots+ alpha_{k_1}mathbf{a}_{k_1} }_{mathbf{v}_1inmathbf{A}}+ underbrace{beta_1 mathbf{b}_1+ldots+ beta_{k_1}mathbf{b}_{k_2} }_{mathbf{v}_2inmathbf{B}}. Базис суммы mathbf{A}+ mathbf{B}= operatorname{Lin} (mathbf{a}_1,ldots, mathbf{a}_{k_1}, mathbf{b}_1, ldots, mathbf{b}_{k_2}) можно найти как максимальную подсистему линейно независимых столбцов.

Пусть подпространства заданы как множества решений однородных систем уравнений (внешнее описание): mathbf{A}={Ax=o} и mathbf{B}={Bx=o}. Тогда, переходя к внутреннему описанию, сводим задачу к предыдущему случаю, а именно нужно выполнить следующие действия:

1) для каждой однородной системы Ax=o и Bx=o найти фундаментальные системы решений varphi_1,ldots,varphi_{n-r} и psi_1,ldots,psi_{n-r} соответственно. При этом получим A=operatorname{Lin} (varphi_1,ldots,varphi_{n-r}) и B=operatorname{Lin}(psi_1,ldots,psi_{n-r}), где r_{A}=operatorname{rg}A, r_{B}=operatorname{rg}B;

2) по правилу (8.19) найти сумму mathbf{A}+mathbf{B}= operatorname{Lin} (varphi_1, ldots,varphi_{n-r},psi_1,ldots,psi_{n-r}).

Пример 8.11. Найти размерность и базис алгебраической суммы mathbf{A}+mathbf{B} подпространств mathbf{A},mathbf{B}triangleleft mathbb{R}^4, если подпространство mathbf{A} задано системой уравнений

begin{cases}x_1+x_2+2x_3+x_4=0,\ 2x_1+3x_2+x_4=0,\ 3x_1+4x_2+2x_3+2x_4=0,end{cases}

подпространство mathbf{B} — линейной оболочкой своих образующих:

mathbf{B}=operatorname{Lin}(b_1,b_2),quad b_1=begin{pmatrix}-4&3&1&-1 end{pmatrix}^T,quad b_2=begin{pmatrix}1&1&1&1end{pmatrix}^T.

Решение. Образующие подпространства mathbf{A} были найдены в примере 8.9: mathbf{A}=operatorname{Lin}(a_1,a_2), где a_1= begin{pmatrix}-6&4&1&0end{pmatrix}^T, a_2=begin{pmatrix}-2&1&0&1 end{pmatrix}^T. По правилу (8.19) получаем mathbf{A}+mathbf{B}= operatorname{Lin}(a_1,a_2,b_1,b_2). Найдем базис этого подпространства как максимальную линейно независимую подсистему столбцов. Составляем из этих столбцов матрицу и приводим ее методом Гаусса к ступенчатому виду:

begin{gathered}begin{pmatrix}-6&-2&-4&1\ 4&1&3&1\ 1&0&1&1\ 0&1&-1&1 end{pmatrix}sim begin{pmatrix}1&0&1&1\ 4&1&3&1\ -6&-2&-4&1\ 0&1&-1&1 end{pmatrix}sim begin{pmatrix}1&0&1&1\ 0&1&-1&-3\ 0&-2&2&7\ 0&1&-1&1 end{pmatrix}sim\[2pt] sim begin{pmatrix}1&0&1&1\ 0&1&-1&-3\ 0&0&0&1\ 0&0&0&4 end{pmatrix}sim begin{pmatrix} 1&0&1&1\ 0&1&-1&-3\ 0&0&0&1\ 0&0&0&0 end{pmatrix}!.end{gathered}

Первый, второй и четвертый столбцы полученной матрицы линейно независимы. Значит, соответствующие столбцы a_1,,a_2,,b_2 исходной матрицы так же линейно независимы (так как выполнялись элементарные преобразования только над строками). Поэтому они являются базисом mathbf{A}+mathbf{B} и dim(mathbf{A}+ mathbf{B})=3.

Нахождение пересечения подпространств

Для заданных подпространств mathbf{A} и mathbf{B} пространства mathbb{R}^n требуется найти размерность и базис их пересечения mathbf{A}cap mathbf{B}. Рассмотрим методику решения этой задачи для двух случаев описания подпространств.

Пусть подпространства заданы как множества решений однородных систем уравнений (внешнее описание): mathbf{A}={Ax=o} и mathbf{B}={Bx=o}. Тогда, приписывая к системе Ax=o, задающей одно подпространство, систему Bx=o, задающую другое подпространство, получаем систему begin{cases} Ax=o,\ Bx=o,end{cases} определяющую пересечение подпространств:

left.{begin{gathered}mathbf{A}={Ax=o},\ mathbf{B}={Bx=o} end{gathered}}right}quad Rightarrowquad mathbf{A}cap mathbf{B}=left{begin{pmatrix}A\ Bend{pmatrix}!x=oright}!.

(8.20)

Базисом пересечения служит ее фундаментальная система решений.

Пусть подпространства mathbf{A} и mathbf{B} пространства mathbb{R}^n заданы линейными оболочками своих образующих (внутреннее описание): mathbf{A}=operatorname{Lin}(a_1,ldots,a_{k_1}) и mathbf{B}= operatorname{Lin}(b_1,ldots,b_{k_2}). Переходя от внутреннего описания подпространств к внешнему, можно свести задачу к предыдущему случаю. Однако удобнее сделать иначе. Пересечению mathbf{A}cap mathbf{B} принадлежат только такие mathbf{x}in mathbb{R}^n, которые можно представить как равные между собой линейные комбинации столбцов a_1,ldots,a_{k_1} и столбцов b_1,ldots,b_{k_2} соответственно:

mathbf{x}=alphacdot mathbf{a}_1+ldots+alpha_{k_1}cdot mathbf{a}_{k_1}= beta_{1}cdot mathbf{b}_{1}+ldots+beta_{k_2}cdot mathbf{b}_{k_2}.

(8.21)

Представим второе равенство в (8.21) в матричном виде Aalpha=Bbeta, где A=begin{pmatrix}a_1&cdots&a_{k_1}end{pmatrix}, B=begin{pmatrix} b_1&cdots&b_{k_2}end{pmatrix} — матрицы, составленные из данных столбцов, alpha= begin{pmatrix}alpha_1&cdots&alpha_{k_1}end{pmatrix}^T, beta= begin{pmatrix} beta_1&cdots&beta_{k_2}end{pmatrix}^T — столбцы коэффициентов линейных комбинаций. Равенство Aalpha=Bbeta можно рассматривать как одно родную систему Aalpha-Bbeta=o n уравнений с (k_1+k_2) неизвестными alpha и beta. Каждому решению этой системы соответствует вектор mathbf{x}= Aalpha=Bbeta, при надлежащий пересечению mathbf{A}cap mathbf{B}. Однако, на практике удобнее вместо системы Aalpha-Bbeta=o рассматривать однородную систему Aalpha+Bbeta=o, решения которой обладают теми же свойствами (тогда вектор mathbf{x}= Aalpha=Bbeta при надлежит пересечению mathbf{A}cap mathbf{B}.

Поэтому для нахождения пересечения подпространств mathbf{A}= operatorname{Lin} (a_1,ldots,a_{k_1}) и mathbf{B}= operatorname{Lin}(b_1,ldots,b_{k_2}) и базиса пересечения нужно выполнить следующие действия.

1. Составить блочную матрицу (Amid B) коэффициентов однородной системы уравнений Aalpha+Bbeta=o, где матрицы A=begin{pmatrix} a_1&cdots&a_{k_1} end{pmatrix}, B=begin{pmatrix} b_1&cdots&b_{k_2}end{pmatrix} образованы из заданных столбцов.

2. Для однородной системы с матрицей (Amid B) найти фундаментальную матрицу Phi. Матрица Phi имеет размеры (k_1+k_2)times (k_1+k_2-r), где r=operatorname{rg}(Amid B).

3. Из первых k_1 строк матрицы Phi составить матрицу Phi_{alpha}= (E_{k_1}mid O)Phi. Столбцы матрицы Phi_{alpha}= begin{pmatrix} varphi_1&cdots &varphi_{k_1+k_2-r}end{pmatrix} содержат искомые коэффициенты alpha=begin{pmatrix}alpha_1&cdots&alpha_{k_1}end{pmatrix}^T линейных комбинаций (8.21).

4. Записать пересечение mathbf{A}cap mathbf{B} как линейную оболочку столбцов матрицы APhi_{alpha}: Acap B=operatorname{Lin}(Avarphi_1,ldots, Avarphi_{k_1+k_2-r}).

5. Найти базис пересечения как максимальную линейно независимую подсистему образующих Avarphi_1,ldots, Avarphi_{k_1+k_2-r}.

Пример 8.12. Найти размерности и базисы суммы mathbf{A}+ mathbf{B} и пересечения mathbf{A}cap mathbf{B} подпространств mathbf{A},mathbf{B}triangleleft mathbb{R}^4, если они заданы линейными оболочками своих образующих: mathbf{A}= operatorname{Lin}(a_1,a_2,a_3) mathbf{B}= operatorname{Lin}(b_1,b_2,b_3), где

a_1=begin{pmatrix}1\1\1\1end{pmatrix}!,quad a_2=begin{pmatrix}1\-1\1\-1 end{pmatrix}!,quad a_3=begin{pmatrix}1\3\1\3end{pmatrix}!,quad b_1=begin{pmatrix} 1\2\0\2 end{pmatrix}!,quad b_2=begin{pmatrix}1\2\1\2end{pmatrix}!,quad b_3=begin{pmatrix} 3\1\3\1 end{pmatrix}!.

Решение. Найдем базис и размерность суммы mathbf{A}+ mathbf{B}. Составим из данных столбцов блочную матрицу

(Amid B)= begin{pmatrix}a_1&a_2&a_3,mid, b_1&b_2&b_3 end{pmatrix}= begin{pmatrix}1&1&1!!&vline!!& 1&1&3\ 1&-1&3!!&vline!!& 2&2&1\ 1&1&1!!&vline!!& 0&1&3\ 1&-1&3!!&vline!!& 2&2&1 end{pmatrix}!.

Элементарными преобразованиями над строками приведем ее к ступенчатому виду:

(Amid B)sim begin{pmatrix}1&1&1!!&vline!!& 1&1&3\ 0&-2&2!!&vline!!& 1&1&-2\ 0&0&0!!&vline!!& -1&0&0\ 0&-2&2!!&vline!!& 1&1&-2end{pmatrix}sim begin{pmatrix} 1&1&1!!&vline!!& 1&1&3\ 0&-2&2!!&vline!!& 1&1&-2\ 0&0&0!!&vline!!& -1&0&0\ 0&0&0!!&vline!!& 0&0&0 end{pmatrix}= (A'mid B').

По ступенчатому виду определяем, что первый, второй и четвертый столбцы линейно независимы. Следовательно, из 6 образующих a_1,a_2,a_3, b_1,b_2,b_3 подпространства mathbf{A}+mathbf{B} максимальную линейно независимую подсистему составляют столбцы a_1,a_2,b_1 (в этих столбцах расположен базисный минор матрицы). Следовательно, эти столбцы служат базисом суммы: mathbf{A}+ mathbf{B}= operatorname{Lin}(a_1,a_2,b_1) и dim(mathbf{A}+mathbf{B})=3. По ступенчатому виду матрицы (Amid B) можно также определить размерности подпространств. В блоке A' две ненулевых строки, следовательно, dimmathbf{A}= operatorname{rg}A= operatorname{rg}A'=2. Ненулевые строки блока В’ линейно независимы, следовательно, dimmathbf{B}= operatorname{rg}B= operatorname{rg}B'=3.

Найдем базис и размерность пересечения mathbf{A}cap mathbf{B}~ (k_1=k_2=3,~ r=operatorname{rg}(Amid B)=3).

1. Первый пункт алгоритма выполнен выше: матрица (Amid B) однородной системы Aalpha+Bbeta=o приведена к ступенчатому виду (A'mid B').

2. Находим фундаментальную систему решений (используя алгоритм, описанный в разд. 5.5). Приводим матрицу (A'mid B') системы к упрощенному виду:

(A'mid B')= begin{pmatrix}1&1&1!!&vline!!& 1&1&3\ 0&-2&2!!&vline!!& 1&1&-2\ 0&0&0!!&vline!!& -1&0&0\ 0&0&0!!&vline!!& 0&0&0end{pmatrix}sim begin{pmatrix}1&0&2!!&vline!!& 0&3/2&2\ 0&1&-1!!&vline!!& 0&-1/2&1\ 0&0&0!!&vline!!& 1&0&0\ 0&0&0!!&vline!!& 0&0&0end{pmatrix}!.

Базисные переменные: alpha_1,,alpha_2,,beta_1; остальные переменные — свободные. Выражаем базисные переменные через свободные: alpha_1=-2alpha_3-frac{3}{2} beta_2-2beta_3; alpha_2=alpha_3+frac{1}{2}beta_2-beta_3; beta_1=0. Придавая свободным переменным наборы значений

alpha_3=1,quad beta_2=0,quad beta_3=0;qquad alpha_3=0,quad beta_2=2,quad beta_3=0;qquad alpha_3=0,quad beta_2=0,quad beta_3=1,

получаем линейно независимые решения

varphi_1=begin{pmatrix} -2&1&1&0&0&0 end{pmatrix}^T,quad varphi_2= begin{pmatrix} -3&1&0&0&2&0 end{pmatrix}^T,quad varphi_3=begin{pmatrix}-2&-1&0&0&0&1 end{pmatrix}^T.

т.е. фундаментальная матрица имеет вид

Phi= begin{pmatrix}-2&-3&-2\ 1&1&-1\ 1&0&0\ 0&0&0\ 0&2&0\ 0&0&1 end{pmatrix}!.

3. Из первых трех строк (k_1=3) матрицы Phi составляем матрицу Phi_{alpha}= begin{pmatrix} -2&-3&-2\ 1&1&-1\ 1&0&0 end{pmatrix}.

4. Вычисляем произведение

AcdotPhi_{alpha}= begin{pmatrix}1&1&1\ 1&-1&3\ 1&1&1\ 1&-1&3 end{pmatrix}! cdot! begin{pmatrix}-2&-3&-2\ 1&1&-1\ 1&0&0end{pmatrix}= begin{pmatrix}0&-2&-3\ 0&-4&-1\ 0&-2&-3\ 0&-4&-1end{pmatrix}= begin{pmatrix}o&c_1&c_2end{pmatrix}!.

Столбцы этой матрицы являются образующими пересечения mathbf{A}cap mathbf{B}= operatorname{Lin}(o,c_1,c_2), где o — нулевой столбец, c_1= begin{pmatrix} -2&-4&-2&-4 end{pmatrix}^T, c_2=begin{pmatrix}-3&-1&-3&-1 end{pmatrix}^T.

5. Найдем базис пересечения mathbf{A}cap mathbf{B}. Для этого матрицу APhi_{alpha} приводим к ступенчатому виду

AcdotPhi_{alpha}= begin{pmatrix}0&-2&-3\ 0&-4&-1\ 0&-2&-3\ 0&-4&-1end{pmatrix}sim begin{pmatrix}0&2&3\ 0&0&5\ 0&0&0\ 0&0&0 end{pmatrix}sim begin{pmatrix}0&1&3/2\ 0&0&1\ 0&0&0\ 0&0&0 end{pmatrix}!.

По ступенчатому виду определяем, что последние два столбца матрицы APhi_{alpha} линейно независимы. Следовательно, два столбца c_1,c_2 являются базисом пересечения mathbf{A}cap mathbf{B}= operatorname{Lin}(c_1,c_2) и dim(mathbf{A}cap mathbf{B})=2.

Проверим размерность пересечения подпространств, которую вычислим, используя формулу (8.13):

dim(mathbf{A}cap mathbf{B})= dim mathbf{A}+dim mathbf{B}-dim(mathbf{A}+ mathbf{B})= 2+3-3=2,

что совпадает с найденной ранее размерностью.

Пример 8.13. Найти размерности и базисы пересечения mathbf{A}cap mathbf{B} и суммы mathbf{A}+ mathbf{B} подпространств mathbf{A}, mathbf{B}triangleleft mathbb{R}^4, если они заданы однородными системами уравнений:

mathbf{A}colon, begin{cases}x_1+x_2+2x_3+x_4=0,\ 2x_1+3x_2+x_4=0,\ 3x_1+4x_2+2x_3+2x_4=0;end{cases}quad mathbf{B}colon, begin{cases}x_1+x_2+x_3=0,\ 2x_1+3x_2+x_3+2x_4=0,\ x_1+2x_2+2x_4=0.end{cases}

Решение. Обозначим матрицы данных систем через mathbf{A} и mathbf{B} соответственно. По правилу (8.20) пересечение mathbf{A}cap mathbf{B} описывается однородной системой begin{cases}Ax=o,\Bx=o.end{cases} Найдем базис пересечения — фундаментальную систему решений этой однородной системы уравнений. Составляем матрицу системы begin{pmatrix}dfrac{A}{B}end{pmatrix} и приводим ее к ступенчатому виду, а затем к упрощенному виду:

begin{gathered} begin{pmatrix}dfrac{A}{B}end{pmatrix}= begin{pmatrix}1&1&2&1\ 2&3&0&1\ 3&4&2&2\hline 1&1&1&0\ 2&3&1&2\ 1&2&0&2 end{pmatrix}sim begin{pmatrix} 1&1&2&1\ 0&1&-4&-1\ 0&1&-4&-1\hline 0&0&-1&-1\ 0&1&-3&0\ 0&1&-2&1 end{pmatrix}sim begin{pmatrix}1&1&2&1\ 0&1&-4&-1\ 0&0&0&0\hline 0&0&-1&-1\ 0&0&1&1\ 0&0&2&2 end{pmatrix}sim begin{pmatrix}1&1&2&1\ 0&1&-4&-1\ 0&0&1&1\hline 0&0&0&0\ 0&0&0&0\ 0&0&0&0 end{pmatrix}sim\[2pt] sim begin{pmatrix}1&0&6&2\ 0&1&-4&-1\ 0&0&1&1\hline 0&0&0&0\ 0&0&0&0\ 0&0&0&0 end{pmatrix}sim begin{pmatrix}1&0&0&-4\ 0&1&0&3\ 0&0&1&1\hline 0&0&0&0\ 0&0&0&0\ 0&0&0&0end{pmatrix}!.end{gathered}

Базисные переменные: x_1,x_2,x_3, свободная переменная — x_4. Выражаем базисные переменные через свободную: x_1=4x_4; x_2=-3x_4; x_3=-x_4. Фундаментальная система содержит одно решение varphi_1= begin{pmatrix} 4&-3&-1&1end{pmatrix}^T, которое получаем, задавая x_4=1. Следовательно, mathbf{A}cap mathbf{B}= operatorname{Lin}(varphi_1) и dim(mathbf{A}cap mathbf{B}).

Найдем теперь сумму mathbf{A}+mathbf{B}. Фундаментальная система решений однородной системы Ax=o была найдена в примере 8.9. Следовательно,

mathbf{A}=operatorname{Lin}(a_1,a_2), где a_1=begin{pmatrix} -6&4&1&0 end{pmatrix}^T,~~ a_2=begin{pmatrix}-2&1&0&1end{pmatrix}^T,~~ dim{mathbf{A}}=2.

Найдем фундаментальную систему решений однородной системы Bx=o. Для этого приводим матрицу системы к ступенчатому виду, а затем к упрощенному:

B=begin{pmatrix}1&1&1&0\ 2&3&1&2\ 1&2&0&2 end{pmatrix}sim begin{pmatrix} 1&1&1&0\ 0&1&-1&2\ 0&1&-1&2 end{pmatrix}sim begin{pmatrix}1&1&1&0\ 0&1&-1&2\ 0&0&0&0 end{pmatrix}sim begin{pmatrix}1&0&2&-2\ 0&1&-1&2\ 0&0&0&0 end{pmatrix}!.

Базисные переменные: x_1,,x_2, свободные переменные: x_3,,x_4. Выражаем базисные переменные через свободные: x_1=-2x_3+2x_4; x_2=x_3-2x_4. Фундаментальная система состоит из двух решений b_1=begin{pmatrix}-2&1&1&0end{pmatrix}^T, b_2=begin{pmatrix}2&-2&0&1end{pmatrix}^T, которые находим, придавая свободным переменным стандартные наборы значений (x_3=1,~x_4=0 и x_3=0,~x_4=1). Следователь но, mathbf{B}= operatorname{Lin}(b_1,b_2) и dim mathbf{B}=2.

По правилу (8.19) находим сумму mathbf{A}+mathbf{B}= operatorname{Lin} (a_1,a_2,b_1,b_2). Чтобы определить базис, составим из столбцов a_1,,a_2,, b_1,,b_2 матрицу и приведем ее к ступенчатому виду:

begin{pmatrix}-6&-2&-2&2\ 4&1&1&-2\ 1&0&1&0\ 0&1&0&1end{pmatrix}sim begin{pmatrix}1&0&1&0\ 0&1&-3&-2\ 0&-2&4&2\ 0&1&0&1 end{pmatrix}sim begin{pmatrix} 1&0&1&0\ 0&1&-3&-2\ 0&0&-2&-2\ 0&0&3&3 end{pmatrix}sim begin{pmatrix}1&0&1&0\ 0&1&-3&-2\ 0&0&1&1\ 0&0&0&0 end{pmatrix}!.

Первые три столбца линейно независимы. Следовательно, mathbf{A}+mathbf{B}= operatorname{Lin}(a_1,a_2,b_1) и dim(mathbf{A}+mathbf{B})=3.

Проверим размерность суммы подпространств. По формуле (8.13) получаем

dim(mathbf{A}+mathbf{B})= dimmathbf{A}+dimmathbf{B}-dim(mathbf{A}cap mathbf{B})=2+2-1=3,

что совпадает с найденной ранее размерностью.

Нахождение относительных алгебраических дополнений подпространств

Пусть дана цепочка подпространств mathbf{A}triangleleft mathbf{B}triangleleft mathbb{R}^n. Требуется найти относительное дополнение mathbf{A}^{+}cap mathbf{B} подпространства mathbf{A} до подпространства mathbf{B}.

Рассмотрим случай внешнего описания подпространств — как множеств решений однородных систем уравнений: mathbf{A}={Ax=o} и mathbf{B}={Ax=o}. Согласно (8.17) базис пространства mathbf{A}^{+} образуют линейно независимые столбцы транспонированной матрицы A^T. Тогда относительное дополнение mathbf{A}^{+}cap mathbf{B} составляют такие векторы x=A^Ty, которые удовлетворяют системе Bx=o. Если обозначить через Phi фундаментальную матрицу системы BA^Ty=o, то линейно независимые столбцы матрицы A^TPhi являются максимальной системой векторов подпространства mathbf{B}, линейно независимой над mathbf{A}, т.е. базисом относительного дополнения.

На практике нахождение базиса mathbf{A}^{+}cap mathbf{B} удобнее производить, используя ступенчатые виды матриц A и B, согласно следующей методике.

1. Привести матрицы A и B при помощи элементарных преобразований строк к ступенчатому виду и удалить нулевые строки. В результате по лучим матрицы (A)_{text{st}} и (B)_{text{st}} модифицированного ступенчатого вида (строки каждой из этих матриц линейно независимые).

2. Найти фундаментальную матрицу Phi однородной системы уравнений (B)_{text{st}}(A)_{text{st}}^Ty=o.

3. Вычислить матрицу (A)_{text{st}}^TPhi. Ее столбцы образуют искомый базис mathbf{A}^{+}cap mathbf{B}.

Рассмотрим случай внутреннего описания подпространства mathbf{A} как линейной оболочки своих образующих: mathbf{A}=operatorname{Lin}(a_1,ldots,a_k). Согласно (8.16) множество решений системы уравнений A^Tx=o (матрица A= begin{pmatrix}a_1&cdots&a_kend{pmatrix} составлена из образующих) является алгебраическим дополнением mathbf{A}^{+}. Тогда множество решений системы begin{cases}A^Tx=o,\Bx=o,end{cases}!!Leftrightarrow, begin{pmatrix} dfrac{A^T}{B} end{pmatrix}!x=o является относительным дополнением mathbf{A}^{+}cap mathbf{B}, а ее фундаментальная система решений — базисом относительного дополнения.

Замечание 8.10. Способы описания подпространств комплексного линейного пространства, а также методы решения типовых задач аналогичны рассмотренным. В отличие от вещественного арифметического пространства mathbb{R}^n вместо операции транспонирования матрицы в комплексном арифметическом пространстве mathbb{C}^n нужно использовать операцию сопряжения матрицы.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Даны две матрицы A [] [] и B [] [] одного порядка m * n . Задача состоит в том, чтобы найти пересечение обеих матриц как C, где:

  • C ij = A ij, если A ij = B ij
  • C = «*», в противном случае.

Примеры:

Input : 
A[N][N] = {{2, 4, 6, 8},
           {1, 3, 5, 7},
           {8, 6, 4, 2},
           {7, 5, 3, 1}};

B[N][N] = {{0, 4, 3, 8},
           {1, 3, 5, 7},
           {8, 3, 6, 2},
           {4, 5, 3, 4}};
Output :
* 4 * 8 
1 3 5 7 
8 * * 2 
* 5 3 *

Поскольку пересечение двух наборов является набором, который включает в себя общие элементы для обоих наборов, аналогично пересечение двух матриц будет включать в себя только соответствующий общий элемент и помещать «*» в положение остальных несогласованных элементов.

Чтобы найти пересечение обеих матриц, просто выполните итерации по их размеру и выведите *, если элемент в определенной позиции в обеих матрицах не равен, иначе выведите элемент.

Ниже приведена реализация вышеуказанного подхода:

C ++

  
#include <bits/stdc++.h>
#define N 4
#define M 4

using namespace std;

void printIntersection(int A[][N], int B[][N])

{

    for (int i = 0; i < M; i++) {

        for (int j = 0; j < N; j++) {

            if (A[i][j] == B[i][j])

                cout << A[i][j] << " ";

            else

                cout << "* ";

        }

        cout << "n";

    }

}

int main()

{

    int A[M][N] = { { 2, 4, 6, 8 },

                    { 1, 3, 5, 7 },

                    { 8, 6, 4, 2 },

                    { 7, 5, 3, 1 } };

    int B[M][N] = { { 2, 3, 6, 8 },

                    { 1, 3, 5, 2 },

                    { 8, 1, 4, 2 },

                    { 3, 5, 4, 1 } };

    printIntersection(A, B);

    return 0;

}

Джава

import java.io.*;

class GFG {

  static int N = 4;

static int M = 4;

static void printIntersection(int A[][], int B[][])

{

    for (int i = 0; i < M; i++) {

        for (int j = 0; j < N; j++) {

            if (A[i][j] == B[i][j])

                System.out.print(A[i][j] +" ");

            else

                System.out.print( "* ");

        }

        System.out.println( " ");

    }

}

    public static void main (String[] args) {

           int A[][] = { { 2, 4, 6, 8 },

                    { 1, 3, 5, 7 },

                    { 8, 6, 4, 2 },

                    { 7, 5, 3, 1 } };

    int B[][] = { { 2, 3, 6, 8 },

                    { 1, 3, 5, 2 },

                    { 8, 1, 4, 2 },

                    { 3, 5, 4, 1 } };

    printIntersection(A, B);

    }

}

python3

N, M = 4, 4

def printIntersection(A, B) :

    for i in range(M) :

        for j in range(N) :

            if (A[i][j] == B[i][j]) :

                print(A[i][j], end = " ")

            else :

                print("* ", end = " ")

        print()

if __name__ == "__main__" :

    A = [ [2, 4, 6, 8 ],

        [ 1, 3, 5, 7 ],

        [ 8, 6, 4, 2 ],

        [ 7, 5, 3, 1 ] ]

    B = [ [ 2, 3, 6, 8 ],

        [ 1, 3, 5, 2 ],

        [ 8, 1, 4, 2 ],

        [ 3, 5, 4, 1 ] ]

    printIntersection(A, B)

C #

using System;

class GFG {

static int N = 4;

static int M = 4;

static void printIntersection(int [,]A, int [,]B)

{

    for (int i = 0; i < M; i++) {

        for (int j = 0; j < N; j++) {

            if (A[i,j] == B[i,j])

                Console.Write(A[i,j] +" ");

            else

                Console.Write( "* ");

        }

        Console.WriteLine( " ");

    }

}

    public static void Main () {

        int [,]A = { { 2, 4, 6, 8 },

                    { 1, 3, 5, 7 },

                    { 8, 6, 4, 2 },

                    { 7, 5, 3, 1 } };

    int [,]B = { { 2, 3, 6, 8 },

                    { 1, 3, 5, 2 },

                    { 8, 1, 4, 2 },

                    { 3, 5, 4, 1 } };

    printIntersection(A, B);

    }

}

PHP

<?php

function printIntersection($A, $B)

{

    $N = 4; $M = 4;

    for ($i = 0; $i < $M; $i++)

    {

        for ($j = 0; $j < $N; $j++)

        {

            if ($A[$i][$j] == $B[$i][$j])

                echo $A[$i][$j] . " ";

            else

                echo "* ";

        }

        echo "n";

    }

}

$A = array(array(2, 4, 6, 8 ),

        array(1, 3, 5, 7 ),

        array(8, 6, 4, 2 ),

        array(7, 5, 3, 1 ) );

$B = array(array(2, 3, 6, 8 ),

        array(1, 3, 5, 2 ),

        array(8, 1, 4, 2 ),

        array(3, 5, 4, 1 ) );

printIntersection($A, $B);

  

?>

Выход:

2 * 6 8 
1 3 5 * 
8 * 4 2 
* 5 * 1

Рекомендуемые посты:

  • Различные операции над матрицами
  • XOR XOR всех подматриц
  • Кронекер Произведение двух матриц
  • Подсчитать подматрицы, имеющие сумму, кратную сумме k
  • Программа для умножения двух матриц
  • Программа Python для добавления двух матриц
  • Программа для вычитания матриц
  • Программа для сложения двух матриц
  • Программа для проверки идентичности двух заданных матриц
  • Программа Python для умножения двух матриц
  • Подсчитать пары из двух отсортированных матриц с заданной суммой
  • Количество матриц (разных порядков) с заданным количеством элементов
  • Запросы на количество двоичных подматриц заданного размера
  • Минимальные элементы, которые нужно добавить, чтобы умножить две матрицы
  • Умножение двух матриц в одной строке с использованием Numpy в Python

Найти пересечение двух матриц

0.00 (0%) 0 votes

Источник

Все курсы > Линейная алгебра > Занятие 6 (часть 1)

Сегодня мы еще раз рассмотрим полученные ранее знания о векторных пространствах, линейных преобразованиях, системе линейных уравнений и определителе матрицы в контексте новых понятий ранга и четырех фундаментальных подпространств матрицы, а именно пространства столбцов, пространства строк, ядра и коядра матрицы.

Продолжим работать в том же ноутбуке⧉

Ранг матрицы

При нулевом определителе в трехмерном пространстве матрица может «схлопнуть» пространство до плоскости, линии или точки (во всех трех случаях определитель равен нулю).

Ранее мы сказали, что для того чтобы в системе уравнений, например, трехмерная матрица $A$ при нулевом определителе все же имела решение, вектор $mathbf b$, на который матрица $A$ переводит вектор $mathbf x$, должен лежать на плоскости или линии, в которые «схлопывается» трехмерное пространство.

Размерность пространства после трансформации принято описывать рангом матрицы (rank).

Если преобразование трехмерной матрицы «сворачивает» размерность до линии, то ранг такого преобразования равен единице, до плоскости — двум и т.д. В случае матрицы $2 times 2$ самый высокий ранг матрицы — два. Это значит, что при преобразовании размерность сохранилась (и соответственно определитель не равен нулю).

Пространство столбцов

Пространством столбцов (column space, а также образом, image) называют множество всех возможных линейных комбинаций вектор-столбцов.

С точки зрения линейных преобразований, пространством столбцов называют векторы, которые определяют пространство после трансформации.

В случае линейно зависимых векторов таких векторов будет меньше, чем в исходной матрице. Приведем пример линейно зависимых векторов и рассчитаем ранг матрицы.

M = np.array([[1,   0,  1],

              [2,   3,  4],

              [–1, –3, –3]])

np.linalg.matrix_rank(M)

Приведем матрицу к упрощенному ступенчатому виду (reduced row-echelon form) с помощью Питона. Для этого воспользуемся методом .rref() библиотеки sympy.

from sympy import *

M = Matrix([[1,   0,  1],

            [2,   3,  4],

            [–1, –3, –3]])

M_rref = M.rref()

M_rref[0]

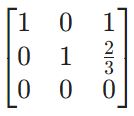
матрица в упрощенном ступенчатом виде

Как мы видим, с одной стороны, пространство сократилось до двух измерений (поэтому ранг матрицы равен двум), с другой, двумерное пространство можно описать первыми двумя столбцами (их еще называют разрещающими, ведущими или базисными, pivot columns), где все элементы кроме одного равны нулю.

Разрешающие столбцы и образуют пространство столбцов. Найдем пространство столбцов с помощью Питона.

# вторым элементом метод .rref() выводит индексы

# разрешающих столбцов (pivot columns)

# используем их для нахождения пространства столбцов

M.col(M.rref()[1])

пространство столбцов

# то же самое можно найти с помощью метода

# sympy.columnspace()

M_columnspace = M.columnspace()

M_columnspace[0]

метод .columnspace() библиотеки sympy

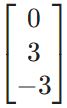
метод .columnspace() библиотеки sympy 2

Откуда такое название? Столбцы матрицы говорят куда «приземлятся» координаты базисных векторов. В этом смысле, оболочка вектор-столбцов то же самое, что и пространство столбцов.

В матрице $2 times 2$ первый столбец показывает, где окажется вектор $mathbf i$, второй — вектор $mathbf j$. И оболочка этих столбцов определит пространство столбцов. Если, например, в матрице $2 times 2$ столбцы линейно независимы и преобразование не приводит к снижению размерности, то пространство столбцов задается этими двумя векторами.

Замечу, что столбцы, не являющиеся разрешающими, называются свободными (free).

Ядро матрицы

Если преобразование уменьшает размерность (например, преобразовывает плоскость в линию), то несколько векторов оказываются в начале координат (становятся нулевыми векторами). Видео ниже прекрасно иллюстрирует эту трансформацию.

Множество таких «исчезающих» векторов называется ядром матрицы или ее нуль-пространством (null space, kernel).

ядро матрицы

Видео про обратные матрицы, ранг и ядро⧉.

Система уравнений

$Ax = b$

Рассмотрим пространство столбцов и ядро с точки зрения системы линейных уравнений. В первую очередь представим пространство столбцов, как решение системы $ A mathbf x = mathbf b $, т.е. линейную комбинацию вектор-столбцов $A$, умноженных на компоненты $mathbf x$.

$$ x_1 begin{bmatrix} vdots \ mathbf a_1 \ vdots end{bmatrix} + x_2 begin{bmatrix} vdots \ mathbf a_2 \ vdots end{bmatrix} + x_3 begin{bmatrix} vdots \ mathbf a_3 \ vdots end{bmatrix} = begin{bmatrix} vdots \ mathbf b \ vdots end{bmatrix} $$

Всегда ли $A mathbf x = mathbf b$ будет иметь решение? Нет. Возьмем некоторую матрицу $A$ и соответствующие ей векторы $mathbf x$ и $mathbf b$.

$$ begin{bmatrix} 1 & 1 & 2 \ 2 & 1 & 3 \ 3 & 1 & 4 \ 4 & 1 & 5 end{bmatrix} begin{bmatrix} x_1 \ x_2 \ x_3 end{bmatrix} = begin{bmatrix} b_1 \ b_2 \ b_3 \ b_4 end{bmatrix} $$

В такой системе будет много векторов $mathbf b$, которые не будут являться линейной комбинацией трех столбцов матрицы A.

вектор b вне пространства столбцов матрицы A

В каком случае такое решение все-таки будет существовать? Если $mathbf b$ будет являться линейной комбинацией векторов $A$, т.е. будет находиться в пространстве столбцов $A$, $mathbf b in col(A) $.

вектор b в пространстве столбцов матрицы A

Например, если $mathbf b$ будет равен одному из столбцов $A$.

$$ begin{bmatrix} 1 & 1 & 2 \ 2 & 1 & 3 \ 3 & 1 & 4 \ 4 & 1 & 5 end{bmatrix} begin{bmatrix} x_1 \ x_2 \ x_3 end{bmatrix} = begin{bmatrix} 1 \ 2 \ 3 \ 4 end{bmatrix} $$

Тогда решением может быть

$$ mathbf x = begin{bmatrix} 1 \ 0 \ 0 end{bmatrix} $$

Что интересно, все возможные решения $mathbf x$ именно такой системы $A mathbf x = mathbf b$, где $mathbf b in col(A) $ сами по себе не образуют векторное пространство (хотя бы потому что нулевой вектор не включен в эти решения).

Дополнительно замечу, что так как в матрице A только два линейно независимых вектора (третий вектор является суммой первых двух), то в данном случае мы имеем двумерное подпространство $R^4$.

$Ax = 0$

В системе линейных уравнений $A mathbf x = mathbf b$, если $mathbf b$ — нулевой вектор, т.е. $A mathbf x = mathbf 0$, то ядро дает все возможные решения этой системы (все возможные $mathbf x$). Можно также сказать, что ядро $mathbf x $ представляет собой комбинацию вектор-столбцов $A$, обращающихся в ноль.

$$ x_1 begin{bmatrix} vdots \ mathbf a_1 \ vdots end{bmatrix} + x_2 begin{bmatrix} vdots \ mathbf a_2 \ vdots end{bmatrix} + x_3 begin{bmatrix} vdots \ mathbf a_3 \ vdots end{bmatrix} = begin{bmatrix} vdots \ mathbf 0 \ vdots end{bmatrix} $$

В примере выше обратите внимание, что $col(A) in R^4$, в то время как $null(A) in R^3$. Решением же этой системы при нулевом векторе $mathbf b$, $A mathbf x = mathbf 0$ будет

$$ null(A) = k begin{bmatrix} 1 \ 1 \ -1 end{bmatrix} $$

где $k in mathbb{R} $. Другими словами, $null(A)$ представляет собой линию в $R^3$.

Убедимся, что для матрицы M выше мы правильно нашли ядро (а также решение $M mathbf x = 0$).

M = np.array([[1,   0,  1],

              [2,   3,  4],

              [–1, –3, –3]])

Null = np.array([–1, –2/3, 1])

M @ Null

Общее и частное решение

Приведем общее решение (complete solution) следующей системы, состоящее из частного решения (particular solution) системы $A mathbf x = mathbf b$ и ядра, то есть решения $A mathbf x = mathbf 0$.

$$ begin{bmatrix} 1 & 1 & 2 \ 2 & 1 & 3 \ 3 & 1 & 4 \ 4 & 1 & 5 end{bmatrix} begin{bmatrix} x_1 \ x_2 \ x_3 end{bmatrix} = begin{bmatrix} 1 \ 2 \ 3 \ 4 end{bmatrix} $$

$$ mathbf x = begin{bmatrix} 1 \ 0 \ 0 end{bmatrix} + k begin{bmatrix} 1 \ 1 \ -1 end{bmatrix} $$

Независимость векторов, базис и размерность

В свете новых знаний еще раз рассмотрим линейную независимость векторов и базис векторного пространства. Возьмем некоторую матрицу $A$.

Независимые вектор-столбцы

Можно сказать, что вектор-столбцы, образующие матрицу $A$ независимы, если ядро матрицы состоит только из нулевого вектора, $null(A) = { mathbf 0 }$ (решением $A mathbf x = mathbf 0$ будет только нулевой вектор $mathbf x$). Одновременно все столбцы такой матрицы являются разрешающими, и матрица имеет полный ранг, равный количеству столбцов $n$, $rank(A) = n$.

Если матрица А квадратная и ее столбцы линейно независимы, то можно сказать, что

  1. Вектор-столбцы матрицы образуют базис $R^n$
  2. Такая матрица будет обратима (!)

Приведем примеры обратимых матриц, столбцы которых формируют базис.

$$ begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end{bmatrix}, begin{bmatrix} 1 & 2 & 3 \ 1 & 2 & 1 \ 2 & 5 & 8 end{bmatrix} $$

A = np.array([[1, 2, 3],

              [1, 2, 1],

              [2, 5, 8]])

np.linalg.matrix_rank(A)

array([[ 5.5, -0.5, -2. ],

       [-3. ,  1. ,  1. ],

       [ 0.5, -0.5,  0. ]])

Зависимые вектор-столбцы

Если же столбцы зависимы, то ядро матрицы содержит также ненулевые векторы и решением $A mathbf x = mathbf 0$ будет или будут некоторые ненулевые векторы $mathbf x$. Столбцы матрицы будут как разрешающими, так и свободными. Ранг матрицы будет равен количеству разрещающих столбцов.

Базис пространства будет определяться именно линейно независимыми векторами, входящими в пространство столбцов. Размерностью (dimension) векторного пространства будет как раз количество векторов базиса.

Например, возьмем следующую матрицу $A$.

$$ A = begin{bmatrix} 1 & 2 & 3 & 1 \ 1 & 1 & 2 & 1 \ 1 & 2 & 3 & 1 end{bmatrix} $$

В данном случае у матрицы два линейно независимых столбца. В частности, это

$$ col(A) = left{ begin{bmatrix} 1 \ 1 \ 1 end{bmatrix}, begin{bmatrix} 2 \ 1 \ 2 end{bmatrix} right} $$

Как следствие,

$$ dim(col(A)) = rank(A) = dim(basis) = text{# of pivots} = 2 $$

Одновременно, нулевое пространство задано векторами

$$ null(A) = left{ begin{bmatrix} -1 \ -1 \ 1 \ 0 end{bmatrix}, begin{bmatrix} -1 \ 0 \ 0 \ 1 end{bmatrix} right} $$

Как следствие,

$$ dim(null(A)) = text{# of free columns} = 2 $$

Код на Питоне для нахождения пространства столбцов и ядра приведен в ноутбуке.

В качестве дополнения, замечу, что размерность векторного пространства характеризуется следом (trace) единичной матрицы этого пространства или суммой элементов главной диагонали. Например, размерность $R^3$ можно охарактеризовать через

$$ dim(col(A)) = tr left( begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 end{bmatrix} right) = 3 $$

Пространство строк и коядро

Пространством строк (row space) называют множество всех возможных линейных комбинаций вектор-строк.

Если матрицу транспонировать, то можно сказать, что

$$ row(A) = col(A^T) $$

Коядром или левым нуль-пространством (left null-space, cokernel) матрицы $A$ будет ядро матрицы $A^T$.

$$ leftnull(A) = null(A^T) $$

Продемонстрируем, почему это пространством называется именно левым нуль-пространством. По определению ядра, как решения $A mathbf x = mathbf 0$, можно сказать, что коядро будет решением $A^T mathbf y = mathbf 0$.

$$ A^T mathbf y = mathbf 0 $$

$$ mathbf y^T(A^T)^T = mathbf 0^T $$

$$ mathbf y^T A = mathbf 0^T $$

Схематично это можно представить следующим образом.

коядро (левое нуль-пространство)

Можно также сказать, что коядро y в системе $ A^T mathbf y = mathbf 0 $ дает все возможные комбинации столбцов $A^T$, дающие нулевой вектор (что то же самое, что линейные комбинации строк $mathbf x^T A = 0$). Приведем пример. Найдем коядро матрицы $A$.

A = Matrix([[1, 2, 3, 1],

            [1, 1, 2, 1],

            [1, 2, 3, 1]])

A.T.nullspace()[0]

коядро матрицы A

Другими словами, нам нужно взять $-1R_1 + 0R_2 + 1R_3$, чтобы получить нулевой вектор. Проверим полученный результат.

A = np.array([[1, 2, 3, 1],

              [1, 1, 2, 1],

              [1, 2, 3, 1]])

Leftnull = np.array([–1, 0, 1])

Leftnull.T @ A

Фундаментальные подпространства матрицы

Обобщим изложенную выше информацию. Возьмем матрицу A размерностью $m times n$. Тогда

  • $ null(A) in R^n$ (так как должно быть решением $A mathbf x = mathbf 0$)
  • $ col(A) in R^m $ (количество строк A)
  • $ row(A) = col(A^T) in R^n $ (количество столбцов A)
  • $ leftnull(A) = null(A^T) in R^m $ (так как должно быть решением $A^T mathbf y = mathbf 0$)

Тогда схематично эти подпространства можно представить следующим образом.

фундаментальные подпространства матрицы

Несколько пояснений и дополнений:

  • $r$ означает ранг (rank) матрицы
  • $r+(n-r) = n$, т.е. столбцы матрицы $A$
  • $r+(m-r) = m$, т.е. строки матрицы $A$ или столбцы $A^T$

Про пересечение подпространств. Может ли вектор $mathbf v = begin{bmatrix} 1 \ 2 end{bmatrix}$ быть одновременно в нуль-пространстве и являться частью пространства строк A (или в целом строкой в A)? Нет.

$$ begin{bmatrix} 1 & 2 \ dots & dots end{bmatrix} begin{bmatrix} 1 \ 2 end{bmatrix} not= begin{bmatrix} 0 \ 0 end{bmatrix} $$

Пересечением пространства строк и нуль-пространства будет только нулевой вектор.

$$ row(A) cap null(A) = { mathbf 0 } $$

Ортогональность подпространств матрицы

Более того, ядро ортогонально пространству строк $row(A) perp null(A)$, так как их скалярное произведение равно нулю. Это следует из определения ядра $A mathbf x = mathbf 0$ (произведение $mathbf x$ на каждую вектор-строку $mathbf a$ равно нулю).

$$ begin{bmatrix} dots & mathbf a_1 & dots \ dots & mathbf a_2 & dots \ dots & mathbf a_3 & dots \ dots & mathbf a_4 & dots end{bmatrix} begin{bmatrix} vdots \ mathbf x \ vdots end{bmatrix} = begin{bmatrix} 0 \ 0 \ 0 \ 0 end{bmatrix} $$

Более того, так как $null(A)$ содержит все векторы, ортогональные $row(A)$, то ядро можно считать ортогональным дополнением (orthogonal complement) пространства строк в $R^n$: $null(A) = row(A)^{perp} $.

То же самое справедливо для пространства столбцов и коядра.

$$ col(A) perp leftnull(A) perp null(A^T) text{ в } R^m $$

$$ leftnull(A), null(A^T) = col(A)^{perp} $$

Количество решений системы уравнений

Систематизируем наши знания о пространствах матрицы с точки зрения возможного количества решений систетемы уравнений.

Система не имеет решений

В случае если система не имеет решений, существует некоторый вектор $mathbf b $, при котором $A mathbf x = mathbf b $ не будет иметь решения.

$$ exists mathbf b implies A mathbf x not= mathbf b $$

С точки зрения матрицы $underset{m times n}{A}$, можно говорить о том, что некоторые строки линейно зависимы и после преобразования метода Гаусса обратятся в нули. Как следствие, ранг матрицы меньше количества строк, $r < m$.

линейно зависимые строки

Система имеет единственное решение

Если мы знаем, что система имеет единственное решение, то это означает, что нуль-пространство матрицы $A$ содержит только нулевой вектор, $null(A) = { mathbf 0 }$ и все столбцы линейно независимы, $ r = n $.

все столбцы линейно независимы

Система имеет множество решений

В этом случае решение состоит из частного решения и решения системы $A mathbf x not= mathbf 0 $. Другими словами, это означает, что нуль-пространство содержит не только нулевой вектор, а значит столбцы матрицы линейно зависимы и $ r < n $.

линейно зависимые столбцы

Теперь рассмотрим пример, иллюстрирующий применение матрицы для моделирования физического процесса и использование знаний о фундаментальных подпространствах матрицы.

Источник

Есть две двухстолбцовые матрицы А и В. Первые столбцы у них имеют одинаковые элементы. Задача: нужно выбрать все строки из второй матрицы В, элементы первого столбца которой совпадают с соотв. элементами первой матрицы А.

Т.е. нужно найти “пересечение” двух матриц по первым столбцам.

Например, если:

А’ = [1 2 4; 34 74 76] (матрицы для наглядности транспонированы)

B’ = [1 2 3 4 5; 16 23 75 46 45],

то нужно получить матрицу С, у которой первый столбец будет сформирован из элементов, общих в первых столбцах А и B (их пересечения), а второй — из элементов В.

Т.е. должно получиться

C’ = [1 2 4; 16 23 46]

Нет ли какой-нибудь функции в матлабе на эту тему?

P.S.

В маткаде такая функция есть — lookup.

lookup(z, A, B) Looks in a vector or matrix, A, for a given value, z, and returns the value(s) in the same position(s) (that is, with the same row and column numbers) in another matrix, B. When multiple values are returned, they appear in a vector in row-wise order, starting with the top left corner of B and sweeping to the right.

Источник

Добавить комментарий