Понятие “Множество” в математике и
информатике играет очень важную роль. В
математике существует целая теория множеств.
Первое знакомство с данной темой может быть у
учащихся как в начальной школе, если у них есть
курс информатики, так и у учащихся 5-6 классов,
которые раньше не изучали информатику. Данный
материал подготовлен для учащихся 5-6 классов.
Теме “Множества” желательно посвятить как
минимум 2 урока. Материал может быть полезен и для
преподавания информатики в начальной школе.
В курсе А.В. Горячева “Информатика в играх и
задачах”, рассчитанного на учащихся начальной
школы, тема “Множества” рассматривается и во 2
классе, и в 3 и в 4 классах. Естественно, что эта
тема прорабатывается с детьми не один урок, а
задания постепенно усложняются.
1. На первом уроке по теме “Множества” важно
сразу же дать четкие определения тех терминов,
которые потом будут использоваться в самых
различных заданиях. Урок основан на
использовании презентации (см.
Приложение 1).
Множество произошло от слова “много”. Но в
математике понятие “множество” используется
более широко.
Множество может объединять любое
количество предметов, чисел, существ. Каждый
предмет множества называется элементом
множества.
Множество, которое не содержит элементов,
называется пустым.
Множество может иметь подмножества.
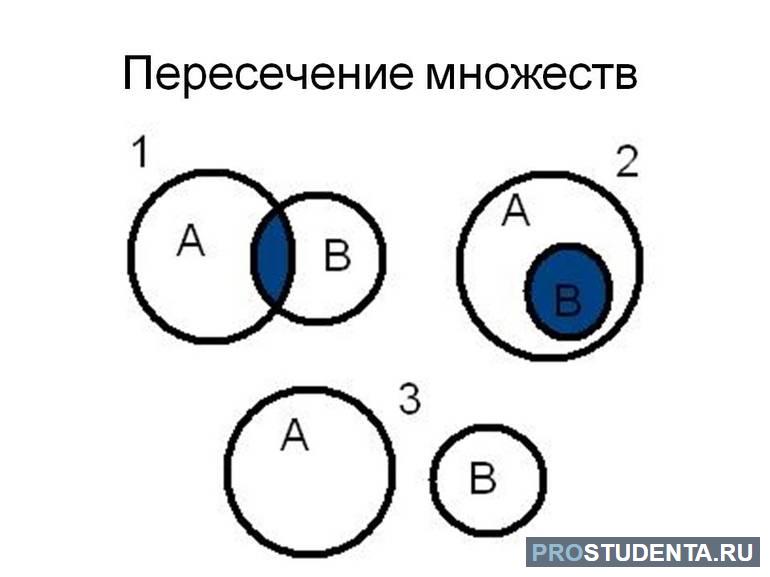
Множества могут пересекаться, не
пересекаться, объединяться.
Равными называются множества, состоящие из одинакового
числа одинаковых элементов.
(Желательно, чтобы эти определения были
записаны учащимися в тетрадь, чтобы потом они
могли к ним вернуться.)
Эти определения необходимо закрепить на
простейших примерах, например: множество
животных имеет несколько подмножеств: рыбы,
птицы, звери, насекомые – и они не пересекаются.
Если же мы возьмем множество морских животных,
то оно будет пересекаться с множеством птиц и
множеством зверей (приводятся несколько
примеров). В качестве пустого множества можно
дать такой пример: в яркий солнечный день на небе
нет облаков, поэтому в этот день множество
облаков (такое множество естественно существует)
– пустое, а в другой день оно уже не будет пустым.
Этот пример используется в тетради А.В. Горячева
“Информатика в играх и задачах” 3 класс, часть 2.
Можно привести и другие примеры, когда какое-то
множество в конкретной ситуации будет пустым.
Также для удобства выполнения различных
заданий необходимо ввести систему обозначения
множеств (геометрические фигуры), подчеркнув,
что это только условное обозначение, но оно очень
удобно. Элементы множеств обозначаются точками.
Для закрепления понятия “элементы множества”
учащимся предлагается следующее задание 1 (приложение 2) (его можно давать
как домашнее задание, которое вклеивается в
тетрадь).
2. Далее вводятся понятия, связанные с
использованием логических связок в названиях
множеств.
В названиях множеств и высказываниях могут
употребляться логические связки: “и”, “не”,
“или” и их комбинация: “не … и”, “не …
или”. “не … и не …”
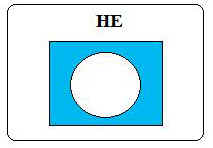
Если в названии множества есть связка “не”,
то его элементы находятся за пределами фигуры,
обозначающей это множество.
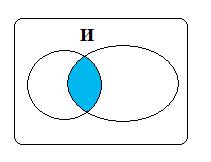
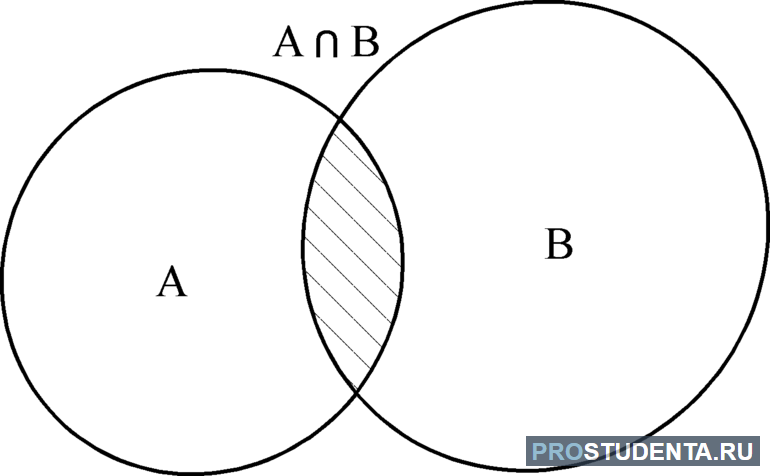
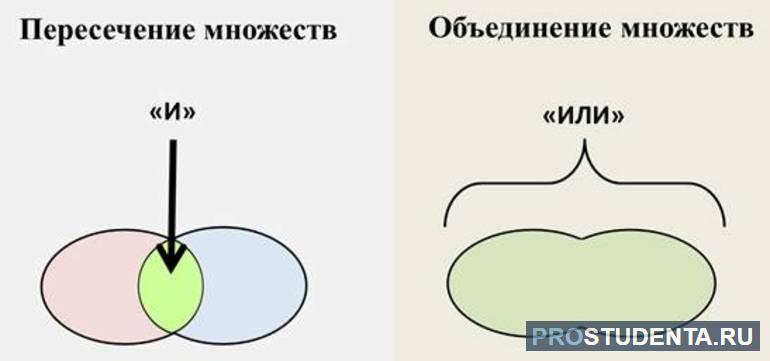
Если в названии множества есть связка “и”,
то его элементы находятся на пересечении фигур,
обозначающих множества.
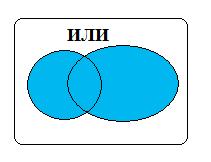
Если в названии множества есть связка “или”,
то это означает, что его элементы находятся в
нескольких фигурах.
Эти схемы также необходимо закрепить с
учащимися на разных примерах, включенных в
задания в тетради (курс Горячева для начальной
школы), а также на тех, где они сами приводят
примеры различных множеств. Для закрепления
понятий пересечения и объединения множеств
учащимся предлагается дополнительное задание 2.
3. На следующем(их) уроке(ах) следует продолжить
подробный разбор заданий, например, включив
задания на пересечение трех множеств. (Желательно
также, чтобы эти схемы были зарисованы учащимися
в тетрадях).
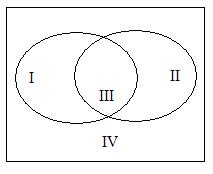
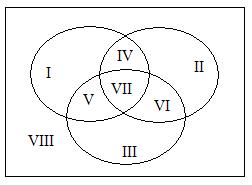
При пересечении 2-х множеств образуется IV
области: 2 области без пересечения, одна область
пересечения множеств и одна область, лежащая за
пределами выделенных множеств.
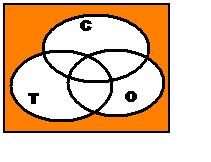
При пересечении 3-х множеств образуется VIII
областей: 3 области без пересечения, 4 области
пересечения множеств и 1 область, лежащая за
пределами выделенных множеств.
Обозначение множеств:
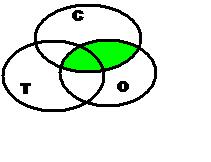
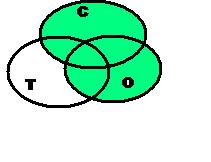
При пересечении двух множеств
закрашивается вся область пересечения этих
множеств. При объединении двух множеств
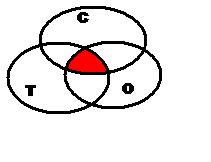
закрашиваются оба множества. При пересечении
трех множеств закрашивается общая часть всех
трех множеств. При отрицании всех трех
множеств закрашивается область, не включающая в
себя сами множества.
Данные схемы сделаны для задания, когда надо
распределить слова, в состав которых входят
буквы “С”, “Т” и “О”. Набор слов должен
включать слова только с “Т”, только с “С”,
только с “О”, а также одновременно с двумя и
тремя буквами. Два-три слова должны быть без букв
“С”, “Т”, “О”. (Например: рельсы, купе,
проводник, скорость, колесо, электровоз, тамбур,
вагон, сумка, место, шпалы, поезд, машинист, билет,
состав, дверь, станция).
В курсе информатики А.В. Горячева в тетради 2
класса есть аналогичное задание на множества
“Круглые”, “Желтые”, “Шары”.
Закрепление теоретического материала должно
сопровождаться решением задач. Простейшие
задачи, например, “Про коз и коров”, “Фиалки и
подруги”, “Газеты и журналы” могут быть
использованы даже во 2 классе (см. приложение
4). Для более сильных учеников и для более
старших классов, соответственно, можно подобрать
задачи нужного уровня, а можно также
использовать какие-то задачи и для проведения
конкурсов, КВНов, школьных олимпиад, недели
математики и информатики. Подобные задачи удобно
решать, используя схему множеств и обозначая
элементы просто точками (если числа малые) или
указывая число элементов в соответствующей
области (в пересечении, без пересечения).
Задачи собраны из самых различных источников,
включая журнал “1 сентября. Информатика”, сайт
Малого Мехмата МГУ и другие сайты, посвященные
решению логических задач.
- Приложение 1. Презентация
“Множества” - Приложение 2. Задание 1.
- Приложение 3. Задание 2.
- Приложение 4. Дополнительные
задачи.
Список литературы.
- Горячев А.В., Горина К.И., Суворова Н.И.
“Информатика в играх и задачах” 2 кл., в 2-х ч. - Горячев А.В., Горина К.И., Суворова Н.И.
“Информатика в играх и задачах” 3 кл., в 2-х ч. - Горячев А.В., Горина К.И., Суворова Н.И.
“Информатика в играх и задачах” 4 кл., в 2-х ч. - Горячев А.В., Горина К.И., Суворова Н.И.
Методические рекомендации для учителя. 2 кл.. - Горячев А.В., Горина К.И., Суворова Н.И.
Методические рекомендации для учителя. 3 кл.. - Горячев А.В., Горина К.И., Суворова Н.И.
Методические рекомендации для учителя. 4 кл. - Горячев А.В., Суворова Н.И. Информатика. Логика и
алгоритмы. 3 кл. - Горячев А.В., Суворова Н.И. Информатика. Логика и
алгоритмы. 4 кл. - Журнал “1 сентября. Информатика”. Сайт https://inf.1sept.ru/
- Фестиваль “Открытый урок”. Сайт https://urok.1sept.ru/ раздел
“Информатика”. - Малый Мехмат МГУ. Сайт http://mmmf.msu.ru/.
- Сайт Логические задачи и головоломки http://www.smekalka.pp.ru/.
- Сайт Логические задачи, головоломки, загадки,
тесты – Лого-рай http://logo-rai.ru/
Всем привет! Я Елена, и на канале TeachYOU мы разбираем задачи из экзаменов по информатике. Обычно я пишу статьи с разбором задач из ЕГЭ, но этот материал пригодится и 9му классу, и 11му. Если вы готовитесь к ЕГЭ и считаете, что эта тема вам не нужна, то советую заглянуть в задания 279 (прототип 24), 5627 (прототип 9) и 2557 (прототип 8) с kompege. Они намного проще решаются, когда обладаешь навыком решения задач на круги Эйлера.
Множества
Чтобы начать говорить о кругах Эйлера, нужно ввести понятие множества. Множество – это набор объектов, объединенных каким-то признаком. Например, множество квадратных объектов, множество предметов, изучаемых в 9 классе и пр.
Рассмотрим множество объектов оранжевого цвета. В него входят рыжий кот, спасательный жилет, апельсин, осенний кленовый лист, и много других объектов оранжевого цвета. На рисунке изобразим круг и будем предполагать, что все оранжевые предметы находятся внутри него:
Теперь возьмем множество животных кошачьего семейства. Здесь будут домашние кошки, тигры, львы, гепарды и остальные представители данного семейства.
Пересечение множеств
Заметим, что рыжий кот входит в оба множества. Поэтому, если мы изобразим эти множества рядом, должны будем расположить их следующим образом:
Область, в которой сидит рыжий кот, называется пересечением множеств. Множества принято обозначать заглавными латинскими буквами: A, B, C, … Пересечение обозначают символом & : A & B, читается как “пересечение множеств A и B“.
В общем случае произвольные два множества располагаются именно так: есть элементы, входящие в оба множества (то есть пересечение множеств непустое), а есть элементы, которые не входят только в одно из множеств.
Объединение
В гости к Пете едет его любимая бабушка. Она поинтересовалась у внука, что можно купить ему в подарок. Он сказал, что любит книжки и машины. В магазине бабушка увидела разные игрушки, и в блокноте изобразила круги Эйлера – один с множеством машин, второй – с множеством книжек. В пересечение этих кругов попала книга о машинах. Вне кругов расположились шарик, вертолет, матрешка и медвежонок – они не входят в множество предполагаемых подарков для Пети:
Область, похожая на перевернутую восьмерку, иллюстрирует множество машинок и книжек – подходящих подарков. Такое множество называется объединением. В него входят все элементы изначальных множеств, причем те, которые находятся на пересечении, входят только один раз:
Мощность множеств
Мощность множества – это количество элементов в нем. Обозначается так: |A|. Мощность множества может быть равна нулю (пустое множество), конечному числу (мощность множества десятичных цифр равна 10) или равна бесконечности (мощность множества натуральных чисел).
Частные случаи расположения элементов двух множеств
Случай 1. Равенство
Рассмотрим картинку с изображениями людей.
Выберем из них два множества:
- А – люди с длинными волосами
- В – женщины
Получилось, что в оба множества входят одни и те же элементы. В этом случае говорят о равенстве множеств:
- A = B – множество А равно множеству В
- A & B = A (= B) – пересечение множеств совпадает с множеством А (или В)
- А | В = А (=В) – объединение множеств равно множеству А (или В)
Что в этом случае происходит с мощностями множеств?
- |A | B| = |A & B| = |A| = |B|
Случай 2. Включение
Все элементы одного множества могут входить в другое множество – тогда говорят о включении одного множества в другое (A ⊂ B). Пусть А – множество домашних кошек. Оно включено в B – множество представителей семейства кошачьих (также можно сказать “множество домашних кошек является подмножеством множества представителей семейства кошачьих”).
Заметим, что пересечение множеств в этом случае совпадает с множеством домашних кошек, а объединение – с множеством представителей семейства кошачьих:
- A ⊂ B (А включено в В, А является подмножеством В)
- A & B = A (пересечение множеств совпадает с множеством А)
- A | B = B (объединение множеств равно множеству В)
Для мощностей множеств можно сформулировать следующие утверждения:
- |A| < |B|
- |A & B| = |A|
- |A | B| = |B|
Случай 3. Непересечение
Бывает, что у множеств нет общих элементов. Про такие множества говорят, что они не пересекаются или что их пересечение равно пустому множеству (A & B = ∅). Давайте изобразим множества представителей кошачьих и собачьих (сложно придумать животного, которое будет одновременно кошкой и собакой):
- A & B = ∅ – множества не пересекаются (пересечение множеств равно пустому множеству)
О мощностях:
- |A & B| = 0
- |A | B| = |A| + |B|
Формула включения/исключения для двух областей
Вернемся к примеру с бабушкой и Петей. Пусть бабушка хочет посчитать, сколько вариантов выбрать один подарок у нее есть. Она знает мощность множества А – подарков на “машинную” тематику, мощность множества книг В и мощность их пересечения A&B.
То, что хочет найти бабушка, называется мощностью объединения множеств A | B. Логично предположить, что для его поиска нужно сложить мощности множеств A и B: 4 “машинковых” подарка + 3 книги = 7 подарков. Но на картинке видно, что всего подарков 6! Дело в том, что при суммировании мощностей множеств A и B элемент, находящийся на их пересечении, мы посчитали два раза. Тогда его нужно один раз отнять. Итого формула нахождения мощности множества объединения двух множеств такова:
|A | B| = |A| + |B| – |A & B|
Ее называют формулой включения – исключения.
Задание 8 ОГЭ по информатике
Наконец мы добрались до заданий из ОГЭ. Оговорюсь, что знание теории, описанной выше, поможет решить не все задачи – в сборниках встречаются задания на три множества. Подобные мы разберем в другой раз.
Задание 1369 с сайта К.Ю. Полякова
Задание: Ниже приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
шахматы | теннис 7770
теннис 5500
шахматы & теннис 1000
Сколько страниц будет найдено по запросу
шахматы?
Решение: обозначим множество страниц, которое находится по запросу шахматы как Ш, а по запросу теннис как Т. Тогда формула включения-исключения примет вид:
|Ш | Т| = |Ш| + |Т| – |Ш & Т|
Подставим в нее известные величины:
7770 = |Ш| + 5500 – 1000
И выразим неизвестную:
|Ш| = 7770 – 5500 + 1000 = 3270
Ответ: 3270
Задание 1365 с сайта К.Ю. Полякова
Задание: Ниже приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
лебедь & (рак | щука) 320
лебедь & рак 200
лебедь & рак & щука 50
Сколько страниц будет найдено по запросу
лебедь & щука?
Решение: может показаться, что эта задача на три множества и силами теории, описанной в этой статье, ее не решить. Но давайте заметим, что во всех строках условия встречается “лебедь &”. Предлагаю на данном этапе не углубляться в теорию множеств, а довериться мне и сократить на лебедя:
лебедь & (рак | щука) 320лебедь & рак 200лебедь & рак & щука 50
Сколько страниц будет найдено по запросу
лебедь & щука?
Теперь это задача на два множества (я их фамильярно называю задачами на два кружочка). Выписываем формулу:
|Р | Щ| = |Р| + |Щ| – |Р & Щ|
Подставляем известные величины, выражаем неизвестную:
|Щ| = 320 + 50 – 200 = 170.
Ответ: 170
Домашнее задание
Сайт К.Ю. Полякова, номера 1368, 1357, 1351, 1364, 1362.
Что с тремя множествами?
Я буду писать статью о трех множествах, где расскажу и об общем случае их пересечения, и о частном под кодовым названием “микки-маус” (или “гусеничка”). Если вам важно, чтобы этот материал вышел поскорее, напишите об этом в комментариях или поставьте лайк – тогда я узнаю, что вы его ждете.
Успехов вам с подготовкой от меня и канала TeachYOU 🙂
Вы
знаете, ученик третьего класса Максим очень хотел объяснить вам эту тему, но
немного приболел и прийти сегодня не смог. Но, благодаря Интернету, мы можем с
ним связаться.
̶
Здравствуй Максим!
̶
Здравствуйте! Проверьте, чтобы ваши соседи по парте были готовы к уроку. И мы
начинаем.
Прослушайте
название пар множеств и попытайтесь заметить, что повторяется в
каждой паре.
Животные
и герои мультфильмов;
Рыбы
и птицы;
Материки
и части света;
Звёзды
и планеты.
Ну,
что заметили? Конечно, повторялся слово «и».
Если
в названии множества есть союз «И», то каждый его элемент должен находиться
на пересечении двух множеств, т.е. находиться одновременно в двух
множествах. Другими словами мы можем сказать, что пересечение множеств
– это их общая часть.
А
теперь задание.
Необходимо
разместить элементы по своим множествам.
Давайте
посмотрим, что за элементы. Так это имена мальчиков и девочек: Коля, Ваня,
Даша, Игорь, Катя, Саша, Дима, Юля, Ира, Женя. Будем размещать имена мальчиков
в синий прямоугольник, а девочек – в розовый. Ага! Так ведь Сашей и Женей могут
звать как мальчиков, так и девочек. Значит, эти два имени будут находиться
сразу в двух множествах, т.е. на пересечении двух множеств.
Итак,
Коля, Ваня – это мальчики, помещаем эти элементы во множество имён мальчиков.
Даша – имя девочки, помещаем в розовый прямоугольник, где находятся имена
девочек. Игорь – имя мальчика, Катя – имя девочки. Саша, так могут звать и
мальчика, и девочку, значит, этот элемент будет находиться на пересечении
двух множеств. Дима – элемент из множества имён мальчиков. Юля, Ира,
конечно элементы из множества имён девочек. И последнее имя, Женя, это имя
могут иметь как девочки, так и мальчики. Значит, этот элемент будет находиться на
пересечении двух множеств.
Теперь
все имена находятся в своих множествах.
А
сейчас я прочитаю названия ещё нескольких пар множеств, а вы попытайтесь
заметить, что повторяется в этих парах.
Яблоки
или груши;
Полевые
или садовые цветы;
Попугаи
или морские свинки;
Рабочие
или выходные дни.
Заметили,
что повторялось в парах множеств? Конечно, это слово «или».
Посмотрите
ещё раз на названия множеств.
Например,
яблоки или груши. А ведь эти множества можно объединить в одно с общим
названием «фрукты» и все элементы будут располагаться в одном новом
множестве.
Попугаи
или морские свинки. Их можно объединить во множество с названием
«домашние
животные» и все попугаи, и все морские свинки будут находиться в новом
множестве.
Значит,
если в названии множества есть слово «или», то его элемент может
находиться в любом множестве и тогда происходит объединение множеств, т.е. эти множества
объединяются.
Давайте
рассмотрим два множества: домашние животные, дикие животные.
Множество
домашние животные содержат следующие элементы: собака, кошка, морская свинка,
попугай.
Множество
дикие животные состоит из следующих элементов: бегемот, леопард, волк, лев.
Какой
общий признак у элементов этих двух множеств? Элементы
каждого из них относятся с животному миру. Значит, можно, объединив эти
множества, создать новое множество под названием животные. Теперь
все элементы находятся в одном множестве.
А
теперь, конечно, задание.
Распределить
элементы по множествам, объединить их и придумать
название для нового множества.
Итак,
смотрим на элементы. Ага, у нас два множества: множество стульев
и множество столов. Распределяем элементы по множествам. Все элементы
стулья во множество стульев, а все элементы столы во множество столов.
Объединяем
множества. Какое название будет у нашего нового множества?
Множество мебели.
Давайте
ещё раз определим разницу между пересечением и объединением множеств.
Если
в названии множества есть слово «И», то это пересечение,
и каждый элемент должен находиться на пересечении двух множеств.
Если
в названии множества есть слово «или», то его элемент может
находиться в любо области объединённых множеств.
Я
надеюсь, что вы поняли разницу между пересечением и объединением
множеств. А давайте проверим?
Итак,
перед вами рисунок с тремя множествами.
Множество
учеников, которые любят математику, множество учеников, которые любят
информатику и множество всех учеников. Но, среди учеников есть и такие, которые
любят и математику и информатику. Значит, эти два множества пересекаются
и одновременно они являются подмножеством множества всех
учеников. А теперь появляются элементы во множествах.
Используя
полученные знания сегодня на уроке, будем отвечать на вопросы. А все ответы
хранятся на этом рисунке, главное внимательно слушать вопросы и внимательно
смотреть на рисунок.
Первый
вопрос:
Сколько
учеников любят математику? Считаем их во множестве учеников, которые любят
математику, и не забываем посчитать тех учеников, которые находятся на пересечении
двух множеств учеников, которые любят и математику, и информатику. Считаем. Их
шесть.
Сколько
учеников любят информатику? Считаем их во множестве учеников, которые любят
информатику и опять считаем тех учеников, которые находятся на пересечении
двух множеств. Считаем. Их пять.
Сколько
учеников любят и математику, и информатику? Будем считать тех учеников, которые
находятся на пересечении двух множеств. Их три.
Сколько
учеников любят или математику или информатику? Если используется слово «или»,
значит элементы находятся в любом месте множеств за исключением любителей двух
предметов сразу. Значит, считаем учеников и в первом множестве и во втором, но
не включаем тех, кто находится в пересечении. Их пять.
Сколько
учеников любят только математику? Любят математику только те, которые находятся
во множестве учеников, которые любят математику. Ученики, которые находятся на
пересечении двух множеств, сюда относится не будут, т.к. они любят и
математику, и информатику. Итак, считаем и получается, что 3 ученика любят
только математику.
Сколько
учеников любят только информатику? Опять, учеников, которые находятся на пересечении
двух множеств, считать не будем. Любителей информатики двое.
Сколько
учеников не любят математику? Надо посчитать их во множестве учеников, которые
любят информатику, кроме тех, которые находятся на пересечении
множеств, т.к. эти ученики любят информатику и математику. А так же надо
посчитать тех учеников, которые находятся во множестве всех учеников, т.к. они
не любят математику. Их всего 5.
Всем
спасибо за отличную работу. Теперь я точно понял, что хочу быть учителем!
Тебе
спасибо, Максим. Тему объяснил хорошо. До свидания! А мы ещё сделаем выводы.
Итак.
Множество
– это объединение некоторых объектов (элементов) в группу по определённым
признакам.
Множество
может быть подмножеством другого множества. Например: множество
собак является подмножеством множества домашние животные.
Множества
могут пересекаться. Например: множество чисел, которые делятся на
2, и множество чисел, которые делятся на 3, пересекаются, т.к. числа, например,
6 и 12 делится и на 2, и на 3.
Множества
могут и не пересекаться. Например: множество телефонов и
множество цветов.
И
множества могут объединяться. Например: множество рабочих дней
недели и множество выходных можно объединить в одно множество дней недели.
Выводы
сделаны, и я желаю вам успехов при выполнении заданий!
Математика тесно связана с различными дисциплинами, одной из которых является информатика. В последней применяются массивы, состоящие из чисел, букв и слов. Чтобы научиться работать с этим типом данных, необходимо разобрать объединение и пересечение множеств, примеры которых разбираются на уроках по алгебре в 8 классе средних образовательных школах. Однако для начала нужно изучить теорию.
Оглавление:
- Общие сведения
- Правила чтения
- Пересечение множеств
- Объединение объектов
Общие сведения
Множеством (массивом) называется математический объект или тип данных (в программировании), состоящий из определенного количества простых элементов. Примером является квартира, в которой находится различная техника, мебель и другие элементы. Следует отметить, что множества также бывают и сложными, однако в 8 классе они не рассматриваются.
Обозначается оно двумя способами:
- Заглавной литерой, после которой идут элементы: D = {1, 2, 3, 4}.
- Только в фигурных скобках.
Первый случай применяется при решении задач с несколькими различными массивами, чтобы их не перепутать между собой. Если в задании используется только одна последовательность, то короткая запись включает только фигурные скобки.
Исключением считается массив информатики в 8 классе, формулы записи которого предусматривают только поименованные объекты, т. е. любая переменная должна иметь определенный идентификатор (имя).
Правила чтения
Очень важно научиться правильно читать множества. Для примера следует разобрать массив чисел-делителей числа 20, имеющий следующий вид: F = {1, 2, 4, 5, 10, 20}. Принадлежность заданного элемента объекту обозначается символом «∈”. Например, запись «5 ∈ F» читается таким образом: элемент «5» принадлежит F. Если число не принадлежит, то знак «∈” перечеркивается, т. е. 7 ∉ F.
В программировании массив обозначается заглавной буквой, и указываются все его элементы. В Турбо Паскале, который изучается в школах и профильных училищах на базе 8 классов, используется для записи ключевое слово «array», т. е. var а: array [ 1, 2, 4, 5, 10, 20 ] of integer.
Сочетание слов «of integer» обозначает тип элементов. Читается строка таким образом: тип данных в виде массива «а», содержащего целые числа (integer). Последние указываются в квадратных скобках. Именно ключевое слово «array» и указывает на принадлежность переменной к этому типу данных.
В учебных заведениях с физико-математическим уклоном изучаются в 3 классе примеры пересечения множеств. Учителя дают только общие понятия в виде презентаций, чтобы постепенно перейти к усиленной программе обучения.
Пересечение множеств
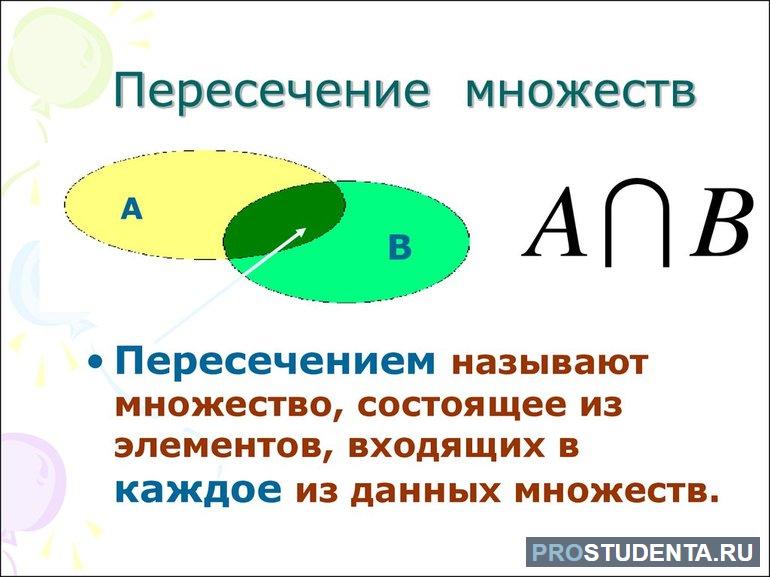
В математике, как и информатике, пересечение множеств является важной операцией. Она позволяет из двух объектов определить только общие элементы, которые в них содержатся. Для обозначения процесса используется специальный знак «∩».
Чтобы не путаться в терминах, математики рекомендуют разобрать основные определения. Пересечение множеств — массив, состоящий только из общих их элементов. Например, дано два объекта S = {1, 2, 4, 6, 7, 8} и I = {3, 4, 7, 12, 18, 20}.
Алгоритм определения
Для определения их пересечения необходимо перебрать все их элементы. Конечный результат «R» вычисляется по такой формуле перебора:
- Записать пустое множество: R = {}.
- Акцентировать внимание на S.
- Первый элемент отсутствует в I, тогда он не записывается в R.
- Второго также нет.
- Третий компонент присутствует в S и I. В этом случае число «4» записывается в R, т. е. R = {4}.
- Четвертого нет в I.
- Пятый: есть. R = {4, 7}.
- Последний — отсутствует.
- Запись результата: {1, 2, 4, 6, 7, 8} ∩ {3, 4, 7, 12, 18, 20} = {4, 7}. Краткая запись имеет следующий вид: S ∩ I = R.
В программировании примером пересечения множеств является объединение двух массивов в один с уникальными элементами. Язык программирования Турбо Паскаль не применяется в написании современных приложений. Он изучается в ознакомительных целях, которые дают базовые знания.
Современные профессиональные языки программирования могут осуществлять доступ к базе данных или к другим массивам информации, в которые не записывается одинаковая информация для экономии оперативной и дисковой памяти компьютера или интернет-ресурса.
Основные свойства
Для решения задач на пересечение объектов, состоящих из числовых или символьных элементов, могут быть полезны свойства. К ним относятся следующие:
- Бинарность.
- Коммутативность.
- Ассоциативность.
- Нейтральность.
- Идемпотентность.
- С пустым объектом.
В первом случае результатом, с точки зрения логической алгебры, являются только 2 значения (пересекает или не пересекает). Коммутативность обусловлена тем, что можно брать первый или второй массив, т. е. S ∩ I = R или I ∩ S = R. Результат от этого не изменится. При рассмотрении трех и более составных объектов справедливо свойство ассоциативности: (S ∩ I) ∩ T = S ∩ (I ∩ T) = (S ∩ T) ∩ I = R.
Четвертое свойство предусматривает существование некоторого нейтрального множества, которое не учитывается при решении. Например, в квартире установлена следующая техника: телевизор, компьютер, кондиционер и т. д. Массивом является «техника», а его компоненты — телевизор, компьютер и другие виды приборов. «Квартира» — нейтральный объект, поскольку он не рассматривается, но включает «технику» и другие группы элементов.
Идемпотентность — пересечение идентичных множеств, т. е. все элементы первого совпадают со вторым. Результатом является искомый объект. Свойство записывается математически таким образом: S ∩ S = S.
Последнее свойство — пересечение объекта с пустым массивом, который обозначается символом «∅”. Результатом является ∅, поскольку оно не содержит общих элементов с исходным.
Объединение объектов
Объединение множеств — математическая операция, которая предусматривает создание массива из всех их элементов. Например, даны два объекта S = {1, 2, 4, 6, 7, 8} и I = {3, 4, 7, 12, 18, 20}. Чтобы их объединить необходимо воспользоваться следующей методикой:
- Записать результирующий массив: R = {}.
- Добавить в R все элементы: R = {1, 2, 4, 6, 7, 8, 3, 4, 7, 12, 18, 20}.
- Выполнить сортировку элементов по возрастанию: R = {1, 2, 3, 4, 4, 6, 7, 7, 8, 12, 18, 20}.
- Исходя из условия задачи, убрать повторяющиеся элементы: R = {1, 2, 3, 4, 6, 7, 8, 12, 18, 20}.
Операция довольно простая, поскольку разобраться с ней не составит труда. При написании программы на языке программирования высокого уровня (например, python) необходимо избегать дублирования элементов. Перед записыванием информации в файл или базу данных нужно убрать одинаковые компоненты при помощи встроенных функций.
Таким образом, изучать операции над множествами необходимо, поскольку эти знания пригодятся при решении сложных задач по высшей математике, а также написании программ на высокоуровневых языках программирования.
На уроке рассматривается разбор 15 задания ЕГЭ по информатике, дается подробное объяснение того, как решать подобные задачи
Содержание:
- Объяснение задания 15 ЕГЭ по информатике
- Элементы математической логики
- Математическая логика и теория множеств
- Задания с отрезками и ДЕЛ
- Задания с поразрядной конъюнкцией
- Решение заданий 15 ЕГЭ по информатике
- Задания с множествами
- Задания с отрезками на числовой прямой
- Задания с ДЕЛ
- Задания с поразрядной конъюнкцией
- Задания на поиск наибольшего или наименьшего числа А
15-е задание: «Основные законы алгебры логики»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 5 минут.
Проверяемые элементы содержания: Знание основных понятий и законов математической логики
До ЕГЭ 2021 года — это было задание № 18 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
“Важно понимать, что выражение должно быть тождественно истинно, т.е. истинно при любых допустимых значениях переменных x и у, а не только при некоторых наборах значений”
ФГБНУ “Федеральный институт педагогических измерений”
Элементы математической логики
-
Для решения 15 задания, потребуется знание таблиц истинности.
- операцию импликация можно преобразовать в операции ИЛИ и НЕ:
- операцию эквивалентность можно преобразовать:
- операцию XOR (сложение по модулю 2) можно преобразовать так:
- кроме того, могут пригодиться базовые аксиомы и формулы:
- Порядок выполнения логических операций:
- выражения в скобках,
- операции «НЕ»,
- операции «И»,
- операции «ИЛИ»,
- операции «импликация»
- операции «эквиваленция»
- последовательность из операций импликации выполняется слева направо (при этом соблюдается принцип «операции с одинаковым приоритетом выполняются слева направо»):
Для выполнения задания рекомендуется повторить следующие темы:
Преобразование логических операций:
A → B = ¬ A ∨ B
или
A → B = A + B
A ↔ B = A ⊕ B = A ∧ B ∨ A ∧ B
или
A ↔ B = A ⊕ B = A · B + A · B
A ⊕ B = (¬A ∧ B) ∨ (A ∧ ¬B)
или
A ⊕ B = (A · B) + (A · B)
Законы алгебры логики:
| Закон двойного отрицания: |
¬¬ A = A |
| Закон исключения третьего: |
A ∧ ¬ A = 0 или A · A = 0 |
| Закон повторения (идемпотентности): |
A ∧ A = A или A · A = A |
| Законы исключения логических констант: |
A ∧ 0 = 0 |
| Переместительный (коммутативный) закон: |
A ∧ B = B ∧ A |
| Сочетательный (ассоциативный) закон: |
(A ∧ B) ∧ C = A ∧ (B ∧ C) |
| Распределительный (дистрибутивный) закон: |
(A ∧ B) ∨ C = (A ∨ C) ∧ (B ∨ C) |
| Закон общей инверсии (Законы де Моргана): |
¬ (A ∧ B) = ¬ A ∨ ¬ B |
| Закон исключения (склеивания): |
(A ∧ B) ∨(¬A ∧ B) = B |
| Упрощать выражения можно с помощью формул: | |
| Закон поглощения: |
A ∨ A ∧ B = A |
A → B → C → D = ((A → B) → C) → D
Математическая логика и теория множеств
- пересечение множеств соответствует логическому умножению, а объединение – логическому сложению;
- пересечением двух множеств называется новое множество, состоящее из элементов, принадлежащих одновременно обеим множествам:
- объединением двух множеств называется новое множество, состоящее из элементов, принадлежащих отдельно каждому из множеств (без повторений);
- пустое множество
∅– это множество, в котором не содержится ни одного элемента; пустому множеству в теории множеств соответствует0; - универсальное множество
U(на кругах Эйлера обозначается в виде прямоугольника) – это множество, содержащее все возможные элементы определенного типа (например, все вещественные числа): - универсальное множество соответствует логической единице: для любого множества целых чисел
Xсправедливы равенства: - разностью двух множеств
AиBназывается новое множество, элементы которого принадлежатA, но не принадлежатB: - дополнение множества
X– это разность между универсальным множествомUи множествомX(например, для целых чисел¬ X– все целые числа, не входящие вX) - пусть требуется выбрать множество
Aтак, чтобы выполнялось равенствоA ∨ X = I; в этом случае множествоAдолжно включать дополнение¬ X, то естьA ≥¬ X(или A ⊇¬ X), то естьAmin = ¬ X - пусть требуется выбрать множество
Aтак, чтобы выполнялось равенство¬ A ∨ X = I, в этом случае множество¬ Aдолжно включать дополнение¬ X, то есть¬ A ⊇ ¬ X; отсюдаA ⊆ X, то естьAmax = X
Пример:
Пример:
X ∨ U = U и X ∧ U = X
Пример разности множеств:
Для большей определенности стоит рассмотреть тему круги Эйлера
Задания с отрезками и ДЕЛ
Для решения заданий необходимо знать рассмотренную тему о множествах.
Для упрощения решений можно пользоваться следующими законами.
1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A без отрицания
то используется закон:
Amin = ¬B
где B — известная часть выражения.
1. Если в задании формула тождественно истинна (равна 1), и
2. после упрощения A с отрицанием
то используется закон:
Amax = B
где B — известная часть выражения.
1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A без отрицания
то используется закон:
Amax = ¬B
где B — известная часть выражения.
1. Если в задании формула тождественно ложна (равна 0), и
2. после упрощения A с отрицанием
то используется закон:
Amin = B
где B — известная часть выражения.
Задания с поразрядной конъюнкцией
В задании 15 ЕГЭ встречаются задачи, связанные с поразрядной конъюнкцией.
Например:
5 & 26
означает поразрядную конъюнкцию (логическое «И») между двоичными значениями двух чисел — 5 и 26. Выполняется так:
5 = 1012 26 = 110102 0 = 000002
Задания, связанные с поразрядной конъюнкцией, решаются несколькими способами. Рассмотрим один из них.
- Обозначим:
(x & K = 0) как Zk
Zk * Zm = Zk or m
(X & 5 = 0) ∧ (X & 26 = 0)
Z5 ∧ Z26
Z5 ∧ Z26 = Z26 or 5 помним, что дизъюнкция - это операция логическое "ИЛИ" (сложение) 5 = 1012 26 = 110102 31 = 111112
Z5 ∧ Z26 = Z31
Zk + Zm = Zk and m
(X & 28 = 0) ∨ (X & 22 = 0)
Z28 ∨ Z22
Z28 ∨ Z22 = Z28 and 22
помним, что конъюнкция - это операция логическое "И" (умножение)
28 = 111002
22 = 101102
101002 = 2010
Z28 ∨ Z22 = Z20
Условие Zk → Zm истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.
- На деле, это означает, что если имеем:
X & 29 = 0 → X & 5 = 0 Истинно или Ложно?
Z29 → Z5
Z29 → Z5 = 1 (истине), тогда, когда: 29 = 111012 5 = 1012 единичные биты двоичного числа 5 входят в единичные биты двоичного числа 29 (совпадают с ними)
Z29 → Z5 = 1 (истинно)
(x & 125 = 5) то же самое, что и
Z120 * ¬Z4 * ¬Z1 = 1 (истине)
- Так, например, если в задании имеем:
X & 130 = 3
X & 130 = 3 то же самое, что и Z127 * ¬Z2 * ¬Z1 т.е. 3 = 2 + 1 : 2 = 10 1 = 01 3 = 11
Решение заданий 15 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Задания с множествами
Множества:
15_16:
Элементами множества А являются натуральные числа. Известно, что выражение
((x ∈ {1, 3, 5, 7, 9, 11}) → ¬(x ∈ {3, 6, 9, 12})) ∨ (x ∈ A)
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное значение суммы элементов множества A.
✍ Решение:
-
✎ Решение аналитическое:
- Введем обозначения:
P ≡ (x ∈ {1, 3, 5, 7, 9, 11}) ;
Q ≡ (x ∈ {3, 6, 9, 12}) ;
A ≡ (x ∈ A).
(P → ¬Q) ∨ A = 1 Избавимся от импликации: ¬P ∨ ¬Q ∨ A = 1
А) была непременно истинной, необходимо, чтобы известная часть была ложна:¬P ∨ ¬Q ∨ А = 1 0 1
¬P ∨ ¬Q = 0, или ¬P = 0 отсюда P = 1 ¬Q = 0 отсюда Q = 1
Q и P. То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно:A = {3,9}
3 + 9 = 12
✎ Решение программированием:
PascalAbc.net:
1 2 3 4 5 6 7 8 9 |
begin var s1 := hset(1, 3, 5, 7, 9, 11); var s2 := hset(3, 6, 9, 12); for var x := 1 to 100 do begin if (x in s1 <= not (x in s2)) = false then print(x) end end. |
Ответ: 12
Аналитическое решение:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Множества:
15_17:
Элементами множества А являются натуральные числа. Известно, что выражение
(x ∈ {2, 4, 6, 8, 10, 12}) → (((x ∈ {3, 6, 9, 12, 15}) ∧ ¬(x ∈ A)) →
→ ¬(x ∈ {2, 4, 6, 8, 10, 12}))
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное значение суммы элементов множества A.
Типовые задания для тренировки
✍ Решение:
- Введем обозначения:
P≡(x ∈ {2, 4, 6, 8, 10, 12}) ;
Q ≡ (x ∈ {3, 6, 9, 12, 15}) ;
A ≡ (x ∈ A).
P → ((Q ∧ ¬A) → ¬P) = P → (¬(Q ∧ ¬А) ∨ ¬P) = ¬P ∨ (¬(Q ∧ ¬А) ∨ ¬P) = ¬P ∨ ¬Q ∨ А.
А) была непременно истинной, необходимо, чтобы известная часть была ложна:¬P ∨ ¬Q ∨ А = 1 0 1
¬P ∨ ¬Q = 0, или ¬P = 0 отсюда P = 1 ¬Q = 0 отсюда Q = 1
Q и P. То есть необходимо выбрать элементы, которые встречаются в обоих множествах одновременно:A = {6,12}
6 + 12 = 18
Ответ: 18
Множества:
15_18: Закон распределения
Элементами множеств А, P, Q являются натуральные числа, причём P = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}, Q = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}. Известно, что выражение
( (x ∈ A) → (x ∈ P) ) ∧ ( (x ∈ Q) → ¬(x ∈ A) )
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наибольшее возможное количество элементов в множестве A.
Типовые задания для тренировки
✍ Решение:
- Введем обозначения:
P ≡ (x ∈ P); Q ≡ (x ∈ Q); A ≡ (x ∈ A).
Избавимся от импликации: (¬A ∨ P) ∧ (¬Q ∨ ¬A) = 1 Применим распределительный закон (но можно вывести самостоятельно): ¬A ∨ (P ∧ ¬Q) = 1
А) была непременно истинной, необходимо, чтобы известная часть была ложна:¬A ∨ (P ∧ ¬Q) = 1 0 1
P ∧ ¬Q = 1, или P = 1 и ¬Q = 1 отсюда Q = 0
Q и P. То есть это новое множество, элементы которого принадлежат P, но не принадлежат Q:A = {2, 4, 8, 10, 14, 16, 20}
Ответ: 7
Множества:
15_20:
Элементами множества А являются натуральные числа. Известно, что выражение
¬(x ∈ A) →¬(x ∈ {1, 3, 7}) ∨ (¬(x ∈ {1, 2, 4, 5, 6}) ∧ (x ∈ {1, 3, 7}))
истинно (т. е. принимает значение 1) при любом значении переменной х.
Определите наименьшее возможное количество элементов множества A.
✍ Решение:
- Введем обозначения:
P ≡ (x ∈ {1, 3, 7});
Q ≡ (x ∈ {1, 2, 4, 5, 6});
A ≡ (x ∈ A).
Избавимся от импликации: A ∨ ¬P ∨ (¬Q ∧ P) = 1 Применим закон поглощения (но можно вывести самостоятельно): A ∨ ¬P ∨ ¬Q = 1
А) была непременно истинной, необходимо, чтобы известная часть была ложна:A ∨ ¬P ∨ ¬Q = 1 1 0
¬P ∨ ¬Q = 0, или P = 1 и Q = 1
Q и P:A = {1}
Ответ: 1
Задания с отрезками на числовой прямой
Отрезки на числовой прямой:
15_3:
На числовой прямой даны два отрезка: P=[44,48] и Q=[23,35].
Укажите наибольшую возможную длину отрезка А, для которого формула
((x ϵ P) → (x ϵ Q)) ∧ (x ϵ A)
тождественно ложна, то есть принимает значение 0 при любом значении переменной x.
✍ Решение:
- Упростим формулу, избавившись от ‘x ϵ‘:
(P → Q) ∧ A
правило импликации: a → b = ¬a ∨ b
(¬P ∨ Q) ∧ A
(¬P ∨ Q) ∧ A = 0
(¬P ∨ Q) ∧ A 0 ∧ 0 = 0 0 ∧ 1 = 0 1 ∧ 0 = 0 1 ∧ 1 = 1
1. (¬P ∨ Q) = 1 ∨ 0 = 1 - на данном отрезке А должно равняться 0
2. (¬P ∨ Q) = 1 ∨ 1 = 1 - на данном отрезке А должно равняться 0
3. (¬P ∨ Q) = 1 ∨ 0 = 1 - на данном отрезке А должно равняться 0
4. (¬P ∨ Q) = 0 ∨ 0 = 0 - на данном отрезке А может! равняться 1
5. (¬P ∨ Q) = 1 ∨ 0 = 1 - на данном отрезке А должно равняться 0
48 - 44 = 4
Результат: 4
✎ Решение 2 (программирование):
Внимание! этот способ подходит НЕ для всех заданий с отрезками!
Python:
1 2 3 4 5 6 7 8 9 |
def f(a1,a2,x): return((44<=x<=48)<=(23<=x<=35))and(a1<=x<=a2) maxim = 0 for a1 in range (1,200): for a2 in range (a1+1,200): if all(f(a1,a2,x)==0 for x in range (1,200)):# если все ложны if a2-a1>maxim: maxim=a2-a1 print(a1,a2, a2-a1) # сами точки отрезка и длина |
Вывод:
44 45 1
44 46 2
44 47 3
44 48 4
PascalABC.net:
Вывод:
С подробным аналитическим решением задания 15 ЕГЭ по информатике можно ознакомиться по видео:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Отрезки на числовой прямой:
15_9:
На числовой прямой даны два отрезка: P = [10,20] и Q = [30,40].
Укажите наибольшую возможную длину отрезка A, для которого формула
((x ∈ P) → (x ∈ Q)) → ¬(x ∈ A)
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
Типовые задания для тренировки
✍ Решение:
- Упростим выражение, введя обозначения:
A: x ∈ A P: x ∈ P Q: x ∈ Q
(P → Q) → ¬A = 1
(P → Q) → ¬A = 1 => ¬(P → Q) ∨ ¬A = 1 => ¬(¬P ∨ Q) ∨ ¬A = 1
¬(¬P ∨ Q) ∨ ¬A = 1 =>
P ∧ ¬Q ∨ ¬A = 1
А = 1 P = 1 ¬Q = 1 или Q = 0
Результат: 10
Отрезки на числовой прямой:
15_10:
На числовой прямой даны два отрезка: P = [3, 20] и Q = [6, 12].
Укажите наибольшую возможную длину отрезка A, для которого формула
((x ∈ P) ~ (x ∈ Q)) → ¬(x ∈ A)
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
✍ Решение:
- Упростим выражение, введя обозначения:
A: x ∈ A P: x ∈ P Q: x ∈ Q
(P ~ Q) → ¬A = 1
(P ~ Q) → ¬A = 1 => ¬(P ~ Q) ∨ ¬A = 1
Далее возможно 2 способа решения.
✎ 1 способ:
(a ~ b) = a * b + ¬a * ¬b
¬(P ~ Q) = ¬((P ∧ Q) ∨ (¬P ∧ ¬Q)) = = ¬(P ∧ Q) ∧ ¬(¬P ∧ ¬Q)
¬(P ∧ Q) ∧ ¬(¬P ∧ ¬Q) = = ¬(P ∧ Q) ∧ (P ∨ Q)
¬(P ∧ Q) ∧ (P ∨ Q) ∨ ¬A = 1
¬(P ∧ Q) ∧ (P ∨ Q) = 1 А = 1
✎ 2 способ:
После того, как мы избавились от импликации, имеем:
¬(P ~ Q) ∨ ¬A = 1
Результат: 8
С решением задания 15 вы также можете ознакомиться, посмотрев видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Отрезки на числовой прямой:
15_11:
На числовой прямой даны два отрезка: P = [11, 21] и Q = [15, 40].
Укажите наибольшую возможную длину отрезка A, для которого формула
(x ∈ A) → ¬((x ∈ P) ~ (x ∈ Q))
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
Типовые задания для тренировки
✍ Решение:
- Упростим выражение, введя обозначения:
A: x ∈ A P: x ∈ P Q: x ∈ Q
A → ¬(P ~ Q) = 1
A → ¬(P ~ Q) = 1 =>
¬A ∨ ¬(P ~ Q) = 1
Результат: 19
Задания с ДЕЛ
Поиск наибольшего А, известная часть Дел ∨ Дел = 1
15_7:
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наибольшего натурального числа А формула
(ДЕЛ(x, 40) ∨ ДЕЛ(x, 64)) → ДЕЛ(x, A)
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Типовые задания для тренировки
✍ Решение:
- Введем обозначения:
A = ДЕЛ(x,A); D40 = ДЕЛ(x, 40); D64 = ДЕЛ(x, 64)
(D40 ∨ D64) → A = 1
¬(D40 ∨ D64) ∨ A = 1 или (¬D40 ∧ ¬D64) ∨ A = 1
(¬D40 ∧ ¬D64) ∨ A = 1 1 2
Т.е. (¬D40 ∧ ¬D64) должно быть = 0. Это нам ничего не дает, т.к. конъюнкция ложна в трех случаях (1*0, 0*1 и 0*0), т.е. D40 и D64 могут быть равны как 0, так и 1 (исключение составляет лишь вариант, когда оба D истинны, тогда логическое умножение 1 * 1 ≠ 0).
¬D40 ∧ ¬D64 = 0 или ¬(¬D40 ∧ ¬D64) = 1 Преобразуем по закону Де Моргана и получим: D40 ∨ D64 = 1
Далее можно решать задание либо с помощью кругов Эйлера, либо с помощью логических рассуждений.
Решение с помощью логических рассуждений:
x, которые делятся на А и при этом делятся на 40 ИЛИ делятся на 64:x/A :x/40 ∨x/64
x = 40, 64, 80, 120, 128, 160, 192, 200, ...
A, начиная с самого наименьшего (единицы), на которые делятся все x без исключения:А = 1, 2, 4, 8
А равно 8.НОД (40,64) = 8
40,64 (64 - 40 = 24)
40,24 (40 - 24 = 16)
24,16 (24 - 16 = 8)
16,8 (16 - 8 = 8)
8,8
Решение с помощью кругов Эйлера:
64 / 40 = 1 (24 остаток) 40 / 24 = 1 (16 остаток) 24 / 16 = 1 (8 остаток) 16 / 8 = 2 (0 остаток) - НОД = 8 +++ 40 / 8 = 5 64 / 8 = 8
Результат: 8
✎ Решение 2 (программирование):
Python:
1 2 3 4 5 6 |
for A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 40 == 0) or (x % 64 == 0))<=(x % A== 0) if OK: print( A ) |
Вывод:
1
2
4
8
PascalABC.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
begin for var A := 1 to 500 do begin var ok := 1; for var x := 1 to 1000 do begin if (((x mod 40 = 0) or (x mod 64 = 0)) <= (x mod A = 0)) = false then begin ok := 0; break; end; end; if (ok = 1) then print(A) end; end. |
Вывод:
1
2
4
8
Результат: 8
Поиск наименьшего А, известная часть Дел ∧ ¬Дел = 1
15_5:
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наименьшего натурального числа А формула
ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Типовые задания для тренировки
✍ Решение:
Имеем:
ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42)) = 1
A = ДЕЛ(x,A); D28 = ДЕЛ(x, 28); D42 = ДЕЛ(x, 42)
A → (¬D28 ∨ D42) = 1
Избавимся от импликации:
¬A ∨ (¬D28 ∨ D42) = 1
¬A ∨ (¬D28 ∨ D42) = 1 1 2
(¬D28 ∨ D42) = 0 один случай: когда ¬D28 = 0 и D42 = 0
x/¬A :x/28 ∧x/¬42
x, которые НЕ делятся на А и при этом делятся на 28 И НЕ делятся на 42:x = 28, 56,84, 112, 140,168, 196, 224, ...
A, начиная с самого наименьшего (единицы), на которые НЕ делятся все x без исключения:А = 1, 2, 3
А равно 3.✎ Решение 2 (программирование). Язык Python, Pascal:
-
Из общего выражения:
ДЕЛ(x, A) → (¬ДЕЛ(x, 28) ∨ ДЕЛ(x, 42)) = 1
А, необходимо рассмотреть диапазон натуральных значений x. Если выражение будет истинным для диапазона всех рассматриваемых х, то такое А необходимо вывести на экран.А (ограничим их числом 50, т.к. необходимо найти наименьшее А), будем запускать внутренний цикл, перебирающий значения х (х ограничим числом 1000, будем рассматривать данный диапазон, как «любое натуральное значение переменной х»).Python:
for A in range(1,50): OK = 1 for x in range(1,1000): OK *= (x % A == 0) <= ((x % 28 != 0) or (x % 42== 0)) if OK: print( A ) break
PascalABC.net:
begin for var A := 1 to 50 do begin var ok := 1; for var x := 1 to 1000 do begin if (x mod A = 0) <= ((x mod 28 <> 0)or (x mod 42 = 0)) = false then begin ok := 0; break; end; end; if (ok = 1) then begin print(A); break; end end; end.
OK — переменная-индикатор: если находится такое А при котором, диапазон всех значений x, подставленных в выражение, возвращает истинное значение выражения, то ОК остается равным 1, т.к. используется операция умножения (до цикла ОК необходимо присвоить единице).
Следует иметь в виду, что в программировании вместо операции импликация (->) можно использовать нестрогое неравенство: <=. Т.к. таблица истинности для операции импликация соответствует операции <=:
a b F(a<=b) 0 0 1 0 1 1 1 0 0 1 1 1
А, т.к. используется оператор break для выхода из цикла после первого найденного значения:3
Результат: 3
15_6:
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m».
Для какого наименьшего натурального числа А формула
(¬ДЕЛ(x, 19) ∨ ¬ДЕЛ(x, 15)) → ¬ДЕЛ(x, A)
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
✍ Решение:
- Введем обозначения:
A = ДЕЛ(x,A); D19 = ДЕЛ(x, 19); D15 = ДЕЛ(x, 15)
(¬D19 ∨ ¬D15) → ¬A = 1
D19 ∧ D15 ∨ ¬A = 1
¬A ∨ D19 ∧ D15 = 1 1 2
¬A ∨ D19 ∧ D15 = 1 0 ∨ 1 = 1
¬A = 0 при D19 ∧ D15 = 1 или A = 1 при D19 = 1 и D15 = 1
A = 1 D19 = 1 D15 = 1
19 * 2 = 38 (38 не делится на 15) 19 * 3 = 57 (57 не делится на 15) 19 * 4 = 76 (76 не делится на 15) 19 * 5 = 95 (95 не делится на 15) ... 19 * 10 = 190 (190 не делится на 15) 19 * 15 = 285 (285 делится на 15)
✎ Решение 2 (программирование). Язык Python:
-
Из общего выражения:
(¬ДЕЛ(x, 19) ∨ ¬ДЕЛ(x, 15)) → ¬ДЕЛ(x, A) = 1
А, необходимо рассмотреть диапазон натуральных значений x. Если выражение будет истинным для диапазона всех рассматриваемых х, то такое А необходимо вывести на экран.А (ограничим их числом 500, т.к. необходимо найти наименьшее А), будем запускать внутренний цикл, перебирающий значения х (х ограничим числом 1000, будем рассматривать данный диапазон, как “любое натуральное значение переменной х”).for A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 19 != 0) or (x % 15 != 0))<= (x % A!= 0) if OK: print( A )
OK – переменная-индикатор: если находится такое А при котором, диапазон всех значений x, подставленных в выражение, возвращает истинное значение выражения, то ОК остается равным 1, т.к. используется операция умножения (до цикла ОК необходимо присвоить единице).
Следует иметь в виду, что в программировании вместо операции импликация (->) можно использовать нестрогое неравенство: <=. Т.к. таблица истинности для операции импликация соответствует операции <=:
a b F(a<=b) 0 0 1 0 1 1 1 0 0 1 1 1
А:285
Результат: 285
Задания с поразрядной конъюнкцией
Поразрядная конъюнкция:
15_1:
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 12&6 = 11002&01102 = 01002 = 4
Для какого наименьшего неотрицательного целого числа A формула
(X & A = 0) ∧ ¬(X & 35 ≠ 0 → X & 52 ≠ 0)
тождественно ложна (то есть принимает значение 0 при любом неотрицательном значении переменной X)?
✍ Решение:
Стоит заметить, что для такого типа задач, нет универсального единственного решения. Поэтому на видео, расположенном ниже, представлено два варианта решения.
✎ Способ 1:
Рассмотрим один из вариантов решения:
- Удалим из формулы X&, чтобы сократить ее запись:
(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0)
(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0)
(A = 0) ∧ ¬(35 ≠ 0 → 52 ≠ 0) 1 2
правило импликации: a → b = ¬a ∨ b
(A = 0) ∧ ¬(35 = 0 ∨ 52 ≠ 0)
т.к. в результате получается отрицание того, что 35 ≠ 0,
то убираем знак "не равно": было 35 ≠ 0, стало 35 = 0
закон де Моргана: ¬ (A ∨ B) = ¬ A ∧ ¬ B
A = 0 ∧ 35 ≠ 0 ∧ 52 = 0 = 0
0 ∧ 0 = 0 0 ∧ 1 = 0 1 ∧ 0 = 0 1 ∧ 1 = 1
(A = 0) ∧ 35 ≠ 0 ∧ 52 = 0 = 0 0 ∧ 1 = 0
35 ≠ 0 ∧ 52 = 0 = истинно (=1) если: 35 ≠ 0 = истинно (=1) и 52 = 0 = истинно (=1) так как стоит логическое умножение ∧ - смотрим выше таблицу истинности для конъюнкции
35 ≠ 0 = 1 (истина) и 52 = 0 = 1 (истина) и A = 0 = 0 (ложь)
35: 100011 (≠ 0) 52: 110100 (= 0)
| 52 | 1 | 1 | 0 | 1 | 0 | 0 |
|---|---|---|---|---|---|---|
| X | 0 | 0 | ? | 0 | ? | ? |
| 35 | 1 | 0 | 0 | 0 | 1 | 1 |
|---|---|---|---|---|---|---|
| X | 1 | ? | ? | ? | 1 | 1 |
0 0 ? 0 ? ? &
1 ? ? ? 1 1
0 0 ? 0 1 1
| X | 0 | 0 | ? | 0 | 1 | 1 |
|---|---|---|---|---|---|---|
| A | 0 | 0 | 0 | 0 | 1 | 1 |
0000112 = 310
Ответ: 3
✎ Способ 2*:
-
Используем метод А.В. Здвижковой.
- Выполним последовательно следующие пункты:
- Произвести замену (x & K = 0) на Zk
- Выполнить преобразования по свойству импликации и закону Де Моргана.
- Стремиться прийти к выражению с конъюнкциями без отрицаний типа: Zk * Zm.
- Все выражения типа Zk * Zm преобразовать по свойству
Zk * Zm = Zk or m. - Путем преобразований прийти к импликации: Zk → Zm.
- Согласно первому пункту производим замену:
A ∧ ¬(¬Z35 → ¬Z52) = 0
¬(A ∧ ¬(¬Z35 → ¬Z52)) = 1
¬A ∨ (¬Z35 → ¬Z52) = 1
¬A ∨ (Z35 ∨ ¬Z52) = 1
¬A ∨ ¬Z52 ∨ Z35 = 1
¬(A ∧ Z52) ∨ Z35 = 1
(A ∧ Z52) → Z35 = 1
ZA ∨ 52 → Z35 = 1
Условие Zk → Zm истинно для любых натуральных значений x тогда и только тогда, когда все единичные биты двоичной записи числа M входят во множество единичных битов двоичной записи числа K.
A = ??0?11 52 = 110100 A or 52 = 110111 35 = 100011
Аmin = 112 = 310
Результат: 3
Детальный разбор данного задания 15 ЕГЭ по информатике предлагаем посмотреть на видео:
Вариант решения №1 (универсальный, теоретический):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Вариант решения №2 (не универсальный, но простой):
📹 YouTube здесь
Поразрядная конъюнкция:
15_2:
Обозначим через m & n поразрядную конъюнкцию неотрицательных целых чисел m и n. Так, например, 12&6 = 11002&01102 = 01002 = 4
Для какого наибольшего неотрицательного целого числа A формула
X & A ≠ 0 → (X & 36 = 0 → X & 6 ≠ 0)
тождественно истинна (то есть принимает значение 1 при любом неотрицательном значении переменной X)?
✍ Решение:
-
✎ Способ 1:
- Произведем замену:
z36 = (x&36 = 0), z6 = (x&6 = 0), A = (x&A = 0)
¬A → (z36 → ¬ z6)
¬A → (z36 → ¬ z6) = A + ¬z36 + ¬z6
A + ¬z36 + ¬z6 = A + ¬(z36 * z6)
A + ¬(z36 * z6) = ¬(z36 * z6) + A = (z36 * z6) → A
z36 * z6 = z36 or 6
1001002 -> 36 1102 -> 6 100100 110 1001102 -> 36 or 6 = 3810
z38 → A
A = 1001102 = 3810
✎ Способ 2:
x&A ≠ 0 → (x&36 = 0 → x&6 ≠ 0) = 1
A = (x&A = 0); P = (x&36 = 0); Q = (x&6 = 0);
¬A → (P → ¬Q) = 1
A ∨ (¬P ∨ ¬Q) = 1
¬P ∨ ¬Q нам необходимо подобрать такой вариант (равный 0 или 1), при котором единственно возможным значением A была бы единица (1). A ∨ (¬P ∨ ¬Q) = 1;
или
1 ∨ (0) = 1
¬P ∨ ¬Q = 0 Отсюда имеем: ¬P = 0 и ¬Q = 0 (дизъюнкция равна 0 в единственном случае, когда все операнды равны 0)
Q = 1 и P = 1
100100 : 36 000110 : 6 0**0** : маска P (x&36 = 0) ***00* : маска Q (x&6 = 0)
0**0** : маска P (x&36 = 0) ***00* : маска Q (x&6 = 0) 0**00* : общая маска x *00**0 : маска для A (x&A = 0) т.е. в тех битах А, где может получиться единица (звездочки в обеих масках),
мы поставили нули.
100110 = 3810
Результат: 38
Подробное решение данного задания 15 ЕГЭ по информатике предлагаем посмотреть в видео уроке:
Способ 1:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Способ 2:
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поразрядная конъюнкция:
15_8:
Определите наименьшее натуральное число А из интервала [43, 55], такое, что выражение
((x & 17 ≠ 0) → ((x & A ≠ 0) → (x & 58 ≠ 0))) → → ((x & 8 = 0) ∧ (x & A ≠ 0) ∧ (x & 58 = 0))
тождественно ложно (то есть принимает значение 0 при любом натуральном значении переменной х)?
Типовые задания для тренировки
✍ Решение:
-
Кратко изложенное решение *:
- Введем обозначения:
(¬Z17 → (¬A → ¬Z58)) → (z8 ∧ ¬A ∧ Z58) = 0
¬(((¬Z17 → (¬A → ¬Z58)) → (z8 ∧ ¬A ∧ Z58)) = 1
Z8 ∧ Z58 = Z8 or 58 :
8 = 1000 or
58 = 111010
111010 = 58
Z8 ∧ Z58 = Z58
¬(¬(Z17 ∨ A ∨ ¬Z58) ∨ (¬A ∧ Z58)) = 1
(Z17 ∨ A ∨ ¬Z58) ∧ ¬(¬A ∧ Z58)) = 1
(Z17 ∨ A ∨ ¬Z58) ∧ (A ∨ ¬Z58) = 1
A ∨ ¬Z58 = 1
¬Z58 ∨ A => Z58 → A = 1
43 = 101011 - не подходит! 58 = 111010 44 = 101100 - не подходит! 58 = 111010 45 = 101101 - не подходит! 58 = 111010 46 = 101110 - не подходит! 58 = 111010 47 = 101111 - не подходит! 58 = 111010 48 = 110000 - подходит! 58 = 111010
Результат: 48
Поразрядная конъюнкция:
15_15:
Определите набольшее натуральное число A, такое что выражение
((x & 26 = 0) ∨ (x & 13 = 0)) → ((x & 78 ≠ 0) → (x & A = 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной х)?
Типовые задания для тренировки:
✍ Решение:
- Для упрощения восприятия введем обозначения:
z26 = (x & 26 = 0) z13 = (x & 13 = 0) z78 = (x & 78 = 0) A = (x & A = 0)
(z26 ∨ z13) → (¬z78 → A) = 1
(z26 ∨ z13) → (z78 ∨ A) = 1
26 : 11010 единичные биты: 4, 3, 1 13 : 1101 единичные биты: 3, 2, 0 ∧ =------------------------ 01000 = 810
z8 → (z78 ∨ A) z78: не влияет на решение, так как операция дизъюнкция истинна тогда, когда хотя бы один операнд истинен z8 → A : ????
Наибольшее А = 1000 = 810
Результат: 8
Задания на поиск наибольшего или наименьшего числа А
Поиск наибольшего или наименьшего числа А:
15_4: 15 задание. Демоверсия ЕГЭ 2018 информатика:
Для какого наибольшего целого числа А формула
тождественно истинна, то есть принимает значение 1 при любых целых неотрицательных x и y?
✍ Решение:
✎ Способ 1 (программный):
Важно: Поскольку используется метод полного перебора, то возможна ситуация, когда транслятор будет работать слишком медленно. Но работоспособность представленного алгоритма проверена на онлайн компиляторах.
Pascalabc.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
begin for var A := 200 downto -100 do begin var OK := 1; for var x := 0 to 100 do for var y := 0 to 100 do if ((x <= 9) <= (x * x <= A)) and ((y * y <= A) <= (y <= 9)) = false then begin OK := 0; break; end; if OK = 1 then begin print(A); break end; end; end. |
| Бейсик: |
Python:
for A in range(200,-100,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK *= ((x<=9) <= (x*x<=A)) and((y*y<=A) <= (y<=9)) if OK: print(A) break |
| С++: |
✎ Способ 2 (теоретическое решение):
- Условно разделим исходное выражение на части:
- Главное действие (внешняя операция) в исходном выражении – это конъюнкция. Конъюнкция истинна, когда все операнды истинны. Т.е. в задаче обе части
1и2должны быть истинными (т.к. по условию общая формула должна быть истинной).
-
Рассмотрим часть
- если в
1.1имеем x > 9, то часть1будет истинна независимо от А. Значит, значение числа А влияет на решение только при выполнении условия: - теперь, для того чтобы в части
1, выражение было истинным, надо чтобы часть1.2была истинной: - таким образом, получаем:
1:
x<=9
(импликация 0 → 0 = 1, 0 → 1 = 1)
x*x <= A
(импликация 1 → 1 = 1)
x <= 9 x2 <= A при любых x
возьмем максимальное натуральное: x=9, тогда A>=81
Рассмотрим часть 2:
2.2 истинно (т.е. y <= 9), то часть 2 будет истинна независимо от А. Значит, значение числа А влияет на решение только при выполнении условия:y > 9
2 выражение было истинным, надо чтобы часть 2.1 была ложной:y * y > A
(импликация 0 → 0 = 1)
y > 9 y2 > A при любых y
возьмем наименьшее возможное по условию натуральное: y = 10, тогда A < 100
Результат: 99
Подробное решение 15 задания демоверсии ЕГЭ 2018 года смотрите на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поиск наибольшего или наименьшего числа А:
✍ Решение:
✎ Способ 1 (программный):
Важно: Поскольку используется метод полного перебора, то возможна ситуация, когда транслятор будет работать слишком медленно. Но работоспособность представленного алгоритма проверена на онлайн компиляторах.
Pascalabc.net:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
begin for var A := -100 to 200 do begin var OK := 1; for var x := 1 to 100 do for var y := 1 to 100 do if ((y+3*x<A) or (x >20)or(y>40)) = false then begin OK := 0; break; end; if OK = 1 then begin print(A); break end; end; end. |
| Бейсик: |
Python:
for A in range(-100,200): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (y+3*x<A) or (x > 20) or (y > 40) if OK: print(A) break |
| С++: |
✎ Способ 2 (теоретическое решение):
- Определим основные части выражения, выделив отдельно неизвестную часть – с А, и, так сказать, известную часть, то есть остальную.
1 2 (y+3x < A) ∨ (x > 20) ∨ (y > 40)
(y+3x < A) ∨ (x > 20) ∨ (y > 40) 1 или 0? 1 = 1 Не подходит!
1. (y+3x < A) = 1 2. (x > 20) ∨ (y > 40) = 0
x <= 20 y <= 40
А > 3x + y A > 3*20 + 40 A > 100
Результат: 101
Подробное решение досрочного ЕГЭ 2018 года смотрите на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поиск наибольшего или наименьшего числа А:
15_0:Разбор 15 задания. Демоверсия егэ по информатике 2019:
Для какого наибольшего целого неотрицательного числа А выражение
(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y)
тождественно истинно, т.е. принимает значение 1 при любых целых неотрицательных x и y?
✍ Решение:
✎ Решение 1 (теоретическое):
- Разделим общее выражение на две части. Выделим неизвестную часть красным:
(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y)
(48 ≠ y + 2x) ∨ (A < x) ∨ (A < y) = 1
0 1
y + 2x = 48 : при x = 0, y = 48 при y = 0, 2x = 48 => x = 24
x + 2x = 48 => 3x = 48 x = 16
✎ Решение 2 (программное):
Python:
1 2 3 4 5 6 7 8 |
for A in range(200,0,-1): OK = 1 for x in range(0,100): for y in range(0,100): OK *= (48!=y+2*x) or(A<x)or (A<y) if OK: print(A) break |
Результат: 15
Видео решения 15 задания демоверсии ЕГЭ 2019 (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поиск наибольшего или наименьшего числа А:
15_19:
Для какого наименьшего целого числа А формула
(y + 5x <= 34) → ((y – x > 4) ∨ (y <= A))
тождественно истинна, т.е. принимает значение 1 при любых целых неотрицательных x и y?
✍ Решение:
- Общая идея такова:
необходимо упростить формулу так, чтобы последняя операция (внешняя) выполнялась со скобкой, в которой находится искомое A. После чего разделить формулу на две части, в одной из которых находится искомое. - Избавимся от импликации, это даст нам возможность опустить общие скобки во второй части формулы:
¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A)
¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A) = 1 1 часть 2 часть
¬(y + 5x <= 34) ∨ (y - x > 4) ∨ (y <= A) = 1 1 часть = 0 2 часть = 1
y + 5x > 34 = 0, значит: 1. y + 5x <= 34 y - x > 4 = 0, значит: 2. y - x <= 4
y <= A или A >= y
34 - 5x = 4 + x 30 = 6x x = 5 Найдем y: y = 4 + 5 = 9
y = 9:
A >= 9 => наименьшее A = 9
✎ Решение 2 (программное):
Python:
1 2 3 4 5 6 7 8 |
for A in range(-100,100): OK = 1 for x in range(0,100): for y in range(0,100): OK *= (y+5*x<=34)<=((y-x >4)or(y<=A)) if OK: print( A ) break |
PascalABC.NET:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
begin for var A := -100 to 100 do begin var OK := true; for var x := 0 to 100 do begin for var y := 0 to 100 do begin OK := (y + 5 * x <= 34) <= ((y - x > 4) or (y <= A)); if OK = false then break; end; if OK = false then break; end; if OK then begin print(A); break; end; end; end. |
Результат: 9
Поиск наибольшего или наименьшего числа А:
15_13:
Укажите наименьшее целое значение А при котором выражение
(2y + 5x < A) ∨ (2x + 4y > 100) ∨ (3x – 2y > 70)
истинно для любых целых положительных значений x и y.
Типовые задания для тренировки
✍ Решение:
-
✎ Решение (программное):
Python:
1 2 3 4 5 6 7 8 |
for A in range(-200,200): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (2*y + 5*x < A) or (2*x + 4*y > 100) or (3*x - 2*y > 70) if OK: print( A ) break |
PascalABC.NET:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
begin for var A := -200 to 200 do begin var OK := true; for var x := 1 to 100 do begin for var y := 1 to 100 do begin OK := (2*y + 5*x < A) or (2*x + 4*y > 100) or (3*x - 2*y > 70); if OK = false then break; end; if OK = false then break; end; if OK then begin print(A); break; end; end; end. |
Результат: 171
Видео разбора задания смотрите на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Поиск наибольшего или наименьшего числа А:
15_14:
Укажите наибольшее целое значение А при котором выражение
(3y – x > A) ∨ (2x + 3y < 30) ∨ (2y – x < –31)
истинно для любых целых положительных значений x и y.
Типовые задания для тренировки
✍ Решение:
-
✎ Решение 1 (теоретическое):
- Разделим выражение на две части: часть с неизвестным = 1, часть известная = 0:
(3y – x > A) ∨ (2x + 3y < 30) ∨ (2y – x < –31) = 1
(1) (2x + 3y) >= 30, y >= (30 - 2x) / 3 x = (30 - 3y) /2
(2) (2y – x >=–31) y >= (x - 31) / 2 x = 2y + 31
(1) x | y 0 | 10 15| 0
(2) x | y 0 | -15 ( целые) 30|0
A<3y-x:A < 3y – x, то будем перемещать А снизу вверх. Наибольшее значение А будет достигнуто в указанной точке пересечения с прямой (2).если y = 1, то x = 2*1 + 31 = 33
А < 3y - x A < 3-33, A < -30, A=-31
✎ Решение (программное):
Python:
1 2 3 4 5 6 7 8 |
for A in range(200,-200,-1): OK = 1 for x in range(1,100): for y in range(1,100): OK *= (3*y-x>A) or (2*x+3*y<30) or (2*y-x<-31) if OK: print(A) break |
Результат: -31
* В некоторых задачах использован метод, предложенный А.В. Здвижковой