Ребят, помогите, объясните. Найдите пересечение множества решений с областью допустимых значений.
Знаток
(384),
закрыт
1 год назад
Татьяна
Оракул
(52104)
1 год назад
Ответ Вам дали верный: { -π/3;0;π/3 } Вы попросили объяснения.
Ваше множество решений состоит из чисел вида πn/3, где n -целое число (скорее всего, вы не указали этого в условии…) π – бесконечная непериодическая дробь, приблизительно равная 3,14. Когда вы начинаете перебирать различные целые п и учитывать при этом приближенное значение π, то только три числа попадут в промежуток [-2 ; 2]
При n= -1, πn/3 ≈ – 3,14*1:3 ≈ – 1,05 ∈ [-2 ; 2].
При n=0, πn/3 = π*0:3= 0∈ [-2 ; 2].
При n=-1, πn/3 ≈ 3,14*1:3 ≈ 1,05 ∈ [-2 ; 2].
Если вместо n подставлять – 2, или 2, то значение выражения πn/3 в первом случае будет < – 2; а во втором >2, т. е уже не будут попадать в промежуток [-2 ; 2], т. е не будут входить в область допустимых значений. .
К. А.
Просветленный
(37886)
1 год назад
{-π/3;0;π/3}
АСВысший разум (140971)
1 год назад
В СССР на тот момент была совсем другая система образования, которая учила и давала понять. – не надо тарахтеть о том чего даже отдаленно не знаешь. У тебя родители закончили ЦПШ и коридор или все же закончили очень среднюю школу, а нынешняя программа, по сравнению с той которую я изучал, примитивна до нельзя, т. к. она направлена на подготовку РАБОВ, а не специалистов и ее разжевать не представляет большого труда, было бы желание, а не ссылки на мифическую занятость.
ВИДЕО УРОК
Под иррациональными неравенствами понимаются неравенства, в которых
неизвестные величины находятся под знаком корня (радикала).
При решении иррационального неравенства следует
сначала найти его ОДЗ, то есть все значения неизвестного, при которых
обе части неравенства определены (имеют смысл).
Обычный способ
решения таких неравенств заключается в сведении их к рациональным неравенствам
(не содержащих корней).
Так при этой операции может получиться неравенство,
неравносильное исходному неравенству, то следует установить, при каких
значениях неизвестного левая и правая части заданного неравенства принимают
положительные или отрицательные значения.
Освободиться от корней иногда удаётся путём возведения
обеих частей неравенства в степень.
При этом (в силу того что проверка
полученных решений подстановкой затруднена) необходимо следить за тем, чтобы
при преобразовании неравенств каждый раз получалось неравенство, равносильное
исходному неравенству.
Если обе части
неравенства принимают на некотором множестве
Х только неотрицательные
значения, то, возведя обе части неравенства в квадрат (или в любую чётную степень) и, сохранив знак исходного неравенства,
получим неравенство, равносильное данному (на множестве Х).
При решении иррациональных неравенств, следует помнить, что при возведении
обеих частей неравенства в нечётную степень всегда получается неравенство,
равносильное исходному неравенству.
ПРИМЕР:
Решите неравенство:
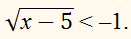
РЕШЕНИЕ:
Найдём область допустимых
значений исходного неравенства
x – 5 ˃ 0, х ∈ [5; +∞).
Обе части исходного неравенства
неотрицательны – можно возводить в квадрат:
x – 5 < 1, x – 6 < 0,
х ∈ (–∞; 6).
Найдём пересечение полученного множества с
областью допустимых значений исходного неравенства

ОТВЕТ: [5; 6)
ПРИМЕР:
Решите неравенство:
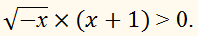
Найдём область допустимых
значений исходного неравенства
–х ≥ 0, х ∈ (–∞;0].
Так как по определению квадратный корень из
любого числа есть величина неотрицательная и
х = 0 не
является решением исходного неравенства, то, разделив обе части неравенства на
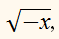
Получим неравенство,
эквивалентное исходному
x + 1 ˃ 0.
Решение этого неравенства
х ∈ (–1; +∞).
Найдём пересечение полученного множества с
областью допустимых значений исходного неравенства

х ∈ (–1; 0].
Учитывая, что х
= 0 не является
решением исходного неравенства, окончательно имеем
х ∈ (–1; 0).
ОТВЕТ: (–1; 0)
ПРИМЕР:
Решите неравенство:
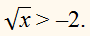
РЕШЕНИЕ:
Область допустимых значений
исходного неравенства
х ∈ [0; +∞).
Одна часть неравенства (левая) неотрицательна, а другая (правая) часть отрицательна.
Следовательно, неравенство выполняется
при всех допустимых значениях х
ОТВЕТ: [0; +∞)
ПРИМЕР:
Решите неравенство:
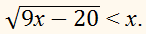
РЕШЕНИЕ:
Найдём область допустимых
значений исходного неравенства
9х – 20 ≥ 0, x ∈ [20/9; +∞).
Правая часть неравенства может
быть отрицательной, но с учётом области допустимых значений обе части
неравенства неотрицательны. Следовательно, обе части неравенства врзвести в
квадрат можно:
9х – 20 < x2,
–x2 + 9x – 20 < 0,
–(x – 4)(x – 5) < 0,
(x – 4)(x – 5) ˃ 0.
Получим
x ∈ (–∞; 4) ∪ (5; +∞).

Найдём пересечение
полученного множества с областью допустимых значений неравенств.

ОТВЕТ:
[20/9; 4) ∪ (5; +∞)
ПРИМЕР:
Решите неравенство:
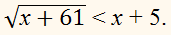
Найдём область допустимых
значений исходного неравенства
х + 61 ≥ 0,
x ∈ [–61; +∞).
Правая часть неравенства
х + 5
может быть отрицательной.
Причём область допустимых значений не выручает, как в предыдущем примере.
Рассмотрим два случая.
1) х + 5 ≥ 0, т. е. х ∈ [–5; +∞).
В этом случае обе части неравенства
неотрицательны. Следовательно, обе части неравенства можно возвести в квадрат:
х + 61 < х2 + 10х + 25,
–х2 –
9х + 36 < 0,
–(х – 3)(х + 12) < 0,
(х – 3)(х + 12) ˃ 0.
Решение этого неравенства
х ∈ (–∞; –12) ∪ (3; + ∞).

Найдём пересечение полученного
множества с множеством
[–5; +∞) – это (3; +∞).

И пересечение последнего
множества с областью допустимых значений исходного неравенства будет
х ∈ (3; +∞).
2) х + 5 < 0, т. е. х ∈ (–∞; –5).
В этом случае левая часть
неравенства неотрицательна, а правая отрицательна. Такое неравенство неверно,
т. е. рассматриваемый промежуток не содержит решений исходного неравенства.
ОТВЕТ: (3; +∞)
ПРИМЕР:
Решите неравенство:
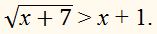
РЕШЕНИЕ:
Найдём область допустимых
значений исходного неравенства
х + 7 ≥ 0,
x ∈ [–7; +∞).
Правая часть неравенства может
быть отрицательной. примере.
Рассмотрим два случая.
1) х + 1 ≥ 0, т. е. х ∈ [–1; +∞).
Возведём обе части неравенства
в квадрат:
х + 7 ˃ х2 + 2х + 1,
–х2 –
х + 6 ˃ 0,
–(х – 2)(х + 3) ˃ 0,
(х – 2)(х + 3) < 0.
Решение последнего неравенства
х ∈ (–3; 2).

Найдём пересечение полученного
множества с множеством
[–1; +∞)
и областью допустимых значений исходного
неравенства

это
[–1; 2).
2) х + 1 < 0, х ∈ (–∞; –1).
В этом случае левая часть неравенства
неотрицательна, а правая отрицательна. Такое неравенство верно. Следовательно,
та часть рассматриваемого участка, которая входит в область допустимых значений
исходного неравенства, является его решением. Находим пересечение
рассматриваемого множества и области допустимых значений

это
[–7; –1).
Ответом является объединение
ответов, полученных в 1) и 2)
случаях:
х ∈ [–7; –1) ∪ [–1; 2), или
х ∈ [–7; 2)
ОТВЕТ: [–7; 2)
ПРИМЕР:
Решите неравенство:
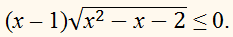
РЕШЕНИЕ:
Найдём область допустимых
значений исходного неравенства
х2 – х – 2 ≥ 0, (x + 1)(х – 2) ≥
0.
Решение этого неравенства
х ∈ (–∞; –1] ∪ [2; +∞)

Множеством решений исходного
неравенства является объединение двух множеств:
множества решений строгого неравенства
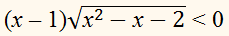
и множества решений
уравнения

Последнее уравнение имеет корни
х1 = 1, х2 = –1, х3 = 2.
Найдём решение строгого неравенства
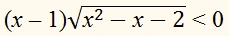
Разделим обе части
неравенства на положительную величину

(значения х, обращающие

в 0 не являются решениями строгого
неравенства). Получим эквивалентное неравенство
х – 1 < 0.
Решим его:
х < 1 или
х ∈ (–∞; 1).
Итак, для окончательного результата нужно найти
пересечение множества (–∞; 1), корней уравнения
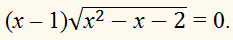
с областью допустимых значений
исходного неравенства.
ОТВЕТ:
–∞ < х
< –1 и х = 2.
ПРИМЕР:
Решите неравенство:
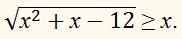
РЕШЕНИЕ:
Решив неравенство
х2 + х – 12 ≥ 0,
найдём ОДЗ
исходного неравенства, то есть множество, которое является объединением
промежутков
(–∞, –4] и [3, +∞).

Рассмотрим два случая:
х ≥ 0 и х < 0.
Первый случай.
х ≥ 0, то
есть х ≥ 3.
Тогда обе части неравенства
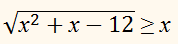
неотрицательны. Возведя их в квадрат,
получаем:
х2 + х – 12 ˃ х2,
откуда х ˃ 12.
Таким
образом, все значения х из
промежутка
(12, +∞)
принадлежат
множеству решений неравенства:
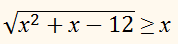
Второй случай.
х < 0,
тогда правая часть неравенства
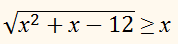
Отрицательна, а его левая часть
неотрицательна. Поэтому все значения х такие, что
х < 0 и х ∈ Е,
то есть значения х из промежутка (–∞, –4], являются решениями исходного неравенства.
ОТВЕТ: х ≤
–4, х ˃ 12
ПРИМЕР:
Решите неравенство:
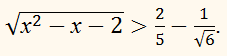
РЕШЕНИЕ:
Множество Е допустимых значений (ОДЗ неравенства) определяется условием
х2 –
х – 2 ≥ 0,
откуда находим:
х ≤ –1, х ≥ 2.
При всех х ∈ Е левая часть неравенства
неотрицательна, а правая часть – отрицательное число, так как
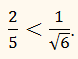
Следовательно, все
значения х ∈ Е и только эти значения являются решениями
неравенства.
ОТВЕТ: х ≤
–1, х ≥ 2
ПРИМЕР:
Решите неравенство:
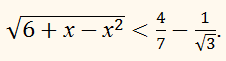
РЕШЕНИЕ:
Рассмотрим правую часть неравенства. Она будет
отрицательной, так как:
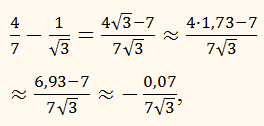
а левая часть неравенства неотрицательна. Поэтому данное
неравенство не имеет решений.
ОТВЕТ: решений
нет
ПРИМЕР:
Решите неравенство:
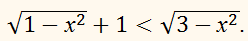
РЕШЕНИЕ:
Левая часть неравенства
определена при условии
1 – х2
≥ 0,
то есть на множестве
Е1 = [–1, 1],
а правая часть неравенства
определена при условии
3 – х2
≥ 0,
то есть на множестве
Е2 = [–√͞͞͞͞͞3, √͞͞͞͞͞3].
Поэтому ОДЗ
неравенства – пересечение множеств Е1 и Е2, то есть множество
Е = Е1 = [–1, 1].
На множестве
Е обе
части неравенства определены и неотрицательны и поэтому обе части неравенства
можно возвести в квадрат.
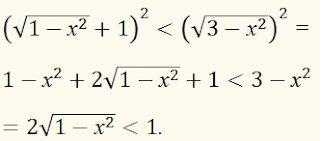
Это
неравенство равносильно на множестве Е каждому из
неравенств:
4(1 – х2)
< 1,
4х2 ˃
3,
х2 ˃ 3/4,
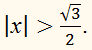
Таким образом, решениями
неравенства являются все те и только те числа
х из
отрезка [–1, 1], которые удовлетворяют
следующим промежуткам:
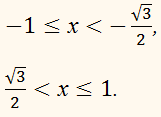
ПРИМЕР:
Решите неравенство:
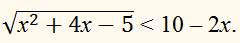
РЕШЕНИЕ:
Первый способ.
Область допустимых значений
неравенства определяется условием:
х2 + 4х – 5
≥ 0,
а множество Е решений неравенства – объединение промежутков
(–∞, –5] и
[1, +∞).
Числа из множества Е, и только они, могут
быть решениями неравенства:
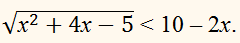
Так как левая часть этого
неравенства неотрицательна при всех
х ∈
Е,
а правая часть меняет знак при
переходе через точку х = 5, поэтому следует рассмотреть два возможных случая:
х < 5 и х ≥ 5.
1) если х ≥ 5, то
10 – 2х ≤ 0
и неравенство

не имеет решений, так как его
левая часть неотрицательна.
2) если х < 5 и х ∈ Е, то обе части неравенства
<
10 – 2х
определены и неотрицательны,
поэтому оно равносильно следующему неравенству
х2 + 4х – 5
< (10 – 2х)2
а
это неравенство равносильно следующему неравенству:
3х2 – 44х + 105 ˃ 0.
Чтобы
решить это неравенство найдём корни уравнения:
3х2 – 44х + 105 = 0.
Получим:

откуда
х1 = 3, х2
= 35/3.
Поэтому множество Е1 решений неравенства
3х2 – 44х + 105 ˃ 0
это объединение интервалов (–∞, 3) и (35/3, +∞).
Условиям х ∈ Е, х < 5 и х ∈ Е1 удовлетворяют значения х из промежутков (–∞, –5] и
[1,
3).
ОТВЕТ:
х ≤ –5, 1 ≤ х <
3
Второй способ.
Построим графики функций
y = f(x) и
у = g(x), где
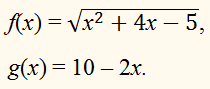

Решить неравенство
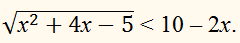
это значит найти все
значения х ∈ Е, при которых график
функции f(x) лежит ниже
графика функции g(x).
Абсциссы точек пересечения этих графиков – корни уравнения
f(x) = g(x).
Это уравнение – следствие
уравнения
f 2(x) = g2(x),
то есть уравнения
х2 + 4х – 5
= (10 – 2х)2,
которое равносильно уравнению
3х2 – 44х + 105 = 0
Из
рисунка

видно,
что прямая
у = 10 – 2х
пересекает
график функции y = f(x) только в точке А, абсцисса
х0 которой – корень уравнения
3х2 – 44х + 105 = 0,
принадлежащий
отрезку [1, 5] то есть
х0 = х1 = 3.
Отметим, что корень х2 уравнения
3х2 – 44х + 105 = 0
это корень уравнения
–f(x) = g(x),
то есть абсцисса точки В,
в которой прямая
у = 10 – 2х
пересекает график функции у = –f(x).
Из рисунка заключаем, что
график функции f(x) лежит ниже графика функции g(x) на промежутках:
(–∞, –5] и
[1,
3).
ОТВЕТ:
х ≤ –5, 1 ≤ х
< 3
Задания к уроку 12
- Задание 1
- Задание 2
- Задание 3
- Урок 1. Числовые неравенства
- Урок 2. Свойства числовых неравенств
- Урок 3. Сложение и умножение числовых неравенств
- Урок 4. Числовые промежутки
- Урок 5. Линейные неравенства
- Урок 6. Системы линейных неравенств
- Урок 7. Нелинейные неравенства
- Урок 8. Системы нелинейных неравенств
- Урок 9. Дробно-рациональные неравенства
- Урок 10. Решение неравенств с помощью графиков
- Урок 11. Неравенства с модулем
- Урок 13. Неравенства с двумя переменными
- Урок 14. Системы неравенств с двумя переменными
- Урок 15. Приближённые вычисления
- Урок 16. Абсолютная и относительная погрешность
В уравнениях и неравенствах вида ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() пересечение областей определения функций
пересечение областей определения функций ![]() и
и ![]() называют областью допустимых значений (ОДЗ) переменной, а также ОДЗ уравнения или неравенства соответственно.
называют областью допустимых значений (ОДЗ) переменной, а также ОДЗ уравнения или неравенства соответственно.
При решении уравнений (неравенств) с одной переменной, когда встает вопрос – находить ли ОДЗ, часто можно услышать категоричное «да» и не менее категоричное «нет». «Сначала нужно найти ОДЗ, а затем приступать к решению уравнения (неравенства)», – утверждают одни. «Незачем тратить время на ОДЗ, по ходу решения будем переходить к равносильному уравнению (неравенству) или к равносильной системе уравнений и неравенств или только неравенств. В конце концов, если это уравнение, то можно сделать проверку», – утверждают другие.
Так находить ли ОДЗ?
Конечно, однозначного ответа на этот вопрос не существует. Нахождение ОДЗ уравнения или неравенства не является обязательным элементом решения. В каждом конкретном примере этот вопрос решается индивидуально.
В одних случаях нахождение ОДЗ упрощает решение уравнения или неравенства (примеры 1-5), а в ряде случаев даже является необходимым этапом решения (примеры 1, 2, 4).
В других случаях (примеры 6, 7) от предварительного нахождения ОДЗ стоит отказаться, так как оно делает решение более громоздким.
Пример 1. Решить уравнение ![]() .
.
Решение.
Возведение обеих частей уравнения в квадрат не упростит, а усложнит его и не позволит избавиться от радикалов. Нужно искать другой способ решения.
Найдем ОДЗ уравнения:
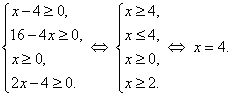
Таким образом, ОДЗ содержит только одно значение ![]() , а, следовательно, корнем исходного уравнения может служить только число 4. Непосредственной подстановкой убеждаемся, что
, а, следовательно, корнем исходного уравнения может служить только число 4. Непосредственной подстановкой убеждаемся, что ![]() – единственный корень уравнения.
– единственный корень уравнения.
Ответ: 4.
Пример 2. Решить уравнение ![]() .
.
Решение.
Наличие в уравнении радикалов различных степеней – второй, третьей и шестой – делает решение сложным. Поэтому, прежде всего, найдем ОДЗ уравнения:
![]()
Непосредственной подстановкой убеждаемся, что ![]() является корнем исходного уравнения.
является корнем исходного уравнения.
Ответ: 2.
Пример 3. Решить неравенство ![]() .
.
Решение.
Конечно, можно решать это неравенство, рассматривая случаи: ![]() ,
, ![]() , но нахождение ОДЗ сразу же упрощает это решение.
, но нахождение ОДЗ сразу же упрощает это решение.
ОДЗ: 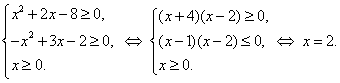
Подставляя это единственное значение ![]() в исходное неравенство, получим ложное числовое неравенство
в исходное неравенство, получим ложное числовое неравенство ![]() . Следовательно, исходное неравенство не имеет решения.
. Следовательно, исходное неравенство не имеет решения.
Ответ: нет решения.
Пример 4. Решить уравнение ![]() .
.
Решение.
Запишем уравнение в виде ![]() .
.
Уравнение вида ![]() равносильно смешанной системе
равносильно смешанной системе 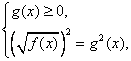 т.е.
т.е. 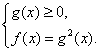
Конечно, здесь нахождение ОДЗ излишне.
В нашем случае получим равносильную систему 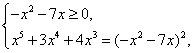 т.е.
т.е. 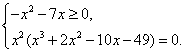
Уравнение ![]() равносильно совокупности
равносильно совокупности 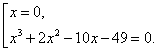 Уравнение
Уравнение ![]() рациональных корней не имеет, но оно может иметь иррациональные корни, нахождение которых вызовет у учащихся затруднения. Поэтому поищем другой способ решения.
рациональных корней не имеет, но оно может иметь иррациональные корни, нахождение которых вызовет у учащихся затруднения. Поэтому поищем другой способ решения.
Вернемся к первоначальному уравнению, запишем его в виде ![]() .
.
Найдем ОДЗ: ![]() .
.
При ![]() правая часть уравнения
правая часть уравнения ![]() , а левая часть
, а левая часть ![]() . Следовательно, исходное уравнение в области допустимых значений переменной х равносильно системе уравнений
. Следовательно, исходное уравнение в области допустимых значений переменной х равносильно системе уравнений 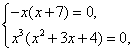 решением которой является только одно значение
решением которой является только одно значение ![]() .
.
Таким образом, в данном примере именно нахождение ОДЗ позволило решить исходное уравнение.
Ответ: 0.
Пример 5. Решить уравнение ![]() .
.
Решение.
Так как ![]() , а
, а ![]() , то при решении исходного уравнения нужно будет избавляться от модулей (раскрывать их).
, то при решении исходного уравнения нужно будет избавляться от модулей (раскрывать их).
Поэтому, сначала имеет смысл найти ОДЗ уравнения:
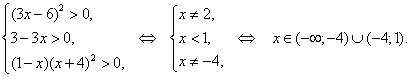
Итак, ОДЗ: ![]()
Упростим исходное уравнение, воспользовавшись свойствами логарифмов.
![]() ,
,
![]() ,
,
![]() .
.
Так как в области допустимых значений переменной х ![]() и
и ![]() , то
, то ![]() , а
, а ![]() , тогда получим равносильное уравнение:
, тогда получим равносильное уравнение:
![]() ,
,
![]() .
.
Учитывая, что в ОДЗ ![]() , перейдем к равносильному уравнению
, перейдем к равносильному уравнению ![]() и решим его, разделив обе части на 3.
и решим его, разделив обе части на 3.
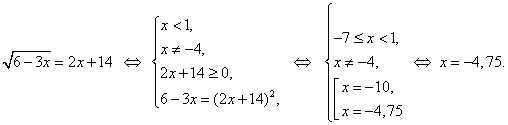
Ответ: − 4,75.
Замечание.
Если не находить ОДЗ, то при решении уравнения ![]() необходимо было бы рассмотреть четыре случая:
необходимо было бы рассмотреть четыре случая: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . На каждом из этих промежутков знакопостоянства выражений, стоящих под знаком модуля, нужно было бы раскрыть модули и решить полученное уравнение. Кроме того еще и выполнить проверку. Мы видим, что нахождение ОДЗ исходного уравнения значительно упрощает его решение.
. На каждом из этих промежутков знакопостоянства выражений, стоящих под знаком модуля, нужно было бы раскрыть модули и решить полученное уравнение. Кроме того еще и выполнить проверку. Мы видим, что нахождение ОДЗ исходного уравнения значительно упрощает его решение.
При решении следующих примеров предварительно ОДЗ находить не будем, так как это сделает решение более громоздким.
Пример 6. Решить неравенство 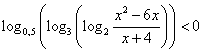 .
.
Решение.
Исходное неравенство запишем в виде 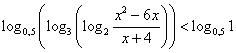 . Учитывая, что функция
. Учитывая, что функция ![]() непрерывна и убывающая при
непрерывна и убывающая при ![]() , перейдем к равносильной системе неравенств:
, перейдем к равносильной системе неравенств:
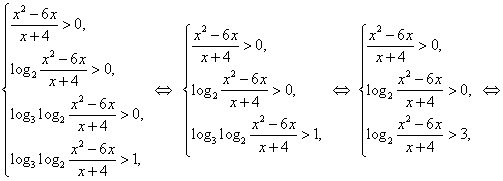
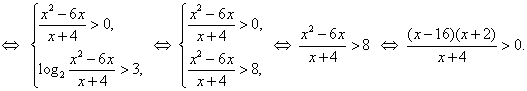
Решением последнего неравенства, а, значит, и исходного является множество ![]() .
.
Ответ: ![]() .
.
Замечание. Если бы мы находили ОДЗ, то нужно было бы решать систему неравенств 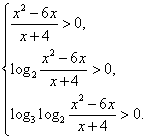 Все эти неравенства вошли в рассматриваемую при решении систему неравенств, причем, в процессе преобразования этой системы, все неравенства, из которых и состоит ОДЗ, оказались лишними. Таким образом, в данном примере нахождение ОДЗ только сделало бы решение более громоздким.
Все эти неравенства вошли в рассматриваемую при решении систему неравенств, причем, в процессе преобразования этой системы, все неравенства, из которых и состоит ОДЗ, оказались лишними. Таким образом, в данном примере нахождение ОДЗ только сделало бы решение более громоздким.
Пример 7. Решить неравенство ![]() .
.
Решение.
Так как переменная х входит и в основание ![]() логарифма, то при решении этого неравенства необходимо будет рассмотреть два случая:
логарифма, то при решении этого неравенства необходимо будет рассмотреть два случая: ![]() и
и ![]() . Поэтому отдельно находить ОДЗ нецелесообразно.
. Поэтому отдельно находить ОДЗ нецелесообразно.
Итак, представим исходное неравенство в виде ![]() и оно будет равносильно совокупности двух систем:
и оно будет равносильно совокупности двух систем:
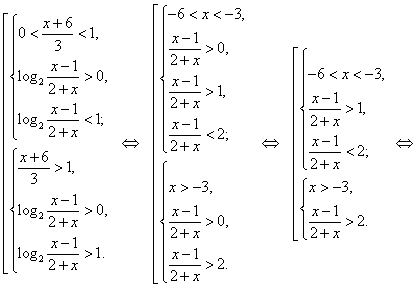
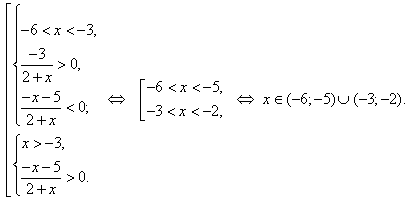
Ответ: ![]() .
.
Приветствую Вас!
Область Допустимых Значений, или по простому ОДЗ. Школьники ненавидят его и боятся. А почему? – Потому что не понимают. Хотя, данная тема затрагивается в учебниках 7-го класса, в самом начале изучения алгебры, но, в своем большинстве, школьные препода не торопятся ее объяснить за ненадобностью.
Затем, наступает 10 класс, и, бах, ребенок в шоке: практически во всех выражениях требуется отыскивать это гребаное ОДЗ. А что это такое, для чего оно, почему без него нельзя, когда его писать, а когда не писать? Вот тут начинаются вопросы.
Давайте разбираться по-тихой. В школьной математике существуют три ограничения:
- 1. На ноль делить нельзя;
- 2. Подкоренное выражение (учитывая, что корень четной степени) должно быть неотрицательным, т.е “больше либо равно нулю”, и число, выходящее из под корня также больше 0;
- 3. Подлогарифмическое выражение должно быть “строго” больше нуля, а основание – “строго” больше нуля и не равно единице.
Тригонометрию не захватываю. Это отдельная история со своими зехерами.
Всего три, понимаете? Не 43, не 128, а всего лишь три! Это же круто. Не нужно запоминать имена всех царей, годы их рождения, смерти, царствования, всяческие войны, стили архитектуры итд итп.
Итак, разберем сначала на элементарных примерах, допустим:
√(2х-5). Видим корень, значит, выражение, которое стоит под корнем, должно быть неотрицательно, а именно: 2х-5>=0. При решении данного неравенства, определяем: x>=2,5. Что это обозначает?
А обозначает это то, что если подставить числа под икс меньше, чем 2,5, то под корнем образуется отрицательное число, а так быть не должно, т.к. мы имеем дело с арифметическим корнем, и именно на него наложено сие ограничение.
Далее дроби:
1. 12/(2х+3), 2. (х+7)/(4х-1).
Рассмотрим первую дробь: у нее сверху стоит число, поэтому нас это не особенно интересует. Всегда интересуемся иксом. Он у нас стоит в знаменателе, а это деление. На ноль делить нельзя. Под икс можно подставлять разные цифры и суметь сосчитать. Ну, если подставить 1/4, получится 12/0. Это не имеет смысла. Ведь, нельзя разделить 12 конфет на друзей, которых нет.
Теперь вторая дробь. Там у нас икс и сверху, и снизу. Если подставить под икс -7, то сверху получится ноль, а снизу 27, т.е 0/27. Что получается: теперь у тебя лично ничего нет, и тебе это “ничего” нужно разделить на 27 друзей. В этом случае можно поделиться хорошим настроением, или плохим, или информацией. В общем, это реально.
Но, подставив 1/4, мы снова теряем друзей. Это печально.
И логарифмы:
Здесь работает ограничение 2х+3>0. А почему? Да потому что, если разобрать логарифм по частям, то получается, что 3 – основание, а 2 – степень. И, возводя любое положительное число, в любую, в том числе и отрицательную степень, ты НИКОГДА не получишь отрицательное число или ноль. Не забываем, что само основание должно быть также больше нуля и плюс не равно 1. Именно поэтому 2х+3 всегда положительно.
Решая данное неравенство, просто определить что х>-1,5. Это обозначает, что числа меньше, или само 1,5 подставлять под икс не имеет смысла.
Теперь скомпонуем всё вместе:
Здесь и корень, и деление на ноль, и логарифм. Не стоит пугаться. Разберемся по порядку. Что видим?
В основании логарифма имеется икс, значит, накладываем туда ограничение, вернее, два: х-2>0, х-2≠1;
Видим квадратный корень, значит то, что стоит под ним, должно быть ≥0, но, само подлогарифмическое должно быть строго >0. Строгость как всегда побеждает. Вспомните своих родителей). Ну, и сам значок > исключает сразу деление на ноль в знаменателе.
Выглядит это все примерно так:
Не нужно записывать в ОДЗ сам значок корня, ведь нас интересует выражение, которое стоит под ним. Таким образом, пересечение штриховок и будет являться допустимой областью, а именно сразу известно какие числа можно подставлять: все, больше двойки, исключая тройку.
Для чего все это? Ну, к примеру, бывает так, что штриховки не пересекаются, а это значит, что нет таких чисел, при подставлении по икс которых, выражение будет иметь смысл. И, если дано уравнение, либо неравенство, то решать его, так же смысла нет. Допустим:
Многие деятели начнут решать неравенство и даже найдут решение. А что мы с вами сделаем? Правильно – распишем ОДЗ:
И, что видно? Штриховочка-то не пересекается. Значит, дальнейшие телодвижения бессмысленны. Само выражение не имеет смысла. Нет таких чисел, чтобы что-либо возможно было решить!
Поэтому ОДЗ вычисляется в первую очередь, а не после основного решения какого-либо выражения.
Конечно же, это все лень писать, да и не всегда надо. Так думают многие. Но вы то не многие. Правильно? Поэтому пишем ОДЗ в первую очередь и ВСЕГДА.
В первой части профильной математики можно встретить уравнения такого типа:
Вот тут то можно и налипнуть, если не просчитать область. Кстати, здесь нужно обратить внимание на то, что выражение с иксом находится как в левой, так и в правой части уравнения. Следовательно, нас интересуют обе стороны.
Составляем и решаем системку:
Почему подписано второе неравенство х≥0? Потому, что √25=5, а не ±5! Следовательно, вычисляя корень, мы можем получить только неотрицательное число.
Решив данное уравнение получим два корня: 6 и -1. А что там просят? А просят записать в ответ наименьший корень, т.е -1. Вот тут вы и попались. Уравнение элементарное, а ответ неверный! -1 не входит в допустимые значения.
Допустим, вы записали в ОДЗ только верхнее неравенство. Опять недолёт. Подкоренному выражению -1 подходит, т.к под корнем получится 1. Только вот при вычислении корня из единицы не получится -1. Факт!
Кто-то скажет: “вот получу я корни при решении, подставлю в исходник и разберусь чё по чём. “
Так то оно так, и даже некоторые авторы учебников демонстрируют именно такой метод. А для более сложных другой, потом третий, четвертый итд. Если ваша голова-дом советов и вы обладаете суперпамятью, то можно действовать разными путями. Я лишь предлагаю упростить задачу.
Возьмите за привычку изначально поставить правильно ограничения, а потом решать, тем более что во второй части присутствуют и неравенства, в которые не очень то удобно подставлять решенные промежутки и проверять их на правильность.
Опять же приведу пример, подтверждающий мою точку зрения:
Некоторые за такое неравенство и не возьмутся, уж больно оно страшное. Но, давайте разберемся: у нас сверху три и снизу два множителя. Чтобы решить его, требуется определить нулевые точки каждого множителя, выставить их на числовую прямую, поставить знаки “+” и “-“, выбрать плюсовые промежутки, т.к значок у неравенства “больше”. И, собственно, ответ.
Проблема стоит в определении нулевых точек. А, если действовать через ОДЗ?
Как видно, первое неравенство при любых икс, больше нуля. Второе также положительно, т.к отрицательный дискриминант.
И помните, если D<0, то это не значит “НЕТ КОРНЕЙ”. Корней, конечно, не будет, но здесь дело в другом: если D<0, то данное квадратное выражение ВСЕГДА будет >0!
Множитель е в степени х, также всегда положителен. А заведомо положительные множители можно исключить из неравенства, т.к они не влияют на его знак. Следовательно, после записи ОДЗ можно записать неравенство в таком виде:
Кайфец! Из грязи – в князи. Ну, а тут уж выставляем нулевые точки числителя и знаменателя на прямую и пишем ответ. Будьте внимательны: в знаменателе стоит икс, значит, возможно деление на ноль. Поэтому при выставлении точек, правильно поставьте шарики: полторашка закрашена, а троечка пустая.
Научитесь думать, анализировать и не пускаться во все тяжкие при виде какой-либо задачи. Не всё так сложно, если разобраться. Ваша математика называется – начало анализа. Значит, требуется помыслить, разложить все по полочкам, а потом уж действовать.
Благодарю за внимание..
Как решать логарифмические неравенства?
Решение неравенств с логарифмами похоже на решение обычных логарифмических уравнений. Но есть несколько моментов, которые необходимо учитывать.
Для начала вспомним, что такое логарифм (log_{a}b) – это в какую степень нужно возвести число (a), чтобы получить (b). Кстати, число (a) называют основанием логарифма, а число (b) – аргументом. Например:
$$log_{3}(27)=3;$$
$$log_{frac{1}{3}}(9)=log_{frac{1}{3}}((frac{1}{3})^{-2})=-2;$$
$$log_{2}(sqrt{2})=log_{2}(2^{frac{1}{2}})=frac{1}{2};$$
Если у вас возникают сложности с вычислением логарифмов настоятельно рекомендую сначала почитать про логарифмы и их свойства.
При этом нужно помнить про ограничения, которые накладываются на логарифм (log_{a}b):
$$ begin{cases}
b>0, \
a>0, \
a neq 1.
end{cases}$$
Начнем изучение неравенств с небольшого примера:
$$log_{2}x>log_{2}4;$$
Сравниваются два логарифма с ОДИНАКОВЫМ основанием, значит вполне логично предположить, что (log_{2}x) будет больше (log_{2}4), при условии, что (x>4). Это и будет решением нашего простого неравенства.
Действительно, согласно определению логарифма, чем больше (х), тем в бОльшую степень нужно возвести (2-ку) в основании логарифма, а значит, и тем больше будет сам логарифм. Подставим в неравенство (х=16) – число большее (4):
$$log_{2}16>log_{2}4;$$
Посчитаем получившиеся логарифмы:
$$4>2;$$
Получили верное неравенство.
И подставляя любые числа большие (4), вы всегда будете получать верное неравенство. Некоторые логарифмы мы не можем посчитать, как например (log_{2}15), но логика сохраняется, если подставлять (x>4), неравенство будет верным. Кстати, калькулятор вам любезно подскажет, что (log_{2}15=3,907>log_{2}4), что нас устраивает.
Ответ: (x>4).
Теперь рассмотрим другой пример:
$$log_{frac{1}{2}}(x)>log_{frac{1}{2}}(4);$$
Обратите внимание, я поменял основания на (frac{1}{2}). Интересно, изменится ли логика рассуждений? Подставим (х=16>4):
$$log_{frac{1}{2}}(16)>log_{frac{1}{2}}(4);$$
$$log_{frac{1}{2}}(2^4)>log_{frac{1}{2}}(2^2);$$
$$log_{frac{1}{2}}((frac{1}{2})^{-4})>log_{frac{1}{2}}((frac{1}{2})^{-2});$$
Посчитаем логарифмы слева и справа:
$$-4>-2;$$
Опа! Получилось неверное неравенство! (-4) конечно же не больше (-2). Мы подставили под левый логарифм число большее, чем у правого, но получили, что значение логарифма меньше.
Другими словами, если основание логарифма будет меньше единицы, то чем бОльший аргумент мы подставляем, тем меньший логарифм будем получать.
Оказывается, если основание у логарифма больше единицы, то логарифм будет возрастающей функцией: чем БОЛЬШЕЕ значение аргумента, тем БОЛЬШЕ сам логарифм. Если основание логарифма меньше единицы, то логарифм будет убывающей функцией: чем БОЛЬШЕЕ значение аргумента, тем МЕНЬШЕ значение логарифма.
Для примера на рисунке показан график логарифмов (log_{2}(x)) с основанием 2 (красным цветом) – возрастающая функция. И (log_{frac{1}{2}}(x)) с основанием 0,5 – синим цветом (убывающая функция).
Находим пересечение указанных областей. И видим, что все (x>8) удовлетворяют ОДЗ, записываем ответ.
Ответ: (x>8.)
Пример 2
$$log_{3}(x+3)>log_{3}(2x-4);$$
Любой пример начинаем с ОДЗ:
$$ begin{cases}
x+3>0, \
2x-4>0. \
end{cases}$$
$$ begin{cases}
x>-3, \
x>2. \
end{cases}$$
Итого ОДЗ получается (x>2).
Теперь приступаем к решению самого неравенства. Слева и справа стоят логарифмы с одинаковыми основаниями большими единицы. Значит просто избавляемся от логарифмов:
$$x+3>2x-4;$$
$$x-2x>-4-3;$$
$$-x>-7;$$
$$x lt 7.$$
Сверяем с ОДЗ ((x>2)) – получается (хin(2;7)).
Ответ: (xin(2;7)).
В примере 2 был важный момент в ОДЗ, на который стоит отдельно обратить внимание. Мы накладывали условия, что оба выражения под логарифмами должны быть больше нуля:
$$ begin{cases}
x+3>0, \
2x-4>0. \
end{cases}$$
Но на самом деле, в этом случае в ОДЗ можно рассмотреть только (2x-4>0). А условие (x+3>0) необязательно! Это следует из простой логики, что если (2x-4>0), то (x+3>0) выполняется автоматически, так как, когда при решении примера избавляемся от логарифмов, мы ищем такие значения (х), при которых (x+3>2x-4>0).
Конкретно в этом примере это не критично, но дальше, когда будут гораздо более сложные примеры, решение дополнительных неравенств в ОДЗ может существенно усложнить жизнь. Особенно это касается заданий с параметром. Настоятельно рекомендую думать, а не просто по схеме накладывать ОДЗ на все подряд.
Пример 3
$$ log_{0,1}(x^2-x-2)>log_{0,1}(3-x);$$
ОДЗ:
$$ begin{cases}
x^2-x-2>0, \
3-x>0. \
end{cases}$$
Для того, чтобы решить первое неравенство в ОДЗ, необходим метод интервалов. Через дискриминант или по теореме Виета (как кому удобно) находим корни квадратного многочлена:
$$D=1-4*(-2)=9;$$
$$x_1=frac{1+3}{2}=2;$$
$$x_2=frac{1-3}{2}=-1;$$
Раскладываем на множители по формуле:
$$ax^2+bx+c=a(x-x_1)(x-x_2);$$
$$x^2-x-2=(x-2)(x+1);$$
$$(x-2)(x+1)>0;$$
Рисуем ось (х), расставляем знаки, отмечаем подходящие промежутки и на этой же оси отмечаем решение второго неравенства в ОДЗ:
$$3-х>0;$$
$$x lt 3;$$
Метод замены переменной в неравенствах с логарифмом
Еще один очень популярный тип неравенств – это неравенства, которые решаются при помощи замены переменной. Как всегда, проще разобраться с этим на примерах:
Пример 5
$$log_{3}^{2}(x)+2>3log_{3}(x);$$
Сперва найдем ОДЗ, здесь оно крайне простое:
$$x>0.$$
Очень легкий пример, который решается при помощи замены. Действительно, обратите внимание, что логарифмы в неравенстве абсолютно одинаковые. Заменим их на какую-нибудь переменную (t):
$$Пусть t=log_{3}(x)$$
Тогда неравенство примет вид:
$$t^2+2>3t;$$
$$t^2-3t+2>0;$$
Получили обыкновенное квадратное неравенство, только относительно переменной не (х), а (t).
Находим корни (t), раскладываем на множители и решаем методом интервалов:
$$(t-1)(t-2)>0;$$
$$tin(-infty;1)cup(2;+infty);$$
То же самое можно переписать в виде совокупности неравенств, смысл остается такой же:
$$left[
begin{gathered}
t lt 1, \
t gt 2. \
end{gathered}
right.$$
Не путайте совокупность и систему! Знак системы используется, когда нужно найти значения (х), удовлетворяющие ОДНОВРЕМЕННО всем неравенствам, входящим в систему.
А знак совокупности используется, когда нужно объединить решение каждого неравенства – то есть решением совокупности будут все корни, полученные в каждом неравенстве по отдельности.
В данном примере мы используем совокупность, так как нас устраивают и (t<1), и (t>2). И то, и то является решением нашего неравенства.
Понимание разницы между совокупностью и системой – принципиальный момент при решении логарифмических и показательных неравенств. С совокупностью мы познакомились в этом примере, а когда используется система, поговорим чуть позже.
Итак, у нас совокупность из двух неравенств относительно переменной (t). Время сделать обратную замену – вместо (t) подставляем выражение, на которое мы его заменяли. Напоминаю (t=log_{3}(x)):
$$left[
begin{gathered}
log_{3}(x) lt 1, \
log_{3}(x) gt 2. \
end{gathered}
right.$$
Ну вот, перед нами два простеньких логарифмических неравенства, которые мы уже научились решать выше:
$$log_{3}(x)<1;$$
$$log_{3}(x)<log_{3}(3);$$
$$x<3.$$
$$log_{3}(x)>2;$$
$$log_{3}(x)>log_{3}(3^2);$$
$$x>9.$$
С учетом ОДЗ ((x>0)), и не забыв про совокупность, получаем:
Ответ: (xin(0;3),cup ,(9;+infty)).
Пример 6
$$frac{log_{4}(64x)}{log_{4}(x)-3}+frac{log_{4}(x)-3}{log_{4}(64x)}geqfrac{log_{4}(x^4)+16}{log_{4}^{2}(x)-9}.$$
Неравенство, на первый взгляд, выглядит немного страшно. Но именно такой пример был на ЕГЭ 2017 года, да и на самом деле оно совсем не страшное.
Запишем ОДЗ:
$$ begin{cases}
x>0, \
log_{4}(x)-3neq 0, \
log_{4}(64x)neq 0, \
log_{4}^{2}(x)-9 neq 0.
end{cases}$$
$$ begin{cases}
x>0, \
log_{4}(x)neq log_{4}(4^3), \
log_{4}(64x)neq log_{4}(4^0), \
(log_{4}(x)-3)(log_{4}(x)+3) neq 0.
end{cases}$$
$$ begin{cases}
x>0, \
log_{4}(x)neq log_{4}(4^3), \
log_{4}(64x)neq log_{4}(4^0), \
log_{4}(x)neq log_{4}({4}^{-3}).
end{cases}$$
В итоге, ОДЗ получается: (xin (0;frac{1}{64}) , cup , (frac{1}{64};64) , cup , (64;+infty).)
Главное помнить про правило: мы должны стараться сделать так, чтобы все логарифмы были с одинаковым основанием, и, по возможности, привести их к одинаковым аргументам.
Здесь у каждого логарифма основание (4) – с этим тут все в порядке. А вот подлогарифмические функции постараемся сделать одинаковыми, воспользовавшись свойствами логарифмов. А именно, нам понадобятся следующие формулы:
$$a=log_{b}(b^a);$$
$$log_{a}(bc)=log_{a}(b)+log_{a}(c);$$
$$log_{a}(b^n)=n*log_{a}(b);$$
Воспользуемся ими для преобразования логарифмов в неравенстве:
$$frac{log_{4}(64)+log_{4}(x)}{log_{4}(x)-3}+frac{log_{4}(x)-3}{log_{4}(64)+log_{4}(x)}geqfrac{4*log_{4}(x)+16}{log_{4}^{2}(x)-9};$$
Заметим, что (log_{4}(64)=3)
$$frac{3+log_{4}(x)}{log_{4}(x)-3}+frac{log_{4}(x)-3}{3+log_{4}(x)}geqfrac{4*log_{4}(x)+16}{log_{4}^{2}(x)-9};$$
Теперь у нас везде одинаковые логарифмы, можно сделать замену. Пусть (t=log_{4}(x):)
$$frac{3+t}{t-3}+frac{t-3}{3+t}geqfrac{4*t+16}{t^2-9};$$
Получилось обыкновенное неравенство из 9-го класса, которое решается методом интервалов. Для этого перекинем все налево, приведем к общему знаменателю, приведем подобные и разложим на множители:
$$frac{3+t}{t-3}+frac{t-3}{3+t}geqfrac{4*t+16}{(t-3)(t+3)};$$
$$frac{(3+t)(t+3)}{(t-3)(t+3)}+frac{(t-3)(t-3)}{(t+3)(t-3)}-frac{4*t+16}{(t-3)(t+3)}geq0;$$
$$frac{9+6t+t^2+t^2-6t+9-4t-16}{(t-3)(t+3)}geq 0;$$
$$frac{2*t^2-4t+2}{(t-3)(t+3)}geq 0;$$
$$frac{2(t-1)^2}{(t-3)(t+3)}geq 0;$$
Воспользуемся методом интервалов, для этого нарисуем ось (х) и расставим знаки:
Обратите внимание, на точку (t=1), она нас устраивает, ведь при этом значении (t) все выражение равно нулю. В ЕГЭ очень часто попадаются отдельные точки, про которые надо не забыть.
$$left[
begin{gathered}
t lt -3, \
t=1, \
t gt 3.\
end{gathered}
right.$$
Сделаем обратную замену (t=log_{4}(x)):
$$left[
begin{gathered}
log_{4}(x)<-3, \
log_{4}(x)=1, \
log_{4}(x)>3. \
end{gathered}
right.$$
Решаем получившиеся простенькие логарифмические неравенства и, неожиданно, одно уравнение. Обратите внимание, что мы решаем опять не систему, а совокупность. Нас устраивают все решения, полученные в каждом уравнениинеравенстве по отдельности.
$$log_{4}(x)<log_{4}({4}^{-3});$$
$$x<{4}^{-3};$$
$$x<frac{1}{64}.$$
$$log_{4}(x)=1;$$
$$log_{4}(x)=log_{4}(4^1);$$
$$x=4.$$
$$log_{4}(x)>3;$$
$$log_{4}(x)>log_{4}(4^3);$$
$$x>64.$$
C учетом ОДЗ записываем ответ:
Ответ: (xin(-infty;frac{1}{64}) , cup , [1] , cup , (64;+infty).)
С основными стандартными типами логарифмических неравенств мы познакомились. Теперь обсудим «подводные камни», которые часто встречаются при решении логарифмических неравенств.
ОДЗ в логарифмических неравенствах. Как сделать проще?
Иногда можно немного упростить себе жизнь при поиске ОДЗ в неравенствах. Для этого нам понадобится немного логики. Разберем на примере:
Пример 7
$$1+log_{6}(4-x)leqlog_{6}(16-x^2).$$
Выпишем ОДЗ, но не будем его решать – да, так можно делать!
ОДЗ:
$$ begin{cases}
4-x>0, \
16-x^2>0.
end{cases}$$
ОДЗ выписали, теперь преобразуем исходное неравенство. Для этого (1) представим в виде логарифма с основанием (6): (1=log_{6}(6)). И воспользуемся формулой:
$$log_{a}(bc)=log_{a}(b)+log_{a}(c).$$
$$log_{6}(6)+log_{6}(4-x)leqlog_{6}(16-x^2).$$
$$log_{6}(6*(4-x))leqlog_{6}(16-x^2).$$
Сравниваются два логарифма с одинаковым основанием, можем смело избавляться от логарифмов, сохраняя знак неравенства:
$$6*(4-x)leq16-x^2;$$
И вот здесь остановимся и поговорим.
Согласно ОДЗ
$$begin{cases}
4-x>0, \
16-x^2>0.
end{cases}$$
Обратите внимание! Что если: (6*(4-x)geq0), то и (16-x^2) будем больше (0) автоматически, так как мы решаем неравенство (6*(4-x)leq16-x^2).
Для нас это означает радостную новость – оказывается необязательно решать все ОДЗ. В данном примере достаточно соблюдать условие (6*(4-x)geq0), а все остальное ОДЗ будет выполняться автоматически, исходя из логики примера. Таким образом, наш пример сводится к решению системы:
$$ begin{cases}
6*(4-x)leq16-x^2, \
6*(4-x)>0.
end{cases}$$
Что избавляет нас от необходимости решать (16-x^2>0), это будет лишним действием.
Конкретно в этом примере нет большой трудности решить все условия из ОДЗ и не думать. Но часто встречаются примеры, в которых выше представленная логика поможет вам не запутаться, ведь иногда это спасает от необходимости решения очень сложных неравенств. Особенно это касается решения заданий с параметрами в профильном ЕГЭ по математике. Вот там каждое лишнее условие в разы увеличивает объем работы.
Дорешаем пример:
$$ begin{cases}
6*(4-x)leq16-x^2, \
6*(4-x)>0.
end{cases}$$
$$ begin{cases}
24-6xleq16-x^2, \
4-x>0.
end{cases}$$
$$ begin{cases}
x^2-6x+8leq0, \
x>4.
end{cases}$$
$$ begin{cases}
2 leq x leq 4, \
4-x>0.
end{cases}$$
Ответ: (x in [2;4).)
Запишем эти правила в общем виде:
$$log_{a}(f(x)>log_{a}(g(x));$$
Эквивалентно
При (a>1):
$$ begin{cases}
f(x)>g(x), \
g(x)>0.
end{cases}$$
При (0 lt a lt 1:)
$$ begin{cases}
f(x) lt g(x), \
f(x) gt 0.
end{cases}$$
Неравенства с логарифмами по переменному основанию
Что, если в основании логарифма будет стоять не положительное число, а некоторое выражение, зависящее от (х – log_{g(x)}(f(x)))? Такие логарифмы называются логарифмами с переменным основанием.
Разберемся, как решать, на примере:
Пример 8
$$ log_{frac{x}{3}}(3x^2-2x+1) ge 0);$$
Начнем решение с ОДЗ. Обратите внимание, что условия накладываются еще и на основание логарифма – оно должно быть больше нуля и не равно единице:
$$ begin{cases}
3x^2-2x+1>0;, \
frac{х}{3}>0; ,\
frac{x}{3}neq1.
end{cases}$$
Заметим, что данный квадратный многочлен больше нуля при любых значениях (х). Второе неравенство имеет решения при (х>0). А третье дает нам (xneq 1).
Объединяя все решения, получаем итоговое ОДЗ:
$$xin(0;3)cup(3;+infty);$$
Приступим к решению.
Мы знаем, чтобы решить неравенство, нужно представить (0) справа в виде логарифма с таким же основанием. Но проблема в том, что основание логарифма слева не число, а выражение, зависящее от (х). Нас не должно это смущать, продолжаем решать точно так же, как если бы в основании было число, то есть, приводим к одинаковому основанию:
$$ log_{frac{x}{3}}(3x^2-2x+1) ge log_{frac{x}{3}}((frac{x}{3})^0);$$
$$ log_{frac{x}{3}}(3x^2-2x+1) ge log_{frac{x}{3}}(1);$$
Получилось, что сравниваются два логарифма с одинаковым основанием. Вот только это основание может быть совершенно любым. Это важно, если вспомнить, как решать классические логарифмические неравенства: знак неравенства должен меняться, если в основании логарифмов стоит число от нуля до единицы, и оставаться таким же, если основание больше единицы. У нас в основании стоит (frac{x}{3}) – выражение, зависящее от (х). Оно может принимать значения, как больше единицы, так и меньше. Поэтому логично было бы рассмотреть два случая, когда основание больше (1), и когда от (0) до (1).
Рассмотрим первый случай:
$$ frac{x}{3}>1;$$
$$ frac{x}{3}-1>0;$$
$$frac{x-3}{3}>0;$$
$$x>3.$$
То есть при (х>3) основание будет больше (1) и знак неравенства должен сохраняться:
$$ begin{cases}
3x^2-2x+1 ge 1, \
х>3.
end{cases}$$
$$ begin{cases}
3x^2-2x ge 0, \
х>3.
end{cases}$$
$$ begin{cases}
x(3x-2) ge 0, \
х>3.
end{cases}$$
Решаем методом интервалов первое неравенство в системе и находим пересечения с условием (x>3):
Метод сужения ОДЗ в логарифмических неравенствах
Эта неприятная штука часто встречается в ЕГЭ по профильной математике и приводит к множеству ошибок и потерянным баллам.
Оказывается, при решении логарифмических неравенств не всегда можно применять формулы из свойств логарифмов (вынесение степени, логарифм от произведения или частного и т.д.). Это связано с изменением области определения логарифмов.
Что это все значит? Проще обсудить на примерах. Рассмотрим простое неравенство с логарифмом:
Пример 11
$$log_{3}(x^2)>4;$$
Как обычно, начинаем с ОДЗ:
$$x^2>0;$$
$$x neq 0.$$
Решаем сам пример, для этого представим (4)-ку справа в виде логарифма с основанием (3).
$$log_{3}(x^2)>log_{3}(3^4);$$
$$x^2>3^4;$$
Разложим в разность квадратов и методом интервалов решим:
$$(x-9)(x+9)>0;$$
$$xin(-infty;-9)cup(9;+infty);$$
А теперь обратите внимание, что этот же самый пример можно было решить по-другому. Согласно формуле вынесения степени из-под логарифма (log_{a}(b^n)=n*log_{a}(b)), можно вынести 2-ю степень. Сделаем это и посмотрим, к чему все это приведет.
$$log_{3}(x^2)>4;$$
$$2*log_{3}(x)>4;$$
Сократим на (2):
$$log_{3}(x)>2;$$
Отдельно обратим внимание на то, как изменилось ОДЗ неравенства после вынесения степени.
$$ОДЗ: x>0;$$
Продолжаем решать неравенство:
$$log_{3}(x)>log_{3}(3^2);$$
$$x>9;$$
Итак, мы решили одно и то же неравенство двумя способами, но ответ получился разный. Как вы думаете, почему? Какое из решений будет верным?
На самом деле, все очень просто. Напоминаю, что логарифм существует только от положительных чисел. Значит, когда под логарифмом стоит (x^2), то вместо (x) можно подставлять любые значения, кроме 0. Вторая степень будет превращать подлогарифмическое выражение в положительное, что нас устраивает. Поэтому могут существовать отрицательные значения (x), при подстановке которых ничего не нарушается. Собственно говоря, у нас так и получилось в первом случае: (xin(-infty;-9)cup(9;+infty)). Есть отрицательные корни, которые удовлетворяют ОДЗ.
А во втором случае, как только мы вынесли из-под логарифма четную степень, отрицательные корни (x) больше не подходят, ведь логарифм не будет существовать, и положительные корни – единственные, которые могут получиться. Другими словами, наше ОДЗ СУЗИЛОСЬ!
И, как мы увидели, ответ получился другой, без отрицательных промежутков. Что, разумеется, неправильно.
Очень важное общее правило. Нельзя с логарифмами производить такие преобразования, при которых происходит сужение области допустимых значений ВСЕГО ПРИМЕРА. Если ОДЗ после преобразования остается прежним или увеличивается, то такое преобразование разрешено.
Отдельная очень важная оговорка про то, что ОДЗ не должно сужаться у всего примера. Посмотрите еще раз на разобранный выше пример 6. Там в одном из логарифмов была четная четвертая степень, которую мы не постеснялись вынести, и ни про какое сужение ОДЗ даже речи не было. Неужели неправильно решили пример? Нет, все абсолютно верно, ведь ОДЗ всего неравенства не сузилось, а значит, можно было пользоваться формулой.
Кстати, все эти размышления касаются не только формул вынесения степени, а всех свойств логарифма (суммы, разности и т.д.), нужно быть внимательными! Но чаще всего встречаются ловушки, связанные с вынесением четной степени.
Пример 12
$$9*log_{7}(x^2+x-2)leq10+log_{7}left(frac{(x-1)^9}{x+2}right).$$
Найдем ОДЗ:
$$ begin{cases}
x^2+x-2>0, \
frac{(x-1)^9}{x+2}>0.
end{cases}$$
$$ begin{cases}
(x+2)(x-1)>0, \
frac{(x-1)^9}{x+2}>0.
end{cases}$$
Решаем методом интервалов:
