Пересечение с осями онлайн
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, предназначен для решения задачи нахождения точек пересечения графика функции с осями координат.
Найти точки пересечения функции с осями координат:
При проведении исследования функции, возникает задача нахождения точек пересечения этой функции с осями координат. Рассмотрим на конкретном примере алгоритм решения такой задачи. Для простоты будем работать с функцией одной переменной:
График данной функции представлен на рисунке:
Как следует из рисунка, наша функция пересекает ось в двух точках, а ось – в одной.
Сначала найдём точки пересечения функции с осью . Сразу отметим, что в этих точках координата . Поэтому для их поиска, нам нужно решить уравнение:
Таким образом, мы нашли две точки пересечения нашей функции с осью абсцисс: и . Стоит отметить, что задача поиска пересечений функции с осью эквивалентна задаче нахождения нулей функции.
Теперь найдём точку пересечения с осью ординат. В этой точке координата . Поэтому для их поиска, просто подставляем значение в нашу функцию:
Таким образом, мы нашли точку пересечения нашей функции с осью ординат .
Другие полезные разделы:
Оставить свой комментарий:
Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме
Как найти пересечение окружности с осями координат
Пересечение с осями онлайн
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, предназначен для решения задачи нахождения точек пересечения графика функции с осями координат.
Найти точки пересечения функции с осями координат:
При проведении исследования функции, возникает задача нахождения точек пересечения этой функции с осями координат. Рассмотрим на конкретном примере алгоритм решения такой задачи. Для простоты будем работать с функцией одной переменной:
График данной функции представлен на рисунке:
Как следует из рисунка, наша функция пересекает ось в двух точках, а ось — в одной.
Сначала найдём точки пересечения функции с осью . Сразу отметим, что в этих точках координата . Поэтому для их поиска, нам нужно решить уравнение:
Таким образом, мы нашли две точки пересечения нашей функции с осью абсцисс: и . Стоит отметить, что задача поиска пересечений функции с осью эквивалентна задаче нахождения нулей функции.
Теперь найдём точку пересечения с осью ординат. В этой точке координата . Поэтому для их поиска, просто подставляем значение в нашу функцию:
Таким образом, мы нашли точку пересечения нашей функции с осью ординат .
Другие полезные разделы:
Оставить свой комментарий:
Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме
Этап: построение окружности и параболы; нахождение точек их пересечения
2 этап: построение окружности и параболы; нахождение точек их пересечения.
3 этап: количество точек пересечения окружности и параболы является ответом на поставленный вопрос.
№2. Найдите множество точек, для каждой из которых расстояния от двух данных точек равны.
Обозначим данные точки через А и В. Выберем систему координат так, чтобы ось Ох совпадала с прямой АВ, а началом координат служила точка А Предположим далее, что АВ=а, тогда в выбранной системе координат А(0,0) и В(а,0). Точка М(х,у) принадлежит искомому множеству тогда и только тогда, когда АМ=МВ, или, что то же самое, АМ 2= МВ 2 . Используя формулу расстояния от одной точки координатной плоскости до другой, получаем АМ 2 =x 2 +y 2 , MB 2 =(x-a) 2 +y 2 . Тогда х 2 +у 2 =(х-а) 2 + у 2
Равенство х 2 +у 2 =(х-а) 2 +у 2 и является алгебраической моделью ситуации, данной в задаче. На этом заканчивается первый этап ее решения (перевод задачи на координатный язык).
На втором этапе осуществляется преобразование полученного выражения, в результате которого получаем соотношение 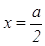 .
.
На третьем этапе осуществляется перевод языка уравнения на геометрический язык. Полученное уравнение является уравнением прямой, параллельной оси Оу и отстоящей от точки А на расстояние 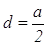 , т.е. серединного перпендикуляра к отрезку АВ.
, т.е. серединного перпендикуляра к отрезку АВ.
2.2 Задачи, обучающие координатному методу
Для разработки методики формирования умения применять координатный метод важно выявить требования, которые предъявляет логическая структура решения задач мышлению решающего. Координатный метод предусматривает наличие у обучающихся умений и навыков, способствующих применению данного метода на практике. Проанализируем решение нескольких задач. В процессе этого анализа выделим умения, являющиеся компонентами умения использовать координатный метод при решении задач. Знание компонентов этого умения позволит осуществить его поэлементное формирование.
Задача №1 . В треугольнике ABC: AC=b, AB=c, ВС=а, BD — медиана. Докажите, что 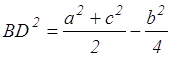 .
.
Выберем систему координат так, чтобы точка А служила началом координат, а осью Ох — прямая АС (рис. 2).
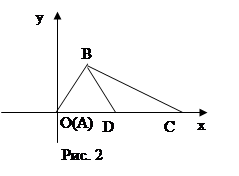 (умение оптимально выбирать систему координат, т. е. так, чтобы наиболее просто находить координаты данных точек).
(умение оптимально выбирать систему координат, т. е. так, чтобы наиболее просто находить координаты данных точек).
В выбранной системе координат точки А, С и D имеют следующие координаты: А(0,0), D(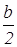 ,0) и С(b,0)
,0) и С(b,0)
(умение вычислять координаты заданных точек). Обозначим координаты точки В через х и у. Тогда используя формулу для нахождения расстояний между двумя точками, заданными своими координатами, получаем:
х 2 +у 2 =с 2 , (x-b) 2 +y 2 =a 2 (1)
(умение находить расстояние между двумя точками, заданными координатами)
По той же формуле 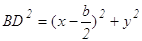 . (2)
. (2)
Используя формулы (1) находим х и у.
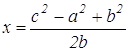 ;
; 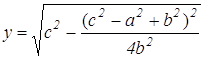 .
.
Далее, подставляя х и у в формулу (2), находим 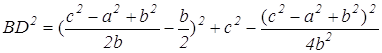 .
.
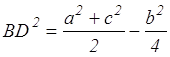 .
.
(умение выполнять преобразования алгебраических выражений)
Задача №2. Найти множество точек, для каждой из которых разность квадратов расстояний от двух данных точек есть величина постоянная.
Обозначим данные точки через А и В. Выберем систему координат так, чтобы ось Ох совпадала с прямой АВ, а началом координат служила точка А.
(умение оптимально выбирать систему координат).
Предположим АВ=а, тогда в выбранной системе координат А(0,0), В(а,0).
(умение находить координаты заданных точек)
Точка М(х,у) принадлежит искомому множеству тогда только тогда, когда AM 2 -MB 2 =b 2 где b — постоянная величина
(умение переводить геометрический язык на аналитический, составлять уравнения фигур).
Используя формулу расстояний между двумя точками, получаем:
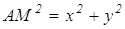 ,
, 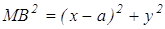 ,
,
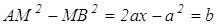
(умение вычислять расстояние между точками, заданными координатами), или 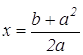 . Данное уравнение является уравнением прямой, параллельной оси Оу и отстоящей от точки А на расстояние
. Данное уравнение является уравнением прямой, параллельной оси Оу и отстоящей от точки А на расстояние 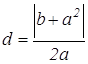 .
.
(умение видеть за уравнением конкретный геометрический образ)
Нетрудно видеть, что и для решения этой задачи необходимо овладение перечисленными выше умениями. Кроме того, для решения приведенной задачи, а также и других задач важно умение «видеть за уравнением» конкретный геометрический образ, которое является обратным к умению составлять уравнения конкретных фигур.
Выделенные умения являются основой при решении и более сложных задач.
Задача №3. В трапеции меньшая диагональ перпендикулярна основаниям. Найти большую диагональ, если сумма противоположных углов равна 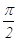 , а основания равны а и b.
, а основания равны а и b.
Направим оси координат по меньшей диагонали и одному из оснований (рис. 3).
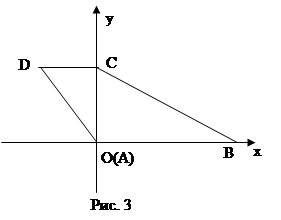 (умение оптимально выбирать систему координат).
(умение оптимально выбирать систему координат).
Тогда точка А имеет координаты (0,0), точка В — (а,0), точка С — (0,c), точка D — (b,c).
(умение находить координаты заданных точек)
Пусть 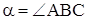 и
и 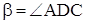 острые углы в трапеции АВСD, тогда их сумма равна
острые углы в трапеции АВСD, тогда их сумма равна 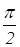 . Для вычисления длины большей диагонали BD надо найти значение с. Его можно вычислить 2 способами. Первый — из прямоугольного треугольника АВС по формуле
. Для вычисления длины большей диагонали BD надо найти значение с. Его можно вычислить 2 способами. Первый — из прямоугольного треугольника АВС по формуле 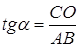 находим
находим 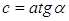 . Второй способ из прямоугольного треугольника ACD:
. Второй способ из прямоугольного треугольника ACD: 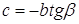 . Отсюда получили, что
. Отсюда получили, что
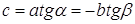 (1)
(1)
Из равенства (1) находим отношение 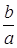 : оно равно —
: оно равно —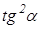 , так как
, так как 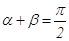 . Выразим
. Выразим 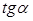 . Он равен
. Он равен 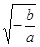 , исходя из этого, пользуясь зависимостью (1), получаем
, исходя из этого, пользуясь зависимостью (1), получаем 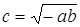 .
.
(умение выразить недостающие координаты через уже известные величины)
Далее воспользовавшись координатной формулой расстояния между двумя точками, найдем длину BD.
(умение вычислять расстояние между точками, заданными координатами)
Она равна 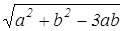 .
.
Итак, компонентами умения применять координатный метод в конкретных ситуациях являются следующие умения:
1. переводить геометрический язык на аналитический для одного типа задач и с аналитического на геометрический для другого;
2. стоить точку по заданным координатам;
3. находить координаты заданных точек;
4. вычислять расстояние между точками, заданными координатами;
5. оптимально выбирать систему координат;
6. составлять уравнения заданных фигур;
7. видеть за уравнением конкретный геометрический образ;
8. выполнять преобразование алгебраических соотношений.
Данные умения можно отработать на примере следующих задач, формирующих координатный метод:
1) задачи на построение точки по ее координатам;
2) задачи на нахождение координат заданных точек;
3) задачи на вычисление расстояния между точками, заданными координатами;
4) задачи на оптимальный выбор системы координат;
5) задачи на составление уравнения фигуры по ее характеристическому свойству;
6) задачи на определение фигуры по ее уравнению;
7) задачи на преобразование алгебраических равенств;
Приведем примеры таких задач.
I. Построение точек на плоскости.
С координатной прямой, а затем и с координатной плоскостью учащиеся знакомятся в 5-6 классах при изучении математического материала. При этом удобно использовать мультимедийные презентации, которые позволяют в динамике излагать необходимый материал, использовать всевозможные иллюстрации и звуковые эффекты, тем самым, заинтересовывая учащихся и являясь хорошим наглядным средством. Одним из примеров является презентация «Метод координат», опирающаяся на учебник [7]. (см. приложение 1). Приведем несколько примеров задач, которые можно использовать при изучении координатной плоскости. Эти задачи могут быть использованы:
— для оттачивания навыков построения точек по их координатам со всем классом;
— для дополнительных заданий отстающим ученикам;
— для развития интереса к изучаемой теме.
1) На координатной плоскости постройте точки А(7,2), B(-2,1), C(0,2).
2) Отметьте на плоскости несколько точек. Начертите произвольную систему координат и найдите в ней координаты заданных точек.
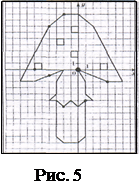
3) 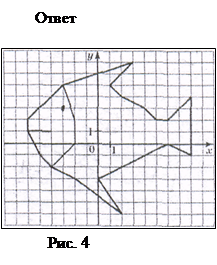 Постройте фигуры по координатам их узловых точек. Указание: узловыми будем называть точки, служащие концами отрезков, образующих фигуры. Точки, координаты которых записаны подряд через запятую, соединяйте последовательно друг с другом. Если же координаты разделяются знаком «;», то соответствующие точки не следует соединять. Они нужны для изображения вспомогательных элементов.
Постройте фигуры по координатам их узловых точек. Указание: узловыми будем называть точки, служащие концами отрезков, образующих фигуры. Точки, координаты которых записаны подряд через запятую, соединяйте последовательно друг с другом. Если же координаты разделяются знаком «;», то соответствующие точки не следует соединять. Они нужны для изображения вспомогательных элементов.
А) Камбала (Рис. 4)
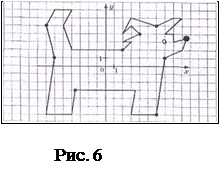
Б)Найдите координаты выделенных на рисунке точек, двигаясь по часовой стрелке от самой жирной точки. (Рис. 5 и 6)
II.Задачи на выбор системы координат
Выбор системы координат имеет очень важное значение при применении метода координат.
Для примера возьмем задачу, которая рассмотрена в учебнике [2] «Середина гипотенузы прямоугольного треугольника равноудалена от его вершин».
Первым шагом при применении метода координат является такой выбор осей и системы координат, при котором алгебраические выкладки становятся более простыми. Для данной задачи удачный выбор системы координат показан на рисунке 7. Таким образом, начало координат помещаем в точку А, а оси проводим через точки В и С так, чтобы эти точки лежали на положительных лучах осей. Следовательно, В(а,0) и С(0,b). Поэтому по формуле середины отрезка D(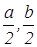 ). Теперь
). Теперь 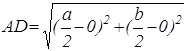 ,
, 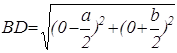 .
.
Поэтому AD=BD. А так как по определению середины отрезка BC=CD, то теорема доказана.
Можно выбрать систему координат и по-другому (рис.8, рис.9). Если выбрать оси совсем случайно, то легкую задачу можно превратить в очень трудную. Чтобы начать доказательство исходя из рисунка 10, нужно найти способ, позволяющий выразить алгебраически, что треугольник ABC имеет при вершине А прямой угол. Сделать это можно, но будет это не очень просто.
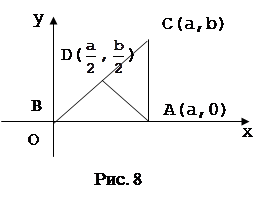
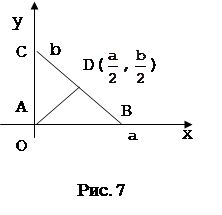
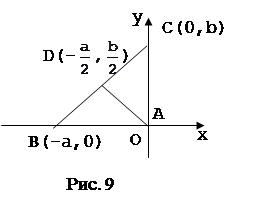
Поэтому необходимо вырабатывать у учащихся, начиная с 6 класса, представления о возможности произвольного выбора системы координат. Эту работу целесообразно вести в процессе решения задач. В целях пропедевтической работы можно рекомендовать в 6 классе задачи из учебника на нахождение координат точек по рисунку, разнообразя их с помощью изменения направления осей и начала координат. (см. приложение1)
1. Длина отрезка АВ равна 5см. а)Выберите систему координат, в которой можно было бы наиболее просто определить координаты концов отрезка. б)Выберите систему координат так, чтобы координаты концов отрезка были бы: А (-2.5,0), В(2.5,0).
2. Постройте квадрат ABCD со стороной 2 см; отметьте точку М- центр квадрата. Поместите начало координат последовательно в точки A, B, C, D и выберите направление осей координат так, чтобы точка М в каждой системе координат имела координаты (1;1). За единичный примите отрезок длиной 1 см.
3. Треугольник ABC равносторонний (длина стороны равна 6 см.). Выберите систему координат так, чтобы можно проще было бы определить координаты его вершин.
III. Расстояние между точками
1) Точка М(а,с) находится от начала координат и точки А(4,0) соответственно на расстояниях 3 и 4 см. Определите координаты точки М.
2) Дан прямоугольник ABCD (АВ=2 см., ВС=4 см.). Как выбрать систему координат, чтобы его вершины имели координаты А(-1,-2), В(-1,2), С(1,2), D(l,-2)?
3) Длины сторон треугольника ABC равны 3, 4 и 5 см. Выберете систему координат и определите в ней координаты вершин треугольника ABC.
4) Вершины четырехугольника ABCD имеют следующие координаты: А(-3,1), В(3,6), С(2,2) и D(-4,3). Установите вид четырехугольника.
IV. Составление уравнения фигур
Это умение является одним из основных умений, которые необходимы при применении метода координат к решению задач.
1) Изобразите систему координат. Отметьте на оси Ох точки А и В. Запишите соотношения, которым удовлетворяют координаты точек, принадлежащих: а)отрезку АВ; б)лучу АВ; в)лучу ВА;
2) Запишите уравнение прямой, содержащей начало координат и точку А(2,5).
3) Запишите уравнение прямой, содержащей точки А(2,7)и В(1,3).
4) Изобразите на координатной плоскости произвольную прямую и найдите ее уравнение.
5) Запишите соотношения, которым удовлетворяю координаты точек прямоугольника с вершинами А(2,3), В(2,5), С(4,5), D(4,3).
6) Что представляют собой множества точек плоскости, координаты которых удовлетворяют неравенствам: а)х≤3; b)-5≤х≤0; c)x>1; d)x 2 +АР 2 не зависит от переменной b. Найдем АМ 2 и АР 2 используя формулу нахождения расстояния между двумя точками по их координатам: 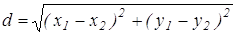 . Они соответственно равны
. Они соответственно равны 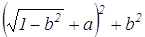 и
и 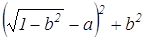 , а их сумма после приведения подобных равна 2а 2 +2. Это число не зависит от переменной b, что и требовалось доказать.
, а их сумма после приведения подобных равна 2а 2 +2. Это число не зависит от переменной b, что и требовалось доказать.
Пример 2. Доказать, что сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналей. (Теорема Эйлера)
Решение: Введем прямоугольную систему координат как показано на рисунке 12.
 Пусть точки А, В, С и D имеют координаты (0,0), (d,0), (c,d) и (0,d) соответственно. Следовательно, координаты точек L и P есть (
Пусть точки А, В, С и D имеют координаты (0,0), (d,0), (c,d) и (0,d) соответственно. Следовательно, координаты точек L и P есть (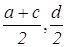 ) и (
) и (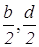 ). Найдем квадраты длин отрезков, с помощью формулы нахождения расстояния между точками по их координатам.
). Найдем квадраты длин отрезков, с помощью формулы нахождения расстояния между точками по их координатам.
AD 2 =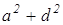 ; BC 2 =
; BC 2 =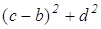 ; DC 2 =
; DC 2 =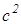 ; AB 2 =
; AB 2 =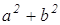 ;
;
AC 2 =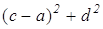 ; BD 2 =
; BD 2 =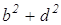 ; LP 2 =
; LP 2 =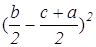 .
.
Запишем выражение, которое необходимо доказать, используя найденные нами значения.
AD 2 +BC 2 +DC 2 +AB 2 =AC 2 +BD 2 +4LP 2

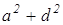 +
+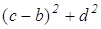 +
+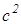 +
+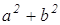 =
=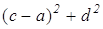 +
+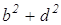 +4
+4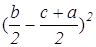
Раскроем скобки, приведем подобные и получим верное равенство 0=0. Значит, сумма квадратов длин сторон четырехугольника равна сумме квадратов длин его диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналей.
Пример 3. Диаметры AB и CD окружности перпендикулярны. Хорда ЕА пересекает диаметр СD в точке К, хорда ЕС пересекает диаметр АВ в точке L. Докажите, что если СК:KD так же как 2:1, то AL:LB так же как 3:1.
Решение: Введем прямоугольную систему координат, направив оси по данным диаметрам AB и CD (рис. 13).
Радиус окружности будем считать равным 1. Тогда точки А, В, С, D будут иметь координаты (-1,0), (1,0), (0,-1), (0,1) соответственно. Так как СК:KD=2:1, то точка К имеет координаты (0,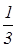 ). Найдем координаты точки Е как точки пересечения прямой АК, имеющей уравнение
). Найдем координаты точки Е как точки пересечения прямой АК, имеющей уравнение 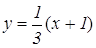 и окружности, заданной уравнением
и окружности, заданной уравнением 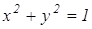 . Получаем, что точка Е имеет координаты (
. Получаем, что точка Е имеет координаты (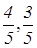 ). Точка L – это точка пересечения прямых СЕ и оси абсцисс, значит ординаты точки L равна 0.
). Точка L – это точка пересечения прямых СЕ и оси абсцисс, значит ординаты точки L равна 0.
Найдем абсциссу точки L. Прямая СЕ задана уравнением 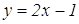 . Она пересекает ось Ох в точке (
. Она пересекает ось Ох в точке (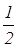 ,0). Отсюда координаты точки L(
,0). Отсюда координаты точки L(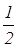 ,0). Найдем отношение AL:LB. Оно равно трем, что и требовалось доказать.
,0). Найдем отношение AL:LB. Оно равно трем, что и требовалось доказать.
1. Доказать, что если в треугольнике две медианы конгруэнтны, то треугольник равнобедренный.
2. Найти множество таких точек Р, что отношение расстояний от каждой из них до двух данных точек равно а.
3. Докажите, что уравнение окружности с центром в точке С (а,с) и радиусом r имеет вид: (х-а) 2 +(у-с) 2 =r 2
4. Найти угол между прямыми Зх-4у+6=0 и 12х+5у+8=0
5. Определите расстояние от точки А(-3,4) до прямой у=х+2.
6. Вычислите площадь треугольника, вершины которого имеют следующие координаты: А (0,-2), В(6,2) и С(2,4) .
7. На прямой с даны три точки А, В, С так, что точка В лежит между точками А и С. В одной полуплоскости с границей а построены равносторонние треугольники АМВ и ВРС. Доказать, что середина отрезка РА, середина отрезка МС и точка В являются вершинами равностороннего треугольника.
8. Доказать, что для любой точки Р лежащей между вершинами В и треугольника ABC, справедливо равенство :
АВ 2 *РС+АС*ВР-АР 2 *ВС=ВС*ВР*РС.
9. Дан прямоугольник. Докажите, что сумма квадратов расстояний от произвольной точки, принадлежащей плоскости этого прямоугольника до его вершин, в два раза больше суммы квадратов расстояний от этой точки до сторон прямоугольника.
10. Доказать, что если через некоторую точку М провести прямую, пересекающую окружность в точках А и В, то произведение МА*МВ постоянно и не зависит от положения прямой.
11. Дан прямоугольник ABCD. Найти множество точек М, для которых MA 2 +MC 2 =MB 2 +MD 2 . (ответ: множество точек М есть плоскость)
Найдите координаты точек пересечения окружности (х — 4)2 + у2 = 25 с осями координат.
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,279
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,949
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Как найти точки пересечения окружности с осью оу
Найти точки пересечения окружности ( x – 1) 2 + (y – 2) 2 = 4 и прямой y = 2x.
Координаты точек пересечения должны удовлетворять обоим указанным уравнениям, так как эти точки находятся как на одной, так и на другой линии. Решим систему уравнений
Подставляя в первое уравнение 2x вместо y и раскрывая скобки, получим
Подставляя эти значения во второе уравнение y = 2x, получим
и .
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/kak-nayti-peresechenie-okruzhnosti-s-osyami-koordinat
http://www.pm298.ru/reshenie/qwq43.php
[/spoiler]
Вопрос по уравнению окружности
™•°•~Pussy~•°•™
Ученик
(48),
закрыт
14 лет назад
Расскажите, как находить координаты точек пересечения окружности с осями Ox и Oy
Например: (x + 6)^2 + (y – 1)^2 = 49
Лучший ответ
Любовь Вингурт
Гуру
(4441)
14 лет назад
Если окружность пересекает ось ох, то у=0. Подставить О в уравнение и найти х. Если окружность пересекает ось оу, то х=0. Аналогично.
Остальные ответы
Таня Грачёва
Знаток
(497)
14 лет назад
тут легко
точки пересечения это х нулевое и у нулевое с противоположенными знаками
в данном случае это будет -6 и 1….а радиус окружности это корень из 49,то есть 7
Похожие вопросы
Исследование свойств окружности по её уравнению
-
Пресечение
с осями координат:
-
С
ОХ: Пусть у=0, тогда
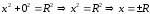 .
.
Отсюда делаем вывод, что (-R;0),
(R;0)-
точки пересечения с осью ОХ. -
С
ОУ: Пусть х=0, тогда 02+у2=R2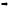
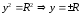 .
.
Отсюда делаем вывод, что (0;-R),(0;R)-
точки пресечения с осью ОУ.
Следовательно,
у окружности с центром в начале координат
область допустимых значений для
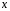 и для
и для закрытый
закрытый
интервал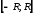 .
.
Вывод:
Окружность вписана в квадрат с размером
стороны 2R.[1.С.99]
2) Симметрия окружности:
-
Относительно
оси ОХ и оси ОУ, так как окружность имеет
общие точки пересечения с осями
координат.
Пусть
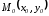 принадлежит окружности, т. Е
принадлежит окружности, т. Е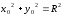 –
–
верное равенство.
Точка
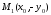 симметрична точкеМ0
симметрична точкеМ0
относительно
оси ОХ. Подставим координаты точки М1
в уравнение окружности
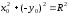 ,отсюда
,отсюда
имеем:
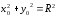 –
–
верное равенство.
Следовательно,
М1
принадлежит
окружности, отсюда следует, что окружность
симметрична относительно оси ОХ.
Точка
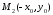 симметрична точкеМ0
симметрична точкеМ0
относительно оси ОУ,
следовательно, окружность симметрична
относительно оси ОУ.
Точка
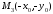 симметрична точке
симметрична точке
М0
относительно О (центра), следовательно,
окружность
симметрична относительно начала
координат. [1.С.99-100]
-
Эксцентриситет
окружности:
Определение
1.2.
Отношение
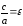 называется эксцентриситетом окружности.
называется эксцентриситетом окружности.
Для окружности эксцентриситет окружности
равен нулю.
-
Касательная
к окружности:
Определение
1.3.
Прямая,
имеющая с окружностью ровно одну общую
точку, называется касательной
к окружности.
Определение
1.4.
Общая точка окружности и касательной
называется точкой касания прямой и
окружности.
Пусть
точка

принадлежит окружности, тогда уравнение
касательной к окружности
в данной точке имеет вид:
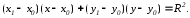 [1.С.100]
[1.С.100]
ЭЛЛИПС
Определение
2.1.
Эллипс – множество точек плоскости, для
каждой из которых сумма расстояний до
двух данных точек F1
и
F2
этой плоскости, называемых фокусами
эллипса, есть заданная постоянная
величина, равная 2а,
а
>
0,
большая,
чем расстояние между фокусами 2с,
с
>
0.
Общий
вид уравнения
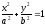
Исследование свойств эллипса по его уравнению
1) Пересечение эллипса с осями координат:
Отсюда
следует, что точки (-a,0),(a,0)
являются точками пересечения с осью
ОХ.
Следовательно,
точки (-b,0),(b,0)являются
точками пересечения с осью ОУ.
Отсюда
заключаем, что границы эллипса
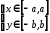 ,
,
отображающие его схематичное построение.
(чертеж
9.)
[1.С. 105]
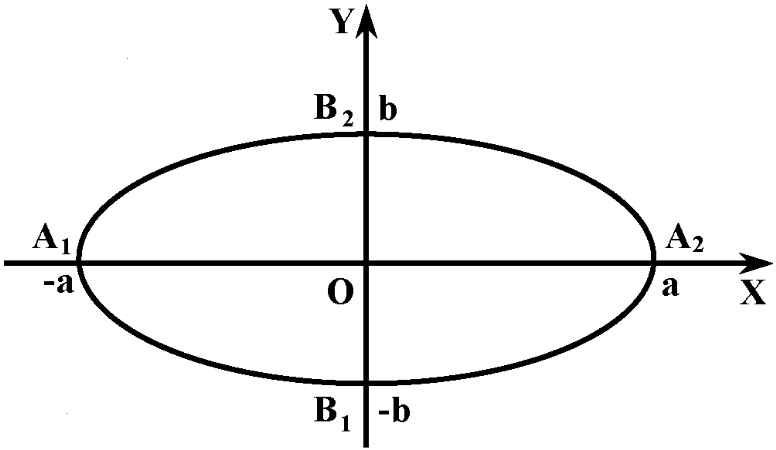
Чертеж
9.
Расстояние
|A1A2|
=
2a называется большой (фокальной) осью
эллипса, расстояние |B1B2|
=
2b называется
малой осью эллипса. Расстояния от начала
координат до вершин A2(a,
0), B2(0,
b) называются соответственно
большой и малой полуосями эллипса.
Вывод:
Таким образом, заключаем,
что эллипс вписан в прямоугольник с
размерами 2a,
2b
(чертеж
10.).
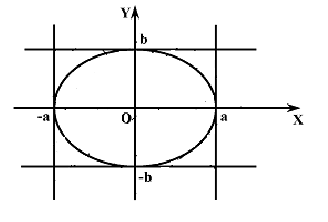
Чертеж
10.
2) Симметрия эллипса относительно координатных осей ox и oy:
Пусть
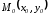 принадлежит эллипсу, т. е
принадлежит эллипсу, т. е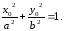 – верное равенство.
– верное равенство.
Точка
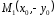 симметрична точке
симметрична точке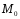 относительно
относительно
оси ОХ
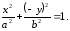
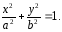 –
–
верное равенство.
Следовательно,
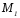 принадлежит эллипсу, отсюда заключаем,
принадлежит эллипсу, отсюда заключаем,
что эллипс симметричен относительно
ОХ
Точка
 симметрична точке
симметрична точке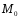 относительно оси ОУ, следовательно,
относительно оси ОУ, следовательно,
эллипс симметричен относительно оси
ОУ.
Точка
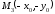 симметрична
симметрична
точке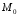 относительно О (центра), следовательно,
относительно О (центра), следовательно,
эллипс симметричен относительно начала
координат.[1.С.105-106]
-
Фокусы
эллипса:
Пусть
фокусы эллипса лежат на оси ОX.
Межфокусное расстояние эллипса равно
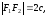
причем
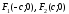 .
.
Заметим, что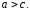
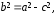
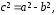
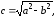
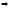
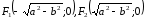 .
.
[1.С.106]
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
0 / 0 / 0 Регистрация: 30.01.2014 Сообщений: 7 |
|
|
1 |
|
По заданным координатам центра окружности и ее радиусу определить координаты точек пересечения окружности с осями координат.31.01.2014, 14:06. Показов 6222. Ответов 3
По заданным координатам центра окружности и ее радиусу определить координаты точек пересечения окружности с осями координат.
0 |
|
49 / 4 / 0 Регистрация: 18.12.2012 Сообщений: 247 Записей в блоге: 1 |
|
|
31.01.2014, 15:03 |
2 |
|
проблема в геометрической реализации или с точки зрения плюсов?
0 |
|
Lefinator 0 / 0 / 0 Регистрация: 30.01.2014 Сообщений: 7 |
||||||||
|
31.01.2014, 21:20 [ТС] |
3 |
|||||||
|
С плюсами проблема Добавлено через 5 часов 11 минут
Если все более менее правильно помогите, как то организовать код, что бы к примеру если R=x0 (и для y0 соответственно) то выводилась одна пара координат, а не две одинаковых и.т.д Добавлено через 41 минуту
Вот собственно Я разбросал все это дело по местам отпишитесь пожалуйста нормальный код или нет.
0 |
|
virtuos553 49 / 4 / 0 Регистрация: 18.12.2012 Сообщений: 247 Записей в блоге: 1 |
||||
|
01.02.2014, 15:10 |
4 |
|||
|
щас , скоро сяду за ноут, помогу с задачей Добавлено через 12 часов 33 минуты Добавлено через 11 минут Добавлено через 30 минут
Вот исправленная версия вашей проги,проверяйте
1 |
Как найти точку пересечения окружностей
Геометрические задачи, решаемые аналитически при помощи приемов алгебры, являются неотъемлемой частью программы школьного обучения. Кроме логического и пространственного мышления они развивают понимание ключевых взаимосвязей между сущностями окружающего мира и абстракциями, применяемыми людьми для формализации отношений между ними. Нахождение точек пересечения простейших геометрических фигур – один из типов подобных задач.
Инструкция
Предположим, что даны две окружности, заданные своими радиусами R и r, а также координатами их центров — соответственно (x1, y1) и (x2, y2). Требуется вычислить, пересекаются ли эти окружности, и если да, то найти координаты точек пересечения.Для простоты можно предположить, что центр одной из заданных окружностей совпадает с началом координат. Тогда (x1, y1) = (0, 0), а (x2, y2) = (a, b). Также имеет смысл предполагать, что a ≠ 0 и b ≠ 0.
Таким образом, координаты точки (или точек) пересечения окружностей, если они есть, должны удовлетворять системе из двух уравнений:x^2 + y^2 = R^2,
(x – a)^2 + (y – b)^2 = r^2.
После раскрытия скобок уравнения приобретают вид:x^2 + y^2 = R^2,
x^2 + y^2 – 2ax – 2by + a^2 + b^2 = r^2.
Теперь первое уравнение можно вычесть из второго. Таким образом, квадраты переменных исчезают, и возникает линейное уравнение: -2ax – 2by = r^2 – R^2 – a^2 – b^2. С его помощью можно выразить y через x:y = (r^2 – R^2 – a^2 – b^2 – 2ax)/2b.
Если подставить найденное выражение для y в уравнение окружности, задача сводится к решению квадратного уравнения: x^2 + px + q = 0, гдеp = -2a/2b,
q = (r^2 – R^2 – a^2 – b^2)/2b – R^2.
Корни этого уравнения позволят найти координаты точек пересечения окружностей. Если уравнение неразрешимо в действительных числах, то окружности не пересекаются. Если корни совпадают между собой, то окружности касаются друг друга. Если корни различны, то окружности пересекаются.
Если a = 0 или b = 0, то исходные уравнения упрощаются. Например, при b = 0 система уравнений примет вид:x^2 + y2 = R^2,
(x – a)^2 + y^2 = r^2.
После вычитания первого уравнения из второго получается:- 2ax + a^2 = r^2 – R^2.Его решение: x = – (r^2 – R^2 – a2)/2a. Очевидно, что в случае b = 0 центры обеих окружностей лежат на оси абсцисс, и у точек их пересечения будет одинаковая абсцисса.
Это выражение для x можно подставить в первое уравнение окружности и получить квадратное уравнение относительно y. Его корни — ординаты точек пересечения, если таковые существуют. Аналогичным образом находится выражение для y, если a = 0.
Если a = 0 и b = 0, но при этом R ≠ r, то одна из окружностей заведомо находится внутри другой, и точки пересечения отсутствуют. Если же R = r, то окружности совпадают, и точек их пересечения бесконечно много.
Если ни у одной из двух окружностей центр не совпадает с началом координат, то их уравнения будут иметь вид:(x – x1)^2 + (y – y1)^2 = R^2,
(x – x2)^2 + (y – y2)^2 = r^2.Если перейти к новым координатам, получающимся из старых методом параллельного переноса: x′ = x + x1, y′ = y + y1, то эти уравнения приобретают вид:x′^2 + y′^2 = R^2,
(x′ – (x1 + x2))^2 + (y′ – (y1 + y2))^2 = r^2.Задача, таким образом, сводится к предыдущей. Найдя решения для x′ и y′, можно легко вернуться к изначальным координатам, обратив уравнения для параллельного переноса.
Источники:
- как найти точки пересечения окружности с прямой

 )
)
