Формула пересечения отрезков на прямой?
Есть прямая на ней два отрезка. Допустим прямая от 0 до 15. Примеры отрезков.
Отрезок А (2, 5) отрезок В (6, 9) не пересекаются.
Отрезок А ( 5, 7) отрезок В ( 3, 9) пересекаются.
Отрезок А (5, 9) отрезок В (7, 11) пересекаются.
Я думаю понятно…
Есть ли формула определить пересекаться отрезки или нет?
-
Вопрос заданболее трёх лет назад
-
2860 просмотров
Пригласить эксперта
эммм…
А(x1, x2)
B(y1, y2)
Если x2 > y1, тогда отрезки пересекаются.
Как то искал ответ на этот вопрос на всякий случай оставлю формулу
(start1 – end2 ) * ( start2 – end1 ) > 0
Если не равенство истинно то отрезки пересекаются.
возьму обозначения из предыдущего ответа
А(x1, x2)
B(y1, y2)
отрезки пересекаются, если выполнено любое из четырёх условий:
y1 <= x1 < y2 или
y1 < x2 <= y2 или
x1 <= y1 < x2 или
x1 < y2 <= x2Если касание в одной точке тоже считать пересечением, то все неравенства должны быть нестрогие.
-
Показать ещё
Загружается…
24 мая 2023, в 02:58
1500 руб./за проект
24 мая 2023, в 02:03
5000 руб./за проект
23 мая 2023, в 23:46
4000 руб./за проект
Минуточку внимания
Я понял, что вопрос в другом, но во избежание споров о том, что можно решить проще, накидал простой пример на C#
void PrintIntersection(int a1, int b1, int a2, int b2)
{
// координаты должны быть упорядочены
if (a1 > b1) (a1, b1) = (b1, a1);
if (a2 > b2) (a2, b2) = (b2, a2);
// первым будет отрезок с наименьшей первой координатой
if (a1 > a2) (a1, b1, a2, b2) = (a2, b2, a1, b1);
if (b1 < a2) {
Console.WriteLine("Пустое множество");
return;
}
if (b1 == a2)
{
Console.WriteLine(b1);
return;
}
Console.WriteLine($"{a2} {b1}");
}
Проверка
PrintIntersection(1, 3, 2, 4);
PrintIntersection(1, 2, 3, 4);
PrintIntersection(5, 6, 6, 8);
PrintIntersection(6, 8, 5, 6);
PrintIntersection(1, 2, 1, 2);
Вывод
2 3
Пустое множество
6
6
1 2
Оглавление
- Расположение отрезков на плоскости
- Параметрическое уравнение отрезка
- Найти точку пересечения двух отрезков
- Отрезки не пересекаются
- Метод SegmentSegment(…)
- Исходник приложения с классом Intersections
Расположение отрезков на плоскости
Два отрезка могут иметь различные положения на плоскости относительно друг друга. Поскольку отрезок ограниченная с двух сторон линия, данная геометрическая фигура предлагает больше вариантов расположения в сравнении с прямой и лучом.
Из вариантов пересечения или непересечения можно выделить несколько особых случаев, например: начала и концы отрезков совпадают, отрезки параллельны и не лежат друг на друге, начало или конец одного отрезка лежит на другом отрезке, совпадают только начальные или конечные точки.
Параметрическое уравнение отрезка
Расположение отрезка в координатной системе и его геометрия, также как прямой и луча, может описываться параметрическими уравнениями. Параметрическое уравнение отрезка(прямой, луча) представляет из себя выражение включающее координату начала, вектор направления и параметр задающий множество точек отрезка(прямой, луча).
Параметр может иметь ограничения или не иметь их.
система из параметрических уравнений: | x = x0 + vt | y = y0 + wt где v и w координаты (x, y) вектора направления v = x1 - x0 w = y1 + y0 при 0 ≤ t ≤ 1 - уравнения описывают отрезок, при 0 ≤ t < +∞ - уравнения описывают луч, при -∞ < t < +∞ - уравнения описывают прямую
Найти точку пересечения двух отрезков
Система из 4-х параметрических уравнений позволяет найти точку пересечения двух отрезков. Нахождение точки пересечения отрезков аналогично описанному для двух лучей.
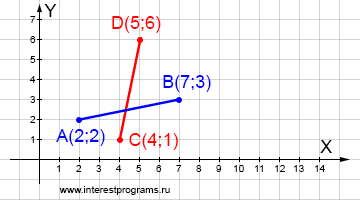
Дано: отрезок AB с координатами начальной и конечной точек – A(2;2) и B(7;3), отрезок CD с координатами – C(4;1) и D(5;6). Найти возможную точку пересечения отрезков AB и CD.
Отрезки имеют точку пересечения если оба параметра отрезков больше или равно нулю и меньше или равно единице.
| x = 2 + (7 - 2)tab | x = 2 + 5tab | y = 2 + (3 - 2)tab => | y = 2 + tab | x = 4 + (5 - 4)tcd | x = 4 + tcd | y = 1 + (6 - 1)tcd | y = 1 + 5tcd
Чтобы узнать есть ли точка пересечения отрезков AB и CD вычислим их параметры:
найдём соотношение параметров через возможно общую координату x 2 + 5tab = 4 + tcd => 5tab = 2 + tcd => tab = (2 + tcd)/5 (у.1) вычислим параметр tcd через возможно общую координату y 2 + tab = 1 + 5tcd => 2 + (2 + tcd)/5 = 1 + 5tcd => 10 + 2 + tcd = 5 + 25cd => tcd = 7/24 ≈ 0.292 вычислим параметр tab использую полученное соотношение (у.1) tab = (2 + 0.292)/5 ≈ 0.458
Оба параметра положительные и меньше единицы – отрезки пересекаются. Найдем точку пересечения используя уравнения из системы для двух отрезков:
x = 2 + 5tab => x = 2 + 5 * 0.458 = 4.29 y = 2 + tab => y = 2 + 0.458 = 2.458
Точка пересечения отрезков AB и CD имеет координаты (4.29; 2.458).
Отрезки не пересекаются
Отсутствие точки пересечения двух отрезков, безусловно, также подтверждается вычислением.
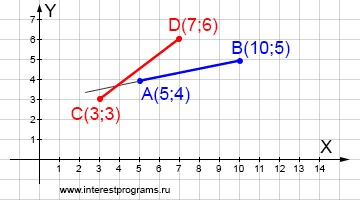
Дано: отрезок AB с координатами начальной и конечной точек – A(5;4) и B(10;5), отрезок CD с координатами – C(3;3) и D(7;6). Определить: отрезки пересекаются или не пересекаются. Если отрезки не пересекаются, найти мнимую точку пересечения.
Отрезки не пересекаются если хотя бы один из параметров отрицательный или больше единицы. Для вычисления используем систему из параметрических уравнений.
| x = 5 + (10 - 5)tab | x = 5 + 5tab | y = 4 + (5 - 4)tab => | y = 4 + tab | x = 3 + (7 - 3)tcd | x = 3 + 4tcd | y = 3 + (6 - 3)tcd | y = 3 + 3tcd
Чтобы узнать пересекаются отрезки или нет вычислим их параметры, вычисление будет происходит аналогично случаю пересечения описанному выше.
3 + 4tcd = 5 + 5tab => 4tcd = 2 + 5tab => tcd = (2 + 5tab)/4 3 + 3tcd = 4 + tab => 3 + 3(2 + 5tab)/4 = 4 + tab => 3 + (6 + 15tab)/4 = 4 + tab => 2 + 11tab = 0 => tab = -2/11 ≈ -0.182 параметр tab меньше нуля, значит отрезки не пересекаются tcd = (2 + 5tab)/4 => tcd = (2 + 5*-0.182)/4 ≈ 0.273 параметр tcd положительный и меньше единицы, значит мнимая точка лежит на отрезке CD
Найдем мнимую точку, расположенную на отрезке CD:
x = 5 + 5 * -0.182 = 4.09 y = 4 - 0.182 = 3.818
Метод SegmentSegment(…)
Метод вычисления точки пересечения отрезков инкапсулирован в классе Intersections. Метод статический, для вычисления точки пересечения не требуется создание экземпляра класса. Методы вычисляющие точки пересечения прямых и лучей описаны на страницах точка пересечения двух прямых на плоскости, пересечение луча и прямой, пересечение двух лучей.
В исходнике приложения, прикрепленного к странице происходит вычисление точки пересечения и создание параметрических уравнений каждого отрезка.
class Intersections
{
// Вычисление точки пересечения отрезков.
public static bool SegmentSegment(Point r1, Point r2, Point p1, Point p2, out Point pCross, out Info info)
{
// Параметрическое уравнение отрезка
// x = x0 + vt
// y = y0 + wt
// где v = x1 - x0
// w = y1 - y0
// при 0 <= t <= 1
// Оповещение о событиях пересечения или не пересечения.
info = new Info();
// Координаты направления вектора синего отрезка
double v = r2.X - r1.X;
double w = r2.Y - r1.Y;
// Координаты направления вектора красного отрезка
double v2 = p2.X - p1.X;
double w2 = p2.Y - p1.Y;
// ===== Частные случаи не пересечения =====
// Отрезки должны быть определены
if (v == 0 && w == 0 && v2 == 0 && w2 == 0)
{
info.Id = 10;
info.Message = "Отрезки неопределённы";
return false;
}
else if (v == 0 && w == 0)
{
info.Id = 11;
info.Message = "Синий отрезка неопределён";
return false;
}
else if (v2 == 0 && w2 == 0)
{
info.Id = 12;
info.Message = "Красный отрезка неопределён";
return false;
}
// Для вычисления параллельности отрезка
// необходимо сравнить направления их векторов.
// Вычисляем длины векторов
double lenBlue = Math.Sqrt(v * v + w * w);
double lenRed = Math.Sqrt(v2 * v2 + w2 * w2);
// Нормализация векторов - создание единичного вектора направления
double x = v / lenBlue;
double y = w / lenBlue;
double x2 = v2 / lenRed;
double y2 = w2 / lenRed;
// Точность совпадения величин double
double epsilon = 0.000001;
// Проверка на совпадение
if (r1.X == p1.X && r1.Y == p1.Y && r2.X == p2.X && r2.Y == p2.Y)
{
info.Id = 20;
info.Message = "Отрезки совпадают";
return false;
}
// Проверка на параллельность с определенной точностью.
if (Math.Abs(x - x2) < epsilon && Math.Abs(y - y2) < epsilon)
{
info.Id = 21;
info.Message = "Отрезки параллельны";
return false;
}
// ===== /Частные случаи не пересечения =====
// ===== Вычисление точки пересечения =====
// Проверка факта пересечения
// x = p1.X + v2t2
// y = p1.Y + w2t2
// r1.X + vt = p1.X + v2t2 => vt = p1.X - r1.X + v2t2 =>
// t = (p1.X - r1.X + v2t2) / v - (у.1) соотношение t-параметров
//
// Вычисление одного параметра с заменой соотношением другого
// r1.Y + wt = p1.Y + w2t2 => wt = p1.Y - r1.Y + w2t2 => t = (p1.Y - r1.Y + w2t2) / w
// (p1.X - r1.X + v2t2) / v = (p1.Y - r1.Y + w2t2) / w =>
// (p1.X - r1.X + v2t2) * w = (p1.Y - r1.Y + w2t2) * v =>
// w * p1.X - w * r1.X + w * v2t2 = v * p1.Y - v * r1.Y + v * w2t2 =>
// w * v2t2 - v * w2t2 = -w * p1.X + w * r1.X + v * p1.Y - v * r1.Y =>
// (w * v2 - v * w2) * t2 = -w * p1.X + w * r1.X + v * p1.Y - v * r1.Y =>
// t2 = (-w * p1.X + w * r1.X + v * p1.Y - v * r1.Y) / (w * v2 - v * w2) - (у.2)
double t2 = (-w * p1.X + w * r1.X + v * p1.Y - v * r1.Y) / (w * v2 - v * w2);
// t = (p1.X - r1.X + v2t2) / v - (у.1)
double t = (p1.X - r1.X + v2 * t2) / v;
// Если один из параметров меньше 0 и больше 1, значит пересечения нет.
if (t < 0 || t > 1 || t2 < 0 || t2 > 1)
{
info.Id = 20;
info.Message = "Пересечения нет";
return false;
}
// Координаты точки пересечения
pCross.X = p1.X + v2 * t2;
pCross.Y = p1.Y + w2 * t2;
info.Id = 0;
info.Message = "Пересечение есть";
return true;
// ===== /Вычисление точки пересечения =====
}
}
public class Info
{
// Для визуального сообщения.
public string Message;
// Для автоматических действий.
public int Id;
}
Исходник приложения с классом Intersections
К странице приложен исходник приложения на языке C#. Приложение демонстрирует вычисление точки пересечения двух отрезков. Графика приложения создает различные положения отрезков на плоскости окна. Управление начальными и конечными точками мышью и служебными клавишами.
Скачать исходник
WpfAppCrossSegmentSegment-vs17.zip
- Размер: 205 Кбайт
- Загрузки: 185
Отметим на координатной прямой точки с координатами –3 и 2. Если точка расположена между ними, то ей соответствует число, которое больше –3 и меньше 2. Верно и обратное: если число х удовлетворяет условию –3 < x < 2.
Множество всех чисел, удовлетворяющих условию –3 < x < 2, называется числовым промежутком или просто промежутком от –3 до 2 и обозначается так: (–3; 2).
На рисунках изображено множество чисел х, для которых выполняется неравенство х < 10 и х ≤ 10. Эти множества представляют собой промежутки, обозначаемые соответственно ((-infty); 10) и ((-infty); 10]. Читается так: число х принадлежит промежутку от минус бесконечности ((-infty)) до 10 (х < 10) и число х принадлежит промежутку от минус бесконечности ((-infty)) до 10, включая число 10 (х ≤ 10). Знак равенства в неравенстве обозначается квадратной скобкой в указании промежутка.
Множество, составляющее общую часть некоторых множеств А и В, называют пересечением этих множеств и обозначают (Acap B).
Промежуток [3; 5] является пересечением промежутков [–1; 5] и [3; 7]. Это можно записать так: [–1; 5] ∩ [3; 7] = [3; 5].
Промежутки [0; 4] и [6; 10] не имеют общих элементов. Если множества не имеет общих элементов, то говорят, что их пересечение пусто. Значит, пересечение промежутков [0; 4] ∩ [6; 10] = 0.
Каждое число из промежутка [1; 7] принадлежит хотя бы одному из промежутков [1; 5] и [3; 7], то есть, либо промежутку [1; 5], либо промежутку [3; 7], либо им обоим.
Множество, состоящее из элементов, принадлежащих хотя бы одному из множеств А и В, называют объединением этих множеств обозначают как (Acup B).
Промежуток [1; 7] является объединением промежутков [1; 5] и [3; 7]. Это можно записать так: ([1;5]cup[3;7]=[1;7].)
Заметим, что объединение промежутков не всегда представляет собой промежуток, например множество ([0;4]cup[6;10]) не является промежутком.
Как найти точку пересечения отрезков
Простейшие геометрические примитивы, такие как точки, прямые, плоскости, фигурируют в большинстве научных и инженерных задач, связанных с проектированием, графическими построениями, визуализацией и машинной графикой. Подобные задачи, как правило, решаются путем применения принципа декомпозиции и сведения их к последовательностям элементарных действий с геометрическими примитивами. Так, сложные трехмерные объекты в машинной графике аппроксимируются полигонами, а те в свою очередь – треугольниками, треугольники задаются отрезками ребер, которые определяются их конечными точками. Именно поэтому понимание того, как решить простейшие геометрические задачи, например того, как найти точки пересечения отрезков, весьма важно для любого технического специалиста.
Вам понадобится
- Лист бумаги, ручка.
Инструкция
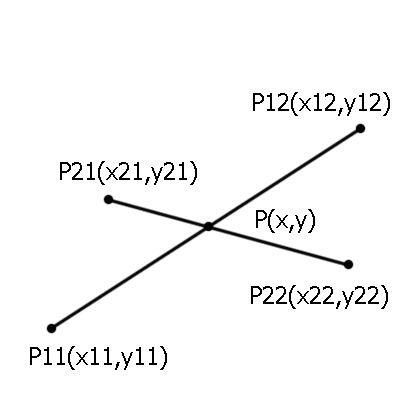
Подготовьте исходные данные. В качестве исходных данных удобно принять отрезки, заданные координатами точек их концов в декартовой системе координат. В данной системе координатные оси ортогональны и имеют одинаковый линейный масштаб. Допустим, имеются отрезки O1 и O2. Отрезок O1 задан точками с координатами P11(x11, y11) и P12(x12, y12), а отрезок O2 задан точками с координатами P21(x21, y21) и P22(x22, y22).
Составьте уравнения прямых, к которым принадлежат отрезки O1 и O2. Уравнение прямой отрезка O1 будет иметь вид: K1*x+d1-y=0. Уравнение прямой отрезка O2 будет иметь вид: K2*x+d2-y=0. Здесь K1=(y12-y11)/(x12-x11), d1=(x12*y11-x11*y12)/(x12-x11), K2=(y22-y21)/(x22-x21), d2=(x22*y21-x21*y22)/(x22-x21).
Решите систему уравнений, состоящую из уравнений прямых, составленных на предыдущем шаге. Вычтя из первого уравнения второе, можно получить: K1*x-K2*x+d1-d2=0. Откуда x=(d2-d1)/(K1-K2). Подставив x в первое уравнение, получим: y=K1*(d2-d1)/(K1-K2)+d1. Значения K1, K2, d1, d2 известны. Точка P(x, y) является пересечением прямых, на которых лежат исходные отрезки.
Проверьте, является ли точка с найденными координатами точкой пересечения именно отрезков, а не прямых, на которых они лежат. Для этого убедитесь, что координата точки x принадлежит одновременно диапазонам значений [x11,x12] и [x21,x22], а координата y принадлежит одновременно диапазонам [y11,y12] и [y21,y22].
Видео по теме
Источники:
- как пересекаются два отрезка
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
 WpfAppCrossSegmentSegment-vs17.zip
WpfAppCrossSegmentSegment-vs17.zip.svg)
.svg)
.svg)

.svg)
.svg)

