Как найти пересечение плоскостей заданных треугольником

Построение линии пересечения плоскостей, заданных различными способами

Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.

Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L₁ и L₂, принадлежащих линии пересечения.

1. Вводим вспомогательную горизонтальную плоскость γ₁. Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1”C” и 2”3”, совпадают с фронтальным следом пл. γ₁. Он обозначен на рисунке как f_0γ1 и расположен параллельно оси x.
2. Определяем горизонтальные проекции 1’C’ и 2’3′ по линиям связи.
3. Находим горизонтальную проекцию точки L₁ на пересечении прямых 1’C’ и 2’3′. Фронтальная проекция точки L₁ лежит на фронтальном следе плоскости γ.
4. Вводим вспомогательную горизонтальную плоскость γ₂. С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L₂.
5. Через L₁ и L₂ проводим искомую прямую l.

Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.

Пересечение плоскостей, заданных следами

Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П₁ и П₂.

1. Находим точку L’₁, расположенную на пересечении горизонтальных следов h_0α и h_0β. Точка L”₁ лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L’₁.
2. Находим точку L”₂ на пересечении фронтальных следов пл. α и β. Точка L’₂ лежит на оси x. Её положение определяется по линии связи, проведенной из L”₂.
3. Проводим прямые l’ и l” через соответствующие проекции точек L₁ и L₂, как это показано на рисунке.

Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.

Пересечение плоскостей треугольников

Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.

1. Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f_0σ. Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3”=A”B”∩f_0σ и 5”=A”С”∩f_0σ, определяем положение (∙)3′ и (∙)5′ по линиям связи на ΔA’B’C’.
2. Находим горизонтальную проекцию N’=D’E’∩3’5′ точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ. Проекция N” расположена на фронтальном следе f_0σ на одной линии связи с N’.

Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f_0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.

Через N и K проводим искомую прямую NK – линию пересечения ΔABC и ΔDEF.

Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₂. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π₂. С противоположной стороны от линии N”K” видимость треугольников меняется.

Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₁. Так как (∙)6” находится выше, чем (∙)7”, то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π₁. С противоположной стороны от линии N’K’ видимость треугольников меняется.

Построить линию пересечения треугольников ABC и EDK и показать видимость их в проекциях.
Определить натуральную величину треугольника ABC.

1. Строим проекции треугольника АВС.

2. Строим проекции треугольника EDK.

3. Находим точку пересечения стороны АС с треугольником EDK

4. Находим точку пересечения стороны А B с треугольником EDK и строим линию пересечения MN

5. С помощью конкурирующих точек 4 и 5 определяем видимость треугольников на фронтальной плоскости проекций.

6. С помощью конкурирующих точек 6 и 7 определяем видимость треугольников на горизонтальной плоскости проекций.

7. В треугольнике ABC проводим горизонталь CL и плоскопараллельным перемещением относительно горизонтальной плоскости проекций располагаем горизонталь перпендикулярно фронтальной плоскости проекций.

Строим фронтальную проекцию треугольника ABC . Треугольник должен проецироваться в прямую линию.

8. Определяем действительную величину треугольника ABC и строим на нем линию пересечения MN.

Пересечение плоскостей треугольников алгоритм

Пошаговое руководство решения задачи №1 — «Нахождение линии пересечения двух плоскостей и определение натуральной величины»

В задаче необходимо найти линию пересечения двух плоскостей и определить натуральную величину одной из них методом плоскопараллельного перемещения.

Для решения такой классической задачи по начертательной геометрии необходимо знать следующий теоретический материал:

— нанесение проекций точек пространства на комплексный чертеж по заданным координатам;

— способы задания плоскости на комплексном чертеже, плоскости общего и частного положения;

— главные линии плоскости;

— определение точки пересечения прямой линии с плоскостью (нахождение «точки встречи»);

— метод плоскопараллельного перемещения для определения натуральной величины плоской фигуры;

— определение видимости на чертеже прямых линий и плоскостей с помощью конкурирующих точек.

Порядок решения Задачи

1. Согласно варианту Задания по координатам точек наносим на комплексный чертеж две плоскости, заданные в виде треугольников ABC (A’, B’, C’; A, B, C) и DKE (D’, K’, E’; D, K, Е) (рис.1.1).

Рис.1.1

2. Для нахождения линии пересечения воспользуемся методом проецирующей плоскости. Суть его в том, что берется одна сторона (линия) первой плоскости (треугольника) и заключается в проецирующую плоскость. Определяется точка пересечения этой линии с плоскостью второго треугольника. Повторив эту задачу еще раз, но для прямой второго треугольника и плоскости первого треугольника, определим вторую точку пересечения. Так как полученные точки одновременно принадлежат обеим плоскостям, они должны находиться на линии пересечения этих плоскостей. Соединив эти точки прямой, будем иметь искомую линию пересечения плоскостей.

3. Задача решается следующим образом:

а) заключаем в проецирующую плоскость Ф(Ф’) сторону AB(A’B’) первого треугольника во фронтальной плоскости проекций V. Отмечаем точки пересечения проецирующей плоскости со сторонами DK и DE второго треугольника, получая точки 1(1’) и 2 (2’). Переносим их по линиям связи на горизонтальную плоскость проекций H на соответствующие стороны треугольника, точка 1(1) на стороне DE и точка 2(2) на стороне DK.

Рис.1.2

б) соединив проекции точек 1 и 2, будем иметь проекцию проецирующей плоскости Ф. Тогда точка пересечения прямой АВ с плоскостью треугольника DKE определится (согласно правилу) вместе пересечения проекции проецирующей плоскости 1-2 и одноименной проекции прямой AB. Таким образом, получили горизонтальную проекцию первой точки пересечения плоскостей – M, по которой определяем (проецируем по линиям связи) её фронтальную проекцию – M’ на прямой A’B’(рис.1.2.а);

в) аналогичным путем находим вторую точку. Заключаем в проецирующую плоскость Г(Г) сторону второго треугольника DK(DK). Отмечаем точки пересечения проецирующей плоскости со сторонами первого треугольника AC и BC во горизонтальной проекции, получая проекции точек 3 и 4. Проецируем их на соответствующие стороны в фронтальной плоскости, получаем 3’ и 4’. Соединив их прямой, имеем проекцию проецирующей плоскости. Тогда вторая точка пересечения плоскостей будет в месте пересечения линии 3’-4’ со стороной треугольника D’K’, которую заключали в проецирующую плоскость. Таким образом, получили фронтальную проекцию второй точки пересечения – N’, по линии связи находим горизонтальную проекцию – N (рис.1.2.б).

г) соединив полученные точки MN(MN) и (M’N’) на горизонтальной и фронтальной плоскостях, имеем искомую линию пересечения заданных плоскостей.

4. С помощью конкурирующих точек определяем видимость плоскостей. Возьмем пару конкурирующих точек, например, 1’=5’ во фронтальной проекции. Спроецируем их на соответствующие стороны в горизонтальную плоскость, получим 1 и 5. Видим, что точка 1, лежащая на стороне DЕ имеет большую координату до оси x, чем точка 5, лежащая на стороне AВ. Следовательно, согласно правилу, большей координаты, точка 1 и сторона треугольника D’Е’ во фронтальной плоскости будут видимые. Таким образом, определяется видимость каждой стороны треугольника в горизонтальной и фронтальной плоскостях. Видимые линии на чертежах проводятся сплошной контурной линией, а не видимые — штриховой линией. Напомним, что в точках пересечения плоскостей (M—N и M’-N’) будет происходить смена видимости.

Рис.1.3

Рис.1.4.

На эпюре дополнительно показано определение видимости в горизонтальной плоскости с использованием конкурирующих точек 3 и 6 на прямых DK и АВ.

5. Методом плоскопараллельного перемещения определяем натуральную величину плоскости треугольника ABC, для чего:

а) в указанной плоскости через точку С(С) проводим фронталь C—F (С-F и C’-F’);

б) на свободном поле чертежа во горизонтальной проекции берем (отмечаем) произвольную точку С₁, считая, что это одна из вершин треугольника (конкретно вершина C). Из нее восстанавливаем перпендикуляр к фронтальной плоскости (через ось х);

Рис.1.5

в) плоскопараллельным перемещением переводим горизонтальную проекцию треугольника ABC, в новое положение A₁B₁C₁ таким образом, чтобы в фронтальной проекции он занял проецирующее положение (преобразовался в прямую линию). Для этого: на перпендикуляре от точки С₁, откладываем фронтальную проекцию горизонтали C₁—F₁ (длина l_CF) получаем точку F₁. Раствором циркуля из точки F₁ величиною F-A делаем дуговую засечку, а из точки C₁ — засечку величиной CA, тогда в пересечении дуговых линий получаем точку A₁ (вторая вершина треугольника);

— аналогично получаем точку B₁ (из точки C₁ делаем засечку величиной C—B (57мм), а из точки F₁ величиной F—B (90мм).Заметим, что при правильном решении три точки A₁ F’₁ и B’₁ должны лежать на одной прямой (сторона треугольника A₁—B₁)две другие стороны С₁—A₁ и C₁—B₁ получаются путем соединения их вершин;

г) из метода вращения следует, что при перемещении или вращении точки в какой-то плоскости проекций — на сопряженной плоскости проекция этой точки должна двигаться по прямой линии, в нашем конкретном случае по прямой параллельной оси х. Тогда проводим из точек A’B’C’ фронтальной проекции эти прямые (их называют плоскостями вращения точек), а из фронтальных проекций перемещенных точек A₁ В₁ C₁ восстановим перпендикуляры (линии связи) (рис.1.6).

Рис.1.6

Пересечения указанных линий с соответствующими перпендикулярами дает новые положения фронтальной проекции треугольника ABC, конкретно A’₁В’₁C’₁ который должен стать проецирующим (прямой линией), поскольку горизонталь h₁ мы провели перпендикулярно фронтальной плоскости проекций (рис.1.6);

5) тогда для получения натуральной величины треугольника достаточно его фронтальную проекцию развернуть до параллельности с горизонтальной плоскостью. Разворот осуществляем с помощью циркуля через точку А’₁, считая ее как центр вращения, ставим треугольник A’₁В’₁C’₁ параллельно оси х, получаем A’₂В’₂C’₂. Как было сказано выше, при вращении точки, на сопряженной (теперь на горизонтальной) проекции они двигаются по прямым параллельным оси х. Опуская перпендикуляры (линии связи) из фронтальных проекций точек A’₂ В’₂ C’₂ пересечения их с соответствующими линиями находим горизонтальную проекцию треугольника ABC (A₂В₂C₂) в натуральную величину (рис.1.7).

Рис. 1.7

У меня есть все готовые решения задач с такими координатами, купить можно >>здесь

Цена 55 руб, чертежи по начертательной геометрии из книжки Фролова Вы легко можете скачать сразу после оплаты или я вышлю Вам на почту. Они находятся в ZIP архиве в различных форматах:
*.jpg – обычный цветной рисунок чертежа в масштабе 1 к 1 в хорошем разрешении 300 dpi;
*.cdw – формат программы Компас 12 и выше или версии LT;
*.dwg и .dxf — формат программы AUTOCAD, nanoCAD;

[spoiler title=”источники:”]

http://student-com.ru/%D0%BF%D0%BE%D1%81%D1%82%D1%80%D0%BE%D0%B5%D0%BD%D0%B8%D0%B5-%D0%BB%D0%B8%D0%BD%D0%B8%D0%B8-%D0%BF%D0%B5%D1%80%D0%B5%D1%81%D0%B5%D1%87%D0%B5%D0%BD%D0%B8%D1%8F-%D0%B4%D0%B2%D1%83%D1%85-%D1%82%D1%80%D0%B5%D1%83%D0%B3%D0%BE%D0%BB%D1%8C%D0%BD%D0%B8%D0%BA%D0%BE%D0%B2.html

http://stud55.ru/peresechenie-treugolnikov-zadacha1/

[/spoiler]

Построение линии пересечения плоскостей, заданных различными способами

Две плоскости пересекаются друг с другом по прямой линии. Чтобы её построить, необходимо определить две точки, принадлежащие одновременно каждой из заданных плоскостей. Рассмотрим, как это делается, на следующих примерах.

Задача

Найдем линию пересечения плоскостей общего положения α и β для случая, когда пл. α задана проекциями треугольника ABC, а пл. β – параллельными прямыми d и e. Решение этой задачи осуществляется путем построения точек L₁ и L₂, принадлежащих линии пересечения.

Решение

1. Вводим вспомогательную горизонтальную плоскость γ₁. Она пересекает α и β по прямым. Фронтальные проекции этих прямых, 1”C” и 2”3”, совпадают с фронтальным следом пл. γ₁. Он обозначен на рисунке как f_0γ1 и расположен параллельно оси x.
2. Определяем горизонтальные проекции 1’C’ и 2’3′ по линиям связи.
3. Находим горизонтальную проекцию точки L₁ на пересечении прямых 1’C’ и 2’3′. Фронтальная проекция точки L₁ лежит на фронтальном следе плоскости γ.
4. Вводим вспомогательную горизонтальную плоскость γ₂. С помощью построений, аналогичных описанным в пунктах 1, 2, 3, находим проекции точки L₂.
5. Через L₁ и L₂ проводим искомую прямую l.

Стоит отметить, что в качестве пл. γ удобно использовать как плоскости уровня, так и проецирующие плоскости.

Пересечение плоскостей, заданных следами

Найдем линию пересечения плоскостей α и β, заданных следами. Эта задача значительно проще предыдущей. Она не требует введения вспомогательных плоскостей. Их роль выполняют плоскости проекций П₁ и П₂.

Алгоритм построения

1. Находим точку L’₁, расположенную на пересечении горизонтальных следов h_0α и h_0β. Точка L”₁ лежит на оси x. Её положение определяется при помощи линии связи, проведенной из L’₁.
2. Находим точку L”₂ на пересечении фронтальных следов пл. α и β. Точка L’₂ лежит на оси x. Её положение определяется по линии связи, проведенной из L”₂.
3. Проводим прямые l’ и l” через соответствующие проекции точек L₁ и L₂, как это показано на рисунке.

Таким образом, прямая l, проходящая через точки пересечения следов плоскостей, является искомой.

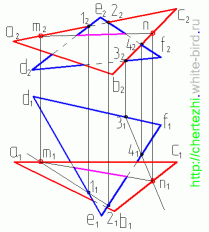
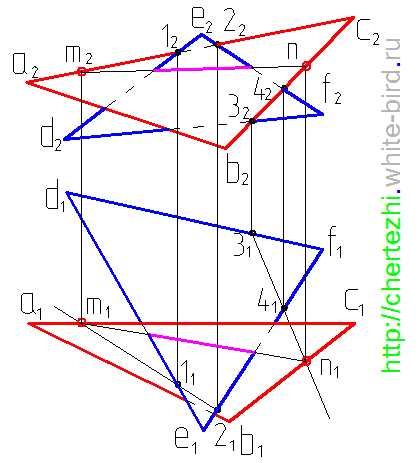
Пересечение плоскостей треугольников

Рассмотрим построение линии пересечения плоскостей, заданных треугольниками ABC и DEF, и определение их видимости методом конкурирующих точек.

Алгоритм построения

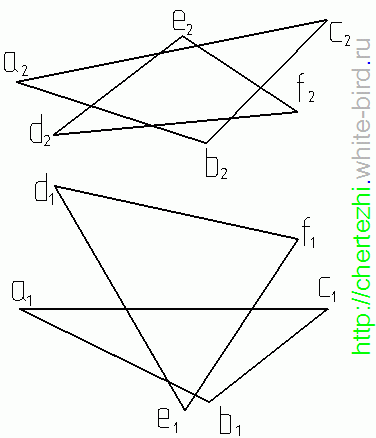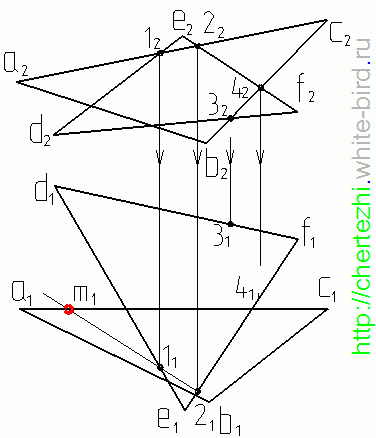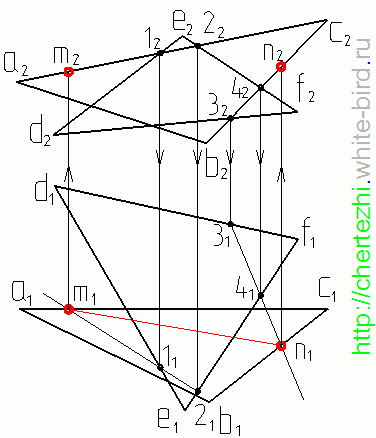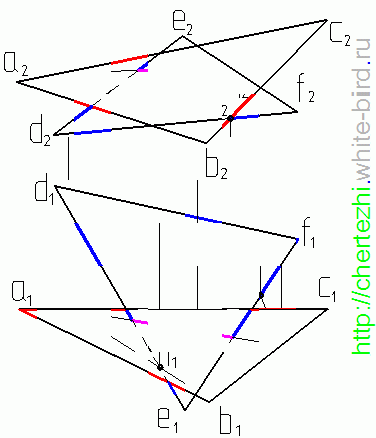
1. Через прямую DE проводим фронтально-проецирующую плоскость σ: на чертеже обозначен ее след f_0σ. Плоскость σ пересекает треугольник ABC по прямой 35. Отметив точки 3”=A”B”∩f_0σ и 5”=A”С”∩f_0σ, определяем положение (∙)3′ и (∙)5′ по линиям связи на ΔA’B’C’.
2. Находим горизонтальную проекцию N’=D’E’∩3’5′ точки N пересечения прямых DE и 35, которые лежат во вспомогательной плоскости σ. Проекция N” расположена на фронтальном следе f_0σ на одной линии связи с N’.

3. Через прямую BC проводим фронтально-проецирующую плоскость τ: на чертеже обозначен ее след f_0τ. С помощью построений, аналогичных тем, что описаны в пунктах 1 и 2 алгоритма, находим проекции точки K.

4. Через N и K проводим искомую прямую NK – линию пересечения ΔABC и ΔDEF.

Определение видимости

Фронтально-конкурирующие точки 4 и 5, принадлежащие ΔDEF и ΔABC соответственно, находятся на одной фронтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₂. Так как (∙)5′ находится ближе к наблюдателю, чем (∙)4′, то отсек ΔABC с принадлежащей ему (∙)5 является видимым в проекции на пл. π₂. С противоположной стороны от линии N”K” видимость треугольников меняется.

Горизонтально-конкурирующие точки 6 и 7, принадлежащие ΔABC и ΔDEF соответственно, находятся на одной горизонтально-проецирующей прямой, но расположены на разном удалении от плоскости проекций π₁. Так как (∙)6” находится выше, чем (∙)7”, то отсек ΔABC с принадлежащей ему (∙)6 является видимым в проекции на пл. π₁. С противоположной стороны от линии N’K’ видимость треугольников меняется.

Дополнительные материалы:

Разделы Уроки по теме Рекомендуем

Построение линии пересечения двух плоскостей. Автор: Moroz Дата: 2010-10-12 Одной из основополагающих задач начертательной геометрии является задача на на построение линии пересечения двух плоскостей общего положения. Случаи задания плоскостей бывают разные, но в любом случае вам встретится задача, в которой будет необходимо построить линию пересечения двух плоскостей заданных треугольниками (или другими плоскими геометрическими фигурами). Алгоритм решения такой задачи я и предлагаю рассмотреть сейчас. (Если же ваши плоскости заданы не треугольниками, а, например, параллельными прямыми, то приглашаю вас прочитать еще один урок, посвященный тому, как найти линию пересечения двух плоскостей.) Итак, даны две плоскости, заданные треугольниками АВС и DEF. Метод сводится к тому, что бы поочередно найти две точки пересечения двух ребер одного треугольника с плоскостью другого. Соединив эти точки мы получим линию пересечения двух плоскостей. Построение точки пересечения прямой с плоскостью более подробно было рассмотрено в предыдущем уроке, напомню только механические действия: – Заключим прямую АС во фронтально-проецирующую плоскость и перенесем по линиям связи на горизонтальную проекцию точки пересечения этой плоскости с прямыми DE и DF – точки 1 и 2 – На горизонтальной проекции соединим проекции точек 1 и 2 и найдем точку пересечения получившейся линии с горизонтальной проекцией той прямой, которую мы заключали во фронтально-проецирующую плоскость, в этом случае – с прямой AC. Мы получили точку M. – Заключим прямую BС во фронтально-проецирующую плоскость и перенесем по линиям связи на горизонтальную проекцию точки пересечения этой плоскости с прямыми EF и DF – точки 3 и 4 Соединим их горизонтальные проекции и получим точку пересечения этой прямой с прямой ВС – точку N. – Соединив точки M и N мы получим линию пересечения плоскостей заданных треугольниками. По сути линия пересечения уже найдена. – Осталось лишь определить видимость ребер треугольников. Это делается методом конкурирующих точек. При помощи наиболее внимательных посетителей сайта удалось найти неточность при определении видимости плоскостей. Ниже приведен чертеж, на котором исправлена видимость линий, ограничивающих плоскости на горизонтальной плоскости проекций: Просмотров: 318763 Вы можете сказать “спасибо!” автору статьи: пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект “White Bird. Чертежи Студентам” или или запишите наш телефон и расскажите о нас своим друзьям – кто-то наверняка ищет способ выполнить чертежи или создайте у себя на страничке или в блоге заметку про наши уроки – и кто-то еще сможет освоить черчение. А вот это – не реклама. Это напоминание, что каждый из нас может сделать. Если хотите – это просьба. Мы действительно им нужны: Комментарии: а я понять не мог никак, спасибо. В рот мне ноги! Ну, тут как говорится, Кесарю – кесарево 🙂 Исключительно , замечательно. Доходчиво и просто. Спасибо большое Большое спасибо, очень доходчиво написано! ААААААААААААААААААААААААА!!! вы спасли меня!!! подскажите пожалуйста. Можно ли строить все тоже самое , но из вида сверху, на вид спереди. т.е из нижних 2х треугольников на верхнии? По такому же алгоритму Вот спасибо, товарищи!)) Отличная статья! Хух спасибо выручили и руп в ближайшее время кину Неправильно определена видимость треугольников в плоскости XY. Легко проверить методом конкурирующих точек. [URL=http://www.radikal.ru][IMG]http://s017.radikal.ru/i401/1211/50/b3aba0648f63.jpg[/IMG][/URL] Хотел вставить картинку с пояснениями, а тут тег [IMG] [/IMG] не работает. Пояснения здесь http://s017.radikal.ru/i401/1211/50/b3aba0648f63.jpg To Дмитрий: Согласен, что ошибка в видимости, но только не в XY, а в XZ. Сделал подобный чертез в простеньком 3D редакторе: http://s59.radikal.ru/i163/1211/8b/bc5f07b225d9.jpg Так должно быть. =) Да и если просто логически подумать, то понятно, что линия df (которая на XY виде выше всех) никак не может на виде сверху (XZ) быть под красным треугольником. Александр, Дмитрий, спасибо за внимательность, исправлю на днях! Как говаривал наш преподаватель по вышке, уже весьма давно: “Молодчики! Бдительность – наше единственное оружие!” Александр, возможно, я ошибся. Но давайте проверим видимость в плоскости XZ с помощью конкурирующих точек. В моем примере это G и H см. рис. http://s47.radikal.ru/i118/1211/b9/d29b24b27c65.jpg Кажется все правильно. Поправьте меня если это не так. Да, Дмитрий, сейчас немного подумал и понял, что просто перепутал фронтальный и горизонтальный виды, поэтому все с точьностью наоборот получилось. Вы правы. =) Бред. Да, согласен. Бред. Так говорят все, это нормально. См. рубрику Юмор спасибо большое! мне эта стаття очень помогла. очень доходчиво был показан алгоритм на анимации. спасибо, еще раз:))) А если у меня не получается одна из точек,т.е точка м не лежит на ас,что делать?     Антон, доброго дня. Если вы имеете ввиду, что линия проведенная через 12 проходит мимо АС- просто продлите отрезок АС таким образом, чтоб все же найти точку пересечения этих ПРЯМЫХ. Их отрезки- лишь обозначенная их часть. Так что смелее. Это часто встречается. помогите сделать контрольную A – 0 55 40 B – 50 110 0 C – 120 40 75 D – 10 80 80 E – 80 20 90 F – 110 80 5 два треуг. ABC и DEF      Дорогие студенты. Если у вас ВДРУГ возникает желание написать подобное сообщение, не закапывайте свой шанс получить быстрый ответ. Пишите сразу на почту, с указанием сроков, телефона для связи и если нужно ОЧЕНЬ БЫСТРО – предлагайте стоимость и способ оплаты. Причем надо быть готовым к оплате вперед. А еще… иногда я бываю занят 🙂 Спасибо огромное! ГИФка просто супер, все понятно) А ведь есть и те, кому не нравится 🙂 Но я не в силах отказаться от этого “спорта”! Жаль только, что никак не найду времени исправить ошибку. Огроменное Вам спасибо!!! мне нужно построить пересечение двух непрозрачных фигур треугольника ABC и параллелограмма DEFG. координаты а(185.140.115)b(0.30.45)c(105.0.15)d(165.115.0)e(215.55.30) f(65.25.115) вот вопрос почему один из треугольников не пересекается с параллелограммом и можно ли решить эту задачу! Спасибо огромное! Мучаюсь уже около часа, методичка не помощник, а Ваша гифка все расставила на свои места! Лера, вы молодец! А ведь что интересно: многие ругают мою псевдонимацию 🙂 Успехов вам! Полностью присоединяюсь к Лере) Ваша гафа просто четкая. Наглядно видно что да как делать. Все супер!!! Спасибо) Спасибо! Всё понятно. Чётко и без мути Добавьте свой комментарий:

Последние уроки Как построить диметрию детали? Построение наклонного сечения, заданного на виде слева Определение линии пересечения двух плоскостей. Метод вспомогательных секущих плоскостей. Наша почта: zakaz@trivida.ru Наша страница в ВК: Случайный комментарий Валерий: Антон, у вас офис только в Москве? или в других городах тоже есть? Валерий, в настоящее время мы не имеем региональных представительств. Хорошо это или нет – не знаю. Сейчас для удаленных пользователей доступны только услуги по выполнению чертежей в электронном виде

Пересечение двух плоскостей треугольников ABC и EDK

Мы уже выполняли задачу на пересечение плоскостей, а также определяли видимость плоскостей.

В этом видеоуроке по начертательной геометрии выполним задачу на пересечение двух плоскостей заданных треугольниками ABC и EDK, т.е. закрепим пройденный материал.

После того как построим линию пересечения плоскостей заданных треугольниками, определим видимость плоскостей способом конкурирующих точек.

Дано:

Таблица значения координат:

Построить:

Пересечение двух плоскостей треугольников ABC и EDK

Более подробно смотрите в видеоуроке.

Пересечение двух плоскостей треугольников ABC и EDK