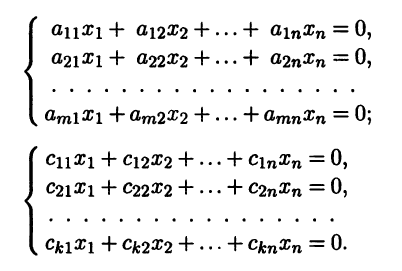Как найти пересечение подпространств заданных векторами - Сайт, где вы сможете решить свои вопросы

Пусть
заданы два подпространства R₁
и R₂
n-мерного
пространства R.

Определение:
Если каждый вектор x
пространства R
можно, и притом единственным образом,
представить как сумму двух векторов:

x
=
x₁+
x₂,

где

, то говорят, что пространство R
разложено в прямую сумму подпространств
R₁
и R₂.
Это записывают так:

R
= R₁+ R₂,

Теорема. Для
того, чтобы пространствоR
разлагалось в прямую сумму подпространств
R₁
и R₂,достаточно,
чтобы:

Подпространства

R₁
и R₂
имели только один общий вектор x
=
0 (нулевой вектор).
Сума
размерностей этих подпространств была
равна размерности пространства R.

Пусть
имеем два произвольных подпространства
R₁
и R₂
линейного пространства R.
Подпространство пересечения
R₁
и R₂
– это совокупность векторов, принадлежащих
обоим подпространствам R₁
и R₂:

☺ Пример
124. Пусть
R₁
и R₂
– два двумерных подпространства
трехмерного прос-транства (две плоскости,
проходящие через начало координат).
Тогда их пересечение

есть одномерное подпространство (прямая,
по которой эти плоскости пересекаются).

По
двум подпространствам
R₁
и R₂

можно построить еще одно подпространство,
которое называют суммой:
векторами этого подпространства являются
всевозможные суммы вида:

x
=
x₁+
x₂, (*)

где

,
его обозначают:
(в
отличие от прямой суммы двух подпрос-транств,
запись (*) элемента из R
может быть неоднозначной. Легко проверить,
что построенные элементы (*) образуют
подпространство.

Теорема. Сумма
размерностей
R₁
и R₂,
равна размерности их суммы плюс
размерность пересечения.

☺ Пример
125. Найдем
базис пересечения подпространств

, если R₁
натянут на векторы a₁и
a₂,
а R₂
– на векторы b₁и
b₂:

, ,

, .

Решение:
Нетрудно заметить, что векторы a₁и
a₂,
b₁и
b₂:
– линейно независимы. Согласно
вышеприведенной теореме запишем
размерность пересечения

в виде d
= k+r-s,
где k
= 2 – число независимых векторов,
порождающих подпространство R₁;
r
= 2 – число независи-мых векторов,
порождающих подпространство R₂;
s
– число независимых векторов, порождающих
подпространство

(его предстоим вычислить).

Применяя
один из способов вычисления ранга
системы векторов, получаем: s
= 3. В таком случае размерность пересечения
d
= 2 + 2 – 3 = 1/

Найдем базис из
условия:

c
= x₁a₁+
x₂
a₂ =
x₃b₁+
x₄
b₂

или

Решая
эту систему одним из способов, изложенных
в Гл.5, получим: x₁=
-s;
x₂=
4s;
x₃=
-3s;
x₄=
s,
где s
– произвольная постоянная. Принимая
s
= -1, получим:

c
= a₁–
4 a₂
= 3b₁–
b₂
= (5, -2, -3, -4).

Ответ:
базис пересечения подпространств: c
=
a₁–
4
a₂
=
3b₁–
b₂
= (5, -2, -3, -4).

☻Решите
примеры:

Пример
126. Найдем
базис пересечения подпространств

, если R₁
натянут на векторы a₁и
a₂,
а R₂
– на векторы b₁и
b₂:

, ,

, .

Ответ:
базис пересечения подпространств: c
=
-4a₁+
13a₂
=
8b₁+
3b₂
= (5, 9, -13, 27).

Пример
127. Найдем
базис пересечения подпространств

, если R₁
натянут на векторы a₁и
a₂,
а R₂
– на векторы b₁и
b₂:

, ,

, .

Ответ:
базис пересечения подпространств: c
=
2a₁–
3
a₂
=
–b₁+
b₂
= (1, 3, -1, 1).

Соседние файлы в папке СРС

Источник

Нахождение дополнения, суммы и пересечения подпространств

Нахождение алгебраического дополнения подпространства

Для заданного подпространства $Ltriangleleft mathbb{R}^n$ требуется найти алгебраическое дополнение подпространства $L^{+}$ , т.е. такое подпространство $L^{+} triangleleftmathbb{R}^n$ , что $mathbb{R}^n=Loplus L^{+}$ .

В зависимости от способа описания подпространства , используем одно из следующих двух утверждений.

1. Если подпространство $Ltriangleleft mathbb{R}^n$ задано как линейная оболочка $L=operatorname{Lin}(a_1,ldots,a_k)$ столбцов матрицы $A=begin{pmatrix} a_1&cdots&a_kend{pmatrix}$ , то множество решений однородной системы A^Tx=o является его алгебраическим дополнением $L^{+}triangleleft mathbb{R}^n$ , т.е.

$L=operatorname{Lin}(a_1,a_2,ldots,a_k)quad Rightarrowquad L^{+}= Bigl{A^Tx=oBigr}.$

(8.16)

2. Если подпространство $Ltriangleleft mathbb{R}^n$ задано как множество решений однородной системы Ax=o уравнений с неизвестными, то линейная оболочка столбцов $a_1^{tau},ldots, a_m^{tau}$ транспонированной матрицы $A^T=begin{pmatrix}a_1^{tau}&cdots& a_m^{tau}end{pmatrix}$ является его алгебраическим дополнением $L^{+}triangleleft mathbb{R}^n$ , т.е.

$L={Ax=o}quad Rightarrowquad L^{+}=operatorname{Lin} (a_1^{tau},ldots,a_m^{tau}),$

(8.17)

где $a_i^{tau}$ — i-й столбец матрицы A^T .

Разумеется, в (8.16) и (8.17) указано одно из возможных алгебраических дополнений подпространства $L^{+}$ (см. свойство 3 алгебраических дополнений подпространств).

Докажем сначала справедливость (8.16) в одномерном случае (k=1) , а потом в общем. Пусть L=operatorname{Lin}(a) — одномерное подпространство R^n , $a=begin{pmatrix}alpha_1&cdots&alpha_nend{pmatrix}^T$ — ненулевой столбец. Найдем алгебраическое дополнение подпространства . Рассмотрим уравнение a^Tx=o в координатной форме: alpha_1x_1+ldots+ alpha_nx_n=0 . Множество ${a^Tx=o}$ решений однородной системы, состоящей из одного уравнения, образует подпространство размерности (n-1) . Найдем пересечение Lcap L' . Подставляя элемент x=lambda a линейной оболочки в уравнение a^Tx=o , получаем lambda[(alpha_1)^2+ (alpha_2)^2+ldots+(alpha_n)^2]=0 , что возможно только при lambda=0 , так как ane o . Следовательно, элемент из принадлежит подпространству только тогда, когда — нулевой столбец, т.е. Lcap L'={o} . Учитывая, что dim{L}+dim{L'}=n , заключаем, что — алгебраическое дополнение подпространства в $mathbb{R}^ncolon, Loplus L'=mathbb{R}^n$ .Таким образом,

$operatorname{Lin}(a)oplus{a^Tx=o}=mathbb{R}^n.$

(8.18)

Учитывая (8.18), докажем (8.16) в общем случае (kgeqslant1) . Представим $L=operatorname{Lin}(a_1,ldots,a_k)$ в виде суммы L=L_1+ldots+L_k , где $L_i=operatorname{Lin}(a_i),$ i=1,ldots,k . Из (8.15) следует, что $(L_1+ldots+L_k)oplus (L_1^{+}+ldots+L_k^{+})= mathbb{R}^n$ . Согласно (8.18), множество $L_1^{+}={(a_i)^Tx=o}$ решений однородной системы, состоящей из одного уравнения, дополняет L_i до всего пространства $mathbb{R}^n$ . Пересечение множеств решений отдельных уравнений дает, разумеется, множество $L_1^{+} capldotscap L_k^{+}={A^Tx=o}$ решений системы этих уравнений. Поэтому $(L_1+ ldots+L_k)oplus{A^Tx=o}=mathbb{R}^n$ , что и требовалось доказать. Утверждение (8.17) доказывается аналогично, используя (8.18).

Пример 8.10. Найти алгебраическое дополнение подпространства $L=operatorname{Lin}[(t-1)^2,(t+1)^3]$ в пространстве $P_3(mathbb{R})$ многочленов не более, чем 3-й степени.

Решение. Сначала нужно переформулировать задачу для арифметического пространства (см. следствие теоремы 8.3 об изоморфизме конечномерных пространств). Для этого возьмем в $P_3(mathbb{R})$ стандартный базис $mathbf{e}_1(t)=1,$ $mathbf{e}_2(t)=t,$ $mathbf{e}_3(t)=t^2,$ $mathbf{e}_4(t)=t^3$ . Пространство $P_3(mathbb{R})$ изоморфно $mathbb{R}^4$ . Найдем координаты многочленов $mathbf{a}_1(t)=(t-1)^2$ и $mathbf{a}_2(t)=(t+1)^3$ в стандартном базисе. Раскладывая $mathbf{a}_1(t)$ по базису, получаем:

$mathbf{a}_1(t)= (t-1)^2= 1-2t+t^2=1cdot mathbf{e}_1(t)+(-2)cdot mathbf{e}_2(t)+ 1cdot mathbf{e}_3(t)+0cdot mathbf{e}_4(t),$

т.е. многочлену $mathbf{a}_1(t)$ соответствует координатный столбец $a_1= begin{pmatrix}1&-2&1&0end{pmatrix}^T$ — элемент пространства $mathbb{R}^4$ . Аналогично получаем координатный столбец $a_2= begin{pmatrix} 1&3&3&1end{pmatrix}^T$ для многочлена $mathbf{a}_2(t)$ .

Таким образом, исходная задача сводится к следующей: требуется найти алгебраическое дополнение подпространства $L=operatorname{Lin}(a_1,a_2)$ в пространстве $mathbb{R}^4$ . Используя правило (8.16), получаем, что $L^{+}$ — это множество решений системы A^Tx=o , где $A^T=begin{pmatrix} a_1&a_2 end{pmatrix}^T= begin{pmatrix}1&-2&1&0\ 1&3&3&1end{pmatrix}$ , т.е. системы $begin{cases} x_1-2x_2+x_3=0,\ x_1+3x_2+3x_3+x_4=0. end{cases}$

Решаем ее методом Гаусса. Приводим матрицу системы к упрощенному виду, прибавляя ко второй строке первую, умноженную на (-1), поделив вторую строку на 5, а затем прибавив ее, умноженную на 2, к первой:

$A^T=begin{pmatrix}1&-2&1&0\ 1&3&3&1end{pmatrix}sim begin{pmatrix}1&-2&1&0\ 0&5&2&1 end{pmatrix}sim begin{pmatrix}1&0&9/5&2/5\ 0&1&2/5&1/5 end{pmatrix}!.$

Базисные переменные x_1,,x_2 , свободные — x_3,,x_4 . Выражаем базисные переменные через свободные: $x_1=-frac{9}{5}x_3-frac{2}{5}x_4;$ $x_2=-frac{2}{5}x_3-frac{1}{5}x_4$ . Находим фундаментальную систему решений. Подставляя стандартные наборы свободных переменных ( x_3=1,,x_4=0 и x_3= 0,,x_4=1 ), получаем решения: $varphi_1=begin{pmatrix}-dfrac{9}{5}&-dfrac{2}{5}& 1&0end{pmatrix}^T,$ $varphi_2=begin{pmatrix}-dfrac{2}{5}&-dfrac{1}{5}&0&1 end{pmatrix}^T$ , которые образуют фундаментальную систему решений и являются базисом алгебраического дополнения $L^{+}=operatorname{Lin}(varphi_1,varphi_2)$ Полученный результат переносим в пространство многочленов. По координатному столбцу находим многочлен

$varphi_1(t)=-frac{9}{9}cdot mathbf{e}_1(t)-frac{2}{5}cdot mathbf{e}_2(t)+ 1cdot mathbf{e}_3(t)+0cdot mathbf{e}_4(t)= -frac{9}{5}-frac{2}{5},t+t^2.$

Аналогично получаем $varphi_2(t)= -frac{2}{5}-frac{1}{5}t+t^3$ . Искомое алгебраическое дополнение имеет вид

$L^{+}=operatorname{Lin}!left[left( -frac{9}{5}-frac{2}{5},t+t^2 right)!,,left( -frac{2}{5} -frac{1}{5}t+ t^3right)right]!,$

Проверим равенство $Lcap L^{+}={mathbf{o}}$ . Для этого приравняем между собой линейные комбинации многочленов $mathbf{a}_1(t),,mathbf{a}_2(t)$ и varphi_1(t),,varphi_2(t):

$alpha(1-t)^2+beta(1+t)^3= gamma!left(-frac{9}{5}-frac{2}{5},t+t^2 right)+delta! left(-frac{2}{5} -frac{1}{5}t+ t^3right)!.$

Преобразовывая, получаем

$(alpha+beta)cdot t^3+(alpha+3beta-gamma)cdot t^2+left(-2alpha+ 3beta+ frac{2}{5},gamma+frac{1}{5},deltaright)!cdot t+alpha+beta+ frac{9}{5},gamma+ frac{2}{5},delta=0.$

Чтобы это равенство выполнялось тождественно, все его коэффициенты должны быть равны нулю:

$begin{cases}beta-delta=0,\ alpha+3beta-gamma=0,\ -2alpha+3beta+ frac{2}{5} gamma+ frac{1}{5}delta=0,\ alpha+beta+ frac{9}{5}gamma+ frac{2}{5}delta=0, end{cases} Leftrightarrowquad underbrace{begin{pmatrix}0&1&0&-1\ 1&3&-1&0\ -2&3&2/5&1/5\ 1&1&9/5&2/5 end{pmatrix}}_{B}!cdot! begin{pmatrix}alpha\ beta\ gamma\ delta end{pmatrix}= begin{pmatrix} 0\0\0\0 end{pmatrix}!.$

Ранг матрицы этой системы равен 4 (находится, например, методом Гаусса). Поэтому однородная система имеет только нулевое решение alpha=beta= gamma= delta=0 . Таким образом, равенство $Lcap L^{+}={mathbf{o}}$ выполняется.

Нахождение алгебраической суммы подпространств

Для заданных подпространств и пространства $mathbb{R}^n$ требуется найти размерность и базис их алгебраической суммы A+B . Рассмотрим методику решения этой задачи для двух случаев описания подпространств.

Пусть подпространства заданы линейными оболочками своих образующих (внутреннее описание): $mathbf{A} =operatorname{Lin}(mathbf{a}_1,ldots, mathbf{a}_{k_1})$ и $mathbf{B} =operatorname{Lin} (mathbf{b}_1,ldots, mathbf{b}_{k_2})$ . Тогда, приписывая к образующим $mathbf{a}_1,ldots, mathbf{a}_{k_1}$ одного подпространства образующие $mathbf{b}_1,ldots, mathbf{b}_{k_2}$ другого подпространства, получаем образующие суммы подпространств и mathbf{B}:

$left.{begin{gathered}mathbf{A} =operatorname{Lin}(mathbf{a}_1,ldots, mathbf{a}_{k_1}),hfill\ mathbf{B}=operatorname{Lin}(mathbf{b}_1,ldots, mathbf{b}_{k_2}) end{gathered}}!right}quad Rightarrowquad mathbf{A}+mathbf{B}=operatorname{Lin} (mathbf{a}_1,ldots, mathbf{a}_{k_1},mathbf{b}_1,ldots, mathbf{b}_{k_2}),$

(8.19)

поскольку любой вектор mathbf{v}in(mathbf{A}+mathbf{B}) имеет вид $mathbf{v}= underbrace{alpha_1 mathbf{a}_1+ldots+ alpha_{k_1}mathbf{a}_{k_1} }_{mathbf{v}_1inmathbf{A}}+ underbrace{beta_1 mathbf{b}_1+ldots+ beta_{k_1}mathbf{b}_{k_2} }_{mathbf{v}_2inmathbf{B}}$ . Базис суммы $mathbf{A}+ mathbf{B}= operatorname{Lin} (mathbf{a}_1,ldots, mathbf{a}_{k_1}, mathbf{b}_1, ldots, mathbf{b}_{k_2})$ можно найти как максимальную подсистему линейно независимых столбцов.

Пусть подпространства заданы как множества решений однородных систем уравнений (внешнее описание): mathbf{A}={Ax=o} и mathbf{B}={Bx=o} . Тогда, переходя к внутреннему описанию, сводим задачу к предыдущему случаю, а именно нужно выполнить следующие действия:

1) для каждой однородной системы Ax=o и Bx=o найти фундаментальные системы решений $varphi_1,ldots,varphi_{n-r}$ и $psi_1,ldots,psi_{n-r}$ соответственно. При этом получим $A=operatorname{Lin} (varphi_1,ldots,varphi_{n-r})$ и $B=operatorname{Lin}(psi_1,ldots,psi_{n-r})$ , где $r_{A}=operatorname{rg}A,$ $r_{B}=operatorname{rg}B$ ;

2) по правилу (8.19) найти сумму $mathbf{A}+mathbf{B}= operatorname{Lin} (varphi_1, ldots,varphi_{n-r},psi_1,ldots,psi_{n-r})$ .

Пример 8.11. Найти размерность и базис алгебраической суммы mathbf{A}+mathbf{B} подпространств $mathbf{A},mathbf{B}triangleleft mathbb{R}^4$ , если подпространство задано системой уравнений

$begin{cases}x_1+x_2+2x_3+x_4=0,\ 2x_1+3x_2+x_4=0,\ 3x_1+4x_2+2x_3+2x_4=0,end{cases}$

подпространство mathbf{B} — линейной оболочкой своих образующих:

$mathbf{B}=operatorname{Lin}(b_1,b_2),quad b_1=begin{pmatrix}-4&3&1&-1 end{pmatrix}^T,quad b_2=begin{pmatrix}1&1&1&1end{pmatrix}^T.$

Решение. Образующие подпространства mathbf{A} были найдены в примере 8.9: $mathbf{A}=operatorname{Lin}(a_1,a_2)$ , где $a_1= begin{pmatrix}-6&4&1&0end{pmatrix}^T,$ $a_2=begin{pmatrix}-2&1&0&1 end{pmatrix}^T$ . По правилу (8.19) получаем $mathbf{A}+mathbf{B}= operatorname{Lin}(a_1,a_2,b_1,b_2)$ . Найдем базис этого подпространства как максимальную линейно независимую подсистему столбцов. Составляем из этих столбцов матрицу и приводим ее методом Гаусса к ступенчатому виду:

$begin{gathered}begin{pmatrix}-6&-2&-4&1\ 4&1&3&1\ 1&0&1&1\ 0&1&-1&1 end{pmatrix}sim begin{pmatrix}1&0&1&1\ 4&1&3&1\ -6&-2&-4&1\ 0&1&-1&1 end{pmatrix}sim begin{pmatrix}1&0&1&1\ 0&1&-1&-3\ 0&-2&2&7\ 0&1&-1&1 end{pmatrix}sim\[2pt] sim begin{pmatrix}1&0&1&1\ 0&1&-1&-3\ 0&0&0&1\ 0&0&0&4 end{pmatrix}sim begin{pmatrix} 1&0&1&1\ 0&1&-1&-3\ 0&0&0&1\ 0&0&0&0 end{pmatrix}!.end{gathered}$

Первый, второй и четвертый столбцы полученной матрицы линейно независимы. Значит, соответствующие столбцы a_1,,a_2,,b_2 исходной матрицы так же линейно независимы (так как выполнялись элементарные преобразования только над строками). Поэтому они являются базисом mathbf{A}+mathbf{B} и dim(mathbf{A}+ mathbf{B})=3 .

Нахождение пересечения подпространств

Для заданных подпространств mathbf{A} и mathbf{B} пространства $mathbb{R}^n$ требуется найти размерность и базис их пересечения mathbf{A}cap mathbf{B} . Рассмотрим методику решения этой задачи для двух случаев описания подпространств.

Пусть подпространства заданы как множества решений однородных систем уравнений (внешнее описание): mathbf{A}={Ax=o} и mathbf{B}={Bx=o} . Тогда, приписывая к системе Ax=o , задающей одно подпространство, систему Bx=o , задающую другое подпространство, получаем систему $begin{cases} Ax=o,\ Bx=o,end{cases}$ определяющую пересечение подпространств:

$left.{begin{gathered}mathbf{A}={Ax=o},\ mathbf{B}={Bx=o} end{gathered}}right}quad Rightarrowquad mathbf{A}cap mathbf{B}=left{begin{pmatrix}A\ Bend{pmatrix}!x=oright}!.$

(8.20)

Базисом пересечения служит ее фундаментальная система решений.

Пусть подпространства mathbf{A} и mathbf{B} пространства $mathbb{R}^n$ заданы линейными оболочками своих образующих (внутреннее описание): $mathbf{A}=operatorname{Lin}(a_1,ldots,a_{k_1})$ и $mathbf{B}= operatorname{Lin}(b_1,ldots,b_{k_2})$ . Переходя от внутреннего описания подпространств к внешнему, можно свести задачу к предыдущему случаю. Однако удобнее сделать иначе. Пересечению mathbf{A}cap mathbf{B} принадлежат только такие $mathbf{x}in mathbb{R}^n$ , которые можно представить как равные между собой линейные комбинации столбцов $a_1,ldots,a_{k_1}$ и столбцов $b_1,ldots,b_{k_2}$ соответственно:

$mathbf{x}=alphacdot mathbf{a}_1+ldots+alpha_{k_1}cdot mathbf{a}_{k_1}= beta_{1}cdot mathbf{b}_{1}+ldots+beta_{k_2}cdot mathbf{b}_{k_2}.$

(8.21)

Представим второе равенство в (8.21) в матричном виде Aalpha=Bbeta , где $A=begin{pmatrix}a_1&cdots&a_{k_1}end{pmatrix},$ $B=begin{pmatrix} b_1&cdots&b_{k_2}end{pmatrix}$ — матрицы, составленные из данных столбцов, $alpha= begin{pmatrix}alpha_1&cdots&alpha_{k_1}end{pmatrix}^T,$ $beta= begin{pmatrix} beta_1&cdots&beta_{k_2}end{pmatrix}^T$ — столбцы коэффициентов линейных комбинаций. Равенство Aalpha=Bbeta можно рассматривать как одно родную систему Aalpha-Bbeta=o уравнений с (k_1+k_2) неизвестными alpha и beta . Каждому решению этой системы соответствует вектор mathbf{x}= Aalpha=Bbeta , при надлежащий пересечению mathbf{A}cap mathbf{B} . Однако, на практике удобнее вместо системы Aalpha-Bbeta=o рассматривать однородную систему Aalpha+Bbeta=o , решения которой обладают теми же свойствами (тогда вектор mathbf{x}= Aalpha=Bbeta при надлежит пересечению mathbf{A}cap mathbf{B} .

Поэтому для нахождения пересечения подпространств $mathbf{A}= operatorname{Lin} (a_1,ldots,a_{k_1})$ и $mathbf{B}= operatorname{Lin}(b_1,ldots,b_{k_2})$ и базиса пересечения нужно выполнить следующие действия.

1. Составить блочную матрицу (Amid B) коэффициентов однородной системы уравнений Aalpha+Bbeta=o , где матрицы $A=begin{pmatrix} a_1&cdots&a_{k_1} end{pmatrix},$ $B=begin{pmatrix} b_1&cdots&b_{k_2}end{pmatrix}$ образованы из заданных столбцов.

2. Для однородной системы с матрицей (Amid B) найти фундаментальную матрицу Phi . Матрица Phi имеет размеры (k_1+k_2)times (k_1+k_2-r) , где r=operatorname{rg}(Amid B) .

3. Из первых k_1 строк матрицы Phi составить матрицу $Phi_{alpha}= (E_{k_1}mid O)Phi$ . Столбцы матрицы $Phi_{alpha}= begin{pmatrix} varphi_1&cdots &varphi_{k_1+k_2-r}end{pmatrix}$ содержат искомые коэффициенты $alpha=begin{pmatrix}alpha_1&cdots&alpha_{k_1}end{pmatrix}^T$ линейных комбинаций (8.21).

4. Записать пересечение mathbf{A}cap mathbf{B} как линейную оболочку столбцов матрицы $APhi_{alpha}:$ $Acap B=operatorname{Lin}(Avarphi_1,ldots, Avarphi_{k_1+k_2-r})$ .

5. Найти базис пересечения как максимальную линейно независимую подсистему образующих $Avarphi_1,ldots, Avarphi_{k_1+k_2-r}$ .

Пример 8.12. Найти размерности и базисы суммы mathbf{A}+ mathbf{B} и пересечения mathbf{A}cap mathbf{B} подпространств $mathbf{A},mathbf{B}triangleleft mathbb{R}^4$ , если они заданы линейными оболочками своих образующих: $mathbf{A}= operatorname{Lin}(a_1,a_2,a_3)$ $mathbf{B}= operatorname{Lin}(b_1,b_2,b_3)$ , где

$a_1=begin{pmatrix}1\1\1\1end{pmatrix}!,quad a_2=begin{pmatrix}1\-1\1\-1 end{pmatrix}!,quad a_3=begin{pmatrix}1\3\1\3end{pmatrix}!,quad b_1=begin{pmatrix} 1\2\0\2 end{pmatrix}!,quad b_2=begin{pmatrix}1\2\1\2end{pmatrix}!,quad b_3=begin{pmatrix} 3\1\3\1 end{pmatrix}!.$

Решение. Найдем базис и размерность суммы mathbf{A}+ mathbf{B} . Составим из данных столбцов блочную матрицу

$(Amid B)= begin{pmatrix}a_1&a_2&a_3,mid, b_1&b_2&b_3 end{pmatrix}= begin{pmatrix}1&1&1!!&vline!!& 1&1&3\ 1&-1&3!!&vline!!& 2&2&1\ 1&1&1!!&vline!!& 0&1&3\ 1&-1&3!!&vline!!& 2&2&1 end{pmatrix}!.$

Элементарными преобразованиями над строками приведем ее к ступенчатому виду:

$(Amid B)sim begin{pmatrix}1&1&1!!&vline!!& 1&1&3\ 0&-2&2!!&vline!!& 1&1&-2\ 0&0&0!!&vline!!& -1&0&0\ 0&-2&2!!&vline!!& 1&1&-2end{pmatrix}sim begin{pmatrix} 1&1&1!!&vline!!& 1&1&3\ 0&-2&2!!&vline!!& 1&1&-2\ 0&0&0!!&vline!!& -1&0&0\ 0&0&0!!&vline!!& 0&0&0 end{pmatrix}= (A'mid B').$

По ступенчатому виду определяем, что первый, второй и четвертый столбцы линейно независимы. Следовательно, из 6 образующих a_1,a_2,a_3, b_1,b_2,b_3 подпространства mathbf{A}+mathbf{B} максимальную линейно независимую подсистему составляют столбцы a_1,a_2,b_1 (в этих столбцах расположен базисный минор матрицы). Следовательно, эти столбцы служат базисом суммы: $mathbf{A}+ mathbf{B}= operatorname{Lin}(a_1,a_2,b_1)$ и dim(mathbf{A}+mathbf{B})=3 . По ступенчатому виду матрицы (Amid B) можно также определить размерности подпространств. В блоке две ненулевых строки, следовательно, dimmathbf{A}= operatorname{rg}A= operatorname{rg}A'=2 . Ненулевые строки блока В’ линейно независимы, следовательно, dimmathbf{B}= operatorname{rg}B= operatorname{rg}B'=3 .

Найдем базис и размерность пересечения $mathbf{A}cap mathbf{B}~ (k_1=k_2=3,~ r=operatorname{rg}(Amid B)=3)$ .

1. Первый пункт алгоритма выполнен выше: матрица (Amid B) однородной системы Aalpha+Bbeta=o приведена к ступенчатому виду (A'mid B') .

2. Находим фундаментальную систему решений (используя алгоритм, описанный в разд. 5.5). Приводим матрицу (A'mid B') системы к упрощенному виду:

$(A'mid B')= begin{pmatrix}1&1&1!!&vline!!& 1&1&3\ 0&-2&2!!&vline!!& 1&1&-2\ 0&0&0!!&vline!!& -1&0&0\ 0&0&0!!&vline!!& 0&0&0end{pmatrix}sim begin{pmatrix}1&0&2!!&vline!!& 0&3/2&2\ 0&1&-1!!&vline!!& 0&-1/2&1\ 0&0&0!!&vline!!& 1&0&0\ 0&0&0!!&vline!!& 0&0&0end{pmatrix}!.$

Базисные переменные: alpha_1,,alpha_2,,beta_1 ; остальные переменные — свободные. Выражаем базисные переменные через свободные: $alpha_1=-2alpha_3-frac{3}{2} beta_2-2beta_3;$ $alpha_2=alpha_3+frac{1}{2}beta_2-beta_3;$ beta_1=0 . Придавая свободным переменным наборы значений

alpha_3=1,quad beta_2=0,quad beta_3=0;qquad alpha_3=0,quad beta_2=2,quad beta_3=0;qquad alpha_3=0,quad beta_2=0,quad beta_3=1,

получаем линейно независимые решения

$varphi_1=begin{pmatrix} -2&1&1&0&0&0 end{pmatrix}^T,quad varphi_2= begin{pmatrix} -3&1&0&0&2&0 end{pmatrix}^T,quad varphi_3=begin{pmatrix}-2&-1&0&0&0&1 end{pmatrix}^T.$

т.е. фундаментальная матрица имеет вид

$Phi= begin{pmatrix}-2&-3&-2\ 1&1&-1\ 1&0&0\ 0&0&0\ 0&2&0\ 0&0&1 end{pmatrix}!.$

3. Из первых трех строк (k_1=3) матрицы Phi составляем матрицу $Phi_{alpha}= begin{pmatrix} -2&-3&-2\ 1&1&-1\ 1&0&0 end{pmatrix}$ .

4. Вычисляем произведение

$AcdotPhi_{alpha}= begin{pmatrix}1&1&1\ 1&-1&3\ 1&1&1\ 1&-1&3 end{pmatrix}! cdot! begin{pmatrix}-2&-3&-2\ 1&1&-1\ 1&0&0end{pmatrix}= begin{pmatrix}0&-2&-3\ 0&-4&-1\ 0&-2&-3\ 0&-4&-1end{pmatrix}= begin{pmatrix}o&c_1&c_2end{pmatrix}!.$

Столбцы этой матрицы являются образующими пересечения $mathbf{A}cap mathbf{B}= operatorname{Lin}(o,c_1,c_2)$ , где — нулевой столбец, $c_1= begin{pmatrix} -2&-4&-2&-4 end{pmatrix}^T,$ $c_2=begin{pmatrix}-3&-1&-3&-1 end{pmatrix}^T$ .

5. Найдем базис пересечения mathbf{A}cap mathbf{B} . Для этого матрицу $APhi_{alpha}$ приводим к ступенчатому виду

$AcdotPhi_{alpha}= begin{pmatrix}0&-2&-3\ 0&-4&-1\ 0&-2&-3\ 0&-4&-1end{pmatrix}sim begin{pmatrix}0&2&3\ 0&0&5\ 0&0&0\ 0&0&0 end{pmatrix}sim begin{pmatrix}0&1&3/2\ 0&0&1\ 0&0&0\ 0&0&0 end{pmatrix}!.$

По ступенчатому виду определяем, что последние два столбца матрицы $APhi_{alpha}$ линейно независимы. Следовательно, два столбца c_1,c_2 являются базисом пересечения $mathbf{A}cap mathbf{B}= operatorname{Lin}(c_1,c_2)$ и dim(mathbf{A}cap mathbf{B})=2 .

Проверим размерность пересечения подпространств, которую вычислим, используя формулу (8.13):

dim(mathbf{A}cap mathbf{B})= dim mathbf{A}+dim mathbf{B}-dim(mathbf{A}+ mathbf{B})= 2+3-3=2,

что совпадает с найденной ранее размерностью.

Пример 8.13. Найти размерности и базисы пересечения mathbf{A}cap mathbf{B} и суммы mathbf{A}+ mathbf{B} подпространств $mathbf{A}, mathbf{B}triangleleft mathbb{R}^4$ , если они заданы однородными системами уравнений:

$mathbf{A}colon, begin{cases}x_1+x_2+2x_3+x_4=0,\ 2x_1+3x_2+x_4=0,\ 3x_1+4x_2+2x_3+2x_4=0;end{cases}quad mathbf{B}colon, begin{cases}x_1+x_2+x_3=0,\ 2x_1+3x_2+x_3+2x_4=0,\ x_1+2x_2+2x_4=0.end{cases}$

Решение. Обозначим матрицы данных систем через mathbf{A} и mathbf{B} соответственно. По правилу (8.20) пересечение mathbf{A}cap mathbf{B} описывается однородной системой $begin{cases}Ax=o,\Bx=o.end{cases}$ Найдем базис пересечения — фундаментальную систему решений этой однородной системы уравнений. Составляем матрицу системы $begin{pmatrix}dfrac{A}{B}end{pmatrix}$ и приводим ее к ступенчатому виду, а затем к упрощенному виду:

$begin{gathered} begin{pmatrix}dfrac{A}{B}end{pmatrix}= begin{pmatrix}1&1&2&1\ 2&3&0&1\ 3&4&2&2\hline 1&1&1&0\ 2&3&1&2\ 1&2&0&2 end{pmatrix}sim begin{pmatrix} 1&1&2&1\ 0&1&-4&-1\ 0&1&-4&-1\hline 0&0&-1&-1\ 0&1&-3&0\ 0&1&-2&1 end{pmatrix}sim begin{pmatrix}1&1&2&1\ 0&1&-4&-1\ 0&0&0&0\hline 0&0&-1&-1\ 0&0&1&1\ 0&0&2&2 end{pmatrix}sim begin{pmatrix}1&1&2&1\ 0&1&-4&-1\ 0&0&1&1\hline 0&0&0&0\ 0&0&0&0\ 0&0&0&0 end{pmatrix}sim\[2pt] sim begin{pmatrix}1&0&6&2\ 0&1&-4&-1\ 0&0&1&1\hline 0&0&0&0\ 0&0&0&0\ 0&0&0&0 end{pmatrix}sim begin{pmatrix}1&0&0&-4\ 0&1&0&3\ 0&0&1&1\hline 0&0&0&0\ 0&0&0&0\ 0&0&0&0end{pmatrix}!.end{gathered}$

Базисные переменные: x_1,x_2,x_3 , свободная переменная — x_4 . Выражаем базисные переменные через свободную: x_1=4x_4; x_2=-3x_4; x_3=-x_4 . Фундаментальная система содержит одно решение $varphi_1= begin{pmatrix} 4&-3&-1&1end{pmatrix}^T$ , которое получаем, задавая x_4=1 . Следовательно, $mathbf{A}cap mathbf{B}= operatorname{Lin}(varphi_1)$ и dim(mathbf{A}cap mathbf{B}) .

Найдем теперь сумму mathbf{A}+mathbf{B} . Фундаментальная система решений однородной системы Ax=o была найдена в примере 8.9. Следовательно,

$mathbf{A}=operatorname{Lin}(a_1,a_2)$ , где $a_1=begin{pmatrix} -6&4&1&0 end{pmatrix}^T,~~ a_2=begin{pmatrix}-2&1&0&1end{pmatrix}^T,~~ dim{mathbf{A}}=2$ .

Найдем фундаментальную систему решений однородной системы Bx=o . Для этого приводим матрицу системы к ступенчатому виду, а затем к упрощенному:

$B=begin{pmatrix}1&1&1&0\ 2&3&1&2\ 1&2&0&2 end{pmatrix}sim begin{pmatrix} 1&1&1&0\ 0&1&-1&2\ 0&1&-1&2 end{pmatrix}sim begin{pmatrix}1&1&1&0\ 0&1&-1&2\ 0&0&0&0 end{pmatrix}sim begin{pmatrix}1&0&2&-2\ 0&1&-1&2\ 0&0&0&0 end{pmatrix}!.$

Базисные переменные: x_1,,x_2 , свободные переменные: x_3,,x_4 . Выражаем базисные переменные через свободные: x_1=-2x_3+2x_4; x_2=x_3-2x_4 . Фундаментальная система состоит из двух решений $b_1=begin{pmatrix}-2&1&1&0end{pmatrix}^T,$ $b_2=begin{pmatrix}2&-2&0&1end{pmatrix}^T$ , которые находим, придавая свободным переменным стандартные наборы значений ( x_3=1,~x_4=0 и x_3=0,~x_4=1 ). Следователь но, $mathbf{B}= operatorname{Lin}(b_1,b_2)$ и dim mathbf{B}=2 .

По правилу (8.19) находим сумму $mathbf{A}+mathbf{B}= operatorname{Lin} (a_1,a_2,b_1,b_2)$ . Чтобы определить базис, составим из столбцов a_1,,a_2,, b_1,,b_2 матрицу и приведем ее к ступенчатому виду:

$begin{pmatrix}-6&-2&-2&2\ 4&1&1&-2\ 1&0&1&0\ 0&1&0&1end{pmatrix}sim begin{pmatrix}1&0&1&0\ 0&1&-3&-2\ 0&-2&4&2\ 0&1&0&1 end{pmatrix}sim begin{pmatrix} 1&0&1&0\ 0&1&-3&-2\ 0&0&-2&-2\ 0&0&3&3 end{pmatrix}sim begin{pmatrix}1&0&1&0\ 0&1&-3&-2\ 0&0&1&1\ 0&0&0&0 end{pmatrix}!.$

Первые три столбца линейно независимы. Следовательно, $mathbf{A}+mathbf{B}= operatorname{Lin}(a_1,a_2,b_1)$ и dim(mathbf{A}+mathbf{B})=3 .

Проверим размерность суммы подпространств. По формуле (8.13) получаем

dim(mathbf{A}+mathbf{B})= dimmathbf{A}+dimmathbf{B}-dim(mathbf{A}cap mathbf{B})=2+2-1=3,

что совпадает с найденной ранее размерностью.

Нахождение относительных алгебраических дополнений подпространств

Пусть дана цепочка подпространств $mathbf{A}triangleleft mathbf{B}triangleleft mathbb{R}^n$ . Требуется найти относительное дополнение $mathbf{A}^{+}cap mathbf{B}$ подпространства до подпространства .

Рассмотрим случай внешнего описания подпространств — как множеств решений однородных систем уравнений: mathbf{A}={Ax=o} и mathbf{B}={Ax=o} . Согласно (8.17) базис пространства $mathbf{A}^{+}$ образуют линейно независимые столбцы транспонированной матрицы A^T . Тогда относительное дополнение $mathbf{A}^{+}cap mathbf{B}$ составляют такие векторы x=A^Ty , которые удовлетворяют системе Bx=o . Если обозначить через Phi фундаментальную матрицу системы BA^Ty=o , то линейно независимые столбцы матрицы A^TPhi являются максимальной системой векторов подпространства mathbf{B} , линейно независимой над mathbf{A} , т.е. базисом относительного дополнения.

На практике нахождение базиса $mathbf{A}^{+}cap mathbf{B}$ удобнее производить, используя ступенчатые виды матриц и , согласно следующей методике.

1. Привести матрицы и при помощи элементарных преобразований строк к ступенчатому виду и удалить нулевые строки. В результате по лучим матрицы $(A)_{text{st}}$ и $(B)_{text{st}}$ модифицированного ступенчатого вида (строки каждой из этих матриц линейно независимые).

2. Найти фундаментальную матрицу Phi однородной системы уравнений $(B)_{text{st}}(A)_{text{st}}^Ty=o$ .

3. Вычислить матрицу $(A)_{text{st}}^TPhi$ . Ее столбцы образуют искомый базис $mathbf{A}^{+}cap mathbf{B}$ .

Рассмотрим случай внутреннего описания подпространства mathbf{A} как линейной оболочки своих образующих: $mathbf{A}=operatorname{Lin}(a_1,ldots,a_k)$ . Согласно (8.16) множество решений системы уравнений A^Tx=o (матрица $A= begin{pmatrix}a_1&cdots&a_kend{pmatrix}$ составлена из образующих) является алгебраическим дополнением $mathbf{A}^{+}$ . Тогда множество решений системы $begin{cases}A^Tx=o,\Bx=o,end{cases}!!Leftrightarrow, begin{pmatrix} dfrac{A^T}{B} end{pmatrix}!x=o$ является относительным дополнением $mathbf{A}^{+}cap mathbf{B}$ , а ее фундаментальная система решений — базисом относительного дополнения.

Замечание 8.10. Способы описания подпространств комплексного линейного пространства, а также методы решения типовых задач аналогичны рассмотренным. В отличие от вещественного арифметического пространства $mathbb{R}^n$ вместо операции транспонирования матрицы в комплексном арифметическом пространстве $mathbb{C}^n$ нужно использовать операцию сопряжения матрицы.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

Ваш е-мэйл

Заполните, если хотите получить ответ

Оцените наш проект

Источник

majestry, действительно формула указанная Veyron несколько упрощает жизнь.
Расскажу как найти пересечение и объединение подпространств, натянутых на Ваши вектора, методом “в лоб”.

У Вас есть две линейные оболочки векторов

$https://www.cyberforum.ru/cgi-bin/latex.cgi?left{{x}_{1},{x}_{2},{x}_{3} right}$

$https://www.cyberforum.ru/cgi-bin/latex.cgi?left{{y}_{1},{y}_{2},{y}_{3} right}$

Для нахождения объединения Вы строите такую матрицу:
Транспонируете Ваши вектора столбцы в вектора строки.
Далее последовательно составляете матрицу 6*3 где i-ая строка отвечает i-ому вектору, а j-столбец j-м координатам соответствующих векторов. Далее, как в методе Гаусса, приводите это дело к диагональному виду откидывая все нулевые строки. Ранг этой матрицы будет отвечать размерности объединения Ваших оболонок.

Пересечение находится так:
Ваши вектора остаются векторами столбцами. Сначала выбрасываете из ваших линейных оболочек те вектора, которые выражаются через другие, то-есть оставляете только базисные вектора. Пускай это будет x1,x2 и y1,y2 Далее составляете такую матрицу

$https://www.cyberforum.ru/cgi-bin/latex.cgi?begin{pmatrix} {x}_{1} & {x}_{2} |&{y}_{1} &{y}_{2} end{pmatrix}$

Далее с помощью преобразований над столбцами, оставляя скажем левую часть не тронутой, Вы приводите подматрицу справа к виду, как можно близкому к диагональному. Делать это надо до тех пор, пока оставшиеся ненулевые вектора станут линейно не зависимыми.
Количество нулевых векторов, которые в итоге останутся и будет размерностью пересечения.

Это можно все делать по разному, но принцип везде работает один и тот же.

Источник

Пусть H₁, H₂ – линейные подпространства в линейном пространстве L.

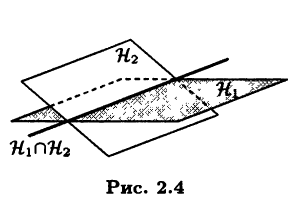
Определение 2.2. Множество Н₁ ∩ Н₂ называют пересечением линейных подпространств Н₁ и Н₂

На рис. 2.4 видим, что два линейных подпространства, изображенные плоскостями, в пересечении дают прямую, также являющуюся представлением некоторого линейного подпространства (см. пример 2.1).

Теорема 2.1. Пересечение Н₁ ∩ Н₂ двух линейных под-пространств Н₁ и Н₂ в линейном пространстве L является линейным подпространством в L.

◄ Проверим, выполняется ли условие 1) определения 2.1. Если векторы x₁ и x₂ принадлежат Н₁ ∩ Н₂ то каждый из этих векторов принадлежит как Н₁ так и H₂. Поскольку Н₁ – линейное подпространство, то, согласно определению 2.1, заключаем, что вектор x₁ + x₂, павный сумме векторов этого линейного подпространства, тоже принадлежит Н₁. Аналогично х₁ + x₂ ∈ H₂ так как каждое из слагаемых является элементом линейного подпространства H₂ Следовательно, x₁ + x₂ ∈ Н₁ ∩ Н₂.

Проверим условие 2) определения 2.1. Выберем произвольный вектор х ∈ Н₁ ∩ Н₂. Тогда х ∈ Н₁ и х ∈ Н₂. Так как H₁ является линейным подпространством, то произведение элемента х этого линейного подпространства на произвольное действительное число λ принадлежит Н₁. Но совершенно аналогично вектор λх принадлежит и H₂. Поэтому λх ∈ Н₁ ∩ Н₂.

Итак, оба условия определения 2.1 выполнены. Следовательно, Н₁ ∩ Н₂ является линейным подпространством. ►

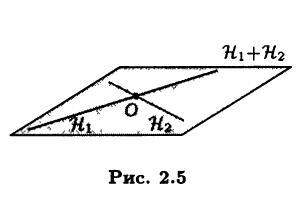
Определение 2.3. Множество Н₁ + Н₂ всех векторов х вида х = х₁ + x₂, где x₁ ∈ Н₁, x₂ ∈ H₂ называют суммой линейных подпространств H₁ и H₂.

На рис. 2.5 линейные подпространства Н₁ и Н₂ представлены несовпадающими прямыми, проходящими через фиксированную точку О. Их сумма представляется плоскостью, содержащей обе прямые.

Теорема 2.2. Сумма линейных подпространств данного линейного пространства является линейным подпространством в том же линейном пространстве.

◄ Рассмотрим два вектора v и w из множества Н₁ + Н₂. Согласно определению 2.3, имеют место представления

v = x₁ + x₂, w = y₁ + y₂,

где векторы x_i, у_i принадлежат H_i, i = 1,2. Складывая эти равенства, получаем

v + w = (x₁ + y₁) + (x₂ + y₂).

Сумма x₁ + y₁ векторов x₁ и y₁ линейного подпространства Н₁ принадлежит H₁. Точно так же сумма x₂ + у₂ векторов x₂ и у₂ линейного подпространства Н₂ принадлежит Н₂. Поэтому вектор v + w принадлежит множеству H₁ + Н₂.

Условие 2) определения 2.1 проверяется аналогично. Произвольный вектор v ∈ H₁ + Н₂ имеет представление v = x₁ + x₂, где x₁ ∈ H₁, x₂ ∈ H₂. Для любого действительного числа λ получаем равенства

λv = λ(x₁ + x₂) = λx₁ + λx₂.

Так как вектор λx₁ принадлежит H₁, а вектор λх₂ – H₂, то вектор λv является элементом множества H₁ + H₂.

Мы доказали, что множество H₁ + Н₂ замкнуто относительно линейных операций объемлющего линейного пространства и поэтому, согласно определению 2.1, оно является линейным подпространством. ►

Пример 2.6. Рассмотрим две однородные системы линей-ных алгебраических уравнений

Множества решений этих систем представляют собой линейные подпространства H₁ и Н₂ линейного арифметического пространства Rⁿ. Объединив обе системы в одну, получим новую
однородную систему, множеством решений которой будет линейное подпространство Н₁ ∩ Н₂.

Пример 2.7. Рассмотрим две системы векторов е₁,…, е_k и f₁, …, f_l в некотором линейном пространстве L. Линейные дболочки этих систем представляют собой линейные подпространства Н₁ = span{e₁,…,е_k} и H₂ = span{f₁,…, f_l} в L. Если мы объединим обе системы в одну, то у новой, объединенной системы линейной оболочкой будет линейное подпространство H₁ + H₂. В самом деле, любой вектор х ∈ Н₁ + Н₂ разлагается в сумму х = х₁ + x₂, где х₁ ∈ H₁, x₂ ∈ H₂. Векторы х₁ и x₂ представляются в виде линейной комбинации, первый – векторов е₁, … , e_k, второй – векторов f₁, …, f_l. Значит, их сумма представляется линейной комбинацией векторов е₁, … ,e_k , f₁, …, f_l т.е. – вектор х принадлежит span{e₁,…,e_k,f₁,..,f_l}. Предположим теперь, что вектор x принадлежит указанной линейной оболочке, т.е. имеет место представление

x = α₁e₁ + … + α_ke_k + β₁f₁ + … +β_lf_l.

Положив

x₁ = α₁e₁+ … + α_ke_k,

x₂ = β₁f₁+ … + β_lf_l

приходим к представлению х = х₁ + x₂, в котором х₁ ∈ H₁, x₂ ∈ H₂. Значит, х ∈ H₁ + H₂.

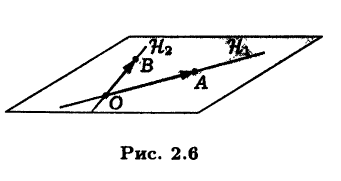
Пример 2.8. Линейное подпространство из примера 2.5, являющееся линейной оболочкой span{OA, OB}, можно представить как сумму подпространств H₁ = span{OA} и H₂ = span{OB} (рис. 2.6).

Линейные операции над векторами
Базис. Cкалярное произведение
Векторное и смешанное произведения векторов
Декартова система координат. прямая на плоскости
Плоскость в пространстве
Прямая в пространстве
Кривые второго порядка — I
Кривые второго порядка — II
Поверхности второго порядка
Матрицы и операции с ними
Обратная матрица
Ранг матрицы
Системы линейных алгебраических уравнений
Свойства решений однородных и неоднородных СЛАУ

Источник

Нахождение дополнения, суммы и пересечения подпространств

Нахождение алгебраического дополнения подпространства

Нахождение алгебраической суммы подпространств

Нахождение пересечения подпространств

Нахождение относительных алгебраических дополнений подпространств

Предложите, как улучшить StudyLib

Линейные операции над векторами

Базис. Cкалярное произведение

Векторное и смешанное произведения векторов

Декартова система координат. прямая на плоскости

Плоскость в пространстве

Прямая в пространстве

Кривые второго порядка — I

Кривые второго порядка — II

Поверхности второго порядка

Матрицы и операции с ними

Обратная матрица

Ранг матрицы

Системы линейных алгебраических уравнений

Свойства решений однородных и неоднородных СЛАУ

Вам также может понравиться

Как найти срок окупаемости dpp

Как исправить ошибки маникюра

Как найти пропавший дом в майнкрафте

Добавить комментарий Отменить ответ