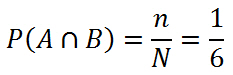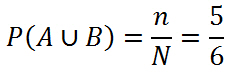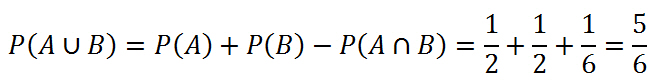Операции над событиями. Теория вероятностей
Пересечение событий
Пусть есть события A и B, у каждого события есть набор элементарных исходов. Пересечением событий A и B называют то событие, в результате которого произошло и событие A и событие B, то есть случился некоторый элементарный исход, который одновременно принадлежит и событию A и событию B.
События не пересекаются
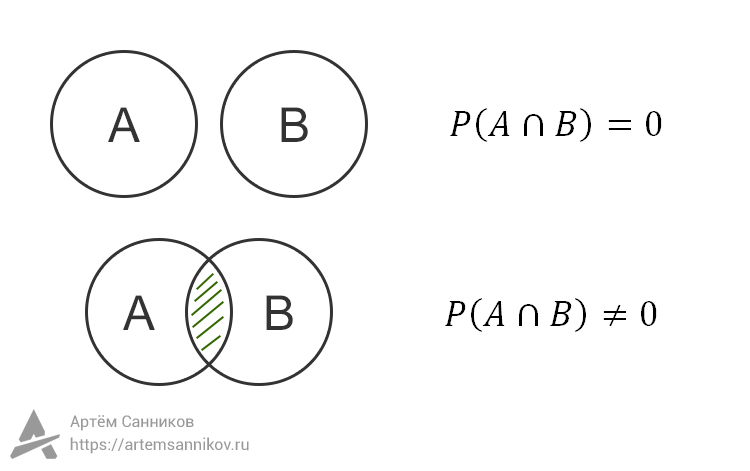
Если у событий A и B нет пересечения (отсутствует элементарный исход), то такая вероятность равна нулю.
События пересекаются
Если события A и B пересекаются (имеют некоторое общее количество элементарных исходов), то вероятность этого пересечения нельзя рассчитать по какой-то универсальной формуле. Эту вероятность нужно подсчитывать, рассматривая общие элементарные исходы.
Объединение событий
Объединением событий A и B называют те события, в результате которых произошло или событие A, или событие B, то есть хотя бы одно из двух.
События не пересекаются
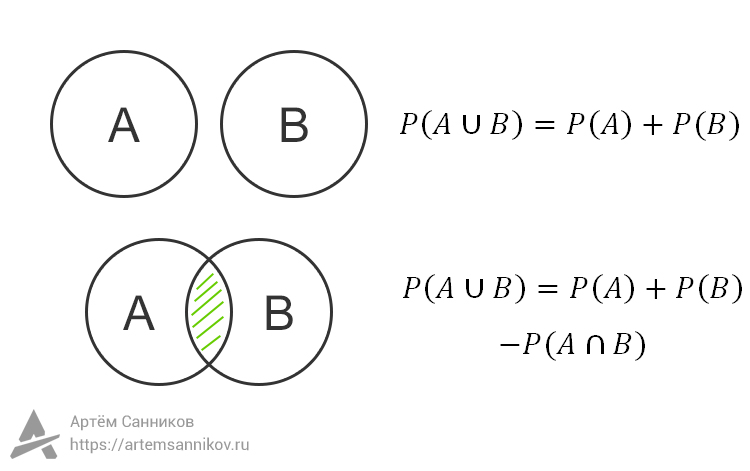
Если события A и B не пересекаются, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B).
События пересекаются
Если события A и B пересекаются, то есть у них есть общие элементарные исходы, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B) — вероятность пересечения событий P(A ∩ B)
Независимые события
События A и B независимы, если наступление одного события не влияет на другое событие.
Практический пример
Будем рассматривать пример с игральным кубиком, для простоты и анализа нашего эксперимента введём следующие обозначения:
- 1 очко = ω1;
- 2 очка = ω2;
- 3 очка = ω3;
- 4 очка = ω4;
- 5 очков = ω5;
- 6 очков = ω6.
Событие A: выпало > 3 очков
Событие B: выпало нечетное число очков
Чтобы приступить к решению задачи выполняем анализ событий.
Анализ события A: этому событию соответствует три элементарных исхода { ω4, ω5, ω6}
Анализ события B: этому событию соответствует три элементарных исхода{ ω1, ω3, ω5}
После анализа событий приступаем к пошаговому решению.
Рассмотрим теперь пересечение события A и B, то есть у нас должно выпасть > 3 очков и при этом число должно быть нечётное. В этом случае у нас есть один элементарный исход: { ω5}.
Отсюда мы можем посчитать вероятность этого события:
- n – элементарный исход, который удовлетворяет нашим условиям;
- N – общее количество исходов.
Далее рассмотрим объединение событий A и B. В данном случае у нас будет следующий набор элементарных условий { ω1, ω3, ω4, ω5, ω6}
Обратите внимание: у нас отсутствует ω2, так как этот исход не фигурирует ни в событии A, ни в событии B.
Поэтому мы можем сказать, что вероятность объединения в этом случае будет:
По факту мы решили задачу, но мы можем её решить намного быстрее, если воспользуемся формулой, которую изучили ранее:
- Вероятность P(A) – выпало > 3 очков
- Вероятность P(B) – выпало нечётное число
- Вероятность P(A ∩ B) – пересечение событий A и B
Метки: Математика, Теория вероятностей.
На этой странице вы узнаете
- Как кот может быть одновременно жив и мертв?
- Можно ли всегда выигрывать спор с монеткой?
- Если рандомно ответить на вопрос теста, какой шанс угадать ответ?
Какова вероятность выиграть в лотерею? Исследователи подсчитали: один на восемь миллионов. «Или выиграю, или проиграю», — решаю я, покупая лотерейный билет. Так понятие вероятности преследует нас в обычной жизни. И не только в лотерее. Давайте разберемся подробнее.
Вероятность
Выходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…
Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться.
Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов.
Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат.
Ученый по имени Эрвин Шредингер провел мысленный эксперимент. Он поместил кота в закрытый ящик, в котором был расположен механизм, содержащий атомное ядро и ёмкость с ядовитым газом.
По эксперименту с вероятностью 0,5 ядро распадется, емкость с газом откроется и кот умрет. Но при этом с вероятностью 0,5 ядро не распадается и кот останется жив.
Пока ящик закрыт, мы не знаем результат эксперимента — такой эксперимент в математике можно назвать случайным. Тем временем кот находится одновременно в двух состояниях: он и жив, и мертв.
Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:
- выпадет орел;
- выпадет решка.
Эти два события образуют множество элементарных событий.
Множество элементарных событий — множество всех возможных результатов случайного эксперимента.
В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации.
Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран.
Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности.
Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу.
(P = frac{m}{n})
Вероятность можно обозначить, как P(x), где х — некоторое событие.
Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.
Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.
Можно, если хитро сформулировать условия. Например: «Орел — я выиграл, решка — ты проиграл». Вероятность выигрыша в этом случае будет равна (P = frac{2}{2} = 1), то есть мы точно выиграем спор.
Однако вероятность не так проста, и даже здесь подготовила ловушку.
В редких случаях есть и третий вариант событий — монетка встанет на ребро. Вероятность такого события составляет (frac{1}{6000}). То есть за миллион бросков это может случиться 150 раз или 1 раз в 2 дня, если подкидывать монету каждый день по 8 часов в течение года. Чтобы монета встала на ребро два раза подряд, придется подбрасывать ее в том же темпе около 35 лет.
Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%.
Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?
Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна
(frac{49}{140} = 0,35)
Выразим в процентах:
0,35 * 100% = 35%
Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ.
Ответ: 0,35
Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой.
(P = frac{m}{n} * 100%)
Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.
Равновозможные и противоположные события
Когда мы бросаем игральную кость, вероятность выпадения любого из чисел равна 16. То есть вероятности выпадения чисел равны между собой. Такие события называются равновозможными.
Равновозможные события — такие события, что по условиям опыта ни одно из них не является более возможным, чем другие.
Вероятности появления событий равны.
Для игрального кубика существует всего шесть событий, которые могут произойти: выпадет число 1, 2, 3, 4, 5 или 6. Все эти события образуют полную группу событий.
Полная группа событий — такая группа событий, если в результате опыта обязательно появится хотя бы одно из них.
В результате подбрасывания монеты выпадет либо орел, либо решка. То есть полная группа событий состоит из двух событий.
Мы подбросили монету и выпал орел. Следовательно, не выпала решка.
А если не выпадет орел? Обязательно выпадет решка. Эти события будут называться противоположными.
Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
Обозначим событие “выпала решка” как A. Противоположное ему событие “выпал орел” обозначим как (overline{A}).
Заметим, что вероятность события A равняется 12, как и вероятность события (overline{A}). Чему равна их сумма?
)frac{1}{2} + frac{1}{2} = 1)
Так мы вывели связь между противоположными событиями. Поскольку они всегда образуют полную группу событий, то сумма их вероятностей будет равна 1.
(P(A) + P(overline{A}) = 1)
Какие еще примеры противоположных событий можно назвать? Ясная и дождливая погода. Если наступает одно из этих событий, то второе уже не может наступить.
Объединение и пересечение событий
Допустим, у нас есть два события: сегодня пойдет снег и сегодня пойдет дождь. Что будет, если мы их объединим?
Объединение событий — событие, состоящее из всех элементарных исходов, благоприятствующих хотя бы одному из событий.
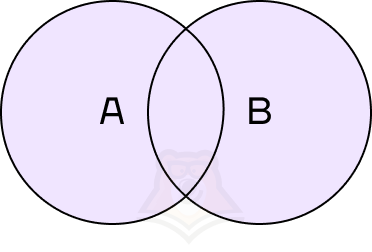
В этом случае мы получим событие, которое будет выполняться при любом из исходов: и если пойдет снег, и если не пойдет снег.
Объединение событий обозначается знаком (cup). Объединение событий А и В можно записать как (A cup B).
Рассмотрим немного другой пример. В первое событие входит, что Илья получит пятерку по физике, а второе событие — Антон получит пятерку по физике. А как можно назвать событие, если оба мальчика получат пятерку по физике?
Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям.
Пересечение событий обозначается знаком (cap). Пересечение событий А и В можно записать как (A cap B).
Несовместные и совместные события
Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.
Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно.
Несовместные события — такие события, появление одного из которых исключает появление другого.
Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?
Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности.
Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.
Сформулируем определение суммы вероятностей двух несовместных событий.
Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей:
(P(A cup B) = P(A) + P(B))
Если существуют несовместные события, то существуют и совместные.
Совместные события — события, наступление одного из которых не исключает наступления другого.
В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят? Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет.
Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”.
Найдем вероятность события А: (frac{1}{6}).
Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна (frac{3}{6} = frac{1}{2})
Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А.
Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги.
А нужно получить вот такую картину:
Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок.
Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения:
(P(A cup B) = P(A) + P(B) — P(A cap B))
В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике.
Независимые и зависимые события
Прогуляемся в магазин за булочками. В упаковке две булочки, а сама упаковка непрозрачная, то есть увидеть булочки до вскрытия упаковки мы не можем.
Известно, что на заводе, где изготавливаются булочки, 5 из 100 булочек подгорают. Значит, 95 из 100 булочек не подгорают. По классическому определению вероятности находим, что вероятность каждой булочки не подгореть равна (frac{95}{100} = 0,95).
Какова вероятность, что в упаковке попадутся только не подгорелые булочки? Как найти вероятность сразу для двух булочек?
Ответим на вопрос: зависят ли булочки друг от друга?
Если подгорит одна из булочек в упаковке, не обязательно подгорит другая. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми.
Независимые события — такие события, появление одного из которых не зависит от появления другого события.
Определим вероятность независимых событий.
Пусть вероятность, что подгорела первая булочка, будет равна Р(А) = 0,95, а вероятность для второй булочки будет равна Р(В) = 0,95.
А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:
(P(A cap B) = P(A) * P(B))
Тогда вероятность, что булочки в одной упаковке не подгорят, равняется P = 0,95 * 0,95 = 0,9025.
В каком случае нужно пользоваться этой формулой? Нужно подставить союз “и”.
Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой.
Приведем еще один пример. В здании два автомата с кофе на разных этажах. Даже если сломается один из них, работа второго не будет зависеть от первого.
Но если автоматы стоят рядом и включены в одну розетку, то при поломке одного из них есть вероятность выхода из строя розетки, а значит, и второй автомат тоже сломается. Такие события будут зависимыми: появление одного из них зависит от появления другого.
Предположим, что в мешке лежит семь кубиков: два из них оранжевые, а пять — фиолетовые. Из мешка дважды вытаскивают кубики. Какова вероятность, достать во второй раз именно фиолетовый кубик?
Нужная последовательность может быть в двух случаях:
- сначала вытащат фиолетовый кубик и потом снова фиолетовый;
- сначала вытащат оранжевый кубик, а потом фиолетовый.
Разберем первый случай. Вероятность в первый раз вытащить фиолетовый кубик равна (frac{5}{7}). После этого в мешке останется шесть кубиков, четыре из которых будут фиолетовые.
Вероятность вытащить во второй раз фиолетовый кубик равна (frac{5}{7} * frac{4}{6} = frac{20}{42} = frac{10}{21}).
Теперь рассмотрим второй случай. Вероятность в первый раз достать оранжевый кубик равна (frac{2}{7}). В мешке останется шесть кубиков, пять из которых будут фиолетовыми.
Вероятность вытащить во второй раз фиолетовый кубик будет уже равна (frac{2}{7} * frac{5}{6} = frac{10}{42} = frac{5}{21}).
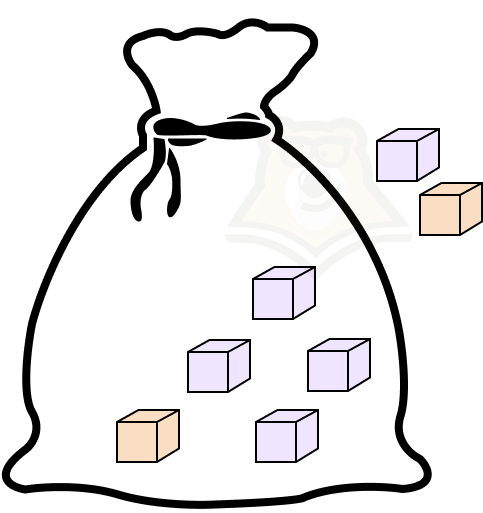
В этом примере очень наглядно видно, что вероятность напрямую зависит от того, какой кубик попался первым. Следовательно, эти события зависимы.
Как отличить зависимые и независимые события? Если после наступления первого события меняется количество благоприятных и всех исходов, то такие события — зависимые. Если количество благоприятных и всех исходов не меняется, то события независимые.
Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Условная вероятность обозначается P(B|A). В нашем примере условной вероятностью будет вычисление, что во второй раз попадется именно фиолетовый кубик.
Найдем вероятность двух зависимых событий. Формула похожа на ту, что используется для независимых событий. Но в этот раз нам нужно применить условную вероятность.
Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило:
(P(A cap B) = P(A) * P(B | A))
Формула Бернулли
Рассмотрим случаи, когда испытание повторяется многократно. Для этого еще раз обратимся к игральному кубику. Подбросим кубик 8 раз. Какова вероятность, что цифра 5 выпала ровно три раза?
Пусть p — вероятность, что выпадет цифра 5. Тогда (p = frac{1}{6}).
Теперь возьмем q — противоположное р событие — вероятность, что цифра 5 не выпадет. (q = frac{5}{6}).
Обозначим количество всех бросков за n, а количество выпадения цифры 5 за k.
Чтобы решить задачу, нужно воспользоваться формулой Бернулли.
(P_n(k) = C_n^k * p^k * q^{n — k})
Множитель (C_n^k) — это число сочетаний. Подробнее узнать про сочетания можно в статье «Основы комбинаторики».
Решим задачу, подставив значения в формулу:
(P_8(3) = C_8^3 * (frac{1}{6})^3 * (frac{5}{6})^5 = frac{8!}{5!3!} * frac{1}{6^3} * frac{5^5}{6^5} = frac{6 * 7 * 8}{1 * 2 * 3} * frac{5^5}{6^8} approx 0,1)
Фактчек
- Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
- События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
- События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: P(A (cup) B) = P(A) + P(B). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: P(A cup B) = P(A) + P(B) — P(A cap B).
- События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события. Вероятность независимых событий можно найти по формуле P(A cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A cap B) = P(A) * P(B | A).
- Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.
Проверь себя
Задание 1.
Какие события являются несовместными?
- Подбрасывание монетки.
- Брак батареек в одной упаковке.
- “Миша идет” и “Миша стоит”.
- Случайное вытаскивание конфет из вазы.
Задание 2.
Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?
- 0,17
- 1
- 0,83
- 1,17
Задание 3.
Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?
- 1
- 0,216
- 0,45
- 1,5
Задание 4.
В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут.
- 0,3
- 0,001
- 2,7
- 0,729
Задание 5.
Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой.
- 0,77
- 0,135
- 0,23
- -0,23
Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1
Пересечение независимых событий
Если события A и B несовместны, то вероятность их объединения равна сумме вероятностей событий A и B:
P(A U B) =P(A) + P(B)
Пересечение независимых событий
Два события A и B называют независимыми, если вероятность каждого из них не зависит от появления или не появления другого события.
Событие C называют пересечением событий A и B (пишут C = A∩B), если событие C означает, что произошли оба события A и B.
Если события A и B независимы, то вероятность их пересечения равна произведению вероятностей событий A и B:
Формула сложения вероятностей совместных событий:
P(A U B) =P(A) + P(B) – P(A∩B)
Несовместные и независимые события.
35. На экзамене по геометрии школьнику достаётся одна задача из сборника. Вероятность того, что эта задача по теме «Углы», равна 0,1. Вероятность того, что это окажется задача по теме «Параллелограмм», равна 0,6. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
Решение. Суммарная вероятность несовместных событий равна сумме вероятностей этих событий: P=0,6+ 0,1 = 0,7.
36. Вероятность того, что на тесте по биологии учащийся О. верно решит больше 11 задач, равна 0,67. Вероятность того, что О. верно решит больше 10 задач, равна 0,74. Найдите вероятность того, что О. верно решит ровно 11 задач.
Решение. Рассмотрим события A = «учащийся решит 11 задач» и В = «учащийся решит больше 11 задач». Их сумма — событие A + B = «учащийся решит больше 10 задач». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B). Тогда, используя данные задачи, получаем: 0,74 = P(A) + 0,67, откуда P(A) = 0,74 − 0,67 = 0,07.
37. Вероятность того, что на тесте по химии учащийся П. верно решит больше 8 задач, равна 0,48. Вероятность того, что П. верно решит больше 7 задач, равна 0,54. Найдите вероятность того, что П. верно решит ровно 8 задач.
39. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых.
Решение.Поскольку биатлонист попадает в мишени с вероятностью 0,8, он промахивается с вероятностью 1 − 0,8 = 0,2. Cобытия попасть или промахнуться при каждом выстреле независимы, вероятность произведения независимых событий равна произведению их вероятностей. Тем самым, вероятность события «попал, попал, попал, промахнулся, промахнулся» равна 0,8•0,8•0,8•0,2•0,2=0,02048. Ответ:0.02048.
40. Ответ: 0,02
3333Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Ответ: 0,91.
Ответ: 0,91
41. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными.
Ответ: 0,8836
2. Если гроссмейстер А. играет белыми, то он выигрывает у гроссмейстера Б. с вероятностью 0,52. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Гроссмейстеры А. и Б. играют две партии, причем во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.
4Ответ: 0,156
3. В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга).
Ответ: 0,027Ответ: 0,062
55 44. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19.
Решение.Рассмотрим события A = «в автобусе меньше 15 пассажиров» и В = «в автобусе от 15 до 19 пассажиров». Их сумма — событие A + B = «в автобусе меньше 20 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B).
Тогда, используя данные задачи, получаем: 0,94 = 0,56 + P(В), откуда P(В) = 0,94 − 0,56 = 0,38.
645. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос на тему «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 0,2 + 0,15 = 0,35.
Ответ: 0,35.
77 46.Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Как найти пересечение событий если известно объединение
Логическое пересечение событий обозначается символом AB и означает, что события A и B происходят одновременно.
Запись 
используется для обозначения объединения событий и означает, что имеет место или событие A, или B, или A и B одновременно.
На рисунке схематически показаны множества событий A и B.
Заштрихованная область является пересечением AB.
Область, ограниченная внешним контуром, является объединением .
.
Операции над вероятностями
Пусть m — число равновозможных элементарных событий, благоприятствующих событию A, k — число равновозможных элементарных событий, благоприятствующих событию B, несовместимому по отношению к событию А. Пусть n — общее число равновозможных элементарных событий, образующих пространство Е всех элементарных событий.
В силу формулы (4.1)
Согласно определению объединения несовместимых событий 
означает: «имеет место или А, или В». Но число событий, благоприятствующих такому событию, равно m+k, поэтому согласно формуле (4.1)
(5.1)
На рисунке 20 дана геометрическая интерпретация формулы (5.1), если m, k и n здесь величины площадей нарисованных фигур.
Последнее равенство выражает следующее правило, которое последовательным применением формулы (5.1) может быть распространено на любое конечное число событий:
Вероятность объединения попарно несовместимых событий равна сумме вероятностей этих событий.
С помощью этого правила мы можем справиться со многими задачами.
Примеры с решением:
Пример 1.
В лотерее выпущено 10 ООО билетов и установлено: 10 выигрышей по 200 р., 100 — по 100 р., 500 — по 25 р. и 1000 выигрышей по 5 р. Гражданин купил один билет. Какова вероятность того, что он выиграет не меньше 25 р.?
А — «выигрыш не менее 25 р.»,
— «выигрыш равен 25 р.»,
— «выигрыш равен 100 р.»,
— «выигрыш равен 200 р.».
Поскольку куплен только один билет, то 
где события 
попарно несовместимы, поэтому
Р (А) = 0,05 + 0,01 + 0,001 = 0,061.
Пример 2.
На военных учениях летчик получил задание «уничтожить» 3 рядом расположенных склада боеприпасов противника. На борту самолета одна бомба. Вероятность попадания в первый склад примерно равна 0,01, во второй — 0,008, в третий — 0,025.
Любое попадание в результате детонации вызывает взрыв и остальных складов. Какова вероятность того, что склады противника будут уничтожены?
А — «склады уничтожены»,
— «попадание в первый склад»,
— «попадание во второй склад»,
— «попадание в третий склад».
Для уничтожения складов достаточно попадания в один из упомянутых трех складов. Поэтому
Пример 3.
Бросают две монеты. Чему равна вероятность появления хотя бы одного герба? Обозначим события:
А — «появление герба при подбрасывании первой монеты», В — «появление герба при подбрасывании второй монеты». Снова предстоит найти вероятность события 
. Но в этом случае 
ибо события А и В совместимы. Поэтому формула (5.1) не применима. Приходится избрать другой путь решения.
Пусть событие 
— «выпадение герба не состоялось». Ясно, что 
, ибо при бросании двух монет могут произойти только следующие события:
Событие 
представляет собой достоверное событие, поэтому 
Вероятность объединения совместимых событии
Пусть m — число равновозможных элементарных событий, благоприятствующих событию A, k — число равновозможных элементарных событий, благоприятствующих событию В. Допустим, что среди упомянутых m + k событий содержится 
таких, которые благоприятствуют и событию А, и событию В. Если n — общее число равновозможных элементарных событий, образующих пространство Е всех элементарных событий, то согласно формуле (4.1)
Запись 
означает: «произойдет или событие А, или событие Ву или то и другое вместе». Но такому событию благоприятствуют (m + k — ) элементарных событий. Поэтому по формуле (4.1) находим:
Подставляя значение, получим:
(5.2)
Ясно, что эта формула представляет собой обобщение формулы (5.1). На основании равенства (5.2) формулируем правило:
Вероятность объединения двух совместимых событий равна сумме вероятностей этих событий без вероятности их совместного осуществления.
Геометрическая интерпретация формулы (5.2) дается на рисунке 21, где m, k, , n представляют величины площадей изображенных фигур.
Примеры с решением:
Пример 1.
Подбрасываем две монеты. Какова вероятность выпадения хотя бы одного герба?
А — «появление герба при подбрасывании первой монеты»,
В — «появление герба при подбрасывании второй монеты».
Нам надо определить вероятность события 
Так как А и В — совместимые события, то
Ясно, что 
Отсюда
Пример 2.
А, В, С — совместимые события. Доказать:
Условные вероятности
Из ящика, в котором 
белых и b черных шаров, наугад вынимают последовательно один за другим два шара. Рассмотрим события:
А — «первый шар белый», В — «второй шар белый». Понятно, что 
. Какова же вероятность события В?
Если событие А произошло, то среди оставшихся + b — 1 шаров только — 1 белых, поэтому вероятность того, что второй шар белый, 
. Если же А не произошло, то среди оставшихся шаров белых , поэтому вероятность того, что второй шар белый, 
. Мы столкнулись с ситуацией, когда вероятность появления события В зависит от того, произошло или не произошло событие А. В таком случае говорим, что событие В зависит от события А, а вероятность появления события В условная.
Найдем способ вычисления таких вероятностей. Условную вероятность появления события В, если событие А произошло, будем обозначать Р (В/А).
Пусть из n равновозможных событий 
составляющих пространство Е всех элементарных событий,
событию А благоприятствуют m событий,
событию В благоприятствуют k событий,
событию 
благоприятствуют r событий (понятно, что 
).
Если событие А произошло, то это означает, что наступило одно из событий 
благоприятствующих событию А. При этом условии событию В благоприятствуют r и только r событий 
благоприятствующих 
(рис. 22). Таким образом,
(5.3)
На основании этих формул находим:
(5.З’)
На основании (5.3) формулируем правило умножения вероятностей :
Вероятность пересечения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого при условии, что первое произошло.
Замечание. Формулы (5.3) имеют смысл в том случае, если имеют смысл события А/В и В/А. А они имеют смысл тогда, когда события А и В совместимы.
Примеры с решением:
Пример 1.
В ящике 
белых и Ь черных шаров. Последовательно вынимаем два шара. Какова вероятность того, что оба они белые?
А — «первый шар белый»,
В — «второй шар белый».
Нам надлежит найти 
Имеем:
Согласно формуле (5.3) находим:
Пример 2.
Из колоды в 32 карты наугад одну за другой вынимают две карты. Найти вероятность того, что:
а) вынуты два валета;
б) вынуты две карты пиковой масти;
в) вынуты валет и дама. Обозначим события:
А — «первая карта — валет», В — «вторая карта — валет», С — «первая карта пиковой масти», D — «вторая карта пиковой масти», Е — «вторая карта — дама».
Нам следует найти 
По формуле (5.3)
Пример 3.
Независимость случайных событии и правило произведения вероятностей
К понятию независимости случайных событий есть несколько подходов.
Событие В называется независимым от А, если его вероятность не зависит от того, произошло или не произошло событие А, т. е.
В случае независимости события В от события А из формулы (5.3) получим:
(5.4)
Сопоставляя формулы (5.3) и (5.4), убеждаемся, что свойство независимости взаимно. Если событие В не зависит от осуществления А, то и А не зависит от осуществления В. На основании (5.4) формулируем правило: Вероятность пересечения двух независимых событий равна произведению вероятностей этих событий.
На практике, как мы убедимся при рассмотрении примеров, для установления независимости событий обычно пользуются соображениями, основанными на опыте обращения с данными объектами, а не анализом формул.
Доказательство правила (5.4) проводилось на основе соотношений
(5.5)
т. е. у нас получилось так: если имеет место (5.5), то имеет место и (5.4). Но читателя может интересовать и обратное: следует ли (5.5) из (5.4)? Пусть
Тогда на основании формул
т. е. из (5.4) следует (5.5). Таким образом, исходной точкой определения независимости А и В может быть и формула (5.4), т. е. мы можем сказать и так:
События А и В называются независимыми тогда и только тогда, когда имеет место условие
(5.6)
Однако определение независимости событий на основе (5.5) более близкое к интуитивному воображению.
Важно запомнить: независимые события с положительными вероятностями не являются несовместимыми. Пусть
(5.7)
Как известно, пересечение несовместимых событий 
V — невозможное событие. Следовательно, для несовместимых событий
Но тогда в силу (5.6) по крайней мере одно из вероятностей Р (А) или Р (В) должно быть равно нулю. Это противоречит (5.7), а значит, подтверждает факт, что независимые события могут быть совместимы.
Приведем любопытный пример, когда интуитивное понимание независимости событий тоже приводит к формальному соотношению (5.4).
Пусть точка М наудачу бросается в прямоугольник с размерами X и Y, стороны которого параллельны координатным осям. Какова вероятность того, что М попадет в прямоугольник с размерами х и у, стороны которого тоже параллельны координатным осям (рис. 23)? Пусть события:
А — «М попала в полосу шириной х». Разумеется, Р(А) 
,
В— «М попала в полосу шириной у». Разумеется, Р(В) 
По формуле (4.3) Р («М попала в маленький прямоугольник») 
но Р(«М попала в маленький прямоугольник») 
Следовательно,
что и требовалось доказать.
Независимость в совокупности
Несколько событий называются независимыми, если любое из них не зависит от любой совокупности остальных. Для независимости событий в их совокупности недостаточно, чтобы они были попарно независимы. Приведем такой пример.
Пусть в ящике 4 шара: черный, красный, белый и один пестрый — окрашенный в полоску всеми этими тремя цветами. Обозначим события: после изъятия одного шара видим
В — «красный цвет»,
Это значит, что А, В, С попарно независимы. Тем не менее 
Значит, в совокупности А, В и С не являются независимыми.
Для независимых в совокупности имеет место
(5.8)
Примеры с решением:
Пример 1.
Бросают две игральные кости. Какова вероятность появления на первой кости нечетного числа очков и на второй пяти очков?
А — «появление нечетного числа очков при бросании первой кости»,
В — «появление пяти очков при бросании второй кости». Нам нужно найти 
Так как события А и В совместимы и независимы, то 
поэтому 
Пример 2.
А, В и С — совместимые и независимые в совокупности события. Доказать, что 
Допустим, что 
Тогда 
Пример 3.
Зашедший в магазин мужчина что-нибудь покупает с вероятностыо 0,1, зашедшая женщина — с вероятностью 0,6. У прилавка один мужчина и две женщины. Какова вероятность того, что по крайней мере одно лицо что-нибудь купит?
А — «покупку сделает мужчина»,
— «покупку сделает первая женщина»,
— «покупку сделает вторая женщина».
Если событие С — «по крайней мере одно лицо что-нибудь купит», то 
По формуле, построенной в примере 2 параграфа 2,
Допуская, что покупатели между собой незнакомы, можем принимать, что 
— события независимы. Тогда в силу (5.6) 
Р (С) = 0,1 + 0,6 + 0,6 — 0,1*0,6 — 0,1*0,6 — 0,6*0,6 + 0,1*0,6*0,6 =0,856.
Пример 4.
Если события А и В независимы, то события А и 
также независимы.
Действительно, поскольку А и В независимы, то Р(В/А) = Р(В) и 
Аналогично убеждаемся, что в случае независимости событий А и В независимыми будут события В и 
Предлагаем вам самостоятельно установить, что в этом случае независимыми будут также события 
Формула полной вероятности
Пусть требуется найти вероятность события А, которое происходит вместе с одним из независимых событий 
(рис. 24).
Если А произошло вместе с одним из событий 
значит, произошло одно из несовместимых событий
Таким образом, событие А представляет или событие 
или 
а это означает, что
Поскольку события взаимно несовместимы, то и события
обладают тем же свойством. Поэтому
(5.9)
Равенство (5.9) носит название формулы полной вероятности. С помощью этой формулы легко находим так называемую формулу Бейеса:
(5.10)
Особенно широко она применяется при решении задач, связанных с вероятностной оценкой гипотез. Докажем справедливость формулы Бейеса. По формуле (5.3′)
Из последнего равенства находим:
Подставляя значение Р (А) из формулы полной вероятности (5.9), получаем формулу Бейеса.
Примеры с решением:
Пример 1.
Охотник сделал три выстрела по кабану. Вероятность попадания первым выстрелом примерно равна 0,4, вторым — 0,5, третьим — 0,7. Одним попаданием кабана можно убить с вероятностью, примерно равной 0,2, двумя попаданиями — с вероятностью 0,6, а тремя наверняка. Найти вероятность того, что кабан будет убит.
Рассмотрим несовместимые события 
— «промах»,
— «одно попадание»,
— «два попадания»,
— «три попадания».
— «попадание с первого выстрела»,
— «попадание со второго выстрела»,
— «попадание с третьего выстрела»,
Согласно формуле полной вероятности
Вспомнив, что события, противополоясные событиям 
обозначаются соответственно 
имеем:
Поскольку независимы в совокупности и независимы, то
Из условия задачи известно, что 
отсюда находим 
Поэтому
Из условия следует:
Подставляя эти результаты в формулу полной вероятности, получим:
Пример 2.
Строительная бригада получает железобетонные перекрытия от трех домостроительных комбинатов (ДСК): от I ДСК — 30%, от II ДСК — 55% и от III ДСК — 15% перекрытий. Известно, что брак продукции I ДСК составляет 5%, II ДСК — 6%, а III ДСК — 10%. Полученные перекрытия хранятся в общем складе. Наугад для контроля проверенное перекрытие оказалось браком. Какова вероятность того, что бракованное перекрытие изготовлено на I ДСК?
А — «наугад проверенное перекрытие — брак»,
— «наугад проверенное перекрытие изготовлено на I ДСК»,
— «наугад проверенное перекрытие изготовлено на II ДСК»,
— «наугад проверенное перекрытие изготовлено на III ДСК».
Нам следует найти 
по формуле (5.10):
Но по условию задачи
Пример 3.
Из 10 учеников, которые пришли на экзамен по математике, трое подготовились отлично, четверо — хорошо, двое — удовлетворительно, а один совсем не готовился — понадеялся на то, что все помнит. В билетах 20 вопросов. Отлично подготовившиеся ученики могут ответить на все 20 вопросов, хорошо — на 16 вопросов, удовлетворительно — на 10, и непод-готовившийся — на 5 вопросов. Каждый ученик получает наугад 3 вопроса из 20. Приглашенный первым ученик ответил на все 3 вопроса. Какова вероятность того, что он отличник?
— «приглашен ученик, подготовившийся отлично»,
— «приглашен ученик, подготовившийся хорошо»,
— «приглашен ученик, подготовившийся удовлетворительно»,
— «приглашенный ученик к экзаменам не готов»,
А — «приглашенный ученик ответил на 3 вопроса».
Согласно условию задачи
Следует найти 
По формуле Бейеса (5.10)
Как видно, искомая вероятность сравнительно невелика. Поэтому учителю придется предложить ученику еще несколько дополнительных вопросов.
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Итак, сегодня у нас из теории вероятностей, задачи об объединении несовместных событий. Мы уже рассмотрели задачи на подбрасывание монеты и кубика, а также задачи средней трудности из ЕГЭ о пересечении независимых событий.
Объединение несовместных событий
Задача 4.1. На экзамене по геометрии школьнику достаётся один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос на тему «Ромб», равна 0,1. Вероятность того, что это вопрос на тему «Описанная окружность», равна 0,15. Вопросов, относящихся одновременно к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение.
Пусть событие А означает, что школьнику достался вопрос по теме «Ромб», событие В — вопрос по теме «Описанная окружность». По условию Р(А)= 0,1, Р(В) = 0,15. По условию события А и В несовместны. Искомая вероятность равна 
= Р(А) + Р(В) = 0,1+ 0,15 = 0,25.
Ответ: 0,25.
Задача 4.2. Вероятность того, что новая кофемолка прослужит больше года, равна 0,93. Вероятность того, что она прослужит больше двух лет, равна 0,81. Найдите вероятность того, что кофемолка прослужит меньше двух лет, но больше года.
Решение.
1-й способ.
Обозначим через А событие «кофемолка прослужит больше года, но меньше двух лет», через В событие «кофемолка прослужит больше двух лет». События А и В несовместны (кофемолка не может прослужить меньше двух лет и одновременно больше двух лет). Объединением событий А и В является событие А и В «кофемолка прослужит больше года». По условию = 0,93, Р(В) = 0,81. Так как А и В несовместны, то = Р(А) + Р(В), откуда Р(А) = — Р(В) = 0,93 — 0,81 = 0,12.
2-й способ.
Будем рассуждать о том, когда может сломаться кофемолка. Она может сломаться уже на первом году работы, может сломаться на втором году работы, а может проработать более двух лет и сломаться потом. Будем заполнять следующую таблицу:
| Событие | сломалась на первом году | сломалась на втором году | сломалась после двух лет работы |
| Вероятность |
Так как вероятность события «кофемолка прослужит больше года» равна 0,93, то вероятность противоположного события «кофемолка сломалась на первом году» равна 1 — 0,93 = 0,07. Вероятность события «кофемолка сломалась после первых двух лет работы» по условию равна 0,81. Вносим найденные значения в таблицу.
| Событие | сломалась на первом году | сломалась на втором году | сломалась после двух лет работы |
| Вероятность | 0,07 | 0,81 |
В таблице перечислены три несовместных события, одно из которых обязательно произойдёт. Поэтому сумма вероятностей в таблице должна быть равна 1. Следовательно, незаполненное искомое значение можно вычислить как 1 — 0,07 — 0,81=0,12.
Ответ: 0,12.
Задача 4.3. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 25 пассажиров, равна 0,91. Вероятность того, что окажется меньше 18 пассажиров, равна 0,39. Найдите вероятность того, что число пассажиров будет от 18 до 24.
Решение.
Обозначим через А событие «в автобусе менее 18 пассажиров», через В событие «в автобусе от 18 до 24» пассажиров. Тогда А U В это событие «в автобусе менее 25 пассажиров». По условию Р (А U В) = 0,91, Р(А) = 0,39. Так как события А и В несовместны, то = Р(А) + Р(В), откуда 0,91 = 0,39 + Р(В), Р(В) = 0,52. Ответ: 0,52.
Задачи об объединении пересечений событий
Задача 4.4. Ковбой Билл попадает в муху на стене с вероятностью 0,8, если стреляет из пристрелянного револьвера. Если Джон стреляет из непристрелянного револьвера, то он попадает в муху с вероятностью 0,25. На столе лежит 5 револьверов, из них только 2 пристрелянные. Ковбой Билл видит на стене муху, наудачу хватает первый попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Билл попадёт в муху.
Решение.
Так как из 5 револьверов 2 пристреляны, то вероятность схватить пристрелянный револьвер равна 
. Вероятность схватить один из трёх непристрелянных револьверов равна 
.
Обозначим через А событие «Билл схватит пристрелянный револьвер и попадёт из него в муху». Так как события «Билл схватит пристрелянный револьвер» и «Билл попадёт из пристрелянного револьвера в муху» независимы, то Р(А) = 
.
Аналогично вероятность события В «Билл схватит непристрелянный револьвер и попадёт из него в муху» равна Р(В) = 
. События А и В несовместны (Билл не может одновременно стрелять как из пристрелянного, так и из непристрелянного револьвера). Искомая вероятность равна
= Р(А)+Р(В) = 0,32+0,15=0,47
Ответ: 0,47.
Задача 4.5. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,98. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,08. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Решение.
Для отбраковки неисправной батарейки должны произойти два независимых события: «линия произвела неисправную батарейку» и «неисправная батарейка забракована». Вероятность события А «произведена и забракована неисправная батарейка» равна Р(А) = 0,05 • 0,98 = 0,049.
Исправную батарейку линия производит с вероятностью 1- 0,05 = 0,95. Для отбраковки исправной батарейки должны произойти два независимых события: «линия произвела исправную батарейку» и «исправная батарейка забракована». Вероятность события В «произведена и забракована исправная батарейка» равна Р(В) = 0,95 • 0,08 = 0,076.
События А и В несовместны. Искомая вероятность равна = Р(А) + Р(В) = 0,049 + 0,076 = 0,125.
Ответ: 0,125.
Задача 4.6. Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков. Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,3.
Решение.
1-й способ.
Так как вероятности выигрыша и проигрыша равны 0,3, то вероятность ничьей равна 1-0,3-0,3 = 0,4. Команда выходит в следующий круг либо после двух выигрышей, либо после выигрыша и ничьей.
1)Вероятность события А «команда выиграла оба матча» по формуле пересечения независимых событий находим как Р(А) = 
.
2)Вероятность события В «команда выиграла первый матч, закончила вничью второй матч» равна Р(В) = 
З. Вероятность события С «команда закончила вничью первый матч, выиграла второй матч» равна Р(В) =
События А, В, С попарно несовместны, вероятность их объединения равна 
= Р(А)+Р(В)+Р(С) = 0,09 + 0,12 + 0,12 = 0,33.
2-й способ.
Составим таблицу возможных результатов матчей и вероятностей этих результатов.
|
Второй матч |
||||
| победа
Р=0,3 |
ничья
Р=0,4 |
поражение Р=0,3 |
||
| Первый матч | победа Р = 0,3 | 0,09 | 0,12 | 0,09 |
| ничья Р = 0,4 | 0,12 | 0,16 | 0,12 | |
| поражение Р = 0,3 | 0,09 | 0,12 | 0,09 |
Числа в ячейках получаются по принципу таблицы умножения (умножение вероятностей соответствующих результатов первого и второго матчей), так как вероятности результатов первого и второго матча не зависят друг от друга. Жирным шрифтом в таблице выделены вероятности тех результатов, при которых команда выходит в следующий круг. Искомая вероятность равна 0,09 + 0,12 + 0,12 = 0,33.
Ответ: 0,33.
Задача 4.7. Две фабрики выпускают одинаковые стёкла для автомобильных фар. Первая фабрика выпускает 60% этих стёкол, вторая-40%. Первая фабрика выпускает 4% бракованных стёкол, а вторая — 3%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Решение.
Вероятность купить стекло первой фабрики равна 0,6. Вероятность брака в стекле первой фабрики равна 0,04. Вероятность события А «куплено бракованное стекло первой фабрики» находим по формуле для пересечения независимых событий: Р (А) = 0,6 • 0,04 = 0,024.
Вероятность купить стекло второй фабрики равна 0,4. Вероятность брака в стекле второй фабрики равна 0,03. Вероятность события В «куплено бракованное стекло второй фабрики» равна Р(В) = 0,4 • 0,03 = 0,012.
Искомая вероятность равна вероятности объединения несовместных событий А и В.
= Р(А) + Р(В) = 0,024 + 0,012 = 0,036.
Ответ: 0,036.
Задачи о частоте
Задача 4.8. Вероятность того, что новый DVD — проигрыватель в течение года поступит в гарантийный ремонт, равна 0,05. В некотором городе из 2000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступили 130 штук. Насколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение.
Частота события «гарантийный ремонт» равна 
. От вероятности она отличается на 0,065 — 0,05 = 0,015.
Ответ: 0,015.
Подведем итог
После изучения материала по решению простых задач по теории вероятностей рекомендую выполнить задачи для самостоятельного решения, которые мы публикуем на нашем канале Telegram.
Также рекомендую изучить простые задачи по теории вероятностей, «Центральные и вписанные углы. Задание № 3 ЕГЭ» и другие уроки по решению заданий ЕГЭ по математике, которые представлены на нашем канале Youtube.
Спасибо, что поделились статьей в социальных сетях
Источник «Подготовка к ЕГЭ. Математика.Теория вероятностей». Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова
Операции над событиями. Диаграммы Эйлера – Венна
Содержание
В теории вероятностей случайными событиями являются подмножества множества элементарных исходов Ω .
Над событиями, как и над любыми множествами, можно совершать следующие операции.
Произведение (пересечение) двух событий
Операцию произведения (пересечения) двух событий A и B обозначают
, или AB, или 
.
ОПРЕДЕЛЕНИЕ 1. Произведением (пересечением) двух событий A и B называют такое событие, которое состоит из всех элементов, входящих как в событие A , так и в событие B (рис. 1).
Рис.1
Сумма (объединение) двух событий
Операцию суммы (объединения) двух событий A и B обозначают
A + B или 
ОПРЕДЕЛЕНИЕ 2. Суммой (объединением) двух событий A и B называют такое событие, которое состоит из элементов события A и элементов события B (рис. 2).
Рис.2
Разность двух событий
Операцию разности двух событий A и B обозначают
A B
ОПРЕДЕЛЕНИЕ 3. Разностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B (рис. 3).
Рис.3
ЗАМЕЧАНИЕ 1. Разностью событий B и A является событие B A , изображенное на рисунке 4.
Рис.4
Симметрическая разность двух событий
Операцию симметрической разности двух событий A и B обозначают
ОПРЕДЕЛЕНИЕ 4 . Симметрической разностью событий A и B называют событие, состоящее из тех элементов события A , которые не входят в событие B , а также из тех элементов события B , которые не входят в событие A (рис. 5).
Рис.5
Переход к противоположному событию
Событие, противоположное к событию A , обозначают
или AC
ОПРЕДЕЛЕНИЕ 5. Противоположным событием к событию A называют событие, состоящее из тех элементов всего множества элементарных событий Ω , которые не входят в событие A (рис. 6).
Рис.6
ЗАМЕЧАНИЕ 2. Справедлива формула
ОПРЕДЕЛЕНИЕ 6. Событие Ω называют достоверным событием, пустое множество 
называют невозможным событием.
ЗАМЕЧАНИЕ 3. Рисунки, на которых наглядно показаны операции над множествами, называют диаграммами Эйлера-Венна. В частности, диаграммами Эйлера-Венна являются рисунки 1-6 .
