Как найти пересечение теория вероятности

Пересечение событий

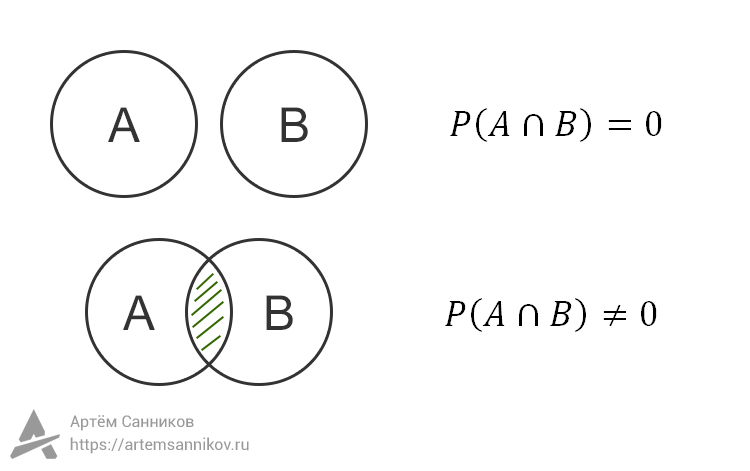
Пусть есть события A и B, у каждого события есть набор элементарных исходов. Пересечением событий A и B называют то событие, в результате которого произошло и событие A и событие B, то есть случился некоторый элементарный исход, который одновременно принадлежит и событию A и событию B.

События не пересекаются

Если у событий A и B нет пересечения (отсутствует элементарный исход), то такая вероятность равна нулю.

События пересекаются

Если события A и B пересекаются (имеют некоторое общее количество элементарных исходов), то вероятность этого пересечения нельзя рассчитать по какой-то универсальной формуле. Эту вероятность нужно подсчитывать, рассматривая общие элементарные исходы.

Объединение событий

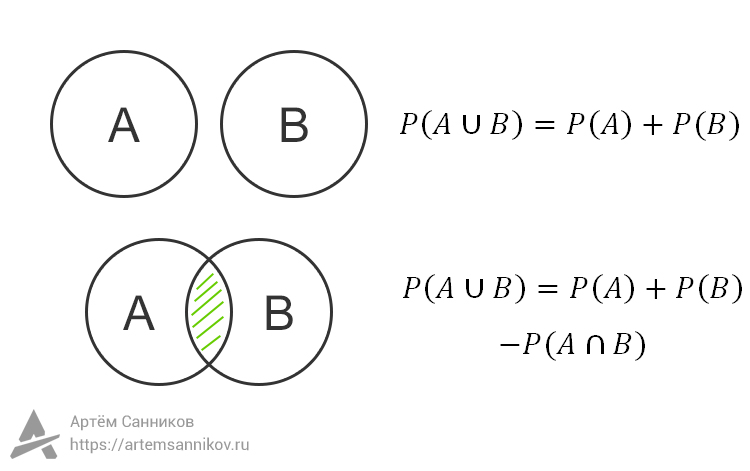
Объединением событий A и B называют те события, в результате которых произошло или событие A, или событие B, то есть хотя бы одно из двух.

События не пересекаются

Если события A и B не пересекаются, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B).

События пересекаются

Если события A и B пересекаются, то есть у них есть общие элементарные исходы, то вероятность их объединения окажется равной = вероятность события P(A) + вероятность события P(B) — вероятность пересечения событий P(A ∩ B)

Независимые события

События A и B независимы, если наступление одного события не влияет на другое событие.

Практический пример

Будем рассматривать пример с игральным кубиком, для простоты и анализа нашего эксперимента введём следующие обозначения:

• 1 очко = ω1;
• 2 очка = ω2;
• 3 очка = ω3;
• 4 очка = ω4;
• 5 очков = ω5;
• 6 очков = ω6.

Событие A: выпало > 3 очков

Событие B: выпало нечетное число очков

Чтобы приступить к решению задачи выполняем анализ событий.

Анализ события A: этому событию соответствует три элементарных исхода { ω4, ω5, ω6}

Анализ события B: этому событию соответствует три элементарных исхода{ ω1, ω3, ω5}

После анализа событий приступаем к пошаговому решению.

Рассмотрим теперь пересечение события A и B, то есть у нас должно выпасть > 3 очков и при этом число должно быть нечётное. В этом случае у нас есть один элементарный исход: { ω5}.

Отсюда мы можем посчитать вероятность этого события:

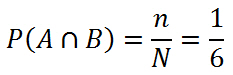
• n – элементарный исход, который удовлетворяет нашим условиям;
• N – общее количество исходов.

Далее рассмотрим объединение событий A и B. В данном случае у нас будет следующий набор элементарных условий { ω1, ω3, ω4, ω5, ω6}

Обратите внимание: у нас отсутствует ω2, так как этот исход не фигурирует ни в событии A, ни в событии B.
Поэтому мы можем сказать, что вероятность объединения в этом случае будет:

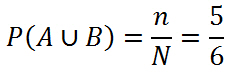
По факту мы решили задачу, но мы можем её решить намного быстрее, если воспользуемся формулой, которую изучили ранее:

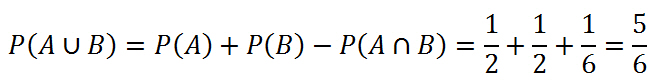
• Вероятность P(A) – выпало > 3 очков
• Вероятность P(B) – выпало нечётное число
• Вероятность P(A ∩ B) – пересечение событий A и B

Метки: Математика, Теория вероятностей.

Материал рассчитан на два урока. В конспекте урока не дается разбивка материала на первый и второй уроки в отдельности.

Этап 1. Введение нового материала.

Учащиеся записывают тему урока – «Пересечение событий» (1 слайд презентации). Учитель начинает объяснять тему, используя материал учебника «Теория вероятностей и статистика» (Ю. Н. Тюрин, А. А. Макаров, И. Р. Высоцкий, И. В. Ященко, МЦНМО, ОАО «Московские учебники» Москва 2008) и работая с доской. Через проектор выводится второй слайд, включающий в себя определение и формульное обозначение ключевого понятия изучаемого материала (Пусть А и В – два события, относящиеся к одному случайному опыту. Взяв все элементарные события, которые благоприятствуют и событию А, и событию В, мы получим новое событие. Это новое событие называют пересечением событий А и В (в русском языке ему соответствует союз И). А ∩ В). Далее выводится третий слайд с продолжением теоретической части (Если события А и В не имеют общих благоприятствующих элементарных событий, то они не могут наступить одновременно в ходе одного и того же опыта. Такие события называют несовместными, а их пересечение – пустое событие. Оно обозначается символом ᴓ ; можно написать А ∩ В = ᴓ).

Этап 2. Закрепление пройденного материала

Упражнение 1 (слайд 4).

Вначале выводится на экран текст «А – «четное число очков». Выпишите элементарные события, составляющие событие А ∩ В, и найдите Р (А ∩ В)».
Учитель: Мы ведем речь о броске игральной кости. Если событие А представляет собой выпадание четного числа очков, то какие же варианты при броске кости могут соответствовать этому событию?
Учащиеся: Если выпадет 2, 4 или 6 очков.
Учитель: Правильно.
На экране появляется табличка «А: 2, 4, 6» и текст «В – выпало число очков, кратное 3».
Учитель: Выпадение какого количества очков соответствует событию В?»
Учащиеся: 3 и 6 очков.
Учитель: Верно.
На экране появляется табличка «В: 3, 6».
Учитель: Давайте подумаем, какие из вариантов войдут в пересечение событий А и В? Как нам известно, это должны быть события, благоприятствующие и А и В одновременно.
Учащиеся: Это 6.
Учитель: Теперь найдем вероятность Р (А ∩ В). Каково общее количество событий?
Учащиеся: Шесть (может выпасть любая грань игральной кости).
Учитель: А благоприятствующих событий?
Учащиеся: Одно – выпадение 6 очков.
Учитель: Так какова вероятность Р (А ∩ В)?
Учащиеся: Одна шестая.
На экране появляется надпись: Выпало 6 очков. Р = 1/6
Учитель: Теперь решим следующую букву номера.
На экране появляется надпись: «б) В – выпало число очков, кратное 4».
Учащимся дается время подумать над решением. Затем на экране появляется табличка «В: 4» и надпись: «Выпало 4 очка. Р = 1/6».
Далее рассматриваются буквы в) и г) номера. На экране появляются надписи «В: 5, 6», «Выпало 6 очков. Р = 1/6», «В: 1,2», «Выпало 2 очка. Р = 1/6».
Учитель обращает внимание учащихся на то, что, невзирая на выпадение различных вариантов, вероятность все время оставалась равной 1/6.

Упражнение 2 (слайд 6)

На экране появляются надписи: «Бросают 2 игральные кости. Событие А – «на первой кости выпало меньше 3 очков». Событие В – «на второй кости выпало больше 4 очков». Пользуясь таблицей элементарных событий этого опыта, выделите цветом все элементарные события, благоприятствующие А, В и А ∩ В, а также найдите Р (А ∩ В)».
На экране появляется таблица всех возможных парных вариантов прокидки кости.
Учитель: Сколько элементарных событий благоприятствуют событиям А и В?
Учащиеся: 12 и 12. А – это все пары, где на первом мест стоит 1 или 2, а В – это все пары, где на втором месте стоит 5 или 6.
На экране данные пары событий выделяются зеленоватым и красноватым оттенками. Соответственно, появляется подсказка к ответу на следующий вопрос, задаваемый учителем.
Учитель: А сколько событий входят в пересечение событий А и В? Что это за события?
Учащиеся: 4 события: (1,5), (1,6), (2,5), (2,6).
Учитель: И какова же вероятность Р (А ∩ В)? Как ее найти?
Учащиеся: Число благоприятствующих событий – 4. Общее число событий – 36. Значит, Р = 4/36=1/9.
На экране появляется надпись: «Р (А ∩ В) = 4/36 =1/9».

Упражнение 4 (слайд 8)

Примечание: Упр. 3 пропускается.
На экран выводится надпись: «D – первый выбранный ученик – девочка; С – второй выбранный ученик – девочка» и таблички «D U С» и «D ∩ С».  
Учитель: Итак, у нас дано два событий и требуется найти их объединение и пересечение. Как вы думаете, какой фразой можно выразить объединение данных событий? А пересечение?
Выслушав ответы учащихся, учитель открывает на слайде надписи: «Первый или второй выбранный ученик – девочка» и «Оба выбранных ученика – девочки».

Упражнение 5 (слайд 9)

Учитель: Это упражнение похоже на предыдущее.
На экране открываются надписи: «А – первый выбранный ученик – девочка; В – среди выбранных учеников есть только одна девочка», « А U В» и «А ∩ В».
Учитель дает время ученикам подумать над формулировками, предлагает им озвучить предполагаемые ответы и выводит на экран надписи: «Среди выбранных учеников есть только одна девочка» и «Первый выбранный ученик – единственная девочка, выбранная среди учеников».

Упражнение 6 (слайд 10)

Учитель: Еще одно похожее упражнение. Давайте поступим с ним так же, как с предыдущим.
По мере необходимости на экран выводятся следующие фрагменты слайда: «С – по дороге из школы домой вам встретится черная кошка; D – по дороге из школы домой вам встретится  злая собака», «D U С» и «D ∩ С», «По дороге из школы домой вам встретится черная кошка или злая собака» и «По дороге из школы домой вам встретятся черная кошка и злая собака».

Упражнение 7 (слайд 11)
Аналогично трем предшествующим. По мере необходимости на экран выводятся следующие фрагменты слайда: «М – вас завтра вызовут к доске на уроке математики; G – вас завтра вызовут к доске на уроке географии», «M U G», «M ∩ G», «Вас завтра вызовут к доске на уроке математики или географии», «Вас завтра вызовут к доске на уроках математики и географии».

Упражнение 8 (слайд 12)
Вначале на экран выводится надпись: «А = 6, В = 8, А ∩ В = 2» и «Событие А наступает, а В – нет».
Учитель: Как вы думаете, сколько событий соответствует данному условию?
Учащиеся: 4 события.
На экране высвечивается табличка: «4 события». Затем появляется условие: «Событие В наступает, а А – нет».
Учитель: А сколько событий соответствует данному условию?
Учащиеся: 6 событий.
На экране высвечивается табличка: «6 событий».
Затем учитель предлагает учащимся изобразить соответствующую диаграмму Эйлера и по прошествии отведенного для этого времени открывает на слайде иллюстрацию.

Упражнение 9 (слайд 13)

На экран выводится надпись: «А = 6, В = 8, А U В = 10. Событие А наступает, а В – нет».
Учитель: Как вы думаете, сколько событий соответствует данному условию?
Учащиеся: 2 события.
На экране высвечивается табличка: «2 события». Затем появляется условие: «Событие В наступает, а А – нет».
Учитель: А сколько событий соответствует данному условию?
Учащиеся: 4 события.
На экране высвечивается табличка: «4 события».
Затем учитель предлагает учащимся изобразить соответствующую диаграмму Эйлера и по прошествии отведенного для этого времени открывает на слайде иллюстрацию.

Упражнение 12 (слайды 14-15)

Примечание: упр. 10-11 пропускаются.
На экран выводится надпись: «Изобразите на диаграмме Эйлера событие» и две таблички  «А ∩`В» и «`А ∩`В ». Учитель специально предлагает к решению сразу два задания, чтобы сильные учащиеся за то время, покуда остальной класс будет обдумывать решение первого, сумели решить оба и (если учитель сочтет это возможным) донести решение второго задания до остальных учащихся.

По прошествии короткого времени учитель вызывает к доске одного из учащихся для решения задания, а затем открывает на слайде соответствующую иллюстрацию.

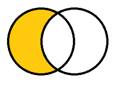
В отношении второго задания решение просто – можно даже не пытаться построить изображение, а ограничиться словом «отсутствует».

На слайде 15 задание выглядит таким образом: «`А ∩ В» и «`А `∩ `В ».

Учитель вновь дает учащимся время на размышления, а затем вызывает к доске двух учащихся для выполнения задания. На слайде имеются соответствующие иллюстрации:

 

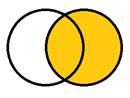
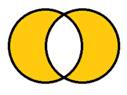
Упражнение 13 (слайд 16)

Докажите, что Р (А ∩ В) ≤ Р(А) и Р (А ∩ В) ≤ Р(В).

Для выполнения данного упражнения учитель должен подвести учащихся к мысли, что при построении диаграммы Эйлера события А и В могут располагаться четырьмя способами. Вначале можно вызвать к доске какого-либо учащегося и попросить изобразить его события А и В с помощью диаграммы Эйлера. Скорее всего, на доске появится один из вариантов. Затем учитель должен спросить, могут ли события располагаться иначе и подтолкнуть учащегося к изображению всех четырех возможных вариантов.

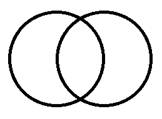
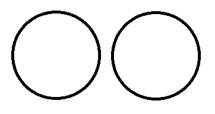
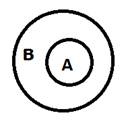
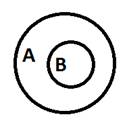
Исходя из каждого из них, можно наглядно убедиться в том, что выражение Р (А ∩ В) ≤ Р(А) и Р (А ∩ В) ≤ Р(В) верно. Для первого рисунка пересечение – это центральная часть, для второго пересечение вообще пусто, для третьего – это множество А, а для четвертого – множество В. Все эти элементы несомненно меньше или равны множествам А и В (для первого – меньше, для второго – меньше, для третьего – равно А, для четвертого – равно В).
Для того, чтобы озвучить и отметить на диаграмме  вышеизложенное, может быть вызван другой ученик или же учитель может предложить учащимся самостоятельно поработать над этим, чтобы проверить решение задания в конце урока.

Упражнение 14 (слайды 17, 18, 19)

На слайде 17 на экран выводится надпись: «Изобразите на диаграмме Эйлера событие» и две таблички  «А ∩ В ∩ С» и «А ∩`В  ∩ С».

Учитель вызывает к доске двух учащихся для решения задания, а после того, как те предложат решение, открывает ответы, находящиеся ниже на слайде. С остальными двумя слайдами работа ведется таким же образом.

 

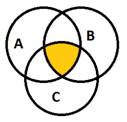
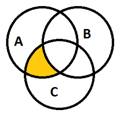
На слайде 18 – «`А ∩ В ∩`С» и «А ∩ В ∩ С».

 

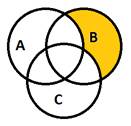
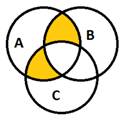
На слайде 19 – «А ∩ В ∩ С».

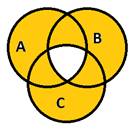
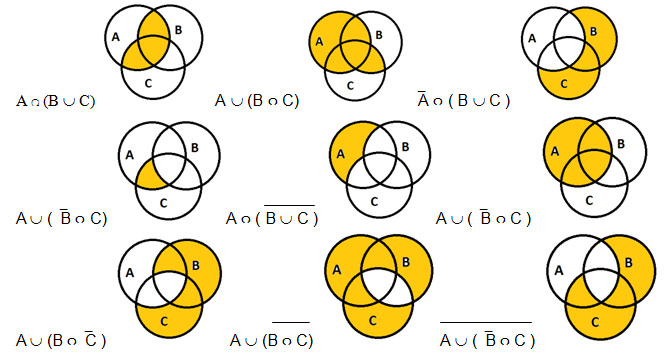
Упражнение 15 (слайды 20, 21, 22, 23, 24)

Учащиеся самостоятельно работают с учебником, заполняя требуемым образом диаграммы Эйлера. После завершения работы с очередным пунктом учитель выводит на экран верное решение, при необходимости поясняя, как оно получено, путем построения промежуточных диаграмм на доске.

Этап 3. Подведение итогов.

Учитель напоминает учащимся, какое понятие было рассмотрено; как выглядит диаграмма Эйлера, касающаяся этого понятия; как выглядит значок пересечения и какой союз в русском языке ему соответствует; чем отличается количество элементарных событий в А ∩ В в случае, если А и В имеют общие элементарные события или не имеют таковых. Возможно также пропустить часть слайдов презентации, дав пропущенные пункты в качестве домашнего задания, и рассмотреть их решение на следующем уроке.

На этой странице вы узнаете

• Как кот может быть одновременно жив и мертв? 
• Можно ли всегда выигрывать спор с монеткой? 
• Если рандомно ответить на вопрос теста, какой шанс угадать ответ?

Какова вероятность выиграть в лотерею? Исследователи подсчитали: один на восемь миллионов. «Или выиграю, или проиграю», — решаю я, покупая лотерейный билет. Так понятие вероятности преследует нас в обычной жизни. И не только в лотерее. Давайте разберемся подробнее.

Вероятность

Выходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…

Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться. 

Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов. 

Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат. 

Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:

• выпадет орел;
• выпадет решка. 

Эти два события образуют множество элементарных событий. 

Множество элементарных событий — множество всех возможных результатов случайного эксперимента. 

В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации. 

Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран. 

Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности. 

Вероятность — отношение количества благоприятных событий к количеству всех возможных событий. 

Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу. 

(P = frac{m}{n})

Вероятность можно обозначить, как P(x), где х — некоторое событие. 

Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.

Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.

Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%. 

Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?

Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна 
(frac{49}{140} = 0,35)

Выразим в процентах:  
0,35 * 100% = 35%

Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ. 

Ответ: 0,35

Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой. 

(P = frac{m}{n} * 100%)

Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.

Равновозможные и противоположные события

Когда мы бросаем игральную кость, вероятность выпадения любого из чисел равна 16. То есть вероятности выпадения чисел равны между собой. Такие события называются равновозможными. 

Равновозможные события — такие события, что по условиям опыта ни одно из них не является более возможным, чем другие. 

Вероятности появления событий равны. 

Для игрального кубика существует всего шесть событий, которые могут произойти: выпадет число 1, 2, 3, 4, 5 или 6. Все эти события образуют полную группу событий. 

Полная группа событий — такая группа событий, если в результате опыта обязательно появится хотя бы одно из них. 

В результате подбрасывания монеты выпадет либо орел, либо решка. То есть полная группа событий состоит из двух событий. 

Мы подбросили монету и выпал орел. Следовательно, не выпала решка. 

А если не выпадет орел? Обязательно выпадет решка. Эти события будут называться противоположными. 

Противоположные события — такие события, если при не наступлении одного обязательно наступает второе. 

Обозначим событие “выпала решка” как A. Противоположное ему событие “выпал орел” обозначим как (overline{A}). 

Заметим, что вероятность события A равняется 12, как и вероятность события (overline{A}). Чему равна их сумма?

)frac{1}{2} + frac{1}{2} = 1) 

Так мы вывели связь между противоположными событиями. Поскольку они всегда образуют полную группу событий, то сумма их вероятностей будет равна 1. 

(P(A) + P(overline{A}) = 1)

Какие еще примеры противоположных событий можно назвать? Ясная и дождливая погода. Если наступает одно из этих событий, то второе уже не может наступить. 

Объединение и пересечение событий 

Допустим, у нас есть два события: сегодня пойдет снег и сегодня пойдет дождь. Что будет, если мы их объединим? 

Объединение событий — событие, состоящее из всех элементарных исходов, благоприятствующих хотя бы одному из событий. 

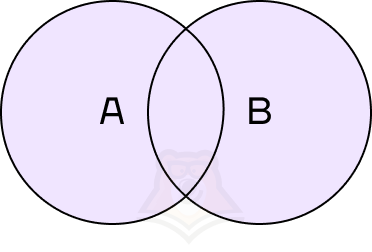
В этом случае мы получим событие, которое будет выполняться при любом из исходов: и если пойдет снег, и если не пойдет снег. 

Объединение событий обозначается знаком (cup). Объединение событий А и В можно записать как (A cup B). 

Рассмотрим немного другой пример. В первое событие входит, что Илья получит пятерку по физике, а второе событие — Антон получит пятерку по физике. А как можно назвать событие, если оба мальчика получат пятерку по физике?

Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям. 

Пересечение событий обозначается знаком (cap). Пересечение событий А и В можно записать как (A cap B). 

Несовместные и совместные события

Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.

Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно. 

Несовместные события — такие события, появление одного из которых исключает появление другого. 

Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?

Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности. 

Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.

Сформулируем определение суммы вероятностей двух несовместных событий. 

Если существуют несовместные события, то существуют и совместные. 

Совместные события — события, наступление одного из которых не исключает наступления другого. 

В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят?  Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет. 

Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”. 

Найдем вероятность события А: (frac{1}{6}). 

Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна (frac{3}{6} = frac{1}{2})

Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А. 

Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги. 

А нужно получить вот такую картину:

Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок. 

В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике. 

Независимые и зависимые события 

Прогуляемся в магазин за булочками. В упаковке две булочки, а сама упаковка непрозрачная, то есть увидеть булочки до вскрытия упаковки мы не можем. 

Известно, что на заводе, где изготавливаются булочки, 5 из 100 булочек подгорают. Значит, 95 из 100 булочек не подгорают. По классическому определению вероятности находим, что вероятность каждой булочки не подгореть равна (frac{95}{100} = 0,95). 

Какова вероятность, что в упаковке попадутся только не подгорелые булочки? Как найти вероятность сразу для двух булочек?

Ответим на вопрос: зависят ли булочки друг от друга? 

Если подгорит одна из булочек в упаковке, не обязательно подгорит другая. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми. 

Независимые события — такие события, появление одного из которых не зависит от появления другого события. 

Определим вероятность независимых событий. 

Пусть вероятность, что подгорела первая булочка, будет равна Р(А) = 0,95, а вероятность для второй булочки будет равна Р(В) = 0,95. 

А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:

(P(A cap B) = P(A) * P(B))

Тогда вероятность, что булочки в одной упаковке не подгорят, равняется P = 0,95 * 0,95 = 0,9025. 

В каком случае нужно пользоваться этой формулой? Нужно подставить союз “и”. 

Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой. 

Приведем еще один пример. В здании два автомата с кофе на разных этажах. Даже если сломается один из них, работа второго не будет зависеть от первого. 

Но если автоматы стоят  рядом и включены в одну розетку, то при поломке одного из них есть вероятность выхода из строя розетки, а значит, и второй автомат тоже сломается. Такие события будут зависимыми: появление одного из них зависит от появления другого. 

Предположим, что в мешке лежит семь кубиков: два из них оранжевые, а пять — фиолетовые. Из мешка дважды вытаскивают кубики. Какова вероятность, достать во второй раз именно фиолетовый кубик?

Нужная последовательность может быть в двух случаях:

• сначала вытащат фиолетовый кубик и потом снова фиолетовый;
• сначала вытащат оранжевый кубик, а потом фиолетовый. 

Разберем первый случай. Вероятность в первый раз вытащить фиолетовый кубик равна (frac{5}{7}). После этого в мешке останется шесть кубиков, четыре из которых будут фиолетовые. 

Вероятность вытащить во второй раз фиолетовый кубик равна (frac{5}{7} * frac{4}{6} = frac{20}{42} = frac{10}{21}). 

Теперь рассмотрим второй случай. Вероятность в первый раз достать оранжевый кубик равна (frac{2}{7}). В мешке останется шесть кубиков, пять из которых будут фиолетовыми. 

Вероятность вытащить во второй раз фиолетовый кубик будет уже равна (frac{2}{7} * frac{5}{6} = frac{10}{42} = frac{5}{21}). 

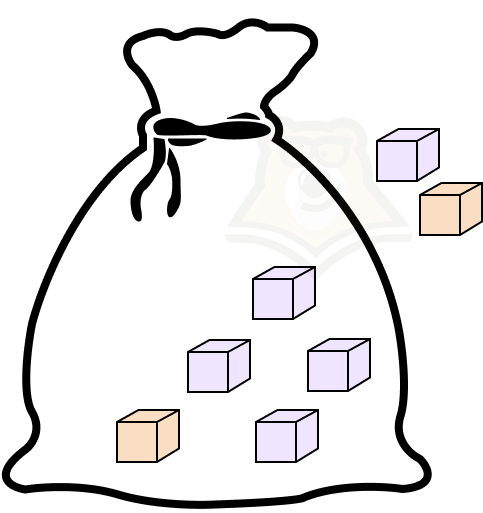
В этом примере очень наглядно видно, что вероятность напрямую зависит от того, какой кубик попался первым. Следовательно, эти события зависимы. 

Как отличить зависимые и независимые события? Если после наступления первого события меняется количество благоприятных и всех исходов, то такие события — зависимые. Если количество благоприятных и всех исходов не меняется, то события независимые.

Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А. 

Условная вероятность обозначается P(B|A). В нашем примере условной вероятностью будет вычисление, что во второй раз попадется именно фиолетовый кубик.   

Найдем вероятность двух зависимых событий. Формула похожа на ту, что используется для независимых событий. Но в этот раз нам нужно применить условную вероятность. 

Формула Бернулли

Рассмотрим случаи, когда испытание повторяется многократно. Для этого еще раз обратимся к игральному кубику. Подбросим кубик 8 раз. Какова вероятность, что цифра 5 выпала ровно три раза?

Пусть p — вероятность, что выпадет цифра 5. Тогда (p = frac{1}{6}). 

Теперь возьмем q — противоположное р событие — вероятность, что цифра 5 не выпадет. (q = frac{5}{6}). 

Обозначим количество всех бросков за n, а количество выпадения цифры 5 за k. 

Чтобы решить задачу, нужно воспользоваться формулой Бернулли. 

(P_n(k) = C_n^k * p^k * q^{n — k}) 

Множитель (C_n^k) — это число сочетаний. Подробнее узнать про сочетания можно в статье «Основы комбинаторики». 

Решим задачу, подставив значения в формулу:

(P_8(3) = C_8^3 * (frac{1}{6})^3 * (frac{5}{6})^5 = frac{8!}{5!3!} * frac{1}{6^3} * frac{5^5}{6^5} = frac{6 * 7 * 8}{1 * 2 * 3} * frac{5^5}{6^8} approx 0,1) 

Фактчек

• Вероятность — отношение количества благоприятных событий к количеству всех возможных событий. 
• События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе. 
• События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: P(A (cup) B) = P(A) + P(B). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: P(A cup B) = P(A) + P(B) — P(A cap B).
• События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события. Вероятность независимых событий можно найти по формуле P(A cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A cap B) = P(A) * P(B | A). 
• Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А. 

Проверь себя

Задание 1. 
Какие события являются несовместными?

1. Подбрасывание монетки.
2. Брак батареек в одной упаковке.
3. “Миша идет” и “Миша стоит”.
4. Случайное вытаскивание конфет из вазы. 

Задание 2. 
Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?

1. 0,17
2. 1
3. 0,83
4. 1,17 

Задание 3. 
Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?

1. 1
2. 0,216
3. 0,45
4. 1,5 

Задание 4. 
В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут. 

1. 0,3
2. 0,001
3. 2,7
4. 0,729 

Задание 5. 
Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой. 

1. 0,77
2. 0,135
3. 0,23
4. -0,23

Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1

Объединением
двух событий А и В называется
событие С, состоящее в выполнении события
А или события В, или обоих событий вместе.

Пересечением
событий А и В называется
событие, состоящее из элементарных
событий принадлежащих и событию А и
событию В.

Разность
двух событий А и В называется
событие, состоящее из элементарных
событий, которые входят в событие А, но
не входят в событие В.

Операции над
событиями:

1)Объединение(Сумма)-это

А
Ṳ В=А+В

ПР:А=(123…9)

В=(56…12)

АṲВ=(123….12)

2)Пересечение(произведение)-

А∩В=А*В

ПР:
А=(123…9)

В=(56…12)

А∩В=(56…9)

3)Разность–

ПР:
А=(123…9)

В
=(56…12)

А/
В=(12…34)

5. Классическое определение вероятности.

Равнозначными
событиями наз – если
условия испытания обеспечивают одинаковую
возможность осуществления , каждого из
них.

Вероятность
события
называется отношение числа исходов
благоприятствующих данному событию, к
числу всех возможных исходов.

.
где
m
– число элементарных исходов,
благоприятствующих событию А;

n–
число
всех равновозможных элементарных
исходов опыта, образующих полную группу
событий.

Напр:
Бросают 2 игральные монеты: Найти
вероятность выпадения герба худобы
один раз.

Ὼ{(гг)(рр)(рг)(гр)}

А=(Выпадает
худобы один раз герб)

Р(А)=?

Р(А)=m/n=3/4

m=3

n=4

6. Геометрическое определение вероятности.

Геометрической
вероятностью
называют вероятность попадания точки
в некоторую область (отрезок, часть
плоскости).

Пусть
отрезок l
составляет
часть отрезка L.

_{Пусть
отрезок} L
наудачу поставлена точка. Тогда
вероятность, что эта точка попадет в
отрезок l
пропорциональна длине отрезка l;
не зависит от расположения l
на L.
И определяется по формуле:

В
области G
содержится область K,
которая может имея Sk.

В
область G
на удачу бросается точка.

Пусть
брошенная точка может попасть в некоторую
часть G.

Требуется
определение вероятности попадания этой
точки в область K
.

P(A)=Sk/Sg

7.Схема выбора без возвращения (сочетания, размещения).

Выборка
без возвращения и без упорядочивания
(Схема выбора проводящая к
сочетанию)Суть выборки из n-элементов
выбирает m-элемент
выбирают без
возвращения и без упорядочивания
следования элементов.

Число
сочетаний из n-элементов
опред.
След. Фор.

1. Схема
   выбора с возвращением (перестановки,
   сочетания и размещения с повторением).

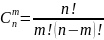
В
магазин привезли мороженое 10 видов.
Сколькими способами можно купить 6
различных пар мороженого.

n=10
m=6

С₁₀⁶
=10!/6!*(10-6)! =10!/6!*4!=7 8 9 10/1234=///

10!=1*2*3*4*5*6*7*8*9*10

Выборка
без возвращения и c
упорядочивания (Схема выбора проводящая
к
размещению)Суть выборки из n-элементов
выбирает m-элемент
выбирают без
возвращения , но с упорядочивания
следования элементов.

Число
размещения из n-элементов
по m-элементам
опред.
След. Фор.

ПР:
Сколько всего существует телефонных
номеров состоящих из 7 различных цифр.

n=10
m=7
А₁₀⁷=10!/(10-7)!=10!/3!=45678910=////

Основные
правила и формулы комбинаторики

	без возвращения	с возвращением
Без порядка
С порядком

Урновая
схема:

Выбор
с возвр-нием:кажд
выбр-ный шарик возвр-ся в урну, т.е. кажд
из а_к
шариков выбир-ся из полной урны. В получ-м
наборе, сост-м из а_к
номеров шариков, могут встреч-ся одни
и те же номера (выборка с повторениями).

Выбор
без возвр-ния:выбр-ные
шарики в урну не возвр-ся, и в получ
наборе не могут встреч-ся одни и те же
номера (выборка без повторений).

Выбор
с учетом порядка:два
набора номеров шариков считаются
различными, если они отличаются составом
или порядком номеров.

Выбор
без учета порядка:два
набора номеров шариков считаются
различными, если они отличаются составом.
Наборы, отличающиеся лишь порядком
следования номеров, считаются одинаковыми.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #