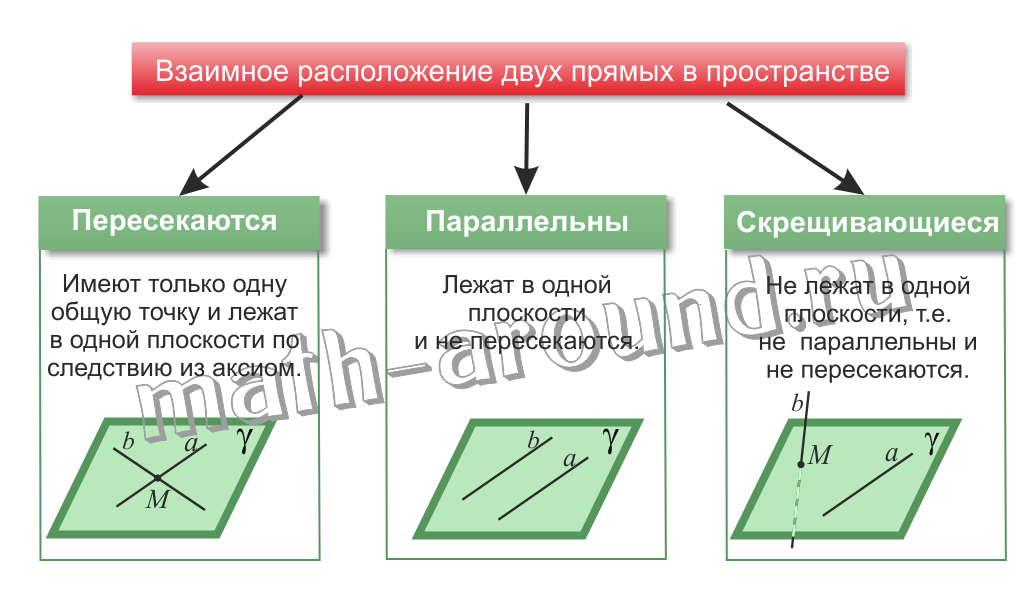
Как известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку).
В пространстве мы можем найти множество примеров ситуаций, когда две прямые не пересекаются, но они и не параллельны.

Рис. (1). Дороги на земле и на эстакадах не пересекаются.
Скрещивающиеся прямые — это прямые, которые не лежат в одной плоскости и не имеют общих точек.
Теорема «Признак скрещивающихся прямых»
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство
Рассмотрим прямую (AB), лежащую в плоскости, и прямую (CD), которая пересекает плоскoсть в точке (D), не лежащей на прямой (AB).

Рис. (2). Скрещивающиеся прямые.
1. Допустим, что прямые (AB) и (CD) всё-таки лежат в одной плоскости.
2. Значит, эта плоскость идёт через прямую (AB) и точку (D), то есть, она совпадает с плоскостью (α).
3. Это противоречит условиям теоремы, по которым прямая (CD) не находится в плоскости (α), а пересекает её.
Теорема доказана.
В пространстве прямые могут пересекаться, скрещиваться или быть параллельными. 
Рис. (3). Параллельные прямые.

Рис. (4). Пересекающиеся прямые.
Рис. (5). Скрещивающиеся прямые.
Теорема
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые (AB) и (CD). 
Рис. (6). Доказательство теоремы.
1. Через точку (D) можно провести прямую (DE), параллельную (AB).
2. Через пересекающиеся прямые (CD) и (DE) можно провести плоскость (α).
3. Так как прямая (AB) не лежит в этой плоскости и параллельна прямой (DE), то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через (CD), будет пересекаться с (DE) и (AB), которая ей параллельна.
Теорема доказана.
1. Если прямые параллельны, то угол между ними —
0°
.
2. Углом между двумя пересекающимися прямыми называют величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол
90°
).
3. Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Обрати внимание!
Провести соответственные прямые, параллельные данным скрещивающимся прямым, можно через любую точку. Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую, параллельную другой из скрещивающихся прямых.
Пример:

Рис. (7). Куб.
Найти угол между
AB
и
B1D1
.
Выберем точку
B
на прямой
AB
и проведём через
B
прямую
BD
параллельно
B1D1
.

Рис. (8). Куб с дополнительными построениями.
Угол между
AB
и
BD
—
45°
, так как
ABCD
— квадрат.
Соотвeтственно, угол между
AB
и
B1D1
— тоже
45°
.
Скрещивающиеся прямые. Расположение прямых в пространстве.
Если две прямые в пространстве параллельны или пересекаются, то они лежат в одной плоскости.
Возможен еще один случай взаимного расположения в пространстве, когда прямые не лежат в одной плоскости.
Определение. Две прямые называются скрещивающимися, если они не лежат в одной плоскости.
Представление о скрещивающихся прямых дают:
- дороги, одна из которых проходит по эстакаде, а другая – под эстакадой;
- детская горка, где одна из скрещивающихся прямых – самая нижняя ступенька лесенки, а вторая – бортик самой горки;
- телеграфные провода и провода антенны.

К кубе АВСDА1В1С1D1 прямые A1D1 и ВВ1, AB и B1C1, В1D и ВC, RL и BC, AB1 и D1C1 являются скрещивающимися.
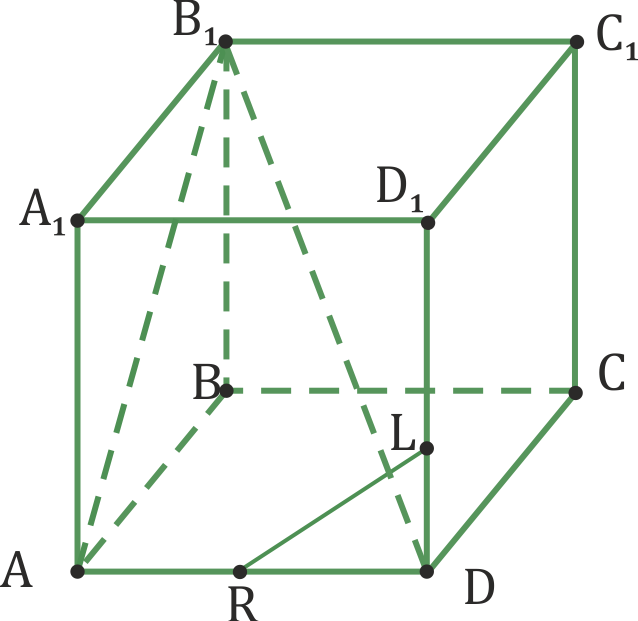
Признак скрещивающихся прямых.
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.
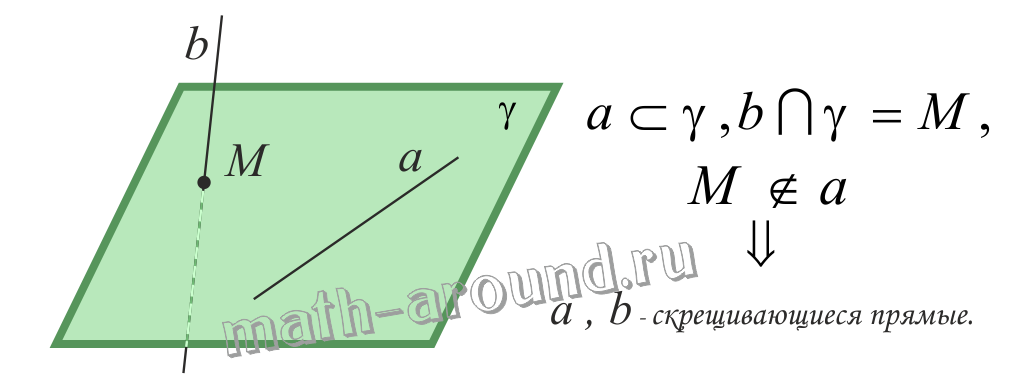
Теорема о скрещивающихся прямых.
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Если Вам понравилась информация и появилось желание поддержать нас, Вы можете:
- отправить денежный перевод с карты на карту мгновенно и без комиссий по ссылке . Ссылка на перевод . В поле «Добавьте комментарий» необходимо указать «в дар» или «подарок».
- оставить комментарий ниже.
Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.
Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.
Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.
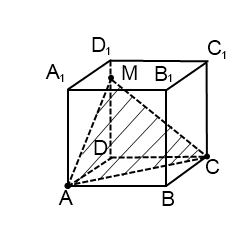
Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.
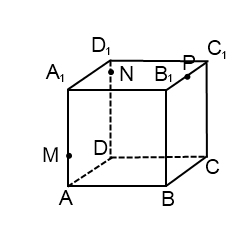
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.
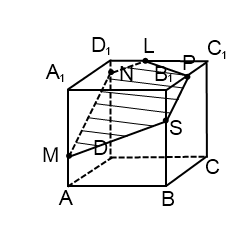 Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).
Через точку P проводим прямую, параллельную MN. Она пересекает ребро BB1 в точке S. PS — след секущей плоскости в грани (BCC1).
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).
Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.
Пятиугольник MNLPS — искомое сечение.
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.
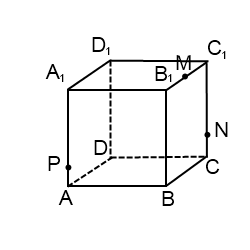
Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).
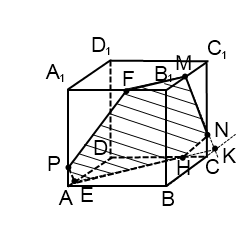
Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.
Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).
Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.
Шестиугольник MNHEPF — искомое сечение.
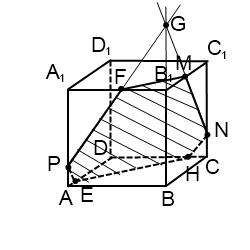
Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.
Работа с прямой PE дает то же сечение MNHEPF.
4) Построить сечение куба плоскостью, проходящей через точку M, N, P.
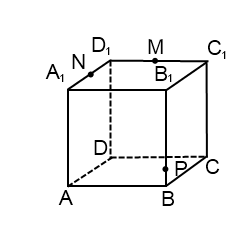 Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.
Здесь можем провести прямую через точки M и N, лежащие в одной плоскости (A1B1C1). Ее след — MN (видимый). Больше нет точек, лежащих в одной плоскости либо в параллельных плоскостях.
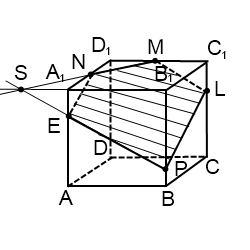 Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.
Продолжим прямую MN. Она лежит в плоскости (A1B1C1), поэтому пересечься может только с одной из прямых этой плоскости. С A1D1 и C1D1 точки пересечения уже есть — N и M. Еще две прямые этой плоскости — A1B1 и B1C1. Точка пересечения A1B1 и MN — S. Поскольку она лежит на прямой A1B1, то принадлежит плоскости ( ABB1), а значит, через нее и точку P, лежащую в этой же плоскости, можно провести прямую. Прямая PS пересекает ребро AA1 в точке E. PE — ее след (видимый). Через точки N и E, лежащие в одной плоскости (ADD1), можно провести прямую, след которой — NE (невидимый). В плоскости (ADD1) есть прямая NE, в параллельной ей плоскости (BCC1) — точка P. Через точку P можем провести прямую PL, параллельную NE. Она пересекает ребро CC1 в точке L. PL — след этой прямой (видимый). Точки M и L лежат в одной плоскости (CDD1), значит, через них можно провести прямую. Ее след — ML (невидимый). Пятиугольник MLPEN — искомое сечение.
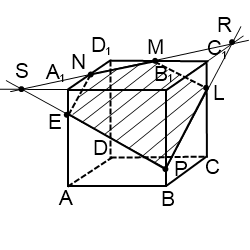 Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.
Можно было продолжать прямую NM в обе стороны и искать ее точки пересечения не только с прямой A1B1, но и с прямой B1C1, также лежащей в плоскости (A1B1C1). В этом случае через точку P проводим сразу две прямые: одну — в плоскости (ABB1) через точки P и S, а вторую — в плоскости (BCC1), через точки P и R. После чего остается соединить лежащие в одной плоскости точки: M c L, E — с N.
Начнем разбирать это задание с самых легких задач. Необходимо найти угол между двумя прямыми в кубе.
В кубе много параллельных ребер, поэтому задачи решаются просто. Если прямые скрещивающиеся, то используем определение угла между скрещивающимися прямыми: “Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым”.
В треугольной призме так же можно найти параллельные прямые.
В треугольной призме можно выполнить дополнительные построения, выходящие за пределы многогранника.
Из треугольника КАС легко можно найти угол КАС.
Вот еще случай, когда точка пересечения прямых лежит вне многогранника
Геометрия, 10 класс
Урок №5. Взаимное расположение прямых в пространстве
Перечень вопросов, рассматриваемых в теме
- признаки скрещивающихся прямых;
- определение углов с сонаправленными сторонами;
- доказательство теоремы о плоскости, проходящей через одну из скрещивающихся прямых;
- доказательство теоремы о равенстве углов с сонаправленными сторонами.
Глоссарий по теме
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.
Два отрезка называются параллельными, если они лежат на паралельных прямых.
Основная литература:
- Учебник Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. Геометрия 10-11 кл.– М.: Просвещение, 2014.
Дополнительная литература:
- Зив Б.Г. Дидактические материалы Геометрия 10 кл.– М.: Просвещение, 2014.
- Глазков Ю.А., Юдина И.И., Бутузов В.Ф. Рабочая тетрадь Геометрия 10 кл.-М.: Просвещение, 2013.
Открытый электронный ресурс:
- https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Мы уже знаем, что прямы в пространстве могут располагаться параллельно или пересекаться. Существует еще один вид- скрещивающиеся прямые. С ним мы мимолетно познакомились на предыдущем уроке. А сегодня нам предстоит разобраться с этой темой более подробно.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости. (рис. 1)

Рисунок 1 – скрещивающиеся прямые
На прошлом уроке в качестве наглядного примера нами был приведен куб.
Сегодня предлагаем вам обратить внимание на окружающую вас обстановку и найти в ней скрещивающиеся прямые.
Примеры скрещивающихся прямых вокруг нас:
|
Одна дорога проходит по эстакаде, а другая под эстакадой |
|
|
Кабели моста |
|
|
Горизонтальные линии крыши и вертикальные линии стен |
|
Разберем и докажем теорему, которая выражает признак скрещивающихся прямых.
Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство.
Рассмотрим прямую AB лежащую в плоскости и прямую CD, которая пересекает плоскoсть в точке D, не лежащей на прямой AB (рис. 2).
- Допустим, что прямые AB и CD всё-таки лежат в одной плоскости.
2. Значит эта плоскость идёт через прямую AB и точку D, то есть она совпадает с плоскостью α.
3. Это противоречит условиям теоремы, что прямая CD не находится в плоскости α, а пересекает её.
Теорема доказана.

Рисунок 2 – скрещивающиеся прямые АВ и СD
Итак, возможны три случая расположения прямых в пространстве:
|
|
|
|
|
|
Разберем и докажем еще одну теорему о скрещивающихся прямых.
Теорема. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые AB и CD.(рис. 3)
1. Через точку D можно провести прямую DE параллельную AB.
2. Через пересекающиеся прямые CD и DE можно провести плоскость α
3. Так как прямая АB не лежит в этой плоскости и параллельна прямой DE, то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через CD, будет пересекаться с DE и AB, которая ей параллельна.
Теорема доказана.

Рисунок 3 – прямые АВ, СD, DЕ
Любая прямая, например ОО1, рассекает плоскость на две полуплоскости. Если лучи ОА и О1А1 параллельны и лежат в одной полуплоскости, то они называются сонаправленными.
Лучи О1А1 и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости. (рис. 4)

Рисунок 4 – сонаправленные лучи
Теорема.Если стороны двух углов соответственно сонаправленны, то такие углы равны. (рис. 5)
Доказательство:
при доказательстве ограничимся случаем, когда углы лежат в разных плоскостях.
- Стороны углов сонаправлены, а, значит, параллельны. Проведем через них плоскости- как показано на чертеже.
Отметим на сторонах угла O произвольные точки A и B.
На соответствующих сторонах угла O1 отложим отрезки OA1 и O₁B₁ равные соответственно ОA и OB.
2. В плоскости рассмотрим четырехугольник OAA1O1.
Так как противолежащие стороны OA и O1A1 этого четырехугольника равны и параллельны по условию, то этот четырехугольник– параллелограмм и, следовательно, равны и параллельны стороны AA1 и OO1.
3. В плоскости, аналогично можно доказать, что OBB1O1 параллелограмм, поэтому равны и параллельны стороны ВВ1 и OO1.
4. Если две отрезка AA1 и BB1 равны параллельны третьему отрезку OO1, значит, они равны и параллельны, т. е. АА1||BB1 и AA1 = BB1.
По определению четырехугольник АВВ1А1 – параллелограмм и из этого получаем АВ=А1В1.
5.Из выше построенного и доказанного АВ=А1В1, ОA =O1A1 и OB =O1B1 следует, что треугольники AOB и A1 O1 B1. равны по трем сторонам, и поэтому О= О1.

Рисунок 5 – равные углы с сонаправленными сторонами
Любые две пересекающиеся прямые лежат в одной плоскости и образуют четыре неразвернутых угла. Если известен один из этих углов, то можно найти и другие три угла. Пусть а – тот из углов, который не превосходит любого из трех остальных углов. Тогда говорят, что угол между пересекающимися прямыми равен а. Очевидно, 0° < а ≤ 90°.
Введем теперь понятие угла между скрещивающимися прямыми(рис. 6, 7).Пусть АВ и СD- две скрещивающиеся прямые (рис. а.) Через произвольную точку М1 проведем прямые А1В1 и С1D1, соответственно параллельные прямым АВ и СВ (рис. б). Если угол между прямыми А1В1 и C1D1 равен φ, то будем говорить, что угол между скрещивающимися прямыми АВ и CD равен φ. Докажем, что угол между скрещивающимися прямыми не зависит от выбора точки М₁.
Действительно, возьмем любую другую точку М₂ и проведем через нее прямые А1В1 и С1D1, соответственно параллельные прямым АВ и СD (рис. б).
Так как А1В1||А1В1, C1D1|| С1D1, то стороны углов с вершинами М1 и М1 попарно сонаправлены (рис. б, такими углами являются ∟A1M1C1 и ∟A1M1C1, ∟A1M1D1 и ∟A1M1D1 и т.д.) Поэтому эти углы соответственно равны. Отсюда следует, что угол между прямыми А1В1 и С1D1 также равен φ. В качестве точки М, можно взять любую точку на одной из скрещивающихся прямых.
На рисунке в на прямой СD отмечена точка М и через нее проведена прямая А’В’, параллельная АВ. Угол между прямыми А’В’ и СD также равен φ.

Рисунок 6 – угол между скрещивающимися прямыми

Рисунок 7 – угол между скрещивающимися прямыми
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Прямая с пересекает прямую а и не пересекает прямую b, параллельна прямой а. Докажите, что b и с- скрещивающиеся прямые .
Доказательство:
- a||b- через a и b проведем плоскость α (эта плоскость существует по определению параллельных прямых);
- пусть с пересекает а в точке М. a||b⇒ М ∉b.
- по теореме о признаке скрещивающихся прямых, с и b скрещиваются.
Пример 2. Выделите цветом верный ответ:
Дано: ОВ||CD
ОА и CD- скрещивающиеся
∟АОВ= 40°
Найти: угол между ОА и CD
- 50°
- 40°
- 140°
Решение:
- D ∈ A1D, A1D||AO
- угол между ОА и CD=∟A1DC
- ∟A1DC=∟AOB=40°.
Ответ: ∟A1DC=40°.
Правильный ответ:
- 50°
- 40°
- 140°






