Что такое периметр параллелограмма
Периметр параллелограмма — это сумма длин всех его сторон.
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно равны и параллельны друг другу. Таким образом, его периметр — это удвоенная сумма двух его смежных ребер.
Свойства
- противоположные стороны равны и параллельны;
- противоположные углы попарно равны;
- сумма соседних углов равна 180 градусов;
- сумма всех углов равна 360 градусов;
- диагонали фигуры делятся пополам в точке пересечения;
- точка пересечения диагоналей — центр симметрии параллелограмма;
- биссектриса образует равнобедренный треугольник.
Как найти периметр
Существует несколько основных способов, с помощью которых можно найти сумму длин всех сторон заданной фигуры. Все они зависят от изначально известных параметров.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
По сумме всех сторон
Так как периметр параллелограмма — это удвоенная сумма двух его смежных ребер, используем формулу:
P=2(a+b),
где a и b — это две смежные стороны данного четырехугольника.
По стороне и двум диагоналям
Если в задаче дана лишь одна сторона, но обе диагонали четырехугольника, мы можем найти вторую сторону. Для этого используем формулу:
(a=frac{sqrt{2d_1^2+2d_2^2-4b^2}}2,)
где (d_1) и (d_2) — это обе диагонали фигуры.
Получается, что расчет суммы длин всех сторон для параллелограмма будет выглядеть так:
(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b).)
По стороне, высоте и синусу угла
В случае, если нам известны лишь одно ребро, высота и один из углов, можем узнать длину второго ребра таким образом:
(a=frac{h_b}{sinalpha})
где (h_b) — высота, проведенная к известной стороне, а (sinalpha) — известный нам угол.
Таким образом, формула для нахождения периметра параллелограмма будет выглядеть так:
(P=2(frac{h_b}{sinalpha}+b))
Примеры решения задач
Попробуем применить полученные знания на практике и рассмотрим несколько задач на периметр параллелограмма.
Задача 1
Дан параллелограмм со сторонами 5 см и 9 см. Вычислить его периметр.
Решение:
Воспользуемся формулой P=2(a+b), так как нам известны обе стороны фигуры. Подставляем значения: P=2(5+9)=28 см.
Ответ: 28 см.
Задача 2
Известно, что одна из сторон параллелограмма равна 4 см, а две его диагонали равны 6 см и 8 см. Найти периметр фигуры.
Решение:
Для расчета суммы длин всех сторон используем формулу:
(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b))
Подставляем известные значения:
(P=2(frac{sqrt{2d_1^2+2d_2^2-4b^2}}2+b)=2(frac{sqrt{2times6^2+2times8^2-4times4^2}}2+4)=2(frac{sqrt{72+128-64}}2+4)=2(frac{2sqrt{34}}2+4)=2sqrt{34}+8) см.
Ответ:( 2sqrt{34}+8) см.
Задача 3
Сторона b параллелограмма равна 2 см, высота, проведенная к b — 1 см, а угол α равен (fracpi6). Найти сумму длин всех сторон фигуры.
Решение:
Для расчета будем использовать уравнение:
(P=2(frac{h_b}{sinalpha}+b))
Подставим известные величины:
(P=2(frac1{sin{displaystylefracpi6}}+2)=2(frac1{displaystylefrac12}+2)=8;)см.
Ответ: 8 см.
В данной публикации мы рассмотрим, каким образом можно посчитать периметр параллелограмма и разберем примеры решения задач.
- Формула вычисления периметра
- Примеры задач
Формула вычисления периметра
Периметр (P) параллелограмма равняется сумме длин всех его сторон. А т.к. противоположные стороны данной фигуры равны, формулу можно представить в следующем виде:
P = 2 * (a + b) или P = 2a + 2b

Примеры задач
Задание 1
Найдите периметр параллелограмма, если его стороны равны 6 и 8 см.
Решение:
Воспользуемся одной из двух формул выше, подставив в нее известные значения: P = 2 * 6 см + 2 * 8 см = 28 см.
Тот же самый результат получится, если применить вторую формулу: P = 2 * (6 см + 8 см) = 28 см.
Задание 2
Периметр параллелограмма равен 50 см. Найдите его вторую сторону, если известно, что первая равна 7 см.
Решение:
Нам известно, что периметр считается по формуле: P = 2a + 2b.
Допустим a – это известная сторона, и нам нужно найти b. Ее длина, умноженная на два, равна: 2b = P – 2a = 50 см – 2 * 7 см = 36 см.
Следовательно, длина неизвестной стороны составляет: b = 36 см / 2 = 18 см.
Параллелограмм — геометрическая фигура, четырехугольник, у которого противоположные стороны попарно параллельны.
Прямоугольник, квадрат и ромб являются частными случаями параллелограмма.
Онлайн-калькулятор периметра параллелограмма
Свойства параллелограмма
Перечислим некоторые свойства параллелограмма:
- Противоположные стороны параллелограмма попарно равны и параллельны.
- Противоположные углы параллелограмма равны.
- Диагонали параллелограмма точкой пересечения делятся пополам.
Формула периметра параллелограмма
Чтобы найти периметр параллелограмма, нужно сложить длины всех его сторон.
P=a+b+a+b=2⋅a+2⋅b=2⋅(a+b)P=a+b+a+b=2cdot a+2cdot b=2cdot (a+b)
a,ba, b — длины двух смежных сторон параллелограмма.
Разберем задачу на нахождение периметра параллелограмма.
Сторона а параллелограмма равна 12 см, а сторона b — 7 см. Чему равен периметр параллелограмма?
Решение
a=12a=12
b=7b=7
Воспользуемся формулой нахождения периметра параллелограмма и подставим вместо aa и bb их численные значения:
P=2⋅(a+b)=2⋅(12+7)=2⋅19=38P=2cdot (a+b)=2cdot (12+7)=2cdot 19=38 см.
Ответ: 38 см.
Не знаете, где можно оформить контрольные работы на заказ? На бирже Студворк сотни авторов, которые готовы выполнить ваше задание!
Тест по теме «Периметр параллелограмма»
Периметр параллелограмма зависит от длины его сторон. И хотя формула для расчета несложная, мы сделали калькулятор, который позволяет рассчитать периметр параллелограмма в режиме онлайн. Наш калькулятор рассчитает периметр параллелограмма по двум сторонам или по двум диагоналям и одной из сторон.
Содержание:
- калькулятор периметра параллелограмма
- формула периметра параллелограмма через две стороны
- формула периметра параллелограмма через диагонали и одну из сторон
- примеры задач
Параллелограмм – четырехугольник, у которого противолежащие стороны попарно параллельны.
На сайте вы можете рассчитать периметры других четырехугольников: квадрат, ромб, прямоугольник.
Формула периметра параллелограмма через две стороны
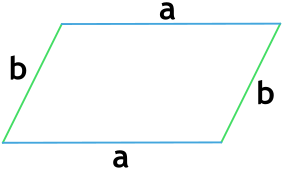
{P = 2 (a + b)}
a и b – стороны параллелограмма
Формула периметра параллелограмма через диагонали и сторону
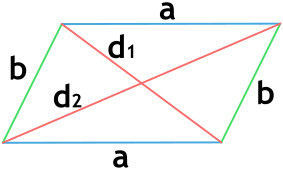
{P = 2a+ sqrt{2{d_1}^2 + 2{d_2}^2 – 4a^2}}
или
{P = 2b+ sqrt{2{d_1}^2 + 2{d_2}^2 – 4b^2}}
a и b – стороны параллелограмма
d1 и d2 – диагонали параллелограмма
Примеры задач на нахождение периметра параллелограмма
Задача 1
Найдите периметр параллелограмма со сторонами 3см и 4.5см.
Решение
Так как из условия задачи мы знаем длины сторон, то воспользуемся первой формулой. Подставим в нее значения длин сторон и произведем расчет:
P = 2 (a + b) = 2 (3 + 4.5) = 2 (7.5) = 15 : см
Ответ: 15см
Воспользуемся калькулятором для проверки полученного ответа.
Задача 2
Найдите периметр параллелограмма, если его стороны равны 5см и 80мм.
Решение
Для начала переведем 80мм в сантиметры и получим, что 80мм = 8см. В остальном задача аналогична предыдущей, так что повторим процесс ее решения:
P = 2 (a + b) = 2 (5 + 8) = 2 (13) = 26 : см
Ответ: 26см
Для проверки снова используем калькулятор . При этом мы можем не переводить 80мм в сантиметры, а просто задать длину стороны в миллиметрах.
Периметр параллелограмма
Формула периметра параллелограмма ABCD со сторонами: (
A B=C D=a, B C=A D=b
) (рис. 1), имеет вид
Примеры решения задач
ПРИМЕР 1
Стороны параллелограмма ABCD равны соответственно 3 и 5 см. Найти его периметр.
По условию обозначим a=3 см и b=5 см. Для нахождения периметра параллелограмма воспользуемся формулой
(
P_{A B C D}=2(a+b)
)
Подставляя исходные данные, получим:
(
P_{A B C D}=2 cdot(3+5)=16
) (см)
Периметр параллелограмма равен
(
P_{A B C D}=16
)см
ПРИМЕР 2
Найти периметр параллелограмма, если одна из его сторон равна 2 см, а меньшая диагональ – (
sqrt{3}
) см, а угол между ним (
30^{circ}
)
Сделаем рисунок (рис. 2).
По условию (
B D=sqrt{3}, A D=2
), а (
angle B D A=30^{circ}
) Рассмотрим (
Delta A B D
). Запишем теорему косинусов, для неизвестной стороны AB:
(
A B^{2}=B D^{2}+A D^{2}-2 B D cdot A D cdot cos angle B D A
)
Подставляя заданные значения, получим?
(
A B^{2}=(sqrt{3})^{2}+2^{2}-2 sqrt{3} cdot 2 cdot cos 30^{circ}
)
(
A B^{2}=3+4-2 sqrt{3} cdot 2 cdot frac{sqrt{3}}{2}
)
(
A B^{2}=7-6 Rightarrow A B=1(mathrm{см})
)
Периметр параллелограмма вычислим по формуле
(
P_{A B C D}=2(a+b)
)
Для данной задачи она запишется следующим образом:
(
P_{A B C D}=2(A B+A D)
)
Подставляя значения AB=1 и AD=2, получим:
(
P_{A B C D}=2 cdot(1+2)=6_{(mathrm{см})}
)
(
P_{A B C D}=6 mathrm{см}
)
