Download Article
Download Article
A trapezoid is defined as a quadrilateral with two parallel sides. As with any polygon, to find the perimeter of a trapezoid you need to add all four of its sides together. However, often you will be missing side lengths but have other information, such as the height of the trapezoid, or the angle measurements. Using this information, you can use rules of geometry and trigonometry to find the unknown lengths of sides.
-

1
Set up the formula for perimeter of a trapezoid. The formula is
, where
equals the perimeter of the trapezoid, and the variables
equals the length of the top base of the trapezoid,
equals the length of the bottom base,
equals the length of the left side, and
equals the length of the right side.[1]
-

2
Plug the side lengths into the formula. If you do not know the length of all four sides of the trapezoid, you cannot use this formula.
- For example, if you have a trapezoid with a top base of 2 cm, a bottom base of 3 cm, and two side lengths of 1 cm, your formula will look like this:
Advertisement
- For example, if you have a trapezoid with a top base of 2 cm, a bottom base of 3 cm, and two side lengths of 1 cm, your formula will look like this:
-

3
Add the side lengths together. This will give you the perimeter of your trapezoid.
Advertisement
-

1
Divide the trapezoid into a rectangle and two right triangles. To do this, draw the height from both top vertices.
- If you cannot form two right triangles because one side of the trapezoid is perpendicular to the base, just note that this side will have the same measurement as the height, and divide the trapezoid into one rectangle and one right triangle.
-

2
Label each height line. Since these are opposite sides of a rectangle, they will be the same length.[2]
- For example, if you have a trapezoid with a height of 6 cm, you should draw a line from each top vertex extending down to the bottom base. Label each line 6 cm.
-

3
Label the length of the middle section of the bottom base. (This is the bottom side of the rectangle.) The length will equal the length of the top base (the top side of the rectangle), because opposite sides of a rectangle are of equal length.[3]
If you do not know the length of the top base, you cannot use this method.- For example, if the top base of the trapezoid is 6 cm, then the middle section of the bottom base is also 6 cm.
-

4
Set up the Pythagorean Theorem formula for the first right triangle. The formula is
, where
is the length of the hypotenuse of the right triangle (the side opposite the right angle),
is the height of the right triangle, and
is the length of the base of the triangle.[4]
-

5
-

6
Square the known values in the equation. Then, subtract to isolate the
variable.
-

7
Take the square root to find the value of
. (For complete instructions on how to simplify square roots, you can read Simplify a Square Root.) The result will give you the value of the missing base of your first right triangle. Label this length on the base of your triangle.
-

8
Find the missing length of the second right triangle. To do this, set up the Pythagorean Theorem formula for the second triangle, and follow the steps to find the length of the missing side. If you are working with an isosceles trapezoid, which is a trapezoid in which the two non-parallel sides are the same length,[5]
the two right triangles are congruent, so you can simply carry the value from the first triangle over to the second triangle. -

9
Add up all the side lengths of the trapezoid. The perimeter of any polygon is the sum of all sides:
. For the bottom base, you will add the bottom side of the rectangle, plus the bases of the two triangles. You will likely have square roots in your answer. For complete instructions on how to add square roots, you can read the article Add Square Roots. You can also use a calculator to convert the square roots to decimals.
Advertisement
-

1
Divide the trapezoid into a rectangle and two right triangles. To do this, draw the height from both top vertices.
- If you cannot form two right triangles because one side of the trapezoid is perpendicular to the base, just note that this side will have the same measurement as the height, and divide the trapezoid into one rectangle and one right triangle.
-

2
Label each height line. Since these are opposite sides of a rectangle, they will be the same length.[6]
- For example, if you have a trapezoid with a height of 6 cm, you should draw a line from each top vertex extending down to the bottom base. Label each line 6 cm.
-

3
Label the length of the middle section of the bottom base. (This is the bottom side of the rectangle.) This length will be equal to the length of the top base, because opposite sides of a rectangle are of equal length.[7]
- For example, if the top base of the trapezoid is 6 cm, then the middle section of the bottom base is also 6 cm.
-

4
-

5
Plug the known values into the sine ratio. Make sure you use the height of the triangle as the length of the opposite side in the formula. You will solve for H.
- For example, if the given interior angle is 35 degrees, and the height of the triangle is 6 cm, your formula will look like this:
- For example, if the given interior angle is 35 degrees, and the height of the triangle is 6 cm, your formula will look like this:
-

6
Find the sine of the angle. Do this by using the SIN button on a scientific calculator. Plug this value into the ratio.
- For example, by using a calculator you will find that the sine of a 35 degree angle is .5738 (rounded). So your formula will now be:
- For example, by using a calculator you will find that the sine of a 35 degree angle is .5738 (rounded). So your formula will now be:
-

7
Solve for H. To do this, multiply each side by H, then divide each side by the angle sine. Or, you can simply divide the height of the triangle by the angle sine.
-

8
Find the length of the hypotenuse of the second right triangle. Set up the sine ratio (
) for the second given interior angle. This will give you the length of the hypotenuse, which is also the first side of the trapezoid.
-

9
Set up the Pythagorean Theorem formula for the first right triangle. The Pythagorean Theorem formula is
, where the length of the hypotenuse is
, and the height of the triangle is
.
-

10
-

11
Solve for
. This will give you the length of base of the first right triangle, and the first missing section of the trapezoid’s bottom base.
-

12
-

13
Add up all the side lengths of the trapezoid. The perimeter of any polygon is the sum of all sides:
. For the bottom base, you will add the bottom side of the rectangle, plus the bases of the two triangles.
- For example,
So, the approximate perimeter of your trapezoid is 45.5059 cm.
- For example,
Advertisement
Add New Question
-
Question
How can I solve the hypotenuse of a right triangle with a height of 2ft?

You don’t have enough information to find the hypotenuse. You would need the lengths of both legs or the size of at least one of the acute angles or the area of the triangle.
-
Question
How do I find the area without knowing the length of the sides of the trapezoid?

You would have to know the height of the trapezoid (h) and the lengths of both parallel sides (a and b). The area formula is [h(a + b)] / 2.
-
Question
Why are there so many formulas?

It’s because there are several possible sets of known dimensions regarding a trapezoid.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
Use the laws of special triangles to find the missing lengths of special triangles without using sine or the Pythagorean Theorem. The laws apply to a 30-60-90 triangle, or a 90-45-45 triangle.
-
Use a scientific calculator to find the sine of an angle by entering the angle measurement, then hitting the “SIN” button. You can also use a trigonometry table.
Thanks for submitting a tip for review!
Advertisement
Things You’ll Need
- Calculator
- Pencil
- Paper
References
About This Article
Article SummaryX
To find the perimeter of a trapezoid if you know the length of both sides and the bases, add together the length of all 4 sides. If you know the height, both side lengths, and the top base length, draw a straight line down from each top corner to form a square and 2 triangles. Then, use the Pythagorean Theorem to find the length of the base of each triangle. Add the length of each triangle base to the length of the top base, then add that to the top base and both sides to get the perimeter. To learn more about using the Pythagorean Theorem, keep reading!
Did this summary help you?
Thanks to all authors for creating a page that has been read 264,394 times.
Did this article help you?
Как найти периметр трапеции
Содержание:
- Основные свойства трапеции
-
Способы нахождений периметра
- По всем сторонам
- По сторонам равнобедренной трапеции
- Через среднюю линию
- Примеры решения задач
Определения
Трапеция — это четырехугольник, у которого лишь одна пара противолежащих сторон параллельна.
Периметр трапеции — это сумма длин всех его сторон.
Основные свойства трапеции
- средняя линия трапеции параллельна ее основаниям, а также равна половине их суммы;
- биссектриса любого угла данного четырехугольника отсекает на его основании отрезок, равный боковой стороне;
- треугольники ABO и DCO (на картинке), образованные диагоналями фигуры и ее основаниями, подобны;
- треугольники OAB и OCD, образованные диагоналями трапеции и ее боковыми сторонами, имеют одинаковую площадь;
- если сумма длин оснований четырехугольника равна сумме его боковых ребер, то в фигуру можно вписать окружность;
- точки M и N середины диагоналей лежат на одной прямой со средней линией фигуры. Также отрезок MN равен полуразность оснований четырехугольника;
- середины оснований фигуры, точка пересечения ее диагоналей, а также точка пересечения продолжений ее боковых сторон лежат на одной прямой;
Свойства равнобедренной трапеции
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- в равнобедренной трапеции углы при обоих ее основаниях одинаковы;
- диагонали равны;
- равнобедренную трапецию всегда можно вписать в окружность или описать окружность вокруг;
- если диагонали перпендикулярны, то высота фигуры равна полусумме ее оснований.
Способы нахождений периметра
Рассмотрим способы, с помощью которых можно найти сумму длин всех сторон данного четырехугольника.
По всем сторонам
Формула для нахождения периметра выглядит так:
P=a+b+c+d
где a, b, c, d — стороны трапеции.
По сторонам равнобедренной трапеции
Если нам известны ребра этого четырехугольника с одинаковыми боковыми сторонами, то находить ее P можно по следующей формуле:
(P=2times a+b+c)
или
(P=2times c+a+b)
Через среднюю линию
Так как средняя линия трапеции равна полусумме ее оснований, то формулу P можно выразить так:
(P=2times l+AB+CD)
где l — средняя линия фигуры.
Примеры решения задач
Давайте рассмотрим наглядные примеры решения задач на нахождение суммы длин всех ребер этой фигуры.
Задача 1
Дана трапеция с боковыми сторонами 4 см и 5 см, а ее основания равны 7 см и 10 см. Найти периметр данного многоугольника.
Решение:
Нам пригодится самая первая формула для расчета:
P=a+b+c+d.
Подставляем значения и получаем:
P=4+7+5+10=26;см.
Ответ: 26 см.
Задача 2
Известно, что у трапеции две боковые стороны равны 7 см, а ее основания равны 5 см и 8 см. Нужно найти P четырехугольника.
Решение:
Так как трапеция равнобедренная, удобнее всего будет использовать формулу:
(P=2times a+b+c)
Таким образом, получается:
(P=2times 7+5+8=27) см.
Ответ: 27 см.
Задача 3
Средняя линия l трапеции равна 6 см, а боковые стороны 5 см и 9 см. Вычислить P фигуры.
Решение:
Считать будем по формуле
(P=2times l+a+c)
(P=2times 6+5+9=26) см.
Ответ: 26 см.
Насколько полезной была для вас статья?
Рейтинг: 3.82 (Голосов: 11)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Трапеция — это геометрическая фигура, четырехугольник, у которого две противоположные стороны параллельны.
Эти параллельные стороны называют основаниями трапеции. Две другие стороны – это боковые стороны трапеции.
Онлайн-калькулятор периметра трапеции
Трапеции бывают равнобедренные, разносторонние и прямоугольные.
У трапеции есть так называемая средняя линия, которая показана на рисунке ниже. Она параллельна двум основаниям, а также равна их полусумме.
Формула периметра трапеции
Для нахождения периметра трапеции нужно сложить длины всех ее сторон.
P=a+b+c+dP = a + b + c + d,
где a,b,c,da, b, c, d — стороны трапеции.
Рассмотрим задачи на нахождение периметра трапеции.
Найти периметр трапеции, стороны которой равны:
a=c=2a = c = 2 см,
d=5d = 5 см,
b=3b = 3 см.
Решение
Нам дана равнобедренная трапеция, так как две ее стороны одинаковой длины. Также известны все стороны фигуры. Воспользуемся формулой и подставим вместо aa, bb, cc, dd их численные значения:
P=2+3+2+5=12P = 2 + 3 + 2 + 5 = 12 (см).
Ответ: P=12P = 12 см.
Рассмотрим еще одну задачу на вычисление стороны равнобедренной трапеции.
У равнобедренной трапеции основания равны 5 см и 3 см, а ее периметр равен 16 см. Чему равны боковые стороны?
Решение
В данной задаче нам известен периметр равнобедренной трапеции и ее основания: P=16P = 16 см, d=5d = 5 см, b=3b = 3 см, но неизвестны боковые стороны.
Воспользуемся формулой нахождения периметра трапеции, обозначив боковую сторону буквой aa:
P=a+a+b+d=2a+b+dP = a + a + b + d = 2a + b + d
Далее выразим 2a2a и найдем длину боковой стороны:
2a=P−b−d2a = P – b – d
2a=16−3−5=16−8=82a = 16 – 3 – 5 = 16 – 8 = 8
a=82=4a = frac{8}{2} = 4 см.
Боковая сторона равнобедренной трапеции равна 4 см.
Ответ: 4 см.
Не знаете, где заказать контрольную работу онлайн? Наши эксперты помогут вам в выполнении работы!
Тест по теме “Периметр трапеции”
Рассчитать периметр трапеции с помощью калькулятора или самостоятельно по формуле поможет материалы этой страницы. Кроме того вы можете рассчитать периметр равнобедренной трапеции.
Содержание:
- калькулятор периметра трапеции
- формула периметра трапеции через 4 стороны
- формула периметра трапеции через среднюю линию и боковые стороны
- примеры задач
Трапеция – выпуклый четырехугольник у которого две стороны параллельны (их называют основаниями), а две другие стороны, которые называют боковые стороны, непараллельны.
Периметр других четырехугольников также можно рассчитать на сайте: квадрат, прямоугольник, параллелограмм, ромб.
Формула периметра трапеции через все стороны
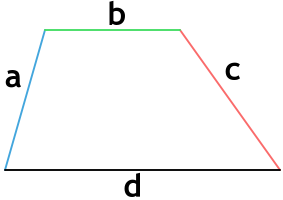
{P = a+b+c+d}
a, b, c и d – стороны трапеции
Формула периметра трапеции через среднюю линию и боковые стороны
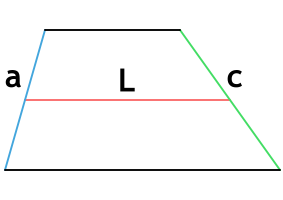
{P = a+c+2L}
a и c – боковые стороны трапеции
L – средняя линия трапеции
Пример задачи на нахождение периметра трапеции
Задача 1
Найдите периметр трапеции если ее основания равны 7см и 10см а боковые стороны 4см и 5см.
Решение
Применим первую формулу. Подставим в нее значения длин сторон трапеции и рассчитаем ее периметр:
P = a+b+c+d = 4+7+5+10 = 26 : см
Ответ: 26 см
Осталось проверить ответ с помощью калькулятора .
Загрузить PDF
Загрузить PDF
Трапеция – это четырехугольник с двумя параллельными сторонами. Чтобы найти периметр трапеции, нужно сложить длины всех четырех сторон. Зачастую в задачах длины некоторых сторон не даны, но известны другие величины, например, высота или угол трапеции. При помощи известных величин, а также геометрических и тригонометрических правил можно найти неизвестные стороны трапеции.
-

1
Запишите формулу для вычисления периметра трапеции. Формула:
, где
– периметр,
– верхнее основание,
– нижнее основание,
– левая боковая сторона,
– правая боковая сторона.[1]
-

2
В формулу подставьте известные длины сторон. Не используйте этот метод, если не даны значения всех четырех сторон.
- Например, верхнее основание трапеции равно 2 см, нижнее основание равно 3 см, а каждая боковая сторона равна 1 см. В этом случае формула примет следующий вид:
- Например, верхнее основание трапеции равно 2 см, нижнее основание равно 3 см, а каждая боковая сторона равна 1 см. В этом случае формула примет следующий вид:
-

3
Сложите длины сторон. Так вы найдете периметр трапеции.
Реклама
-

1
Разбейте трапецию на прямоугольник и два прямоугольных треугольника. Для этого из каждой вершины трапеции проведите высоту.
- Если одна сторона трапеции перпендикулярна основаниям, вы не сможете получить два прямоугольных треугольника. В этом случае боковая сторона, перпендикулярная основаниям, равна высоте, а трапеция разбивается на прямоугольник и один прямоугольный треугольник.
-

2
Обозначьте каждую высоту. Так как высоты являются противоположными сторонами прямоугольника, они равны.[2]
- Например, высота трапеции равна 6 см. Из вершин трапеции проведите две высоты (к нижнему основанию). Возле каждой высоты напишите «6 см» (без кавычек).
-

3
Обозначьте среднюю часть нижнего основания (она является нижней стороной прямоугольника). Эта часть равна верхнему основанию (то есть верхней стороне прямоугольника), так как противоположные стороны прямоугольника равны.[3]
Не используйте этот метод, если не дано значение верхнего основания.- Например, если верхнее основание трапеции равно 6 см, то средняя часть нижнего основания также равна 6 см.
-

4
Запишите теорему Пифагора для первого прямоугольного треугольника. Формула:
, где
– гипотенуза треугольника (сторона, противоположная прямому углу),
– высота треугольника,
– основание треугольника.[4]
-

5
-

6
Возведите в квадрат известные значения. Затем при помощи вычитания обособьте переменную
.
-

7
Извлеките квадратный корень, чтобы найти
. (Чтобы получить информацию об упрощении квадратных корней, прочитайте эту статью.) Вы найдете основание первого прямоугольного треугольника. Напишите найденное значение под основанием соответствующего треугольника.
-

8
Найдите неизвестную сторону второго прямоугольного треугольника. Для этого запишите теорему Пифагора для второго треугольника и действуйте так, как описано выше. Если дана равнобедренная трапеция, у которой боковые стороны равны,[5]
то два прямоугольных треугольника являются равными, то есть любая сторона одного треугольника равна соответствующей стороне другого. -

9
Сложите значения всех сторон трапеции. Периметр любого многоугольника равен сумме всех его сторон:
. Нижнее основание трапеции равно сумме нижней стороны прямоугольника и оснований двух треугольников. В интернете поищите информацию о том, как складывать квадратные корни, или просто воспользуйтесь калькулятором, чтобы преобразовать квадратные корни в десятичные дроби.
Реклама
-

1
Разбейте трапецию на прямоугольник и два прямоугольных треугольника. Для этого из каждой вершины трапеции проведите высоту.
- Если одна сторона трапеции перпендикулярна основаниям, вы не сможете получить два прямоугольных треугольника. В этом случае боковая сторона, перпендикулярная основаниям, равна высоте, а трапеция разбивается на прямоугольник и один прямоугольный треугольник.
-

2
Обозначьте каждую высоту. Так как высоты являются противоположными сторонами прямоугольника, они равны.[6]
- Например, высота трапеции равна 6 см. Из вершин трапеции проведите две высоты (к нижнему основанию). Возле каждой высоты напишите «6 см» (без кавычек).
-

3
Обозначьте среднюю часть нижнего основания (она является нижней стороной прямоугольника). Эта часть равна верхнему основанию (то есть верхней стороне прямоугольника), так как противоположные стороны прямоугольника равны.[7]
- Например, если верхнее основание трапеции равно 6 см, то средняя часть нижнего основания также равна 6 см.
-

4
-

5
В формулу синуса подставьте известные величины. Вместо противоположной стороны подставьте высоту треугольника. Вы найдете гипотенузу, то есть боковую сторону трапеции.
- Например, если нижний угол трапеции равен 35 градусов, а высота треугольника равна 6 см, то формула запишется так:
- Например, если нижний угол трапеции равен 35 градусов, а высота треугольника равна 6 см, то формула запишется так:
-

6
Найдите синус угла. Это делается при помощи научного калькулятора, а именно клавиши SIN. Найденное значение подставьте в формулу.
- При помощи калькулятора вы найдете, что синус угла в 35 градусов приблизительно равен 0,5738. Таким образом, формула примет следующий вид:
- При помощи калькулятора вы найдете, что синус угла в 35 градусов приблизительно равен 0,5738. Таким образом, формула примет следующий вид:
-

7
Найдите переменную H. Для этого каждую сторону уравнения (формулы) умножьте на Н, а затем каждую сторону уравнения разделите на синус угла. Или просто разделите высоту треугольника на синус угла.
-

8
Найдите гипотенузу второго прямоугольного треугольника. Напишите функцию (формулу) синуса угла второго прямоугольного треугольника:
. Так вы найдете гипотенузу второго треугольника, которая является второй боковой стороной трапеции.
-

9
Запишите теорему Пифагора для первого прямоугольного треугольника. Формула:
, где
– гипотенуза треугольника (сторона, противоположная прямому углу),
– высота треугольника.
-

10
-

11
Найдите
. Вы получите основание первого прямоугольного треугольника, которое является первой неизвестной частью нижнего основания трапеции.
-

12
-

13
Сложите значения всех сторон трапеции. Периметр любого многоугольника равен сумме всех его сторон:
. Нижнее основание трапеции равно сумме нижней стороны прямоугольника и оснований двух треугольников.
- В нашем примере:
Таким образом, приблизительный периметр трапеции равен 45,5059 см.
Реклама
- В нашем примере:
Советы
- Для специальных прямоугольных треугольников (треугольник 30-60-90[8]
или треугольник 90-45-45[9]
) существуют формулы, при помощи которых можно найти неизвестные стороны без использования функции синуса или теоремы Пифагора. - Чтобы найти синус угла, воспользуйтесь научным калькулятором – введите угол, а затем нажмите клавишу SIN. Или используйте тригонометрические таблицы.[10]
Реклама
Что вам понадобится
- Калькулятор
- Карандаш
- Бумага
Об этой статье
Эту страницу просматривали 118 976 раз.






