Как найти периметр балки

Периметр Т-образной формы с заданной высотой и длиной балки Решение

ШАГ 0: Сводка предварительного расчета

Используемая формула

Периметр Т-образной формы = 2*(Длина луча Т-образной формы+Высота Т-образной формы)
P = 2*(l_Beam+h)
В этой формуле используются 3 Переменные

Используемые переменные

Периметр Т-образной формы – (Измеряется в метр) – Периметр Т-образной формы — это общая длина всех граничных линий Т-образной формы.
Длина луча Т-образной формы – (Измеряется в метр) – Длина балки Т-образной формы — это длина от левого конца до правого конца верхней балки Т-образной формы, которая направлена горизонтально.
Высота Т-образной формы – (Измеряется в метр) – Высота Т-образной формы — это перпендикулярное расстояние от самой нижней точки до самой верхней точки Т-образной формы.

ШАГ 1. Преобразование входов в базовый блок

Длина луча Т-образной формы: 15 метр –> 15 метр Конверсия не требуется
Высота Т-образной формы: 10 метр –> 10 метр Конверсия не требуется

ШАГ 2: Оцените формулу

Подстановка входных значений в формулу

P = 2*(l_Beam+h) –> 2*(15+10)

Оценка … …

P = 50

ШАГ 3: Преобразуйте результат в единицу вывода

50 метр –> Конверсия не требуется

ОКОНЧАТЕЛЬНЫЙ ОТВЕТ

50 метр <– Периметр Т-образной формы

(Расчет завершен через 00.004 секунд)

Источник

Перейти к содержимому Меню Закрыть

ГДЗ, ответы, контрольные работы, решение заданий, тесты на Знания.ком

Искать:

Знания.ком

Меню

Знания.ком

Искать:

Меню

ГДЗ, ответы, контрольные работы, решение заданий, тесты на Знания.ком

Искать:

Кнопка

Главная страница

Вопросы

как найти периметр балки?

11 просмотров10.07.2022Геометрия

admin304.70K 10.07.2022 0 комментариев

как найти периметр балки?

Регистрация или Вход

Вопросы

Информатика. 9 класс. 3 ответа | 0 Голосов

характеристика автора романа Бедная Лиза 2 ответа | 0 Голосов

Пример со скрытым числом 1 ответ | 0 Голосов

Разработка на Python 1 ответ | 0 Голосов

Обществознание законы 1 ответ | 0 Голосов

Источник

Двутавр

Балки двутавровые по ГОСТ 8239-89

N профиля	^Масса ^кг/м	Высота основания, h, мм	Высота полки, b мм	Площадь сечения см²	Периметр мм	Приведенная толщина мм
10	9,46	100	55	12,0	420	2,86
12	11,5	120	64	14,7	496	2,96
14	13,7	140	73	17,4	572	3,04
16	15,9	160	81	20,2	644	3,14
18	18,4	180	90	23,4	720	3,25
20	21,0	200	100	26,8	800	3,40
22	24,0	220	110	30,6	880	3,48
24	27,3	240	115	34,8	940	3,70
27	31,5	270	125	40,2	1040	3,87
30	36,51	300	135	46,5	1140	4,08
33	42,2	330	140	53,8	1220	4,41
36	46,8	360	145	61,9	1300	4,76
40	56,1	400	155	71,4	1420	5,03
45	65,2	450	160	83,0	1540	5,39
50	76,8	500	170	97,8	1680	5,82
55	89,8	550	180	114	1820	6,26
60	104	600	190	132	1960	6,73
65	120	650	200	153	2100	7,29
70	138	700	210	176	2240	7,86

погода

курс валют

Источник

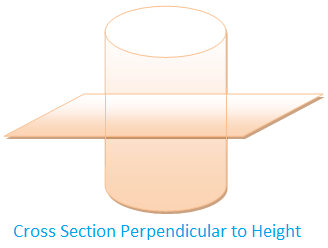
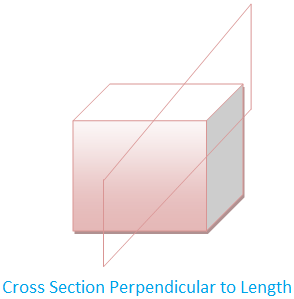
The cross section of a solid is a plane section resulting
from a cut (real or imaginary) perpendicular to the length (or breadth of
height) of the solid.

If the shape and size of the cross section is the same at
every point along the length (or breadth or height) of the solid then the cross
section is uniform.

The two solids shown above have uniform cross sections.

The figure given below is a solid (Cone) whose cross sections perpendicular to height are not uniform.

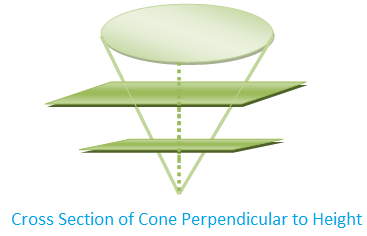
Volume of a solid figure with uniform cross section

= (Area of the cross section) × length (or height or breadth)

= A × h

Lateral surface area of a solid figure with uniform cross section

= (Perimeter of the cross section) × length (or height or breadth)

= P × h

Cross Section of Sold Figure

Total surface area of a solid figure with uniform cross section

= Lateral surface area + Sum of the areas of the two plane ends

= P × h + 2 × A

9th Grade Math

From Cross Section to HOME PAGE

Didn’t find what you were looking for? Or want to know more information
about Math Only Math.
Use this Google Search to find what you need.

Источник

Сечения трехмерных фигур — площади и периметр

Умеешь строить сечения трехмерных фигур – точно не пропадешь.

В этой статье я расскажу тебе об алгоритме построения сечений и разберу пример!

Поехали!

Алгоритм определения площади и периметра сечения объемных фигур

Нарисовать сечение.
Определить фигуру, которая получилась в этом сечении.
Вспомнить формулы площади/периметра этой фигуры.
Найти площадь/периметр фигуры.

Стандартное сечение имеет вид треугольника, круга или четырехугольника. Следовательно, нам необходимо искать площади именно этих фигур.

Площадь сечения

Площадь треугольника

Площадь круга

Площадь прямоугольника

Пример решения задачи

Диаметр основания конуса ( displaystyle left( AB right)) равен ( displaystyle 8) см.

Длина образующей ( displaystyle left( AC; BC right)) равна ( displaystyle 5) см (линия от вершины конуса до любой точки его основания).

Найдите площадь осевого сечения этого конуса.

Осевое сечение конуса – это равнобедренный треугольник ( displaystyle left( ABC right)), высота которого совпадает с высотой конуса ( displaystyle left( CO right)), а основание ( displaystyle left( AB right)) является диаметром основания конуса.

Значит, ( displaystyle S) осевого сечения конуса =( displaystyle S) треугольника ( displaystyle ABC).

Вспомним формулу площади треугольника:

( displaystyle S=frac{(COcdot AB)}{2} )

begin{matrix}
AB -длина стороны треугольника \
CO – высота, опущенная на сторону AB \
end{matrix}

Найдем высоту ( displaystyle Delta ABC):

Рассмотрим ( displaystyle Delta COA).

т.к. ( displaystyle OC) – высота ( displaystyle Delta ABC rightarrow angle COA=90{}^circ rightarrow Delta COA) – прямоугольный.

( displaystyle AO=frac{AB}{2}=frac{8}{2}=4) (т.к. ( displaystyle AO) – радиус окружности, ( displaystyle AB) – диаметр).

Найдем ( displaystyle AC):

По теореме Пифагора:

( displaystyle A{{C}^{2}}=C{{O}^{2}}+A{{O}^{2}}; C{{O}^{2}}=A{{C}^{2}}-A{{O}^{2}}={{5}^{2}}-{{4}^{2}}=9см; CO=sqrt{9}=3см)

Подставим получившиеся значения в формулу площади:

( displaystyle {{S}_{ABC}}=frac{left( COcdot AB right)}{2}=frac{3cdot 8}{2}=)( displaystyle 12см{{ }^{2}})

Площадь осевого сечения этого конуса равна ( displaystyle 12см{{ }^{2}}).

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук — ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 — WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org — email для записи

тысячи учеников, поступивших в лучшие ВУЗы страны
автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
закончил МФТИ, преподавал на малом физтехе;
репетиторский стаж — c 2003 года;
в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».

Источник

Периметр Т-образной формы с заданной высотой и длиной балки Решение

как найти периметр балки?