Расчёт периметра прямоугольника по диагонали и стороне
Периметр прямоугольника равен сумме длин его сторон.
Прямоугольник это параллелограмм с прямыми углами.
Калькулятор рассчитывает периметр прямоугольника по диагонали и стороне.
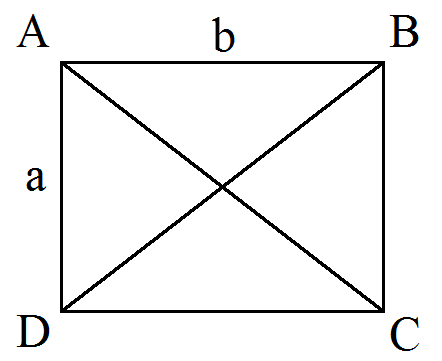
Формула периметра прямоугольника
color{#0000FF}{P = 2a+2b}
color{#0000FF}{P = 2(a+b)}
По теореме пифагора зная диагональ и сторону выразим другую сторону
color{#0000FF}{a = sqrt{{BD}^2-b^2}}
color{#0000FF}{b = sqrt{{BD}^2-a^2}}
В прямоугольнике диагонали равны
color{#0000FF}{BD = AC}
Формула периметра прямоугольника через диагональ и сторону
color{#0000FF}{P = 2(sqrt{{BD}^2-b^2}+b)}
color{#0000FF}{P = 2(a+sqrt{{BD}^2-a^2})}
Значащих цифр:
Периметр прямоугольника равен сумме длин его сторон. Для расчета можно указать либо длину и ширину прямоугольника, либо его диагональ и одну из сторон.
Содержание:
- калькулятор периметра прямоугольника
- формула периметра прямоугольника через стороны
- формула периметра прямоугольника через диагональ и сторону
- примеры задач
Прямоугольник – четырехугольник, у которого все углы равны 90 градусов, т. е. прямые.
Периметры других четырехугольников на сайте – ромб, квадрат, параллелограмм.
Формула периметра прямоугольника через стороны

{P = 2 (a + b)}
a и b – стороны прямоугольника
Формула периметра прямоугольника через диагональ и сторону
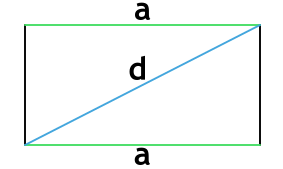
{P = 2(a+sqrt{d^2-a^2})}
a – сторона прямоугольника
d – диагональ прямоугольника
Примеры задач на нахождение периметра прямоугольника
Задача 1
Найдите периметр прямоугольника со сторонами 4см и 2см.
Решение
Решить задачу поможет первая формула. Подставим в нее значение длин сторон и рассчитаем периметр прямоугольника:
P = 2 (a + b) = 2 (4 + 2) = 2 (6) = 12 : см
Ответ: 12 см
Убедимся в правильности решения с помощью калькулятора .
Задача 2
Найдите периметр прямоугольника одна сторона которого равна 9см а диагональ 15см.
Решение
А в этом случае воспользуемся второй формулой.
P = 2(a+sqrt{d^2-a^2}) = 2(9+sqrt{15^2-9^2}) = 2(9+sqrt{(15+9)(15-9)}) = 2(9+sqrt{24 cdot 6}) = 2(9+sqrt{144}) = 2(9+12) = 2 cdot 21 = 42 : см
Ответ: 42 см
Проверим ответ на калькуляторе .
Задача 3
Найдите периметр прямоугольника со сторонами 12см и 9см.
Решение
Задача похожа на первую и решается аналогичным образом.
P = 2 (a + b) = 2 (12 + 9) = 2 (21) = 42 : см
Ответ: 42 см
Проверка .
Как найти периметр прямоугольника
Вас ждут четыре простых способа.

Напомним, периметром называют суммарную длину всех сторон. Вычислить её можно по‑разному. Выбирайте формулу в зависимости от известных вам данных.
Зная все или две соседние стороны
Для полноты упомянем простейшие классические формулы.
- Если известна длина всех сторон прямоугольника, просто посчитайте сумму этих величин.
- Если вы знаете только две соседние стороны, суммируйте их и умножьте результат на два.
- P — искомый периметр;
- a, b, c, d — стороны прямоугольника.
Зная любую сторону и площадь
- Поделите площадь на длину известной стороны.
- Прибавьте результат к известной стороне.
- Умножьте полученное число на два.
- P — искомый периметр прямоугольника;
- a — известная сторона;
- S — площадь прямоугольника.
Зная любую сторону и диагональ
- Посчитайте разность квадратов диагонали и стороны.
- Найдите корень из результата.
- Прибавьте полученное число к известной стороне.
- Умножьте результат на два.
- P — искомый периметр прямоугольника;
- a — известная сторона;
- d — диагональ прямоугольника.
Зная одну любую сторону и радиус описанной окружности
- Умножьте квадрат радиуса на четыре.
- Посчитайте разность полученного числа и квадрата известной стороны.
- Найдите корень из результата.
- Прибавьте полученное число к известной стороне.
- Умножьте результат на два.
- P — искомый периметр прямоугольника;
- a — известная сторона;
- R — радиус окружности, описанной вокруг прямоугольника.
Читайте также 📐✂️📌
- Как научить ребёнка считать играючи
- Как перевести обычную дробь в десятичную
- 6 способов посчитать проценты от суммы с калькулятором и без
- 9 логических задач, которые по зубам только настоящим интеллектуалам
- 11 книг, которые прокачают математическое мышление
Как рассчитать периметр прямоугольника
На данной странице калькулятор поможет рассчитать периметр прямоугольника онлайн. Для расчета задайте длину сторон или длины диагоналей и угол между ними.
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).
Через стороны
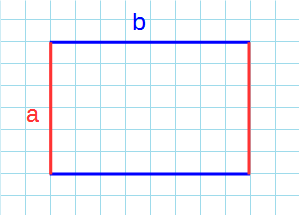
Формула для нахождения периметра прямоугольника через стороны:
a, b – стороны прямоугольника.
Через диагонали и сторону
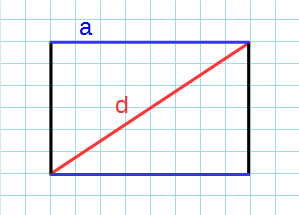
Формула для нахождения периметра прямоугольника через сторону и диагональ:
d – диагональ; a – сторона прямоугольника.
Периметр прямоугольника — это сумма
всех сторон прямоугольника.
Периметр прямоугольника можно рассчитать
через четыре стороны, через смежные стороны,
через диагональ, через площадь,
через радиус описанной окружности.
Самый простой способ найти периметр
прямоугольника, это сложить все стороны.
Также, исходя из свойства прямоугольника, — «противоположные
стороны равны и параллельны», можно сказать, что периметр
численно равен удвоенной сумме ширины и высоты — двух
смежных сторон прямоугольника.
Кроме этих двух способов периметр прямоугольника
можно найти через другие величины. Например, через
площадь прямоугольника, диагональ прямоугольника, и так далее.
В прямоугольник невозможно вписать окружность,
поэтому выразить периметр через вписанную
окружность не получится.
Единицы измерения периметра прямоугольника:
км, м, дм, см, мм.
Содержание
- Формулы периметра прямоугольника
- Полупериметр
- Основные определения и величины
Формулы периметра прямоугольника
- Периметр прямоугольника через четыре стороны
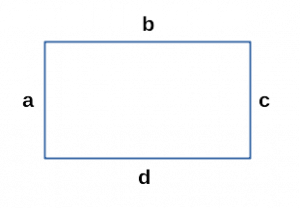
[ P = a + b + c + d ]
a, b, c, d — стороны прямоугольника;
a || c, b || d;
a = c, b = d; - Периметр прямоугольника через смежные стороны
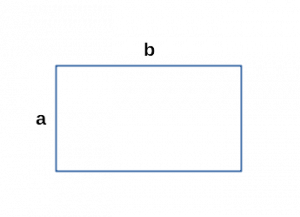
[ P = 2a + 2b = 2(a+b) ]
a, b — смежные стороны;
a ≠ b; - Периметр прямоугольника через любую сторону и диагональ
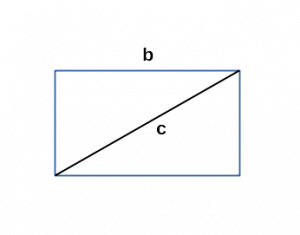
[ P = 2(b + (sqrt{c^2-b^2})) ]
b — любая сторона;
c — диагональ; - Периметр прямоугольника через любую сторону и площадь

[ P = 2 * (b + S : b) ]
b — любая сторона;
S — площадь; - Периметр прямоугольника через любую сторону и радиус описанной окружности
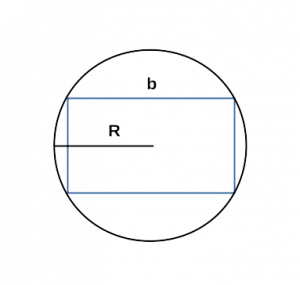
[ P = 2 cdot (b + sqrt{4R^2 — b^2}), ]
b — любая сторона;
R — радиус описанной окружности;
Полупериметр
Полупериметр — это половина периметра.
Обозначается латинской буквой p.
Чтобы найти полупериметр нужно разделить
периметр на два, или домножить периметр на 0.5.
[ p = frac{P}{2} = P cdot 0.5 ]
Полупериметр применяется в некоторых формулах
нахождения разных величин прямоугольника. Вместо того,
чтобы вычислять периметр, в таких формулах
удобней вычислять полупериметр.
Основные определения и величины
Длина прямоугольника — это длинная сторона
/ наибольшая сторона прямоугольника.
Обозначается латинской буквой a.
Ширина прямоугольника — это широкая сторона
/ наименьшая сторона прямоугольника.
Обозначается латинской буквой b.
Сторона прямоугольника — это ширина или длина прямоугольника,
в зависимости от численного значения длины стороны.
Обозначается латинской буквой a или b.
Диагональ прямоугольника — это отрезок, соединяющий
противоположные стороны прямоугольника.
Обозначается латинской буквой c или d.
Средняя линия прямоугольника — это отрезок, соединяющий
наименьшие параллельные стороны прямоугольника друг с
другом, причем делящий их пополам на равные отрезки.
Обозначается латинской буквой l.
Радиус описанной окружности прямоугольника — это отрезок,
соединяющий центр описанной около треугольника
окружности и произвольную точку на окружности.
Обозначается латинской буквой R.
Высота прямоугольника — это любая сторона прямоугольника,
а также любой отрезок в прямоугольнике, образующий угол в 90 градусов.
Обозначается латинской буквой h.
