Четырехугольники, вписанные в окружность. Теорема Птолемея
Вписанные четырёхугольники и их свойства
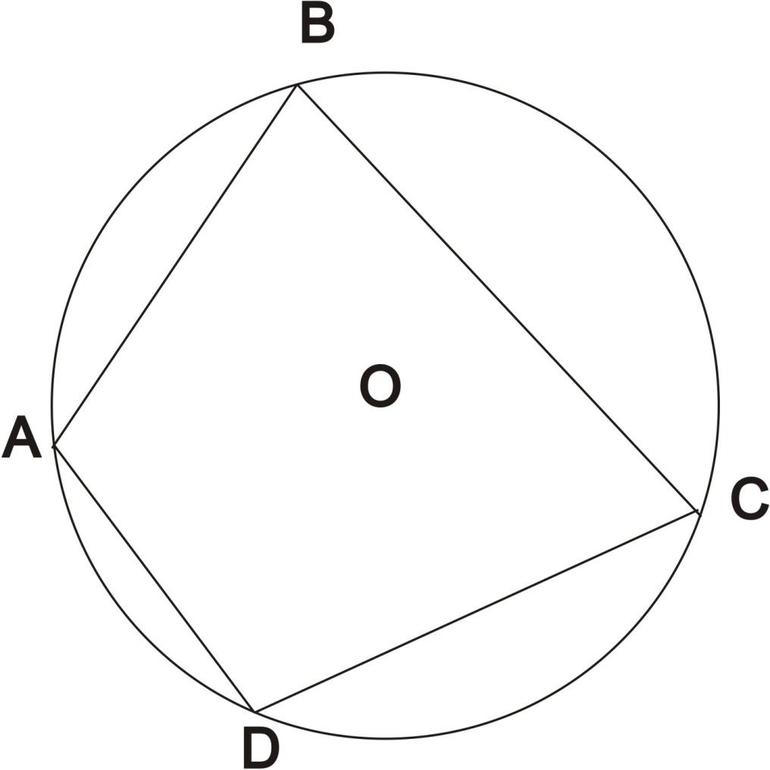
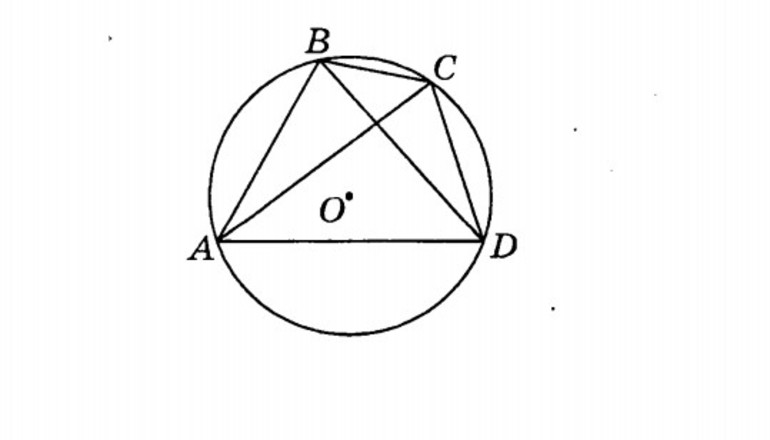
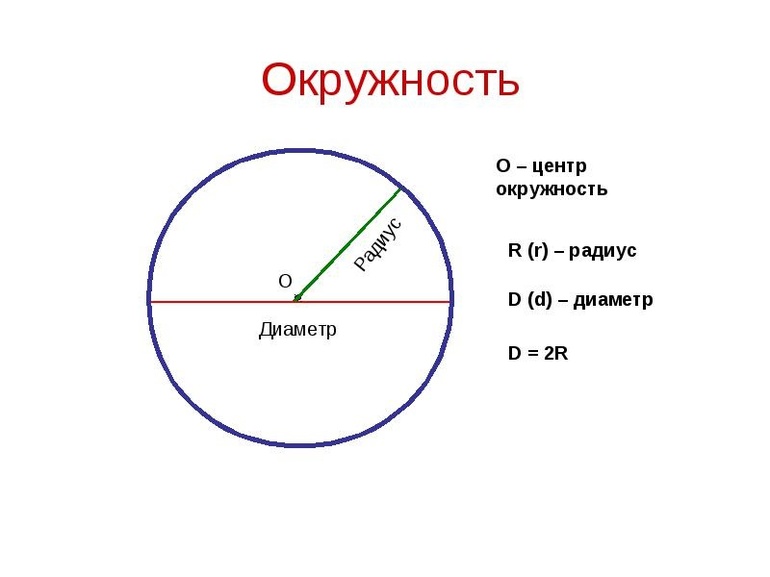
Определение 1 . Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником .
Теорема 1 . Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180° .
Доказательство . Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC . Угол ADC является вписанным углом, опирающимся на дугу ABC . Поэтому величина угла ADC равна половине угловой величины дуги ABC . Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180° .
Если рассмотреть углы BCD и BAD , то рассуждение будет аналогичным.
Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
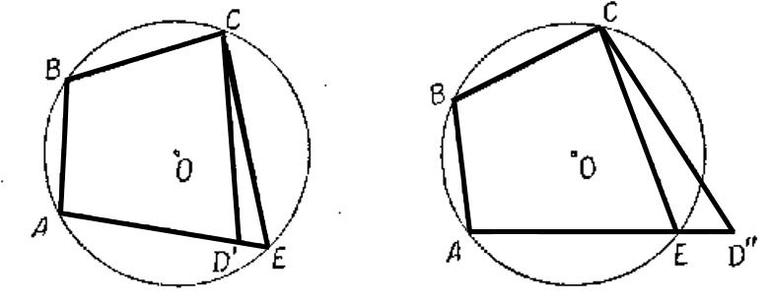
Доказательство . Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A , B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D . Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).
Продолжим отрезок CD за точку D до пересечения с окружностью в точке E , и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180° . При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC . Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC , не смежного с ним.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Теорема 2 доказана.
Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:
где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.
| Фигура | Рисунок | Свойство |
| Окружность, описанная около параллелограмма |  |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба |  |
Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
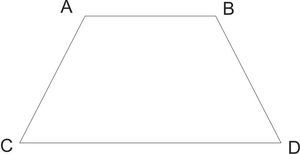
| Окружность, описанная около трапеции |  |
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида |  |
Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник |  |
Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:
где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.
| Окружность, описанная около параллелограмма | |
 |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба | |
 |
Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
| Окружность, описанная около трапеции | |
 |
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида | |
 |
Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник | |
 |
| Окружность, описанная около параллелограмма |
 |
Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником.
Окружность, описанная около ромба
Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом.
Окружность, описанная около трапеции
Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией.
Окружность, описанная около дельтоида
Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников.
Произвольный вписанный четырёхугольник
Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты:
где a, b, c, d – длины сторон четырёхугольника,
а p – полупериметр, т.е.
Теорема Птолемея
Теорема Птолемея . Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
Доказательство . Рассмотрим произвольный четырёхугольник ABCD , вписанный в окружность (рис.3).
Докажем, что справедливо равенство:
Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).
Заметим, что треугольник ABD подобен треугольнику BCE . Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E ), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
откуда вытекает равенство:
 |
(1) |
Заметим, что треугольник ABE подобен треугольнику BCD . Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
Как найти периметр сторон четырехугольника, формула нахождения
Совсем недавно в России родители отправляли своих детей в первый класс и с нетерпением ждали их первых заданий. Они с удовольствием наблюдали за тем, как их дети знакомятся с буквами русского алфавита, учатся считать палочки и точечки, выводить различные кривые и прямые линии. Родители помогали знакомиться своим детям с тем, что тетрадь в клеточку предназначена для написания цифр, а тетрадь в линеечку — для письма.
Сегодня, будучи второклассниками, ученики России достигли больших успехов в сфере начального образования, а точнее, в математическом прогрессе. Учителя научили их складывать и вычитать, умножать, делить, измерять.
Кстати, по поводу измерения: с линейкой ребята вторых классов России уже знакомы, и применение ей, кроме как стрелять с задней парты в соседа бумажки, они тоже знают. Именно об измерениях мы и заведем сегодняшний разговор.
Как мы видим, прогресс обучения нынешних учеников проходит слегка в ускоренном режиме. С теми темами, например, такими как периметр, дети 90-х знакомились позже, а наши ребята узнают сегодня. Конечно, в этом нет ничего страшного. Время меняется, и программа обучения тоже должна не стоять на месте. Зато, как считают многие, наши дети будут умнее нас.
Школьное задание
Наверное, многих родителей сегодня удивляют нынешние задания для второклассников. В учебнике по математике для второго класса можно встретить такое задание, как, например: «Найди периметр четырехугольника, две стороны которого равны по 2 сантиметра, а другие две будут по 3 сантиметра». Как справиться с данным заданием?
Многие родители настоящего времени являются теми самыми детьми девяностых годов, и, естественно, в большинстве случаев, мало кто помнит, что такое периметр. Особенно, если учились не на отлично, да и не совсем на «хорошо».
Естественно, каждому родителю хотелось бы, чтоб его ребенку было проще в обучении, и они всеми силами стараются ему в этом помочь. Некоторым родителям сначала приходится справиться со своей душевной паникой, а уже потом продолжать объяснять своему ребенку. В этом случае многим помогает интернет, место, где можно найти ответы на все тревожные вопросы. Во времена девяностых, к сожалению, такой «роскоши» не было.
Вопросы:
- Что такое «периметр»?
- Как находить периметр четырехугольника?
Ответы на вопросы:
Для тех, кто знает, вспоминаем, а кто не знает — объясняем:
- Периметр — это сумма всех сторон четырехугольника. Всего лишь каждая грань по отдельности будет равна после сложения единому числу.
- Найти периметр, значит, что нужно взять линейку и измерить каждую границу четырехугольника. После выполнения данного действия необходимо сложить полученные числа между собой. Общая полученная сумма и будет являться периметром.
Решение:
В данном случае, по действиям нашей задачи, нам известны суммы сторон четырехугольника, а именно две из них по 2 сантиметра и две по 3 сантиметра. Поэтому нам остается всего лишь перечертить четырехугольник в тетрадь и сложить известные нам суммы каждой грани.
2+2+3+3=10
Как мы видим, периметр нашей четырехугольной фигуры равен 10.
В математике сумму всех сторон (периметр) мы обозначаем символом Р.
Теперь записываем правильное решение этой задачи:
Р=2+2+3+3;
Ответ: Р=10.
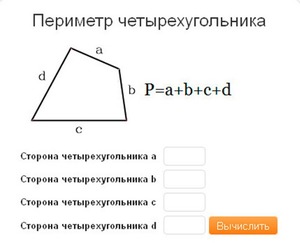
В математике существует формула, запомнив которую, вы никогда не будете забывать, как найти периметр (общую сумму всех сторон) четырехугольника и выглядит она так:
P = a + b + c + d (где a , b, c, d являются границами четырехугольника).
Кроме того, хотелось бы обратить внимание, что четырехугольник не обязательно будет являться прямоугольником. Это может быть и квадрат, у которого все стороны равны, и любая другая геометрическая фигура, у которой есть четыре стороны и такое же количество углов.
Грани произвольного четырехугольника могут совсем не совпадать ни с одной из сторон фигуры. Это могут быть совершенно разные числа. И, в итоге, получаются фигуры с четырьмя сторонами и теми же четырьмя углами. Фигура не будет похожа ни на квадрат, ни на прямоугольник, так как углы ее прямыми не будут. И периметр, соответственно мы вычисляем по той же самой единой формуле.
Или взять, например трапецию. Обычно у трапеции две стороны одинаковые, а другие две совсем не совпадают, но между собой параллельные.
На примере трапеция может выглядеть так: верхняя грань равна 2 сантиметра, левая и правая стороны по 3 сантиметра, соединяем их с нижней гранью и получаем трапецию. Высчитываем каждую ее сторону и снова получаем периметр четырехугольника.
Вычислить по формуле всегда будет проще, и не важно, каким числам равна каждая сторона.
Так как современные дети страны уже дошли до таблицы умножения, с периметром квадрата у них проблем не будет. Зная размер одной стороны квадрата, нужно умножить ее на все четыре равные стороны.
В общем, теперь стоит взять линейку с карандашом и лист бумаги. После этого следует начертить произвольные фигуры с четырьмя углами и высчитать общую сумму ее сторон.
Четырехугольник, вписанный в окружность – основные свойства, признаки и формулы
Общие сведения
Фигура является вписанной в окружность, когда все ее вершины лежат на ней. Произвести вписание в окружность четырехугольника можно только в том случае, когда он выпуклый. Все его точки находятся по одну сторону от произвольной прямой, которая проходит через соседние вершины фигуры. Нужно отметить, что в этом случае окружность является описанной вокруг фигуры. Если в параллелограмм вписана окружность, то ее центр совпадает с центром окружности, которая описана вокруг него.
Четырехугольники бывают самопересекающимися. Они также могут быть вписанными, однако это встречается крайне редко. Не каждую фигуру можно вписать в круг, поскольку существуют определенные законы. Например, вокруг ромба нельзя описать круг — исключение составляет случай, когда ромб является квадратом.
Основные правила
Выпуклый четырехугольник можно вписать в окружность. Однако для этого существуют некоторые правила (критерии) или признаки. Некоторые задачи сформулированы таким образом, что нужно знать основные критерии, а также уметь доказывать возможность вписывать или описывать окружность. Около четырехугольника можно описать окружность, если выполняются следующие условия:
- Сумма углов, которые являются противоположными, соответствует 180 градусам.
- Соблюдается равенство смежного и противоположного углов.
- Угол между стороной и диагональю равен углу между противоположной стороной и диагональю.
- Произведение двух диагоналей соответствует размерности суммы произведений противоположных сторон.
- Четыре точки лежат на окружности, когда две прямые АС и BD, образующие диагонали, пересекаются в некоторой точке P, а также выполняется следующее равенство: AP * PC = BP * PD.
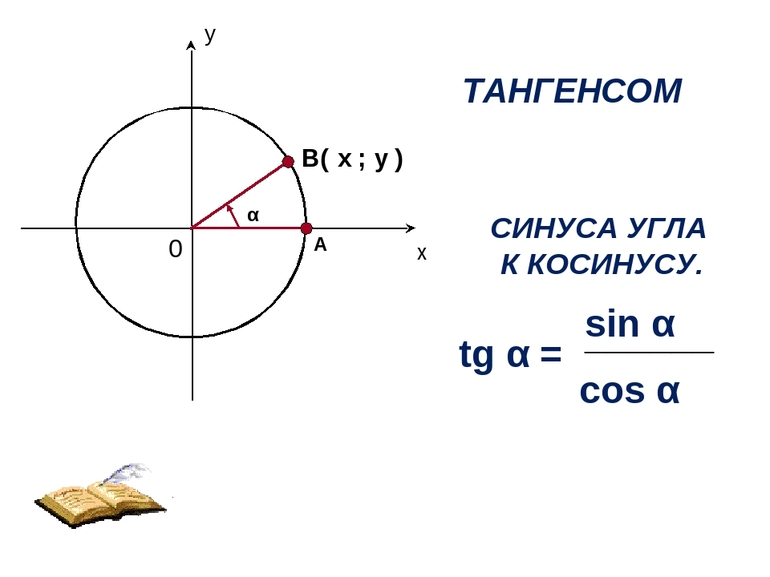
- Произведения тангенсов половины двух противоположных углов равны 1. Кроме того, значения произведений эквивалентны друг другу (tg (A/2) * tg (C/2) = tg (B/2) * tg (D/2) = 1).
Четвертое утверждение является теоремой Птолемея. Все эти правила являются следствиями, полученными при доказательстве различных гипотез. Правила можно применять в зависимости от условия поставленной задачи. Любой параллелограмм можно вписать в окружность, когда он является прямоугольником или квадратом.
Свойства и утверждения
При решении можно воспользоваться некоторыми свойствами, которые были доказаны. Это нужно для того, чтобы не тратить время на выведение какой-либо формулы. Применяется методика для оптимизации вычислений. К ним можно отнести следующие:
- Если вокруг четырехугольника описана окружность, то центры окружностей, которые вписанных в треугольники, образованные диагоналями фигуры, являются вершинами прямоугольника.
- Не бывает четырехугольников, вписанных в окружность, с рациональной площадью и сторонами, которые образуют арифметический или геометрический тип прогрессии.
- При продолжении сторон до точек пересечения Y и Z, внутренние биссектрисы углов Y и Z являются перпендикулярными.
Данные утверждения применяются не всегда. В некоторых случаях можно ограничиться формулами и основными соотношениями — они позволяют легко и быстро искать нужные величины.
Формулы и соотношения
Очень часто необходимо перерыть горы информации для поиска нужной формулы. Это сказывается на оптимизации решения. Кроме того, некоторые соотношения могут содержать ошибки, поскольку материал излагается неквалифицированными специалистами.
Педагоги утверждают, что обучение какой-либо дисциплине с физико-математическим уклоном должно быть основано на алгоритмах. Кроме того, рекомендуется прочитать условие задачи несколько раз до полного его понимания. В основном необходимо находить площадь, диагонали и углы четырехугольника.
Периметр и полупериметр
Периметром выпуклого четырехугольника со сторонами a, b, c и d называется сумма длин всех его сторон. Величина обозначается литерой «Р», и вычисляется по следующей формуле: P = a + b + c +d. Кроме того, в некоторых формулах встречается величина, которая называется полупериметром. Обозначается она литерой «р». Для ее нахождения применяется такое соотношение: p = P / 2 = (a + b + c +d) / 2. Единицей измерения полупериметра являются метрические величины: мм, см, дм, м и т. д.
Для квадрата формула периметра имеет вид: P = 4 * a. Равенство легко доказывается для фигуры со стороной а. Из определения периметра получается соотношение: P = a + a + a + a. Если привести подобные слагаемые, то результирующая формула имеет вид: P = 4 * a. У прямоугольника противоположные стороны равны. Чтобы найти его периметр, нужно воспользоваться равенством: P = a + b + a + b = 2 * (a + b). Необходимо отметить, что квадрат является правильным четырехугольником, поскольку его стороны равны между собой.
Понятие площади
Площадь двумерных фигур — понятие геометрии, которое показывает ее численную характеристику или размер. Очень часто она обозначается литерой S. Измеряется величина в квадратных единицах (см 2 , м 2 и т. д. ). Фигура, имеющая характеристику S, называется квадратируемой.
Для нахождения S применяется интегральный метод, но существуют частные случаи, при которых интегрировать необязательно. Очень часто возникает необходимость перевода одной единицы в другую. Для этого существует простой алгоритм, позволяющий корректно выполнить данную операцию. Например, нужно перевести м 2 в см 2 . Необязательно заучивать единицы площади и их эквивалентность другим. Достаточно выполнить следующие действия:
- Определить базовую единицу: м и см.
- Выполнить перевод одной метрической величины в другую: 1 м = 100 см.
- Возвести обе части выражения во втором пункте в квадрат: 1 м 2 = 100 2 см 2 = 10000 см 2 .
Однако бывают и другие единицы, которые применяются для измерения размерности земельных участков: 1 ар (сокращенно а) = 1 сотке = 100 м 2 и 1 гектар (га) = 10000 м 2 .
Когда известны все стороны четырехугольника (a, b, c и d), который вписан в окружность, можно найти его S. Для этого нужно знать еще одну величину. Она называется полупериметром. Расчет выполняется по формуле: S = [(p — a) * (p — b) * (p — c) * (p — d)]^(½). Соотношение называется формулой Брахмагупты.
Необходимо отметить, что вписанный четырехугольник обладает максимальным значением S среди остальных эквивалентных фигур. Если известны четыре стороны, которые являются последовательными (a, b, c и d), а также угол В между a и b, то можно воспользоваться более упрощенной формулой: S = [(a * b + c * d) * sin (B)] / 2. В случае, когда известны все стороны и любой угол (Y) между диагоналями, соотношение можно записать таким образом: S = [(a * с + и * d) * sin (Y)] / 2.
Площадь можно выразить и другим соотношением, когда известны все стороны и угол А, который не является прямым: S = [(a 2 — b 2 — c 2 + d 2 ) * tg (A)] / 4. При известном радиусе описанной окружности и углах (A, B и Y) можно воспользоваться такой формулой: S = 2 * R^(2) * sin (A) * sin (B) * sin (Y). Следствием из последнего соотношения является S 2 . Если четырехугольник является квадратом, то неравенство преобразуется в равенство, т. е. S = 2 * R 2 .
Диагонали и углы
Для вписанного четырехугольника ABCD существуют определенные соотношения, по которым можно найти его диагонали. Для фигуры со сторонами a = AB, b = BC, c = CD и d = DA диагонали (s = АС и t = DA) находятся таким образом: s = [((a * c + b * d) * (a * d + b * c)) / (a * b + c * d)]^(½) и t = [((a * c + b * d) * (a * b + d * c)) / (a * d + c * b)]^(½). Если умножить диагональ s на t и привести подобные слагаемые, то в результате получится формула Птолемея: s * t = a * c + b * d.
При отношении двух диагоналей получается вторая теорема Птолемея: s / t = (a * d + b * c) / (a * b + d * c). Сумма диагоналей — есть неравенство такого вида: s + t >= 2 * [a * c + b * d]^(½). Неравенство преобразуется в равенство, когда диагонали равны. Однако в этом случае можно воспользоваться следующим выражением: [s + t]^(½) >= [a * c]^(2) + [b * d]^(2).
Необходимо отметить, что в произвольном выпуклом четырехугольнике диагонали делят его на 4 треугольника, которые являются между собой подобными по парам. Кроме того, при пересечении двух диагоналей AC и BD в некоторой точке М, справедливо следующее соотношение: AM / CM = (AB * AD) / (CB * CD).
Можно находить и некоторые углы фигуры. Для этого существуют определенные соотношения. Во вписанном четырехугольнике со сторонами, которые соответствуют значениям a, b, c и d, углом A между сторонами a и d, а также полупериметром p, функции тригонометрического типа для А вычисляются таким образом:
- cos (A) = (a 2 + d 2 — b 2 — c 2 ) / (2 * (a * d + b + c)).
- sin (A) = [(p — a) * (p — b) * (p — c) * (p — d)]^(½) / (a * d + b + c).
- tg (A/2) = [((p — a) * (p — d)) / ((p — b) * (p — c))]^(½).
В некоторых случаях нужно вычислить значение тангенса для угла Y, который находится между диагоналями, по формуле: tg (Y/2) = [((p — b) * (p — d)) / ((p — a) * (p — c))]^(½).
В геометрии существует вписанный четырехугольник, стороны которого являются целыми числами. Кроме того, целочисленными являются также его диагонали и площадь. Он называется четырехугольником Брахмагупты. Однако для преобразования любого четырехугольника в данную фигуру необходимо выполнить некоторые математические операции. Пусть он имеет следующие целочисленные параметры:
- Стороны: a, b, c и d.
- Диагонали: s и t.
- Площадь: S.
- Радиус описанной окружности: R.
В некоторых случаях возникает необходимость избавиться от рациональных значений в знаменателе. При значениях дробных параметров k, l и m нужно использовать такие соотношения:
- a = [k * (l + m) + (1 — (l * m))] * [l + m — k * (1 — (l * m))].
- b = (1 — l 2 ) * (m — k) * (1 + k * m).
- c = k * (1 + l 2 ) * (1 + m 2 ).
- d = (1 + m 2 ) * (l — k) * (1 + k * l).
- s = l * (1 + k 2 ) * (1 + m 2 ).
- t = m * (1 + k 2 ) * (1 + l 2 ).
- S = l * m * [2 * k * (1 — l * m) — (l + m) * (1 — k 2 )] * [2 * k (l + m) + (1 — l * m) * (1 — k 2 )].
- 4 * R = (1 + l 2 ) * (1 + m 2 ) * (1 + k 2 ).
Существуют также соотношения для описанной вокруг четырехугольника окружности. Математики утверждают, что при комбинации двух и более геометрических фигур время поиска некоторых параметров увеличивается.
Параметры для окружности
Радиус окружности R для четырехугольника c полупериметром р и со сторонами a, b, c, d находится по формуле Парамешвары: R = (¼) * [((a * b + c * d) * (a * c + b * d) * (a * d + b * c)) / ((p — a) * (p — b) * (p — c) * (p — d))]^(½). Соотношение было выведено в XV веке математиком из Индии Ватассери Парамешварой.
При комбинации данной формулы с соотношением Брахмагупты можно получить следующее соотношение: 4 * S * R = [(a * b + c * d) * (a * c + b * d) * (a * d + b *c)]^(½). Следует отметить, что величина S является площадью вписанного четырехугольника. Для ортогонального четырехугольника с перпендикулярными диагоналями, которые делятся на отрезки s1, s2, t1 и t2, существует некоторое соотношение, позволяющее найти диаметр окружности (D): D 2 = (s1)^2 + (s2)^2 + (t1)^2 + (t2)^2 = a 2 + c 2 = b 2 + d 2 .
Радиус в этом случае находится таким образом: R = D / 2 = [(s1)^2 + (s2)^2 + (t1)^2 + (t2)^2] / 2 = [a 2 + c 2 ] / 2 = [b 2 + d 2 ] / 2. Если выполнить сложение квадратов сторон, то получится такое равенство: 8 * R = a 2 + b 2 + c 2 + d 2 . По формуле Эйлера R можно также выразить через диагонали (s и t) и расстояние v между их серединами: R = [(s 2 + t 2 + 4 * v 2 ) / 8]^(½).
Таким образом, специалисты рекомендуют на начальных этапах обучения использовать уже готовые формулы для вычисления основных параметров выпуклого четырехугольника, вписанного в окружность.
[spoiler title=”источники:”]
http://liveposts.ru/articles/education-articles/matematika/kak-najti-perimetr-storon-chetyrehugolnika-formula-nahozhdeniya
http://nauka.club/matematika/chetyrekhugolnik-vpisan-v-okruzhnost.html
[/spoiler]
формулы и примеры заданий для второго класса
Совсем недавно в России родители отправляли своих детей в первый класс и с нетерпением ждали их первых заданий. Они с удовольствием наблюдали за тем, как их дети знакомятся с буквами русского алфавита, учатся считать палочки и точечки, выводить различные кривые и прямые линии. Родители помогали знакомиться своим детям с тем, что тетрадь в клеточку предназначена для написания цифр, а тетрадь в линеечку — для письма.
Сегодня, будучи второклассниками, ученики России достигли больших успехов в сфере начального образования, а точнее, в математическом прогрессе. Учителя научили их складывать и вычитать, умножать, делить, измерять.
Кстати, по поводу измерения: с линейкой ребята вторых классов России уже знакомы, и применение ей, кроме как стрелять с задней парты в соседа бумажки, они тоже знают. Именно об измерениях мы и заведем сегодняшний разговор.
Как мы видим, прогресс обучения нынешних учеников проходит слегка в ускоренном режиме.
С теми темами, например, такими как периметр, дети 90-х знакомились позже, а наши ребята узнают сегодня. Конечно, в этом нет ничего страшного. Время меняется, и программа обучения тоже должна не стоять на месте. Зато, как считают многие, наши дети будут умнее нас.
Содержание:
- Школьное задание
Наверное, многих родителей сегодня удивляют нынешние задания для второклассников. В учебнике по математике для второго класса можно встретить такое задание, как, например: «Найди периметр четырехугольника, две стороны которого равны по 2 сантиметра, а другие две будут по 3 сантиметра». Как справиться с данным заданием?
Многие родители настоящего времени являются теми самыми детьми девяностых годов, и, естественно, в большинстве случаев, мало кто помнит, что такое периметр. Особенно, если учились не на отлично, да и не совсем на «хорошо».
Естественно, каждому родителю хотелось бы, чтоб его ребенку было проще в обучении, и они всеми силами стараются ему в этом помочь.
Некоторым родителям сначала приходится справиться со своей душевной паникой, а уже потом продолжать объяснять своему ребенку. В этом случае многим помогает интернет, место, где можно найти ответы на все тревожные вопросы. Во времена девяностых, к сожалению, такой «роскоши» не было.
Вопросы:
- Что такое «периметр»?
- Как находить периметр четырехугольника?
Ответы на вопросы:
Для тех, кто знает, вспоминаем, а кто не знает — объясняем:
- Периметр — это сумма всех сторон четырехугольника. Всего лишь каждая грань по отдельности будет равна после сложения единому числу.
- Найти периметр, значит, что нужно взять линейку и измерить каждую границу четырехугольника. После выполнения данного действия необходимо сложить полученные числа между собой. Общая полученная сумма и будет являться периметром.
Решение:
В данном случае, по действиям нашей задачи, нам известны суммы сторон четырехугольника, а именно две из них по 2 сантиметра и две по 3 сантиметра.
2+2+3+3=10
Как мы видим, периметр нашей четырехугольной фигуры равен 10.
В математике сумму всех сторон (периметр) мы обозначаем символом Р.
Теперь записываем правильное решение этой задачи:
Р=2+2+3+3;
Ответ: Р=10.
В математике существует формула, запомнив которую, вы никогда не будете забывать, как найти периметр (общую сумму всех сторон) четырехугольника и выглядит она так:
P = a + b + c + d
(где a , b, c, d являются границами четырехугольника).
Кроме того, хотелось бы обратить внимание, что четырехугольник не обязательно будет являться прямоугольником. Это может быть и квадрат, у которого все стороны равны, и любая другая геометрическая фигура, у которой есть четыре стороны и такое же количество углов.
Грани произвольного четырехугольника могут совсем не совпадать ни с одной из сторон фигуры. Это могут быть совершенно разные числа. И, в итоге, получаются фигуры с четырьмя сторонами и теми же четырьмя углами. Фигура не будет похожа ни на квадрат, ни на прямоугольник, так как углы ее прямыми не будут. И периметр, соответственно мы вычисляем по той же самой единой формуле.
Или взять, например трапецию. Обычно у трапеции две стороны одинаковые, а другие две совсем не совпадают, но между собой параллельные.
На примере трапеция может выглядеть так: верхняя грань равна 2 сантиметра, левая и правая стороны по 3 сантиметра, соединяем их с нижней гранью и получаем трапецию. Высчитываем каждую ее сторону и снова получаем периметр четырехугольника.
Вычислить по формуле всегда будет проще, и не важно, каким числам равна каждая сторона.
Так как современные дети страны уже дошли до таблицы умножения, с периметром квадрата у них проблем не будет. Зная размер одной стороны квадрата, нужно умножить ее на все четыре равные стороны.
В общем, теперь стоит взять линейку с карандашом и лист бумаги. После этого следует начертить произвольные фигуры с четырьмя углами и высчитать общую сумму ее сторон.
Как найти периметр? — Занимательная математика — Математика
- 27 ноября 2020 года
- Теги: квадрат, треугольник, периметр, прямоугольник
Комментариев: 0
Периметр — это расстояние вокруг фигуры.
В реальной жизни периметр — это забор вокруг двора или рамка вокруг картины. Периметр образует двухмерную форму.
Как найти периметр четырехугольника
Чтобы найти периметр четырехугольника, сложите размеры четырех сторон фигуры. Формула: a+b+c+d=P
Четырехугольник — это многоугольник, имеющий четыре стороны и четыре угла. Наиболее распространенные типы четырехугольников — квадрат, прямоугольник, ромб, трапеция и параллелограмм.
Как найти периметр квадрата и ромба
У квадрата и ромба по четыре равные стороны, но у квадрата четыре прямых угла.
Как найти периметр прямоугольника и параллелограмма
Формулы для периметра прямоугольника и параллелограмма одинаковы, потому что каждый многоугольник имеет два набора равных сторон. Формула 2*(a + b) = P, где a обозначает длину, а b обозначает ширину. Рассмотрим прямоугольник длиной 2 сантиметра и шириной 4 сантиметра. Сумма длины и ширины равна 6. Умножьте 6 на 2, и вы получите периметр в 12 сантиметров.
Как найти периметр трапеции
Формула для трапеции немного отличается, потому что трапеция — это четырехугольник, у которого есть две параллельные стороны неравной длины. Две стороны имеют одинаковую длину. Две другие стороны имеют равную длину друг друга, но длина этих двух сторон отличается от длины двух других сторон.
Как найти периметр неправильного четырехугольника
Формула неправильного четырехугольника — многоугольника с четырьмя сторонами разной длины — такая же, как у трапеции. Формула: a + b + c + d = P. Например, предположим, что четырехугольник имеет стороны длиной 1, 5, 3 и 4 см. Периметр равен 1 + 5 + 3 + 4 или 13 см.
Использование координат для определения длины стороны
Если вам известны только координаты фигуры, найдите размеры сторон, определив расстояние между точками. Например, найдите расстояние между точками A и B для одной стороны и расстояние между точками B и C для другой стороны. Затем подставьте боковые размеры в соответствующую формулу, чтобы определить периметр.
Периметр четырехугольника – определение, формула и примеры
Периметр четырехугольника – это общая длина его границы. Четырехугольник — это четырехугольник, который может быть правильным или неправильным. В правильном четырехугольнике все стороны равны по длине и все углы равны, тогда как в неправильном четырехугольнике стороны и углы не равны. Существует 6 конкретных типов четырехугольников — квадрат, прямоугольник, параллелограмм, ромб, воздушный змей и трапеция. Давайте узнаем, как найти периметр четырехугольника на этой странице.
| 1. | Что такое периметр четырехугольника? |
| 2. | Периметр четырехугольника Формула |
| 3. | Формулы периметра четырехугольников различных типов |
| 4. | Периметр четырехугольника с вписанной окружностью |
| 5. | Часто задаваемые вопросы о периметре четырехугольника |
Что такое периметр четырехугольника?
Периметр четырехугольника — это длина его границы, т.
Периметр четырехугольника Формула
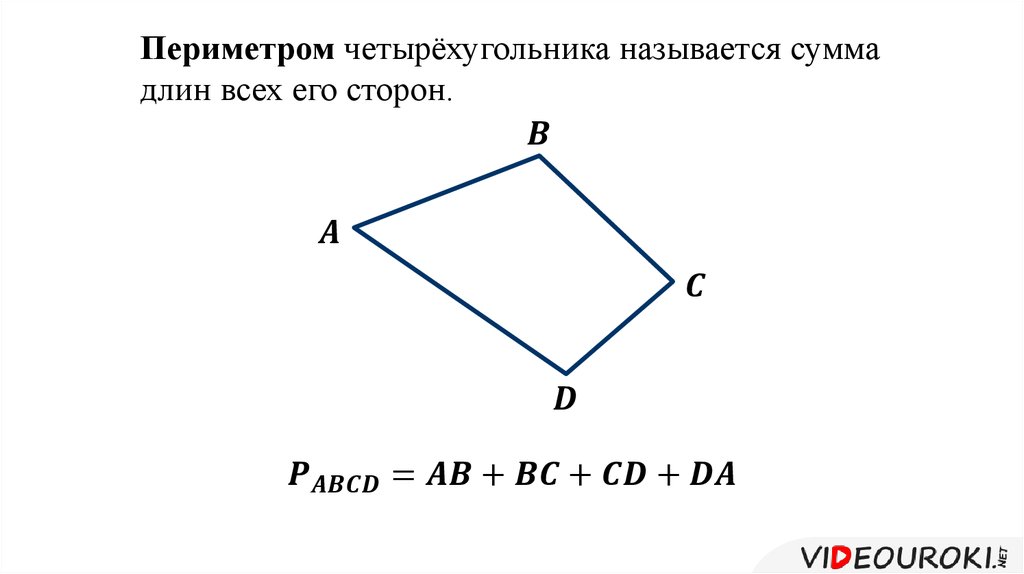
Мы знаем, что периметр четырехугольника можно получить, сложив длины всех его сторон. Это можно выразить простой формулой. Например, формула для периметра четырехугольника ABCD может быть выражена как
Периметр = AB + BC + CD + DA
Формулы периметра четырехугольников различных типов
Мы уже видели, что существует 6 конкретных типов четырехугольников: квадрат, прямоугольник, параллелограмм, ромб, воздушный змей и трапеция. Хотя периметр четырехугольника представляет собой сумму всех его сторон, иногда не все длины сторон могут быть заданы. В таких случаях нам нужно вспомнить свойства четырехугольников относительно сторон, чтобы получить длины сторон, которые не даны.
Периметр четырехугольника с вписанной окружностью
Иногда внутри четырехугольника находится окружность. Это называется описанным четырехугольником или четырехугольником с вписанной окружностью. В таких случаях мы используем свойство касательной окружности, которое гласит: «любые две касательные, проведенные к окружности из точки, имеют одинаковую длину». Мы увидим, как найти периметр описанного четырехугольника (или) периметр четырехугольника с окружностью внутри него на приведенном ниже примере.
Пример: Найдите периметр следующего четырехугольника.
Решение:
Используя свойство касательных «Любые две касательные, проведенные к окружности из точки, имеют одинаковую длину», найдем периметр четырехугольника с вписанной окружностью.
PT = PU = 5 дюймов
QV = QU = 2 дюйма
RW = RV = 3 дюйма
ST = SW = 4 дюйма
Теперь периметр четырехугольника равен
PQ + QR + RS + SP
= (PU + UQ) + (QV + VR) + (RW + WS) + (ST + TP)
= (5 + 2) + (2 + 3) + (3 + 4) + (4 + 5)
= 28 дюймов
Следовательно, периметр данного четырехугольника = 28 дюймов.
Примечание: Мы можем использовать то же свойство касательных окружности «две касательные, проведенные к окружности из точки, имеют одинаковую длину», чтобы найти периметр вписанного в окружность четырехугольника (четырехугольник, вписанный в окружность) также.
Решенные примеры на периметре четырехугольника
-
Пример 1: Найдите периметр воздушного змея, смежные стороны которого равны 7 единицам и 13 единицам.
Решение:
Мы знаем, что у воздушного змея две пары равных смежных сторон. Итак, используя формулу периметра четырехугольника, мы сложим стороны воздушного змея. Стороны данного воздушного змея составляют 7 единиц, 7 единиц, 13 единиц и 13 единиц.
Таким образом, периметр данного воздушного змея равен
7 + 7 + 13 + 13 = 40 единиц.
Ответ: Периметр данного воздушного змея = 40 единиц.
-
Пример 2: Найдите периметр трапеции, стороны которой равны 4, 6, 7 и 9 единицам.
Решение:
Мы знаем, что периметр четырехугольника можно получить, сложив все его стороны. В случае трапеции периметр можно рассчитать по формуле P = a + b + c + d.
Подставляя значения в формулу, Периметр трапеции = 4 + 6 + 7 + 9 = 26 единиц.
Ответ: Периметр данной трапеции равен 26 единицам.
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила.
Записаться на бесплатный пробный урок
Практические вопросы по периметру четырехугольника
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о периметре четырехугольника
Что означает периметр четырехугольника?
Периметр четырехугольника равен общей длине его границы. Например, периметр четырехугольника ABCD можно выразить как Периметр = AB + BC + CD + DA. Это означает, что если известны все стороны четырехугольника, мы можем получить его периметр, сложив все его стороны.
Какая формула периметра четырехугольника?
Основная формула, которая используется для нахождения периметра четырехугольника: Периметр = a + b + c + d, где a, b, c и d — четыре стороны четырехугольника. Хотя эта формула используется для всех четырехугольников, для некоторых четырехугольников, таких как квадрат и прямоугольник, эту формулу можно упростить, потому что в квадрате все стороны равны, поэтому формула периметра принимает вид a + a + a + a = 4a.
Как найти периметр четырехугольника с отсутствующей стороной?
Недостающую сторону четырехугольника можно найти, используя свойства четырехугольников. Как только все недостающие стороны найдены, мы можем найти периметр четырехугольника, сложив все длины сторон. Например, если мы знаем одну сторону квадрата, мы можем найти остальные 3 стороны, потому что мы знаем, что все стороны квадрата равны. После этого можем найти периметр.
Как найти периметр четырехугольника с вписанной окружностью?
Когда четырехугольник имеет вписанную окружность, стороны четырехугольника становятся касательными к окружности. Следовательно, свойство касательных можно использовать для нахождения периметра данного четырехугольника. Свойство касательной гласит: «Любые две касательные, проведенные из точки в некоторые точки окружности, всегда имеют одинаковую длину».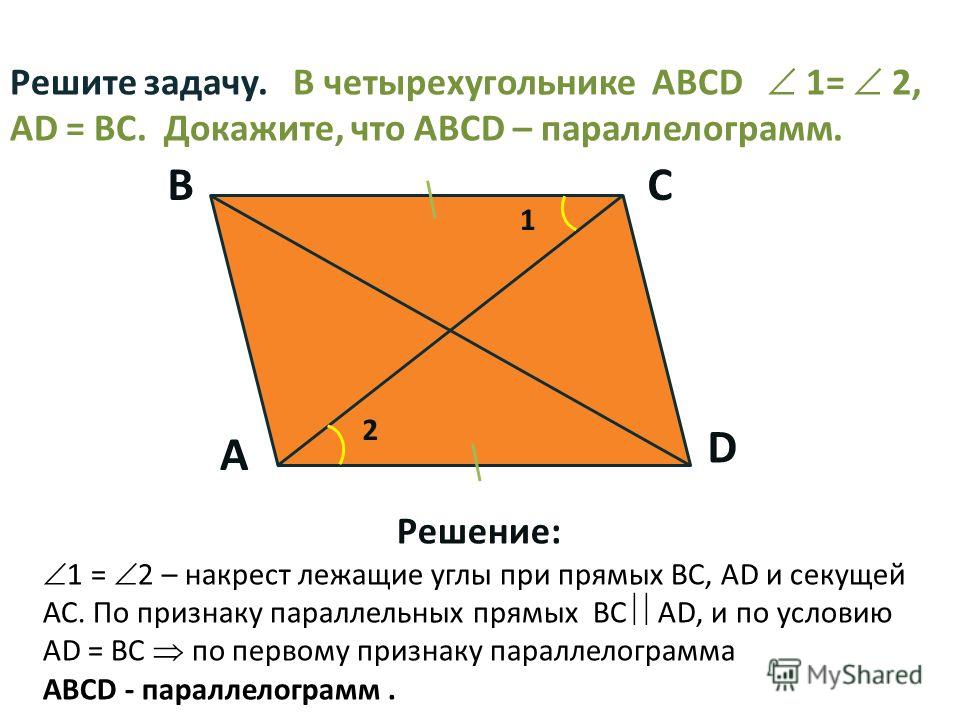
Как найти периметр четырехугольника с координатами?
Когда известны координаты вершин четырехугольника, мы сначала находим длины его сторон, используя формулу расстояния. Затем мы складываем все четыре стороны, чтобы найти его периметр.
Как найти периметр четырехугольника на графике?
Чтобы найти периметр четырехугольника на графике, мы используем следующие шаги.
- Шаг 1: Найдите координаты вершин на графике.
- Шаг 2: Примените формулу расстояния, чтобы найти длины сторон четырехугольника.
- Шаг 3: Сложите все длины сторон, и сумма даст периметр четырехугольника.
Как найти периметр четырехугольника, вписанного в окружность?
Когда четырехугольник вписан в окружность, он называется вписанным четырехугольником.
Как вычислить периметр четырехугольника
Обновлено 13 марта 2018 г.
Автор: Tabitha Burgtorf
Чтобы вычислить периметр четырехугольника, сложите измерения четырех сторон. Периметр — это расстояние вокруг фигуры. В реальных приложениях периметром является забор вокруг двора или рамка вокруг картины. Периметр простирается по всему периметру двумерной формы. Четырехугольник — это многоугольник , имеющий четыре стороны и четыре угла. К наиболее распространенным типам четырехугольников относятся квадрат, прямоугольник, ромб, трапеция и параллелограмм.
Периметр квадрата и ромба
У квадрата и ромба по четыре равные стороны, а у квадрата четыре прямых угла.
Периметр прямоугольника и параллелограмма
Формулы для периметра прямоугольника и параллелограмма одинаковы, потому что каждый многоугольник имеет два набора равных сторон. Формула: 2 (l + w) = периметр, , где l представляет длину, а w представляет ширину. Рассмотрим прямоугольник, длина которого 2 дюйма, а ширина 4 дюйма. Сумма длины и ширины равна 6. Умножьте 6 на 2, и вы получите периметр 12 дюймов.
Периметр трапеции
Формула для трапеции немного отличается, потому что трапеция — это четырехугольник, у которого две параллельные стороны неравной длины.
Формула a + b + c + d = периметр. Каждая буква соответствует разной стороне или основанию фигуры. Например, предположим, что размеры ребер трапеции равны 2, 3, 2 и 5 дюймам. Периметр равен 2 + 3 + 2 + 5, что равно 12 дюймам.
Периметр неправильного четырехугольника
Формула неправильного четырехугольника — многоугольника с четырьмя сторонами разной длины — такая же, как и у трапеции. Формула a + b + c+ d = периметр. Например, предположим, что четырехугольник имеет длины сторон 1, 5, 3 и 4 дюйма. Периметр равен 1 + 5 + 3 + 4 или 13 дюймов.
Использование координат для определения длины стороны
Если вы знаете только координаты фигуры, найдите размеры сторон, найдя расстояние между точками.
Четырехугольник не является прямоугольником.
Периметр искать легко в отличие от площади. В периметре сложить величины всех сторон четырехугольника можно за несколько секунд, потому что стороны редко бывают больше 10 сантиметров, значит все подсчеты производим в уме.
Это четырехугольник.
Это формула периметра, обозначается буквой Р.
автор вопроса выбрал этот ответ лучшим
Tanyetta
[298K]
9 лет назад
Вспоминая уроки геометрии. Найти периметр четырехугольника очень просто! Для этого надо сложить длину всех его сторон. А если четырехугольник прямоугольный, то короткая сторона плюс длинная сторона умножить на 2! Удачных решений примеров и задач!
Носорог
[63.1K]
9 лет назад
Четырехугольник не всегда является прямоугольником или квадратом, все верно было сказано. И в то же время квадрат и прямоугольник можно назвать четырехугольниками. Четырехугольник может иметь как одинаковую длину сторон, так и разную. Ну а что такое периметр, периметр плоской фигуры (а в данном случае четырехугольник как раз плоская двухмерная фигура) – это сумма сторон. Так что чтобы узнать, вычислить периметр, необходимо знать длину каждой из сторон, а затем складываем длины и получаем конечную сумму.
У квадрата измеряем одну сторону и умножаем на 4. У квадрата же все стороны равны по длине. Это известно еще со школы с уроков геометрии.
Четырехугольник-это геометрическая фигура с четырьмя углами и с четырьмя сторонами. Так что найти периметр легко. Нужно измерить длину всех сторон и сложить их длины. И данный ответ и будит являться периметром.
ИнгаМус
[16.7K]
9 лет назад
Четырехугольник имеет четыре стороны, как мы видим уже из названия. Еще со школьных времен прочно запомнилась формула нахождения периметра четырехугольника.
Если он не является прямоугольником, то нам надо будет знать длину его каждой стороны по отдельности. Сложив их все вместе, мы и узнаем периметр этой фигуры.
Если кому – то потребуется вот здесь есть калькулятор расчета периметра четырехугольника.
elena-kh
[245K]
9 лет назад
Чтобы найти периметр, нужно сложить длины всех сторон. Если бы являлся прямоугольником, было бы проще, ведь можно было каждую длину умножить на 2, а потом сложить. У квадрата все еще проще – нужно длину одной стороны умножить на 4. У остальных прямоугольников, как правило, необходимо просто сложить все стороны. Хотя для параллелограммов тоже есть свои формулы.
Афанасий44
[443K]
9 лет назад
Четырёхугольник может быть неправильной формы и все стороны его могут иметь разную длину. Например, такие четырёхугольники:
В таких случаях, чтобы найти периметр неправильного четырёхугольника, надо просто измерить длину каждой его стороны и потом всё сложить.
Для того чтобы вам найти периметр четырёхугольника вам нужно вспомнить уроки геометрии в школе которые раньше для меня были очень интересными, так вот что надо сделать, надо сложить все длины четырёх сторон и у вас получится периметр.
Edvard
[10.5K]
9 лет назад
Найти периметр четырехугольника не представляет из себя ничего сложного. Надо всего лишь найти сумму длин всех четырех сторон четырехугольника. Этот нехитрый способ известен нам еще со школьной скамьи.
Безразличный
[257K]
10 лет назад
Сложите длины всех четырех сторон и получите периметр.
Агафья
[118K]
8 лет назад
Вообще просто для этого достаточно перемерить все стороны прямоугольника и их величины сложить вместе. Вот эта сумма и будет являться периметром неправильного четырёхугольника. Меня этому ещё в школе научили.
Знаете ответ?

Помогите,периметр правильного четырех угольника вписанного в окружность равен 16 см найдите периметр и площаь треугольника вписаного в ту окружность

Правильный четырехугольник, вписанный в окружность, – это квадрат.Его сторона а = 16/4 = 4.
Радиус окружности, в которую вписан этот квадрат, равен R = а/√2 = = а√2/2 = 4√2/2 = 2√2.
Сторона треугольника.вписанного в эту окружность, равна R√3 = 2√2*√3 = 2√6.
Площадь такого треугольника равна S = a²√3/4 = 24√3/4 = 6√3 кв.ед.

Если вы не нашли ответа на свой вопрос, или сомневаетесь в его правильности, то можете воспользоваться формой ниже и уточнить решение. Или воспользуйтесь формой поиска и найдите похожие ответы по предмету Геометрия.
6
Пожалуйста. объясните как решить эту задачу. Найдите наименьший возможный периметр четырехугольника, вписанного в единичный квад
Пожалуйста. объясните как решить эту задачу.
Найдите наименьший возможный периметр четырехугольника, вписанного в единичный квадрат так, что на каждой стороне квадрата находится по одной вершине четырехугольника, причем одна из вершин делит соответствующую сторону квадрата в отношении 3 : 2.
Ответ 2*корень из 2
1 ответ:
0
0
Заберу я эти баллы уж больно задача понравилась!
оптика! представь что внутри квадрата зеркало. и построй отражения одной заданной точки – сначала на боковых сторонах квадрата в обе стороны. потом одного из изображений от зеркала на противоположной стороне квадрата и соедини с другим первым отражением. Свет идет по кратчайшему расстоянию – минимальному периметру.
самое главное – ответ не зависит от начального положения первой точки!
Читайте также
По формуле Герона находим площадь тр-ка АВС: S=√p(p-a)(p-b)(p-c), где р – полупериметр, а a,b,c – стороны тр-ка. Имеем:S= √21*8*7*6 = √7056 = 84см².
Площадь равна произведению половины омнования на высоту, то есть расстояние АН (перпендикуляр) от точки А до стороны ВС равно: 84:7 = 12см.
Тогда <span>расстояние от точки D до стороны ВС</span> по Пифагору равно √(АD²+АН²) =
√169 = 13см.
В треугольниках <span>ADB </span><span>и </span><span>DBC </span><span>углы </span><span>ADB </span><span>и </span><span>DBC </span><span>равны как накрест лежащие, кроме того, </span><span> Поэтому указанные треугольники подобны по двум пропорциональным сторонам и углу между ними.</span>
В задаче явно опечатка..Угол С и Угол ВСD-Это один и тот же угол,так что либо вы не правильно посмотрели,либо Опечатка от автора
А)3х*5х^2=15х^3
б)3аb*9a*6a^2b=162a^4b^2
сечением будет круг, часть, заключенная между конусом и шаром—кольцо
радиус меньшей окружности r—средняя линия треугольника, являющегося осевым сечением конуса, равен R/2
радиус большей окружности(G)—половина хорды окружности, являющейся сечением шара, проходящим через центр,—катет прямоугольного треугольника, в кот. гипотенуза R и второй катет R/2
G^2 = R^2 – R^2/4 = 3R^2/4
Sкольца = Sкруга_радиуса_G – Sкруга_радиуса_r = п * 3R^2/4 – п * R^2/4 = пR^2/2