Как найти периметр фигуры с одинаковыми сторонами

Как найти периметр фигуры с одинаковыми сторонами

Нахождение периметра треугольника: формула и задачи

В данной публикации мы рассмотрим, каким образом можно посчитать периметр треугольника и разберем примеры решения задач.

Формула вычисления периметра

Периметр (P) любого треугольника равняется сумме длин всех его сторон.

P = a + b + c

Периметр равнобедренного треугольника

Равнобедренным называют треугольник, у которого две боковые стороны равны (примем их за b). Сторона a, имеющая отличную от боковых длину, является основанием. Таким образом, периметр можно считать так:

P = a + 2b

Периметр равностороннего треугольника

Равносторонним или правильным называется треугольник, у которого все стороны равны (примем ее за a). Периметр такой фигуры вычисляется так:

P = 3a

Примеры задач

Задание 1
Найдите периметр треугольника, если его стороны равны: 3, 4 и 5 см.

Решение:
Подставляем в формулу известные по условиям задачи величины и получаем:
P = 3 см + 4 см + 5 см = 12 см.

Задание 2
Найдите периметр равнобедренного треугольника, если его основание равняется 10 см, а боковая сторона- 8 см.

Решение:
Как мы знаем, боковые стороны равнобедренного треугольника равны, следовательно:
P = 10 см + 2 ⋅ 8 см = 26 см.

Как найти периметр треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

P = √ b 2 + с 2 – 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.

Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

P = √ c 2 – a 2 + (a + c), где a — любой катет, c — гипотенуза.

Гипотенуза — сторона, которая лежит напротив прямого угла.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Как найти периметр треугольника если известны не все стороны

Периметр — это величина, подразумевающая длину всех сторон плоской (двумерной) геометрической фигуры. Для разных геометрических фигур существуют разные способы нахождения периметра.

В данной статье вы узнаете как находить периметр фигуры разными способами, в зависимости от известных его граней.

Возможные методы:

  • известны все три стороны равнобедренного или любого другого треугольника;
  • как найти периметр прямоугольного треугольника при двух известных его гранях;
  • известны две грани и угол, который расположен между ними (формула косинусов) без средней линии и высоты.

Это интересно: что микроэкономика изучает, кратко об основателях и основах науки.

Первый метод: известны все стороны фигуры

Как находить периметра треугольника, когда известны все три грани, необходимо использовать следующую формулу: P = a + b + c, где a,b,c — известные длины всех сторон треугольника, P — периметр фигуры.

Например, известны три стороны фигуры: a = 24 см, b = 24 см, c = 24 см. Это правильная равнобедренная фигура, чтобы вычислить периметр пользуемся формулой: P = 24 + 24 + 24 = 72 см.

Данная формула подходит к любому треугольнику, необходимо просто знать длины всех его сторон. Если хотя бы одна из них неизвестна, необходимо воспользоваться другими способами, о которых мы поговорим ниже.

Еще один пример: a = 15 см, б = 13 см, c = 17 см. Вычисляем периметр: P = 15 + 13 + 17 = 45 см.

Очень важно помечать единицу измерения в полученном ответе. В наших примерах длины сторон указаны в сантиметрах (см), однако, существуют разные задачи, в условиях которых присутствуют другие единицы измерения.

Второй метод: прямоугольный треугольник и две известные его стороны

В том случае, когда в задании, которое нужно решить, дана прямоугольная фигура, длины двух граней которой известны, а третья нет, необходимо воспользоваться теоремой Пифагора.

Теорема Пифагора описывает соотношение между гранями прямоугольного треугольника. Формула, описываемая этой теоремой, является одной из самых известных и наиболее часто применяемых теорем в геометрии. Итак, сама теорема:

Стороны любого прямоугольного треугольника описываются таким уравнением: a^2 + b^2 = c^2, где а и b — катеты фигуры, а c — гипотенуза.

  • Гипотенуза. Она всегда расположена противоположно прямому углу (90 градусов), а также является самой длинной гранью треугольника. В математике принято обозначать гипотенузу буквой c.
  • Катеты — это грани прямоугольного треугольника, которые относятся к прямому углу и обозначаются буквами а и b. Один из катетов одновременно является и высотой фигуры.

Таким образом, если условиями задачи заданы длины двух из трех граней такой геометрической фигуры, с помощью теоремы Пифагора необходима найти размерность третьей грани, после чего воспользоваться формулой из первого метода.

Например, мы знаем длину 2-х катетов: a = 3 см, b = 5 см. Подставляем значения в теорему: 3^2 + 4^2 = c^2 => 9 + 16 = c^2 => 25 = c^2 => c = 5 см. Итак, гипотенуза такого треугольника равна 5 см. К слову, данный пример является самым распространенным и называется «Египетский треугольник». Иными словами, если два катета фигуры равны 3 см и 4 см, то гипотенуза составит 5 см соответственно.

Если неизвестна длина одного из катетов, необходимо преобразовать формулу следующим образом: c^2 — a^2 = b^2. И наоборот для другого катета.

Продолжим пример. Теперь необходимо обратиться к стандартной формуле поиска периметра фигуры: P = a + b + c. В нашем случае: P = 3 + 4 + 5 = 12 см.

Третий метод: по двум граням и углу между ними

В старшей школе, а также университете, чаще всего приходится обращаться именно к данному способу нахождения периметра. Если условиями задачи заданы длины двух сторон, а также размерность угла между ними, то необходимо воспользоваться теоремой косинусов.

Данная теорема применима абсолютно к любому треугольнику, что и делает ее одной из наиболее полезных в геометрии. Сама теорема выглядит следующим образом: c^2 = a^2 + b^2 — (2 * a * b * cos(C)), где a,b,c — стандартно длины граней, а A,B и С — это углы, которые лежат напротив соответствующих граней треугольника. То есть, A — угол, противолежащий стороне a и так далее.

Представим, что описан треугольник, стороны а и б которого составляют 100 см и 120 см соответственно, а угол, лежащий между ними, составляет 97 градусов. То есть а = 100 см, б = 120 см, C = 97 градусов.

Все, что нужно сделать в данном случае — это подставить все известные значения в теорему косинусов. Длины известных граней возводятся в квадрат, после чего известные стороны перемножаются между друг другом и на два и умножаются на косинус угла между ними. Далее, необходимо сложить квадраты граней и отнять от них второе полученное значение. Из итоговой величины извлекается квадратный корень — это будет третья, неизвестная до этого сторона.

После того как все три грани фигуры известны, осталось воспользоваться уже полюбившейся нам стандартной формулой поиска периметра описываемой фигуры из первого метода.

[spoiler title=”источники:”]

http://skysmart.ru/articles/mathematic/perimetr-treugolnika

Как найти периметр треугольника если известны не все стороны

[/spoiler]

Источник

Содержание:

  • Определения
  • Формулы периметра основных геометрических фигур

Определения

Определение

Периметр – общая длина границы фигуры, которая чаще всего находится на плоскости.

Периметр имеет ту же размерность величин, что и длина. Иногда периметром называют границу геометрической фигуры.
Чаще всего этот термин применяется к треугольнику и многоугольникам и в этом случае означает сумму длин всех сторон фигуры.
То есть периметр – это сумма длин сторон какой-либо геометрической фигуры.

Определение

Полупериметр – половина периметра. Употребляется в основном в геометрии треугольника.

Формулы периметра основных геометрических фигур

Периметр треугольника

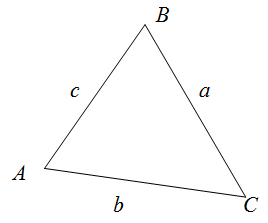
Чтобы найти периметр треугольника $ABC$,
необходимо сложить длины всех его сторон.

$$P_{Delta A B C}=a+b+c$$

Читать дальше: формула периметра треугольника и примеры решений →

Периметр круга

Чтобы найти периметр круга, необходимо вычислить длину окружности, которая его ограничивает.

Для нахождения длины окружности можно использовать одну из формул

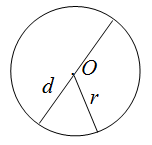
Читать дальше: формула периметра круга и примеры решений →

Периметр квадрата

Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.

$$P_{Delta A B C D}=a+a+a+a=4 a$$

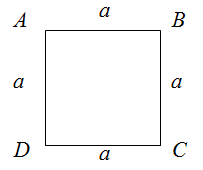
Читать дальше: формула периметра квадрата и примеры решений →

Периметр прямоугольника

Чтобы найти периметр прямоугольника, нужно сумму его ширины и длины умножить на два.

$$P_{Delta A B C D}=a+b+a+b=2 a+2 b=2(a+b)$$

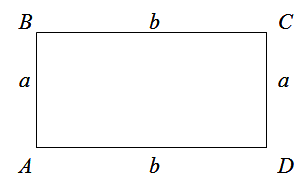
Читать дальше: формула периметра прямоугольника и примеры решений →

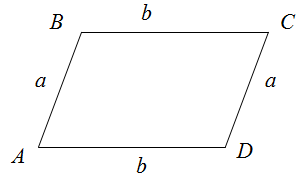
Периметр параллелограмма

Чтобы найти периметр параллелограмма, нужно сумму двух непараллельных сторон умножить на два.

$$P_{Delta A B C D}=a+b+a+b=2 a+2 b=2(a+b)$$

Читать дальше: формула периметра параллелограмма и примеры решений →

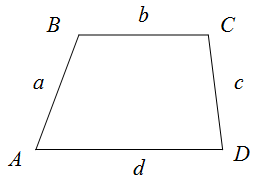
Периметр трапеции

Чтобы найти периметр трапеции необходимо найти сумму длин её сторон.

$$P_{Delta A B C D}=a+b+c+d$$

Читать дальше: формула периметра трапеции и примеры решений →

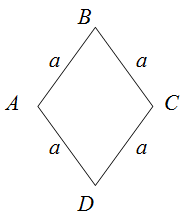
Периметр ромба

Чтобы найти периметр ромба, необходимо длину его стороны умножить на четыре.

$$P_{Delta A B C D}=a+a+a+a=4 a$$

Читать дальше: формула периметра ромба и примеры решений →

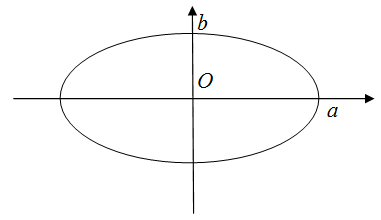
Периметр эллипса

Чтобы найти периметр эллипса
$frac{x^{2}}{a^{2}}+frac{y^{2}}{b^{2}}=1$, нужно воспользоваться формулой

$$P=4 cdot frac{pi a b+(a-b)}{a+b}$$

Читать дальше: формула периметра эллипса и примеры решений →

  • Как найти периметр треугольника
  • Как найти периметр трапеции
  • Как найти периметр ромба
  • Как найти периметр эллипса
  • Как найти периметр многоугольника
  • Как найти периметр прямоугольного треугольника
  • Как найти периметр равнобедренного треугольника
  • Как найти периметр равностороннего треугольника
  • Как найти периметр круга
  • Как найти длину окружности
  • Как найти периметр квадрата
  • Как найти периметр прямоугольника
  • Как найти периметр параллелограмма
Источник


Download Article


Download Article

A polygon is any two-dimensional shape that has straight lines. There are both regular polygons, which are shapes with equal sides, and irregular polygons, which are shapes with different side lengths. The methods for finding the perimeter of regular and irregular polygons are a little different, but both are simple once you know what to do. You can also find the perimeter of them on a coordinate grid. If you’re trying to find the perimeter of a regular polygon, just use the formula: perimeter = number of sides x the length of any side.

  1. Image titled Find the Perimeter of a Polygon Step 1

    1

    Check that the sides of the polygon are all the same length. Regular polygons are polygons that have equal sides. If the sides of the polygon you’re looking at aren’t all the same length, you’ll need to find the perimeter using the method for irregular polygons instead. If the side lengths are equal, you’re working with a regular polygon.[1]

    Tip: If some of the sides aren’t labeled, try looking at the rest of the polygon to determine what the lengths are. For example, if you have a square with only 1 labeled side, you know the other sides are the same length since squares have equal sides.

  2. Image titled Find the Perimeter of a Polygon Step 2

    2

    Write down the length of 1 side of the polygon. It doesn’t matter which side you choose since all of the side lengths are equal. Just make sure you’re only writing down the length of 1 side.[2]

    • For example, if you’re working with a square that has a side length of 6, you would write down “6.”

    Advertisement

  3. Image titled Find the Perimeter of a Polygon Step 3

    3

    Write down the total number of sides that the polygon has. Don’t worry about the side lengths at this point. Just count how many sides the polygon has and write it down.[3]

    • For a square, you’d write down “4” since a square has 4 sides.

  4. Image titled Find the Perimeter of a Polygon Step 4

    4

    Multiply the side length by the number of sides to get the perimeter. The formula for finding the perimeter of a regular polygon is just the number of sides x the length of any side. Once you’ve multiplied those 2 numbers together, you’ve found the perimeter of the polygon![4]

    • In the square example, you know that the square has a side length of 6 and a total of 4 sides. Therefore, you’d just multiply 6 by 4 to get 24, which would be the perimeter of the square.
    • Or, say you were working with a triangle that has a side length of 3. Since a triangle has 3 sides, you would multiply 3 (the number of sides) by 3 (the side length) to get 9. Therefore, the perimeter of the triangle would be 9.

    5. Advertisement

  1. Image titled Find the Perimeter of a Polygon Step 5

    1

    Look at the length of the polygon’s sides to determine if it’s irregular. An irregular polygon is a polygon that doesn’t have equal sides. If the sides of the polygon are all the same length, that means the polygon is regular, not irregular.[5]

    Did you know? You can use the same method for finding the perimeter of an irregular polygon to find the perimeter of a regular polygon, but not the other way around.

  2. Image titled Find the Perimeter of a Polygon Step 6

    2

    Write down the length of each side of the polygon. Since not all sides of an irregular polygon are equal, you’ll need to write out each individual side length. Even if some of the sides are equal, you should still write each length out individually.[6]

    • For example, if you’re working with a rectangle that has 2 sides that are 4 units long and 2 sides that are 3 units long, you would write “4, 4, 3, 3.”
    • If you’re working with an irregular polygon that has 1 side that’s 2 units, 1 side that’s 3 units, and 1 side that’s 4 units, you would write “2, 3, 4.”

  3. Image titled Find the Perimeter of a Polygon Step 7

    3

    Add up all of the lengths to find the perimeter. To find the perimeter of an irregular polygon, all you need to do is find the total of all of its side lengths. Simply add up each side length that you wrote down to find the perimeter of the polygon![7]

    • For example, if the side lengths for the polygon were 4, 4, 3, and 3, they would add up to 14. Therefore, 14 would be the perimeter of the polygon.

    4. Advertisement

  1. Image titled Find the Perimeter of a Polygon Step 8

    1

    Draw a coordinate grid with an x- and y-axis. A coordinate grid is a graph with an x- and y-axis that you can plot coordinates on. To draw a coordinate grid, get a piece of graph paper or draw your own grid lines on a blank piece of paper using a ruler. Then, draw a horizontal line through the middle for the x-axis and a vertical line down the center for the y-axis. Finally, number the points on each axis, starting with “0” where the x- and y-axis intersect.[8]

    • When you number your grid, the numbers above and to the right of the 0 will be positive, while the numbers below and to the left of the 0 will be negative.

  2. Image titled Find the Perimeter of a Polygon Step 9

    2

    Plot the given coordinates on the graph. You should have been given coordinates for each vertex, or angular point, of the polygon you’re trying to find the perimeter of. Each coordinate should look something like “(1,2).” Use the numbers you marked on the coordinate grid to plot each of the coordinates. When you’re finished, connect the points with straight lines to see the shape of the polygon you’re working with.[9]

    Tip: When plotting coordinates, remember that the first number represents the x-axis and the second number represents the y-axis. For example, if you were plotting (2,4), you would count 2 over on the x-axis and 4 up on the y-axis and then mark where those 2 points meet on the grid.

  3. Image titled Find the Perimeter of a Polygon Step 10

    3

    Find vertical and horizontal side lengths by counting the units. You’ll need to know the length of each side of the polygon to determine its perimeter. For vertical or horizontal sides, simply count how many units there are between the points on each end. Then, write down the number next to that side so you can refer to it later.[10]

    • For example, if you’re trying to find the length of a horizontal side, start at one end and count the number of boxes between that point and the other end. If you counted 6, that would mean the length of that side is 6 units.

  4. Image titled Find the Perimeter of a Polygon Step 11

    4

    Use the distance formula to find the length of diagonal sides. Unfortunately, you can’t count the units on a grid to find the length of diagonal sides like you can with vertical or horizontal sides. Instead, you’ll need to use the distance formula, which is d={sqrt {(x_{{2}}-x_{{1}})^{{2}}+(y_{{2}}-y_{{1}})^{{2}}}}. Just plug in the values of the x and y coordinates for the 2 points at the ends of the side you’re trying to find the distance of and solve to find the length.[11]

    • For example, if you’re trying to find the distance (length) between 2 points with the coordinates (4,7) and (1,3), you would plug those coordinates into the formula and get d={sqrt {(4_{{2}}-1_{{1}})^{{2}}+(7_{{2}}-3_{{1}})^{{2}}}}
    • Then, you would simplify the equation to get d={sqrt {25}}.
    • Finally, you would solve d={sqrt {25}} and get 5. Therefore, the length of the side would be 5.

  5. Image titled Find the Perimeter of a Polygon Step 12

    5

    Add the length of each side together to find the polygon’s perimeter. The perimeter of a polygon is equal to the sum of all of its side lengths. Once you’ve determined all of these lengths using the coordinates you were given, all you need to do is add them together and then you’re done!

    • For example, if you plotted the coordinates of a triangle and found that the side lengths are 3, 2, and 5, you would add these numbers together to get 10. Therefore, the perimeter of the triangle is 10.

    6. Advertisement

Add New Question

  • Question

    What should I do when I don’t feel motivated to do homework?

    Jake Adams

    Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University.

    Jake Adams

    Academic Tutor

    Expert Answer

    Support wikiHow by
    unlocking this expert answer.

    First, create a plan for doing the homework and build in breaks or rewards. For example, get one task done and then set a reward for yourself to take a 15-minute break to call a friend or to go outside for a walk.

  • Question

    If I get stressed while studying, how can I stay positive so I can do better on exams?

    Jake Adams

    Jake Adams is an academic tutor and the owner of Simplifi EDU, a Santa Monica, California based online tutoring business offering learning resources and online tutors for academic subjects K-College, SAT & ACT prep, and college admissions applications. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients the very best online tutoring experience and access to a network of excellent undergraduate and graduate-level tutors from top colleges all over the nation. Jake holds a BS in International Business and Marketing from Pepperdine University.

    Jake Adams

    Academic Tutor

    Expert Answer

    Support wikiHow by
    unlocking this expert answer.

    Build a positive reinforcement loop for yourself by having a plan. For example, take the test day and then work backwards from that and decide what things you need to get done during the time you have. Then work towards those things. It’s putting one foot in front of the other. It’s also being realistic. If you realize the plan is not possible, but you’ll still get through about 80% of it, you’re still going to probably do okay in the class. You’ve done the best that you can. It takes this weight off of your shoulders of having to be perfect. Instead, it’s I have to do the best that I can in any given circumstance and that’s all I can do.

  • Question

    How do you find the perimeter and area of a polygon?

    wikiHow Staff Editor

    This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

    wikiHow Staff Editor

    wikiHow Staff Editor

    Staff Answer

    Support wikiHow by
    unlocking this staff-researched answer.

    To find the perimeter, add up the lengths of all the sides of the polygon. Finding the area can be a little more complicated, since it depends on what kind of shape you’re dealing with. To calculate the area of a regular polygon, multiply ½ x p (the perimeter) x a (the apothem, or the distance from the center of the polygon to the midpoint of any side). If the polygon is irregular, you’ll need to divide it up into regular shapes (e.g., a rectangle and a triangle), find the area of each part, and add them together.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Advertisement

References

About This Article

Article SummaryX

To find the perimeter of a regular polygon, which is a polygon with equal sides, start by writing down the length of 1 side and the total number of sides. Then, multiply those 2 numbers together to find the perimeter. If you’re trying to find the perimeter of an irregular polygon, which is a polygon with different side lengths, start by writing down the length of each side. Then, simply add up all of the lengths to find the perimeter. To learn how to find the perimeter of a polygon using coordinates, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 155,020 times.

Did this article help you?

Источник

Периметр многоугольника – это сумма длин всех его сторон.

Многоугольник – эта фигура, которая имеет, как минимум, 3 вершины.

Если многоугольник является правильным (равносторонний треугольник, квадрат и т.п.), то достаточно знать длину одной стороны. Периметр многоугольника в этом случае находится путём умножения длины его стороны на число вершин многоугольника n.

Например, периметр правильного шестиугольника со стороной 6 сантиметров будет равен:

Рмн = 6*6 см = 36 см.

Если многоугольник имеет 2 параллельные стороны, равные между собой (параллелограмм и прямоугольник), то нужно знать длины 2 сторон (длину и ширину).

Для нахождения периметра нужно сложить длину и ширину, а затем результат умножить на 2.

Например, периметр прямоугольника со сторонами 6 и 8 сантиметров будет равен:

Рмн = (6+8)*2 см = 28 см.

Если треугольник прямоугольный, то нужно знать 2 любых стороны, а если равнобедренный – длину боковой стороны и основания.

Для нахождения периметра равнобедренной трапеции нужно знать длины 2 оснований и боковой стороны.

В других случаях (если многоугольник не является правильным), то нужно находить длины всех сторон.

Источник

Среди геометрических фигур очень большую часть составляют многоугольники. Это квадрат, прямоугольник, параллелограмм, ромб, треугольник, трапеция и другие n-угольники (n — количество сторон многоугольника).

Периметр любого многоугольника – это сумма длин всех его сторон.

Онлайн-калькулятор периметра многоугольника

Формула периметра многоугольника

Общая формула периметра многоугольника

P=a+b+c+d+e+…P=a+b+c+d+e+…,

где a,b,c,d,e,…a, b, c, d, e,… — длины сторон многоугольника.

Частным случаем многоугольника является так называемый правильный многоугольник.

Определение правильного многоугольника

Правильный многоугольник – это такой многоугольник, у которого все стороны равной длины.

Если говорить о периметре правильного многоугольника, то его можно найти, умножив длину стороны фигуры на количество сторон.

Периметр правильного многоугольника

P=n⋅aP=ncdot a

aa — длина стороны многоугольника;
nn — количество сторон многоугольника.

Разберем задачи на нахождение периметра правильного и неправильного многоугольников.

Задача 1

Найти периметр правильного шестиугольника со стороной 10 см.

Решение

a=10a=10
n=6n=6

Воспользуемся формулой для нахождения периметра правильного шестиугольника и подставим вместо aa численное значение:

P=n⋅a=6⋅10=60P=ncdot a=6cdot 10=60 см.

Ответ: P=60P=60 см.

Задача 2

Стороны многоугольника равны 6 см, 5 см, 2 см, 3 см и 1 см. Найти периметр данной фигуры.

Решение

a=6a=6
b=5b=5
c=2c=2
d=3d=3
e=1e=1

В данной задаче нам дан неправильный многоугольник, так как его стороны разной длины. В этом случае нам подходит первая стандартная формула нахождения периметра. Сложим длины всех сторон многоугольника и найдем его периметр:

P=a+b+c+d+e=6+5+2+3+1=17P=a+b+c+d+e=6+5+2+3+1=17 см.

Ответ: P=17P=17 см.

Ищете, где где можно заказать контрольную работу недорого? Обратитесь к нашим экспертам!

Тест по теме “Периметр многоугольника”

Источник

Добавить комментарий