Как найти периметр грани тетраэдра

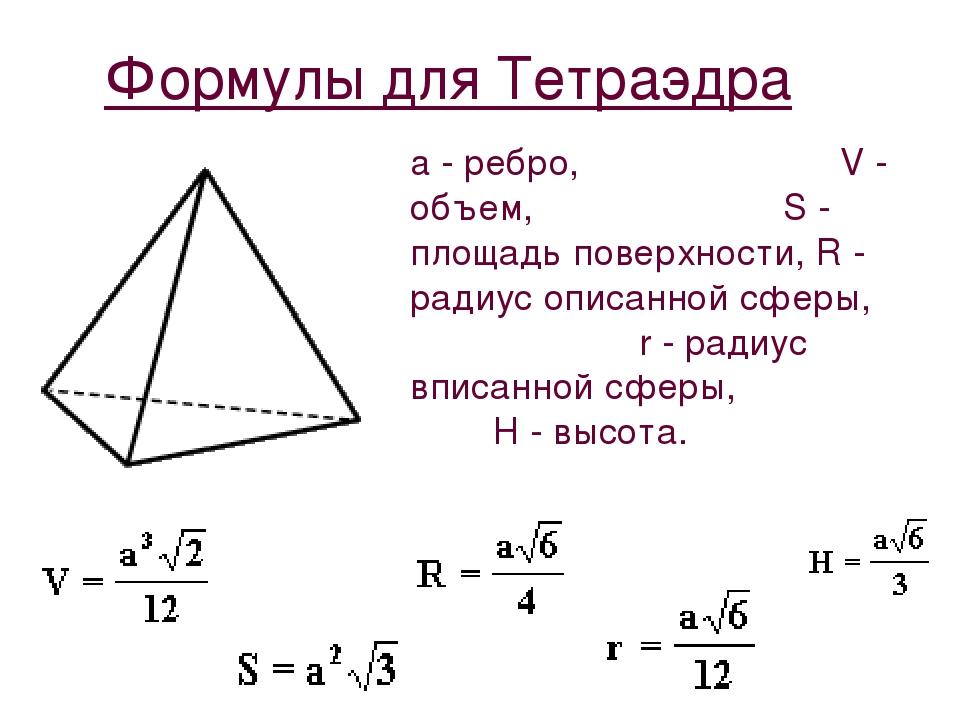
Зная ребро тетраэдра, нужно в первую очередь найти площадь одной его грани, а также радиус вписанной и описанной окружностей грани. Периметр тетраэдра равен стороне, умноженной на их количество, а площадь одной грани тетраэдра – произведению квадрата стороны на корень из трех, деленный на четыре. Соответственно площадь полной поверхности будет представлять собой четыре площади одной грани – по их количеству.
P=6a
S_1=(√3 a^2)/4
S_(п.п.)=4S_1=√3 a^2

Чтобы найти радиусы вписанной и описанной в грань окружностей для тетраэдра, необходимо взять стандартные формулы для равностороннего треугольника и подставить в них значение ребра тетраэдра.
r=a/(2√3)
R=a/√3

Вычислив все параметры одной грани, можно перейти к объемным показателям тетраэдра, таким как высота и апофема. И для высоты, и для апофемы тетраэдра можно вывести индивидуальные формулы из теоремы Пифагора в прямоугольных треугольниках с радиусами вписанных и описанных окружностей грани, являющейся основанием тетраэдра. (рис. 60.1)
h=√(2/3) a
l=(√3 a)/2

Объем тетраэдра вычисляется через ребро тетраэдра по преобразованной формуле для простой пирамиды.
V=a^3/(6√2)

Поскольку тетраэдр является правильной пирамидой, у которой все ребра равны, в него можно вписать сферу, а также описать сферу около него. Радиус вписанной в тетраэдр сферы будет равен ребру тетраэдра, деленному на два корня из шести, а радиус сферы, описанной около тетраэдра, – боковому ребру тетраэдра, умноженному на коэффициент корень из трех, деленный на два корня из двух. (рис.60.2, 60.3)
r_1=a/(2√6)
R_1=(√3 a)/(2√2)

Источник

Как найти периметр тетраэдра?

На этой странице находится вопрос Как найти периметр тетраэдра?. Здесь же – ответы на него,
и похожие вопросы в категории Геометрия, которые можно найти с помощью
простой в использовании поисковой системы. Уровень сложности вопроса
соответствует уровню подготовки учащихся 5 – 9 классов. В комментариях,
оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
ними можно обсудить тему вопроса в режиме on-line. Если ни один из
предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
строке, расположенной вверху, и нажмите кнопку.

Источник

Найдите периметр и площадь сечения тетраэдра. Дополнительные задачи 102, Геометрия, 10-11 класс, Атанасян Л.С.

Дочка просит помочь, а я уже и не помню геометрию(

Докажите, что плоскость α, проходящая через середины двух ребер основания тетраэдра и вершину, не принадлежащую основанию, параллельна третьему ребру основания. Найдите периметр и площадь сечения тетраэдра плоскостью а, если длины всех ребер тетраэдра равны 20 см.

Здравствуйте. Могу поделиться)
По теореме I пл. DNM || DC (MN – средняя линия ААВС, поэтому МН || ВС ).
Если все ребра тетраэдра равны, тогда в ΔADC отрезок DM – ме диана, а значит и высота и биссектриса. Из ΔADM:

ΔAND – ΔAMD (они – прямоугольные, AD – общая гипотенуза,
AM=AN) из равенства треугольников DM= DN;

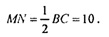
Рассмотрим ΔMDN.

Проведем в равнобедренном ΔМDN высоту DK.

Как найти периметр сторон четырехугольника, формула нахождения

Совсем недавно в России родители отправляли своих детей в первый класс и с нетерпением ждали их первых заданий. Они с удовольствием наблюдали за тем, как их дети знакомятся с буквами русского алфавита, учатся считать палочки и точечки, выводить различные кривые и прямые линии. Родители помогали знакомиться своим детям с тем, что тетрадь в клеточку предназначена для написания цифр, а тетрадь в линеечку — для письма.

Сегодня, будучи второклассниками, ученики России достигли больших успехов в сфере начального образования, а точнее, в математическом прогрессе. Учителя научили их складывать и вычитать, умножать, делить, измерять.

Кстати, по поводу измерения: с линейкой ребята вторых классов России уже знакомы, и применение ей, кроме как стрелять с задней парты в соседа бумажки, они тоже знают. Именно об измерениях мы и заведем сегодняшний разговор.

Как мы видим, прогресс обучения нынешних учеников проходит слегка в ускоренном режиме. С теми темами, например, такими как периметр, дети 90-х знакомились позже, а наши ребята узнают сегодня. Конечно, в этом нет ничего страшного. Время меняется, и программа обучения тоже должна не стоять на месте. Зато, как считают многие, наши дети будут умнее нас.

Школьное задание

Наверное, многих родителей сегодня удивляют нынешние задания для второклассников. В учебнике по математике для второго класса можно встретить такое задание, как, например: «Найди периметр четырехугольника, две стороны которого равны по 2 сантиметра, а другие две будут по 3 сантиметра». Как справиться с данным заданием?

Многие родители настоящего времени являются теми самыми детьми девяностых годов, и, естественно, в большинстве случаев, мало кто помнит, что такое периметр. Особенно, если учились не на отлично, да и не совсем на «хорошо».

Естественно, каждому родителю хотелось бы, чтоб его ребенку было проще в обучении, и они всеми силами стараются ему в этом помочь. Некоторым родителям сначала приходится справиться со своей душевной паникой, а уже потом продолжать объяснять своему ребенку. В этом случае многим помогает интернет, место, где можно найти ответы на все тревожные вопросы. Во времена девяностых, к сожалению, такой «роскоши» не было.

Вопросы:

Что такое «периметр»?
Как находить периметр четырехугольника?

Ответы на вопросы:

Для тех, кто знает, вспоминаем, а кто не знает — объясняем:

Периметр — это сумма всех сторон четырехугольника. Всего лишь каждая грань по отдельности будет равна после сложения единому числу.
Найти периметр, значит, что нужно взять линейку и измерить каждую границу четырехугольника. После выполнения данного действия необходимо сложить полученные числа между собой. Общая полученная сумма и будет являться периметром.

Решение:

В данном случае, по действиям нашей задачи, нам известны суммы сторон четырехугольника, а именно две из них по 2 сантиметра и две по 3 сантиметра. Поэтому нам остается всего лишь перечертить четырехугольник в тетрадь и сложить известные нам суммы каждой грани.

2+2+3+3=10

Как мы видим, периметр нашей четырехугольной фигуры равен 10.

В математике сумму всех сторон (периметр) мы обозначаем символом Р.

Теперь записываем правильное решение этой задачи:

Р=2+2+3+3;

Ответ: Р=10.

В математике существует формула, запомнив которую, вы никогда не будете забывать, как найти периметр (общую сумму всех сторон) четырехугольника и выглядит она так:

P = a + b + c + d (где a , b, c, d являются границами четырехугольника).

Кроме того, хотелось бы обратить внимание, что четырехугольник не обязательно будет являться прямоугольником. Это может быть и квадрат, у которого все стороны равны, и любая другая геометрическая фигура, у которой есть четыре стороны и такое же количество углов.

Грани произвольного четырехугольника могут совсем не совпадать ни с одной из сторон фигуры. Это могут быть совершенно разные числа. И, в итоге, получаются фигуры с четырьмя сторонами и теми же четырьмя углами. Фигура не будет похожа ни на квадрат, ни на прямоугольник, так как углы ее прямыми не будут. И периметр, соответственно мы вычисляем по той же самой единой формуле.

Или взять, например трапецию. Обычно у трапеции две стороны одинаковые, а другие две совсем не совпадают, но между собой параллельные.

На примере трапеция может выглядеть так: верхняя грань равна 2 сантиметра, левая и правая стороны по 3 сантиметра, соединяем их с нижней гранью и получаем трапецию. Высчитываем каждую ее сторону и снова получаем периметр четырехугольника.

Вычислить по формуле всегда будет проще, и не важно, каким числам равна каждая сторона.

Так как современные дети страны уже дошли до таблицы умножения, с периметром квадрата у них проблем не будет. Зная размер одной стороны квадрата, нужно умножить ее на все четыре равные стороны.

В общем, теперь стоит взять линейку с карандашом и лист бумаги. После этого следует начертить произвольные фигуры с четырьмя углами и высчитать общую сумму ее сторон.

A В D АВСD – ромб, сторона которого 6 см, СNSD – параллелограмм. Найдите периметр четырехугольника АВNS, если СN = 4 см и угол ADS равен 60 0. C N S 6. – презентация

Презентация была опубликована 8 лет назад пользователемВсеволод Степухин

Презентация на тему: ” A В D АВСD – ромб, сторона которого 6 см, СNSD – параллелограмм. Найдите периметр четырехугольника АВNS, если СN = 4 см и угол ADS равен 60 0. C N S 6.” — Транскрипт:

2 A В D АВСD – ромб, сторона которого 6 см, СNSD – параллелограмм. Найдите периметр четырехугольника АВNS, если СN = 4 см и угол ADS равен C N S 6 см 4 см Повторение

3 Многоугольник ABCDNH – фигура, составленная из отрезков. А ВС D H N А1А1А1А1 А2А2А2А2 А3А3А3А3 А4А4А4А4 А5А5А5А5 А6А6А6А6 А7А7А7А7 Многоугольник A 1 А 2 А 3 А 4 А 5 А 6 А 7 – часть плоскости, ограниченная линией A 1 А 2 А 3 А 4 А 5 А 6 А 7.

4 D А С В … Поверхность, составленная из четырех треугольников … тетраэдром называется тетраэдром Грани Вершины Ребра

5 Тетраэдр. Тетраэдр. Слово составлено из греческих «четыре» и – «основание». Буквальное значение – «четырехгранник». По-видимому, термин впервые употреблен Евклидом. После Платона чаще встречается «пирамида», / С А В SS

6 D А С В Противоположные ребра основание А С В Dоснование

7 Параллелепипед АВСDA 1 B 1 C 1 D 1 – АВСD и A 1 B 1 C 1 D 1 Параллелепипед АВСDA 1 B 1 C 1 D 1 – поверхность, составленная из двух равных параллелограммов АВСD и A 1 B 1 C 1 D 1 и четырех параллелограммов АВВ 1 А 1, ADD 1 A 1, CDD 1 C 1 и ВСС 1 В 1 А В С D D1D1 С1С1 A1A1 B1B1

8 А В С D D1D1 С1С1 A1A1 B1B1 Параллелепипед АВСDA 1 B 1 C 1 D 1 Грани Вершины Ребра Противоположные грани

9 Параллелепипед. Параллелепипед. Слово составлено из греческих «плоскость» «поверхность». Слово встречалось у Эвклида и Герона, но его еще не было у Архимеда.

10 А В С D А1А1 D1D1 С1С1 B1B1 Диагональ параллелепипеда – Диагональ параллелепипеда – отрезок, соединяющий противоположные вершины.

11 Прямоугольный параллелепипед Две грани параллелепипеда называются параллельными, если их плоскости параллельны.

12 А В С D D1D1 С1С1 A1A1 B1B1 Свойства параллелепипеда Противоположные грани параллелепипеда параллельны и равны.

13 А В С D D1D1 С1С1 A1A1 B1B1 Свойства параллелепипеда Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

14 А D С В B1B1 С1С1 D1D1 А1А1 Каково взаимное положение прямых А 1 D и MN, А 1 D и В 1 С 1, МN и A 1 B 1 ? N MRОшибка

15 АD С В B1B1 С1С1 D1D1 А1А1 F E F и E – средины ребер куба. Определите взаимное расположение прямых и угол между прямыми EF и AC.

16 АD С В B1B1 С1С1 D1D1 А1А1 F F – средина ребра DD 1 куба. Определите взаимное расположение прямых BD и B 1 F.R

17 АD С В B1B1 С1С1 D1D1 А1А1 F E F и E – средины ребер куба. Определите взаимное расположение прямых и угол между прямыми В 1 Е и ОF. О

18 АD С В B1B1 С1С1 D1D1 А1А1 F F и Е – средины ребер куба. Определите взаимное расположение прямых АС и FЕ и угол между ними. Е

19 АD С В B1B1 С1С1 D1D1 А1А1 F F и Е – средины ребер куба. Определите взаимное расположение прямых ОЕ и FВ 1. Е О

20 А В С D N M E F F, Е, N, M – средины ребер тетраэдра. Определите взаимное расположение прямых NM и FЕ и угол между ними.

21 А В С D N M N, M – средины ребер тетраэдра. Определите взаимное расположение прямых NM и ВС.

22 А В С D N M N, M, Р и К – средины ребер тетраэдра. Определите взаимное расположение прямых NК и МС. Р К

23 А В С D N N, Р и К – средины ребер тетраэдра. Определите взаимное расположение прямых NВ и РК. Р К

24 А В С D N N и Р – средины ребер тетраэдра. Определите взаимное расположение прямой NР и плоскости АСD Р

25 А В С D Определите взаимное расположение прямой DВ и плоскости АСD

26 А В С D N F, S, N и Р – средины ребер тетраэдра. Определите взаимное расположение прямой CF и плоскости NPS Р S F

27 А В С D N K, F, S, N и Р – средины ребер тетраэдра. Определите взаимное расположение прямой KF и плоскости NPS Р S F K

28 С А В S D В тетраэдре DABC DBC = DBA = ABC = 60 0, BD = BA = BC = 4 см. Найдите площадь грани ADC

29 С А В S D В тетраэдре DABC DBC = DBA = ABC = 90 0, BD = BA = BC = 2 см. Найдите площадь грани ADC

30 А С В D В тетраэдре точка Е – середина ребра ВС. Постройте сечение тетраэдра плоскостью, проходящей через точку Е, параллельно плоскости АDC N Е Р

31 А С В D Е Р N Еще один эскиз к задаче

32 Р E F M S R Пример неудачного эскиза В тетраэдре SMEF все ребра равны 4 см. Найдите периметр сечения, проведенного параллельно ребру MF и проходящего через точки Е и Р, где Р – середина SF.

33 E F M S В тетраэдре SMEF все ребра равны 4 см. Найдите периметр сечения, проведенного параллельно ребру MF и проходящего через точки Е и Р, где Р – середина SF. P Еще один эскиз к задаче R F P S E

34 С А В D В тетраэдре DABC точка М – середина АС, DB=6 см, MD=10см, DBM = Постройте сечение тетраэдра плоскостью, проходящей через середину ребра DC параллельно плоскости DMB, и найдите площадь сечения. M Е R R 6 10

[spoiler title=”источники:”]

http://liveposts.ru/articles/education-articles/matematika/kak-najti-perimetr-storon-chetyrehugolnika-formula-nahozhdeniya

http://www.myshared.ru/slide/553248/

[/spoiler]

Источник

Свойства тетраэдра, виды и формулы

Сегодня поговорим об элементах и свойствах тетраэдра, а также узнаем формулы нахождения у этих элементов площади, объема и других параметров.

Элементы четырехгранника

Вам будет интересно: Петрозаводский педагогический колледж: стать специалистом заочно

Отрезок, выпущенный из любой вершины тетраэдра и опущенный на точку пересечения медиан грани, являющейся противоположной, называется медианой.

Высота многоугольника представляет собой нормальный отрезок, опущенный из вершины напротив.

Бимедианой называется отрезок, соединяющий центры скрещивающихся ребер.

Свойства тетраэдра

1) Параллельные плоскости, которые проходят через два скрещивающихся ребра, образуют описанный параллелепипед.

3) Плоскость разделяет тетраэдр на две равные по объему части, если проходит через середину двух скрещивающихся ребер.

Виды тетраэдра

Видовое разнообразие фигуры достаточно широко. Тетраэдр может быть:

Остановимся подробно на правильном тетраэдре, свойства которого практически не отличаются.

Формулы четырехгранника

Высота тетраэдра равна произведению корня из 2/3 и длины ребра.

Объем тетраэдра находится так же, как объем пирамиды: корень квадратный из 2 разделить на 12 и умножить на длину ребра в кубе.

Остальные формулы для расчета площади и радиусов окружностей представлены выше.

Источник

Тетраэдр.

Тетраэдр — правильный многогранник (четырёхгранный), имеющий 4 грани, они, в свою очередь, оказываются правильными треугольниками. У тетраэдра 4 вершины, к каждой из них сходится 3 ребра. Общее количество ребер у тетраэдра 6.

Свойства тетраэдра.

Параллельные плоскости, которые проходят через пары рёбер тетраэдра, что скрещиваются, и определяют описанный параллелепипед около тетраэдра.

Плоскость, которая проходит сквозь середины 2-х рёбер тетраэдра, что скрещиваются, и делит его на 2 части, одинаковые по объему.

Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, если считать от вершины. Она же делит бимедианы на две равные части.

Типы тетраэдров.

У правильного тетраэдра каждый двугранный угол при рёбрах и каждый трёхгранный угол при вершинах имеют одинаковую величину.

Тетраэдр состоит из 4 граней, 4 вершин и 6 ребер.

Кроме правильного тетраэдра, заслуживают внимания такие типы тетраэдров:

— Равногранный тетраэдр, у него каждая грань представляет собой треугольник. Все грани-треугольники такого тетраэдра равны.

— Ортоцентрический тетраэдр, у него каждая высота, опущенная из вершин на противоположную грань, пересекается с остальными в одной точке.

— Прямоугольный тетраэдр, у него каждое ребро, прилежащее к одной из вершин, перпендикулярно другим ребрам, прилежащим к этой же вершине.

— Каркасный тетраэдр — тетраэдр, который таким условиям:

— Соразмерный тетраэдр, бивысоты у него одинаковы.

— Инцентрический тетраэдр, у него отрезки, которые соединяют вершины тетраэдра с центрами окружностей, которые вписаны в противоположные грани, пересекаются в одной точке.

Формулы для определения элементов тетраэдра.

Высота тетраэдра:

Объем тетраэдра рассчитывается по классической формуле объема пирамиды. В нее нужно подставить высоту тетраэдра и площадь правильного (равностороннего) треугольника.

Основные формулы для правильного тетраэдра:

Источник

Как найти высоту тетраэдра формула

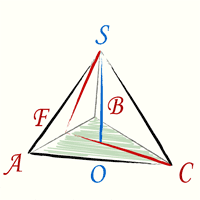
Высота тетраэдра — равна корню квадратному из двух третих, помноженному на длину ребра тетраэдра

(h – высота тетраэдра, a – ребро тетраэдра)

Вывод формулы высоты тетраэдра

Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:

Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).

Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.

Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.

Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле

Правильный тетраэдр – частный вид тетраэдра

Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:

, где
BM=, DM=, BD=a,
p=1/2 (BM+BD+DM)=
Подставим эти значения в формулу высоты. Получим

Вынесем 1/2a. Получим

Применим формулу разность квадратов

После небольших преобразований получим

Объем любого тетраэдра можно рассчитать по формуле
,
где ,

Подставив эти значения, получим

Таким образом формула объема для правильного тетраэдра

где a –ребро тетраэдра

Вычисление объема тетраэдра, если известны координаты его вершин

Пусть нам даны координаты вершин тетраэдра

Из вершины проведем векторы , , .
Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим

Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула

Свойства

Зная высоту тетраэдра, можно вычислить его ребро, перевернув формулу так, чтобы ребро было равно корню из трех вторых, умноженному на высоту. a=√(3/2) h

Выразив таким образом ребро тетраэдра через его высоту, можно найти периметр тетраэдра, то есть длину всех его ребер, площадь одной грани и площадь полной поверхности тетраэдра. Периметр тетраэдра будет равен шести длинам его ребер, площадь одной грани – ребру в квадрате, умноженному на корень из трех, деленный на четыре, а площадь полной поверхности – четырем площадям одной грани. P=6a=6√(3/2) h S_1=(√3 a^2)/4=(3√3 h^2)/8 S_(п.п.)=4S_1=(3√3 h^2)/2

Через высоту, подставленную вместо ребра в определенном соотношении можно найти соответственно и радиусы вписанной и описанной окружностей в основание тетраэдра. r=h/(2√2) R=h/√2

Апофема тетраэдра проходит из вершины к противоположной стороне грани под прямым углом и рассчитать ее можно как из прямоугольного треугольника с боковым ребром по той же грани, так и из прямоугольного треугольника во внутреннем пространстве тетраэдра с высотой. l=3h/(2√2)

Чтобы вычислить объем тетраэдра, необходимо возвести в куб ребро и разделить полученное значение на шесть корней из двух, либо подставить вместо ребра корень из трех вторых, умноженный на высоту и преобразовать формулу объема для высоты. V=(√3 h^3)/8

В тетраэдр можно вписать сферу или описать сферу около него, тогда, зная высоту, чтобы вычислить радиусы вписанной и описанной сфер, необходимо воспользоваться следующими, уже готовыми формулами. (рис.60.2, 60.3) r_1=h/4 R_1=3h/4

Источник

Высота тетраэдра

Свойства

Источник

Тетраэдр

Тетраэдр имеет следующие характеристики:

Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.
Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.

Является ли тетраэдр пирамидой? Да, тетраэдр это треугольная пирамида у которой все стороны равны.

Может ли пирамида быть тетраэдром? Только если это пирамида с треугольным основанием и каждая из её сторон равносторонний треугольник.

Отметим, что очень редко, но встречаются геометрические тела, составленные не из правильных треугольников, и их тоже называют тетраэдры, так как они имеют четыре грани.

Математические характеристики тетраэдра

Тетраэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.

Радиус описанной сферы тетраэдра определяется по формуле:

R tetr

Сфера может быть вписана внутрь тетраэдра.

Радиус вписанной сферы тетраэдра определяется по формуле:

r1 tetr

Площадь поверхности тетраэдра

Для наглядности, площадь поверхности тетраэдра можно представить в виде площади развёртки. Площадь поверхности можно определить как площадь одной из сторон тетраэдра (это площадь правильного треугольника) умноженной на 4. Либо воспользоваться формулой: S tetr

Объем тетраэдра определяется по следующей формуле:

V tetr

6 tert

Высота тетраэдра определяется по следующей формуле:

Расстояние до центра основания тетраэдра определяется по формуле:

Вариант развертки

platon

Древнегреческий философ Платон ассоциировал тетраэдр с «земным» элементом огонь, поэтому для построения модели этого правильного многогранника мы выбрали красный цвет.