The perimeter of a shape is the total distance around it. To find the perimeter, add every side of the shape to find the total. If one or more sides are fractions, you will have to follow the rules for adding fractions to add each side and find the perimeter.
Identify All Sides
No matter what the shape is, add all sides to find the perimeter. If the shape has equal sides, there are formulas to simplify the process. To find the perimeter of an equilateral triangle, multiply the side length by 3. To find the perimeter of a square, multiply the side length by 4. If the shape is a rectangle, add the long side and the short side, and multiply that total by two: P = 2(x+y). These formulas still work with fractions. If your shape is a polygon with sides as fractions, follow the rules for adding fractions to find the perimeter.
Find the Common Denominator
Before you can add fractions, you must find a common denominator. The common denominator will be the Least Common Multiple (LCM): the smallest number that all of your denominators will divide into evenly. For example, if you have a 4-sided polygon with sides 1/2, 1/3, 3/4 and 5/6, you will have to change all of the denominators so they are all the same. Each of these denominators can divide evenly into 12, so 12 will be your new denominator. To change the fraction, multiply the numerator and denominator by the same number to keep the value the same. Multiply 1/2 by 6/6 to get 6/12. Multiply 1/3 by 4/4 to get 4/12. Multiply 2/4 by 3/3 to get 6/12. Multiply 5/6 by 2/2 to get 10/12. Now, every denominator is the same.
Use the Numerators
Once the denominators are the same, keep the denominator and only add the numerators. If your common denominator is 12, that will be the denominator of your answer. To add 6/12, 4/12, 6/12, and 10/12, add 6+4+6+10 and put the answer over 12. Your total, and your perimeter, will be 26/12.
If you have a shape with even sides and use a multiplication formula, only multiply the numerator. For example, to find the perimeter of a square with the formula P=4x, and your side length is 3/4, multiply 3×2 and put the product over 4. Your perimeter will be 6/4.
Simplify Your Results
After you find the perimeter, simplify your total fraction. If your total is an improper fraction, follow your directions to know whether to leave it as improper or turn it into a mixed number. To simply 26/12, for example, divide the numerator and denominator by the same number. Both 26 and 12 are divisible by 2, and after you divide, you will have 13/6. If your directions say to turn this into a mixed number, divide 6 into 13 and write your remainder as a fraction. Six will go into 13 two times with a remainder of 1. Put that remainder over your denominator for a final answer of 2 1/6.
Найти периметр квадрата если длина его стороны равна 1 / 10 ( дроби).
Перед вами страница с вопросом Найти периметр квадрата если длина его стороны равна 1 / 10 ( дроби)?, который относится к
категории Математика. Уровень сложности соответствует учебной программе для
учащихся 1 – 4 классов. Здесь вы найдете не только правильный ответ, но и
сможете ознакомиться с вариантами пользователей, а также обсудить тему и
выбрать подходящую версию. Если среди найденных ответов не окажется
варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском»,
который откроет все похожие ответы, или создайте собственный вопрос, нажав
кнопку в верхней части страницы.
Периметр квадрата калькулятор онлайн умеет вычислять периметр пятью способами:
- По стороне квадрата.
- По диагонали квадрата.
- По площади квадрата.
- По радиусу описанной окружности.
- По радиусу вписанной окружности.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
Периметр квадрата – это сумма четырех его сторон.
Так как у квадрата все стороны равны, то для вычисления периметра достаточно знать длину всего одной стороны.
Периметр может быть найден и по другим формулам, например через диагональ или площадь квадрата. В этих случаях сначала находится длина одной стороны квадрата, а затем и сам периметр.
Как найти периметр квадрата?
Найти периметр квадрата очень просто на нашем онлайн калькуляторе. Так же периметр может быть найден самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По стороне
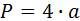
где а – сторона квадрата.
2) По диагонали
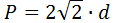
где d – диагональ квадрата.
3) По площади
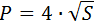
где S – площадь квадрата.
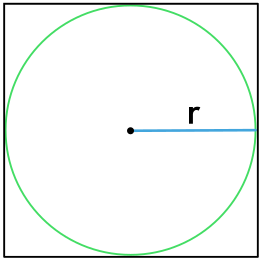
4) По радиусу описанной окружности
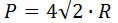
где R – радиус описанной окружности.
5) По радиусу вписанной окружности
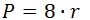
где r – радиус вписанной окружности.
Скачать все формулы в формате Word/PDF
{P = 4 cdot a}
Периметр квадрата рассчитывается довольно просто, но если вы забыли формулу или не имеете под рукой калькулятора, мы собрали для вас формулы для расчета периметра квадрата и онлайн калькулятор, который рассчитает периметр по длине стороны, диаметру, радиусам вписанной или описанной окружности, площади.
Содержание:
- калькулятор периметра квадрата
- формула периметра квадрата через длину стороны
- формула периметра квадрата через диагональ
- формула периметра квадрата через площадь
- формула периметра квадрата через радиус описанной окружности
- формула периметра квадрата через радиус вписанной окружности
- примеры задач
Квадрат – четырехугольник, у которого все стороны равны и все углы равны (прямые, 90 градусов). Квадрат так же называют правильным четырехугольником. Квадрат является частным случаем прямоугольника и ромба.
Кроме квадрата на сайте вы можете найти периметр ромба, прямоугольника, параллелограмма.
Формула периметра квадрата через длину стороны
{P = 4 cdot a}
a – сторона квадрата
Формула периметра квадрата через диагональ
{P = 2 sqrt{2} cdot d}
d – диагональ квадрата
Формула периметра квадрата через площадь
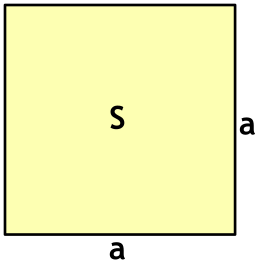
{P = 4sqrt{S}}
S – площадь квадрата
Формула периметра квадрата через радиус описанной окружности
{P = 4sqrt{2} cdot R}
R – радиус описанной около квадрата окружности
Формула периметра квадрата через радиус вписанной окружности
{P = 8r}
r – радиус вписанной в квадрат окружности
Примеры задач на нахождение периметра квадрата
Задача 1
Найти периметр квадрата, вписанного в окружность с R = 4√2.
Решение
Среди формул для решения этой задачи используем наиболее подходящую формулу №4. В условии сказано про квадрат, вписанный в окружность. Но при этом окружность будет описана около квадрата. Именно поэтому мы используем эту формулу. Подставим в нее известный из условия радиус вписанной окружности (в нашем случае он будет являться радиусом описанной окружности):
P = 4sqrt{2} cdot R = 4sqrt{2} cdot 4sqrt{2} = ({4sqrt{2}})^2 = {4^2 cdot ({sqrt{2}})^2} = 16 cdot 2 = 32 : см
Ответ: 32
Проверить полученный ответ можно с помощью калькулятора . Однако, радиус задан не просто числом, а выражением с квадратным корнем – 4√2. К счастью, наш калькулятор может анализировать математические выражения и производить с ними вычисления. Так как на клавиатуре компьютера нет знака квадратного корня, ввести значение радиуса необходимо в таком виде – 4*sqrt(2).
Задача 2
Найдите периметр квадрата сторона которого 13см.
Решение
Чтобы решить эту задачу используем первую формулу:
P = 4 cdot a = 4 cdot 13 = 52 : см
Ответ: 52 см
Проверить ответ поможет калькулятор .
Задача 3
Найдите периметр квадрата сторона которого 5см.
Решение
Для решения этой задачи также используем первую формулу:
P = 4 cdot a = 4 cdot 5 = 20 : см
Ответ: 20 см
Проверить ответ поможет калькулятор .
Задача 4
Найдите периметр квадрата с диагональю 2√2.
Решение
При решении этой задачи воспользуемся формулой №2:
P = 2 sqrt{2} cdot d = 2 sqrt{2} cdot 2 sqrt{2} = ({2 sqrt{2}})^2 = 2^2 cdot ({sqrt{2}})^2 = 4 cdot 2 = 8 : см
Ответ: 8 см
Проверить ответ к этой задаче можно с помощью калькулятора . Диагональ задана выражением с квадратным корнем, введем ее в виде, который сможет распознать наш калькулятор – 2 * sqrt(2).
Содержание:
- Формула
- Примеры вычисления периметра квадрата
Формула
Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.
По определению, квадрат – это правильный четырехугольник, у которого все углы и стороны равны. Тогда, если задан квадрат
$ABCD$ со стороной
$a$, то для него формула для нахождения периметра примет вид:
$$P_{Delta A B C D}=a+a+a+a=4 a$$
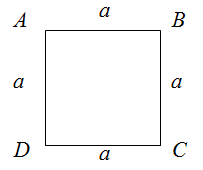
Примеры вычисления периметра квадрата
Пример
Задание. Дан квадрат
$ABCD$ со стороной
$a=0,25$ см. Вычислить периметр заданного квадрата.
Решение. Для нахождения периметра квадрата воспользуемся формулой
$$P_{Delta A B C D}=4a$$
Подставляя в неё значение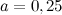 
, получим:
$P_{Delta A B C D}=4 cdot 0,25=1$ (см)
Ответ. $P_{Delta A B C D}=1$ (см)
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти периметр квадрата
$ABCD$, который вписан в окружность радиуса
$r=2$ дм.
Решение. Сделаем рисунок.
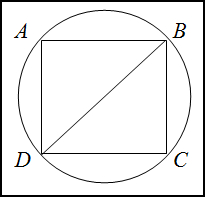
Диаметр описанной окружности является диагональю вписанного в неё квадрата, то есть
$DB=d=2r=2 cdot 2=4$ (дм)
Известно, что сторона квадрата $AB$ связана с его диагональю
$DB$ соотношением:
$$D B=A B sqrt{2}$$
Откуда получаем, что
$A B=frac{D B}{sqrt{2}}=frac{4}{sqrt{2}}=2 sqrt{2}$ (дм)
А тогда искомый периметр:
Ответ. $P_{Delta A B C D}=8 sqrt{2}$ (дм)
Читать дальше: как найти периметр прямоугольника.
