Как найти периметр квадрата, если известна его площадь
Квадрат представляет собой правильный четырехугольник (или ромб), в котором все углы являются прямыми, а стороны равны между собой. Как и у любого иного правильного многоугольника, у квадрата можно высчитать периметр и площадь. Если площадь квадрата уже известна, то найти его стороны, а затем и периметр не составит труда.

Инструкция
Площадь квадрата находится по формуле:
S = a²
Это означает, что для того, чтобы вычислить площадь квадрата, нужно умножить длины двух его сторон друг на друга. Как следствие, если знать площадь квадрата, то при извлечении корня из данного значения можно узнать длину стороны квадрата.
Пример: площадь квадрата 36 см², чтобы узнать сторону данного квадрата, необходимо извлечь квадратный корень из значения площади. Таким образом, длина стороны данного квадрата 6 см
Для нахождения периметра квадрата необходимо сложить длины всех его сторон. С помощью формулы это можно выразить так:
P = a+a+a+a.
Если извлечь корень из значения площади квадрата, а затем сложить получившуюся величину 4 раза, то можно найти периметр квадрата.
Пример: Дан квадрат с площадью 49 см². Требуется найти его периметр.
Решение:
Сначала необходимо извлечь корень площади квадрата: √49 = 7 см
Затем, вычислив длину стороны квадрата, можно вычислить и периметр: 7+7+7+7 = 28 см
Ответ: периметр квадрата площадью 49 см² составляет 28 см
Обратите внимание
Для квадрата справедливы следующие определения:
Квадрат – это прямоугольник, который обладает равными между собой сторонами.
Квадрат – это особая разновидность ромба, у которого каждый из углов равен 90 градусам.
Являясь правильным четырехугольником, вокруг квадрата можно описать или вписать окружность. Радиус вписанной в квадрат окружность можно найти по формуле:
R = t/2, где t – сторона квадрата.
Если же окружность описана вокруг него, то ее радиус находится так:
R = (√2*t)/2
Исходя из данных формул, можно вывести новые для нахождения периметра квадрата:
P = 8*R, где R – радиус вписанной окружности;
P = 4*√2*R, где R – радиус описанной окружности.
Квадрат является уникальной геометрической фигурой, поскольку он абсолютно симметричен, независимо от того, как и где провести ось симметрии.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Лучший ответ
****Nastyusha****
Знаток
(325)
11 лет назад
площадь например: 25 значит сторона квадрата будет 5 см, а чтобы узнать периметр нужно сторону квадрата умшожить на 4
Остальные ответы
Безнадежный Романтик
Просветленный
(29859)
11 лет назад
Площадь подели на четыре
Дмитрий Чабанов
Знаток
(262)
11 лет назад
периметр равен сумме всех сторон
сторона равна квадратному корню из площади
Вера Вера
Знаток
(408)
11 лет назад
Площадь квадрата равна: сторона в квадрате. Зная площадь, можно узнать чему равна одна сторона (извлечь кв. корень) , потом умножить на четыре.
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* – обязательно заполнить
Площадь (S) = 10
Cторона, диаметр вписанной окружности (L) = (sqrt{S}) = (sqrt{10}) = 3.16
Диагональ, диаметр описанной окружности (M) = (sqrt{2*L^{2}}) = (sqrt{2*3.16^{2}}) = 4.47
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{3.16}{2}) = 1.58
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{4.47}{2}) = 2.24
Периметр (P) = (L*4) = (3.16*4) = 12.64

{P = 4 cdot a}
Периметр квадрата рассчитывается довольно просто, но если вы забыли формулу или не имеете под рукой калькулятора, мы собрали для вас формулы для расчета периметра квадрата и онлайн калькулятор, который рассчитает периметр по длине стороны, диаметру, радиусам вписанной или описанной окружности, площади.
Содержание:
- калькулятор периметра квадрата
- формула периметра квадрата через длину стороны
- формула периметра квадрата через диагональ
- формула периметра квадрата через площадь
- формула периметра квадрата через радиус описанной окружности
- формула периметра квадрата через радиус вписанной окружности
- примеры задач
Квадрат – четырехугольник, у которого все стороны равны и все углы равны (прямые, 90 градусов). Квадрат так же называют правильным четырехугольником. Квадрат является частным случаем прямоугольника и ромба.
Кроме квадрата на сайте вы можете найти периметр ромба, прямоугольника, параллелограмма.
Формула периметра квадрата через длину стороны

{P = 4 cdot a}
a – сторона квадрата
Формула периметра квадрата через диагональ

{P = 2 sqrt{2} cdot d}
d – диагональ квадрата
Формула периметра квадрата через площадь
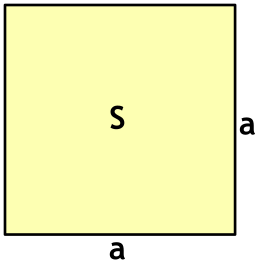
{P = 4sqrt{S}}
S – площадь квадрата
Формула периметра квадрата через радиус описанной окружности

{P = 4sqrt{2} cdot R}
R – радиус описанной около квадрата окружности
Формула периметра квадрата через радиус вписанной окружности
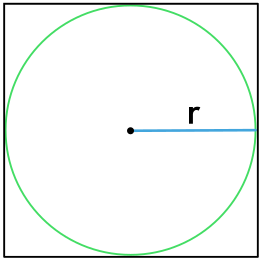
{P = 8r}
r – радиус вписанной в квадрат окружности
Примеры задач на нахождение периметра квадрата
Задача 1
Найти периметр квадрата, вписанного в окружность с R = 4√2.
Решение
Среди формул для решения этой задачи используем наиболее подходящую формулу №4. В условии сказано про квадрат, вписанный в окружность. Но при этом окружность будет описана около квадрата. Именно поэтому мы используем эту формулу. Подставим в нее известный из условия радиус вписанной окружности (в нашем случае он будет являться радиусом описанной окружности):
P = 4sqrt{2} cdot R = 4sqrt{2} cdot 4sqrt{2} = ({4sqrt{2}})^2 = {4^2 cdot ({sqrt{2}})^2} = 16 cdot 2 = 32 : см
Ответ: 32
Проверить полученный ответ можно с помощью калькулятора . Однако, радиус задан не просто числом, а выражением с квадратным корнем – 4√2. К счастью, наш калькулятор может анализировать математические выражения и производить с ними вычисления. Так как на клавиатуре компьютера нет знака квадратного корня, ввести значение радиуса необходимо в таком виде – 4*sqrt(2).
Задача 2
Найдите периметр квадрата сторона которого 13см.
Решение
Чтобы решить эту задачу используем первую формулу:
P = 4 cdot a = 4 cdot 13 = 52 : см
Ответ: 52 см
Проверить ответ поможет калькулятор .
Задача 3
Найдите периметр квадрата сторона которого 5см.
Решение
Для решения этой задачи также используем первую формулу:
P = 4 cdot a = 4 cdot 5 = 20 : см
Ответ: 20 см
Проверить ответ поможет калькулятор .
Задача 4
Найдите периметр квадрата с диагональю 2√2.
Решение
При решении этой задачи воспользуемся формулой №2:
P = 2 sqrt{2} cdot d = 2 sqrt{2} cdot 2 sqrt{2} = ({2 sqrt{2}})^2 = 2^2 cdot ({sqrt{2}})^2 = 4 cdot 2 = 8 : см
Ответ: 8 см
Проверить ответ к этой задаче можно с помощью калькулятора . Диагональ задана выражением с квадратным корнем, введем ее в виде, который сможет распознать наш калькулятор – 2 * sqrt(2).
