Квадрат — это геометрическая фигура, правильный четырехугольник, у которого все углы и стороны равны.
Онлайн-калькулятор периметра квадрата
Противоположные стороны квадрата параллельны.
Другими словами, квадрат — это прямоугольник, у которого все стороны равны, или квадрат — это ромб, у которого все углы прямые. Квадрат имеет две диагонали, которые делятся точкой их пересечения пополам. Диагонали квадрата также делят его углы пополам и соединяют несмежные вершины.
Формула периметра квадрата
Для того чтобы найти периметр квадрата, нужно сложить длины всех его сторон.
P=a+a+a+a=4⋅aP=a+a+a+a=4cdot a
aa — длина стороны квадрата.
Разберем задачу на нахождение периметра квадрата.
Найти периметр квадрата со стороной 12 см.
Решение
a=12a=12
Воспользуемся формулой нахождения периметра квадрата и подставим вместо aa его численное значение:
P=4⋅a=4⋅12=48P=4cdot a=4cdot 12=48 см.
Ответ: 48 см.
Ищете, где заказать решение контрольной работы? Эксперты Студворк с радостью помогут вам!
Тест по теме «Периметр квадрата»
Увидев этот вопрос, мы с сыном, который перешёл в пятый класс, улыбнулись, и начали вспоминать, когда же нахождение периметра проходили в школе. После небольшой, но оживлённой дискуссии, я решил этот вопрос, пробежав программу по математике в начальной школе на сайте Министерства образования и науки Украины. Как оказалось, мой мальчик был прав, что ещё во 2-ом классе, а не в 3-ем, как запомнилось мне, детям уже даются основы геометрический знаний.
Итак, квадрат – это плоская геометрическая фигура состоящая из четырёх отрезков, каждый из которых пересекается с двумя другими под углом в 90 градусов. Соответственно стороны данного четырёхугольника равны.
Для того же, чтобы узнать периметр (сумму всех сторон), достаточно измерить длину одного из отрезков и полученную величину умножить на 4.
Для наглядности проиллюстрирую ниже.
Как видите, всё довольно просто ! Успехов в учёбе !

{P = 4 cdot a}
Периметр квадрата рассчитывается довольно просто, но если вы забыли формулу или не имеете под рукой калькулятора, мы собрали для вас формулы для расчета периметра квадрата и онлайн калькулятор, который рассчитает периметр по длине стороны, диаметру, радиусам вписанной или описанной окружности, площади.
Содержание:
- калькулятор периметра квадрата
- формула периметра квадрата через длину стороны
- формула периметра квадрата через диагональ
- формула периметра квадрата через площадь
- формула периметра квадрата через радиус описанной окружности
- формула периметра квадрата через радиус вписанной окружности
- примеры задач
Квадрат – четырехугольник, у которого все стороны равны и все углы равны (прямые, 90 градусов). Квадрат так же называют правильным четырехугольником. Квадрат является частным случаем прямоугольника и ромба.
Кроме квадрата на сайте вы можете найти периметр ромба, прямоугольника, параллелограмма.
Формула периметра квадрата через длину стороны
{P = 4 cdot a}
a – сторона квадрата
Формула периметра квадрата через диагональ
{P = 2 sqrt{2} cdot d}
d – диагональ квадрата
Формула периметра квадрата через площадь
{P = 4sqrt{S}}
S – площадь квадрата
Формула периметра квадрата через радиус описанной окружности
{P = 4sqrt{2} cdot R}
R – радиус описанной около квадрата окружности
Формула периметра квадрата через радиус вписанной окружности
{P = 8r}
r – радиус вписанной в квадрат окружности
Примеры задач на нахождение периметра квадрата
Задача 1
Найти периметр квадрата, вписанного в окружность с R = 4√2.
Решение
Среди формул для решения этой задачи используем наиболее подходящую формулу №4. В условии сказано про квадрат, вписанный в окружность. Но при этом окружность будет описана около квадрата. Именно поэтому мы используем эту формулу. Подставим в нее известный из условия радиус вписанной окружности (в нашем случае он будет являться радиусом описанной окружности):
P = 4sqrt{2} cdot R = 4sqrt{2} cdot 4sqrt{2} = ({4sqrt{2}})^2 = {4^2 cdot ({sqrt{2}})^2} = 16 cdot 2 = 32 : см
Ответ: 32
Проверить полученный ответ можно с помощью калькулятора . Однако, радиус задан не просто числом, а выражением с квадратным корнем – 4√2. К счастью, наш калькулятор может анализировать математические выражения и производить с ними вычисления. Так как на клавиатуре компьютера нет знака квадратного корня, ввести значение радиуса необходимо в таком виде – 4*sqrt(2).
Задача 2
Найдите периметр квадрата сторона которого 13см.
Решение
Чтобы решить эту задачу используем первую формулу:
P = 4 cdot a = 4 cdot 13 = 52 : см
Ответ: 52 см
Проверить ответ поможет калькулятор .
Задача 3
Найдите периметр квадрата сторона которого 5см.
Решение
Для решения этой задачи также используем первую формулу:
P = 4 cdot a = 4 cdot 5 = 20 : см
Ответ: 20 см
Проверить ответ поможет калькулятор .
Задача 4
Найдите периметр квадрата с диагональю 2√2.
Решение
При решении этой задачи воспользуемся формулой №2:
P = 2 sqrt{2} cdot d = 2 sqrt{2} cdot 2 sqrt{2} = ({2 sqrt{2}})^2 = 2^2 cdot ({sqrt{2}})^2 = 4 cdot 2 = 8 : см
Ответ: 8 см
Проверить ответ к этой задаче можно с помощью калькулятора . Диагональ задана выражением с квадратным корнем, введем ее в виде, который сможет распознать наш калькулятор – 2 * sqrt(2).
Содержание:
- Формула
- Примеры вычисления периметра квадрата
Формула
Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.
По определению, квадрат – это правильный четырехугольник, у которого все углы и стороны равны. Тогда, если задан квадрат
$ABCD$ со стороной
$a$, то для него формула для нахождения периметра примет вид:
$$P_{Delta A B C D}=a+a+a+a=4 a$$
Примеры вычисления периметра квадрата
Пример
Задание. Дан квадрат
$ABCD$ со стороной
$a=0,25$ см. Вычислить периметр заданного квадрата.
Решение. Для нахождения периметра квадрата воспользуемся формулой
$$P_{Delta A B C D}=4a$$
Подставляя в неё значение 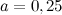
$P_{Delta A B C D}=4 cdot 0,25=1$ (см)
Ответ. $P_{Delta A B C D}=1$ (см)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти периметр квадрата
$ABCD$, который вписан в окружность радиуса
$r=2$ дм.
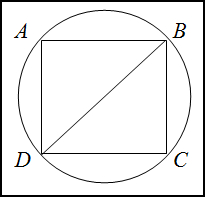
Решение. Сделаем рисунок.
Диаметр описанной окружности является диагональю вписанного в неё квадрата, то есть
$DB=d=2r=2 cdot 2=4$ (дм)
Известно, что сторона квадрата $AB$ связана с его диагональю
$DB$ соотношением:
$$D B=A B sqrt{2}$$
Откуда получаем, что
$A B=frac{D B}{sqrt{2}}=frac{4}{sqrt{2}}=2 sqrt{2}$ (дм)
А тогда искомый периметр:
Ответ. $P_{Delta A B C D}=8 sqrt{2}$ (дм)
Читать дальше: как найти периметр прямоугольника.
Загрузить PDF
Загрузить PDF
Периметр двумерной фигуры – это общая длина ее границы, равная сумме длин сторон фигуры.[1]
Квадрат – это фигура с четырьмя сторонами одинаковой длины, которые пересекаются под углом 90°.[2]
Так как в квадрате все стороны имеют одинаковую длину, то вычислить его периметр очень легко. Эта статья расскажет вам, как вычислить периметр квадрата по одной данной стороне, по данной площади и по данному радиусу окружности, описанной вокруг квадрата.
-
1
Формула для вычисления периметра квадрата: P = 4s, где s – длина стороны квадрата.
-
2
Определите длину одной стороны квадрата и умножьте ее на 4, чтобы найти периметр. Чтобы определить длину стороны, измерьте ее линейкой или посмотрите ее значение в учебнике (задаче). Вот некоторые примеры вычисления периметра:
- Если сторона квадрата равна 4, то P = 4 * 4 = 16.
- Если сторона квадрата равна 6, то P = 4 * 6 = 36.
Реклама
-
1
Формула для вычисления площади квадрата. Площадь любого прямоугольника (а квадрат – это частный случай прямоугольника) равна произведению его длины на его ширину.[3]
Поскольку длина и ширина квадрата равны, то его площадь вычисляется по формуле: A = s*s = s2, где s – длина стороны квадрата. -
2
Извлеките квадратный корень из значения площади, чтобы найти сторону квадрата. Для этого в большинстве случаев воспользуйтесь калькулятором (введите значение площади и нажмите клавишу “√”). Вы также можете вычислить квадратный корень вручную.
- Если площадь квадрата равна 20, то его сторона равна: s = √20 = 4,472.
- Если площадь квадрата равна 25, то s = √25 = 5.
-
3
Умножьте найденную сторону на 4, чтобы найти периметр. Вычисленное значение стороны подставьте в формулу для нахождения периметра: P = 4s. Вы найдете периметр квадрата.
- В нашем первом примере: P = 4 * 4,472 = 17,888.
- Периметр квадрата, площадь которого равна 25, а сторона равна 5, равен Р = 4 * 5 = 20.
Реклама
-
1
Вписанный квадрат – это квадрат, вершины которого лежат на окружности.[4]
-
2
Отношение между радиусом окружности и длиной стороны квадрата. Расстояние от центра описанной окружности до вершины вписанного в нее квадрата равно радиусу окружности. Чтобы найти сторону квадрата s, необходимо диагональю разделить квадрат на 2 прямоугольных треугольника. Каждый из этих треугольников будет иметь равные стороны a и b и общую гипотенузу с, равную удвоенному радиусу описанной окружности (2r).
-
3
Воспользуйтесь теоремой Пифагора, чтобы найти сторону квадрата. Теорема Пифагора гласит, что в любом прямоугольном треугольнике с катетами а и b и гипотенузой с: a2 + b2 = c2.[5]
Так как в нашем случае а = b (не забывайте, что мы рассматриваем квадрат!), и мы знаем, что с = 2r, то мы можем переписать и упростить это уравнение:- a2 + a2 = (2r)2“‘; теперь упростим это уравнение:
- 2a2 = 4(r)2; теперь разделим обе стороны уравнения на 2:
- (a2) = 2(r)2; теперь извлечем квадратный корень из обеих сторон уравнения:
- a = √(2r). Таким образом, s = √(2r).
-
4
Умножьте найденную сторону квадрата на 4, чтобы найти его периметр. В этом случае периметр квадрата: P = 4√(2r). Эту формулу можно переписать так: Р = 4√2 * 4√r = 5,657r, где r – радиус описанной окружности.[6]
-
5
Пример. Рассмотрим квадрат, вписанный в окружность радиусом 10. Это означает, что диагональ квадрата равна 2 * 10 = 20. Используя теорему Пифагора, мы получим: 2(a2) = 202, то есть 2a2 = 400. Теперь разделим обе стороны уравнения на 2 и получим: a2 = 200. Теперь извлечем квадратный корень из обеих сторон уравнения и получим: а = 14,142. Умножим это значение на 4 и вычислим периметр квадрата: P = 56,57.
- Обратите внимание, что вы могли бы получить тот же результат, просто умножив радиус (10) на 5,657: 10 * 5,567 = 56,57; но такой метод трудно запомнить, поэтому лучше пользоваться процессом вычисления, описанным выше.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 413 196 раз.