- Следить
- Отметить нарушение!
Ответы и объяснения
Периметр – это сумма всех сторон. У квадрата все стороны равны.
Следовательно, P квадрата = 4*a, где a – это сторона квадрата.
Вычислим периметр квадрата, подставив значения:
P = 4 * 3 = 12 см
Ответ: периметр квадрата равен 12 см
- 0 комментариев
- Отметить нарушение!
- Спасибо 0
- Учебники
- 4 класс
- Математика 👍
- Моро
- №409

авторы: Моро, Бантова, Бельтюкова.
издательство: Просвещение 2016 год
Раздел:
- ЧАСТЬ 1
- ЧИСЛА, КОТОРЫЕ БОЛЬШЕ 1000
- Умножение и деление
- Деление на однозначное число (страница 81)
Найди периметр квадрата со стороной 3 см 2 мм.

reshalka.com
Математика 4 класс Моро. Часть 1. Деление на однозначное число. Номер №409
Решение
Периметр квадрата − это сумма длин всех его сторон, тогда:
P = 3 см 2 мм * 4 = 32 * 4 = 128 (мм) = 12 см 8 мм
Ответ: 12 см 8 мм
- Предыдущее
- Следующее
![]()
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Каллимах
27 сентября, 22:39
-

Митяй
27 сентября, 23:31
0
3 умножить на 3 будет площадь, а периметр такой: 3 + 3+3+3 = 12
- Комментировать
- Жалоба
- Ссылка
-

Костюха
28 сентября, 00:21
0
Площадь 3*3=9 (см) Периметр (3+3) * 2 = 3+3+3+3=12 (см)
- Комментировать
- Жалоба
- Ссылка
Найди верный ответ на вопрос ✅ «Вычисли периметр и площадь квадрата со стороной 3 сантиметра …» по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Новые вопросы по математике
Главная » Математика » Вычисли периметр и площадь квадрата со стороной 3 сантиметра
Введите данные:
Достаточно ввести только одно значение, остальное калькулятор посчитает сам.
Cторона квадрата, диаметр вписанной окружности (L)
Диагональ квадрата, диаметр описанной окружности (M)
Радиус вписанной окружности (R1)
Радиус описанной окружности (R2)
Округление:
* – обязательно заполнить
Cторона, диаметр вписанной окружности (L) = 3
Диагональ, диаметр описанной окружности (M) = (sqrt{2*L^{2}}) = (sqrt{2*3^{2}}) = 4.24
Радиус вписанной окружности (R1) = (frac{L}{2}) = (frac{3}{2}) = 1.5
Радиус описанной окружности (R2) = (frac{M}{2}) = (frac{4.24}{2}) = 2.12
Периметр (P) = (L*4) = (3*4) = 12
Площадь (S) = (L^{2}) = (3^{2}) = 9

{P = 4 cdot a}
Периметр квадрата рассчитывается довольно просто, но если вы забыли формулу или не имеете под рукой калькулятора, мы собрали для вас формулы для расчета периметра квадрата и онлайн калькулятор, который рассчитает периметр по длине стороны, диаметру, радиусам вписанной или описанной окружности, площади.
Содержание:
- калькулятор периметра квадрата
- формула периметра квадрата через длину стороны
- формула периметра квадрата через диагональ
- формула периметра квадрата через площадь
- формула периметра квадрата через радиус описанной окружности
- формула периметра квадрата через радиус вписанной окружности
- примеры задач
Квадрат – четырехугольник, у которого все стороны равны и все углы равны (прямые, 90 градусов). Квадрат так же называют правильным четырехугольником. Квадрат является частным случаем прямоугольника и ромба.
Кроме квадрата на сайте вы можете найти периметр ромба, прямоугольника, параллелограмма.
Формула периметра квадрата через длину стороны

{P = 4 cdot a}
a – сторона квадрата
Формула периметра квадрата через диагональ

{P = 2 sqrt{2} cdot d}
d – диагональ квадрата
Формула периметра квадрата через площадь
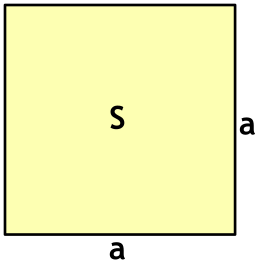
{P = 4sqrt{S}}
S – площадь квадрата
Формула периметра квадрата через радиус описанной окружности

{P = 4sqrt{2} cdot R}
R – радиус описанной около квадрата окружности
Формула периметра квадрата через радиус вписанной окружности
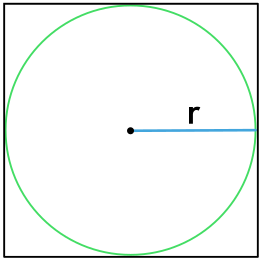
{P = 8r}
r – радиус вписанной в квадрат окружности
Примеры задач на нахождение периметра квадрата
Задача 1
Найти периметр квадрата, вписанного в окружность с R = 4√2.
Решение
Среди формул для решения этой задачи используем наиболее подходящую формулу №4. В условии сказано про квадрат, вписанный в окружность. Но при этом окружность будет описана около квадрата. Именно поэтому мы используем эту формулу. Подставим в нее известный из условия радиус вписанной окружности (в нашем случае он будет являться радиусом описанной окружности):
P = 4sqrt{2} cdot R = 4sqrt{2} cdot 4sqrt{2} = ({4sqrt{2}})^2 = {4^2 cdot ({sqrt{2}})^2} = 16 cdot 2 = 32 : см
Ответ: 32
Проверить полученный ответ можно с помощью калькулятора . Однако, радиус задан не просто числом, а выражением с квадратным корнем – 4√2. К счастью, наш калькулятор может анализировать математические выражения и производить с ними вычисления. Так как на клавиатуре компьютера нет знака квадратного корня, ввести значение радиуса необходимо в таком виде – 4*sqrt(2).
Задача 2
Найдите периметр квадрата сторона которого 13см.
Решение
Чтобы решить эту задачу используем первую формулу:
P = 4 cdot a = 4 cdot 13 = 52 : см
Ответ: 52 см
Проверить ответ поможет калькулятор .
Задача 3
Найдите периметр квадрата сторона которого 5см.
Решение
Для решения этой задачи также используем первую формулу:
P = 4 cdot a = 4 cdot 5 = 20 : см
Ответ: 20 см
Проверить ответ поможет калькулятор .
Задача 4
Найдите периметр квадрата с диагональю 2√2.
Решение
При решении этой задачи воспользуемся формулой №2:
P = 2 sqrt{2} cdot d = 2 sqrt{2} cdot 2 sqrt{2} = ({2 sqrt{2}})^2 = 2^2 cdot ({sqrt{2}})^2 = 4 cdot 2 = 8 : см
Ответ: 8 см
Проверить ответ к этой задаче можно с помощью калькулятора . Диагональ задана выражением с квадратным корнем, введем ее в виде, который сможет распознать наш калькулятор – 2 * sqrt(2).
