Голосование за лучший ответ
аня вилкова
Знаток
(472)
10 лет назад
(4+4)*2 вот
Источник: голова
Байтаков Жаслан
Мыслитель
(9019)
10 лет назад
Периметр – это сумма всех сторон. У квадрата все стороны равны. Т. е. P=a+a+a+a=4*a =4*4 = 16 (см)
Игорь Самарев
Знаток
(474)
10 лет назад
4 стороны, значит периметр 4*4=16
poli сныткина
Знаток
(351)
10 лет назад
Р=a*4
P=4*4
P=16см
Источник: Ум
Игорь Морозов
Знаток
(373)
6 лет назад
Всё просто!
2 способа.
1 сп.:
4+4+4+4=16(см) – периметр квадрата (или: Р квадрата, без разницы)
Ответ: 16 см.
——-
2 сп.
4х4=16(см) – периметр/Р квадрата
Ответ: 16 см.
——
То есть, и в 1 и во 2 способе – ответ – 16 см., значит задача решена верно!
—
Удачи в учёбе!
Содержание:
- Формула
- Примеры вычисления периметра квадрата
Формула
Чтобы найти периметр квадрата, необходимо длину его стороны умножить на четыре.
По определению, квадрат – это правильный четырехугольник, у которого все углы и стороны равны. Тогда, если задан квадрат
$ABCD$ со стороной
$a$, то для него формула для нахождения периметра примет вид:
$$P_{Delta A B C D}=a+a+a+a=4 a$$
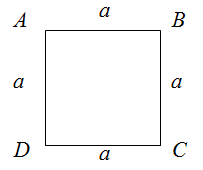
Примеры вычисления периметра квадрата
Пример
Задание. Дан квадрат
$ABCD$ со стороной
$a=0,25$ см. Вычислить периметр заданного квадрата.
Решение. Для нахождения периметра квадрата воспользуемся формулой
$$P_{Delta A B C D}=4a$$
Подставляя в неё значение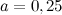 
, получим:
$P_{Delta A B C D}=4 cdot 0,25=1$ (см)
Ответ. $P_{Delta A B C D}=1$ (см)
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти периметр квадрата
$ABCD$, который вписан в окружность радиуса
$r=2$ дм.
Решение. Сделаем рисунок.
Диаметр описанной окружности является диагональю вписанного в неё квадрата, то есть
$DB=d=2r=2 cdot 2=4$ (дм)
Известно, что сторона квадрата $AB$ связана с его диагональю
$DB$ соотношением:
$$D B=A B sqrt{2}$$
Откуда получаем, что
$A B=frac{D B}{sqrt{2}}=frac{4}{sqrt{2}}=2 sqrt{2}$ (дм)
А тогда искомый периметр:
Ответ. $P_{Delta A B C D}=8 sqrt{2}$ (дм)
Читать дальше: как найти периметр прямоугольника.
Главная
-
- 0
-
Сторона квадрата равна 4 см. Найти площадь и периметр квадрата.
P.S. На вложения внимание не обращайте))
Лина Бредишева
Вопрос задан 24 сентября 2019 в
5 – 9 классы,
Геометрия.
-
Комментариев (0)
Добавить
Отмена
2 Ответ (-а, -ов)
- По голосам
- По дате
-
- 0
-
Площадь ( длину умножить на ширину) квадрата
S = a x b = 4см x 4см= 16 кв.см
Периметр(сумма всех сторон) квадрата P = a x 4 = 4cм х 4 = 16 см
Отмена
Вера Маратенкова
Отвечено 24 сентября 2019
-
Комментариев (0)
Добавить
Отмена
-
- 0
-
Отмена
Эмиль Гаптрахманов
Отвечено 24 сентября 2019
-
Комментариев (0)
Добавить
Отмена
Ваш ответ
{P = 4 cdot a}
Периметр квадрата рассчитывается довольно просто, но если вы забыли формулу или не имеете под рукой калькулятора, мы собрали для вас формулы для расчета периметра квадрата и онлайн калькулятор, который рассчитает периметр по длине стороны, диаметру, радиусам вписанной или описанной окружности, площади.
Содержание:
- калькулятор периметра квадрата
- формула периметра квадрата через длину стороны
- формула периметра квадрата через диагональ
- формула периметра квадрата через площадь
- формула периметра квадрата через радиус описанной окружности
- формула периметра квадрата через радиус вписанной окружности
- примеры задач
Квадрат – четырехугольник, у которого все стороны равны и все углы равны (прямые, 90 градусов). Квадрат так же называют правильным четырехугольником. Квадрат является частным случаем прямоугольника и ромба.
Кроме квадрата на сайте вы можете найти периметр ромба, прямоугольника, параллелограмма.
Формула периметра квадрата через длину стороны
{P = 4 cdot a}
a – сторона квадрата
Формула периметра квадрата через диагональ
{P = 2 sqrt{2} cdot d}
d – диагональ квадрата
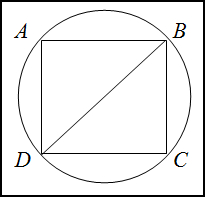
Формула периметра квадрата через площадь
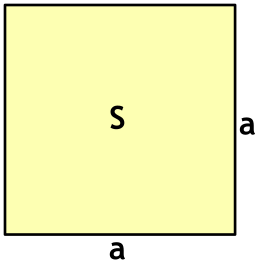
{P = 4sqrt{S}}
S – площадь квадрата
Формула периметра квадрата через радиус описанной окружности
{P = 4sqrt{2} cdot R}
R – радиус описанной около квадрата окружности
Формула периметра квадрата через радиус вписанной окружности
{P = 8r}
r – радиус вписанной в квадрат окружности
Примеры задач на нахождение периметра квадрата
Задача 1
Найти периметр квадрата, вписанного в окружность с R = 4√2.
Решение
Среди формул для решения этой задачи используем наиболее подходящую формулу №4. В условии сказано про квадрат, вписанный в окружность. Но при этом окружность будет описана около квадрата. Именно поэтому мы используем эту формулу. Подставим в нее известный из условия радиус вписанной окружности (в нашем случае он будет являться радиусом описанной окружности):
P = 4sqrt{2} cdot R = 4sqrt{2} cdot 4sqrt{2} = ({4sqrt{2}})^2 = {4^2 cdot ({sqrt{2}})^2} = 16 cdot 2 = 32 : см
Ответ: 32
Проверить полученный ответ можно с помощью калькулятора . Однако, радиус задан не просто числом, а выражением с квадратным корнем – 4√2. К счастью, наш калькулятор может анализировать математические выражения и производить с ними вычисления. Так как на клавиатуре компьютера нет знака квадратного корня, ввести значение радиуса необходимо в таком виде – 4*sqrt(2).
Задача 2
Найдите периметр квадрата сторона которого 13см.
Решение
Чтобы решить эту задачу используем первую формулу:
P = 4 cdot a = 4 cdot 13 = 52 : см
Ответ: 52 см
Проверить ответ поможет калькулятор .
Задача 3
Найдите периметр квадрата сторона которого 5см.
Решение
Для решения этой задачи также используем первую формулу:
P = 4 cdot a = 4 cdot 5 = 20 : см
Ответ: 20 см
Проверить ответ поможет калькулятор .
Задача 4
Найдите периметр квадрата с диагональю 2√2.
Решение
При решении этой задачи воспользуемся формулой №2:
P = 2 sqrt{2} cdot d = 2 sqrt{2} cdot 2 sqrt{2} = ({2 sqrt{2}})^2 = 2^2 cdot ({sqrt{2}})^2 = 4 cdot 2 = 8 : см
Ответ: 8 см
Проверить ответ к этой задаче можно с помощью калькулятора . Диагональ задана выражением с квадратным корнем, введем ее в виде, который сможет распознать наш калькулятор – 2 * sqrt(2).
