Квадрат — это геометрическая фигура, правильный четырехугольник, у которого все углы и стороны равны.
Онлайн-калькулятор периметра квадрата
Противоположные стороны квадрата параллельны.
Другими словами, квадрат — это прямоугольник, у которого все стороны равны, или квадрат — это ромб, у которого все углы прямые. Квадрат имеет две диагонали, которые делятся точкой их пересечения пополам. Диагонали квадрата также делят его углы пополам и соединяют несмежные вершины.
Формула периметра квадрата
Для того чтобы найти периметр квадрата, нужно сложить длины всех его сторон.
P=a+a+a+a=4⋅aP=a+a+a+a=4cdot a
aa — длина стороны квадрата.
Разберем задачу на нахождение периметра квадрата.
Найти периметр квадрата со стороной 12 см.
Решение
a=12a=12
Воспользуемся формулой нахождения периметра квадрата и подставим вместо aa его численное значение:
P=4⋅a=4⋅12=48P=4cdot a=4cdot 12=48 см.
Ответ: 48 см.
Ищете, где заказать решение контрольной работы? Эксперты Студворк с радостью помогут вам!
Тест по теме «Периметр квадрата»
Загрузить PDF
Загрузить PDF
Периметр двумерной фигуры – это общая длина ее границы, равная сумме длин сторон фигуры.[1]
Квадрат – это фигура с четырьмя сторонами одинаковой длины, которые пересекаются под углом 90°.[2]
Так как в квадрате все стороны имеют одинаковую длину, то вычислить его периметр очень легко. Эта статья расскажет вам, как вычислить периметр квадрата по одной данной стороне, по данной площади и по данному радиусу окружности, описанной вокруг квадрата.
-

1
Формула для вычисления периметра квадрата: P = 4s, где s – длина стороны квадрата.
-

2
Определите длину одной стороны квадрата и умножьте ее на 4, чтобы найти периметр. Чтобы определить длину стороны, измерьте ее линейкой или посмотрите ее значение в учебнике (задаче). Вот некоторые примеры вычисления периметра:
- Если сторона квадрата равна 4, то P = 4 * 4 = 16.
- Если сторона квадрата равна 6, то P = 4 * 6 = 36.
Реклама
-

1
Формула для вычисления площади квадрата. Площадь любого прямоугольника (а квадрат – это частный случай прямоугольника) равна произведению его длины на его ширину.[3]
Поскольку длина и ширина квадрата равны, то его площадь вычисляется по формуле: A = s*s = s2, где s – длина стороны квадрата. -

2
Извлеките квадратный корень из значения площади, чтобы найти сторону квадрата. Для этого в большинстве случаев воспользуйтесь калькулятором (введите значение площади и нажмите клавишу “√”). Вы также можете вычислить квадратный корень вручную.
- Если площадь квадрата равна 20, то его сторона равна: s = √20 = 4,472.
- Если площадь квадрата равна 25, то s = √25 = 5.
-

3
Умножьте найденную сторону на 4, чтобы найти периметр. Вычисленное значение стороны подставьте в формулу для нахождения периметра: P = 4s. Вы найдете периметр квадрата.
- В нашем первом примере: P = 4 * 4,472 = 17,888.
- Периметр квадрата, площадь которого равна 25, а сторона равна 5, равен Р = 4 * 5 = 20.
Реклама
-

1
Вписанный квадрат – это квадрат, вершины которого лежат на окружности.[4]
-

2
Отношение между радиусом окружности и длиной стороны квадрата. Расстояние от центра описанной окружности до вершины вписанного в нее квадрата равно радиусу окружности. Чтобы найти сторону квадрата s, необходимо диагональю разделить квадрат на 2 прямоугольных треугольника. Каждый из этих треугольников будет иметь равные стороны a и b и общую гипотенузу с, равную удвоенному радиусу описанной окружности (2r).
-

3
Воспользуйтесь теоремой Пифагора, чтобы найти сторону квадрата. Теорема Пифагора гласит, что в любом прямоугольном треугольнике с катетами а и b и гипотенузой с: a2 + b2 = c2.[5]
Так как в нашем случае а = b (не забывайте, что мы рассматриваем квадрат!), и мы знаем, что с = 2r, то мы можем переписать и упростить это уравнение:- a2 + a2 = (2r)2“‘; теперь упростим это уравнение:
- 2a2 = 4(r)2; теперь разделим обе стороны уравнения на 2:
- (a2) = 2(r)2; теперь извлечем квадратный корень из обеих сторон уравнения:
- a = √(2r). Таким образом, s = √(2r).
-

4
Умножьте найденную сторону квадрата на 4, чтобы найти его периметр. В этом случае периметр квадрата: P = 4√(2r). Эту формулу можно переписать так: Р = 4√2 * 4√r = 5,657r, где r – радиус описанной окружности.[6]
-

5
Пример. Рассмотрим квадрат, вписанный в окружность радиусом 10. Это означает, что диагональ квадрата равна 2 * 10 = 20. Используя теорему Пифагора, мы получим: 2(a2) = 202, то есть 2a2 = 400. Теперь разделим обе стороны уравнения на 2 и получим: a2 = 200. Теперь извлечем квадратный корень из обеих сторон уравнения и получим: а = 14,142. Умножим это значение на 4 и вычислим периметр квадрата: P = 56,57.
- Обратите внимание, что вы могли бы получить тот же результат, просто умножив радиус (10) на 5,657: 10 * 5,567 = 56,57; но такой метод трудно запомнить, поэтому лучше пользоваться процессом вычисления, описанным выше.
Реклама
Похожие статьи
Об этой статье
Эту страницу просматривали 413 196 раз.
Была ли эта статья полезной?
Увидев этот вопрос, мы с сыном, который перешёл в пятый класс, улыбнулись, и начали вспоминать, когда же нахождение периметра проходили в школе. После небольшой, но оживлённой дискуссии, я решил этот вопрос, пробежав программу по математике в начальной школе на сайте Министерства образования и науки Украины. Как оказалось, мой мальчик был прав, что ещё во 2-ом классе, а не в 3-ем, как запомнилось мне, детям уже даются основы геометрический знаний.
Итак, квадрат – это плоская геометрическая фигура состоящая из четырёх отрезков, каждый из которых пересекается с двумя другими под углом в 90 градусов. Соответственно стороны данного четырёхугольника равны.
Для того же, чтобы узнать периметр (сумму всех сторон), достаточно измерить длину одного из отрезков и полученную величину умножить на 4.
Для наглядности проиллюстрирую ниже.

Как видите, всё довольно просто ! Успехов в учёбе !

{P = 4 cdot a}
Периметр квадрата рассчитывается довольно просто, но если вы забыли формулу или не имеете под рукой калькулятора, мы собрали для вас формулы для расчета периметра квадрата и онлайн калькулятор, который рассчитает периметр по длине стороны, диаметру, радиусам вписанной или описанной окружности, площади.
Содержание:
- калькулятор периметра квадрата
- формула периметра квадрата через длину стороны
- формула периметра квадрата через диагональ
- формула периметра квадрата через площадь
- формула периметра квадрата через радиус описанной окружности
- формула периметра квадрата через радиус вписанной окружности
- примеры задач
Квадрат – четырехугольник, у которого все стороны равны и все углы равны (прямые, 90 градусов). Квадрат так же называют правильным четырехугольником. Квадрат является частным случаем прямоугольника и ромба.
Кроме квадрата на сайте вы можете найти периметр ромба, прямоугольника, параллелограмма.
Формула периметра квадрата через длину стороны

{P = 4 cdot a}
a – сторона квадрата
Формула периметра квадрата через диагональ

{P = 2 sqrt{2} cdot d}
d – диагональ квадрата
Формула периметра квадрата через площадь
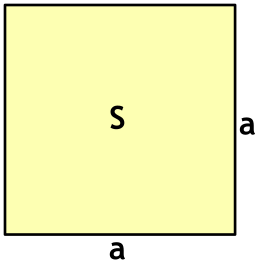
{P = 4sqrt{S}}
S – площадь квадрата
Формула периметра квадрата через радиус описанной окружности

{P = 4sqrt{2} cdot R}
R – радиус описанной около квадрата окружности
Формула периметра квадрата через радиус вписанной окружности
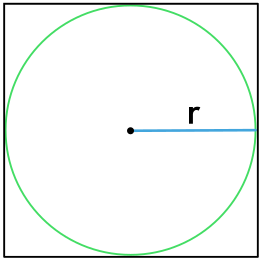
{P = 8r}
r – радиус вписанной в квадрат окружности
Примеры задач на нахождение периметра квадрата
Задача 1
Найти периметр квадрата, вписанного в окружность с R = 4√2.
Решение
Среди формул для решения этой задачи используем наиболее подходящую формулу №4. В условии сказано про квадрат, вписанный в окружность. Но при этом окружность будет описана около квадрата. Именно поэтому мы используем эту формулу. Подставим в нее известный из условия радиус вписанной окружности (в нашем случае он будет являться радиусом описанной окружности):
P = 4sqrt{2} cdot R = 4sqrt{2} cdot 4sqrt{2} = ({4sqrt{2}})^2 = {4^2 cdot ({sqrt{2}})^2} = 16 cdot 2 = 32 : см
Ответ: 32
Проверить полученный ответ можно с помощью калькулятора . Однако, радиус задан не просто числом, а выражением с квадратным корнем – 4√2. К счастью, наш калькулятор может анализировать математические выражения и производить с ними вычисления. Так как на клавиатуре компьютера нет знака квадратного корня, ввести значение радиуса необходимо в таком виде – 4*sqrt(2).
Задача 2
Найдите периметр квадрата сторона которого 13см.
Решение
Чтобы решить эту задачу используем первую формулу:
P = 4 cdot a = 4 cdot 13 = 52 : см
Ответ: 52 см
Проверить ответ поможет калькулятор .
Задача 3
Найдите периметр квадрата сторона которого 5см.
Решение
Для решения этой задачи также используем первую формулу:
P = 4 cdot a = 4 cdot 5 = 20 : см
Ответ: 20 см
Проверить ответ поможет калькулятор .
Задача 4
Найдите периметр квадрата с диагональю 2√2.
Решение
При решении этой задачи воспользуемся формулой №2:
P = 2 sqrt{2} cdot d = 2 sqrt{2} cdot 2 sqrt{2} = ({2 sqrt{2}})^2 = 2^2 cdot ({sqrt{2}})^2 = 4 cdot 2 = 8 : см
Ответ: 8 см
Проверить ответ к этой задаче можно с помощью калькулятора . Диагональ задана выражением с квадратным корнем, введем ее в виде, который сможет распознать наш калькулятор – 2 * sqrt(2).
В данной публикации мы рассмотрим, каким образом можно посчитать периметр квадрата и разберем примеры решения задач.
-
Формула вычисления периметра
-
По длине стороны
- По длине диагонали
-
По длине стороны
- Примеры задач
Формула вычисления периметра
По длине стороны
Периметр (P) квадрата равняется сумме длин его сторон.
P = a + a + a + a

Так как все стороны квадрата равны, формулу можно представить в виде произведения:
P = 4 ⋅ a
По длине диагонали
Периметр (P) квадрата равен произведению длины его диагонали на число 2√2:
P = d ⋅ 2√2

Данная формула следует из соотношения длин стороны (a) и диагонали (d) квадрата:
d = a√2.
Примеры задач
Задание 1
Найдите периметр квадрата, если его сторона равна 6 см.
Решение:
Используем формулу, в которой участвует значение стороны:
P = 6 см + 6 см + 6 см + 6 см = 4 ⋅ 6 см = 24 см.
Задание 2
Найдите периметр квадрата, диагональ которого равняется √2 см.
Решение 1:
С учетом известной нам величины воспользуемся второй формулой:
P = √2 см ⋅ 2√2 = 4 см.
Решение 2:
Выразим длину стороны через диагональ:
a = d / √2 = √2 см / √2 = 1 см.
Теперь, используя первую формулу, получаем:
P = 4 ⋅ 1 см = 4 см.
