Четырехугольник не является прямоугольником.
Периметр искать легко в отличие от площади. В периметре сложить величины всех сторон четырехугольника можно за несколько секунд, потому что стороны редко бывают больше 10 сантиметров, значит все подсчеты производим в уме.
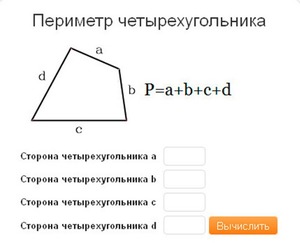
Это четырехугольник.
Это формула периметра, обозначается буквой Р.
автор вопроса выбрал этот ответ лучшим
Tanyetta
[298K]
9 лет назад
Вспоминая уроки геометрии. Найти периметр четырехугольника очень просто! Для этого надо сложить длину всех его сторон. А если четырехугольник прямоугольный, то короткая сторона плюс длинная сторона умножить на 2! Удачных решений примеров и задач!
Носорог
[63.1K]
9 лет назад
Четырехугольник не всегда является прямоугольником или квадратом, все верно было сказано. И в то же время квадрат и прямоугольник можно назвать четырехугольниками. Четырехугольник может иметь как одинаковую длину сторон, так и разную. Ну а что такое периметр, периметр плоской фигуры (а в данном случае четырехугольник как раз плоская двухмерная фигура) – это сумма сторон. Так что чтобы узнать, вычислить периметр, необходимо знать длину каждой из сторон, а затем складываем длины и получаем конечную сумму.
У квадрата измеряем одну сторону и умножаем на 4. У квадрата же все стороны равны по длине. Это известно еще со школы с уроков геометрии.
Четырехугольник-это геометрическая фигура с четырьмя углами и с четырьмя сторонами. Так что найти периметр легко. Нужно измерить длину всех сторон и сложить их длины. И данный ответ и будит являться периметром.
ИнгаМус
[16.7K]
9 лет назад
Четырехугольник имеет четыре стороны, как мы видим уже из названия. Еще со школьных времен прочно запомнилась формула нахождения периметра четырехугольника.
Если он не является прямоугольником, то нам надо будет знать длину его каждой стороны по отдельности. Сложив их все вместе, мы и узнаем периметр этой фигуры.
Если кому – то потребуется вот здесь есть калькулятор расчета периметра четырехугольника.
elena-kh
[245K]
9 лет назад
Чтобы найти периметр, нужно сложить длины всех сторон. Если бы являлся прямоугольником, было бы проще, ведь можно было каждую длину умножить на 2, а потом сложить. У квадрата все еще проще – нужно длину одной стороны умножить на 4. У остальных прямоугольников, как правило, необходимо просто сложить все стороны. Хотя для параллелограммов тоже есть свои формулы.
Афанасий44
[442K]
9 лет назад
Четырёхугольник может быть неправильной формы и все стороны его могут иметь разную длину. Например, такие четырёхугольники:
В таких случаях, чтобы найти периметр неправильного четырёхугольника, надо просто измерить длину каждой его стороны и потом всё сложить.
Для того чтобы вам найти периметр четырёхугольника вам нужно вспомнить уроки геометрии в школе которые раньше для меня были очень интересными, так вот что надо сделать, надо сложить все длины четырёх сторон и у вас получится периметр.
Edvard
[10.5K]
9 лет назад
Найти периметр четырехугольника не представляет из себя ничего сложного. Надо всего лишь найти сумму длин всех четырех сторон четырехугольника. Этот нехитрый способ известен нам еще со школьной скамьи.
Безразличный
[256K]
10 лет назад
Сложите длины всех четырех сторон и получите периметр.
Агафья
[118K]
8 лет назад
Вообще просто для этого достаточно перемерить все стороны прямоугольника и их величины сложить вместе. Вот эта сумма и будет являться периметром неправильного четырёхугольника. Меня этому ещё в школе научили.
Знаете ответ?
Как найти периметр сторон четырехугольника, формула нахождения
Совсем недавно в России родители отправляли своих детей в первый класс и с нетерпением ждали их первых заданий. Они с удовольствием наблюдали за тем, как их дети знакомятся с буквами русского алфавита, учатся считать палочки и точечки, выводить различные кривые и прямые линии. Родители помогали знакомиться своим детям с тем, что тетрадь в клеточку предназначена для написания цифр, а тетрадь в линеечку — для письма.
Сегодня, будучи второклассниками, ученики России достигли больших успехов в сфере начального образования, а точнее, в математическом прогрессе. Учителя научили их складывать и вычитать, умножать, делить, измерять.
Кстати, по поводу измерения: с линейкой ребята вторых классов России уже знакомы, и применение ей, кроме как стрелять с задней парты в соседа бумажки, они тоже знают. Именно об измерениях мы и заведем сегодняшний разговор.
Как мы видим, прогресс обучения нынешних учеников проходит слегка в ускоренном режиме. С теми темами, например, такими как периметр, дети 90-х знакомились позже, а наши ребята узнают сегодня. Конечно, в этом нет ничего страшного. Время меняется, и программа обучения тоже должна не стоять на месте. Зато, как считают многие, наши дети будут умнее нас.
Школьное задание
Наверное, многих родителей сегодня удивляют нынешние задания для второклассников. В учебнике по математике для второго класса можно встретить такое задание, как, например: «Найди периметр четырехугольника, две стороны которого равны по 2 сантиметра, а другие две будут по 3 сантиметра». Как справиться с данным заданием?
Многие родители настоящего времени являются теми самыми детьми девяностых годов, и, естественно, в большинстве случаев, мало кто помнит, что такое периметр. Особенно, если учились не на отлично, да и не совсем на «хорошо».
Естественно, каждому родителю хотелось бы, чтоб его ребенку было проще в обучении, и они всеми силами стараются ему в этом помочь. Некоторым родителям сначала приходится справиться со своей душевной паникой, а уже потом продолжать объяснять своему ребенку. В этом случае многим помогает интернет, место, где можно найти ответы на все тревожные вопросы. Во времена девяностых, к сожалению, такой «роскоши» не было.
Вопросы:
- Что такое «периметр»?
- Как находить периметр четырехугольника?
Ответы на вопросы:
Для тех, кто знает, вспоминаем, а кто не знает — объясняем:
- Периметр — это сумма всех сторон четырехугольника. Всего лишь каждая грань по отдельности будет равна после сложения единому числу.
- Найти периметр, значит, что нужно взять линейку и измерить каждую границу четырехугольника. После выполнения данного действия необходимо сложить полученные числа между собой. Общая полученная сумма и будет являться периметром.
Решение:
В данном случае, по действиям нашей задачи, нам известны суммы сторон четырехугольника, а именно две из них по 2 сантиметра и две по 3 сантиметра. Поэтому нам остается всего лишь перечертить четырехугольник в тетрадь и сложить известные нам суммы каждой грани.
2+2+3+3=10
Как мы видим, периметр нашей четырехугольной фигуры равен 10.
В математике сумму всех сторон (периметр) мы обозначаем символом Р.
Теперь записываем правильное решение этой задачи:
Р=2+2+3+3;
Ответ: Р=10.
В математике существует формула, запомнив которую, вы никогда не будете забывать, как найти периметр (общую сумму всех сторон) четырехугольника и выглядит она так:
P = a + b + c + d (где a , b, c, d являются границами четырехугольника).
Кроме того, хотелось бы обратить внимание, что четырехугольник не обязательно будет являться прямоугольником. Это может быть и квадрат, у которого все стороны равны, и любая другая геометрическая фигура, у которой есть четыре стороны и такое же количество углов.
Грани произвольного четырехугольника могут совсем не совпадать ни с одной из сторон фигуры. Это могут быть совершенно разные числа. И, в итоге, получаются фигуры с четырьмя сторонами и теми же четырьмя углами. Фигура не будет похожа ни на квадрат, ни на прямоугольник, так как углы ее прямыми не будут. И периметр, соответственно мы вычисляем по той же самой единой формуле.
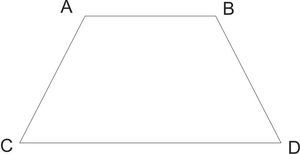
Или взять, например трапецию. Обычно у трапеции две стороны одинаковые, а другие две совсем не совпадают, но между собой параллельные.
На примере трапеция может выглядеть так: верхняя грань равна 2 сантиметра, левая и правая стороны по 3 сантиметра, соединяем их с нижней гранью и получаем трапецию. Высчитываем каждую ее сторону и снова получаем периметр четырехугольника.
Вычислить по формуле всегда будет проще, и не важно, каким числам равна каждая сторона.
Так как современные дети страны уже дошли до таблицы умножения, с периметром квадрата у них проблем не будет. Зная размер одной стороны квадрата, нужно умножить ее на все четыре равные стороны.
В общем, теперь стоит взять линейку с карандашом и лист бумаги. После этого следует начертить произвольные фигуры с четырьмя углами и высчитать общую сумму ее сторон.
Четырехугольник, вписанный в окружность – основные свойства, признаки и формулы
Общие сведения
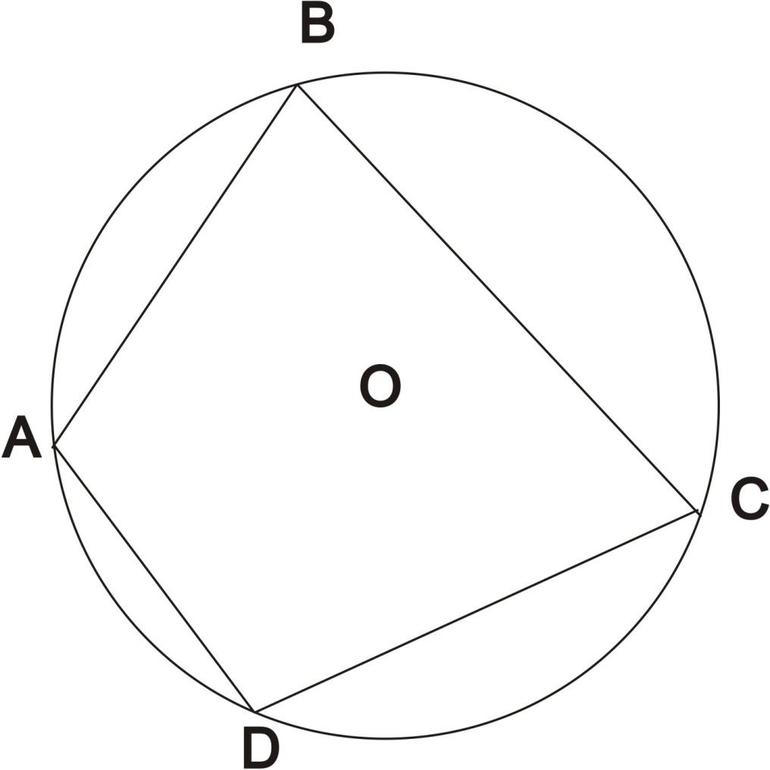
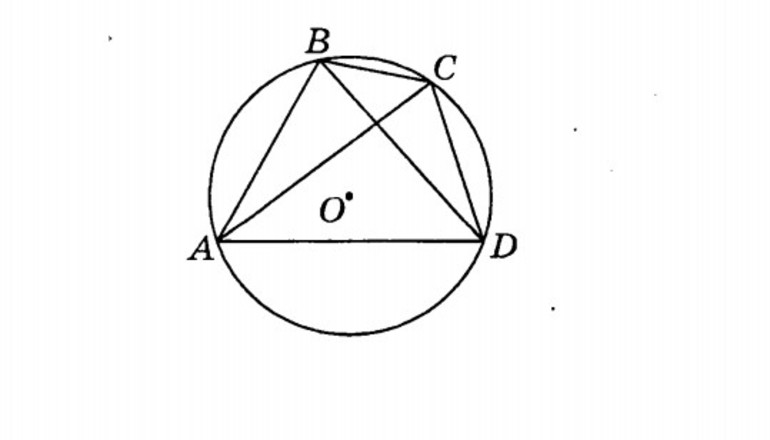
Фигура является вписанной в окружность, когда все ее вершины лежат на ней. Произвести вписание в окружность четырехугольника можно только в том случае, когда он выпуклый. Все его точки находятся по одну сторону от произвольной прямой, которая проходит через соседние вершины фигуры. Нужно отметить, что в этом случае окружность является описанной вокруг фигуры. Если в параллелограмм вписана окружность, то ее центр совпадает с центром окружности, которая описана вокруг него.
Четырехугольники бывают самопересекающимися. Они также могут быть вписанными, однако это встречается крайне редко. Не каждую фигуру можно вписать в круг, поскольку существуют определенные законы. Например, вокруг ромба нельзя описать круг — исключение составляет случай, когда ромб является квадратом.
Основные правила
Выпуклый четырехугольник можно вписать в окружность. Однако для этого существуют некоторые правила (критерии) или признаки. Некоторые задачи сформулированы таким образом, что нужно знать основные критерии, а также уметь доказывать возможность вписывать или описывать окружность. Около четырехугольника можно описать окружность, если выполняются следующие условия:
- Сумма углов, которые являются противоположными, соответствует 180 градусам.
- Соблюдается равенство смежного и противоположного углов.
- Угол между стороной и диагональю равен углу между противоположной стороной и диагональю.
- Произведение двух диагоналей соответствует размерности суммы произведений противоположных сторон.
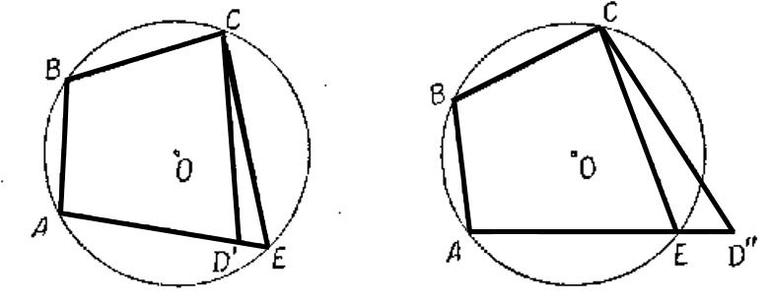
- Четыре точки лежат на окружности, когда две прямые АС и BD, образующие диагонали, пересекаются в некоторой точке P, а также выполняется следующее равенство: AP * PC = BP * PD.
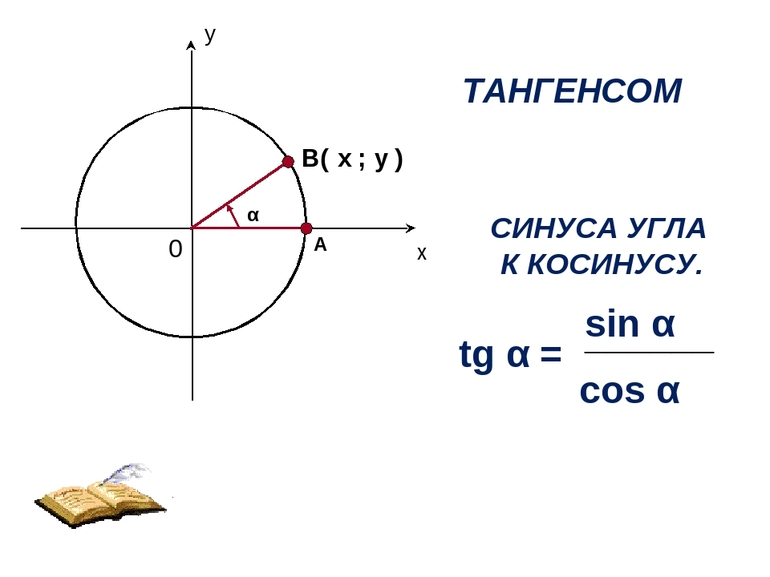
- Произведения тангенсов половины двух противоположных углов равны 1. Кроме того, значения произведений эквивалентны друг другу (tg (A/2) * tg (C/2) = tg (B/2) * tg (D/2) = 1).
Четвертое утверждение является теоремой Птолемея. Все эти правила являются следствиями, полученными при доказательстве различных гипотез. Правила можно применять в зависимости от условия поставленной задачи. Любой параллелограмм можно вписать в окружность, когда он является прямоугольником или квадратом.
Свойства и утверждения
При решении можно воспользоваться некоторыми свойствами, которые были доказаны. Это нужно для того, чтобы не тратить время на выведение какой-либо формулы. Применяется методика для оптимизации вычислений. К ним можно отнести следующие:
- Если вокруг четырехугольника описана окружность, то центры окружностей, которые вписанных в треугольники, образованные диагоналями фигуры, являются вершинами прямоугольника.
- Не бывает четырехугольников, вписанных в окружность, с рациональной площадью и сторонами, которые образуют арифметический или геометрический тип прогрессии.
- При продолжении сторон до точек пересечения Y и Z, внутренние биссектрисы углов Y и Z являются перпендикулярными.
Данные утверждения применяются не всегда. В некоторых случаях можно ограничиться формулами и основными соотношениями — они позволяют легко и быстро искать нужные величины.
Формулы и соотношения
Очень часто необходимо перерыть горы информации для поиска нужной формулы. Это сказывается на оптимизации решения. Кроме того, некоторые соотношения могут содержать ошибки, поскольку материал излагается неквалифицированными специалистами.
Педагоги утверждают, что обучение какой-либо дисциплине с физико-математическим уклоном должно быть основано на алгоритмах. Кроме того, рекомендуется прочитать условие задачи несколько раз до полного его понимания. В основном необходимо находить площадь, диагонали и углы четырехугольника.
Периметр и полупериметр
Периметром выпуклого четырехугольника со сторонами a, b, c и d называется сумма длин всех его сторон. Величина обозначается литерой «Р», и вычисляется по следующей формуле: P = a + b + c +d. Кроме того, в некоторых формулах встречается величина, которая называется полупериметром. Обозначается она литерой «р». Для ее нахождения применяется такое соотношение: p = P / 2 = (a + b + c +d) / 2. Единицей измерения полупериметра являются метрические величины: мм, см, дм, м и т. д.
Для квадрата формула периметра имеет вид: P = 4 * a. Равенство легко доказывается для фигуры со стороной а. Из определения периметра получается соотношение: P = a + a + a + a. Если привести подобные слагаемые, то результирующая формула имеет вид: P = 4 * a. У прямоугольника противоположные стороны равны. Чтобы найти его периметр, нужно воспользоваться равенством: P = a + b + a + b = 2 * (a + b). Необходимо отметить, что квадрат является правильным четырехугольником, поскольку его стороны равны между собой.
Понятие площади
Площадь двумерных фигур — понятие геометрии, которое показывает ее численную характеристику или размер. Очень часто она обозначается литерой S. Измеряется величина в квадратных единицах (см 2 , м 2 и т. д. ). Фигура, имеющая характеристику S, называется квадратируемой.
Для нахождения S применяется интегральный метод, но существуют частные случаи, при которых интегрировать необязательно. Очень часто возникает необходимость перевода одной единицы в другую. Для этого существует простой алгоритм, позволяющий корректно выполнить данную операцию. Например, нужно перевести м 2 в см 2 . Необязательно заучивать единицы площади и их эквивалентность другим. Достаточно выполнить следующие действия:
- Определить базовую единицу: м и см.
- Выполнить перевод одной метрической величины в другую: 1 м = 100 см.
- Возвести обе части выражения во втором пункте в квадрат: 1 м 2 = 100 2 см 2 = 10000 см 2 .
Однако бывают и другие единицы, которые применяются для измерения размерности земельных участков: 1 ар (сокращенно а) = 1 сотке = 100 м 2 и 1 гектар (га) = 10000 м 2 .
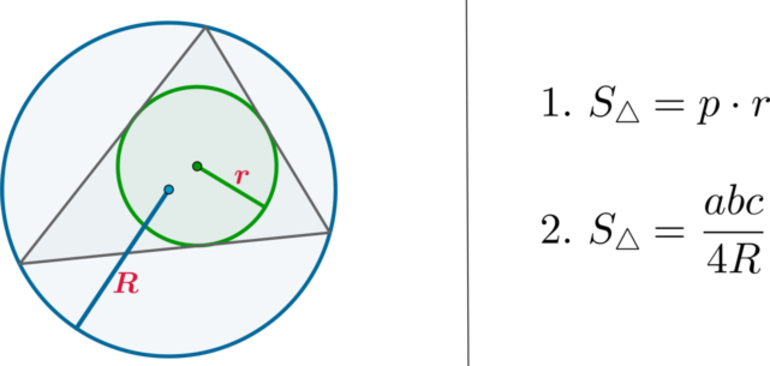
Когда известны все стороны четырехугольника (a, b, c и d), который вписан в окружность, можно найти его S. Для этого нужно знать еще одну величину. Она называется полупериметром. Расчет выполняется по формуле: S = [(p — a) * (p — b) * (p — c) * (p — d)]^(½). Соотношение называется формулой Брахмагупты.
Необходимо отметить, что вписанный четырехугольник обладает максимальным значением S среди остальных эквивалентных фигур. Если известны четыре стороны, которые являются последовательными (a, b, c и d), а также угол В между a и b, то можно воспользоваться более упрощенной формулой: S = [(a * b + c * d) * sin (B)] / 2. В случае, когда известны все стороны и любой угол (Y) между диагоналями, соотношение можно записать таким образом: S = [(a * с + и * d) * sin (Y)] / 2.
Площадь можно выразить и другим соотношением, когда известны все стороны и угол А, который не является прямым: S = [(a 2 — b 2 — c 2 + d 2 ) * tg (A)] / 4. При известном радиусе описанной окружности и углах (A, B и Y) можно воспользоваться такой формулой: S = 2 * R^(2) * sin (A) * sin (B) * sin (Y). Следствием из последнего соотношения является S 2 . Если четырехугольник является квадратом, то неравенство преобразуется в равенство, т. е. S = 2 * R 2 .
Диагонали и углы
Для вписанного четырехугольника ABCD существуют определенные соотношения, по которым можно найти его диагонали. Для фигуры со сторонами a = AB, b = BC, c = CD и d = DA диагонали (s = АС и t = DA) находятся таким образом: s = [((a * c + b * d) * (a * d + b * c)) / (a * b + c * d)]^(½) и t = [((a * c + b * d) * (a * b + d * c)) / (a * d + c * b)]^(½). Если умножить диагональ s на t и привести подобные слагаемые, то в результате получится формула Птолемея: s * t = a * c + b * d.
При отношении двух диагоналей получается вторая теорема Птолемея: s / t = (a * d + b * c) / (a * b + d * c). Сумма диагоналей — есть неравенство такого вида: s + t >= 2 * [a * c + b * d]^(½). Неравенство преобразуется в равенство, когда диагонали равны. Однако в этом случае можно воспользоваться следующим выражением: [s + t]^(½) >= [a * c]^(2) + [b * d]^(2).
Необходимо отметить, что в произвольном выпуклом четырехугольнике диагонали делят его на 4 треугольника, которые являются между собой подобными по парам. Кроме того, при пересечении двух диагоналей AC и BD в некоторой точке М, справедливо следующее соотношение: AM / CM = (AB * AD) / (CB * CD).
Можно находить и некоторые углы фигуры. Для этого существуют определенные соотношения. Во вписанном четырехугольнике со сторонами, которые соответствуют значениям a, b, c и d, углом A между сторонами a и d, а также полупериметром p, функции тригонометрического типа для А вычисляются таким образом:
- cos (A) = (a 2 + d 2 — b 2 — c 2 ) / (2 * (a * d + b + c)).
- sin (A) = [(p — a) * (p — b) * (p — c) * (p — d)]^(½) / (a * d + b + c).
- tg (A/2) = [((p — a) * (p — d)) / ((p — b) * (p — c))]^(½).
В некоторых случаях нужно вычислить значение тангенса для угла Y, который находится между диагоналями, по формуле: tg (Y/2) = [((p — b) * (p — d)) / ((p — a) * (p — c))]^(½).
В геометрии существует вписанный четырехугольник, стороны которого являются целыми числами. Кроме того, целочисленными являются также его диагонали и площадь. Он называется четырехугольником Брахмагупты. Однако для преобразования любого четырехугольника в данную фигуру необходимо выполнить некоторые математические операции. Пусть он имеет следующие целочисленные параметры:
- Стороны: a, b, c и d.
- Диагонали: s и t.
- Площадь: S.
- Радиус описанной окружности: R.
В некоторых случаях возникает необходимость избавиться от рациональных значений в знаменателе. При значениях дробных параметров k, l и m нужно использовать такие соотношения:
- a = [k * (l + m) + (1 — (l * m))] * [l + m — k * (1 — (l * m))].
- b = (1 — l 2 ) * (m — k) * (1 + k * m).
- c = k * (1 + l 2 ) * (1 + m 2 ).
- d = (1 + m 2 ) * (l — k) * (1 + k * l).
- s = l * (1 + k 2 ) * (1 + m 2 ).
- t = m * (1 + k 2 ) * (1 + l 2 ).
- S = l * m * [2 * k * (1 — l * m) — (l + m) * (1 — k 2 )] * [2 * k (l + m) + (1 — l * m) * (1 — k 2 )].
- 4 * R = (1 + l 2 ) * (1 + m 2 ) * (1 + k 2 ).
Существуют также соотношения для описанной вокруг четырехугольника окружности. Математики утверждают, что при комбинации двух и более геометрических фигур время поиска некоторых параметров увеличивается.
Параметры для окружности
Радиус окружности R для четырехугольника c полупериметром р и со сторонами a, b, c, d находится по формуле Парамешвары: R = (¼) * [((a * b + c * d) * (a * c + b * d) * (a * d + b * c)) / ((p — a) * (p — b) * (p — c) * (p — d))]^(½). Соотношение было выведено в XV веке математиком из Индии Ватассери Парамешварой.
При комбинации данной формулы с соотношением Брахмагупты можно получить следующее соотношение: 4 * S * R = [(a * b + c * d) * (a * c + b * d) * (a * d + b *c)]^(½). Следует отметить, что величина S является площадью вписанного четырехугольника. Для ортогонального четырехугольника с перпендикулярными диагоналями, которые делятся на отрезки s1, s2, t1 и t2, существует некоторое соотношение, позволяющее найти диаметр окружности (D): D 2 = (s1)^2 + (s2)^2 + (t1)^2 + (t2)^2 = a 2 + c 2 = b 2 + d 2 .
Радиус в этом случае находится таким образом: R = D / 2 = [(s1)^2 + (s2)^2 + (t1)^2 + (t2)^2] / 2 = [a 2 + c 2 ] / 2 = [b 2 + d 2 ] / 2. Если выполнить сложение квадратов сторон, то получится такое равенство: 8 * R = a 2 + b 2 + c 2 + d 2 . По формуле Эйлера R можно также выразить через диагонали (s и t) и расстояние v между их серединами: R = [(s 2 + t 2 + 4 * v 2 ) / 8]^(½).
Таким образом, специалисты рекомендуют на начальных этапах обучения использовать уже готовые формулы для вычисления основных параметров выпуклого четырехугольника, вписанного в окружность.
Как найти периметр фигуры
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Определение периметра
Периметр — это сумма длин всех сторон многоугольника.
Какой буквой обозначается периметр? Заглавной латинской P. Под обозначением P удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах по ходу решения.
В чем измеряется периметр? В тех же единицах измерения, что и длина — например, миллиметр, сантиметр, метр, фут, дюйм, локоть и др.
Если в условиях задачки длины сторон переданы в разных единицах длины, мы не сможем узнать периметр фигуры. Для правильного решения нужно перевести все данные в одну единицу измерения.
Формулы нахождения периметра
Как мы только что узнали, периметр — это сумма длин всех сторон многоугольника. А значит, чтобы его найти, нам надо знать длины этих сторон. Давайте посмотрим, как найти периметр, на примерах нескольких фигур.
Равносторонний многоугольник
У равностороннего треугольника все стороны равны. А значит, периметр равностороннего треугольника можно найти как произведение длины стороны на их количество, т. е. на 3.
P = 3 ⋅ a, где a — длина стороны.
Периметр любого другого равностороннего многоугольника можно найти тем же способом: умножив длину его стороны на их количество. Например, у квадрата и ромба все стороны равны, а значит, их периметр можно найти по формуле P = 4 ⋅ a, где a — длина стороны.
А формула для любого равностороннего n-угольника будет такая: P = n ⋅ a, где a — длина стороны, n — количество сторон.
Прямоугольник и параллелограмм
У прямоугольника и параллелограмма противоположные стороны равны, а значит, найти их периметр легко, зная две соседние стороны.
P = 2 ⋅ (a + b), где a — одна сторона, b — соседняя сторона.
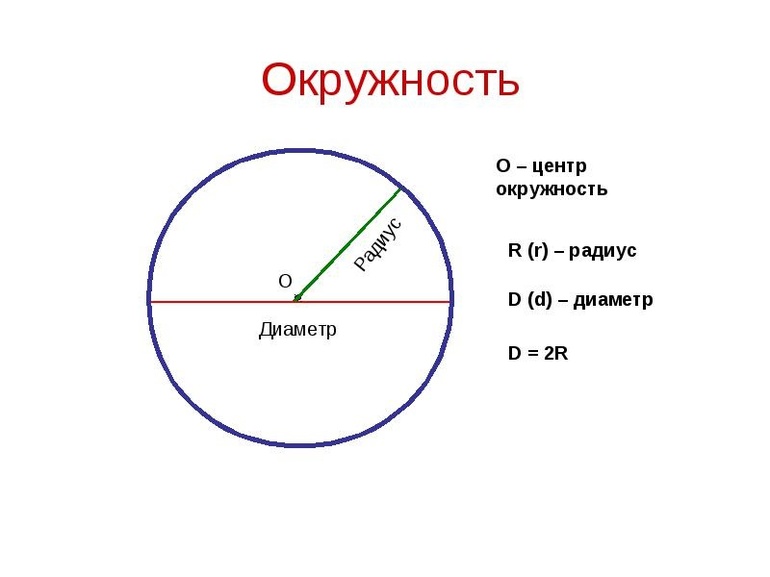
Окружность
У окружности нет периметра, потому что это не многоугольник. Но у нее есть длина, которую можно найти, зная радиус. Длина окружности — это произведение пи на два радиуса или произведение пи на диаметр.
L = d ⋅ π = 2 ⋅ r ⋅ π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она приблизительно равна 3,14.
Можно выучить все формулы, а можно, запомнив определение о сумме всех сторон, каждый раз проявлять смекалку и вычислять самостоятельно. Давайте потренируемся, как определять периметр фигур!
Решение задач
Площадь прямоугольника равна 80 см 2 , длина составляет 10 см. Чему равен периметр фигуры?
- Для использования формулы P = 2 × (a + b), нам нужно найти ширину;
- Так как S = a × b, для поиска одной стороны необходимо разделить площадь на известную сторону: 80 : 10 = 8 см;
- Далее подставляем известные данные в формулу: (10 + 8) × 2 = 36 см;
Равнобедренный треугольник имеет периметр 40 см, длина его основания составляет 6 см. Какую длину будут иметь две другие стороны?
- Мы знаем, что периметр — это сумма длин всех сторон, а значит, если вычесть из данного периметра сторону основания — получим сумму двух оставшихся сторон: 40 − 6 = 34 см;
- Известно, что равнобедренный треугольник имеет две равные стороны;
- Далее делим получившуюся сумму на два: 34 : 2 = 17 см;
Ответ: две другие стороны равны по 17 см.
Радиус окружности равен периметру равностороннего пятиугольника со стороной 4 см. Найдите длину окружности.
- Периметр равностороннего пятиугольника равен 4 × 5 = 20 см, значит, радиус окружности равен 20 см;
- Длина окружности равна π × 2 × 20 = 40π см;
Еще больше практических заданий — на курсах по математике в онлайн-школе Skysmart!
[spoiler title=”источники:”]
http://nauka.club/matematika/chetyrekhugolnik-vpisan-v-okruzhnost.html
http://skysmart.ru/articles/mathematic/perimetr-figury
[/spoiler]
Как найти периметр четырехугольника: простые методы решения
Периметр – это сумма всех сторон многоугольника. Поэтому найти периметр четырехугольника нужно просто сложить все его стороны.
Существует несколько способов найти периметр четырехугольника:
1. Сложение всех сторон. Для этого необходимо измерить каждую сторону четырехугольника с помощью линейки и сложить их значения.
2. Использование формулы. Известно, что периметр четырехугольника равен сумме длин всех его сторон: P = a + b + c + d. Где a, b, c и d – длины соответствующих сторон.
3. Разложение на составные части. Обратите внимание, что для некоторых четырехугольников более удобно разложить его на более простые составные части, например, на два треугольника. Затем вычислить периметр каждого треугольника и сложить их значения.
Зная формулу для периметра четырехугольника и простые методы его вычисления, вы можете быстро и легко определить периметр любого четырехугольника. Будьте внимательны и не перепутайте порядок сложения сторон или пропуска измерения стороны – это может повлиять на результат вычислений.
Периметр четырехугольника
Сергей Феликсович Савельев
Эксперт по предмету «Калькуляторы»
Задать вопрос автору статьи
В этой статье мы расскажем вам, как найти периметр четырехугольника, зная его стороны, а также о том, какие бывают четырёхугольники.
Для удобства на страницу добавлен онлайн-калькулятор для расчёта периметра произвольного четырёхугольника.
Определение 1
Четырёхугольником называют геометрический объект, состоящий из четырёх вершин, три из которых не лежат на одной прямой, и четырёх отрезков.
Различают выпуклые и невыпуклые четырёхугольники. К выпуклым относят ромбы, трапеции, параллелограммы и некоторые другие фигуры.
Расчет периметра четырехугольника
Периметр любого четырёхугольника можно рассчитать путём суммирования его сторон:
$P = a + b + c + d$, где
$a, b, c, d$ — стороны четырёхугольника.
Рассмотрим, как использовать формулу для расчёта периметра четырехугольника.
Пример 1
Задача
Дан четырёхугольник со сторонами $a, b, c$ и $d$, равными соответственно $3, 4, 5$ и $6$ см. Найдите его периметр.
Решение:
Для получения ответа сложим все стороны:
$P = 3 + 4 + 5 + 6 = 18$ см.
Ответ совпадает с ответом онлайн-калькулятора, а значит, решение найдено верно.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата написания статьи: 07.07.2019
Как найти периметр четырехугольника
Нахождение периметра четырехугольника – важный процесс в понимании задач с повышенной сложностью. Несмотря на это, процесс не составляет большого труда. Данная статья рассмотрит варианты и примеры нахождения периметра четырехугольника.
1
Суть периметра
Периметр – не только геометрическое понятие. Он используется и в жизни. Умением находить периметр пользуются в строительном бизнесе, при ремонте квартир, постройке частных домов. Вам понадобится вычислить периметр фигуры, которая будет окружать ваш дом. Если вы осознаете, насколько важно уметь применять периметр в разных сферах деятельности реальной жизни, то изучать данную тему будет намного интереснее.
Не важно с какой геометрической фигурой вы имеете дело – квадратом, ромбом, треугольником или шестиугольником. Важным является то, что периметром любой фигуры, в независимости от ее формы и количества углов, будет сумма длин всех сторон. Для нахождения периметра необходимо знать значение всех сторон. Если значение какой-либо из сторон не приведено в условии задачи, нужно будет сначала найти его.
2
Виды четырехугольников
В геометрии существует большое количество фигур. Любая фигура, имеющая четыре угла (четыре стороны) является четырехугольником.
Ниже приведены основные виды четырехугольников, которые встречаются в книгах по геометрии:
- Квадрат. Все стороны данной фигуры равны. Чтобы найти периметр, необходимо сложить их или умножить величину одной стороны на 4. Формула выглядит следующим образом: P = a + a + a + a, P = 4a. P – периметра и a – длина стороны.
Пример: Найдите периметр квадрата, если известно что его сторона равна 6.Решение и рассуждения: Мы уже знаем, что для нахождения периметра квадрата необходимо умножить значение его стороны на количество. Подставив значения в формулу, получим: P = 4×6 = 24. - Прямоугольник. Прямоугольник – это такая фигура, где параллельные стороны равны. Он имеет две длины и две ширины. Длина фигуры обозначается латинской буквой a, ширина же – латинской буквой b. Формула нахождения периметра прямоугольника будет иметь следующий вид: P = 2a + 2b. Таким образом, зная ширину и длину мы сможем найти периметр. Важно помнить, что если нам знакомо значение только длины или только ширины, найти периметр невозможно.
Пример: Найти P прямоугольника, если его длина = 5, а ширина = 3.Решение: Подставим значения сторон в формулу: P = 2a + 2b = 2×5 + 2×3 = 10 + 6 = 16 - Ромб. У ромба, как и квадрата, все стороны равны. Легко догадаться, что по отношению к ромбу применяется та же формула, что и квадрату: P = a + a + a + a, P = 4a. P – периметра и a – длина стороны.
Пример: Какому значению будет равен периметр ромба, если его сторона равна 7 см.Решение: Мы уже знаем, что для нахождения периметра ромба необходимо умножить значение его стороны на количество. Подставив значения в формулу, получим: P = 4×7 = 28. - Параллелограмм. У данной фигуры стороны, которые лежат друг против друга (параллельные) равны. Таким образом, формула нахождения периметра для параллелограмма идентична формуле периметра для прямоугольника. P = 2a + 2b.
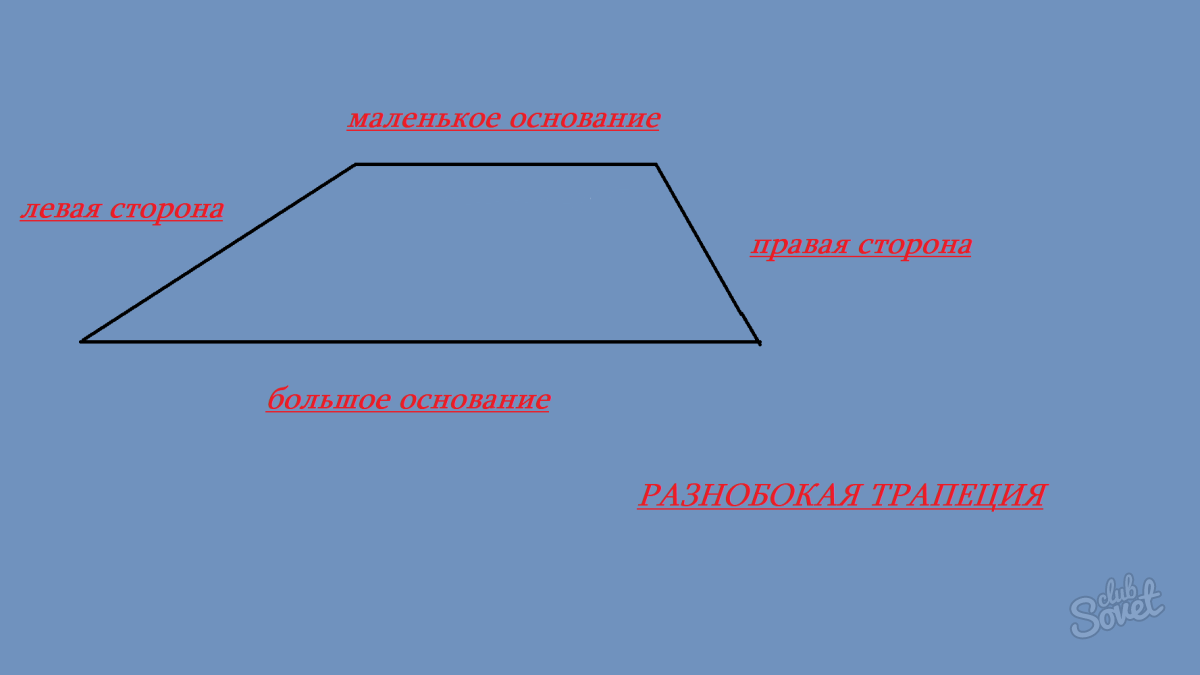
Пример: Найти значение периметра, если одна сторона параллелограмма равна 9, а вторая – 7.Решение: Подставив значения в формулу, получим: P = 2×9 + 2×7 = 18 + 14 = 32. - Трапеция (Равнобокая трапеция, Прямоугольная трапеция).Трапеция может быть как разнобокой, так и равнобокой, а также прямоугольной. В независимости от этого, исходя из сути периметра, для его нахождения необходимо сложить все стороны. Трапеция имеет следующие стороны: маленькой основание, большое основание, левая и правая стороны). Формула будет иметь следующий вид: P = a + b + c + d, где a и b – числовые значения оснований трапеции и c, d – левая и правая стороны.
Пример: Маленькое основание трапеции = 3, большое – 5. Левая сторона рана 2, правая – 4. Найти периметр.Решение: Применяя приведенную выше формулу, получим: P = 3 + 5 + 2 + 4 = 14
Все те же действия будет необходимо проделать с равнобокой и прямоугольной трапецией. Единственное различие – это то, что в равнобокой трапеции левая и правая стороны равны друг другу. Логично, что идентичными будут и углы при большом основании. Прямоугольная трапеция имеет 1 прямоугольный угол, который находится у большого основания фигуры.
3
Онлайн калькулятор
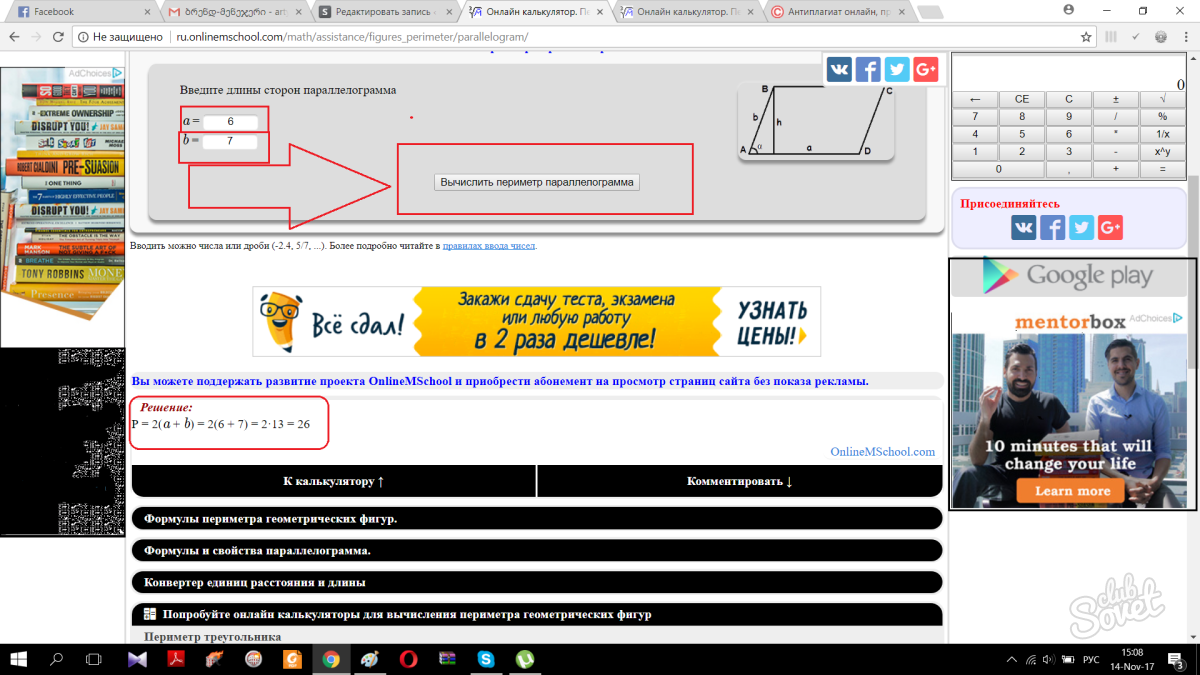
Помимо всего прочего, вы можете использовать онлайн калькулятор, который за считанные секунды расcчитает вам значение периметра любой фигуры. В сети существует много калькуляторов, для разных фигур.
Когда вы перейдете на страницу расчета, необходимо будет вписать длину сторон и затем нажать на кнопку вычисления. Онлайн программа при помощи специальных несложных алгоритмов найдет необходимое вам значение. Несмотря на существование таких способов вычисления, не стоит ими злоупотреблять. Вы всегда должны уметь самостоятельно находить все значения и помнить наизусть все формулы.
На контрольной работе или экзамене таких вычислительных хитростей вам никто не предоставит. Они и не понадобятся, ведь выполнить все это не составит большого труда. Ниже будет приведен список страниц для разных фигур:
- Прямоугольник
- Квадрат
- Ромб
- Параллелограмм
Как вы уже могли убедиться, найти периметр четырехугольника, да и вообще любой фигуры – очень легко. Хорошо изучите эту тему, она поможет вам в решении более сложных задач, где нахождение периметра будет лишь одним из шагов к правильному решению геометрической задачи.
Помните, что любой материал требует закрепления и практических занятий. Поэтому ниже будут приведены ресурсы, перейдя на которые вы сможете отточить мастерство решений задач на нахождение периметра четырехугольника:
- http://www.myshared.ru/slide/370862/
- https://profmeter.com.ua/communication/learning/course/course7/lesson59/
- https://www.math10.com/ru/zadachi/perimetr/easy/
Почитайте теорию, она также важна как и практическое решение задач. Совмещайте практику и теорию, тогда любая тема будет даваться вам легко.