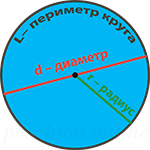
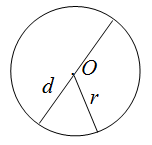Периметр круга
- Главная
- /
- Математика
- /
- Геометрия
- /
- Периметр круга
Чтобы посчитать периметр круга просто воспользуйтесь нашим онлайн калькулятором:
Онлайн калькулятор
Для того чтобы рассчитать периметр круга (длину граничной окружности) вам необходимо знать его радиус или диаметр, либо его площадь.
Ликбез: Круг — часть плоскости, лежащая внутри окружности.
Как посчитать периметр круга зная радиус
Чему равен периметр круга если
его радиус ?
Ответ:
0
Каков периметр круга (L) если его радиус r ?
Формула
L = 2⋅π⋅r, где π ≈ 3.14
Пример
Если радиус круга равен 0.5 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная диаметр
Чему равен периметр круга если
его диаметр ?
Ответ:
0
Каков периметр круга (L) если его диаметр d?
Формула
L = π⋅d, где π ≈ 3.14
Пример
Если диаметр круга d = 1 см, то его периметр равен числу π, то есть ≈ 3.14 см.
Как посчитать периметр круга зная его площадь
Чему равен периметр круга если
его площадь ?
Ответ:
0
Каков периметр круга (L) если его площадь S?
Формула
L = 2π⋅√S/π, где π ≈ 3.14
Пример
Если площадь круга равна 8 см2, то его периметр ≈ 10 см.
См. также
В данной публикации мы рассмотрим, каким образом можно посчитать длину/периметр окружности (круга) и разберем примеры решения задач.
- Формула вычисления длины/периметра
- Примеры задач
Формула вычисления длины/периметра
1. Через радиус
Периметр круга или длина окружности (C) равняется удвоенному произведению ее радиуса на число π:
C = 2 * π * r
Радиус (r) – это отрезок, который соединяет центр окружности и любую точку на ней.
2. Через диаметр
Периметр/длина окружности считается как произведение ее диаметра на число π:
C = π * d
Диаметр (d) равен двум радиусам (d=2r). Это отрезок, соединяющий две противоположные точки на окружности.
Примечание: в расчетах значение числа π округляется до 3,14.
Примеры задач
Задание 1
Найдите длину окружности, если ее радиус равен 12 см.
Решение:
Воспользуемся первой формулой, в которой участвует значение радиуса: C = 2 * 3,14 * 12 см = 75,36 см.
Задание 2
Найдите периметр круга, если ее диаметр составляет 15 см.
Решение:
Применим формулу, в которой используется диаметр: C = 3,14 * 15 см = 47,1 см.
Способы расчета периметра круга и длины окружности
Содержание:
- Периметр круга — что это, определение
-
Как рассчитать периметр круга или длину окружности
- Через радиус
- Через диаметр
- Примеры решения задач
Периметр круга — что это, определение
Определение
Круг — это геометрическое множество точек на плоскости, расстояние от которых до данной точки, называемой центром круга, не превосходит заданного неотрицательного числа.
Оределение
Окружность — замкнутая кривая на плоскости, все точки которой равноудалены от центра окружности.
Эти определения плотно связаны друг с другом. Круг — это часть плоскости, ограниченная окружностью. Окружность — это граница круга.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Радиус — расстояние от центра окружности до любой ее точки. Это отрезок, который соединяет центр круга с его границей.
Определение
Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр. Он равен двум радиусам.
Определение
Периметр — это длина окружности, ограничивающей круг.
Понятия «периметр круга» и «длина окружности» считаются синонимичными.
Как рассчитать периметр круга или длину окружности
Чтобы вычислить периметр круга, необходимо ввести постоянную величину — число Пи. Оно равно отношению длины окружности к ее диаметру. Это отношение идентично для всех окружностей и равно (pi=3,14159…)
Чтобы произвести расчет периметра круга, достаточно помнить это число до двух знаков после запятой:
(pi=3,14)
Помимо этого, для вычисления необходимо знать длину радиуса или диаметра.
Через радиус
Длину окружности L можно найти по формуле через радиус:
(L=2pi R)
где (pi ) — число Пи, R — радиус.
Через диаметр
Длину окружности L можно найти по формуле через диаметр. Поскольку диаметр D равен двум радиусам:
(L=pi D)
Примеры решения задач
Задача
Каков периметр круга, если его радиус равен 0,5 см?
Решение
По формуле, (L= 2pi R). Отсюда:
(L=2pi R=2cdot0,5pi=piapprox3,14)
Ответ: 3,14 см.
Задача
Какова длина окружности, если ее диаметр равен 2 см?
Решение
По формуле, (L=pi D). Отсюда:
(L=pi D=picdot2approx3,14cdot2=6,28)
Ответ: 6,28 см.
Насколько полезной была для вас статья?
Рейтинг: 3.00 (Голосов: 2)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Содержание:
- Формула
- Примеры вычисления периметра круга
Формула
Чтобы найти периметр круга, необходимо вычислить длину окружности, которая его ограничивает.
Для нахождения длины окружности можно использовать одну из формул
$l=2 pi r$ или $l=pi d$
где $r$ и $d$ соответственно радиус и диаметр круга, а
$pi approx 3,1415926535 ldots$. Радиусом окружности называется отрезок,
соединяющий центр окружности с точкой окружности. Диаметр – это отрезок, который соединяет две точки окружности и проходящий
через её центр. Число $pi$ – математическая константа,
выражающая отношение длины окружности к длине её диаметра.
Примеры вычисления периметра круга
Пример
Задание. Найти периметр круга, радиус которого равен 2 см.
Решение. Периметр круга – это не что иное, как длина ограничивающей его окружности. Так как
нам задан радиус круга, то для вычисления длины окружности будем использовать формулу:
$l=2 pi r$
Получим:
$P_{k}=l=2 cdot pi cdot 2=4 pi approx 12,56$ (см)
Ответ. $P_{k}=4 pi approx 12,56$ (см)

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Круг вписан в квадрат со стороной
$a=5$ мм. Найти периметр круга.
Решение. Сторона квадрата для круга является диаметром, то есть $a=d=5$ мм. Периметр круга равен длине окружности его
ограничивающей. Вычислим указанную длину по формуле:
$l=pi d$
Тогда искомый периметр равен:
$P_{k}=l=5 pi approx 15.7$ (мм)
Ответ. $P_{k}=l=5 pi approx 15.7$ (мм)
Читать дальше: как найти длину окружности.
Круг – двухмерная геометрическая фигура, границей которого по определению является окружность. Центром фигуры становится зафиксированная на плоскости точка, равноудаленная от любого места на замкнутой кривой. Прямая линия, соединяющая центр с каждой точкой окружности называется радиусом — R. Рассчитать длину окружности можно по одной из известных величин – радиусу или диаметру.
Достоверная формула для определения периметра и длины круга была выведена древнегреческим математиком Архимедом Сиракузским в III веке до нашей эры. Ученый первый обнаружил закономерность в соотношении общей длины тела к его диаметру, и предложил обозначить константой ∏. Абстрактное число было равно 3,14159265359 … и до бесконечности. Голландский математик Лудольф ван Цейлен рассчитал и ограничил ∏ до 32 знаков после запятой. Константа стала основой для современной формулы вычисления периметра и длины окружности через радиус.
В калькуляторе периметра круга используется классический принцип расчета:
- По радиусу: P=2∏r, где P — периметр (длина) окружности, r – радиус, ∏ — число Пи (3.1415)
- По диаметру: P=∏D, где D — диаметр
- Формула для определения диаметра: D=2r
Для вычисления параметров круга, достаточно вставить в строку известное значение радиуса и получить результат.
Примеры вычисления
С помощью удобного инструмента можно быстро и просто найти длину любого круглого тела. Например, чтобы узнать периметр экватора Земли, необходимо подставить значения в поля калькулятора. Согласно географическим данным, экваториальный радиус составляет 6 378.1 километра:
P=2∏r=2х∏х6378.1=40074.7842 км
Значение полностью соответствует официально установленной протяженности экватора.
Расчет может применяться не только для определения абстрактных величин. В повседневной жизни формула является одной из самых востребованных. Например, чтобы сделать удачную покупку ювелирного кольца в интернет-магазине, не обязательно примерять десятки изделий для уточнения размера в традиционном бутике. Достаточно сантиметром измерить диаметр старого украшения, и разделить значение на 2. Например, если радиус кольца 9 мм, то длина равна:
P=2∏r=2х∏х9=56.548 мм
Круг – одно из самых распространенных геометрических тел в повседневной жизни. Целая фигура и её отдельные части используются во всех сферах промышленности и народного хозяйства, от крупномасштабного строительства до производства посуды. Необходимость быстро вычислить параметры окружности возникает часто. Онлайн калькулятор периметра круга можно использовать для решения элементарных математических и бытовых задач.