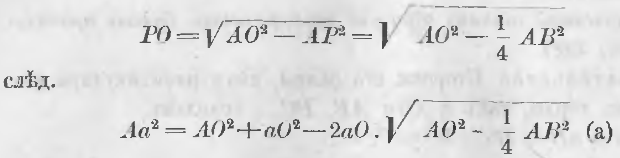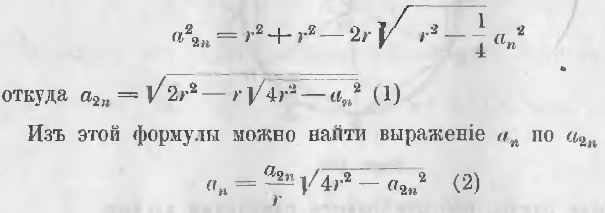Как найти периметр правильного многоугольника
Периметром многоугольника называют замкнутую ломаную линию, составленную из всех его сторон. Нахождение длины этого параметра сводится к суммированию длин сторон. Если все отрезки, образующие периметр такой двухмерной геометрической фигуры, имеют одинаковые размеры, многоугольник называется правильным. В этом случае вычисление периметра значительно упрощается.
Инструкция
В самом простом случае, когда известны длина стороны (а) правильного многоугольника и число вершин (n) в нем, для вычисления длины периметра (Р) просто перемножьте эти две величины: Р = а*n. Например, длина периметра правильного шестиугольника со стороной в 15 см должна быть равна 15*6=90 см.
Вычислить периметр такого многоугольника по известному радиусу (R) описанной около него окружности тоже возможно. Для этого придется сначала выразить длину стороны с использованием радиуса и количества вершин (n), а затем умножить полученную величину на число сторон. Чтобы рассчитать длину стороны умножьте радиус на синус числа Пи, поделенного на количество вершин, а результат удвойте: R*sin(π/n)*2. Если вам удобнее вычислять тригонометрическую функцию в градусах, замените число Пи на 180°: R*sin(180°/n)*2. Периметр вычислите умножением полученной величины на число вершин: Р = R*sin(π/n)*2*n = R*sin(180°/n)*2*n. Например, если шестиугольник вписан в круг с радиусом 50 см, его периметр будет иметь длину 50*sin(180°/6)*2*6 = 50*0,5*12 = 300 см.
Схожим способом можно посчитать периметр, не зная длины стороны правильного многоугольника, если он описан около окружности с известным радиусом (r). В этом случае формула для вычисления размера стороны фигуры будет отличаться от предыдущей лишь задействованной тригонометрической функцией. Замените в формуле синус на тангенс, чтобы получить такое выражение: r*tg(π/n)*2. Или для расчетов в градусах: r*tg(180°/n)*2. Для вычисления периметра увеличьте полученную величину в число раз, равное количеству вершин многоугольника: Р = r*tg(π/n)*2*n = r*tg(180°/n)*2*n. Например, периметр восьмиугольника, описанного возле круга с радиусом в 40 см, будет приблизительно равен 40*tg(180°/8)*2*8 ≈ 40*0,414*16 = 264,96 см.
Источники:
- периметр многоугольника формула
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d19e973b9d47b5f • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Периметр описанного около окружности правильного многоугольника
Ключевые слова: многоугольник, правильный многоугольник, сторона, угол, вписанная, описанная окружность
Выпуклый многоугольник называется правильным, если у него все стороны равны и все углы равны.
Центром правильного многоугольника называется точка, равноудаленная от всех его вершин и всех его сторон.
Центральным углом правильного многоугольника называется угол, под которым видна сторона из его центра.
См. также:
Вписанная окружность, Описанная окружность, Выпуклый четырёхугольник, Произвольный выпуклый многоугольник
Правильный многоугольник
Формулы, признаки и свойства правильного многоугольника
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие: все стороны и углы одинаковы.
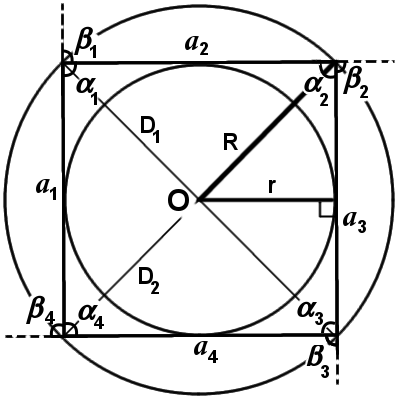
a 1 = a 2 = a 3 = … = a n-1 = a n ,
α 1 = α 2 = α 3 = … = α n-1 = α n
где a1 … an — длины сторон правильного многоугольника,
α 1 … α n — внутренние углы между стронами правильного многоугольника.
Основные свойства правильного многоугольника
- Все стороны равны: a 1 = a 2 = a 3 = … = a n-1 = a n
- Все углы равны: α 1 = α 2 = α 3 = … = α n-1 = α n
- Центр вписанной окружности Oв совпадает с центром описанной окружности Oо, что и образуют центр многоугольникаO.
- Сумма всех углов n-угольника равна: 180° · n – 2
- Сумма всех внешних углов n-угольника равна 360°: β 1 + β 2 + β 3 + … + β n-1 + β n = 360°
- Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины: D n = n · n – 3 2
- В любой многоугольник можно вписать окружность и описать круг; при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника: S = π 4 · a 2
- Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O .
Формулы правильного n-угольника
Формулы длины стороны правильного n-угольника
Формула стороны правильного n-угольника через радиус вписанной окружности
a = 2 · r · tg 180° n (через градусы),
a = 2 · r · tg π n (через радианы)
Формула стороны правильного n-угольника через радиус описанной окружности
a = 2 · R · sin 180° n (через градусы),
a = 2 · R · sin π n (через радианы)
Формулы радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны
r = a : 2 · tg 180° n (через градусы),
r = a : 2 · tg π n (через радианы)
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны
R = a : 2 · sin 180° n (через градусы),
R = a : 2 · sin π n (через радианы)
Формулы площади правильного n-угольника
Формула площади n-угольника через длину стороны
Формула площади n-угольника через радиус вписанной окружности
Формула площади n-угольника через радиус описанной окружности
Формула периметра правильного многоугольника
Формула периметра правильного n-угольника
Периметр правильного n-угольника равен произведению длины одной стороны правильного n-угольника на количество его сторон.
Формула определения угла между сторонами правильного многоугольника
Формула угла между сторонами правильного n-угольника
Правильный треугольник
Правильный треугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного треугольника равны между собой, все углы также равны и составляют 60°.
Формулы правильного треугольника
Формула стороны правильного треугольника через радиус вписанной окружности
Сторона правильного треугольника равна удвоенному произведению радиуса вписанной окружности на корень из трёх.
Формула стороны правильного треугольника через радиус описанной окружности
Сторона правильного треугольника равна произведению радиуса описанной окружности на корень из трёх.
Формула площади правильного треугольника через длину стороны
Формула площади правильного треугольника через радиус вписанной окружности
Формула площади правильного треугольника через радиус описанной окружности
Углы между сторонами правильного треугольника
Правильный четырехугольник
Правильный четырехугольник — это квадрат.
Формулы правильного четырехугольника
Формула стороны правильного четырехугольника через радиус вписанной окружности
Сторона правильного четырехугольника равна двум радиусам вписанной окружности.
Формула стороны правильного четырехугольника через радиус описанной окружности
Сторона правильного четырехугольника равна произведению радиуса описанной окружности на корень из двух.
Формула радиуса вписанной окружности правильного четырехугольника через длину стороны
Радиус вписанной окружности правильного четырехугольника равен половине стороны четырехугольника.
Формула радиуса описанной окружности правильного четырехугольника через длину стороны
Радиус описанной окружности правильного четырехугольника равен половине произведения стороны четырехугольника на корень из двух.
Формула площади правильного четырехугольника через длину стороны
Площадь правильного четырехугольника равна квадрату стороны четырехугольника.
Формула площади правильного четырехугольника через радиус вписанной окружности
Площадь правильного четырехугольника равна четырем радиусам вписанной окружности четырехугольника.
Формула площади правильного четырехугольника через радиус описанной окружности
Площадь правильного четырехугольника равна двум квадратам радиуса описанной окружности.
Углы между сторонами правильного четырехугольника
Правильный шестиугольник
Правильный шестиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного шестиугольника равны между собой, все углы также равны и составляют 120°.
Формулы правильного шестиугольник
Формула стороны правильного шестиугольника через радиус вписанной окружности
Формула стороны правильного шестиугольника через радиус описанной окружности
Длина стороны правильного шестиугольника равна радиусу описанной окружности.
Формула радиуса вписанной окружности правильного шестиугольника через длину стороны
Формула радиуса описанной окружности правильного шестиугольника через длину стороны
Формула площади правильного шестиугольника через длину стороны
Формула площади правильного шестиугольника через радиус вписанной окружности
Формула площади правильного шестиугольника через радиус описанной окружности
Углы между сторонами правильного шестиугольника
Правильный восьмиугольник
Правильный восьмиугольник — это правильный многоугольник с тремя сторонами. Все стороны правильного восьмиугольник равны между собой, все углы также равны и составляют 135°.
[spoiler title=”источники:”]
http://uztest.ru/abstracts/?idabstract=50
http://urokmatematiki.ru/reference-information/formuly-po-geometrii/pravilny-mnogougolnik.php
[/spoiler]
| Правильный многоугольник | |
|---|---|
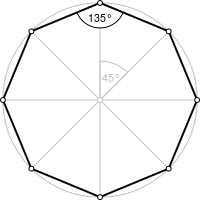 Правильный восьмиугольник |
|
| Тип | Многоугольник |
| Символ Шлефли |
 |
| Вид симметрии |
Диэдрическая группа  |
| Площадь |
 |
| Внутренний угол |
 |
| Свойства | |
| выпуклый, вписанный, равносторонний, равноугольный[en], изотоксальный | |
Пра́вильный многоуго́льник — выпуклый многоугольник, у которого равны все стороны и все углы между смежными сторонами.
Определение правильного многоугольника может зависеть от определения многоугольника: если он определён как плоская замкнутая ломаная, то появляется определение правильного звёздчатого многоугольника как невыпуклого многоугольника, у которого все стороны между собой равны и все углы между собой равны.
Связанные определения[править | править код]
- Центром правильного многоугольника называется его центр масс, совпадающий с центрами его вписанной и описанной окружностей.
Свойства[править | править код]
Координаты[править | править код]
Пусть 



где 


Размеры[править | править код]
Правильный многоугольник, вписанный и описанный около окружности
Пусть 
,
а длина стороны многоугольника равна
Площадь[править | править код]
Площадь правильного многоугольника с числом сторон 

.
Площадь правильного многоугольника с числом сторон 

.
Площадь правильного многоугольника с числом сторон 

Площадь правильного многоугольника с числом сторон 
,
где 


Периметр[править | править код]
Если нужно вычислить длину стороны 

— длина стороны правильного n-угольника.
Периметр 
где 
Свойства диагоналей правильных многоугольников[править | править код]
- Максимальное количество диагоналей правильного
-угольника, пересекающихся в одной точке, не являющейся его вершиной или центром, равно:
- Существуют лишь три исключения: данное число равно
в треугольнике,
в шестиугольнике и
в двенадцатиугольнике.[4].
- При чётном
в центре многоугольника пересекается
диагонали.
Введём функцию 




- Количество точек пересечения диагоналей правильного
-угольника равно
- Где
– число сочетаний из
по
[4].
- Количество частей, на которые правильный
-угольник делят его диагонали, равно
- [4].
Применение[править | править код]
Правильными многоугольниками по определению являются грани правильных многогранников.
Древнегреческие математики (Антифонт, Брисон Гераклейский, Архимед и др.) использовали правильные многоугольники для вычисления числа π. Они вычисляли площади вписанных в окружность и описанных вокруг неё многоугольников, постепенно увеличивая число их сторон и получая таким образом оценку площади круга.[5]
История[править | править код]
Построение циркулем и линейкой правильного многоугольника с 

Евклид в своих «Началах» занимался построением правильных многоугольников в книге IV, решая задачу для 















Средневековая математика почти никак не продвинулась в этом вопросе. Лишь в 1796 году Карлу Фридриху Гауссу удалось доказать, что если число сторон правильного многоугольника равно простому числу Ферма, то его можно построить при помощи циркуля и линейки. На сегодняшний день известны следующие простые числа Ферма: 

Из результата Гаусса мгновенно следовало, что правильный многоугольник возможно построить, если число его сторон равно 


Последними результатами в области построения правильных многоугольников являются явные построения 17-, 257- и 65537-угольника. Первое было найдено Йоханнесом Эрхингером в 1825 году, второе — Фридрихом Юлиусом Ришело в 1832 году, а последнее — Иоганном Густавом Гермесом в 1894 году.
См. также[править | править код]
- Правильный многогранник
Примечания[править | править код]
- ↑ (unspecified title)
- ↑ МАТВОКС
- ↑ treugolniki.ru. Дата обращения: 12 мая 2020. Архивировано 2 июля 2020 года.
- ↑ 1 2 3 Bjorn Poonen and Michael Rubinstein “The number of intersection points made by thediagonals of a regular polygon”. Дата обращения: 16 июля 2020. Архивировано 17 июля 2020 года.
- ↑ А. В. Жуков. О числе π. — М.: МЦНМО, 2002. ISBN 5-94057-030-5.
- ↑ Лабуда
Правильные вписанные и описанные многоугольники
Правильный многоугольник. Правильным называется такой многоугольник, у которого все стороны и все углы равны.
Правильный треугольник есть равносторонний треугольник, каждый угол которого равен (2/3)d или 60°.
Правильный четырехугольник есть квадрат, каждый угол которого равен прямому углу или 90°.
Правильный многоугольник, имеющий n сторон, есть многоугольник, каждый угол которого равен 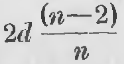
Таким образом, полагая n = 3, 4, 5, 6, мы имеем для каждого угла величину (2/3)d, d, (6/5)d, (4/3)d и т. д.
Угол правильного пятиугольника равен (6/5)d = 108°, угол правильного шестиугольника равен (4/3)d = 120° и т. д.
Одноименные многоугольники. Все многоугольники, имеющие одинаковое число углов, называются одноименными многоугольниками.
Все правильные одноименные многоугольники имеют одинаковые углы и различаются только величиной сторон.
Подобие правильных многоугольников. Одноименные правильные многоугольники подобны, ибо у них углы равны и стороны пропорциональны.
Из подобия их вытекает, что периметры одноименных правильных многоугольников относятся как стороны.
Теорема 117. Около правильного многоугольника всегда можно описать окружность.
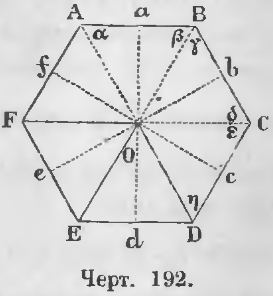
Дан правильный многоугольник ABCDEF (черт. 192). Стороны его и углы равны между собой:
AB = BC = CD = DE = EF = AF и
A = B = C = D = E = F
Требуется доказать, что существует точка, равноотстоящая от всех его вершин.
Доказательство. Проведем через три точки A, B, C окружность. Для этого из середины линий AB и BC восставляем перпендикуляры до взаимного их пересечения в точке O. Точка O есть центр круга, проходящего через три точки A, B, C. Докажем, что эта окружность пройдет и через точки D, E, F. Для этого соединим точку O с вершинами многоугольника отрезками AO, BO, CO, DO, EO, FO.
1. Все эти отрезки разделяют углы многоугольника пополам.
Из равнобедренных треугольников AOB и BOC видно, что
∠α = ∠β, ∠γ = ∠δ
Так как ΔABO = ΔBCO, то
∠β = ∠γ = ½B,
т. е. угол B делится пополам.
Из равенств
∠δ = ½B = ½C
следует, что угол C тоже делится пополам.
Точно также легко доказать, что угол D тоже делится пополам.
Треугольники BOC и COD равны, ибо OC сторона общая, BC = CD как стороны правильного многоугольника, ∠δ = ∠ε, следовательно, ∠γ = ∠η.
Так как ∠γ = ½B = ½C = ½D, то и угол η = ½D, т. е. угол D делится тоже пополам.
Подобным образом легко доказать, что все углы многоугольника делятся пополам отрезками, соединяющими точку O с вершинами многоугольника.
2. Все отрезки OA, OB, OC, OD, OE, OF равны.
Действительно, по построению следует, что
OA = OB = OC
Из равенства треугольников BOC и COD следует, что
OC = OD
Из равенства треугольников COD и DOE следует, что
OD = OE и т. д.
Таким образом точка O находится на равном расстоянии от всех вершин многоугольника, т. е. окружность, описанная радиусом OA, пройдет через все вершины многоугольника, и точка O будет центром описанного многоугольника (ЧТД).
Теорема 118. Центр описанного круга будет также центром круга, вписанного в правильный многоугольник.
Доказательство. Из точки O центра описанного многоугольника (черт. 192) опустим перпендикуляры Oa, Ob, Oc, Od, Oe, Of на стороны многоугольника. Так как треугольники ABO, BCO равнобедренные и многоугольники правильные, то
Aa = aB = Bb = bC = Cc = cD = …
Два прямоугольных треугольника aBO и BbO равны, ибо BO сторона общая
aB = Bb
следовательно, Oa = Ob.
Точно также легко доказать, что Ob = Oc и т. д.
Следовательно, вообще Oa = Ob = Oc = Od = Oe = Of.
Если мы радиусом Oa опишем окружность, то она коснется сторон правильного многоугольника в точках a, b, c, … т. е. она будет вписана в многоугольник.
Точки a, b, c, … делят стороны многоугольника пополам.
Таким образом точка O, будучи центром описанного, есть в то же время и центр круга, вписанного в правильный многоугольник (ЧТД).
Апофема. Перпендикуляр, опущенный из центра на сторону правильного многоугольника, называется апофемой.
Теорема 119. Периметры одноименных правильных многоугольников относятся как радиусы описанных и вписанных кругов.
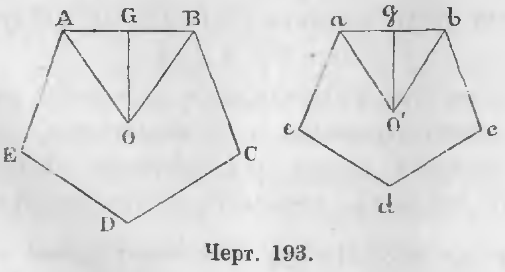
Даны два правильных одноименных многоугольника (черт. 193). Из центров O и O’ проведем радиусы кругов описанных и вписанных.
Требуется доказать, что
(AB + BC + CD + DE + EA) / (ab + bc + cd + de + ea) = OA/O’a = OG/O’g
Доказательство. Два треугольника GOB и gOb подобны, ибо они прямоугольны и ∠GBO = ∠gbO’, следовательно,
GB/gb = OB/O’b = GO/gO’
Так как GB = ½AB, gb = ½ab, то
AB/ab = OB/O’b = GO/gO’ (a)
Кроме того имеют место следующие равенства отношений:
AB/ab = BC/bc = CD/cd = DE/de = EA/ea
откуда по свойству пропорций имеем:
(AB + BC + CD + DE + EA) / (ab + bc + cd + de + ea) = AB/ab
Обозначим периметры этих многоугольников через P и p, имеем:
P/p = AB/ab (b)
Сравнивая пропорции (a) и (b), получаем равные отношения:
P/p = AB/ab = OB/O’b = GO/gO’ (ЧТД).
Теорема 120. Если углы описанного многоугольника равны, то и стороны равны, т. е. равноугольный описанный есть многоугольник правильный.
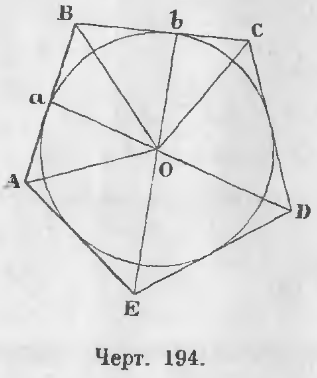
Дано. В описанном многоугольнике ABCDE углы равны (черт. 194):
A = B = C = D = E.
Требуется доказать, что AB = BC = CD = DE = EA.
Доказательство. Соединим вершины описанного многоугольника и точки прикосновения с центром круга O.
1. Два прямоугольных треугольника aBO и BbO равны, ибо у них BO сторона общая, aO = bO как радиусы, следовательно, ∠aOB = ∠Bob и ∠aBO = ∠bBO, т. е. отрезки, соединяющие вершины описанного многоугольника с центром, делят углы многоугольника пополам.
2. Треугольники AOB и BOC равны, ибо BO сторона общая, ∠ABO = ∠CBO по доказанному, ∠BAO = ∠BCO по условию, следовательно, AB = BC.
Таким образом можно доказать равенство остальных сторон описанного многоугольника, имеющего равные углы (ЧТД).
Теорема 121. По данному вписанному правильному многоугольнику можно описать правильный многоугольник того же числа сторон.
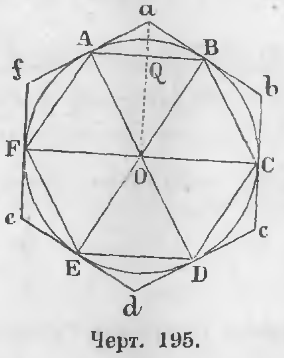
Дан правильный вписанный многоугольник (черт. 195) ABCDEF, следовательно, стороны и углы его равны.
AB = BC = CD = DE = EF = FA и
◡AB = ◡BC = ◡CD = ◡DE = ◡EF = ◡FA
Для построения правильного описанного многоугольника по данному вписанному применяют два способа.
Первый способ. Нужно центр правильного вписанного многоугольника соединить с вершинами и в вершинах провести к этим отрезкам перпендикуляры, которые, пересекаясь, образуют правильный описанный многоугольник.
Проведем радиусы AO, BO, CO, и т. д. и в вершинах A, B, C, D, E, F проведем перпендикуляры к этим радиусам до взаимного их пересечения в точках a, b, c, d, e, f. Образуется многоугольник abcdef.
Требуется доказать, что многоугольник abcdef будет правильным описанным многоугольником.
Доказательство. Многоугольник abcdef будет описанным многоугольником, потому что ab, bc, … будут касательными к окружности, так как они проведены перпендикулярно к радиусам из их концов.
2. Треугольники AaB, BbC … равнобедренны, ибо
∠aAB = ∠aBA
∠bBC = ∠bCB и т. д.
так как они измеряются половиной одной и той же дуги, следовательно, и соответствующие стороны равны
aA = aB, bB = bC, cC = Dc и т. д.
3. Треугольники AaB и BbC равны, ибо AB = BC как стороны правильного вписанного многоугольника
∠aAB = ∠bCB
∠aBA = ∠bBC
ибо они измеряются половиной равных дуг.
Из равенства треугольников AaB и BbC вытекает, что aB = Bb, т. е.
Каждая сторона таким образом описанного многоугольника делится в точке прикосновения пополам.
4. Кроме того,
aA = aB, или ½af = ½ab = ½bc и т. д.
следовательно,
af = ab = bc = cd и т. д.,
т. е. все стороны многоугольника равны.
5. Наконец, ∠a = ∠b, следовательно и все углы многоугольника abcdef равны. Поэтому этот многоугольник правильный (ЧТД).
Второй способ. Нужно из центра на стороне правильного вписанного многоугольника опустить перпендикуляры, продолжить их до пересечения с окружностью и в точках пересечения провести касательные прямые до взаимного их пересечения. Эти точки пересечения и будут вершинами правильного описанного многоугольника.
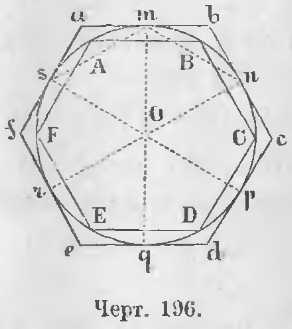
Дан правильный вписанный многоугольник ABCDEF (черт. 196).
Из центра O опустим перпендикуляр на стороны вписанного многоугольника и в точках m, n, p, q, r, s их встречи с окружностью проведем касательные до их взаимного пересечения в точках a, b, c, d, e, f.
Требуется доказать, что abcdef есть правильный описанный многоугольник.
Доказательство. 1. Стороны многоугольника abcdef касательны к окружности, следовательно, abcdef есть многоугольник описанный.
2. Его стороны параллельны сторонам правильного вписанного многоугольника, поэтому его углы равны
∠a = ∠b = ∠c = ∠d = ∠e = ∠f.
3. Соединим точки m, n, p, q … прямыми линиями.
Точки m, n, p, q … суть середины дуг AB, BC и т. д., следовательно, для дуг и хорд имеют место равенства:
sm = mn = np = pq = qr = rs.
4. Треугольники sam, mbn, ncp … равнобедренны, ибо
∠asm = ∠ams, ∠bmn = ∠bnm и т. д.
следовательно,
as = am, bm = bn, cn = cp и т. д.
5. Треугольники sam и mbn равны, ибо
∠ams = ∠bmn
∠asm = ∠bnm
следовательно, am = bm, т. е. стороны описанного многоугольника делятся в точках прикосновения пополам.
6. Наконец из равенства as = am следует равенство
½af = ½ab или af = ab, т. е.
стороны описанного многоугольника равны.
Таким образом многоугольник abcdef есть правильный описанный многоугольник (ЧТД).
Теорема 122. По данному правильному описанному можно вписать правильный многоугольник того же числа сторон.
Здесь тоже имеют место два способа.
Первый способ. Чтобы по данному правильному описанному вписать правильный многоугольник, нужно соединить точки прикосновения описанного многоугольника между собой.
Дан описанный правильный многоугольник abcdef, следовательно,
ab = bc = cd = de = ef = fa и
∠a = ∠b = ∠c = ∠d = ∠e = ∠f.
Стороны правильного описанного многоугольника (черт. 195) делятся в точках прикосновения пополам, следовательно,
aB = bB = bC = Cc = …
Соединим точки прикосновения A, B, C, D, E, F между собой.
Требуется доказать, что ABCDEF есть правильный вписанный многоугольник, т. е.
AB = BC = CD = DE = EF = FA и
∠A = ∠B = ∠C = ∠D = ∠E = ∠F.
Доказательство. 1. Треугольники AaB и BbC равны, ибо они имеют по равному углу, содержащемуся между двумя равными сторонами. Действительно,
aA = bC
aB = bB
∠a = ∠b
следовательно, AB = BC.
Точно также можно доказать, что
BC = CD = DE = EF = FA,
следовательно, и стороны и дуги AB, BC, CD … равны.
Таким образом стороны вписанного многоугольника равны.
2. Сравнивая две дуги BCDEF и CDEFA, мы находим, что
BCDEF = окружности – AB – AF
CDEFA = окружности – AB – BC.
Так как ◡AF = ◡BC, то
◡BCDEF = ◡CDEFA
следовательно,
∠A = ∠B.
Подобным же образом можно доказать равенство других углов, следовательно,
∠A = ∠B = ∠C = ∠D = ∠E = ∠F
Таким образом углы вписанного многоугольника как и стороны тоже равны, следовательно, ABCDEF правильный вписанный многоугольник (ЧТД).
Второй способ. Чтобы по данному правильному описанному многоугольнику вписать правильный одноименный многоугольник, соединим его вершины с центром круга и точки пересечения этих отрезков с окружностью соединим между собой.
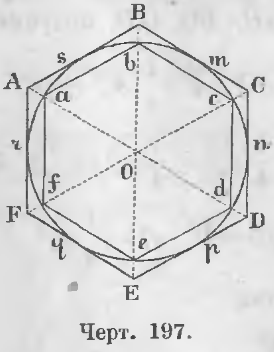
Дан правильный описанный многоугольник ABCDEFA (черт. 197), следовательно,
AB = BC = CD = DE = EF = FA
∠A = ∠B = ∠C = ∠D = ∠E = ∠F
и стороны его делятся в точках прикосновения пополам, т. е.
As = Bs = Cm = Cn = Dn = и т. д.
Соединим вершины его с центром и означим точки пересечения этих линий с окружностью через a, b, c, d, e, f.
Требуется доказать, что многоугольник abcdef правильный.
Доказательство. 1. Углы при центре AOB, BOC, COD и т. д. равны, а следовательно и дуги ab, bc, de, ef, fa равны.
Отсюда вытекает, что стороны тоже равны
ab = bc = cd = de = ef = fa
2. Углы многоугольника тоже равны, ибо измеряются дугами одинаковой величины.
Теорема 123. По данной стороне правильного вписанного многоугольника можно определить сторону описанного многоугольника того же числа сторон.
Означим длину стороны вписанного правильного многоугольника имеющего n сторон через an и одноименного описанного многоугольника через An, а радиус круга через r (черт. 195)
AB = BC = CD = DE = … = an
ab = bc = cd = de = … An
Соединим точку a с O, тогда
aB = ½An, BQ = ½an
Из треугольника aBO имеем:
формулу, определяющую сторону правильного вписанного многоугольника по стороне одноименного правильного описанного многоугольника.
Удвоение числа сторон правильного вписанного многоугольника
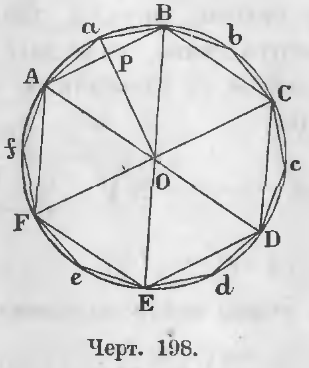
Чтобы удвоить число сторон правильного вписанного многоугольника, опускают из центра перпендикуляры на его стороны, соединяют с вершинами данного многоугольника точки пересечения их с окружностью.
1. Полученный таким образом многоугольник будет правильным (черт. 198).
Доказательство. Стороны его равны, ибо перпендикуляры делят как хорды, так и дуги AB, BC, … пополам, следовательно,
Aa = aB = Bb = bC = Cc = …
Углы тогда равны, ибо измеряются одинаковыми дугами.
2. Периметр многоугольника при удвоении числа сторон увеличивается.
Действительно,
Aa + aB > AB
Bb + bC > BC и т. д.
Складывая эти неравенства, получим
Aa + aB + Bb + bC + … > AB + BC + …
Обозначив периметр правильного многоугольника, имеющего n сторон, через pn, имеем:
p2n >pn
Теорема 124. Можно определить длину стороны вписанного многоугольника с удвоенным числом сторон по радиусу и стороне данного многоугольника.
Из треугольника AaO (черт. 198) длина стороны Aa, как стороны, лежащей против острого угла, выражается равенством:
Aa2 = AO2 + aO2 – 2aO · PO.
Из треугольника APO имеем:
Обозначив через r радиус круга, an длину стороны правильного вписанного многоугольника, имеющего n сторон, и через a2n сторону многоугольника с удвоенным числом сторон, мы имеем по формуле (a)
Удвоение числа сторон правильного описанного многоугольника
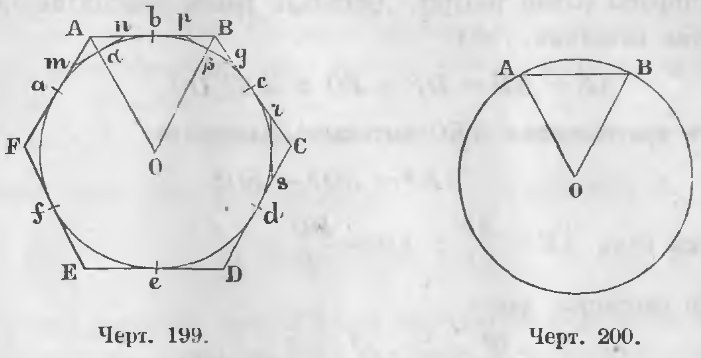
Чтобы удвоить число сторон правильного описанного многоугольника нужно разделить дуги ab, bc, cd, … пополам и провести через точки деления отрезки mn, pg, rs, … до пересечения их со сторонами данного многоугольника (черт. 199).
В этом случае образуется многоугольник равноугольный, ибо его углы измеряются одинаковой мерой. В равноугольном же описанном многоугольнике стороны равны (теорема 120).
Периметр описанного многоугольника с удвоенным числом сторон уменьшается.
Действительно,
An > αn
Bp > βp, следовательно,
AB > αn + np + pβ
Такие же равенства имеют место и для сторон BC, CD, … и т. д. Сложив их, находим, что
AB + BC + CD + … > mn + np + pq + …
или Pn > P2n
где Pn и P2n означают периметры правильных описанных многоугольников, имеющих n и 2n сторон.
Теорема 125. Сторона правильного вписанного шестиугольника равна радиусу (a6 = r).
Дано. Пусть AB сторона правильного шестиугольника (черт. 200), вписанного в круг, радиус которого обозначим через r.
Требуется доказать, что AB = a6 = r.
Доказательство. Дуга AB равна 60°. Соединив A и B с центром O, имеем треугольник ABO, у которого угол AOB имеет 60° = (2/3)d.
Углы A и B равны, следовательно, из равенства A + B + O = 2d, имеем:
2A + (2/3)d = 2d, откуда A = B = (2/3)d
Таким образом треугольник ABO равносторонний и следовательно AB = AO = r.
Теорема 126. Сторона правильного вписанного треугольника равна радиусу, умноженному на √3 (a3 = r√3).
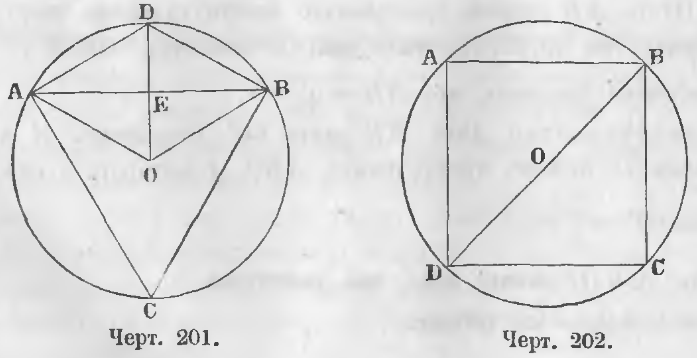
Дан правильный вписанный треугольник ABC (черт. 201).
Требуется доказать, что AB = r√3.
Доказательство. Из центра O опустим перпендикуляр OD к стороне AB и соединим D с вершинами A и B. Стороны AD и DB как стороны правильного вписанного шестиугольника равны радиусу. Четырехугольник ADBO есть ромб, ибо у него все стороны равны радиусу. Диагонали ромба перпендикулярны и делятся пополам, следовательно,
AE = EB = DE = EO и AB ⊥ DO.
Из треугольника AEO вытекает равенство
AE2 = AO2 – EO2
Так как AE = AB/2, EO = DO/2 = r/2, то это равенство дает
AB2/4 = r2 – r2/4 = (3/4)r2, откуда
AB = a3 = r√3 (ЧТД).
Теорема 127. Сторона вписанного квадрата равна радиусу, умноженному на √2.
Дан правильный вписанный четырехугольник или квадрат ABCD (черт. 202).
Требуется доказать, что AB = r√2.
Доказательство. Соединим B с D. Отрезок BD есть диаметр, ибо прямой угол B опирается на концы диаметра.
Из прямоугольного треугольника ABD вытекает равенство
AB2 + AD2 = BD2
Так как AB = AD, BD = 2r, то
2AB2 = 4r2, откуда AB = a4 = r√2 (ЧТД).
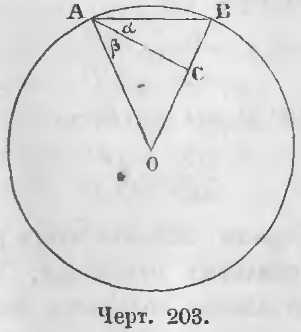
Теорема 128. Сторона правильного вписанного десятиугольника равна большей части радиуса, разделенного в крайнем и среднем отношении.
Дано. Положим AB есть сторона правильного вписанного десятиугольника (черт. 203), следовательно, дуга AB = 1/10 окружности и
∠AOB = (4d)/10 = (2/5)d.
Требуется доказать, что AB есть большая часть радиуса среднепропорциональная между целым радиусом и меньшей его частью.
Доказательство. Соединим точки A и B с центром и разделим угол BAO пополам.
∠AOB = (2/5)d
В равенстве ∠BAO + ∠ABO + ∠AOB = 2d
∠BAO = ∠ABO, следовательно, ∠BAO = ∠ABO = (4/5)d.
Так как ∠α = ∠β по построению, то из равенства
∠α + ∠β = (4/5)d следует, что ∠α = ∠β = (2/5)d
Треугольник ABC равнобедренный, ибо
∠α = (2/5)d, ∠B = (4/5)d,
следовательно, из равенства
∠α + ∠B + ∠ACB = 2d имеем:
(2/5)d + (4/5)d + ∠ACB = 2d и ∠ACB = (4/5)d.
Таким образом
∠ACB = ∠ABC = (4/5)d
следовательно,
AB = AC
Треугольник ACO тоже равнобедренный, ибо
∠β = (2/5)d и ∠AOB = (2/5)d
следовательно, AC = CO и таким образом AB = AC = CO.
Так как отрезок AC делит угол треугольника пополам, то имеет место пропорция (теорема 98)
AO/AB = OC/CB
Так как AB = OC и AO = OB, то
OB/OC = OC/CB
откуда видно, что OC равно большей части радиуса OB, разделенного в крайнем и среднем отношении. Так как OC = AB, то и сторона десятиугольника обладает тем же свойством.
Обозначив ее через a10, а радиус через r, имеем пропорцию
r/a10 = a10/(r – a10)
откуда положительное решение квадратного уравнения, определяющее сторону правильного вписанного десятиугольника, будет:
a10 = ((√5 – 1)/2)r.
Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника
Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
Признаки правильного многоугольника
Многоугольник будет правильным, если выполняется следующее условие:
Все стороны и углы одинаковы:
a1 = a2 = a3 = … = an-1 = an
α1 = α2 = α3 = … = αn-1 = αn
Основные свойства правильного многоугольника
1. Все стороны равны:
a1 = a2 = a3 = … = an-1 = an
2. Все углы равны:
α1 = α2 = α3 = … = αn-1 = αn
3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O
4. Сумма всех углов n-угольника равна:
180° · (n – 2)
5. Сумма всех внешних углов n-угольника равна 360°:
β1 + β2 + β3 + … + βn-1 + βn = 360°
6. Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:
7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O
Правильный n-угольник – формулы
Формулы длины стороны правильного n-угольника
1. Формула стороны правильного n-угольника через радиус вписанной окружности:
2. Формула стороны правильного n-угольника через радиус описанной окружности:
Формула радиуса вписанной окружности правильного n-угольника
Формула радиуса вписанной окружности n-угольника через длину стороны:
Формула радиуса описанной окружности правильного n-угольника
Формула радиуса описанной окружности n-угольника через длину стороны:
Формулы площади правильного n-угольника
1. Формула площади n-угольника через длину стороны:
2. Формула площади n-угольника через радиус вписанной окружности:
3. Формула площади n-угольника через радиус описанной окружности:
Формула периметра правильного многоугольника:
Формула периметра правильного n-угольника:
P = na
Формула определения угла между сторонами правильного многоугольника:
Формула угла между сторонами правильного n-угольника:
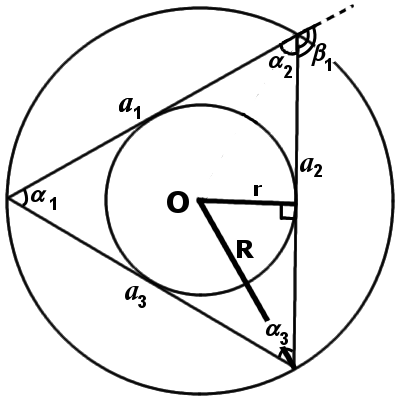 |
| Рис.3 |
Правильный треугольник
Формулы правильного треугольника:
1. Формула стороны правильного треугольника через радиус вписанной окружности:
a = 2r √3
2. Формула стороны правильного треугольника через радиус описанной окружности:
a = R√3
3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:
4. Формула радиуса описанной окружности правильного треугольника через длину стороны:
5. Формула площади правильного треугольника через длину стороны:
6. Формула площади правильного треугольника через радиус вписанной окружности:
S = r2 3√3
7. Формула площади правильного треугольника через радиус описанной окружности:
8. Угол между сторонами правильного треугольника:
α = 60°
 |
| Рис.4 |
Правильный четырехугольник
Правильный четырехугольнику – квадрат.
Формулы правильного четырехугольника:
1. Формула стороны правильного четырехугольника через радиус вписанной окружности:
a = 2r
2. Формула стороны правильного четырехугольника через радиус описанной окружности:
a = R√2
3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
5. Формула площади правильного четырехугольника через длину стороны:
S = a2
6. Формула площади правильного четырехугольника через радиус вписанной окружности:
S = 4 r2
7. Формула площади правильного четырехугольника через радиус описанной окружности:
S = 2 R2
8. Угол между сторонами правильного четырехугольника:
α = 90°
Правильный шестиугольник
Формулы правильного шестиугольника:
1. Формула стороны правильного шестиугольника через радиус вписанной окружности:
2. Формула стороны правильного шестиугольника через радиус описанной окружности:
a = R
3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны:
R = a
5. Формула площади правильного шестиугольника через длину стороны:
6. Формула площади правильного шестиугольника через радиус вписанной окружности:
S = r2 2√3
7. Формула площади правильного шестиугольника через радиус описанной окружности:
8. Угол между сторонами правильного шестиугольника:
α = 120°
Правильный восьмиугольник
Формулы правильного восьмиугольника:
1. Формула стороны правильного восьмиугольника через радиус вписанной окружности:
a = 2r · (√2 – 1)
2. Формула стороны правильного восьмиугольника через радиус описанной окружности:
a = R√2 – √2
3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:
4. Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:
5. Формула площади правильного восьмиугольника через длину стороны:
S = a2 2(√2 + 1)
6. Формула площади правильного восьмиугольника через радиус вписанной окружности:
S = r2 8(√2 – 1)
7. Формула площади правильного восьмиугольника через радиус описанной окружности:
S = R2 2√2
8. Угол между сторонами правильного восьмиугольника:
α = 135°